Environmental Factors Controlling the Precipitation in California
Abstract
1. Introduction
2. Data and Method
2.1. Data
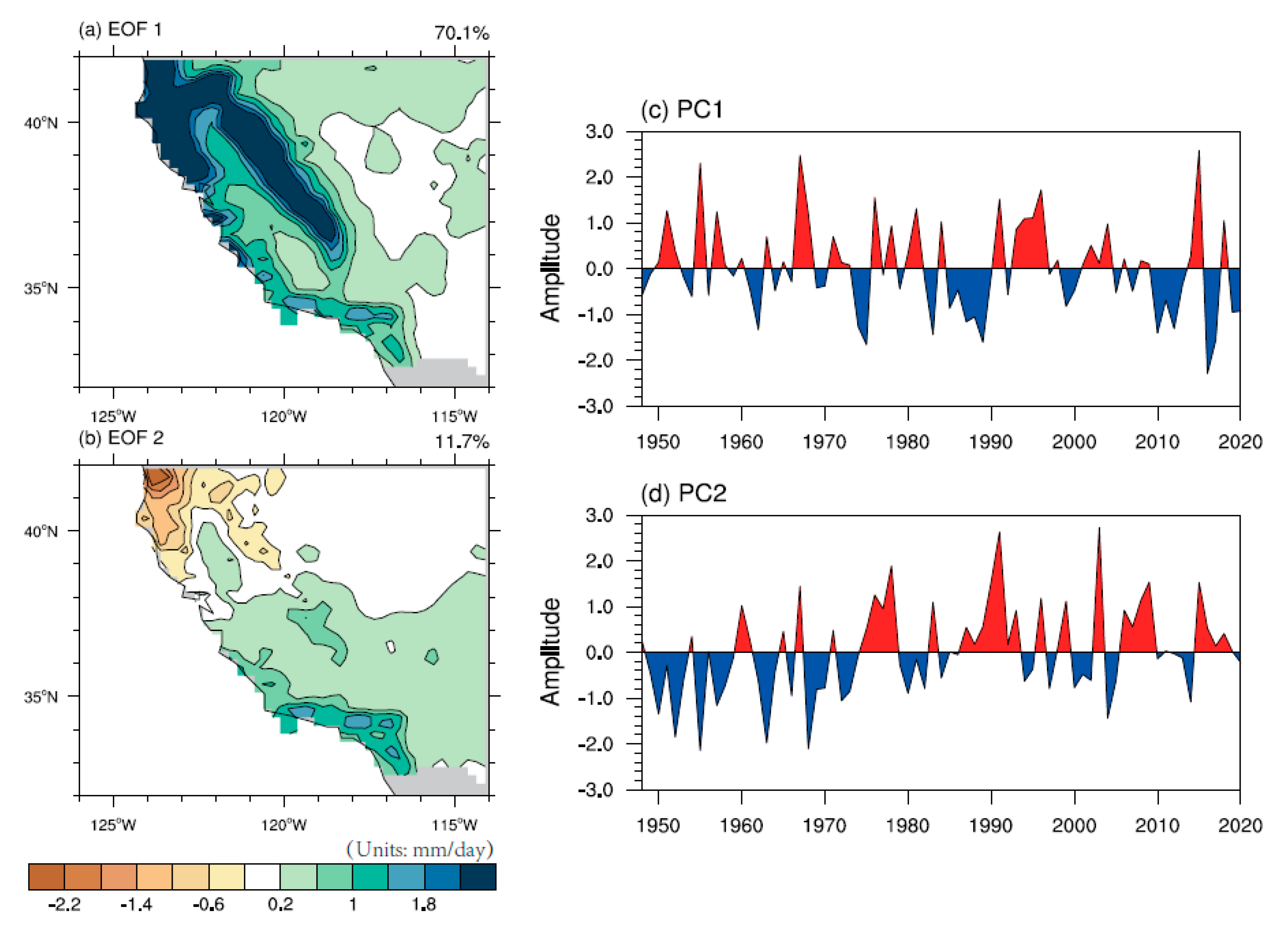
2.2. Empirical Orthogonal Function (EOF) Analysis
2.3. Regression Analysis
2.4. Anomaly General Circulation Model
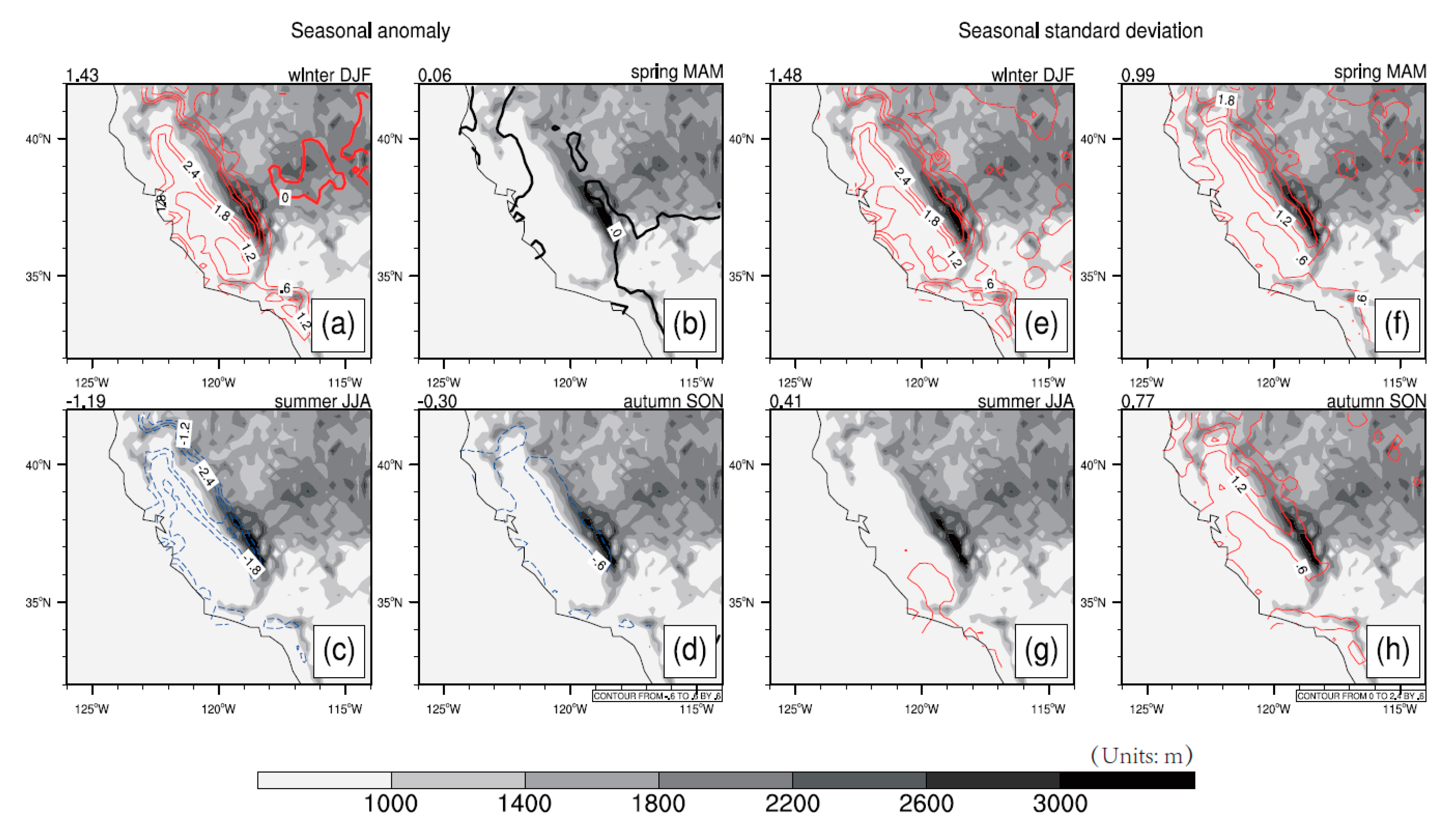
3. Basic Evolution of Precipitation
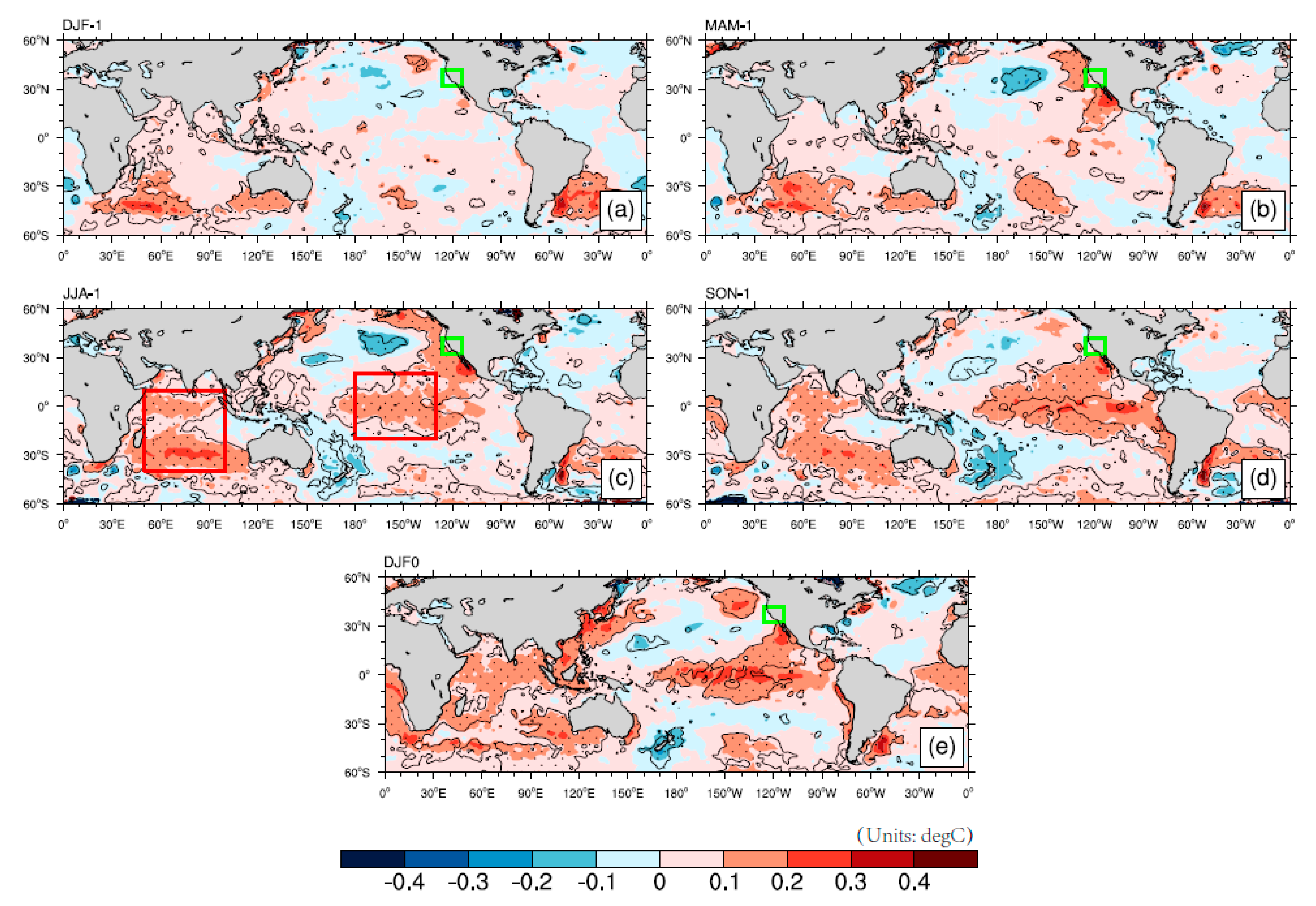
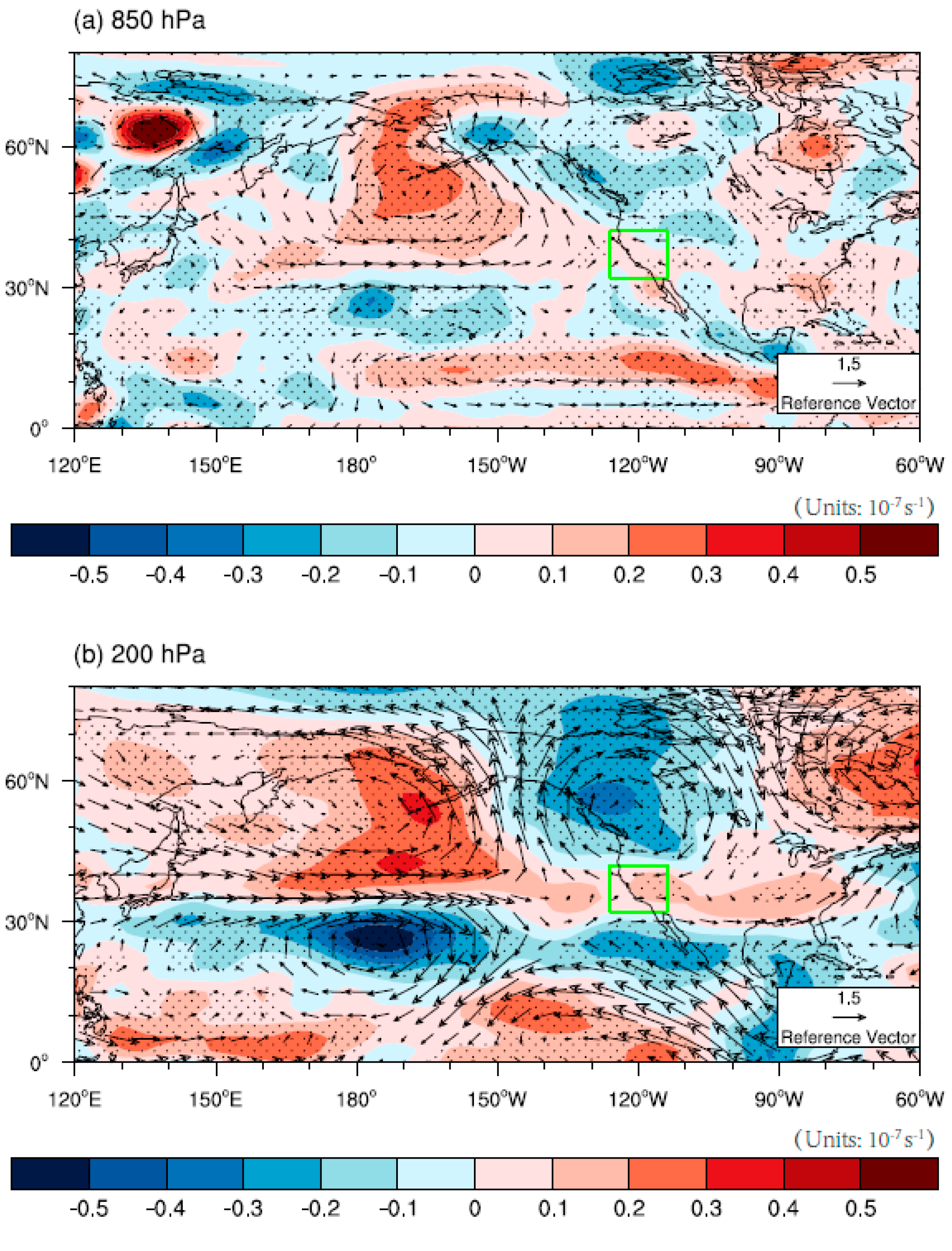
4. Environmental Factors Affecting PC1 Changes
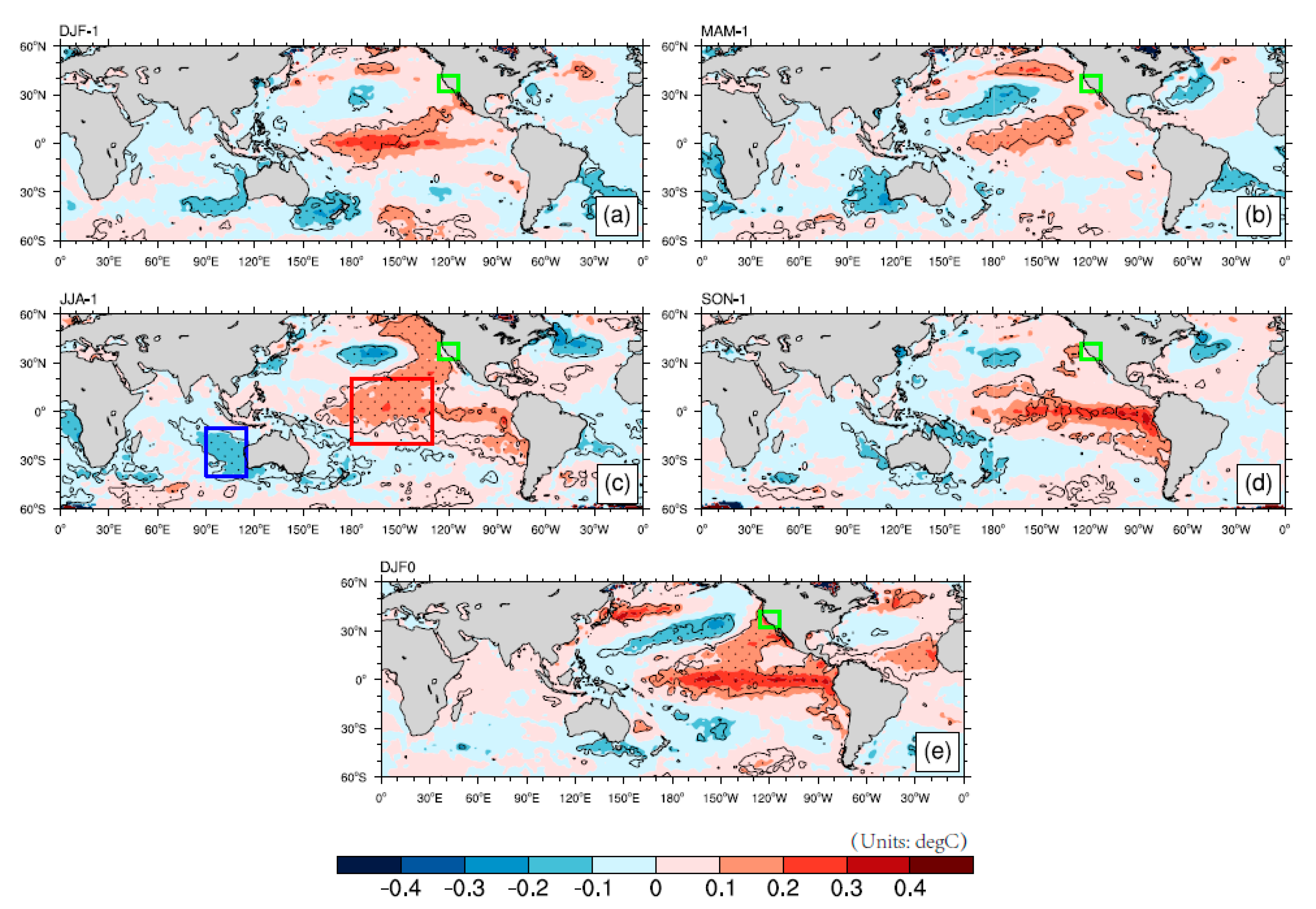
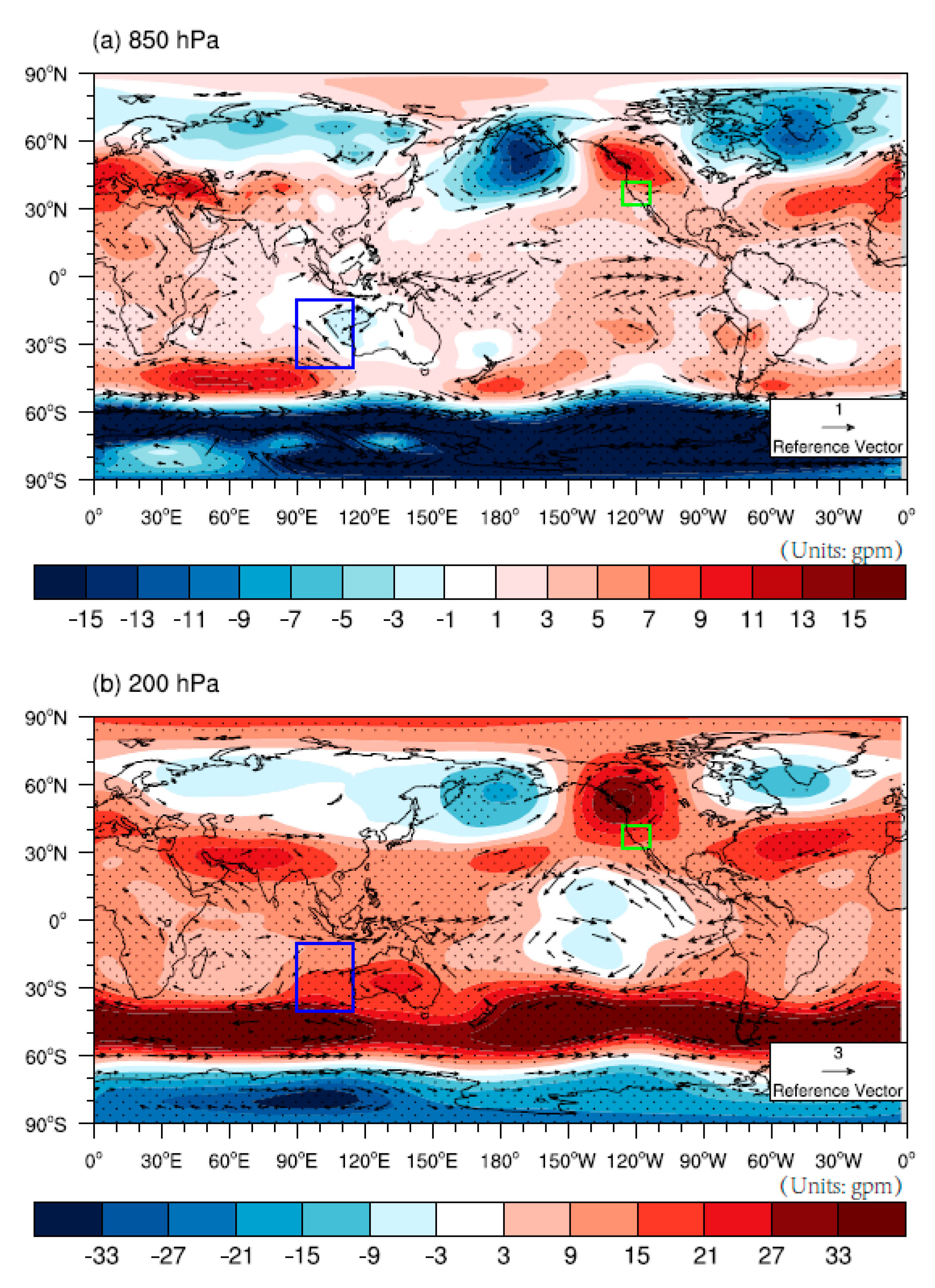
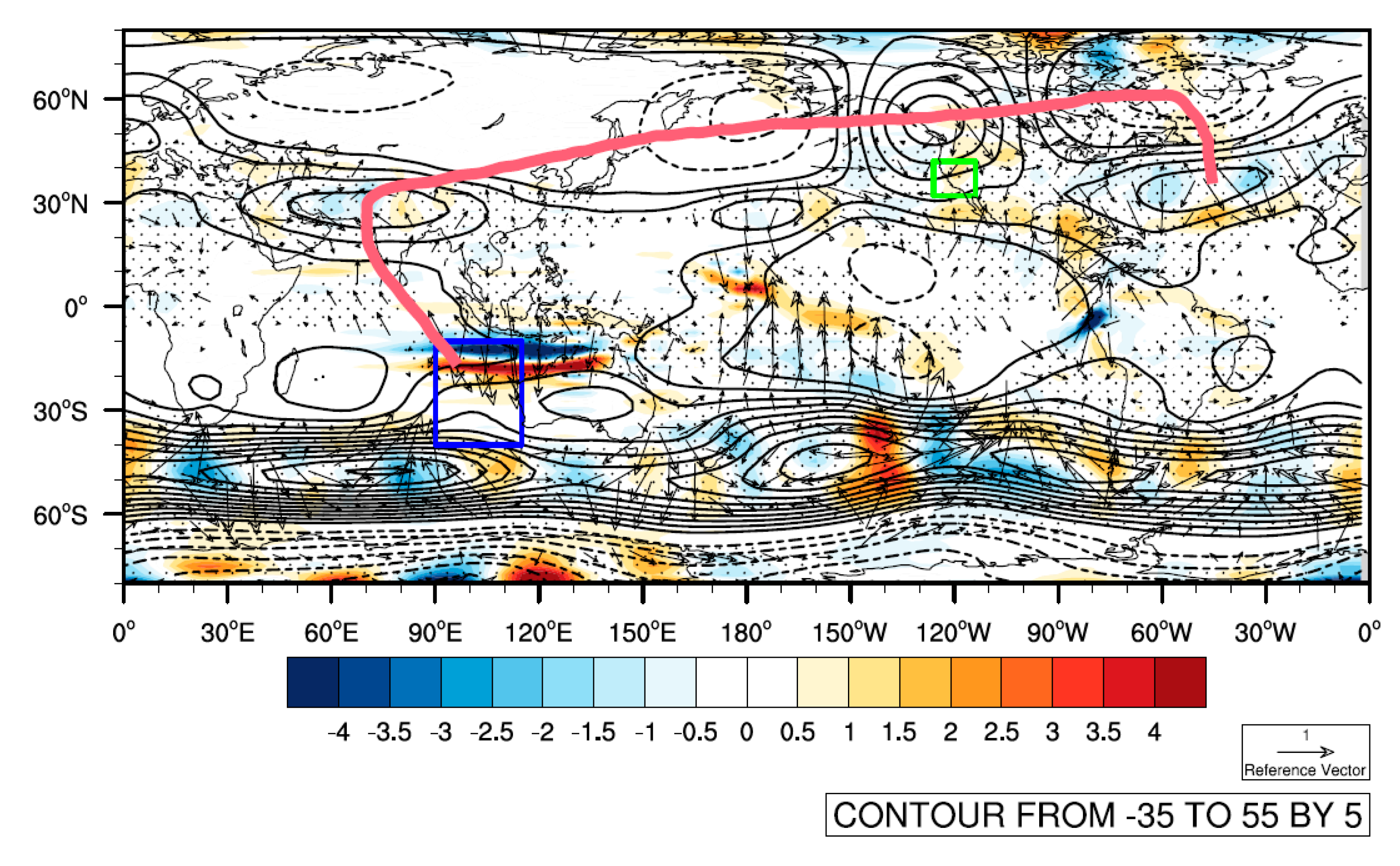
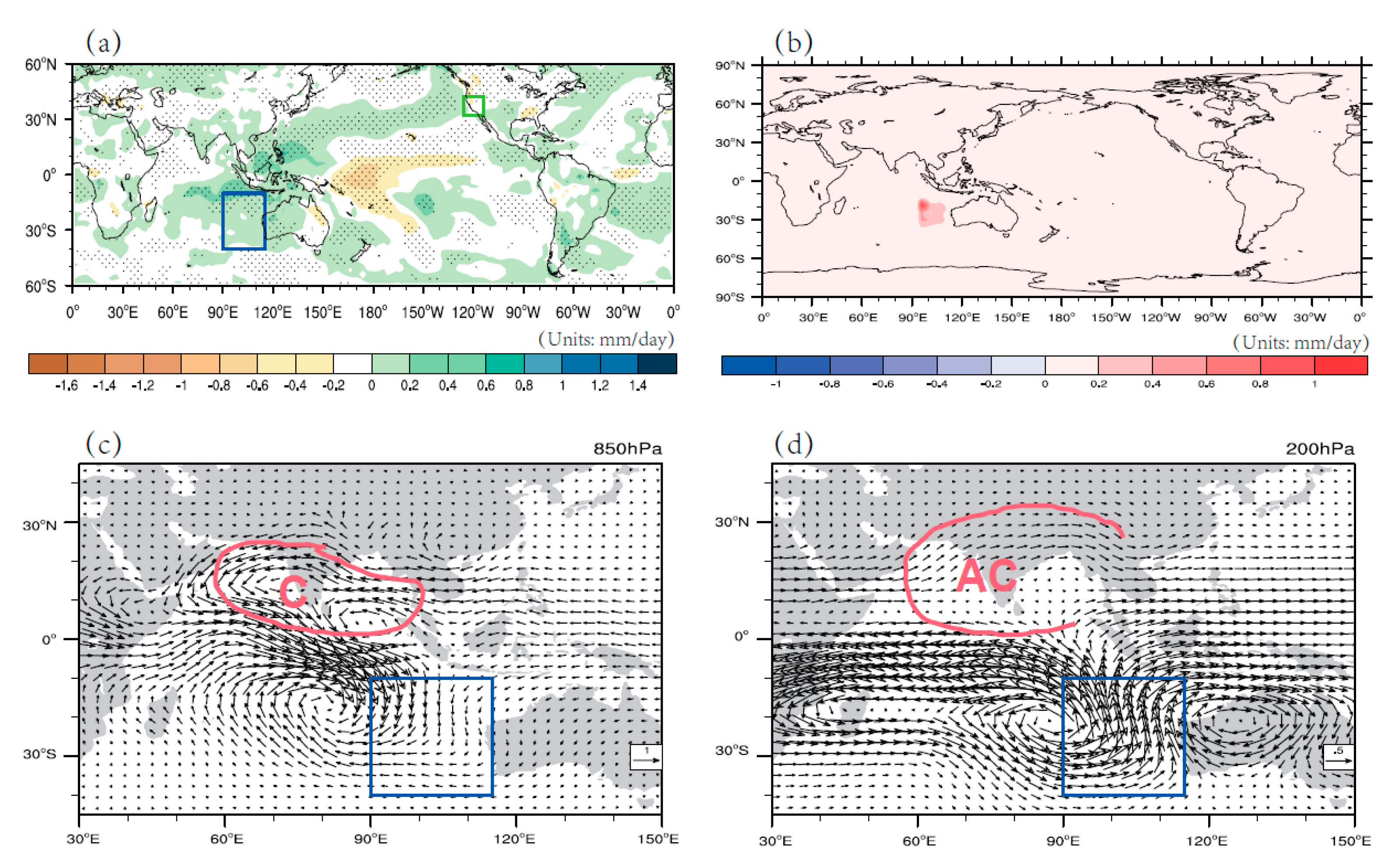
4.1. Central Pacific Ocean
4.2. Southeast Indian Ocean
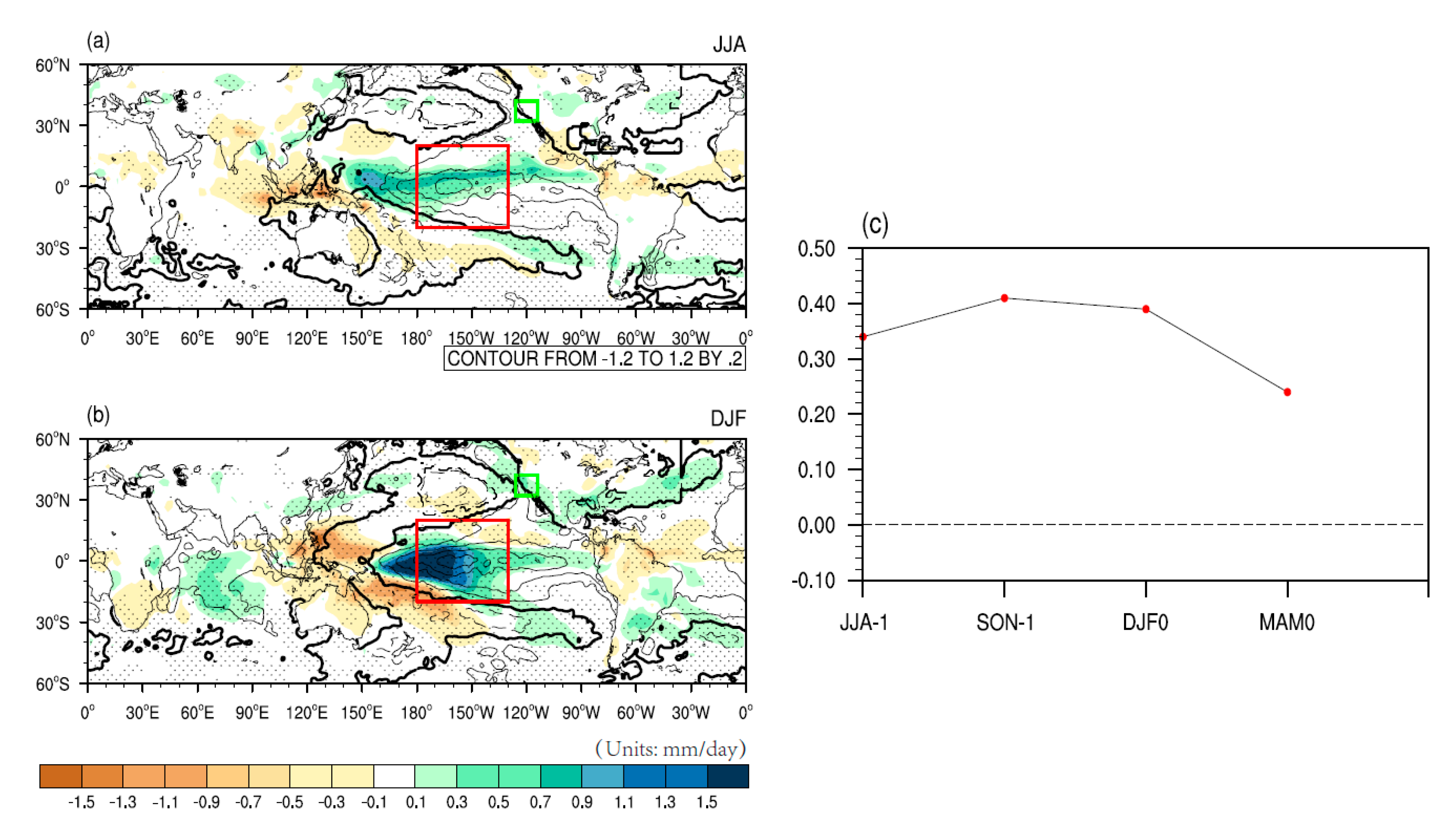
5. Environmental Factors Affecting PC2 Changes
6. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seager, R.; Hoerling, M.P.; Schubert, S.; Wang, H.; Lyon, B.; Kumar, A.; Nakamura, J.; Henderson, N. Causes of the 2011–2014 California Drought. J. Clim. 2015, 28, 6997–7024. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef]
- US Census Bureau. State and County QuickFacts. 2014. Available online: Quickfacts.census.gov/qfd/states/06000.html (accessed on 20 March 2021).
- US Bureau of Economic Analysis. Bureau of Economic Analysis Interactive Data. 2014. Available online: www.bea.gov/ (accessed on 20 March 2021).
- US Department of Agriculture. CALIFORNIA Agricultural Statistics 2012 Crop Year. 2013. Available online: www.nass.usda.gov/Statistics_by_State/California/Publications/California_Ag_Statistics/Reports/2012cas-all.pdf (accessed on 20 March 2021).
- Zhu, Z.; Li, T. Amplified contiguous United States summer rainfall variability induced by East Asian monsoon interdecadal change. Clim. Dyn. 2017, 50, 1–14. [Google Scholar] [CrossRef]
- Manuel, J. Drought in the Southeast: Lessons for Water Management. Environ. Health Perspect. 2008, 116, A168–A171. [Google Scholar] [CrossRef] [PubMed]
- Gotvald, A.J.; Mccallum, B.E. Epic Flooding in Georgia, 2009. In U.S. Geological Survey Fact Sheet 2010-3107; U.S. Geological Survey: Reston, VA, USA, 2012; 2p. [Google Scholar]
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 California drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef]
- Williams, A.P.; Seager, R.; Abatzoglou, J.T.; Cook, B.I.; Smerdon, J.E.; Cook, E.R. Contribution of anthropogenic warming to California drought during 2012–2014. Geophys. Res. Lett. 2015, 42, 6819–6828. [Google Scholar] [CrossRef]
- Mao, Y.; Nijssen, B.; Lettenmaier, D.P. Is climate change implicated in the 2013–2014 California drought? A hydrologic perspective. Geophys. Res. Lett. 2015, 42, 2805–2813. [Google Scholar] [CrossRef]
- Nitta, T. Convective activities in the tropical western Pacific and their impact on the northern hemisphere summer circulation. J. Meteorol. Soc. Jpn. 1987, 65, 373–390. [Google Scholar] [CrossRef]
- Huang, R. The numerical simulation of the three-dimensional teleconnections in the summer circulation over the Northern Hemisphere. Adv. Atmos. Sci. 1985, 2, 81–92. [Google Scholar]
- Lau, K.M.; Weng, H. Recurrent Teleconnection Patterns Linking Summertime Precipitation Variability over East Asia and North America. J. Meteorol. Soc. Jpn. 2002, 80, 1309–1324. [Google Scholar] [CrossRef]
- Lau, K.M. Dynamics of atmospheric teleconnections during the Northern Hemisphere summer. J. Clim. 1992, 5, 140–158. [Google Scholar] [CrossRef]
- Ting, M.; Wang, H. Summertime, U.S. Precipitation Variability and Its Relation toPacific Sea Surface Temperature. J. Clim. 2010, 10, 1853–1873. [Google Scholar] [CrossRef]
- Hui, W.; Ting, M.; Ming, J. Prediction of seasonal mean United States precipitation based on El Niño sea surface temperatures. Geophys. Res. Lett. 1999, 26, 1341–1344. [Google Scholar]
- Li, C.; Zhang, L. Summer monsoon activities in South China Sea and its impacts. Chinese. Sci. Atmos. Sin. 1999, 3, 23. [Google Scholar]
- Lau, K.M. Dynamical and Boundary Forcing Characteristics of Regional Components of the Asian Summer Monsoon. J. Clim. 2000, 13, 2461–2482. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Lau, K.M. Interannual Variability of the Asian Summer Monsoon: Contrasts between the Indian and the Western North Pacific–East Asian Monsoons*. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Guillemot, C.J. Physical Processes Involved in the 1988 Drought and 1993 Floods in North America. J. Clim. 1996, 9, 1288–1298. [Google Scholar] [CrossRef]
- Mo, K.C.; Paegle, J.N.; Higgins, R.W. Atmospheric Processes Associated with Summer Floods and Droughts in the Central United States. J. Clim. 1997, 10, 3028–3046. [Google Scholar] [CrossRef]
- Livezey, R.E.; Smith, T.M. Covariability of Aspects of North American Climate with Global Sea Surface Temperatures on Interannual to Interdecadal Timescales. J. Clim. 1999, 12, 289–302. [Google Scholar] [CrossRef]
- Mo, K.C. Intraseasonal Modulation of Summer Precipitation over North America. Mon. Weather Rev. 2000, 128, 1490–1505. [Google Scholar] [CrossRef]
- Higgins, R.W.; Leetmaa, A.; Xue, Y.; Barnston, A. Dominant factors influencing the seasonal predictability of United States precipitation and surface air temperature. J. Clim. 2000, 13, 3994–4017. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. North American Precipitation and Temperature Patterns Associated with the El Nio/Southern Oscillation (ENSO). Mon. Weather Rev. 1985, 114, 12. [Google Scholar]
- Palmer, T.N.; Brankovi, C. The 1988 US drought linked to anomalous sea surface temperature. Nature 1989, 338, 54–57. [Google Scholar] [CrossRef]
- Mo, K.C.; Schemm, J.E. Relationships between ENSO and drought over the southeastern United States. Geophys. Res. Lett. 2008, 35, 212–222. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Kushnir, Y. Variation of the North Atlantic subtropical high western ridge and its implication to Southeastern US summer precipitation. Clim. Dyn. 2012, 39, 1401–1412. [Google Scholar] [CrossRef]
- Dai, A. The influence of the inter-decadal Pacific oscillation on US precipitation during 1923–2010. Clim. Dyn. 2013, 41, 633–646. [Google Scholar] [CrossRef]
- Enfield, D.B. Relationships of inter-american rainfall to tropical Atlantic and Pacific SST variability. Geophys. Res. Lett. 1996, 23, 3305–3308. [Google Scholar] [CrossRef]
- Wang, H.; Fu, R.; Kumar, A.; Li, W. Intensification of Summer Rainfall Variability in the Southeastern United States during Recent Decades. J. Hydrometeorol. 2010, 11, 1007–1018. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S.; Oglesby, R.J. Variations in North American Summer Precipitation Driven by the Atlantic Multidecadal Oscillation. J. Clim. 2010, 1, 8. [Google Scholar] [CrossRef]
- Curtis, S. The Atlantic multidecadal oscillation and extreme daily precipitation over the US and Mexico during the hurricane season. Clim. Dyn. 2008, 30, 343–351. [Google Scholar] [CrossRef]
- McCabe, G.J.; Palecki, M.A.; Betancourt, J.L. Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc. Natl. Acad. Sci. USA 2004, 101, 4136–4141. [Google Scholar] [CrossRef] [PubMed]
- Horel, J.D.; Wallace, J.M. Planetary-Scale Atmospheric Phenomena Associated with the Southern Oscillation. Mon. Weather Rev. 1981, 109, 813–829. [Google Scholar] [CrossRef]
- Leathers, D.J.; Yarnal, B.; Palecki, M.A. The Pacific/North American Teleconnection Pattern and United States Climate. Part I: Regional Temperature and Precipitation Associations. J. Clim. 1991, 4, 517–528. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Branstator, G.W.; Karoly, D.; Kumar, A.; Lau, N.C.; Ropelewski, C. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures. J. Geophys. Res. Ocean. 1998, 103, 14291–14324. [Google Scholar] [CrossRef]
- Coleman, J.S.M.; Rogers, J.C. Ohio River Valley Winter Moisture Conditions Associated with the Pacific–North American Teleconnection Pattern. J. Clim. 2003, 16, 969–981. [Google Scholar] [CrossRef]
- Ge, Y.; Gong, G.; Frei, A. Physical Mechanisms Linking the Winter Pacific–North American Teleconnection Pattern to Spring North American Snow Depth. J. Clim. 2009, 22, 5135–5148. [Google Scholar] [CrossRef]
- Xie, P.; Chen, M.; Yang, S.; Yatagai, A.; Hayasaka, T.; Fukushima, Y.; Liu, C. A Gauge-Based Analysis of Daily Precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626. [Google Scholar] [CrossRef]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P. Global Land Precipitation: A 50-yr Monthly Analysis Based on Gauge Observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Rayner, N.A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, D14. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; Whie, G.; Woolled, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Technology; China Meteorological Press: Beijing, China, 1956. [Google Scholar]
- Venkateshan, S.P. Regression Analysis. Mechanical Measurements; Springer International Publishing: Cham, Switzerland, 2021; pp. 49–77. [Google Scholar]
- Fisher, R.A. Accuracy of observation, A mathematical examination of the methods of determining, by the mean error and by the mean square error. Mon. Not. R. Astron. Soc. 1920, 80, 443–450. [Google Scholar] [CrossRef]
- Held, I.M.; Suarez, M.J. A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models. Bull. Am. Meteorol. Soc. 1994, 75, 1825–1830. [Google Scholar] [CrossRef]
- Jiang, X.A.; Li, T. Reinitiation of the boreal summer intraseasonal oscillation in the tropical Indian Ocean. J. Clim. 2005, 18, 3777–3795. [Google Scholar] [CrossRef][Green Version]
- Li, T.; Liu, P.; Fu, X.; Wang, B.; Meehl, G.A. Spatiotemporal Structures and Mechanisms of the Tropospheric Biennial Oscillation in the Indo-Pacific Warm Ocean Regions*. J. Clim. 2006, 19, 3070–3087. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather. Rev. 1982, 110, 699. [Google Scholar] [CrossRef]
- Bridge, N. The Climate of Southern California; University of California Press: Oakland, CA, USA, 1901. [Google Scholar]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Nigam, S. On the Role of Sea Surface Temperature Gradients in Forcing Low-Level Winds and Convergence in the Tropics. J. Atmos. Sci. 1987, 45, 2418–2436. [Google Scholar] [CrossRef]
- Nakamura, H.; Nakamura, M.; Anderson, J.L. The Role of High- and Low-Frequency Dynamics in Blocking Formation. Mon. Weather Rev. 1997, 125, 2074–2093. [Google Scholar] [CrossRef]
- Gill, A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 2010, 106, 447–462. [Google Scholar] [CrossRef]
- Yang, H.; Lohmann, G.; Lu, J.; Gowan, E.J.; Shi, X.; Liu, J.; Wang, Q. Tropical Expansion Driven by Poleward Advancing Midlatitude Meridional Temperature Gradients. J. Geophys. Res. Atmos. 2020, 125, e2020JD033158. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, F.; Zhang, L.; Liu, Q.; Chyi, D. Environmental Factors Controlling the Precipitation in California. Atmosphere 2021, 12, 997. https://doi.org/10.3390/atmos12080997
Hu F, Zhang L, Liu Q, Chyi D. Environmental Factors Controlling the Precipitation in California. Atmosphere. 2021; 12(8):997. https://doi.org/10.3390/atmos12080997
Chicago/Turabian StyleHu, Feng, Leying Zhang, Qiao Liu, and Dorina Chyi. 2021. "Environmental Factors Controlling the Precipitation in California" Atmosphere 12, no. 8: 997. https://doi.org/10.3390/atmos12080997
APA StyleHu, F., Zhang, L., Liu, Q., & Chyi, D. (2021). Environmental Factors Controlling the Precipitation in California. Atmosphere, 12(8), 997. https://doi.org/10.3390/atmos12080997




