Abstract
Drought is one of the disasters that causes the most extensive and severe damage. Therefore, drought prevention must be performed for administrative districts at the national level rather than the individual level. This study proposes a drought index estimation method for Gyeongsangnamdo, South Korea that evaluates its appropriateness through a comparison with damage data over several years. The standardized precipitation index (SPI) by duration was used as the drought index that was estimated for 13 rainfall stations located inside and outside Gyeonsangnam-do using the Thiessen method and cluster analysis. The SPI of Gyeongsangnamdo by duration based on the Thiessen method and cluster analysis for the years when drought damage occurred was compared with an SPI value of −2.0, which is the extreme drought condition, to determine its appropriateness. For the evaluation of the appropriateness, the performance indicators of the mean absolute deviation (MAD), mean squared error (MSE), and root mean square error (RMSE) were used. The analysis results showed that SPI by duration based on the cluster analysis method was more appropriate for damage data over many years than that based on the Thiessen method.
1. Introduction
Drought is a natural disaster characterized by the lack of precipitation (i.e., rain, snow, or sleet) for a protracted period (i.e., more than 3 to 12 months), resulting in water shortage that greatly affects a wide range of socioeconomic sectors including agriculture, living, and industry. In recent years, the acceleration of climate change leads to changes in the intensity, spatial extent, frequency, duration, and timing of weather and climate extremes that worsens drought conditions, which vary in frequency, duration, and severity per climatic zone, experienced across vast portions of the world [1,2,3]. Particularly, South Korea has faced continuous severe droughts, which is normally concentrated in spring and autumn, and experiences varying drought damages depending on regional characteristics. In addition, the annual average rainfall that occurs in summer is approximately 60%, indicating the necessity for proper management of the supply and distribution of water resources especially during drought. To prevent drought impacts, drought risk assessments and drought pattern identification need to be implemented to establish prevention and response systems for each administrative district rather than point-based planning.
Various drought indices have been developed for drought evaluation, including the standardized precipitation index (SPI), standardized precipitation evapotranspiration index (SPEI), reconnaissance drought index (RDI), Palmer drought severity index (PDSI), and effective drought index (EDI) [4,5,6,7,8]. Among them, SPI can evaluate drought using only precipitation, is less complex to calculate, and is more comparable across regions with different climates. Therefore, the World Meteorological Organization has recommended SPI as a standard index and has become one of the most widely used drought indices [9].
SPI is an index that is widely used to characterize drought on a range of timescales for national disaster management policies and drought evaluation, prediction, and monitoring in several countries in America, Asia, Europe, Africa, and Oceania [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. In addition, statistical methods were applied for analyzing the spatiotemporal impacts of drought and its annual or seasonal variability [22,38,39,40,41,42,43,44,45]. In the field of water resources, SPI is utilized in agricultural, environmental, and hydrological evaluations of the impact of drought on these fields. Moreover, the effects of groundwater, river flow, and water circulation on the characteristics of drought, such as periodicity, duration, and severity, were analyzed [46,47,48,49,50,51]. Recently, climate change data, including RCP (Representative Concentration Pathway) and GCM (General Circulation Models), were used, and the impact of global warming and climate change on drought was presented [52,53,54,55,56,57]. Here, RCP is a greenhouse gas concentration trajectory adopted by the IPCC and GCM is a type of climate model. However, most evaluation and prevention studies using SPI use point-based analysis based on rainfall stations. In some studies, spatial analysis was conducted using the arithmetic mean method, area-weighted mean method, isohyetal method, and Kriging method. However, no research has been conducted on the evaluation of their appropriateness for drought.
In many countries, point-based observations are performed for weather observations, but the influence of drought damage is expanded in a spatial range. Measures for national administrative districts must be prepared to prevent or respond to drought. Various methods have been applied to this end. The influence of drought on national administrative districts was evaluated by rainfall estimation and SPI analysis using the arithmetic mean and Thiessen methods [58,59,60,61,62,63,64,65]. In the analysis based on the Thiessen method, the (1) mean rainfall was estimated and SPI was analyzed by applying the Thiessen weight to observed rainfall, or (2) observed rainfall was analyzed as SPI and compared with the mean SPI estimated through the application of the Thiessen weight [10,66,67,68,69,70]. In addition, drought was evaluated by selecting rainfall stations that affect administrative districts and watersheds through cluster analysis and analysis of SPI [47,71]. SPI was analyzed by estimating rainfall that represents administrative districts or watersheds, but the appropriateness of methodologies for areal rainfall estimation has not been researched. If the point rainfall is estimated as the rainfall of an administrative district, the area-averaged rainfall is calculated to be small. Therefore, it is difficult to reflect all extreme rainfall or drought indices of each point. In addition, the utilization of SPI-based drought analysis has been mostly emphasized for national disaster prevention and disaster response, but comparisons with past damage are insufficient.
Therefore, in this study, SPI by duration was analyzed using the Thiessen weight of rainfall stations for the Thiessen method and the k-means method for cluster analysis on 13 rainfall stations located in the administrative district of Gyeongsangnamdo, South Korea, which experienced frequent drought damage in the past. The SPI results by duration estimated for the administrative district were compared with past damage data to evaluate the appropriateness of the drought index estimation method.
2. Materials and Methods
2.1. SPI
SPI was developed by McKee et al. [4,72] to analyze the size of drought, considering that the lack of water supply due to the reduction of precipitation with increasing demand causes drought [4,72]. The SPI by duration was analyzed by estimating hourly or monthly cumulative precipitation time series. In addition, the cumulative probability of the variance was estimated by analyzing the time-series rainfall by duration for each month and applying it to the standard normal distribution. The drought indices for 3, 6, 9, and 12 months were estimated for each time axis based on the periodic distribution of precipitation for the corresponding observation point using the gamma probability density function. Moreover, the SPI was used to identify the spatiotemporal variability of drought. Table 1 shows the drought classification.

Table 1.
Drought classification using SPI values and corresponding event probabilities.
The SPI parameters were estimated using the maximum likelihood method. The cumulative probability of rainfall events for the time interval of the target point was analyzed using the parameters calculated using Equation (1).
where is the shape parameter, is the scale parameter, and is the estimated rainfall for each observation point according to the time scale designated as the coefficient of the gamma probability density function. The estimates of and can be calculated using the following equations, respectively:
where and n is the amount of precipitation data. The obtained parameters are applied to the cumulative probability distribution functional formula defined in Equation (4).
Equation (4) can be rewritten into Equation (5) by applying .
The Gamma function is not defined as x = 0, but there are cases where the precipitation is zero. Thus, the cumulative probability is given by:
where is the probability when the precipitation is zero. The probability of no rainfall, , can be expressed as using the assumption that is the number of days with no rainfall and is the number of days that rainfall occurred. If the cumulative probability H(x) is converted to express a random variable Z of the standard normal distribution with a mean of zero and a variance of 1, then it becomes:
where , , , , , and . These variables, , , , , , and , are constants. Moreover, x is the precipitation and H(x) is the cumulative probability of the observed precipitation value.
2.2. Thiessen Method
The Thiessen method is a trigonometric network that does not include other points in the circumscribed circle of a triangle that connects three nodes to a Thiessen polygon, which is also referred as the Voronoi diagram. This method can be considered as a Delaunay triangulation because it performs spatial calculations on a set of irregular points and polygons made of bisectors on each side [73]. Figure 1a shows the Delaunay triangulations on JLO, OLU, ULV, VLW, and WLJ, which are trigonometric networks connected with each other and do not include other points in the circumscribed circle of a triangle that connects points arranged on a plane [74]. A Thiessen polygon converts irregularly arranged points into a structure based on a certain principle. A polygon containing points that are closer to the arbitrary point L than points J, O, U, V, and W can be assigned for point L, which is made of vertical bisectors of segments LJ, LO, LU, LV, and LW. Moreover, points J, O, U, V, and W are referred to as the Thiessen neighbors of point L. The construction of Thiessen polygons is shown in Figure 1b.
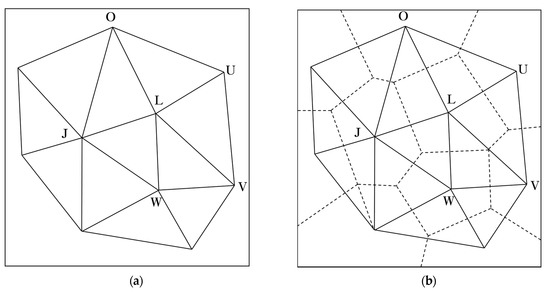
Figure 1.
Construction of the irregular trigonometric network: (a) Delaunay triangulation); (b) Thiessen polygon.
The Thiessen polygon method considers the influence of irregularly located rainfall stations on the target area during flood estimation in a watershed. The areal average rainfall is estimated by creating Thiessen polygons for each rainfall station based on the observed rainfall at that station. Then, the ratio of the area and the total area is expressed, and becomes a weight, as shown in Equation (11).
where is the average rainfall of the watershed, are the rainfall observed at n stations in the watershed, and are the commanded areas of each observation point.
2.3. Cluster Analysis
The k-means method of cluster analysis is an algorithm proposed by MacQueen for classifying experimental results or the data obtained from samples according to certain properties [75,76]. Homogeneous patterns are classified into k clusters, while the average was calculated as the central value of a cluster.
In this method, objects at a closer distance are connected by measuring the degree of similarity or dissimilarity between objects when variables are measured for data. The i-th observed value of y for data is set as vector . It is assumed that the of each data that is composed of k groups belongs to only one group for and the average of each group is expressed as , as shown in Equation (12). Among the n data, the set of the observed values that belong to the i-th group is presented as , and the classification of that minimizes cluster analysis is shown in Equation (13).
Clusters are created based on the proximity of each data point when the initial value of n data is composed of k clusters. The center of a cluster repeats separation and combination with the data included in the range, and cluster analysis was conducted, as shown in Table 2.

Table 2.
Cluster analysis procedure.
2.4. Drought Damage Status and Target Area Selection
In recent years, the increase in temperature, reduced rainfall occurrence, and increase in evapotranspiration have been observed due to the influence of climate change, resulting in the worldwide occurrence of drought damage in United States, Australia, Europe, and Africa [77]. In South Korea, drought damage frequently occurred in the region before the 1980s as the economic development is starting. After the economic development, significant drought damage occurred every five or ten years despite the construction of dams, reservoirs, and water supply facilities.
Before 2000, the status of damage in South Korea was investigated, and reports were prepared for administrative districts where large-scale drought damage occurred. Reports on administrative districts have been published each year since 2010 because of the constant occurrence of various disasters, including drought. The status of drought damage that occurred from 1965 to 2019 is recorded in the “drought record survey report (1995 and 2001)” and “abnormal weather report (2010 to 2019)” for administrative districts.
Damages occurred at least 1 to 16 times with an average of 4 times for each administrative district in South Korea, except in Daejeon and Ulsan in which no damage was reported. It occurred most frequently in Gyeongsangnamdo (16 times), as shown in Figure 2a. Drought damage occurred in 1 to 11 administrative districts each year for 27 years in 122 regions from 1965 to 2019, as shown in Figure 2b. The blue bar graph is the administrative district where drought damage occurred by year, and the red line is the cumulative administrative district. Drought damage occurred in two administrative districts on average each year, and the most extensive damage occurred over nine regions in 1994 and 11 regions in 1977 and 2018 (Figure 2a).
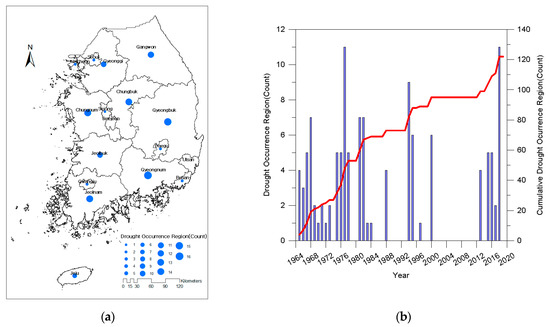
Figure 2.
Drought damage status in South Korea (1965 to 2018): (a) Number of drought damage occurrences by region; (b) Number of drought damage occurrences by year.
In this study, Gyeongsangnamdo, where drought damage occurred most frequently among the 17 administrative districts in South Korea, was selected as the target area (Figure 3). Moreover, the influence of precipitation is used as an analysis factor because drought damage develops when there is insufficient water supply catering a large demand. Precipitation varies depending on regional characteristics, and rainfall stations that affect the target area are located inside and outside the area. Thirteen rainfall stations affected the target area in which ten of them are located inside the area and three are outside the area.
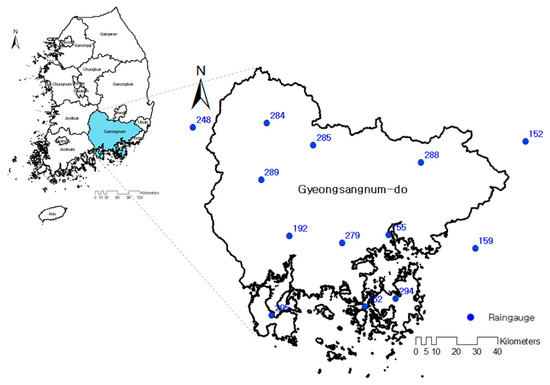
Figure 3.
Map of Gyeongsangnamdo, South Korea.
Figure 4 shows that out of the 27 times drought damage occurred in South Korea, 16 times it was experienced in Gyeongsangnamdo. The blue bar graph is the year of drought damage, and the red line is the cumulative number of drought damage. The drought in Gyeongsangnamdo lasted for two to three years with the addition occurrence of short-term drought that lasted for a year, resulting in more serious drought damage compared to other regions. A total of 50% of drought damage occurred before 1980; then, it periodically occurred every ten or five years since then. Although the number of drought damage occurrences has decreased through various water resource policies, the severity of drought was found to significantly increase.
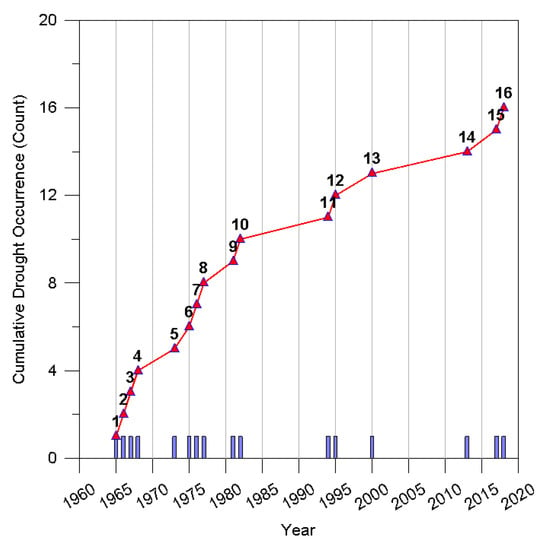
Figure 4.
Status of drought damage in Gyeongsangnamdo by year.
3. Results
3.1. SPI Analysis
In this study, SPI, which is a method used to analyze the influence of drought using rainfall on various meteorological factors, was selected to identify the spatiotemporal scale and drought situation in Gyeongsangnamdo. It is easy and is the most widely used. There were 13 rainfall stations for Gyeonsangnam-do, and 57 weather data were observed, including rainfall, temperature, wind speed, and humidity. Rainfall stations were installed according to the importance of the region and applicability, and the observation of weather data begins on different dates. Table 3 shows the station index, station name, and observation date for 13 rainfall stations.

Table 3.
Status of rainfall stations for Gyeongsangnamdo.
The observation dates of each rainfall station must be unified for drought analysis in Gyeongsangnamdo using the SPI. Four stations began observations between 1965 and 1970, seven stations between 1970 and 1980, and two stations after 1980. Therefore, in this study, SPI was analyzed for the rainfall period from 1973 to 2019 because the rainfall observation data of at least 30 years and drought damage of more than ten years could be compared. Among the rainfall stations, Changwon and Jangju were analyzed based on their observation dates.
The duration of SPI was divided into 3, 6, 9, and 12 months, considering that spring and autumn droughts occur in South Korea based on the monsoon season during the summer. Therefore, the SPI analysis period of each rainfall station for Gyeongsangnamdo was 47 years, from January 1973 to December 2019, and the analysis was conducted for the durations of 3, 6, 9, and 12 months. Figure 5 shows the results of the SPI analysis by duration for each rainfall station. Moreover, the SPI range for the 13 rainfall stations are as follows: SPI3 ranged from −7.08 to 4.09, SPI6 ranged from −3.94 to 3.64, SPI9 ranged from −3.42 to 3.84, and SPI12 ranged from −2.87 to 3.75.
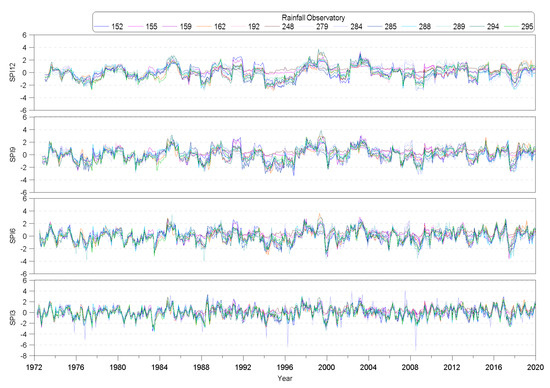
Figure 5.
Results of SPI analysis by duration for the rainfall stations affecting Gyeonsangnamdo.
SPI3 ranged from −3.15 to 2.91 on average for each station, and the minimum and maximum SPI ranging from −7.08 to 4.09 were observed from the Geochang station (no. 284). In addition, SPI6 ranged from −2.65 to 2.69 on average, and the minimum SPI ranging from −3.94 to 3.49 was observed from the Sancheong station (no. 289) and the maximum SPI ranging from −3.00 to 3.64 was observed from the Tongyeong station (no. 162). On the other hand, SPI9 ranged from −2.49 to 2.59 on average, and the minimum SPI ranging from −3.42 to 2.98 was observed from the Ulsan station (no. 152) and the maximum SPI ranging from −2.36 to 3.84 was observed from the Geoje station (no. 294). Meanwhile, SPI12 ranged from −2.26 to 2.79 on average, and the minimum SPI ranging from −2.87 to 3.45 was observed from the Geochang station (no. 284) and the maximum SPI ranging from −2.38 to 3.75 was observed from the Geoje station (no. 294). The SPI analysis results for each rainfall station showed that the maximum and minimum ranges and the drought index decreased as the duration increased.
3.2. Drought Index Analysis Using the Thiessen Method
In this study, the Thiessen method was used to estimate the areal average rainfall at each station by creating a Thiessen polygon based on the 13 rainfall stations affecting Gyeongsangnamdo shown in Figure 6 and calculating the area ratio of the Thiessen polygon as a weight. In various studies, Thiessen polygons have been applied as a method to analyze the meteorological factors of a watershed or administrative district [10,58,59,60,61,62,63,64,65,66,67,68,69,70].
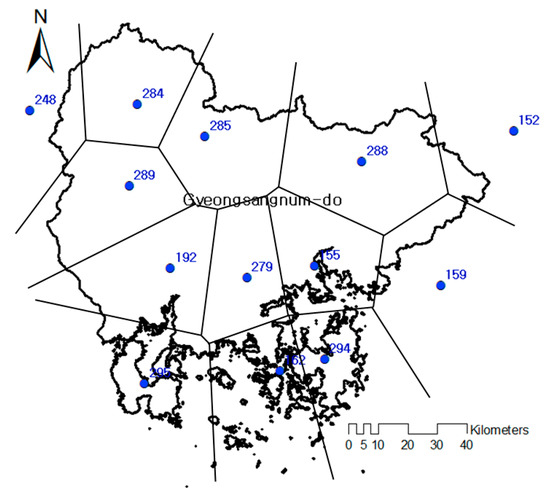
Figure 6.
Thiessen polygon distribution for Gyeongsangnamdo.
The rainfall stations for Gyeongsangnamdo were analyzed starting from January 1973, but the observation dates for Changwon (no. 155) and Geochang (no. 284) started in January 1988. As the observation dates were different, the area ratio of a Thiessen polygon was calculated as the weight for 11 stations before 1988 and 13 stations after 1988. Table 4 lists the weights of rainfall stations according to the analysis period. The Changwon (no. 155) and Geochang (no. 284) stations represented approximately 20% of the total weight, and the weights after 1988 were reduced by 0.6 to 3.8% compared to those before 1988.

Table 4.
Thiessen weight by rainfall station.
The SPI by duration of Gyeongsangnamdo was calculated by applying the area weight of the Thiessen polygon for each rainfall station, as shown in Figure 7. The SPI3 ranged from −3.09 to 2.76, and the quartiles were found to be −0.53 for Q1, 0.07 for Q2, and 0.68 for Q3. Moreover, SPI6 ranged from −2.49 to 2.25, and the quartiles were found to be −0.61 for Q1, 0.13 for Q2, and 0.66 for Q3. Meanwhile, SPI9 ranged from −2.15 to 2.07, and the quartiles were found to be −0.61 for Q1, 0.15 for Q2, and 0.65 for Q3. On the other hand, SPI12 ranged from −2.36 to 2.59, and the quartiles were found to be −0.54 for Q1, 0.19 for Q2, and 0.62 for Q3. The “extremely dry” condition, which is an SPI of −2 or less, was found to occur ten times for SPI3, six times for SPI6, once for SPI9, and thrice for SPI12.
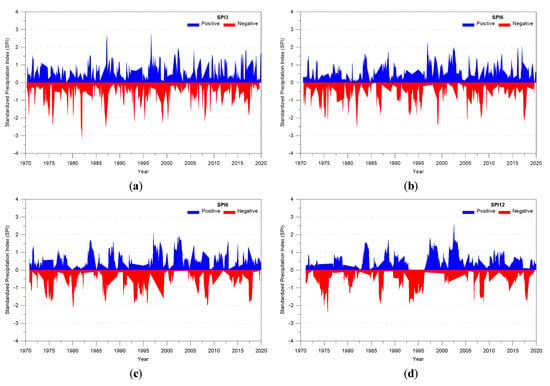
Figure 7.
Analysis of the SPI of Gyeongsangnamdo by duration through the application of Thiessen polygons: (a) SPI3; (b) SPI6; (c) SPI9; (d) SPI12.
3.3. Analysis of the Drought Index Using Cluster Analysis
The SPI by duration was estimated for the 13 rainfall stations affecting Gyeongsangnamdo using cluster analysis. The cluster analysis method used in this study is the k-means method, which is an unsupervised learning method. The k-means method proposed by MacQueen is an algorithm that divides the given data into k clusters [76]. For the k-means method, the analyzer must set the initial number of clusters. It was determined by drawing a graph with a function using R, a statistical software program, among various setting methods.
The monthly SPI of Gyeongsangnamdo for the 13 stations was analyzed by setting the number of clusters to two to six. Figure 8 shows the cluster results of the D index and Best.partition for setting the appropriate number of clusters for SPI by duration. For the D index, the point at which the slope of the Y-axis sharply decreased was selected as the appropriate number of clusters, and the slope was largest at three. For Best.partition, the highest point was selected as the appropriate number of clusters, and the value was the highest (more than 40%) at three. Therefore, in this study, the number of clusters for the k-means method was set to three.
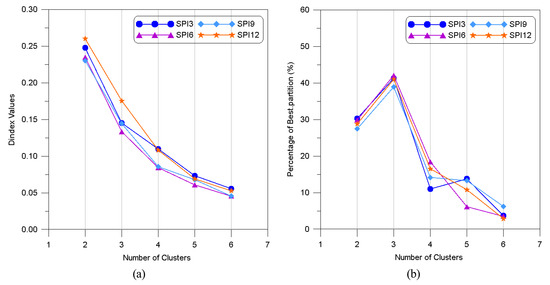
Figure 8.
Setting the number of clusters for cluster analysis: (a) D index; (b) Best.partition.
The SPI by duration of Gyeongsangnamdo based on cluster analysis was analyzed using three clusters, as shown in Figure 9. The minimum value of SPI3 ranged from −3.30 to −2.96 and the maximum value ranged from 1.80 to 2.96. On the other hand, the minimum value of SPI6 ranged from −2.94 to −2.37 and the maximum value ranged from 1.69 to 2.57. Meanwhile, the minimum value of SPI9 ranged from −2.37 to −2.02 and the maximum value ranged from 1.82 to 2.82. Moreover, the minimum value of SPI12 ranged from −2.50 to −1.95 and the maximum value ranged from 1.72 to 2.97. The analysis results of SPI by duration showed that the minimum value ranged from −3.30 to −1.95 and the maximum value ranged from 1.69 to 2.97. The difference in the cluster analysis of SPI by duration was 1.35 for the minimum value and 1.28 for the maximum value.
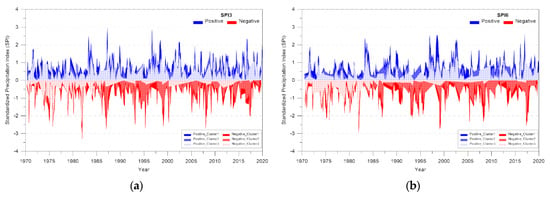
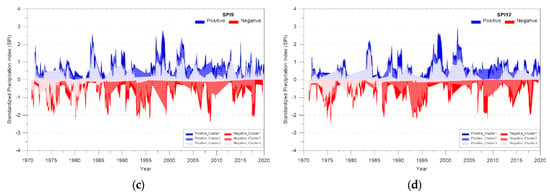
Figure 9.
SPI of Gyeongsangnamdo by duration based on cluster analysis: (a) SPI3; (b) SPI6; (c) SPI9; (d) SPI12.
As for the SPI of Gyeongsangnamdo by duration, the minimum value among the three clusters analyzed was set as the representative SPI by duration (Figure 10). The SPI3 of Gyeongsangnamdo ranged from −3.30 to 1.80, and the quartiles were found to be −0.78 for Q1, −0.18 for Q2, and 0.44 for Q3. SPI6 ranged from −2.94 to 1.69, and the quartiles were found to be −0.88 for Q1, −0.18 for Q2, and 0.40 for Q3. SPI9 ranged from −2.37 to 1.82, and the quartiles were found to be −0.95 for Q1, −0.20 for Q2, and 0.39 for Q3, respectively. SPI12 ranged from −2.50 to 1.72, and the quartiles were found to be −0.97 for Q1, −0.28 for Q2, and 0.38 for Q3, respectively. In addition, the “extremely dry” condition, for which SPI is –2 or less, was found to occur 20 times for SPI3, 19 times for SPI6, 14 times for SPI9, and 10 times for SPI12.
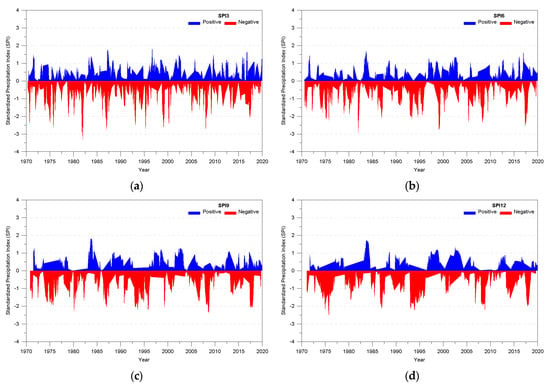
Figure 10.
SPI of Gyeongsangnamdo by duration based on k-means cluster analysis: (a) SPI3; (b) SPI6; (c) SPI9; (d) SPI12.
3.4. Examination of Drought Damage and the Appropriateness of the Drought Index
In this study, SPI by duration was estimated using the Thiessen method and cluster analysis from the data of Gyeongsangnamdo, which were constructed based on reports that include the damage status per year that indicates that the start and end time points of drought are not clear. Therefore, the minimum SPI value by year was calculated for the quantitative evaluation of SPI by duration and drought damage data. Figure 11a shows the minimum value of SPI by year for the durations of 3, 6, 9, and 12 months. SPI by year and duration ranged from −3.09 to 1.06 for the Thiessen method and from −3.30 to 1.30 for cluster analysis, showing that cluster analysis had higher minimum and maximum values than the Thiessen method.
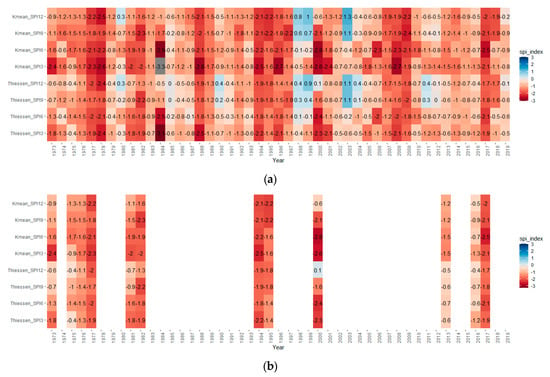
Figure 11.
SPI by duration according to the analysis method: (a) Minimum value of SPI by year; (b) Minimum value of SPI for each year with drought damage.
In Gyeongsangnamdo, drought damage occurred 12 times between 1973 and 2019 (i.e., in 1973, 1975, 1976, 1977, 1981, 1982, 1994, 1995, 2000, 2013, 2016, and 2017). However, there is no report showing the severity, range, and duration of drought in these years. Moreover, the maximum duration of drought in South Korea does not exceed 12 months since the monsoon season occurs during the summer. Therefore, SPI by duration was compared for 12 months or less. Figure 11b shows the SPI by duration when drought damage occurred in Gyeongsangnamdo. The SPI by duration based on the Thiessen method ranged from −2.41 to 0.07 in terms of years.
The severity of the drought was divided into seven categories for the SPI. An SPI of −1.00 indicates the start of drought, and values from −2.00 or less mean that extreme drought is experienced, and the evaluation occurs. It is not possible to accurately determine which drought categories cause drought damage, but an SPI value of −2.00 is evaluated as drought in various papers. Therefore, in this study, the SPI by duration analyzed using the Thiessen method and cluster analysis was compared with an SPI value of −2.00, which is a criterion for extremely dry conditions, to determine its appropriateness. The mean absolute deviation (MAD), mean squared error (MSE), and root mean square error (RMSE) were used as performance indicators for determining the appropriateness of time-series analysis. We found that the appropriateness is higher as they come closer to zero.
Table 5 shows the results of analyzing drought damage by year and the appropriateness of the SPI by duration analyzed using the Thiessen method and cluster analysis based on MAD, MSE, and RMSE. Particularly, the appropriateness of the SPI by duration using the Thiessen method for drought damage by year was found to be higher than 0.5 and lower than 1.0. The accuracy of each performance indicator was found to be high for SPI3 and SPI6. Meanwhile, the appropriateness of the SPI by duration analyzed using the cluster analysis for drought damage by year was higher than 0.3 and lower than 0.8. Moreover, the accuracy for each performance indicator was high for SPI3 and SPI9. The results show that cluster analysis exhibited higher accuracy than the Thiessen method, indicating that the cluster analysis method has higher precision in estimating SPI by duration for drought damage.

Table 5.
SPI and accuracy analyses using the Thiessen method and cluster analysis for drought damage.
4. Discussion
Drought is a disaster that needs to be prevented at the national level using disaster management plans proposed by administrative districts in many countries. However, in most studies, the drought index was analyzed using observation stations and estimated by the Thiessen method in which the extreme values for each station tend to be underestimated [58,59,60,61,62,63,64,65]. To address this problem, we proposed a method using cluster analysis to analyze these underestimated extreme values of the drought index. Moreover, its appropriateness was presented through a comparison with past drought damage.
The SPI by duration for 13 rainfall stations in Gyeongsangnamdo, an administrative district in South Korea where drought damage occurred most frequently, was analyzed, and the representative drought index was calculated using the Thiessen method and cluster analysis. In addition, both past drought damage and SPI by duration were analyzed to examine the appropriateness of the analysis methods, resulting in a more accurate result for the cluster analysis. The difference in the appropriateness results of MAD, MSE, and RMSE for drought damage and analysis methods ranged from 0.1 to 0.3, which does not indicate that the estimation method based on the Thiessen method is incorrect. Moreover, it is apparent that drought damage will be reduced if methodologies with higher appropriateness are developed for disaster prevention.
For the analysis of drought, SPI was analyzed and evaluated using the arithmetic mean, Thiessen, and inverse distance weighting methods, which consider the influence of rainfall stations on administrative districts, watersheds, and spatial ranges [58,59,60,61,62,63,64,65,66,67,68,69,70]. These methods were compared based on the analysis results and the ranges of the drought index. Moreover, the appropriateness was evaluated while adjusting the drought index estimation method or the spatial range for rainfall stations [62]. On the other hand, three regions from 144 rainfall stations in Portugal were divided through cluster analysis, and the period of drought was proposed using SPI [71]. The analysis of the spatial range for rainfall stations is important for drought evaluation, and research on various methods is required. Most previous studies have limitations in terms of accuracy because only the development of indices for evaluating drought or comparisons were presented, indicating the need for a qualitative analysis and appropriateness verification using past drought damage data.
In this study, SPI by duration based on the Thiessen method and cluster analysis was analyzed, and its accuracy was calculated for Gyeongsangnamdo, Korea. However, there are limitations in evaluating drought using SPI that considers only rainfall, since drought is a disaster that occurs due to various causes and complex relationships. Moreover, the occurrence of past drought damage under extreme drought conditions cannot be accurately verified. However, despite these aforementioned limitations, a more reliable disaster prevention will be possible if a more accurate methodology is used to analyze the influence of drought.
In future research, it will be necessary to propose quantitative linkage methods with the drought index through quantitative analysis of drought damage. In addition, most of the current drought analyses propose various durations, but it will be possible to secure durations for disaster prevention if drought damage is linked to the drought index by duration.
5. Conclusions
Drought is a slow-onset natural hazard in which its effects accumulate slowly over a certain period and may persist for years after the termination of the event. Therefore, determining the exact time of occurrence of drought is difficult. However, various disaster management studies were conducted to prevent its damaging effects. In this study, we proposed a drought analysis method using SPI in Gyeongsangnamdo, where drought damages frequently occurred in South Korea.
SPI by duration was analyzed for 13 rainfall stations located inside and outside Gyeongsangnamdo. The representative SPI of Gyeongsangnamdo was estimated by applying the SPI of each station by duration based on the Thiessen method and cluster analysis. For the Thiessen method, the SPI by duration was estimated by applying the area weight of the Thiessen polygon for each rainfall station, resulting in the range −3.09 to 2.76. For cluster analysis, clusters were divided into three clusters using the k-means method, and the minimum value was calculated as the SPI by duration. SPI by duration based on cluster analysis ranged from −3.30 to 1.82.
The minimum value per year was calculated as the representative SPI to compare the SPI of the past damage data of Gyeongsangnamdo by duration using the Thiessen method and cluster analysis. Moreover, appropriateness was compared based on the years the drought damage occurred, since the past drought damage data only present the damage status per year without accurate drought start points. The SPI by duration for the years with drought damage was set to -2.00, which is the criterion for extremely dry conditions, and the accuracy of each analysis method was analyzed using the MAD, MSE, and RMSE.
The appropriateness of SPI by duration for the past drought damage was found to be higher than 0.5, which is lower than 1.0, for the Thiessen method. Meanwhile, for cluster analysis, it was higher than 0.3 and lower than 0.8, indicating that cluster analysis exhibited higher accuracy. Therefore, it is possible to predict drought damage more accurately if cluster analysis is utilized during the analysis of the drought index for rainfall stations in administrative districts.
Author Contributions
Conceptualization, Y.S. and M.P.; methodology, Y.S. and M.P.; validation, Y.S.; formal analysis: Y.S.; resources, Y.S.; data curation, Y.S. and M.P.; writing—original draft preparation, Y.S.; writing—review and editing, M.P.; visualization, Y.S.; supervision, Y.S. and M.P.; project administration, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the Fundamental Technology Development Program for Extreme Disaster Response] grant number [2019-MOIS31-010] And The APC was funded by [MOIS].
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to [national policy research result].
Acknowledgments
This study was supported by the Fundamental Technology Development Program for Extreme Disaster Response (Grant No. 2019-MOIS31-010) funded by the Korean Ministry of Interior and Safety (MOIS).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rossi, G.; Benedini, M.; Tsakiris, G.; Giakoumakis, S. On regional drought estimation and analysis. Water Resour. Manag. 1992, 6, 249–277. [Google Scholar] [CrossRef]
- Obasi, G.O.P. Wmo’s role in the international decade for natural disaster reduction. Bull. Am. Meteorol. Soc. 1994, 75, 1655–1661. [Google Scholar] [CrossRef] [Green Version]
- Mpelasoka, F.; Hennessy, K.; Jones, R.; Bates, B. Comparison of suitable drought indices for climate change impacts assessment over australia towards resource management. Int. J. Climatol. 2008, 28, 1283–1292. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9, 3–11. [Google Scholar]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Byun, H.-R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The lincoln declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef] [Green Version]
- Livada, I.; Assimakopoulos, V. Spatial and temporal analysis of drought in Greece using the standardized precipitation index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Smakhtin, V.; Hughes, D. Automated estimation and analyses of meteorological drought characteristics from monthly rainfall data. Environ. Model Softw. 2007, 22, 880–890. [Google Scholar] [CrossRef]
- Naresh Kumar, M.; Murthy, C.; Sesha Sai, M.; Roy, P. On the use of standardized precipitation index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Kisi, O.; Gorgij, A.; Zounemat-Kermani, M.; Mahdavi-Meymand, A.; Kim, S. Drought forecasting using novel heuristic methods in a semi-arid environment. J. Hydrol. 2019, 578, 124053. [Google Scholar] [CrossRef]
- Agnew, C.T.; Chappell, A. Drought in the Sahel. GeoJournal 1999, 48, 299–311. [Google Scholar] [CrossRef]
- Cheo, A.E.; Voigt, H.J.; Mbua, R.L. Vulnerability of water resources in northern Cameroon in the context of climate change. Environ. Earth Sci. 2013, 70, 1211–1217. [Google Scholar] [CrossRef]
- Dhakar, R.; Sehgal, V.K.; Pradhan, S. Study on inter-seasonal and intra-seasonal relationships of meteorological and agricultural drought indices in the Rajasthan State of India. J. Arid. Environ. 2013, 97, 108–119. [Google Scholar] [CrossRef]
- Dutra, E.; Di Giuseppe, F.; Wetterhall, F.; Pappenberger, F. Seasonal forecasts of droughts in African basins using the Standardized Precipitation Index. Hydrol. Earth Syst. Sci. 2013, 17, 2359–2373. [Google Scholar] [CrossRef] [Green Version]
- Edossa, D.C.; Babel, M.S.; Gupta, A.D. Drought analysis in the Awash River basin, Ethiopia. Water Resour. Manag. 2010, 24, 1440–1460. [Google Scholar] [CrossRef]
- Feng, J.; Yan, D.H.; Li, C.Z. Evolutionary trends of drought under climate change in the Heihe River basin, Northwest China. J. Food Agric. Environ. 2013, 11, 1025–1031. [Google Scholar]
- Ford, T.; Labosier, C.F. Spatial patterns of drought persistence in the Southeastern United States. Int. J. Climatol. 2014, 34, 2229–2240. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Evaluation of trends and multivariate frequency analysis of droughts in three meteorological subdivisions of western India. Int. J. Climatol. 2014, 34, 911–928. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.D.; Wihite, D.A.; Vanyarhko, O.V. Monitoring the 1996 drought using the standardized precipitation index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef] [Green Version]
- Karavitis, C.A.; Chortaria, C.; Alexandris, S.; Vasilakou, C.G.; Tsesmelis, D.E. Development of the standardised precipitation index for Greece. Urban Water J. 2012, 9, 401–417. [Google Scholar] [CrossRef]
- Khan, S.; Gabriel, H.F.; Rana, T. Standard precipitation index to track drought and assess impact of rainfall on watertables in irrigation areas. Irrig. Drain. Syst. 2008, 22, 159–177. [Google Scholar] [CrossRef]
- Liu, X.C.; Xu, Z.X.; Yu, R.H. Spatiotemporal variability of drought and the potential climatological driving factors in the Liao River basin. Hydrol. Process. 2012, 26, 1–14. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Guhathakurta, P.; Hatwar, H.R. District-wide drought climatology of the southwest monsoon season over India based on standardized precipitation index (SPI). Nat. Hazards 2011, 59, 1797–1813. [Google Scholar] [CrossRef]
- Seiler, R.; Hayes, M.; Bressan, L. Using the standardized precipitation index for flood risk monitoring. Int. J. Climatol. 2002, 22, 1365–1376. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef] [Green Version]
- Tabari, H.; Abghari, H.; Talaee, P.H. Temporal trends and spatial characteristics of drought and rainfall in arid and semiarid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Towards a drought watch system based on spatial SPI. Water Resour. Manag. 2004, 18, 1–12. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A.; Liberis, N. A water balanced derived drought index for Pinios River Basin, Greece. Water Resour. Manag. 2010, 25, 1087–1101. [Google Scholar] [CrossRef]
- Vincente-Serrano, S.M.; Gonzalez-Hidalgo, J.C.; Luis, M.; Raventos, J. Drought pattern in the Mediterranean area: The Valencia region (eastern Spain). Clim. Res. 2004, 26, 5–15. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Ringler, C.; Zhu, T.J.; Waqas, A. Droughts in Pakistan: A spatiotemporal variability analysis using the Standardized Precipitation Index. Water Int. 2013, 38, 620–631. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.F.; Singh, V.P.; Bai, Y.G. SPI-based evaluation of drought events in Xinjiang, China. Nat. Hazards 2012, 64, 481–492. [Google Scholar] [CrossRef]
- Zin, W.Z.W.; Jemain, A.A.; Ibrahim, K. Analysis of drought condition and risk in Peninsular Malaysia using Standardised Precipitation Index. Theor. Appl. Climatol. 2013, 111, 559–568. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Zhang, Z.X. Observed changes of drought/wetness episodes in the Pearl River basin, China, using the standardized precipitation index and aridity index. Theor. Appl. Climatol. 2009, 98, 89–99. [Google Scholar] [CrossRef]
- Du, J.; Fang, J.; Xu, W.; Shi, P.J. Analysis of dry/wet conditions using the standardized precipitation index and its potential usefulness for drought/flood monitoring in Hunan Province, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 377–387. [Google Scholar] [CrossRef]
- Fischer, T.; Gemmer, M.; Su, B.; Scholten, T. Hydrological long-term dry and wet periods in the Xijiang River basin, South China. Hydrol. Earth Syst. Sci. 2013, 17, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Sun, S.L.; Xue, Y.; Li, J.J.; Zhang, J.C. Spatial and Temporal Variability of Precipitation and Dryness/Wetness during 1961–2008 in Sichuan province, West China. Water Resour. Manag. 2014, 28, 1655–1670. [Google Scholar] [CrossRef]
- Raziei, T.; Bordi, I.; Pereira, L.S.; Corte-Real, J.; Santos, J.A. Relationship between daily atmospheric circulation types and winter dry/wet spells in western Iran. Int. J. Climatol. 2012, 32, 1056–1068. [Google Scholar] [CrossRef] [Green Version]
- Tosic, I.; Unkasevic, M. Analysis of wet and dry periods in Serbia. Int. J. Climatol. 2014, 34, 1357–1368. [Google Scholar] [CrossRef]
- Li, B.; Su, H.B.; Chen, F.; Li, S.G.; Tian, J.; Qin, Y.C.; Zhang, R.H.; Chen, S.H.; Yang, Y.M.; Rong, Y. The changing pattern of droughts in the Lancang River Basin during 1960–2005. Theor. Appl. Climatol. 2013, 111, 401–415. [Google Scholar] [CrossRef]
- Zhao, G.J.; Mu, X.M.; Hormann, G.; Fohrer, N.; Xiong, M.; Su, B.D.; Li, X.C. Spatial patterns and temporal variability of dryness/wetness in the Yangtze River Basin, China. Quat. Int. 2012, 282, 5–13. [Google Scholar] [CrossRef]
- Bokal, S. Standardized Precipitation Index Tool for Drought Monitoring—Examples from Slovenia, Drought Management Centre for South-Eastern Europe; DMCSEE: Ljubljana, Slovenia, 2017. [Google Scholar]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of drought in Portugal. Water Resour. Res. 2010, 46, W03503. [Google Scholar] [CrossRef] [Green Version]
- Moreira, E.E.; Martins, D.S.; Pereira, L.S. Assessing drought cycles in SPI time series using a Fourier analysis. NHESS 2015, 15, 571–585. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- val Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Barker, L.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardized indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef] [Green Version]
- Mavromatis, T. Drought index evaluation for assessing future wheat production in Greece. Int. J. Climatol. 2007, 27, 911–924. [Google Scholar] [CrossRef]
- Kempes, C.; Myers, O.; Breshears, D.; Ebersole, J. Comparing response of Pinus edulis tree-ring growth to five alternate moisture indices using historic meteorological data. J. Arid Environ. 2008, 72, 350–357. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J.; Angulo, M.; El Kenawy, A. A new global 0.5 gridded dataset (1901–2006) of a multiscalar drought index: Comparison with current drought index datasets based on the Palmer Drought Severity Index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef] [Green Version]
- Taylor, C.; de Jeu, R.; Guichard, F.; Harris, P.; Dorigo, W. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [Green Version]
- Teuling, A.; Van Loon, A.; Seneviratne, S.; Lehner, I.; Aubinet, M.; Heinesch, B.; Spank, U. Evapotranspiration amplifies European summer drought. Geophys. Res. Lett. 2013, 40, 2071–2075. [Google Scholar] [CrossRef]
- Zhang, B.; He, C. A modified water demand estimation method for drought identification over arid and semiarid regions. Agric. For. Meteorol. 2016, 230, 58–66. [Google Scholar] [CrossRef]
- Asrari, E.; Masoudi, M. A new methodology for drought vulnerability assessment using SPI (standardized precipitation index). Int. J. Sci. Knowl. 2014, 2, 425–432. [Google Scholar] [CrossRef]
- Masoudi, M.; Hakimi, S. A new model for vulnerability assessment of drought in Iran using percent of normal precipitation index (PNPI). Iran. J. Sci. Technol. Sci. 2014, 38, 435–440. [Google Scholar]
- Zarei, A.; Masoudi, M.; Mahmodi, A.R. Analyzing spatial pattern of drought changes in Iran, using standardized precipitation index (SPI). Ecol. Environ. Conserv. 2014, 20, 427–432. [Google Scholar]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based joint drought index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef]
- Rhee, J.; Carbone, G.J.; Hussey, J. Drought index mapping at different spatial units. J. Hydrometeorol. 2008, 9, 1523–1534. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE groundwater drought index: Evaluation of California Central Valley groundwater drought. Remote. Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Zhang, H.; Song, J.; Wang, G.; Wu, X.; Li, J. Spatiotemporal characteristic and forecast of drought in northern Xinjiang, China. Ecol. Indic. 2021, 127, 107712. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y. SPI based meteorological drought assessment over a humid basin: Effects of processing schemes. Water 2016, 8, 373. [Google Scholar] [CrossRef] [Green Version]
- Zhai, J.; Su, B.; Krysanova, V.; Vetter, T.; Gao, C.; Jiang, T. Spatial variation and trends in PDSI and SPI indices and their relation to streamflow in 10 large regions of China. J. Clim. 2010, 23, 649–663. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, Y. Spatio-temporal variation of hydrological drought under climate change during the period 1960–2013 in the Hexi Corridor, China. J. Arid Land 2016, 8, 157–171. [Google Scholar] [CrossRef] [Green Version]
- Dash, B.K.; Rafiuddin, M.; Khanam, F.; Islam, M.N. Characteristics of meteorological drought in Bangladesh. Nat. Hazards 2012, 64, 1461–1474. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P.; Desai, V.R. Drought characterization: A probabilistic approach. Stoch. Environ. Res. Risk Assess. 2007, 23, S11–S19. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in spatial patterns of drought on different time scales: An analysis of the Iberian Peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
- Shamshirband, S.; Gocić, M.; Petković, D.; Javidnia, H.; Ab Hamid, S.H.; Mansor, Z.; Qasem, S.N. Clustering project management for drought regions determination: A case study in Serbia. Agric. For. Meteorol. 2015, 200, 57–65. [Google Scholar] [CrossRef]
- McKee, T.B. Drought Monitoring with Multiple Time Scales. In Proceedings of the 9th Conference on Applied Climatology, Boston, MA, USA, 15–20 January 1995. [Google Scholar]
- Rebay, S. Efficient Unstructured mesh generation by mean of Delaunay triangulation and Bowyer-Watson algorithm. J. Comput. Phys. 1993, 106, 125–138. [Google Scholar] [CrossRef]
- Pedrini, H. An Adaptive Method for Terrain Surface Approximation Based on Triangular Meshes. Ph.D. Thesis, Rensselaer Institute Troy, New York, NY, USA, 2000. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observation, in 5th Berkeley Symposium on Mathematical Statistics and Probability; Statistical Laboratory University: California, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Trenberth, K.; Overpeck, J.; Solomon, S. Exploring drought and its implications for the future. EOS Trans. Am. Geophys. Union 2007, 85, 27. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).