Next Article in Journal
On the Problem of Critical Electric Field of Atmospheric Air
Next Article in Special Issue
Investigation of Air-Sea Turbulent Momentum Flux over the Aegean Sea with a Wind-Wave Coupling Model
Previous Article in Journal
Predicting the Nonlinear Response of PM2.5 and Ozone to Precursor Emission Changes with a Response Surface Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 12
Issue 8
10.3390/atmos12081045
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Representation of the Southern Annular Mode Signal in the Brazilian Earth System Model

by
Luciana F. Prado
1,*,
Ilana Wainer
1 and
Ronald B. de Souza
2
1
Instituto Oceanográfico, Universidade de São Paulo, Praça do Oceanográfico, 191, Cidade Universitária, São Paulo 05508-120, Brazil
2
Divisão de Modelagem Numérica do Sistema Terrestre, Centro de Previsão de Tempo e Estudos Climáticos, Instituto Nacional de Pesquisas Espaciais (CPTEC-INPE), Rodovia Presidente Dutra km 40, Cachoeira Paulista, São Paulo 12630-000, Brazil
*
Author to whom correspondence should be addressed.
Atmosphere 2021, 12(8), 1045; https://doi.org/10.3390/atmos12081045
Submission received: 27 June 2021 / Revised: 9 August 2021 / Accepted: 11 August 2021 / Published: 14 August 2021
(This article belongs to the Special Issue Atmosphere-Ocean Interactions)
Browse Figures
Versions Notes

Abstract

:
The Southern Annular Mode (SAM, also known as the Antarctic Oscillation—AAO) explains most of the climate variability in the Southern Hemisphere. A ring pattern in mean sea level pressure (MSLP) or 500 hPa geopotential height around Antarctica characterizes SAM. Differences of MSLP values between SH mid and high latitudes define positive and negative SAM phases with impacts on mean atmospheric circulation. Thus, investigating how different models represent SAM is of paramount importance, as it can improve their ability to describe or even predict most of the SH climate variability. Here we examine how the Brazilian Earth System Model (BESM) represents SAM’s signal compared with observations, reanalysis, and other climate models contributing to the Coupled Modeling Intercomparison Project version 5 (CMIP5). We also evaluate how SAM relates to the South American surface temperature and precipitation and discuss the models’ limitations and biases compared with reanalysis data.

1. Introduction

The Southern Annular Mode (SAM) pattern dominates Southern Hemisphere (SH) extratropical climate variability [1,2,3]. SAM is defined by a regular atmospheric pressure pattern in the 500 hPa geopotential height or in mean sea level pressure (MSLP) anomalies. A “ring-shape” spatial structure of successive and opposite signs between high and midlatitudes reflects SAM variability. The SAM signal corresponds to 22–34% of the SH atmospheric circulation variance [4,5] and 10% of global atmospheric mass transport variance [6]. SAM presents both positive and negative phases, depending on the difference of MSLP anomalies’ sign between high and midlatitudes. Positive SAM corresponds to negative MSLP anomalies above 60 °S and positive MSLP anomalies below 60 °S and is associated with stronger circumpolar westerlies, increased cyclone activity, and stronger zonal winds [7,8]. Negative SAM corresponds to the opposite pattern, with positive MSLP anomalies above 60 °S and negative MSLP anomalies in midlatitudes.
SAM induces seasonal precipitation and monthly temperature anomalies in the Southern Hemisphere [3,5] and influences the preferable tracks of cyclones by modifying their latitudinal occurrence density [8,9]. As SAM results in changes in the SH meridional atmospheric pressure gradient, it can change the location and intensity of the SH polar jet [10]. The polar jet changes with the SAM phase and intensity. These changes are related to the eddy momentum flux convergence, and to the mean atmospheric circulation strength (Ferrel and Hadley cells) [5]. The association between SAM and the SH polar jet indicates the connections between SAM and the tropical variability [11].
In South America, part of southeastern and central-west Brazil is among the most affected regions by SAM, with responses varying at the monthly scale. A weakening of the South Atlantic Convergence Zone (SACZ) from November to March is expected during negative SAM episodes [12]. Positive (negative) SAM enhances (weakens) frontogenesis in South America and South Atlantic, with positive (negative) precipitation anomalies over southeast South America [13].
A polar vortex that extends throughout the troposphere associates with SAM [7], being strongly influenced by ozone concentration [14] and the El Niño—Southern Oscillation (ENSO) [15]. Changes in SAM since the 1970s are associated with a cooling of the Antarctic lower stratosphere caused by ozone loss at that atmospheric level [16]. These changes include a positive trend in SAM observed along the past decades, a strengthening of the circumpolar vortex, and an intensification of the westerlies around Antarctica [17]. Paleoclimate studies report changes in SAM along the past centuries, with a positive SAM trend since 1600 AD, around 1850, and in the early and late 1900s [18].
SAM time series is obtained through Marshall’s observational index [17], which uses MSLP anomalies to compute MSLP differences between high and midlatitudes from surface observations. Alternatively, time series can be obtained through Gong and Wang’s index [4]. This index consists of the difference between MSLP at the 45 °S and 60 °S latitudinal belts. Thus, we used these two indexes to evaluate how different datasets represent the SAM signal or pattern. In this sense, the historical period (1850–2005) is ideal for model performance evaluation compared with the present climate and observed climate change, promoting the assessment of human impacts on climate, and contributing to improving future scenario experiments [19].
In this paper, we evaluate how the Brazilian Earth System Model version OA2.5 (BESM-OA2.5) represents SAM and its main effects on precipitation, and surface temperature, in eastern South America. BESM is the Brazilian contribution to the Coupled Model Intercomparison Project—CMIP [20,21]. Previous studies examined BESM-OA2.5 performance, where results in assessing polar climate response to global warming were comparable to other CMIP models [22,23,24]. For example, Casagrande et al. [23] examined BESM simulations under the Abrupt-4xCO2 scenario reporting a systematical polar amplification in both poles and all climate models’ results, including BESM-OA2.5′s, despite the asymmetry in warming between the Arctic and Antarctic.
Here we compare BESM results for SAM to observations, reanalysis, and the ensemble mean of CMIP5 models. We characterize SAM using MSLP anomalies to compare Gong and Wang’s [4] with Marshall’s [17] observational SAM indices and discuss how the different datasets represent SAM and its impacts on precipitation and surface temperature.

2. Materials and Methods

2.1. Brazilian Earth System Model (BESM)

BESM’s main characteristics are described in [20,21]. The model has been set up and run at the Weather Forecast and Climate Studies (CPTEC) of the Brazilian National Institute for Space Research (INPE) in Cachoeira Paulista, São Paulo State, Brazil, and consists of a land-ocean-atmosphere coupled model. The BESM version used in this study (BESM-OA2.5) uses the FMS coupler from the Geophysical Fluid Dynamics Laboratory (GFDL) of the National Oceanic and Atmospheric Administration (NOAA). The atmospheric component is the Brazilian Global Atmosphere Model (BAM) [25] with a horizontal resolution of ~1.875°, 28 levels in the vertical, and upper boundary at 2.73 hPa. The Modular Ocean Model version 4p1 (MOM4p1) [26] is the oceanic component of BESM, with a zonal resolution of 1°, meridional resolution from 0.25° to 2°, and 50 vertical levels. MOM4p1 includes the Sea Ice Simulator (SIS), a built-in ice model [27].
The CMIP5 Historical experiment was performed with the BESM-OA2.5 following Taylor et al. [28] protocols, and it is described by Veiga et al. [29]. The model was forced by the historical atmospheric equivalent CO2 concentration from January/1850 to December/2005. We used monthly mean sea level pressure (MSLP) to reconstruct the SAM index and correlate it to precipitation and air temperature. Outputs were regridded to 2° × 2° resolution to facilitate the comparison among the datasets. We applied a bilinear interpolation available in the Climate Data Operators (CDO) [30].

2.2. CMIP5 Models Outputs

Monthly MSLP, precipitation, and temperature outputs of the Historical Experiment [28] from eight CMIP5 models (Table 1) were compared with BESM outputs. The Historical Experiment consists of simulations of the recent past (1850–2005) forced by changing conditions consistent with observations. These changes may include atmospheric composition, solar forcing, emissions and concentration of aerosols, and land use and may vary among models [19]. All model outputs were regridded (2° × 2°) to compute the ensemble results.

2.3. Observations and Reanalysis

To evaluate the models’ performance, we used monthly precipitation and surface temperature from the Global Precipitation Climatology Project (GPCP) v2.3 combined dataset [38]. This observational dataset integrates satellite, soundings, and gauge data, resulting in precipitation estimates over land and ocean. The different datasets composing the GPCP were merged in a 2.5° × 2.5° resolution grid, dating from January/1979 to the present.
Surface temperature products combine air temperature over land and sea surface temperature over the ocean. We used two datasets derived from observations, both consisting of surface temperature anomalies. The GISS Surface Temperature Analysis v4 (GISTEMP v4) [39] uses the timeframe 1951–1980 as the reference period and combines Global Historical Climatology Network v4 (GHCN) air temperature over land with Extended Reconstructed SST v5 (ERSST), on a 2° × 2° grid. In this study, we used the GISTEMP v4 1200 km smoothed version provided by the National Aeronautics and Space Administration (NASA).
We also used the Met Office Hadley Centre/Climatic Research Unit v5 dataset (HadCRUT5) [40] that consists of surface temperature anomalies concerning the 1961–1990 base period. HadCRUT5 combines air temperature from land stations with SST from ships and buoys on a 5° × 5° grid, available from 1850 to 2018.
Models’ results were also compared with reanalysis, using the National Oceanic and Atmospheric Administration 20th Century Reanalysis version 2 (NOAA-20Cv2) [41] and version 3 and (NOAA-20Cv3) [42]. Some differences between the two NOAA-20C versions include upgraded data assimilation methods, datasets, parameterization, an ensemble-based estimate of confidence, among others. Our study period is from January/1871 to December/2005 because the NOAA-20Cv2 dataset is available from 1871.

2.4. SAM Indices

Here we used two SAM indices. The Gong and Wang index [4], referred to as GW99 hereafter, was applied to the models and reanalysis outputs. The Marshall index [17], on the other hand, uses MSLP observations from surface stations.
The GW99 SAM index is defined as the difference of MSLP normalized monthly anomalies between 40 °S ( P 40 ° S * ) and 65 °S ( P 65 ° S * ) latitudinal belts:
SAM = P 40 ° S * − P 60 ° S *
The SAM Marshall index [17] is based on the GW99 definition but uses MSLP values recorded in six surface stations near the latitudes of 40 °S and 65 °S. Monthly values from January/1957 to the present are available on Marshall’s website (https://legacy.bas.ac.uk/met/gjma/sam.html, accessed on 11 August 2021). Anomalies were normalized using the standard deviation.
We applied a 10-yr moving average to SAM indices to facilitate the examination of long-term changes. We compared the smoothed SAM indices with the standard deviation of the CMIP5 ensemble mean to evaluate the spread of the models.
We employed the Pearson correlation to verify the relationship of the MSLP spatial pattern with the reconstructed SAM indices and to examine the relation between SAM, the seasonal precipitation, and the monthly temperature anomalies fields in South America. A T-test was applied to identify the 5% significance level. A 10-yr moving average was applied to seasonal indices to evaluate their evolution along the 20th and 21st centuries.
Composite analysis was performed to investigate the spatial structure of the precipitation and temperature anomalies associated with the SAM phases. Precipitation and temperature anomalies were composited considering the SAM standardized index monthly values higher (lower) than 2 (-2) for the positive (negative) phase. For seasonal composites (see Supplementary Materials), we applied the threshold of |1| as seasonal time series are shorter than monthly ones. This analysis considers the time interval from January/1979 to December/2005 so that model-derived data can be compared with observations. Comparison among the composites was qualitative.

3. Results

For the analysis of the atmospheric pressure and SAM climatological fields, the time interval from January/1957 to December/2005 was adopted as the reference period due to its correspondence to the available Marshall index time interval. To all datasets, we averaged the MSLP annual cycle over 40 °S and 65 °S that are the SAM GW99 index latitudes (Figure 1). In the 40 °S latitude belt (Figure 1a), the MSLP presents values higher than 1013 hPa when compared with the 65 °S latitude belt (Figure 1b). At the 40 °S belt (Figure 1a), all datasets present a similar annual pattern, with the major MSLP peak occurring in March-April. However, reanalysis (green and purple triangles) and models (BESM, black squares; CMIP5 ensemble mean, blue diamonds) present a 1–2 months delay in respect to observations for the second MSLP peak. MSLP minima higher than observations occurred during austral summer and winter (Marshall index, red circles), except for the CMIP5 Ensemble mean (blue diamonds).
At the 65 °S belt (Figure 1b), the reanalysis MSLP monthly means (purple and green triangles) are closer to the observational annual pace (Marshall index, red circles) than to model-derived results (BESM, black squares; CMIP5 ensemble mean, blue diamonds). The major MSLP peak occurs during the austral summer (December-January), while minima occur during austral spring and autumn. However, models disagree with observations and reanalysis in the second maxima, with a 2-months delay and a sub-estimation of MSLP values. This bias in BESM-OA2.5 response is probably related to radiative processes that warm anomalously the ocean mixing layer, mainly during summer. The stored heat in the upper ocean warms the atmosphere for two months more after the end of summer and induces a delay on MSLP peaks [20,21,29]. BESM model (black squares) outputs present the largest differences in MSLP when compared with observations (> 5 hPa).
Seasonal reconstructions of the GW99 SAM index time series were filtered using a 10-yr moving average to examine its decadal behavior (Figure 2). We compare the indices to the CMIP5 ensemble mean spread (2 standard deviations, light blue shaded area). The two reanalysis reconstructions (purple and green lines) tend to agree in more recent times and show a difference to the Marshall index (red lines) during all seasons (Figure 2a–d). CMIP5 ensemble-derived index (blue lines) is smoothed in amplitude compared with other reconstructions because of the members averaging. However, it follows the general trend of the Marshall index in the more recent decades. The BESM index (black lines) shows amplitude variations comparable to reanalysis but mostly distinct in phase. Differences present between indices are expected because, as pointed out before in this text, Marshall’s index uses surface stations observations while the GW99 index uses MSLP latitudinal anomalies from gridded datasets. We computed the absolute error between Marshall’s index and the other reconstructions (Figure S1) and obtained mostly positive values in all seasons for all the reconstructions. BESM presented a negative absolute error during the 1990s, except for austral winter (JJA, Figure S1c). CMIP5 ensemble mean and BESM also presented negative values in the 1970s for JJA (Figure S1c) and in the 1960s for SON (Figure S1d).
Previous studies found the highest positive trend during austral winter in the NCAR reanalysis, and during austral summer for Marshall’s index [7]. A positive trend starting in the 1970s is observed in the Marshall index time series (red lines) in austral summer (Figure 2a) and autumn (Figure 2b). BESM index (black line) is the only one that does not follow the DJF trend (Figure 2a), although it follows the MAM reconstructions (Figure 2b). During JJA (Figure 2c), the positive trend is not clear in observations (red line), CMIP5 models (blue line), and BESM (black line), but very noticeable in reanalysis data (green and purple lines). Reanalysis data (green and purple lines) and CMIP5 models outputs (blue line) also show a positive trend during austral spring (SON). BESM (black line) outputs agree with Marshall’s index (red line) with no trend in SON (Figure 2d).
Other previous studies associate the recent SAM positive trend with changes in the stratosphere and the circumpolar westerlies, as changes in the atmosphere’s vertical shear influences SAM [43]. The circumpolar vortex enhances with increased vertical shear in the zonal wind because of a stratospheric meridional temperature gradient intensification, a reduction in stratospheric ozone concentration, and an increase in other greenhouse gas concentrations [44]. However, the positive SAM trend started ten years before the known ozone loss described for the SH stratosphere, suggesting that the observed trend may be related to a non-linear interaction between natural and anthropogenic forcings [45]. Previous studies report the persistence and enhancement of SAM positive phase with BESM-OA2.5 outputs for CMIP5 future scenarios [22] and associated with thermal expansion of the oceans in the upper 700 m of up to 0.23 m until 2100 [46]. In quadrupling atmospheric CO2 scenarios, seasonality in the polar amplification occurs in both north and south poles, with a decrease in sea-ice near the Antarctic Peninsula in BESM-OA2.5 and other CMIP5 models’ results [23].
To reconstruct the spatial pattern of SAM, we correlated the GW99 SAM index for each dataset with the seasonal MSLP anomalies from 20 °S to 90 °S, from January/1871 to December/2005 (Figure 3). All results show an annular pattern, with a negative correlation above 60 °S, and a positive correlation below 40 °S. Spatial variations occur among seasons, where wavenumber 3 or 4 patterns become somehow evident, mainly for the reanalysis results (Figure 3, first and second columns). For CMIP5 models and BESM, however, the SAM wave patterns are not clear (Figure 3, third and fourth columns). For all datasets, the correlation is weaker during austral autumn (MAM, Figure 3e–h) and winter (JJA, Figure 3i–l) and stronger during austral summer (DJF, Figure 3a–d) and spring (SON, Figure 3m–p). BESM outputs (Figure 3, fourth column) present the highest correlation values among all datasets.
CMIP5 models present an improvement in simulating SAM structure over CMIP3, but half of the models comprising the CMIP5 experiment fail in representing recent SAM decadal phases [3]. Previous studies report a seasonal correlation between SAM and surface weather. Hendon et al. [47], e.g., show a correlation during austral winter and austral summer, probably related to changes in teleconnection between polar and subtropical circulation features. Nonetheless, SAM amplifies with height during late spring due to planetary wave-mean flow interaction favored by the zonal flow [2]. These changes in circulation could facilitate the correlation between SAM and weather conditions during other seasons than austral winter.
SAM was previously evaluated using BESM-OA2.5 outputs [29]. The authors applied EOF analysis to the monthly mean 500 hPa geopotential height field from 20 °S to 90 °S over 1950–2005 and compared their results with NOAA-20Cv2 reanalysis. They reported differences in the amplitude of the signal but not in its spatial pattern. In this study, the explained variance was also higher for BESM-OA2.5 (34.1%) than for reanalysis (21%) [29], but the values were within the variance range reported in other studies [5].

4. Discussion and Conclusions

Previous statistical studies report that SAM climate impacts the SH in latitudes ranging from Antarctica and the Southern Ocean [48] to midlatitudes [49], with effects in precipitation, surface air temperature, and sea level pressure [5]. Here we investigate how the BESM and other CMIP5 climate models reproduce the relationship between SAM, precipitation, and air temperature, comparing our results with others previously reported.

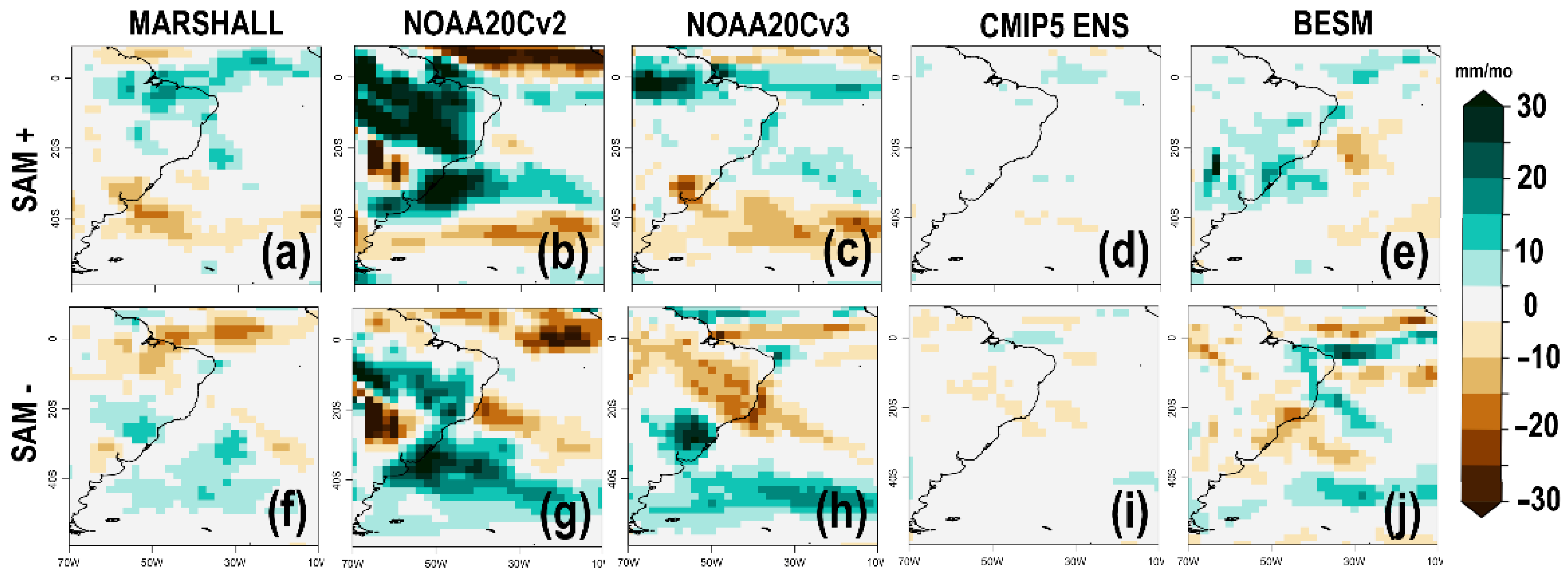
4.1. Precipitation

In South America, SAM impacts the precipitation through changes in the frontogenesis properties [13] and in the South Atlantic Convergence Zone (SACZ) variability [12]. The SACZ, for instance, occurs mainly in southeastern South America and may be related to SAM phases and other modes of climate variability such as El Niño-Southern Oscillation [50,51]. During the austral wet season (November to March), a weakening of the SACZ is associated with a negative SAM signal [12]. Sea level pressure, precipitation, and air temperature in SH are influenced by changes in cyclones’ density and SAM phase [9] and by differences in frontogenesis during the positive and negative phases of SAM [13].
In our results, observations and reanalysis data show a positive correlation between SAM and seasonal precipitation in the Amazon during austral autumn (MAM) and spring (SON) that are not reproduced by BESM-OA2.5 (Figure 4, second and fourth lines). BESM-OA2.5 presented a bias in the Amazon region reported by [29]. Their results point out a convergence bias during MAM over the Amazon, an underestimation of the precipitation in the subtropics, and an overestimation at midlatitudes, when compared with the GPCP dataset. In northeastern and southern Brazil, however, BESM-OA2.5 seems to reproduce the precipitation pattern associated with SAM, with negative and positive anomalies, respectively, during DJF (Figure 4, first line, fifth column) and JJA (Figure 4, third line, fifth column). An opposite pattern occurs during SON (Figure 4, fourth line, fifth column).
The negative correlation between SAM and precipitation anomalies during SON in southeastern South America is consistent with the findings of Silvestri and Vera [52]. BESM-OA2.5 also presents difficulties in representing cloudiness, mainly in the high latitudes of the Southern Hemisphere [29]. CMIP5 models (Figure 4, fourth column) reproduce the SAM and precipitation relationship in all seasons except the austral winter (JJA, fourth line). Spatial patterns obtained with the reanalysis datasets (Figure 4, second and third columns) agree with observations (Figure 4, first column), but overestimate the magnitude of the correlation, especially in the Amazon region, and in midlatitudes (~50 °S).
To examine the relationship between SAM phases and precipitation, we performed a composite analysis. The observations indicate that during the positive phase of SAM, positive precipitation anomalies occur in northeastern Brazil and the equatorial and tropical southwestern Atlantic. Negative anomalies occur in southern Brazil and Uruguay and the mid-latitudes of the South Atlantic Ocean (Figure 5a). NOAA-20Cv3 reanalysis can reproduce this pattern (Figure 5c). NOAA-20Cv2 agrees in sign, although overestimated in magnitude (Figure 5b). CMIP5 ensemble mean agrees in sign but underestimates the magnitude of the precipitation signal (Figure 5d). BESM-OA2.5 composite is consistent with the precipitation observations, mainly over the ocean, but presents opposite signs over the continent (Figure 5e).
The negative phase of SAM presents an opposite precipitation response compared with the positive phase: negative precipitation anomalies occur in northeastern Brazil and the equatorial and tropical Atlantic Ocean; positive anomalies are present in southern Brazil and the southwestern South Atlantic Ocean (Figure 5f). NOAA-20Cv3 reanalysis can reproduce this pattern (Figure 5h), but the earlier version of the dataset (NOAA-20Cv2) presents similarities with the precipitation patterns only over the ocean (Figure 5g). CMIP5 ensemble mean composite agrees in sign but underestimates the magnitude of the precipitation fields (Figure 5i). BESM-OA2.5 results are comparable to the precipitation observations over the ocean, but the relation is not clear over the continent (Figure 5j).
Seasonal composites (Figures S2–S5) show a similar representation of SAM positive and negative phases in terms of precipitation. NOAA-20Cv2 overestimates precipitation anomalies in all seasons and the sign of anomalies for positive SAM changes. NOAA-20Cv3 agrees in sign with observations for precipitation anomalies, mainly for negative SAM. CMIP5 ensemble mean underestimate precipitation anomalies in all seasons. BESM agrees with observational reconstruction mainly for austral summer (Figure S2) and spring (Figure S5).
Previous studies investigated the relationship between SAM phases and precipitation. During the 1960s-1970s spring, SAM impacted on southeastern South America precipitation as enhanced moisture convergence caused the intensification of an upper-level anticyclonic anomaly in the southwestern subtropical Atlantic Ocean. It resulted in an increase in precipitation associated with a positive SAM [52]. However, this relationship changed during the 1980s–1990s, when the anticyclonic anomaly moved towards southern South America, producing the opposite response of weakened moisture convergence and a decreased precipitation rate. Similar results were found for the latter decades, indicating a modulation of ENSO impacts in the precipitation of southeastern South America by the forcing of SAM [50].
Changes in the subtropical and polar jet associated with the SAM also impact the precipitation anomalies over South America. The positive SAM phase results in a weakening of the subtropical jet in both hemispheres, and a strengthening of the SH polar jet, with opposite responses during the negative phase of SAM [53]. Similar results were found by subsequent studies [10], but with no evidence of change in the subtropical jet position as the polar jet moves polewards during a positive SAM. Indeed, the strengthening and poleward displacement of the polar jet during the positive SAM show zonal wind anomalies that occur on the poleward side of the tropospheric jet, near 60 °S [54]. The opposite pattern occurs during negative SAM phase. SAM phases also affect extratropical cyclogenesis in South America with an impact on the precipitation. Teleconnections between SAM, ENSO and the Indian Ocean Dipole (IOD) modify the mean position of cyclones’ occurrence, ultimately changing the cyclones’ track density [9].

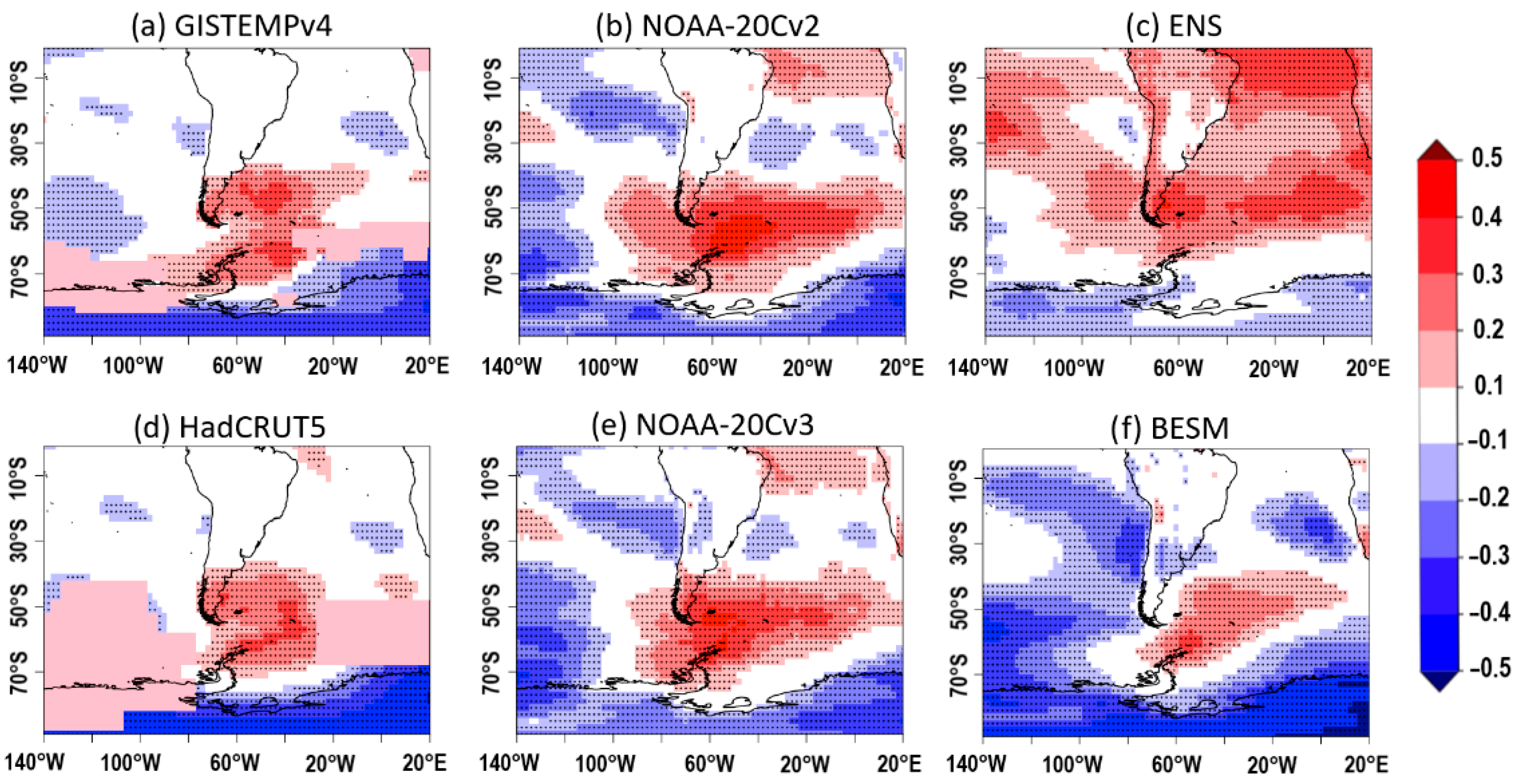
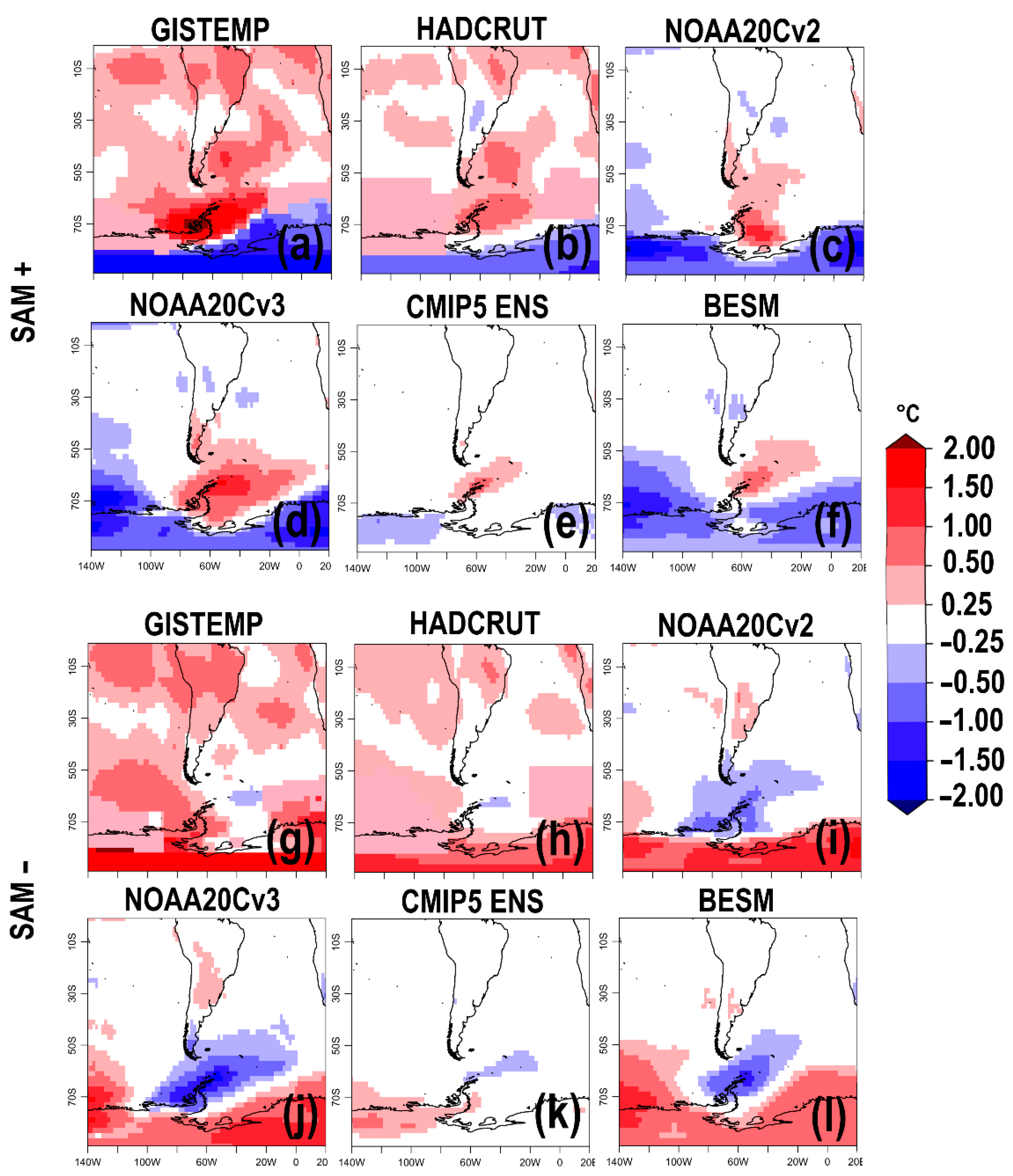
4.2. Surface Temperature

CMIP5 projections using RCP4.5 show a weak negative trend in the SAM time series but a robust positive trend in the RCP8.5 scenario [3]. More recently, Ibebuchi [8] identified a positive trend in SAM under the RCP8.5 simulations and updated ssp585 CMIP6 simulations. Zheng et al. [3] reconstructed the SAM pattern using Empirical Orthogonal Function (EOF) considering the 700 hPa geopotential height south of 20 °S. They found explained variances ranging from 44% to 79% among CMIP5 models and 39% in reanalysis data [3]. Although reproducing the spatial patterns, CMIP5 models diverge in SAM amplitude. Nonetheless, all 12 analyzed models could reproduce the long-term SAM positive trend, as observed in Marshall’s index [3]. A higher spatial resolution did not appear to be a determining factor for a better representation of the SAM pattern. Differences may also reflect the jet stream dynamic behavior in each model [55].
Changes in surface air temperature associated with changes in the SAM patterns are stronger over the eastern Antarctic Peninsula (AP) compared with western AP because of lee side compressional warming during the period dominated by strong westerly (upwind) flows [56]. Surface current circulation and sea surface temperature (SST) patterns observed in the Southern Ocean over Antarctica relate to the SAM positive trend [16].
Air surface temperature anomalies are related to SAM and changes in the MSLP. This relationship is clear in our results for all examined datasets (Figure 6), with negative correlations over Antarctica’s center, and positive correlations over the AP and southern South America. Our results are consistent with the previous studies [57]. The authors suggested that recent changes in SAM resulted in negative surface air temperature anomalies over the entire Antarctic continent, except for the AP region.
BESM-OA2.5 has difficulties in representing the warming trend of the historical period because it does not include aerosol processes if compared with other CMIP5 models [29]. However, in this study BESM-OA2.5 shows a more realistic relationship between SAM and surface air temperature when compared with other CMIP5 models (Figure 6).
Previous studies indicate a good agreement between CMIP5 models and observations when reproducing SAM and surface air temperature during austral winter (JJA) when SAM shows a less annular pattern [58]. However, we only computed monthly correlations (Figure 6) as recent studies report that the most important correlations between SAM and surface air temperature occur on a monthly scale [5].
BESM-OA2.5 also presents a noticeable SST bias in the tropical Atlantic Ocean, concerning the ERSSTv4 dataset [29]. This bias is higher than in other CMIP5 models, being positive in the eastern tropical Atlantic Ocean. However, biases in BESM are within the range reported by other CMIP5 models. Positive biases in the major eastern coastal upwelling regions also occur in BESM, but this is a systematic error common to many state-of-the-art models and is related to underestimated winds in coastal zones [29]. In experiments with quadrupling the atmospheric CO2 concentration, BESM-OA-2.5 presented bias in lapse rate, humidity feedback, and albedo over the ocean near Antarctica, when compared with the CMIP5 multi-model ensemble [24]. Despite the biases, our results indicate that BESM-OA2.5 reproduces the SST seasonal variability, presenting the same correlation sign over the ocean if compared with the observations (Figure 6).
Surface air temperature composites (Figure 7) reveal a more robust response to the SAM positive and negative phases, mainly over Antarctica, the AP, and the southernmost region of South America. During the positive SAM phase, observations indicate a positive surface air temperature anomaly over the PA, the Weddell Sea, the northern and southern regions of South America, and over the southwestern Atlantic Ocean. Negative anomalies occur in Antarctica (Figure 7a,b). Model results present similar responses, but limited to the mid and high latitudes, with some variations in surface temperature anomalies magnitude among all models (Figure 7c–f).
During the negative phase of SAM, an opposed response occurs in Antarctica if compared with the positive SAM, except in the PA region. The opposed pattern does not occur over South America and the Atlantic Ocean (Figure 7g,h). However, reanalysis, CMIP5 ensemble, and BESM-OA2.5 show an opposed response of surface air temperature anomalies during the SAM negative phase, if compared with the positive phase (Figure 7i–l).
Seasonal composite analysis of surface temperature (Figures S6–S9) does not reveal a consistent opposition between positive and negative SAM phases in observations, except for austral winter (JJA, Figure S8). BESM disagrees with the observational reconstruction sign of SAM phases. These results partially agree with previous studies, which report a more consistent relationship between SAM and precipitation on the seasonal scale, and with the surface temperature on the monthly scale [5].
Previous studies relate SAM phases and the surface air temperature anomalies with perturbations in atmospheric circulation, mainly associated with changes in subtropical and polar jets. Adiabatic responses of the meridional circulation during a positive SAM, the strengthening of the zonal westerly flow, and of the polar jet, which also moves poleward, are caused by changes in atmospheric zonal mean temperature [5]. Indeed, [52] reported the occurrence of an anticyclonic anomaly over southern South America that favored positive advection of temperature anomalies in this region during the positive phase of SAM.
In conclusion, we found that the BESM-OA2.5 model was able to reproduce most of the SAM patterns and their effects on climate variables if compared with other CMIP5 models, reanalysis, and observations. The MSLP climatology over latitudinal belts used in the SAM index computation was consistent in BESM-OA2.5 outputs and other examined datasets, despite the BESM-OA2.5 bias in higher latitudes. The SAM index obtained for all datasets presents a positive trend since the 1970s in agreement with previous studies. All analyzed datasets were able to represent the SAM spatial pattern, but BESM-OA2.5 tends to enhance MSLP anomalies’ magnitudes in comparison with observations, reanalysis, and other CMIP5 models.
The relationship between the SAM mean pattern and phases with precipitation and surface temperature was also represented, albeit with the intrinsic limitations of all data used here. BESM-OA2.5 was able to represent the seasonal relationship between precipitation and SAM in eastern South America and to express the effects of SAM phases on eastern South American precipitation, mostly on the seasonal scale (during austral summer and spring). For surface temperature, BESM-OA2.5 was able to reproduce the monthly relationship between surface temperature and SAM in the South America region if compared with observations. On the other hand, most of the examined datasets (including BESM-OA2.5) showed an unclear relationship between SAM phases and surface temperature on the seasonal timescale, except for austral winter. This result agrees with recent studies that report a well-defined relationship between surface temperature and SAM on the month-time scale.
Biases in the tropical Atlantic and over the Amazon, combined with the poor representation of cloudiness by the BESM-OA2.5 model in higher latitudes, seem to contribute to the seasonal discrepancies found in our results for these regions. However, identifying these biases will certainly lead to refinements in BESM and contribute to improving studies of climate variability and change.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/atmos12081045/s1, Figure S1: SAM GW99 index absolute error compared with the observational reconstruction fromthe Marshall index (Figure 1). Figure S2: DJF precipitation anomalies composites according to SAM phases. Figure S3: MAM precipitation anomalies composites according to SAM phases. Figure S4: JJA precipitation anomalies composites according to SAM phases. Figure S5: SON precipitation anomalies composites according to SAM phases. Figure S6: DJF surface temperature anomalies composites according to SAM phases. Figure S7: MAM surface temperature anomalies composites according to SAM phases. Figure S8: JJA surface temperature anomalies composites according to SAM phases. Figure S9: SON surface temperature anomalies composites according to SAM phases.

Author Contributions

Study conceptualization: L.F.P., I.W., R.B.d.S.; data analyses: L.F.P.; manuscript main writing: L.F.P.; manuscript editing and review: L.F.P., I.W., R.B.d.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Brazilian Agencies CNPq, CAPES and FAPERGS to the following projects: (i) National Institute for Science and Technology of the Cryosphere (CNPq 704222/2009 and FAPERGS 17/2551-0000518-0); Use and Development of the BESM Model for Studying the Ocean-Atmosphere-Cryosphere in high and medium latitudes (CAPES 88887-145668/2017-00). This study was also financed by CAPES—Finance Code 001 (88887.495715/2020-00; 88887.136384/2017-00), FAPESP: 2018/14789-9; CNPq: 301726/2013-2, 405869/20134.

Data Availability Statement

CMIP5 models’ data is available at ESGF website (https://esgf-node.llnl.gov/projects/cmip5/ accessed on 10 August 2021).

Acknowledgments

We are thankful to the ESGF Portal for making CMIP5 data available, and to Fernanda Casagrande and André Lanfer for the support with BESM-OA2.5 technical information. We also thank three anonymous referees that contributed to the improvement of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rogers, J.C.; van Loon, H. Spatial variability of sea level pressure and 500 mb height anomalies over the Southern Hemisphere. Mon. Weather Rev. 1982, 110, 1375–1392. [Google Scholar] [CrossRef] [Green Version]
  2. Thompson, D.W.J.; Wallace, J.M. Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Clim. 2000, 13, 1000–1016. [Google Scholar] [CrossRef]
  3. Zheng, F.; Li, J.; Clark, R.T.; Nnamchi, H.C. Simulation and projection of the Southern Hemisphere annular mode in CMIP5 models. J. Clim. 2013, 26, 9860–9879. [Google Scholar] [CrossRef] [Green Version]
  4. Gong, D.; Wang, S. Definition of Antarctic oscillation index. Geophys. Res. Lett. 1999, 26, 459–462. [Google Scholar] [CrossRef] [Green Version]
  5. Fogt, R.L.; Marshall, G.J. The Southern Annular Mode: Variability, trends, and climate impacts across the Southern Hemisphere. WIREs Clim. Chang. 2020, 11, e652. [Google Scholar] [CrossRef]
  6. Trenberth, K.E.; Stepaniak, D.P.; Smith, L. Interannual variability of the patterns of atmospheric mass distribution. J. Clim. 2005, 18, 2812–2825. [Google Scholar] [CrossRef]
  7. Russell, A.; McGregor, G.R. Southern hemisphere atmospheric circulation: Impacts on Antarctic climate and reconstructions from Antarctic ice core data. Clim. Chang. 2010, 99, 155–195. [Google Scholar] [CrossRef] [Green Version]
  8. Ibebuchi, C.C. On the relationship between circulation patterns, the Southern Annular Mode, and rainfall variability in Western Cape. Atmosphere 2021, 12, 753. [Google Scholar] [CrossRef]
  9. Reboita, M.S.; Rocha, R.P.; Ambrizzi, T.; Gouveia, C.D. Trend and teleconnection patterns in the climatology of extratropical cyclones over the Southern Hemisphere. Clim. Dyn. 2015, 45, 1929–1944. [Google Scholar] [CrossRef]
  10. Gallego, D.; Ribera, P.; Garcia-Herrera, R.; Hernandez, E.; Gimeno, L. A new look for the Southern Hemisphere jet stream. Clim. Dyn. 2005, 24, 607–621. [Google Scholar] [CrossRef]
  11. L’Heureux, M.L.; Thompson, D.W.J. Observed relationships between the El Niño–Southern Oscillation and the extratropical zonal-mean circulation. J. Clim. 2006, 19, 276–287. [Google Scholar] [CrossRef]
  12. Vasconcellos, F.C.; Pizzochero, R.M.; Cavalcanti, I.F.A. Month-to-month impacts of Southern Annular Mode over South America climate. Anuário Inst. Geociências 2019, 42, 783–792. [Google Scholar] [CrossRef]
  13. Reboita, M.S.; Ambrizzi, T.; Rocha, R.P. Relationship between the Southern Annular Mode and Southern Hemisphere atmospheric systems. Rev. Bras. Meteorol. 2009, 24, 48–55. [Google Scholar] [CrossRef] [Green Version]
  14. McLandress, C.; Shepherd, T.G.; Scinocca, J.F.; Plummer, D.A.; Sigmond, M.; Jonsson, A.I.; Reader, M.C. Separating the dynamical effects of climate change and ozone depletion. Part II: Southern Hemisphere troposphere. J. Clim. 2011, 24, 1850–1868. [Google Scholar] [CrossRef] [Green Version]
  15. Gong, T.; Feldstein, S.B.; Luo, D. The impact of ENSO on wave breaking and Southern Annular Mode events. J. Atmos. Sci. 2010, 67, 2854–2870. [Google Scholar] [CrossRef] [Green Version]
  16. Thompson, D.W.J.; Solomon, S. Interpretation of recent Southern Hemisphere climate change. Science 2002, 296, 895–899. [Google Scholar] [CrossRef] [Green Version]
  17. Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
  18. Goodwin, I.D.; van Ommen, T.D.; Curran, M.A.J.; Mayewski, P.A. Mid latitude winter climate variability in the South Indian and southwest Pacific regions since 1300 AD. Clim. Dyn. 2004, 22, 783–794. [Google Scholar] [CrossRef]
  19. Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. A Summary of the CMIP5 Experiment Design. 2009. Available online: https://pcmdi.llnl.gov/mips/cmip5/experiment_design.html (accessed on 17 August 2020).
  20. Nobre, P.; Siqueira, L.S.P.; De Almeida, R.A.F.; Malagutti, M.; Giarolla, E.; Castelão, G.P.; Bottino, M.J.; Kubota, P.; Figueroa, S.N.; Costa, M.C.; et al. Climate simulation and change in the brazilian climate model. J. Clim. 2013, 26, 6716–6732. [Google Scholar] [CrossRef]
  21. Giarolla, E.; Siqueira, L.S.P.; Bottino, M.J.; Malagutti, M.; Capistrano, V.B.; Nobre, P. Equatorial Atlantic Ocean dynamics in a coupled ocean atmosphere model simulation. Ocean Dynam. 2015, 65, 831–843. [Google Scholar] [CrossRef] [Green Version]
  22. Figueroa, S.N.; Bonatti, J.P.; Kubota, P.Y.; Grell, G.A.; Morrison, H.; Barros, S.R.M.; Fernandez, J.P.R.; Ramirez, E.; Capistrano, V.B.; Alvim, D.S.; et al. The Brazilian Global Atmospheric Model (BAM): Performance for Tropical Rainfall Forecasting and Sensitivity to Convective Scheme and Horizontal Resolution. Weather Forecast. 2016, 31, 1547–1572. [Google Scholar] [CrossRef]
  23. Prado, L.F.; Wainer, I.; de Souza, R.B. Positive SAM trend as seen in the Brazilian Earth System Model (BESM) future scenarios. Ann. Brazil. Acad. Sci. 2021, in press. [Google Scholar]
  24. Casagrande, F.; de Souza, R.B.; Nobre, P.; Marquez, A.L. An inter-hemispheric seasonal comparison of polar amplification using radiative forcing of a quadrupling CO2 experiment. Ann. Geophys. 2020, 38, 1123–1138. [Google Scholar] [CrossRef]
  25. Capistrano, V.B.; Nobre, P.; Veiga, S.F.; Tedeschi, R.; Silva, J.; Bottino, M.; Silva, M.B., Jr.; Menezes Neto, O.L.; Figueroa, S.N.; Bonatti, J.P.; et al. Assessing the performance of climate change simulation results from BESM-OA2.5 compared with a CMIP5 model ensemble. Geosci. Model Dev. 2020, 13, 2277–2296. [Google Scholar] [CrossRef]
  26. Griffies, S.M. Elements of MOM4p1. NOAA/Geophysical Fluid Dynamics Laboratory; Ocean Group Technical Report 6; 2009, 444p. Available online: https://www.gfdl.noaa.gov/wp-content/uploads/files/model_development/ocean/guide4p1.pdf (accessed on 11 August 2021).
  27. Winton, M. A reformulated three-layer sea ice model. J. Atmos. Ocean. Tech. 2000, 17, 525–531. [Google Scholar] [CrossRef] [Green Version]
  28. Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
  29. Veiga, S.F.; Nobre, P.; Giarolla, E.; Capistrano, V.; Baptista Jr., M.; Marquez, A.L.; Figueroa, S.N.; Bonatti, J.P.; Kubota, P.; Nobre, C.A. The Brazilian Earth System Model ocean-atmosphere (BESM-OA) version 2.5: Evaluation of its CMIP5 historical simulation. Geosci. Model. Dev. 2019, 12, 1613–1642. [Google Scholar] [CrossRef] [Green Version]
  30. Jones, P.W. A User’s Guide for SCRIP: A Spherical Coordinate Remapping and Interpolation Package. Los Alamos National Laboratory 1998, 29p. Available online: https://www.researchgate.net/publication/258437800_A_User’s_Guide_for_SCRIP_A_Spherical_Coordinate_Remapping_and_Interpolation_Package_Version_14 (accessed on 11 August 2021).
  31. Bi, D.; Dix, M.; Marsland, S.; Hirst, T.; O’Farrell, S.; Uotila, P.; Sullivan, A.; Yan, H.; Kowalczyk, E.; Rashid, H.; et al. ACCESS: The Australian coupled climate model for IPCC AR5 and CMIP5. In Climate Change Beijing; Chinese Academy of Science: Beijing, China, 2012. [Google Scholar]
  32. Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
  33. Voldoire, A.; Sanchez-Gomez, E.; Salas y Mélia, D.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef] [Green Version]
  34. Bao, Q.; Lin, P.; Zhou, T.; Liu, Y.; Yu, Y.; Wu, G.; He, B.; He, J.; Li, L.; Li, J.; et al. The Flexible Global Ocean-Atmosphere-Land System model, spectral version 2: FGOALS-s2. Adv. Atmos. Sci. 2012, 30, 561–576. [Google Scholar] [CrossRef]
  35. Collins, M.; Tett, S.F.B.; Cooper, C. The internal climate variability of HadCM3, a version of the Hadley Centre Coupled Model without flux adjustments. Clim. Dyn. 2001, 17, 61–81. [Google Scholar] [CrossRef]
  36. Dufresne, J.-L.; Foujols, M.-A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth system model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef]
  37. Yukimoto, S.; Adachi, Y.; Hosaka, M.; Sakami, T.; Yoshimura, H.; Hirabara, M.; Tanaka, T.Y.; Shindo, E.; Tsujino, H.; Deushi, M.; et al. A new global climate model of the meteorological research institute: MRI-CGCM3—model description and basic performance. J. Meteor. Soc. 2011, 90, 23–64. [Google Scholar] [CrossRef] [Green Version]
  38. Adler, R.F.; Sapiano, M.R.P.; Huffman, G.J.; Wang, J.-J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E.; et al. The Global Precipitation Climatology Project (GPCP) monthly analysis (new version 2.3) and a review of 2017 global precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef] [Green Version]
  39. Lenssen, N.; Schmidt, G.; Hansen, J.; Menne, M.; Persin, A.; Ruedy, R.; Zyss, D. Improvements in the GISTEMP uncertainty model. J. Geophys. Res. Atmos. 2019, 124, 6307–6326. [Google Scholar] [CrossRef]
  40. Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Winn, J.P.; Hogan, E.; Killick, R.E.; Dunn, R.J.H.; Osborn, T.J.; Jones, P.D.; Simpson, I.R. An updated assessment of near-surface temperature change from 1850: The HADCRUT5 dataset. J. Geophys. Res. 2021, 126, e2016JD032361. [Google Scholar] [CrossRef]
  41. Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemouin, P.; et al. The Twentieth Century Reanalysis Project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
  42. Slivinski, L.C.; Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Giese, B.S.; McColl, C.; Allan, R.; Yin, X.; Vose, R.; Titchner, H.; et al. Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteorol. Soc. 2019, 145, 2876–2908. [Google Scholar] [CrossRef] [Green Version]
  43. Limpasuvan, V.; Hartmann, D.L. Eddies and the annular modes of climate variability. Geophys. Res. Lett. 1999, 26, 3133–3136. [Google Scholar] [CrossRef] [Green Version]
  44. Hartmann, D.L.; Wallace, J.M.; Limpasuvan, V.; Thompson, D.W.J.; Holton, J.R. Can ozone depletion and global warming interact to produce rapid climate change? Proc. Natl. Acad. Sci. USA 2000, 97, 1412–1417. [Google Scholar] [CrossRef] [Green Version]
  45. Marshall, G.J.; Stott, P.A.; Turner, J.; Connolley, W.M.; King, J.C.; Lachlan-Cope, T.A. Causes of exceptional atmospheric circulation changes in the Southern Hemisphere. Geophys. Res. Lett. 2004, 31, L14205. [Google Scholar] [CrossRef]
  46. Giarolla, E.; Veiga, S.F.; Nobre, P.; Silva Jr., M. B.; Capistrano, V.B.; Callegare, A.O. Sea surface height trends in the Southern hemisphere oceans simulated by the Brazilian Earth System Model under RCP4.5 and RCP8.5 scenarios. J. South Hemisph. Earth. Sys. Sci. 2020, 70, 280–289. [Google Scholar]
  47. Hendon, H.H.; Lim, E.P.; Nguyen, H. Seasonal variations of subtropical precipitation associated with the Southern Annular Mode. J. Clim. 2014, 27, 3446–3460. [Google Scholar] [CrossRef]
  48. Gillet, N.P.; Kell, T.D.; Jones, P.D. Regional impacts of the Southern Annular Mode. Geophys. Res. Lett. 2006, 33, L23704. [Google Scholar] [CrossRef]
  49. Jones, M.E.; Bromwich, D.H.; Nicolas, J.P.; Carrasco, J.; Plavcová, E.; Zou, X.; Wang, S.-H. Sixty years of widespread warming in the Southern middle and high latitudes (1957–2016). J. Clim. 2019, 32, 6875–6898. [Google Scholar] [CrossRef] [Green Version]
  50. Silvestri, G.E.; Vera, C. Antarctic Oscillation signal on precipitation anomalies over southeastern South America. Geophys. Res. Lett. 2003, 30, 2115. [Google Scholar] [CrossRef] [Green Version]
  51. Vera, C.S.; Osman, M. Activity of the Southern Annular Mode during 2015–2016 El Niño event and its impact on Southern Hemisphere climate anomalies. Int. J. Climatol. 2018, 38, e1288–e1295. [Google Scholar] [CrossRef]
  52. Silvestri, G.; Vera, C. Nonstationary impacts of the Southern Annular Mode on Southern Hemisphere climate. J. Clim. 2009, 22, 6142–6148. [Google Scholar] [CrossRef]
  53. Carvalho, L.; Jones, C.; Ambrizzi, T. Opposite phases of the Antarctic Oscillation and relationships with intraseasonal to interannual activity in the tropics during the austral summer. J. Clim. 2005, 18, 702–718. [Google Scholar] [CrossRef] [Green Version]
  54. Kidson, J.W.; Sinclair, M.R. The influence of persistent anomalies on Southern Hemisphere storm tracks. J. Clim. 1995, 8, 1938–1950. [Google Scholar] [CrossRef] [Green Version]
  55. Schenzinger, V.; Osprey, S.M. Interpreting the nature of Northern and Southern Annular Mode variability in CMIP5 Models. J. Geophys. Res. Atmos. 2015, 120, 11,203–11,214. [Google Scholar] [CrossRef]
  56. van Lipzig, N.P.M.; Marshall, G.J.; Orr, A.; King, J.C. The relationship between the Southern Hemisphere annular mode and Antarctic peninsula summer temperatures: Analysis of a high-resolution model climatology. J. Clim. 2008, 21, 1649–1668. [Google Scholar] [CrossRef]
  57. Kwok, R.; Comiso, J.C. Spatial patterns of variability in Antarctic surface temperature: Connections to the Southern Hemisphere annular mode and the southern oscillation. Geophys. Res. Lett. 2002, 29, 50-1–50-4. [Google Scholar] [CrossRef] [Green Version]
  58. Marshall, G.J.; Bracegirdle, T.J. An examination of the relationship between the Southern Annular Mode and Antarctic surface air temperatures in the CMIP5 historical runs. Clim. Dyn. 2015, 45, 1513–1535. [Google Scholar] [CrossRef]
Atmosphere 12 01045 g001 550
Figure 1. Monthly Mean Sea Level Pressure (MSLP, hPa) averaged over SAM GW99 index latitudes, (a) 40 °S, and (b) 65 °S, from January/1957 to December/2005. Black squares: BESM; blue diamonds: CMIP5 ensemble mean; purple triangles: NOAA-20Cv2 reanalysis; green upside-down triangles: NOAA-20Cv3 reanalysis; and red circles: Marshall index, surface-station derived pressure values.
Figure 1. Monthly Mean Sea Level Pressure (MSLP, hPa) averaged over SAM GW99 index latitudes, (a) 40 °S, and (b) 65 °S, from January/1957 to December/2005. Black squares: BESM; blue diamonds: CMIP5 ensemble mean; purple triangles: NOAA-20Cv2 reanalysis; green upside-down triangles: NOAA-20Cv3 reanalysis; and red circles: Marshall index, surface-station derived pressure values.
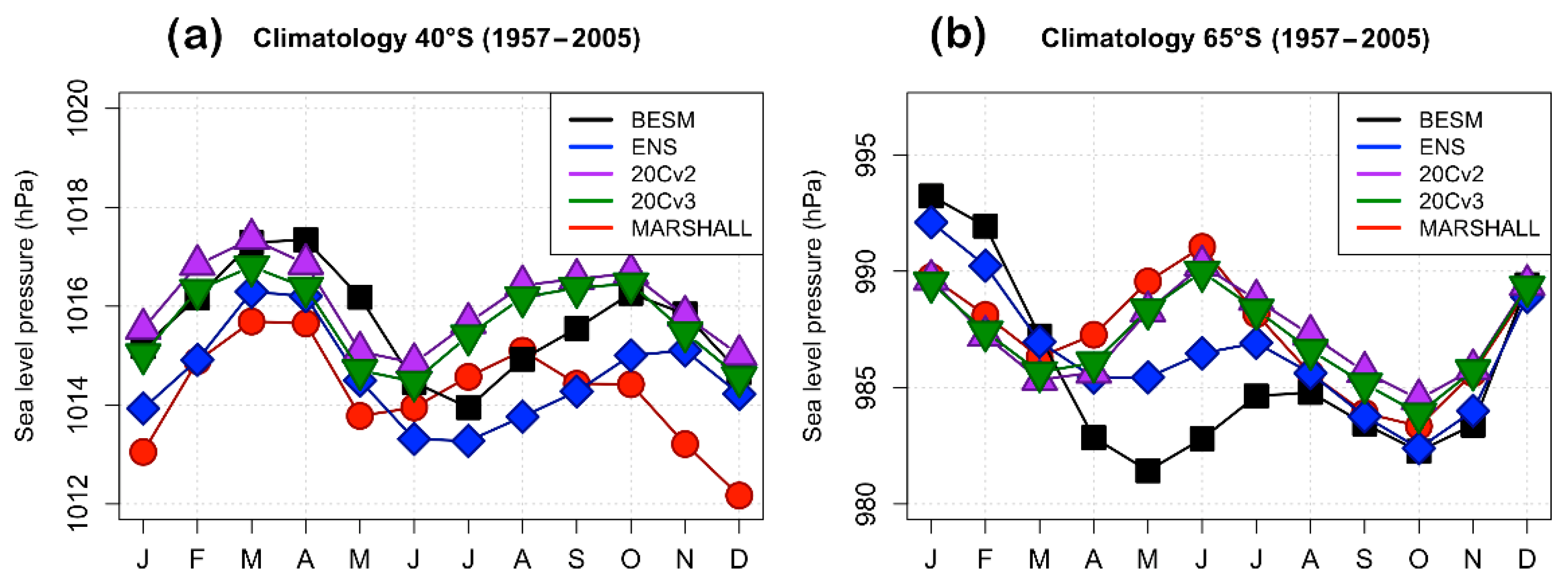
Atmosphere 12 01045 g001
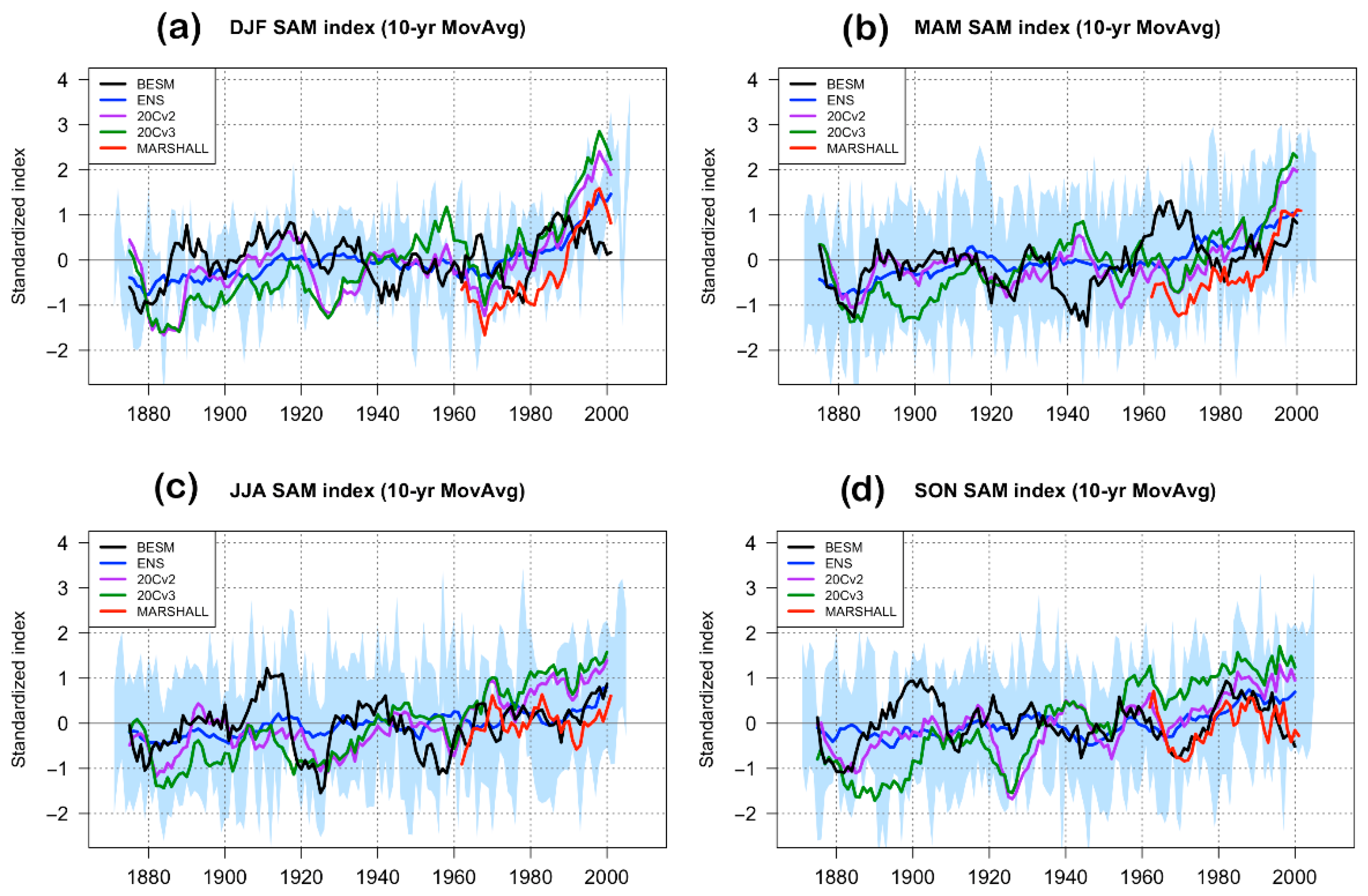
Atmosphere 12 01045 g002 550
Figure 2. SAM GW99 index seasonal reconstruction from 1871 to 2005, compared with observations-derived Marshall index (red lines, available since January 1957). (a) austral summer (DJF); (b) austral autumn (MAM); (c) austral winter (JJA); and (d) austral spring (SON). Black lines: BESM; blue lines: CMIP5 ensemble mean; purple lines: NOAA-20Cv2 reanalysis; green lines: NOAA-20Cv3 reanalysis. SAM indices time series were smoothed by a 10-yr moving average. Light blue shaded area corresponds to 2 standard deviations of the ensemble mean (blue line).
Figure 2. SAM GW99 index seasonal reconstruction from 1871 to 2005, compared with observations-derived Marshall index (red lines, available since January 1957). (a) austral summer (DJF); (b) austral autumn (MAM); (c) austral winter (JJA); and (d) austral spring (SON). Black lines: BESM; blue lines: CMIP5 ensemble mean; purple lines: NOAA-20Cv2 reanalysis; green lines: NOAA-20Cv3 reanalysis. SAM indices time series were smoothed by a 10-yr moving average. Light blue shaded area corresponds to 2 standard deviations of the ensemble mean (blue line).
Atmosphere 12 01045 g002
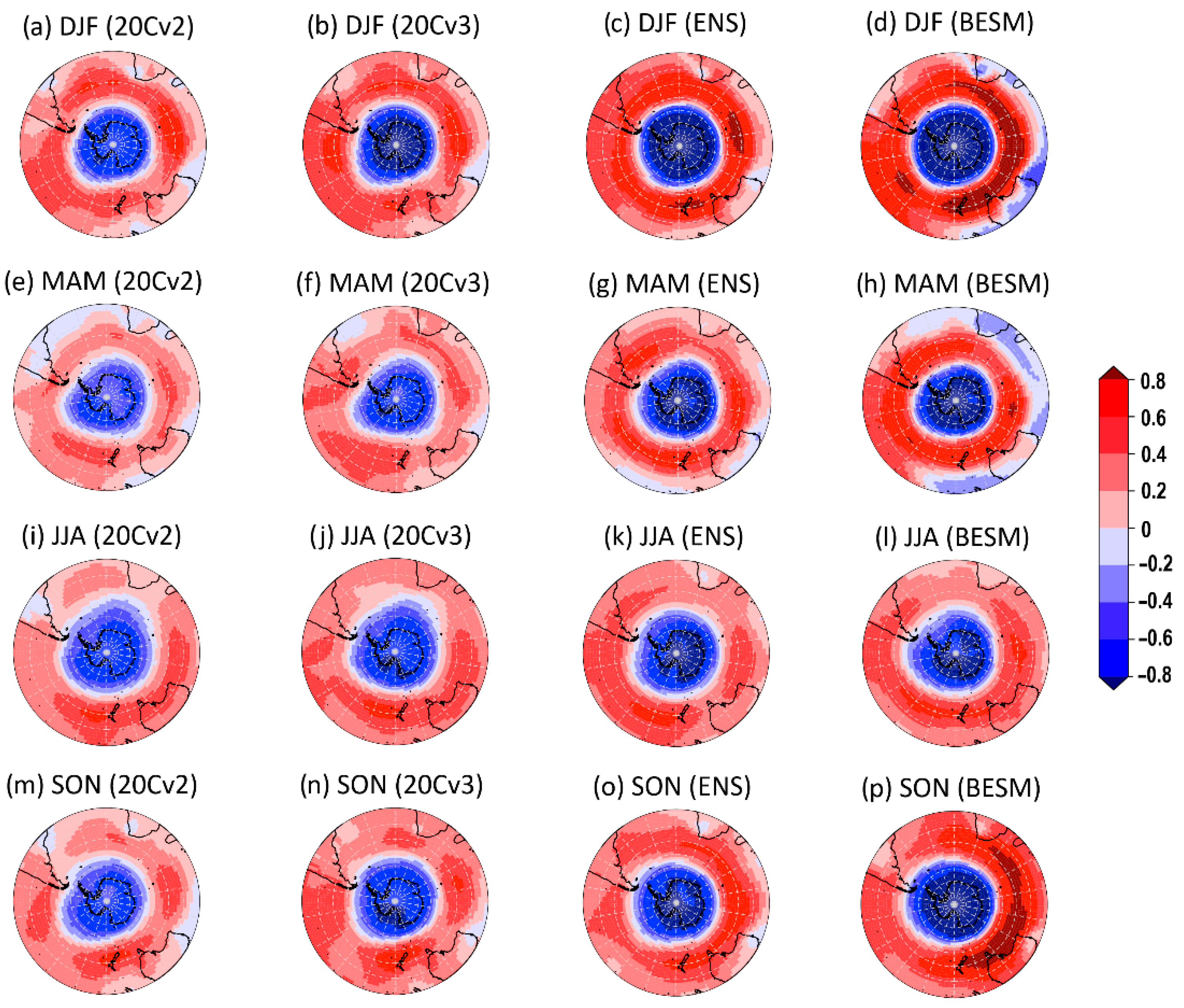
Atmosphere 12 01045 g003 550
Figure 3. SAM GW99 index correlation with seasonal SLP anomalies. DJF: (a–d); MAM: (e–h); JJA: (i–l); SON: (m–p). First column: NOAA-20Cv2 reanalysis; second column: NOAA-20Cv3 reanalysis; third column: CMIP5 ensemble mean; and fourth column: BESM. Reference period: 1871–2005.
Figure 3. SAM GW99 index correlation with seasonal SLP anomalies. DJF: (a–d); MAM: (e–h); JJA: (i–l); SON: (m–p). First column: NOAA-20Cv2 reanalysis; second column: NOAA-20Cv3 reanalysis; third column: CMIP5 ensemble mean; and fourth column: BESM. Reference period: 1871–2005.
Atmosphere 12 01045 g003
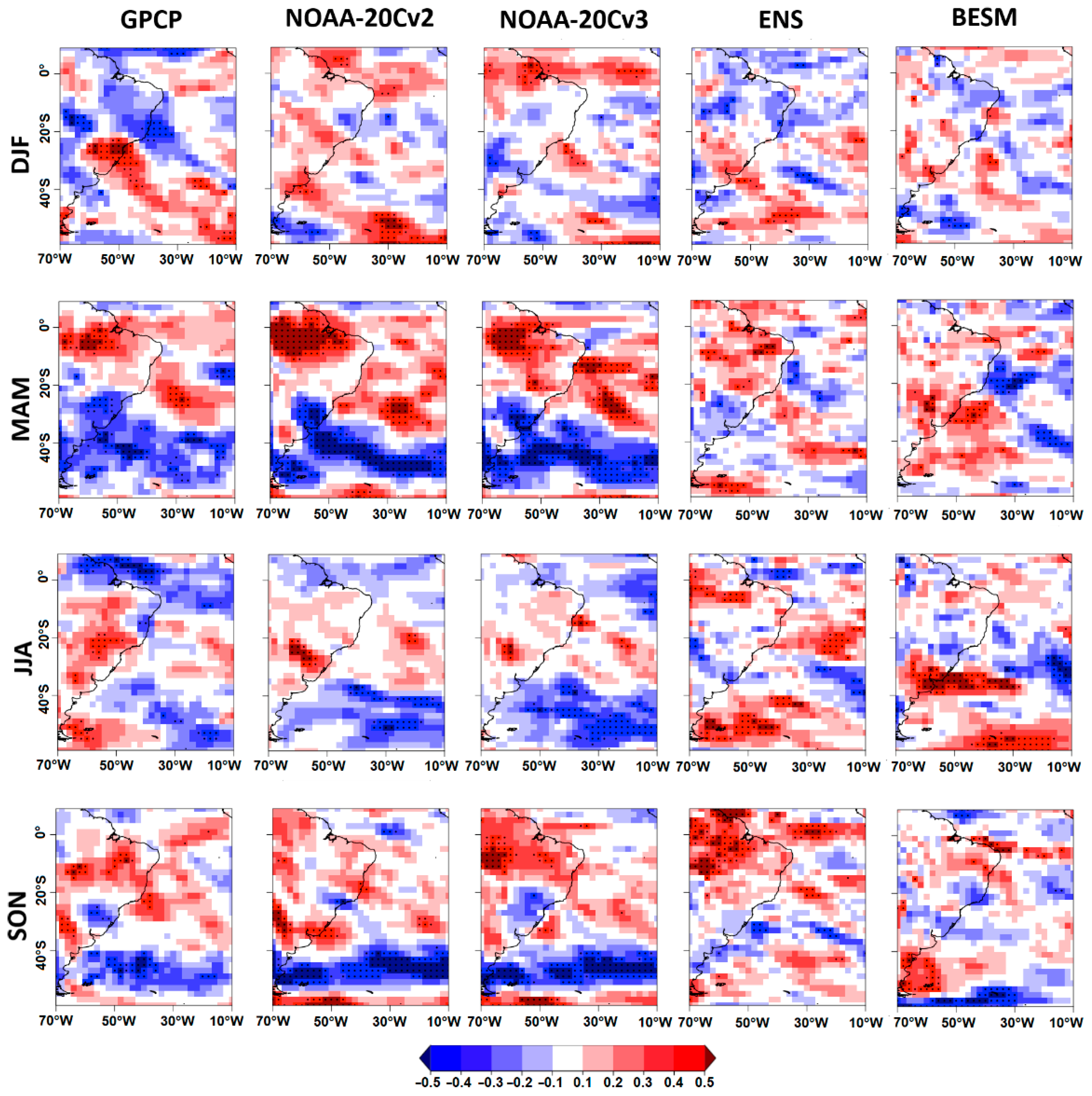
Atmosphere 12 01045 g004 550
Figure 4. SAM index correlation with seasonal precipitation anomalies (1979–2005). Precipitation values: first column, GPCP; second column, NOAA-20Cv2 reanalysis; third column, NOAA-20Cv3 reanalysis; fourth column, CMIP5 ensemble mean; and fifth column, BESM. Lines refer to seasons: first line, December to February (DJF); second line, March to May (MAM); third line, June to August (JJA); and fourth line, September to November (SON). Dotted areas correspond to 5% significance level.
Figure 4. SAM index correlation with seasonal precipitation anomalies (1979–2005). Precipitation values: first column, GPCP; second column, NOAA-20Cv2 reanalysis; third column, NOAA-20Cv3 reanalysis; fourth column, CMIP5 ensemble mean; and fifth column, BESM. Lines refer to seasons: first line, December to February (DJF); second line, March to May (MAM); third line, June to August (JJA); and fourth line, September to November (SON). Dotted areas correspond to 5% significance level.
Atmosphere 12 01045 g004
Atmosphere 12 01045 g005 550
Figure 5. Precipitation anomalies composites according to SAM phases. (a–e), positive SAM; (f–j), negative SAM. Composites were obtained by averaging precipitation anomalies in months with SAM standardized index values higher than |2|. Precipitation values are in millimeters per month (mm/month). Datasets: (a,f), Marshall SAM index and GPCP; (b,g), NOAA-20Cv2; (c,h), NOAA-20Cv3; (d,i), CMIP5 ensemble mean; (f,j), BESM. Reference period: 1979–2005.
Figure 5. Precipitation anomalies composites according to SAM phases. (a–e), positive SAM; (f–j), negative SAM. Composites were obtained by averaging precipitation anomalies in months with SAM standardized index values higher than |2|. Precipitation values are in millimeters per month (mm/month). Datasets: (a,f), Marshall SAM index and GPCP; (b,g), NOAA-20Cv2; (c,h), NOAA-20Cv3; (d,i), CMIP5 ensemble mean; (f,j), BESM. Reference period: 1979–2005.
Atmosphere 12 01045 g005
Atmosphere 12 01045 g006 550
Figure 6. SAM index correlation with monthly surface temperature anomalies (1979–2005). (a) GISTEMPv4, (b) NOAA-20Cv2 reanalysis, (c) CMIP5 ensemble mean, (d) HadCRUT5, (e) NOAA-20Cv3 reanalysis, (f) BESM. GISTEMPv4 and HadCRUT5 temperature anomalies were correlated with Marshall observational index, while reanalysis and models’ temperature anomalies were correlated with GW99 index. Dotted areas correspond to 5% significance level.
Figure 6. SAM index correlation with monthly surface temperature anomalies (1979–2005). (a) GISTEMPv4, (b) NOAA-20Cv2 reanalysis, (c) CMIP5 ensemble mean, (d) HadCRUT5, (e) NOAA-20Cv3 reanalysis, (f) BESM. GISTEMPv4 and HadCRUT5 temperature anomalies were correlated with Marshall observational index, while reanalysis and models’ temperature anomalies were correlated with GW99 index. Dotted areas correspond to 5% significance level.
Atmosphere 12 01045 g006
Atmosphere 12 01045 g007 550
Figure 7. Surface temperature anomalies composites according to SAM phases. (a–f), positive SAM; (g–l), negative SAM. Composites were obtained by averaging temperature anomalies in months with SAM standardized index values higher than |2|. Temperature values are in celsius (°C). Datasets: (a,g), Marshall SAM index and GISTEMP; (b,h), Marshall SAM index and HadCRUT; (c,i), NOAA-20Cv2; (d,j), NOAA-20Cv3; (e,k), CMIP5 ensemble meanr.
Figure 7. Surface temperature anomalies composites according to SAM phases. (a–f), positive SAM; (g–l), negative SAM. Composites were obtained by averaging temperature anomalies in months with SAM standardized index values higher than |2|. Temperature values are in celsius (°C). Datasets: (a,g), Marshall SAM index and GISTEMP; (b,h), Marshall SAM index and HadCRUT; (c,i), NOAA-20Cv2; (d,j), NOAA-20Cv3; (e,k), CMIP5 ensemble meanr.
Atmosphere 12 01045 g007
Table
Table 1. CMIP5 models used in this study. Grid refers to atmospheric horizontal spacing (longitude × latitude, in degrees).
Table 1. CMIP5 models used in this study. Grid refers to atmospheric horizontal spacing (longitude × latitude, in degrees).
ModelInstitutionGrid
ACCESS1.0 [31]Centre for Australian Weather and Climate Research (CAWCR)1.875 × 1.25
BESM-OA2.5 [20]Brazilian National Institute for Space Research (INPE)1.875 × 1.875
CCSM4 [32]National Center for Atmospheric Research (NCAR)1.25 × 0.9424
CNRM-CM5 [33]Centre National de Recherches Météorologiques/Centre Européen de Recherche et Formation Avancées en Calcul Scientifique (CNRM-CERFACS)1.40625 × 1.4008
FGOALS-s2 [34]Institute of Atmospheric Physics, Chinese Academy of Sciences (LASG-IAP)2.8125 × 1.6590
GISS-E2-HNASA Goddard Institute for Space Sciences (GISS)2.5 × 2
HadCM3 2 [35]Met Office Hadley Centre (MOHC)3.75 × 2.5
IPSL-CM5A-LR [36]Institute Pierre Simon Laplace (IPSL)3.75 × 1.8947
MRI-CGCM3 [37]Meteorological Research Institute (MRI)1.125 × 1.12148
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Prado, L.F.; Wainer, I.; de Souza, R.B. The Representation of the Southern Annular Mode Signal in the Brazilian Earth System Model. Atmosphere 2021, 12, 1045. https://doi.org/10.3390/atmos12081045

AMA Style

Prado LF, Wainer I, de Souza RB. The Representation of the Southern Annular Mode Signal in the Brazilian Earth System Model. Atmosphere. 2021; 12(8):1045. https://doi.org/10.3390/atmos12081045

Chicago/Turabian Style

Prado, Luciana F., Ilana Wainer, and Ronald B. de Souza. 2021. "The Representation of the Southern Annular Mode Signal in the Brazilian Earth System Model" Atmosphere 12, no. 8: 1045. https://doi.org/10.3390/atmos12081045

APA Style

Prado, L. F., Wainer, I., & de Souza, R. B. (2021). The Representation of the Southern Annular Mode Signal in the Brazilian Earth System Model. Atmosphere, 12(8), 1045. https://doi.org/10.3390/atmos12081045

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop