On the Problem of Critical Electric Field of Atmospheric Air

Abstract

It is traditionally accepted to define the dielectric strength of air as an electric field corresponding to the balance between the rates of impact ionization and electrons’ attachment to neutrals. Its reduced value is known to be about 110 Td regardless of the altitude above the mean sea level. In this study, the altitude profile of the critical electric field of atmospheric air in the 0–40 km altitude range is specified. Unlike the conventional approach, a wide range of additional plasma-chemical processes occurring in atmospheric air, such as electron detachment from negative ions and ion-ion conversion is taken into account. Atmospheric air is considered to be a mixture of N${}_2$:O${}_2$ = 4:1 containing a small amount of chemically active small gas components, such as water vapor, atomic oxygen, ozone, and several types of nitrogen oxides. It is shown that the dielectric strength of air falls noticeably compared to its conventional value. The results of the study can be important to solve the problems of initiation and propagation of lightning discharges, blue starters, and blue jets.

1. Introduction

The breakdown electric field, which separates the dielectric state of the medium from the ionized one, is an important property of atmospheric air. It is traditionally accepted to define the breakdown threshold $E_b$ taking into account only ionization (production of electrons) and attachment (the loss of electrons) processes. This concept involves a single equation for the electron concentration $\left[e\right]$ temporal evolution:

$$\frac{\partial \left[e\right]}{\partial t}=({\nu }_i-{\nu }_a)\left[e\right],$$

(1)

where ${\nu }_i$ and ${\nu }_a$ are the ionization and attachment frequencies, respectively, which are both sharp functions of the electric field [1]. In the framework of Equation (1), electron multiplication is impossible when ${\nu }_a>{\nu }_i$ and the threshold of their number density exponential growth is determined from the relation:

$${\nu }_i(E_b)-{\nu }_a(E_b)=0.$$

(2)

In atmospheric air, which in the first approximation can be considered as a nitrogen-oxygen mixture, there are two main ionization reactions:

$$e+{\mathrm{N}}_2\Rightarrow 2e+{\mathrm{N}}_2^{+},$$

(3)

$$e+{\mathrm{O}}_2\Rightarrow 2e+{\mathrm{O}}_2^{+}.$$

(4)

In the lower atmosphere, the key process responsible for the loss of electrons is their attachment to oxygen molecules:

$$e+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}^{-}+\mathrm{O},$$

(5)

$$e+{\mathrm{O}}_2+\mathrm{M}\Rightarrow {\mathrm{O}}_2^{-}+\mathrm{M}.$$

(6)

Under normal conditions, the attachment frequency ${\nu }_a$ varies from ${10}^7$ s${}^{-1}$ (for three-body attachment (6) which prevails for reduced electric fields smaller than 55 Td [2]) to ${10}^8$ s${}^{-1}$ (for two-body attachment (5) which prevails for reduced electric fields higher than 55 Td [2]). Table 4 reported in [3] allows one to estimate the electron lifetime as 10–100 ns. When attached to neutrals, electrons form negative ions, the relatively low mobility of which significantly complicates further ionization. The air breakdown field $E_b$ at the sea level found from Equation (2) varies from 2.6 to 3.2 MV/m [1] and exponentially decreases with increasing height because of the reduction in the number density of air molecules. It must be noted that the balance relation (2) works well at times that do not exceed ${\nu }_a^{-1}$, while at larger time scales an additional consideration of slower processes, the main of which is detachment of electrons from negative ions, is needed.

There are numerous studies (see [2,4,5,6,7] and references therein) discussing the influence of electron detachment from negative ions on the critical breakdown field of air. In [4], two additional (with respect to impact ionization and attachment) plasma-chemical processes were employed: detachment of electrons from ${\mathrm{O}}_2^{-}$ ions

$${\mathrm{O}}_2^{-}+\mathrm{M}\Rightarrow {\mathrm{O}}_2+\mathrm{M}+e$$

(7)

and conversion of ${\mathrm{O}}^{-}$ ions into ${\mathrm{O}}_2^{-}$ ones:

$${\mathrm{O}}^{-}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{-}+\mathrm{O}.$$

(8)

A joint consideration of reactions (3)–(5), (7) and (8) allowed the authors to compile a linear system of three differential equations describing the temporal evolution of electron, ${\mathrm{O}}^{-}$, and ${\mathrm{O}}_2^{-}$ concentrations and to derive the formula for the effective ionization frequency, which becomes positive under the conventional threshold $E_b$. In [2], reactions (3)–(5) and (7) were supported by associative detachment

$${\mathrm{O}}^{-}+{\mathrm{N}}_2\Rightarrow {\mathrm{N}}_2\mathrm{O}+e$$

(9)

and three-body conversion

$${\mathrm{O}}^{-}+{\mathrm{O}}_2+\mathrm{M}\Rightarrow {({\mathrm{O}}_3^{-})}^{*}+\mathrm{M}\Rightarrow {\mathrm{O}}_3^{-}+\mathrm{M}$$

(10)

reactions. Similarly to [4], it was shown that the resultant system of four differential equations that involves the number densities of electrons and ${\mathrm{O}}^{-}$, ${\mathrm{O}}_2^{-}$, ${\mathrm{O}}_3^{-}$, ${\mathrm{N}}_2^{+}$, and ${\mathrm{O}}_2^{+}$ ions loses stability when ${\nu }_i<{\nu }_a$. This result was later refined in [5] with additional consideration of reactions (6) and (8) along with the following detachment processes involving $\mathrm{O}$ atoms:

$${\mathrm{O}}^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_2+e,$$

(11)

$${\mathrm{O}}_2^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_3+e,$$

(12)

$${\mathrm{O}}_3^{-}+\mathrm{O}\Rightarrow 2{\mathrm{O}}_2+e.$$

(13)

The authors of [6] developed a simple model with reactions (3)–(5) and (9) to show that in the upper atmosphere electrons multiply under electric fields significantly below the conventional breakdown threshold because, at high altitude (low pressure), the electron associative detachment from atomic oxygen ions counteracts the effect of dissociative attachment. In a recent study [7] devoted to the problem of lightning initiation in a thundercloud, it was shown that the involvement of detachment reactions (7), (9), and (13) together with the conversion ones (8) and (10) and

$${\mathrm{O}}_3^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{O}}_2$$

(14)

provides a significant (15–30%, see their Figure 1(a)) reduction in the critical electric field compared to the traditionally accepted value $E_b$. In their calculations, the authors first considered the process of ion loss to hydrometeors, which can be important for intracloud conditions, and analyzed the 0–20 km altitude range. Among other results of [7], there is the fact that the gap between the reduced critical field $E_c/N$, which falls with the altitude above the mean sea level (AMSL) h, and the reduced conventional breakdown field $E_b/N$, which does not noticeably depend on h, increases with increasing values of h reaching approximately 35 Td at the height of 20 km.

In the present study, the quantity of the critical electric field of atmospheric air is refined. The advantage of our model is that it considers both the wide range of plasma-chemical reactions (72 in total, see Appendix A) and the presence of chemically active small gas components (SGCs), such as ${\mathrm{H}}_2\mathrm{O}$, $\mathrm{O}$, ${\mathrm{O}}_3$, $\mathrm{NO}$, ${\mathrm{NO}}_2$, ${\mathrm{NO}}_3$, and ${\mathrm{N}}_2\mathrm{O}$ inhomogeneously distributed over the analyzed 0–40 km altitude range.

The content of the paper is the following. In Section 2, the composition and thermodynamical properties of virgin atmospheric air in the considered 0–40 km altitude range (Section 2.1) and the numerical scheme used to define the altitude profile of its reduced critical electric field and to analyze its ion composition in suprathreshold conditions (Section 2.2) are given. In Section 3, the model results which are further discussed in Section 4 are presented. The main findings of our study are formulated in Section 5. Appendix A and Appendix B provide the list of considered plasma-chemical reactions and components of the system evolution matrix, respectively.

2. Materials and Methods

The main purpose of the study is to specify the critical electric field, exceeding of which ensures exponential growth of charged particle concentrations in atmospheric air, and to analyze the system behavior in the fields slightly exceeding its value. In this section, the composition and properties of the analyzed medium, which is atmospheric air in the 0–40 km altitude range, are described and the numerical approach used is discussed.

2.1. Ambient Conditions

In this study, the basic parameters of the atmospheric air correspond to the standard atmosphere approximation which is widely used in solving various technical and thermophysical problems and implies the averaged, i.e. not attached to some specific conditions, values of air pressure and temperature. Altitude distributions of atmospheric air parameters and composition were obtained by digitizing data from the following sources:

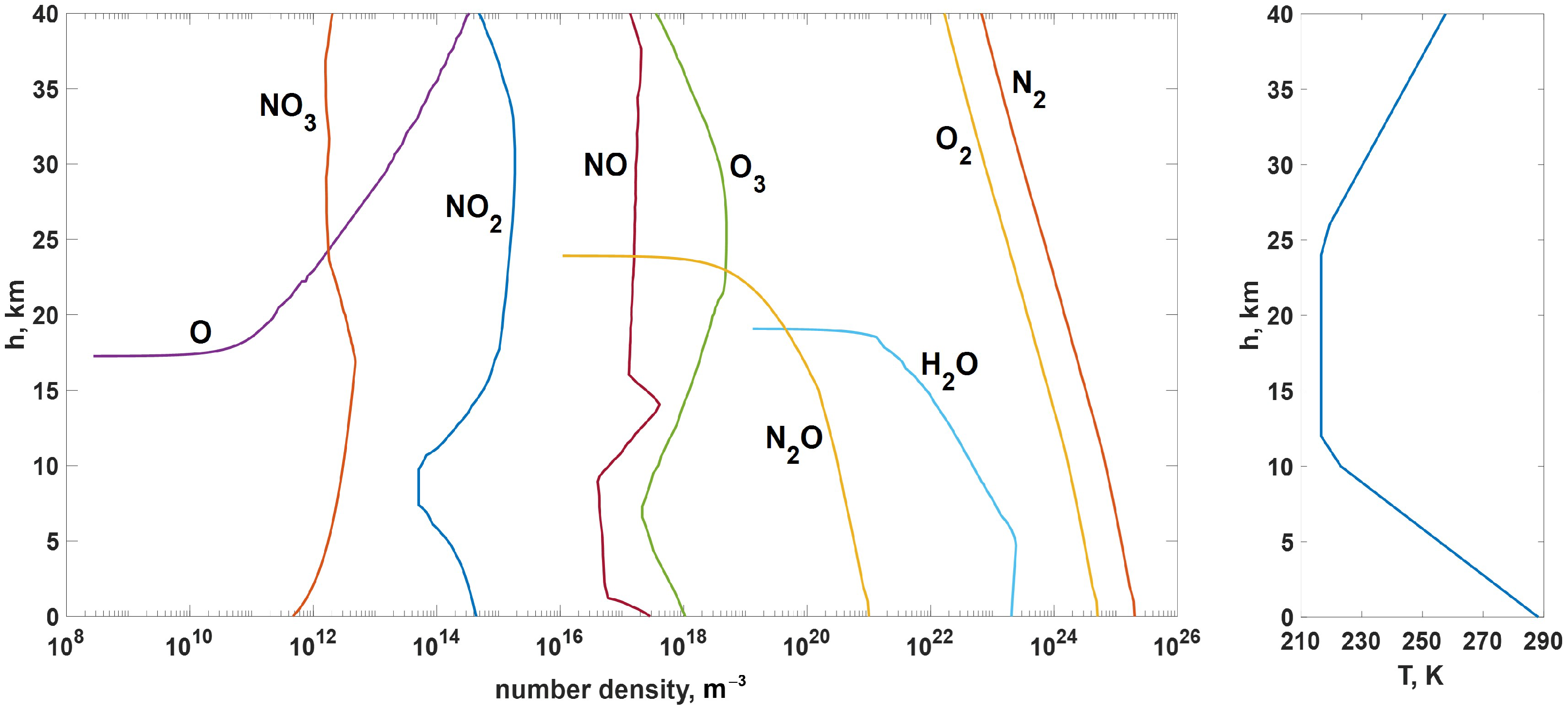
• Air temperature (T) and pressure (p) altitude distributions—Table 1 from the peer-reviewed web resource [8];
• Water vapor number density ([${\mathrm{H}}_2\mathrm{O}$])—Figure 2 from the peer-reviewed web resource [8];
• Atomic oxygen number density ([$\mathrm{O}$])—Figure VIII-10 from [9];
• Ozone number density ([${\mathrm{O}}_3$])—Figure 1.4 from [10];
• Nitric oxide (II) number density ([$\mathrm{NO}$])—Figure 1 from [11];
• Nitric oxide (IV) number density ([${\mathrm{NO}}_2$])—Figure 5 from [12];
• Nitric oxide number density ([${\mathrm{NO}}_3$])—Figure 1(b) from [13];
• Nitric oxide (I) number density ([${\mathrm{N}}_2\mathrm{O}$])—Figure 8 from [14].

The air number density N, which determines the reduced electric field $E/N$, was calculated as

$$N(h)=\frac{p(h)}{k_{B}T(h)},$$

(15)

where $k_B=1.38\times {10}^{-23}$ J/K is the Boltzmann constant. In the altitude range of 0–40 km AMSL, the air can be considered as a mixture of N${}_2$:O${}_2$ = 4:1 (see Figure 1 in [8]) containing SGCs whose number densities are many orders of magnitude smaller than $N=\left[{\mathrm{N}}_2\right]+\left[{\mathrm{O}}_2\right]$. Altitude distributions of the discussed quantities in the considered range of 0–40 km AMSL are presented in Figure 1.

In a recent study [7], it was shown that the frequency of ion loss to hydrometeors is ${\nu }_h=$ 0.1–1 s${}^{-1}$ in thundercloud conditions. It is unknown how ${\nu }_h$ depends on the altitude AMSL beyond the cloud volume. On the other hand, it follows from general considerations that ${\nu }_h$ must fall when moving away from the cloud center where the concentration of hydrometeors is maximal. Because of this, it is conditionally assumed in the study that

$${\nu }_h\left[{\mathrm{s}}^{-1}\right]=exp\left[-{\left(\frac{h\left[\mathrm{km}\right]-5}{10}\right)}^2\right].$$

(16)

In Equation (16), the 5-km altitude, where ${\nu }_h$ has a maximum, approximately corresponds to the peak of the used water vapor altitude profile (see Figure 2 in [8]), while the characteristic scale of 10 km is comparable to the vertical extent of a thundercloud where the vast majority of hydrometeors is located.

2.2. Evolution Matrix

In conditions when the electric field exceeds the air breakdown threshold, there appear an increasing number of electrons and ions. In this study, a wide range of atmospheric positive (${\mathrm{N}}_2^{+}$, ${\mathrm{O}}_2^{+}$, ${\mathrm{O}}_4^{+}$, ${\mathrm{N}}_4^{+}$, ${\mathrm{O}}_2^{+}·{\mathrm{N}}_2$, ${\mathrm{H}}_2{\mathrm{O}}^{+}$) and negative (${\mathrm{O}}^{-}$, ${\mathrm{O}}_2^{-}$, ${\mathrm{O}}_3^{-}$, ${\mathrm{O}}_4^{-}$, ${\mathrm{NO}}^{-}$, ${\mathrm{NO}}_2^{-}$, ${\mathrm{NO}}_3^{-}$, ${\mathrm{NO}}_3^{-*}$, ${\mathrm{NO}}_3^{-}({\mathrm{H}}_2\mathrm{O})$, ${\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_2$, ${\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_3$) ions is considered. The model includes several types of plasma-chemical processes (see Appendix A), such as ionization, electrons’ attachment to neutrals and detachment from negative ions, and ion-ion conversions. The set of considered reactions can be presented in the form of an evolution matrix $\widehat{A}$ (see Appendix B) so that

$$\frac{d\mathbf{x}}{dt}=\widehat{A}\mathbf{x},$$

(17)

where $\mathbf{x}$ is a vector of variables that includes concentrations of electrons and positive and negative ions. Since in sub-threshold electric fields the ambient concentrations of electrons and atmospheric ions are negligible compared to those under suprathreshold conditions, the equilibrium state of the system can be considered as zero. This circumstance allows one to neglect quadratic recombination processes (at least when the electric field is not far from the ionization threshold) and to operate with the linearized system of Equation (17). As in previous studies (for example, [2,4,5,6,7]), the sought critical electric field $E_c$ is defined as a field at which the first positive eigenvalue ${\lambda }^{+}$ of the matrix $\widehat{A}$, which can also be called an effective ionization frequency ${\nu }_{\mathrm{eff}}$, appears. It should be noted that some components of the evolution matrix $\widehat{A}$ are sharp functions of both reduced electric field $E/N$ and air temperature T. The components of the eigenvector ${\mathbf{x}}^{+}$ corresponding to the eigenvalue ${\lambda }^{+}$, which characterize ion composition of atmospheric air, also depend on electric field and altitude AMSL.

The described numerical method allows one to answer the following questions (see Section 3):

1.

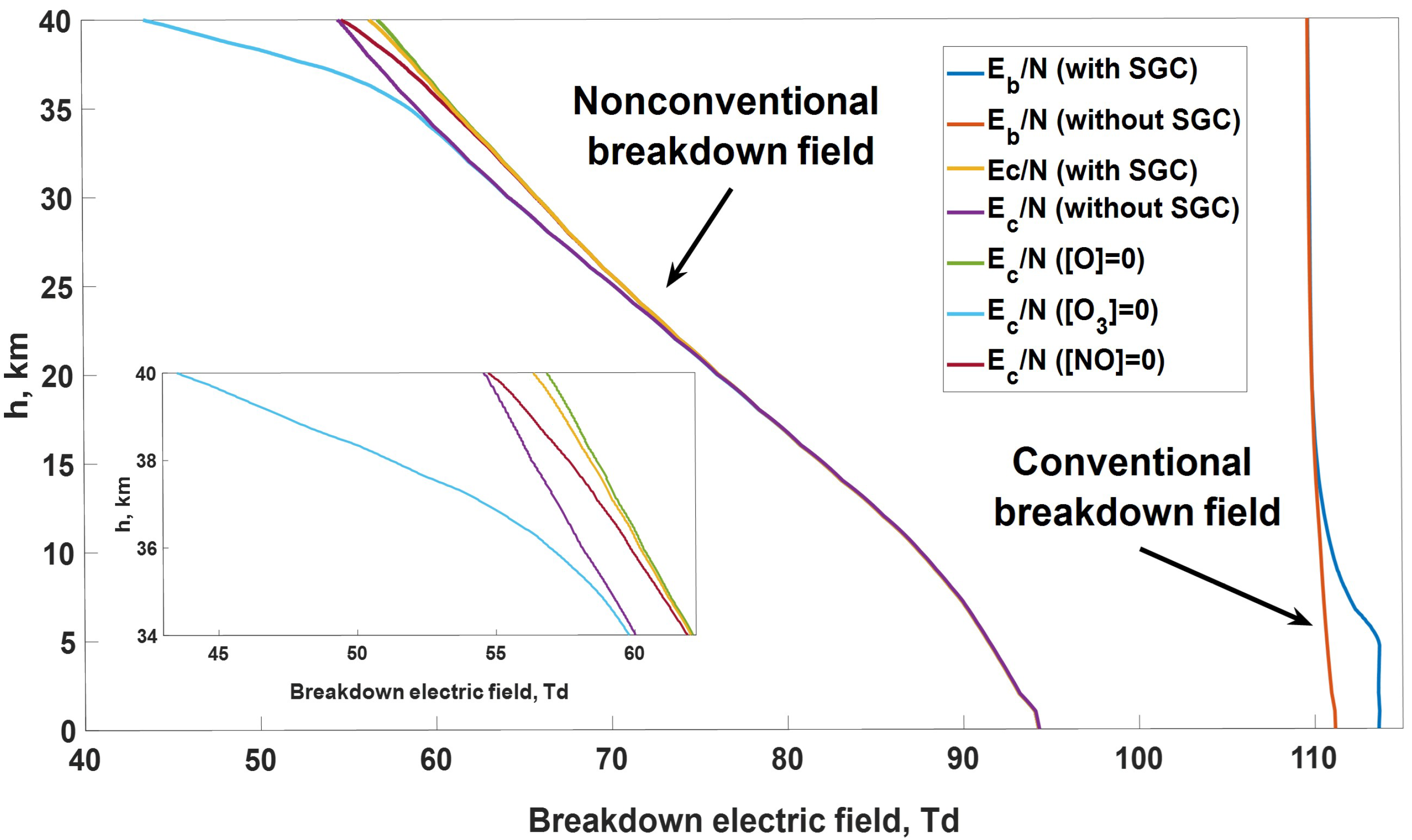
How does the critical electric field of atmospheric air depend on altitude AMSL?

2.

How does the presence of SGCs influence the critical electric field altitude profile?

3.

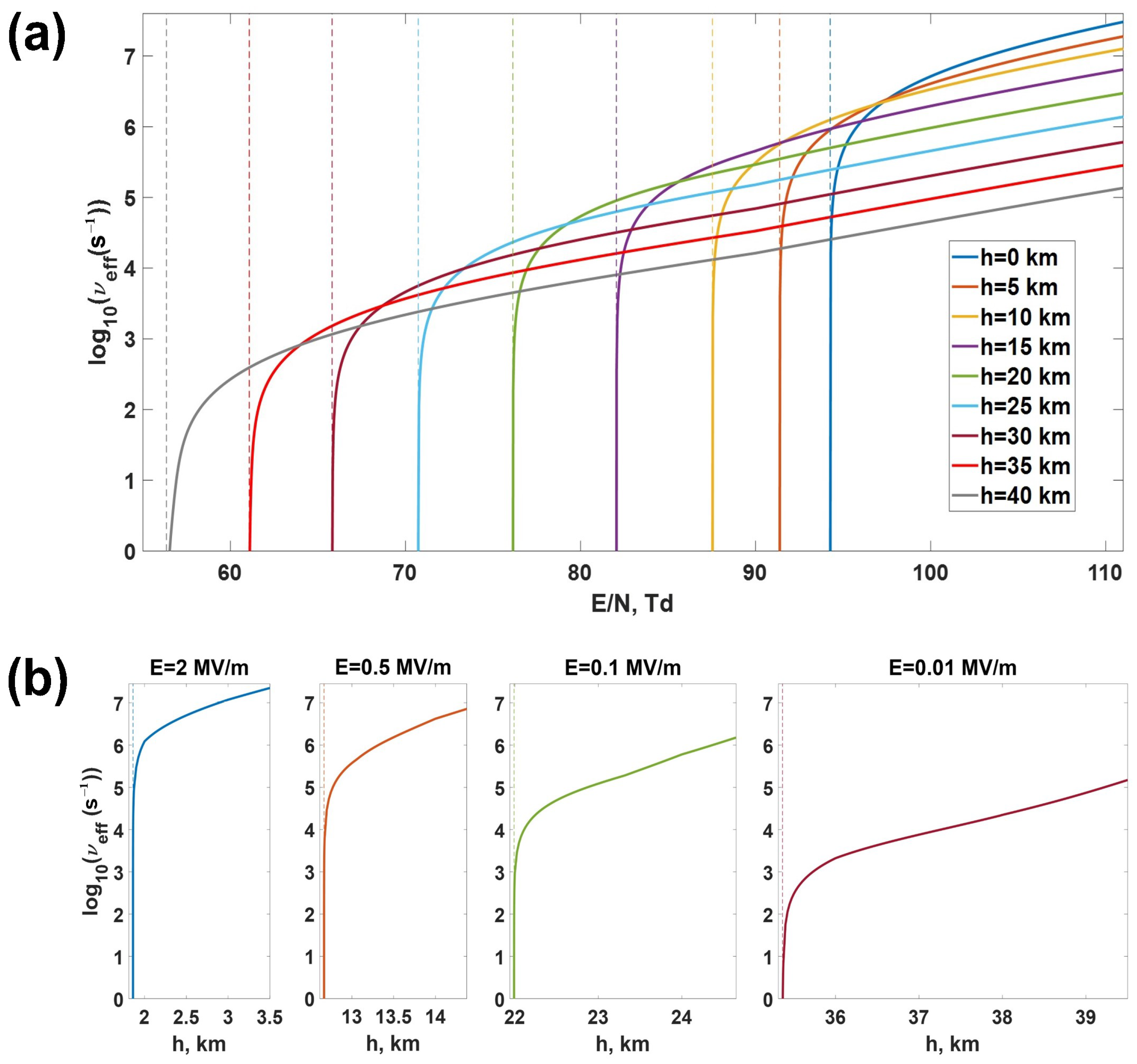
How does the effective ionization frequency depend on electric field and altitude AMSL?

4.

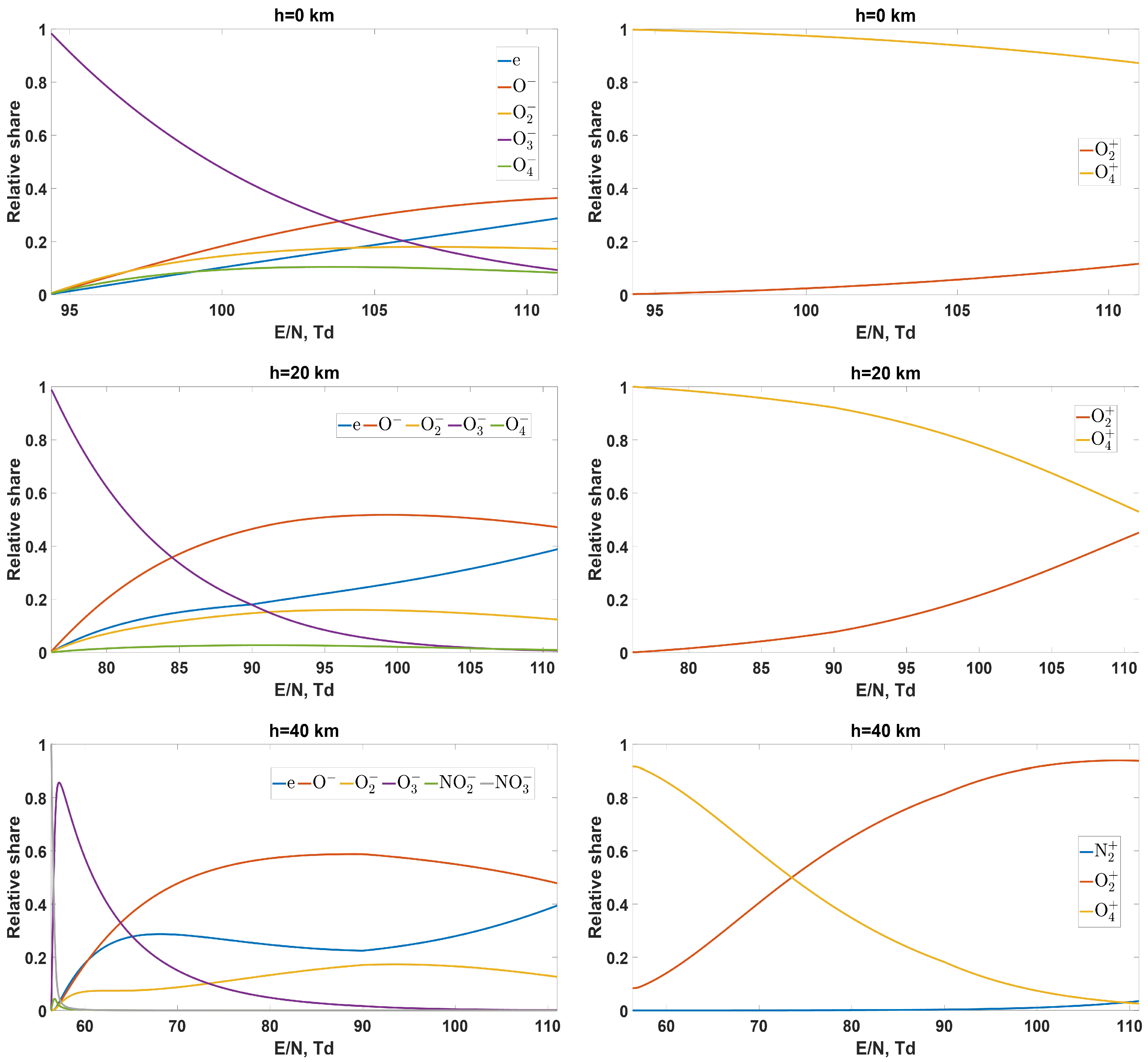
How does the composition of charged particles (electrons and ions) vary with both electric field and altitude AMSL?

5.

What is the ratio of detachment frequency to ionization frequency at different electric fields and altitudes AMSL?

3. Results

Figure 2 presents altitude profiles of reduced conventional ($E_b/N$) and critical ($E_c/N$) breakdown electric fields obtained for different atmospheric air compositions. The values of $E_b$ were obtained from Equation (2) with ${\nu }_i={\nu }_{i1}+{\nu }_{i2}$ and ${\nu }_a={\sum }_{k=1}^{12}{\nu }_{ak}$ (see Appendix A). It follows from Figure 2 that the field $E_c$, whose calculation involves a wide set of plasma-chemical reactions (see Appendix A), is significantly smaller than the conventional field $E_b$, the concept of which assumes that only ionization and attachment processes are significant. This is because, in agreement with previous studies [2,4,5,6,7], the role of electrons’ detachment from negative ions cannot be neglected. Conversions between different types of negative ions are also important because each detachment reaction involves a specific sort of negative ions. It is also seen that the gap between $E_b$ and $E_c$ increases (from 15% at the ground level to 50% at the height of 40 km) with increasing altitude AMSL. The possible factors of this can be the reduction of the role of three-body reactions with a decreasing molecule concentration and the non-monotonous altitude profile of the air temperature $T(h)$ (see Figure 1). The latter is important because the temperature of neutrals T influences both the rates of some plasma-chemical reactions (see Appendix A) and the altitude dependence of molecule concentration $N(h)$ (see Equation (15)). Further, it is seen from Figure 2 that the role of SGCs in determining the altitude profiles of $E_b$ and $E_c$ is generally not significant. For a reduced conventional breakdown field $E_b/N$, the presence of water vapor provides insignificant growth (about 2.5 Td) at altitudes smaller than 10 km because of the detachment reaction (2l) (see Appendix A), while its influence on the critical electric field $E_c$ is negligible. For the nonconventional breakdown field $E_c$, the role of SGCs becomes noticeable above approximately 25 km altitude. In particular, an exclusion of ozone results in a significant (more than 10 Td for 40 km altitude) reduction of $E_c/N$ at altitudes above 35 km because the presence of ozone provides attachment processes (2f)–(2h) (see Appendix A). Calculations show that ${\mathrm{NO}}_2$, ${\mathrm{NO}}_3$, and ${\mathrm{N}}_2\mathrm{O}$ molecules do not noticeably affect the breakdown field, at least at the considered altitudes.

Figure 3 presents several examples of dependencies of the model-predicted effective ionization frequency ${\nu }_{\mathrm{eff}}$ on the reduced electric field $E/N$ for several different altitudes and on the altitude AMSL h for different values of the electric field E. It follows from Figure 3 that the rapid growth of the increment ${\nu }_{\mathrm{eff}}$ at electric fields and altitudes slightly exceeding the critical levels quickly transfers into the mode of smoother growth. The bigger the altitude AMSL is, the smaller the rate of ${\nu }_{\mathrm{eff}}$ increment. This feature partially compensates for the critical electric field reduction with increasing altitude (see Figure 2). In this and all the following figures, (1) the presented model results were obtained with all the SGCs taken into account; (2) for panels with fixed values of h, the upper reduced electric field limit of 111 Td corresponds to the conventional breakdown field $E_b$; (3) for panels with fixed values of E, the upper altitude limits correspond to the electric field E being equal to $E_b$. Thus, in our model results we do not touch upon the area of $E>E_b$.

Figure 4 and Figure 5 demonstrate dependence curves of relative shares of positive and negative (including electrons) charged particles on the reduced electric field for several altitudes and on altitude AMSL for several fixed values of the electric field, respectively. The presented fractions correspond to normalized components of the eigenvector ${\mathbf{x}}^{+}$ of the matrix $\widehat{A}$ conjugated to the eigenvalue ${\lambda }^{+}={\nu }_{\mathrm{eff}}$ (see Section 2.2). It is seen from Figure 4 and Figure 5 that at reduced electric fields (altitudes) corresponding to the conventional breakdown threshold $E_b/N\approx$ 111 Td (the heights where $E=E_b$), the system already contains a sufficiently large amount of not only ions but also free electrons which are very important for the breakdown development. Near the critical threshold $E_c$ (the altitude at which $E=E_c$), a negative charge exists predominantly in the form of negative ions, while electrons do not survive under these conditions because of the rapid attachment to neutrals. As the electric field (altitude) increases, the role of detachment grows rapidly which is accompanied by the decay of the relative fraction of negative ions in the “community” of negatively charged particles and release of electrons. As a result, the balance gradually changes in favor of the latter.

Figure 6 shows how the ratio of effective detachment frequency to the attachment frequency ${\nu }_d^{\mathrm{eff}}/{\nu }_a$ depends on the reduced electric field $E/N$ for several altitudes and on altitude AMSL h for several fixed values of the electric field E. The total attachment frequency is ${\nu }_a={\sum }_{k=1}^{12}{\nu }_{ak}$ (see Appendix A), while the effective detachment frequency ${\nu }_d^{\mathrm{eff}}$ is calculated taking into account the relative contributions of negative ions involved in reactions (3a)–(3h) from

Table A1. The list of model reactions.

Reaction	Frequency, s${}^{-1}$	Rate Constant k, m${}^{-3}$s${}^{-1}$ or m${}^{-6}$s${}^{-1}$	Study
Impact ionization
(1a) $e+{\mathrm{N}}_2\Rightarrow 2e+{\mathrm{N}}_2^{+}$	${\nu }_{i1}=\left[{\mathrm{N}}_2\right]k$	$\begin{array}{c}{10}^{-14.09-402.9/\breve{E}},\breve{E}=80--300\mathrm{Td}\\ {10}^{-13.37-618.1/\breve{E}},\breve{E}=300--1000\mathrm{Td}\end{array}$	[19]
(1b) $e+{\mathrm{O}}_2\Rightarrow 2e+{\mathrm{O}}_2^{+}$	${\nu }_{i2}=\left[{\mathrm{O}}_2\right]k$	$\begin{array}{c}{10}^{-14.31-285.7/\breve{E}},\breve{E}=60--260\mathrm{Td}\\ (1+4·{10}^{-10}{\breve{E}}^3)\times \\ \times {10}^{-13.54-485.7/\breve{E}},\breve{E}=260--1000\mathrm{Td}\end{array}$	[19]
Electron attachment to neutrals
(2a) $e+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}^{-}+\mathrm{O}$	${\nu }_{a1}=\left[{\mathrm{O}}_2\right]k$	$\begin{array}{cc}\hfill {10}^{-15.42-127/\breve{E}},& \breve{E}=30--90\mathrm{Td}\hfill \\ \hfill {10}^{-16.21-57/\breve{E}},& \breve{E}=90--300\mathrm{Td}\hfill \end{array}$	[19]
(2b) $e+2{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{O}}_2$	${\nu }_{a2}={\left[{\mathrm{O}}_2\right]}^{2}k$	$\begin{array}{c}\hfill 1.4·{10}^{-41}(300/T_e)·exp(-600/T)\times \\ \hfill \times exp(700(T_e-T)/(T_e·T))\end{array}$	[17]
(2c) $e+{\mathrm{O}}_2+{\mathrm{N}}_2\Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{N}}_2$	${\nu }_{a3}=\left[{\mathrm{O}}_2\right]\left[{\mathrm{N}}_2\right]k$	$\begin{array}{c}\hfill 1.07·{10}^{-43}{(300/T_e)}^2·exp(-70/T)\times \\ \hfill \times exp(1500(T_e-T)/(T_e·T))\end{array}$	[17]
(2d) $e+{\mathrm{O}}_2+\mathrm{O}\Rightarrow {\mathrm{O}}^{-}+{\mathrm{O}}_2$	${\nu }_{a4}=\left[{\mathrm{O}}_2\right]\left[\mathrm{O}\right]k$	${10}^{-43}$	[17]
(2e) $e+{\mathrm{O}}_2+\mathrm{O}\Rightarrow {\mathrm{O}}_2^{-}+\mathrm{O}$	${\nu }_{a5}=\left[{\mathrm{O}}_2\right]\left[\mathrm{O}\right]k$	${10}^{-43}$	[17]
(2f) $e+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}^{-}+{\mathrm{O}}_2$	${\nu }_{a6}=\left[{\mathrm{O}}_3\right]k$	${10}^{-17}$	[17]
(2g) $e+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}_2^{-}+\mathrm{O}$	${\nu }_{a7}=\left[{\mathrm{O}}_3\right]k$	${10}^{-15}$	[17]
(2h) $e+{\mathrm{O}}_2+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{a8}=\left[{\mathrm{O}}_2\right]\left[{\mathrm{O}}_3\right]k$	the same as in (2b)	[17]
(2i) $e+\mathrm{M}+\mathrm{NO}\Rightarrow {\mathrm{NO}}^{-}+\mathrm{M}$	${\nu }_{a9}=\left[\mathrm{M}\right]\left[\mathrm{NO}\right]k$	${10}^{-42}$	[17]
(2g) $e+{\mathrm{NO}}_2\Rightarrow {\mathrm{O}}^{-}+\mathrm{NO}$	${\nu }_{a10}=\left[{\mathrm{NO}}_2\right]k$	${10}^{-17}$	[17]
(2k) $e+{\mathrm{NO}}_2(+\mathrm{M})\Rightarrow {\mathrm{NO}}_2^{-}(+\mathrm{M})$	${\nu }_{a11}=\left[{\mathrm{NO}}_2\right]k$	$3·{10}^{-17}$	[17]
(2l) $\begin{array}{c}e+{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\Rightarrow \\ \Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{H}}_2\mathrm{O}\end{array}$	${\nu }_{a12}=\left[{\mathrm{O}}_2\right]\left[{\mathrm{H}}_2\mathrm{O}\right]k$	$1.4·{10}^{-41}$	[20]
Electron detachment from negative ions
(3a) ${\mathrm{O}}^{-}+{\mathrm{N}}_2\Rightarrow {\mathrm{N}}_2\mathrm{O}+e$	${\nu }_{d1}=\left[{\mathrm{N}}_2\right]k$	$\begin{array}{c}\hfill 1.16·{10}^{-18}·exp(-{(48.9/(11+\breve{E}))}^2)\end{array}$	[2]
(3b) ${\mathrm{O}}^{-}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_3+e$	${\nu }_{d2}=\left[{\mathrm{O}}_2\right]k$	$5·{10}^{-21}$	[17]
(3c) ${\mathrm{O}}_2^{-}+\mathrm{M}\Rightarrow {\mathrm{O}}_2+\mathrm{M}+e$	${\nu }_{d3}=\left[\mathrm{M}\right]k$	$\begin{array}{c}\hfill 1.24·{10}^{-17}·exp(-{(179/(8.8+\breve{E}))}^2)\end{array}$	[2]
(3d) ${\mathrm{O}}^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_2+e$	${\nu }_{d4}=\left[\mathrm{O}\right]k$	$5·{10}^{-16}$	[17]
(3e) ${\mathrm{O}}^{-}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_2+e$	${\nu }_{d5}=\left[\mathrm{NO}\right]k$	$2.6·{10}^{-16}$	[17]
(3f) ${\mathrm{O}}_2^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_3+e$	${\nu }_{d6}=\left[\mathrm{O}\right]k$	$1.5·{10}^{-16}$	[17]
(3g) ${\mathrm{O}}_3^{-}+\mathrm{O}\Rightarrow 2{\mathrm{O}}_2+e$	${\nu }_{d7}=\left[\mathrm{O}\right]k$	$3·{10}^{-16}$	[17]
(3h) ${\mathrm{NO}}_2^{-}+\mathrm{O}\Rightarrow {\mathrm{NO}}_3+e$	${\nu }_{d8}=\left[\mathrm{O}\right]k$	${10}^{-18}$	[17]
Ion-ion conversion without nitrogen oxides
(4a) $\begin{array}{c}{\mathrm{O}}^{-}+{\mathrm{O}}_2\Rightarrow {({\mathrm{O}}_3^{-})}^{*}\Rightarrow \\ \Rightarrow {\mathrm{O}}_2^{-}+\mathrm{O}\end{array}$	${\nu }_{c1}=\left[{\mathrm{O}}_2\right]k$	$\begin{array}{c}6.96·{10}^{-17}·exp(-{(198/(5.6+\breve{E}))}^2)\end{array}$	[2]
(4b) $\begin{array}{c}{\mathrm{O}}^{-}+{\mathrm{O}}_2+\mathrm{M}\Rightarrow \\ \Rightarrow {({\mathrm{O}}_3^{-})}^{*}+\mathrm{M}\Rightarrow {\mathrm{O}}_3^{-}+\mathrm{M}\end{array}$	${\nu }_{c2}=\left[{\mathrm{O}}_2\right]\left[\mathrm{M}\right]k$	$\begin{array}{c}1.1·{10}^{-42}·exp(-{(\breve{E}/65)}^2)\end{array}$	[2]
(4c) ${\mathrm{O}}^{-}+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}_3^{-}+\mathrm{O}$	${\nu }_{c3}=\left[{\mathrm{O}}_3\right]k$	$5.3·{10}^{-16}$	[17]
(4d) $\begin{array}{c}{\mathrm{O}}_2^{-}+{\mathrm{O}}_2+\mathrm{M}\Rightarrow {\mathrm{O}}_4^{-}+\mathrm{M}\end{array}$	${\nu }_{c4}=\left[{\mathrm{O}}_2\right]\left[\mathrm{M}\right]k$	$3.5·{10}^{-43}\times (300/T)$	[17]
(4e) ${\mathrm{O}}_2^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}^{-}+{\mathrm{O}}_2$	${\nu }_{c5}=\left[\mathrm{O}\right]k$	$3.3·{10}^{-16}$	[17]
(4f) ${\mathrm{O}}_2^{-}+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{c6}=\left[{\mathrm{O}}_3\right]k$	$4·{10}^{-16}$	[17]
(4g) ${\mathrm{O}}_3^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{O}}_2$	${\nu }_{c7}=\left[\mathrm{O}\right]k$	$3.2·{10}^{-16}$	[17]
(4h) ${\mathrm{O}}_4^{-}+\mathrm{M}\Rightarrow {\mathrm{O}}_2^{-}+{\mathrm{O}}_2+\mathrm{M}$	${\nu }_{c8}=\left[\mathrm{M}\right]k$	${10}^{-16}·exp(-1044/T)$	[17]
(4i) ${\mathrm{O}}_4^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}^{-}+2{\mathrm{O}}_2$	${\nu }_{c9}=\left[\mathrm{O}\right]k$	$3·{10}^{-16}$	[17]
(4j) ${\mathrm{O}}_4^{-}+\mathrm{O}\Rightarrow {\mathrm{O}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{c10}=\left[\mathrm{O}\right]k$	$4·{10}^{-16}$	[17]
(4k) ${\mathrm{N}}_2^{+}+2{\mathrm{N}}_2\Rightarrow {\mathrm{N}}_4^{+}+{\mathrm{N}}_2$	${\nu }_{c11}={\left[{\mathrm{N}}_2\right]}^{2}k$	$5·{10}^{-41}$	[17]
(4l) ${\mathrm{N}}_2^{+}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{+}+{\mathrm{N}}_2$	${\nu }_{c12}=\left[{\mathrm{O}}_2\right]k$	$6·{10}^{-17}{(300/T)}^{0.5}$	[17]
(4m) ${\mathrm{N}}_2^{+}+{\mathrm{O}}_3\Rightarrow {\mathrm{O}}_2^{+}+\mathrm{O}+{\mathrm{N}}_2$	${\nu }_{c13}=\left[{\mathrm{O}}_3\right]k$	${10}^{-16}$	[17]
(4n) ${\mathrm{N}}_2^{+}+{\mathrm{H}}_2\mathrm{O}\Rightarrow {\mathrm{H}}_2{\mathrm{O}}^{+}+{\mathrm{N}}_2$	${\nu }_{c14}=\left[{\mathrm{H}}_2\mathrm{O}\right]k$	$1.8·{10}^{-15}$	[21]
(4o) $\begin{array}{c}{\mathrm{O}}_2^{+}+2{\mathrm{N}}_2\Rightarrow {\mathrm{O}}_2^{+}·{\mathrm{N}}_2+{\mathrm{N}}_2\end{array}$	${\nu }_{c15}={\left[{\mathrm{N}}_2\right]}^{2}k$	$9·{10}^{-43}·{(300/T)}^2$	[17]
(4p) ${\mathrm{O}}_2^{+}+2{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_4^{+}+{\mathrm{O}}_2$	${\nu }_{c16}={\left[{\mathrm{O}}_2\right]}^{2}k$	$2.4·{10}^{-42}{(300/T)}^{3.2}$	[17]
(4q) ${\mathrm{O}}_4^{+}+{\mathrm{N}}_2\Rightarrow {\mathrm{O}}_2^{+}·{\mathrm{N}}_2+{\mathrm{O}}_2$	${\nu }_{c17}=\left[{\mathrm{N}}_2\right]k$	$4.61·{10}^{-18}·{(T/300)}^{2.5}·exp(-2650/T)$	[17]
(4r) ${\mathrm{O}}_4^{+}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{+}+2{\mathrm{O}}_2$	${\nu }_{c18}=\left[{\mathrm{O}}_2\right]k$	$3.3·{10}^{-12}·{(300/T)}^4·exp(-5030/T)$	[17]
(4s) ${\mathrm{O}}_4^{+}+\mathrm{O}\Rightarrow {\mathrm{O}}_2^{+}+{\mathrm{O}}_3$	${\nu }_{c19}=\left[\mathrm{O}\right]k$	$3·{10}^{-16}$	[17]
(4t) ${\mathrm{N}}_4^{+}+{\mathrm{N}}_2\Rightarrow {\mathrm{N}}_2^{+}+2{\mathrm{N}}_2$	${\nu }_{c20}=\left[{\mathrm{N}}_2\right]k$	${10}^{-20.6+0.0036(T-300)},T=300$–$900\mathrm{K}$	[17]
(4u) ${\mathrm{N}}_4^{+}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{+}+2{\mathrm{N}}_2$	${\nu }_{c21}=\left[{\mathrm{O}}_2\right]k$	$2.5·{10}^{-16}$	[17]
(4v) ${\mathrm{N}}_4^{+}+{\mathrm{H}}_2\mathrm{O}\Rightarrow {\mathrm{H}}_2{\mathrm{O}}^{+}+2{\mathrm{N}}_2$	${\nu }_{c22}=\left[{\mathrm{H}}_2\mathrm{O}\right]k$	$2.4·{10}^{-15}$	[21]
(4w) $\begin{array}{c}{\mathrm{O}}_2^{+}·{\mathrm{N}}_2+{\mathrm{N}}_2\Rightarrow {\mathrm{O}}_2^{+}+2{\mathrm{N}}_2\end{array}$	${\nu }_{c23}=\left[{\mathrm{N}}_2\right]k$	$1.1·{10}^{-12}·{(300/T)}^{5.3}·exp(-2357/T)$	[17]
(4x) ${\mathrm{O}}_2^{+}·{\mathrm{N}}_2+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_4^{+}+{\mathrm{O}}_2$	${\nu }_{c24}=\left[{\mathrm{O}}_2\right]k$	${10}^{-15}$	[17]
(4y) ${\mathrm{H}}_2{\mathrm{O}}^{+}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{+}+{\mathrm{H}}_2\mathrm{O}$	${\nu }_{c25}=\left[{\mathrm{O}}_2\right]k$	$4.1·{10}^{-16}$	[21]
Ion-ion conversion involving nitrogen oxides
(5a) ${\mathrm{O}}^{-}+{\mathrm{N}}_2\mathrm{O}\Rightarrow {\mathrm{NO}}^{-}+\mathrm{NO}$	${\nu }_{n1}=\left[{\mathrm{N}}_2\mathrm{O}\right]k$	$2·{10}^{-16}$	[17]
(5b) ${\mathrm{O}}^{-}+\mathrm{NO}+\mathrm{M}\Rightarrow {\mathrm{NO}}_2^{-}+\mathrm{M}$	${\nu }_{n2}=\left[\mathrm{NO}\right]\left[\mathrm{M}\right]k$	${10}^{-41}$	[17]
(5c) ${\mathrm{O}}^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_2^{-}+\mathrm{O}$	${\nu }_{n3}=\left[{\mathrm{NO}}_2\right]k$	$1.2·{10}^{-15}$	[17]
(5d) ${\mathrm{O}}_2^{-}+{\mathrm{N}}_2\mathrm{O}\Rightarrow {\mathrm{O}}_3^{-}+{\mathrm{N}}_2$	${\nu }_{n4}=\left[{\mathrm{N}}_2\mathrm{O}\right]k$	${10}^{-18}$	[17]
(5e) ${\mathrm{O}}_2^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{O}}_2$	${\nu }_{n5}=\left[{\mathrm{NO}}_2\right]k$	$8·{10}^{-16}$	[17]
(5f) ${\mathrm{O}}_2^{-}+{\mathrm{NO}}_3\Rightarrow {\mathrm{NO}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{n6}=\left[{\mathrm{NO}}_3\right]k$	$5·{10}^{-16}$	[17]
(5g) ${\mathrm{O}}_3^{-}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{O}}_2$	${\nu }_{n7}=\left[\mathrm{NO}\right]k$	$2.6·{10}^{-18}$	[17]
(5h) ${\mathrm{O}}_3^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{O}}_3$	${\nu }_{n8}=\left[{\mathrm{NO}}_2\right]k$	$7·{10}^{-16}$	[17]
(5i) ${\mathrm{O}}_3^{-}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_3^{-}+\mathrm{O}$	${\nu }_{n9}=\left[\mathrm{NO}\right]k$	${10}^{-17}$	[17]
(5j) ${\mathrm{O}}_3^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{n10}=\left[{\mathrm{NO}}_2\right]k$	$2·{10}^{-17}$	[17]
(5k) ${\mathrm{O}}_3^{-}+{\mathrm{NO}}_3\Rightarrow {\mathrm{NO}}_3^{-}+{\mathrm{O}}_3$	${\nu }_{n11}=\left[{\mathrm{NO}}_3\right]k$	$5·{10}^{-16}$	[17]
(5l) ${\mathrm{O}}_4^{-}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_3^{-*}+{\mathrm{O}}_2$	${\nu }_{n12}=\left[\mathrm{NO}\right]k$	$2.5·{10}^{-16}$	[17]
(5m) ${\mathrm{NO}}^{-}+{\mathrm{O}}_2\Rightarrow {\mathrm{O}}_2^{-}+\mathrm{NO}$	${\nu }_{n13}=\left[{\mathrm{O}}_2\right]k$	$5·{10}^{-16}$	[17]
(5n) ${\mathrm{NO}}^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_2^{-}+\mathrm{NO}$	${\nu }_{n14}=\left[{\mathrm{NO}}_2\right]k$	$7.4·{10}^{-22}$	[17]
(5o) ${\mathrm{NO}}^{-}+{\mathrm{N}}_2\mathrm{O}\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{N}}_2$	${\nu }_{n15}=\left[{\mathrm{N}}_2\mathrm{O}\right]k$	$2.8·{10}^{-20}$	[17]
(5p) ${\mathrm{NO}}_2^{-}+{\mathrm{O}}_3\Rightarrow {\mathrm{NO}}_3^{-}+{\mathrm{O}}_2$	${\nu }_{n16}=\left[{\mathrm{O}}_3\right]k$	$1.8·{10}^{-17}$	[17]
(5q) $\begin{array}{c}{\mathrm{NO}}_2^{-}+{\mathrm{NO}}_2\Rightarrow {\mathrm{NO}}_3^{-}+\mathrm{NO}\end{array}$	${\nu }_{n17}=\left[{\mathrm{NO}}_2\right]k$	$4·{10}^{-18}$	[17]
(5r) $\begin{array}{c}{\mathrm{NO}}_2^{-}+{\mathrm{NO}}_3\Rightarrow {\mathrm{NO}}_3^{-}+{\mathrm{NO}}_2\end{array}$	${\nu }_{n18}=\left[{\mathrm{NO}}_3\right]k$	$5·{10}^{-16}$	[17]
(5s) $\begin{array}{c}{\mathrm{NO}}_3^{-}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{NO}}_2\end{array}$	${\nu }_{n19}=\left[\mathrm{NO}\right]k$	$3·{10}^{-21}$	[17]
(5t) $\begin{array}{c}{\mathrm{NO}}_3^{-}+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\Rightarrow \\ \Rightarrow {\mathrm{NO}}_3^{-}({\mathrm{H}}_2\mathrm{O})+{\mathrm{O}}_2\end{array}$	${\nu }_{n20}=\left[{\mathrm{H}}_2\mathrm{O}\right]\left[{\mathrm{O}}_2\right]k$	$7.5·{10}^{-41}$	[22]
(5u) $\begin{array}{c}{\mathrm{NO}}_3^{-*}+\mathrm{NO}\Rightarrow {\mathrm{NO}}_2^{-}+{\mathrm{NO}}_2\end{array}$	${\nu }_{n21}=\left[\mathrm{NO}\right]k$	$1.5·{10}^{-17}$	[17]
(5v) $\begin{array}{c}{\mathrm{NO}}_3^{-}({\mathrm{H}}_2\mathrm{O})+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\Rightarrow \\ \Rightarrow {\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_2+{\mathrm{O}}_2\end{array}$	${\nu }_{n22}=\left[{\mathrm{H}}_2\mathrm{O}\right]\left[{\mathrm{O}}_2\right]k$	$4·{10}^{-41}$	[22]
(5w) $\begin{array}{c}{\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_2+{\mathrm{O}}_2\Rightarrow \\ \Rightarrow {\mathrm{NO}}_3^{-}({\mathrm{H}}_2\mathrm{O})+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\end{array}$	${\nu }_{n23}=\left[{\mathrm{O}}_2\right]k$	$1.6·{10}^{-19}$	[22]
(5x) $\begin{array}{c}{\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_2+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\Rightarrow \\ \Rightarrow {\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_3+{\mathrm{O}}_2\end{array}$	${\nu }_{n24}=\left[{\mathrm{H}}_2\mathrm{O}\right]\left[{\mathrm{O}}_2\right]k$	$3·{10}^{-41}$	[22]
(5y) $\begin{array}{c}{\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_3+{\mathrm{O}}_2\Rightarrow \\ \Rightarrow {\mathrm{NO}}_3^{-}{({\mathrm{H}}_2\mathrm{O})}_2+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\end{array}$	${\nu }_{n25}=\left[{\mathrm{O}}_2\right]k$	$1.1·{10}^{-18}$	[22]

:

$${\nu }_d^{\mathrm{eff}}=\frac{({\nu }_{d1}+{\nu }_{d2}+{\nu }_{d4}+{\nu }_{d5})x_2+({\nu }_{d3}+{\nu }_{d6})x_3+{\nu }_{d7}{x}_4+{\nu }_{d8}{x}_7}{x_2+x_3+x_4+x_7},$$

(18)

where $x_2$, $x_3$, $x_4$, and $x_7$ are components of the vector of variables $\mathbf{x}$ corresponding to ${\mathrm{O}}^{-}$, ${\mathrm{O}}_2^{-}$, ${\mathrm{O}}_3^{-}$, and ${\mathrm{NO}}_2^{-}$ ions (see Appendix B) that vary with the electric field and altitude AMSL (see Figure 4 and Figure 5). It follows from Figure 6 that the role of the detachment process quickly becomes significant at electric fields exceeding the critical threshold $E_c$, especially for high altitudes. The knowledge of this ratio is important because, if these conditions can be considered as quasi-equilibrium, it characterizes the balance between electron ($n_e$) and atmospheric negative ion ($n_n$) number densities:

$$\frac{n_e}{n_n}\approx \frac{{\nu }_d^{\mathrm{eff}}}{{\nu }_a}.$$

(19)

4. Discussion

The concept of a critical electric field of air breakdown is closely related to the problem of lightning initiation which heads the list of ten top questions in the physics of lightning [15]. Indeed, maximal electric fields measured in clouds are about an order of magnitude lower than the conventional breakdown value at the same altitude (see, for example, Table 3.2 in [16] and Table 3.1 in [15]) which means that there must be some physical mechanisms making electrical breakdown possible in conditions of smaller electric fields. In this study, we developed a numerical model which takes into account a wide list of plasma-chemical processes and the presence of atmospheric SGCs to show that the critical electric field, at which charged particles multiplication begins, is noticeably lower than the conventional breakdown threshold and that the gap between their values increases with increasing altitude (see Figure 2). It was also shown that at electric fields higher than $E_c$ there is some amount of free electrons (see Figure 4 and Figure 5) which are the key element of any electrical breakdown. The fact that, even in electric fields smaller than the conventional breakdown threshold, the air contains some amount of not only ions but also free electrons sheds some light on how lightning initiation in sub-breakdown intracloud conditions is possible at all (see [7] for more details).

In our model, we deal with a linearized system of differential equations and neglect the higher order processes, the most significant of which are electron-ion and ion-ion recombination. This is valid because near the critical threshold $E_c$ the measure of air ionization is low. For electric fields significantly higher than $E_c$, recombination becomes noticeable which makes the used approach inoperable. That is why in the presentation of our model results we limit ourselves to electric fields ranging from critical $E_c$ to conventional $E_b$ breakdown thresholds. Production and chemical transformations of SGCs are also not taken into account assuming that their concentrations do not differ significantly from that of the virgin air. Effective generation of SGC molecules (some reactions are shown in Appendix A) is possible at relatively high concentrations of charged particles which is not the case near their multiplication threshold. Regarding the transformations between neutrals, the rate constants of their reactions are functions of the air temperature [17]. As there must not be significant air heating at the considered electric field range, SGC number densities must not change significantly. Although the described model limitations can be crucial far above $E_c$, it is believed that they do not significantly affect the model predictions described in the paper.

In this study, the used altitude profiles of nitrogen oxides were taken, for lack of anything better, from particular experiments [11,12,13,14] conducted at certain times and places which can potentially be a source of inaccuracy of the model results. On the other hand, it follows from Figure 2 that the most “important” SGC noticeably influencing the nonconventional breakdown field is ozone whose averaged number density altitude profile is relatively well known. For the conventional case, the most “influential” SGC is the water vapor which is also well measured near the ground. So, the use of locally measured altitude profiles of nitrogen oxides is believed to be justified.

The altitude range of 0–40 km AMSL is considered in the study. At higher altitudes, the atmosphere becomes strongly ionized by cosmic rays (see Figure 1.3 in [16]) regardless of the electric field. Because of this, it can hardly be considered as a dielectric medium which significantly complicates the concept of its breakdown field. For the considered altitude range, we suppose that below the critical electric field concentrations of all the charged particles are negligible which allows us to work with a zero equilibrium state.

5. Conclusions

The concept of a critical breakdown field of atmospheric air taking into account the wide range of plasma-chemical reactions and the presence of SGCs is refined in the study. In addition, the model results allow to analyze the dynamics of charged components composition and the relative share of free electrons among negatively charged particles near the critical breakdown threshold. The main findings of the study are the following:

1.

The critical electric field of atmospheric air, at which the multiplication of charged particles begins, is significantly smaller than the conventional value, mostly due to electrons’ detachment from negative ions. The gap between conventional and nonconventional thresholds increases with increasing altitude AMSL from 15% at the ground level to 50% at the height of 40 km.

2.

The presence of SGCs does not significantly influence the critical electric field.

3.

Close to the critical threshold, the effective ionization frequency is a sharp function of the reduced electric field. The rate of its growth decreases with increasing altitude AMSL which partially compensates for the critical electric field reduction.

4.

Above the critical electric field, ionized air contains some amount of free electrons. Their relative share in “community” of negatively charged particles, which can be expressed via the ratio of effective detachment frequency to the attachment frequency, generally increases with increasing reduced electric field.

The results of the study testify that discharge development in atmospheric air actually begins in electric fields significantly smaller than the conventional breakdown threshold which is important for the lightning initiation problem.