1. Introduction
Estimating pan evaporation (PE) is essential for monitoring, surveying, and managing water resources. In many arid and semi-arid regions, water resources are scarce and seriously endangered by overexploitation. Therefore, the precise estimation of evaporation becomes imperative for the planning, managing, and scheduling irrigation practices. Evaporation happens if there is an occurrence of vapor pressure differential between two surfaces, i.e., water and air. The most general and essential meteorological parameters that influence the rate of evaporation are relative humidity, temperature, solar radiation, the deficit of vapor pressure, and wind speed. Thus, for the estimation of evaporation losses, these parameters should be considered for the precise planning and managing of different water supplies [
1,
2].
In the global hydrological cycle, the evaporation stage is defined as transforming water from a liquid to a vapor state [
3]. In recent decades, evaporation losses have increased significantly, especially in semi-arid and arid regions [
4,
5]. Many factors, such as water budgeting, irrigation water management, hydrology, agronomy, and water supply management require a reliable evaporation rate estimation. The water budgeting factor has been modeled on estimates and the responses of cropping water to varying weather conditions. The daily evaporation of the pan (Epan) was considered a significant parameter. It was widely used as an index of lake and reservoir evaporation, evapotranspiration, and irrigation [
6].
It is usually calculated in one of two ways, either (a) directly with pan evaporimeters or (b) indirectly with analytical and semi-empirical models dependent on climatic variables [
7,
8]. However, the calculation has proved sensitive to multiple sources of error, including strong wind circulation, pan visibility, and water depth measurement in the pan, for various reasons, including physical activity in and around the pan, water litter, and pan construction material and pan height. It can also be a repetitive, costly, and time-consuming process to estimate monthly pan evaporation (EP
m) using direct measurement. As a result, in the hydrological field, the introduction of robust and reliable intelligent models is necessary for precise estimation [
9,
10,
11,
12,
13,
14].
Several researchers have used meteorological variables to forecast E
pan values, as reported by [
15,
16,
17,
18]. Since evaporation is a non-linear, stochastic, and complex operation, a reliable formula to represent all the physical processes involved is difficult to obtain [
19]. In recent years, most researchers have commonly acknowledged the use of artificial intelligence techniques, such as artificial neural networks (ANNs), adaptive neuro-fuzzy inference method (ANFIS), and genetic programming (G.P.) in hydrological parameter estimation [
15,
20,
21,
22]. In estimating E
pan, Sudheer et al. [
23] used an ANN. They found that the ANN worked better than the other traditional approach. For modeling western Turkey’s daily pan evaporation, Keskin et al. [
24] used a fuzzy approach. To estimate regular E
pan, Keskin and Terzi [
25] developed multi-layer perceptron (MLP) models. They found that the ANN model showed significantly better performance than the traditional system. Tan et al. [
26] applied the ANN methodology to model hourly and daily open water evaporation rates. In regular E
pan modeling, Kisi and Çobaner [
27] used three distinct ANN methods, namely, the MLP, radial base neural network (RBNN), and generalized regression neural network (GRNN). They found that the MLP and RBNN performed much better than GRNN. In a hot and dry climate, Piri et al. [
28] have applied the ANN model to estimate daily E
pan. Evaporation estimation methods discussed by Moghaddamnia et al. [
19] were implemented based on ANN and ANFIS. The ANN and ANFIS techniques’ findings were considered superior to those of the analytical formulas. The fuzzy sets and ANFIS were used for regular modeling of E
pan by Keskin et al. [
29] and found that the ANFIS method could be more efficiently used than fuzzy sets in modeling the evaporation process. Dogan et al. [
30] used the approach of ANFIS for the calculation of evaporation of the pan from the Yuvacik Dam reservoir, Turkey. Tabari et al. [
31] looked at the potential of ANN and multivariate non-linear regression techniques to model normal pan evaporation. Their findings concluded that the ANN performed better than non-linear regression. Using linear genetic programming techniques, Guven and Kişi [
20] modeled regular pan evaporation by gene-expression programming (GEP), multi-layer perceptrons (MLP), radial basis neural networks (RBNN), generalized regression neural networks (GRNN), and Stephens–Stewart (SS) models. Two distinct evapotranspiration models have been used and found that the subtractive clustering (SC) model of ANFIS produces reasonable accuracy with less computational amounts than the ANFIS-GP ANN models [
32].
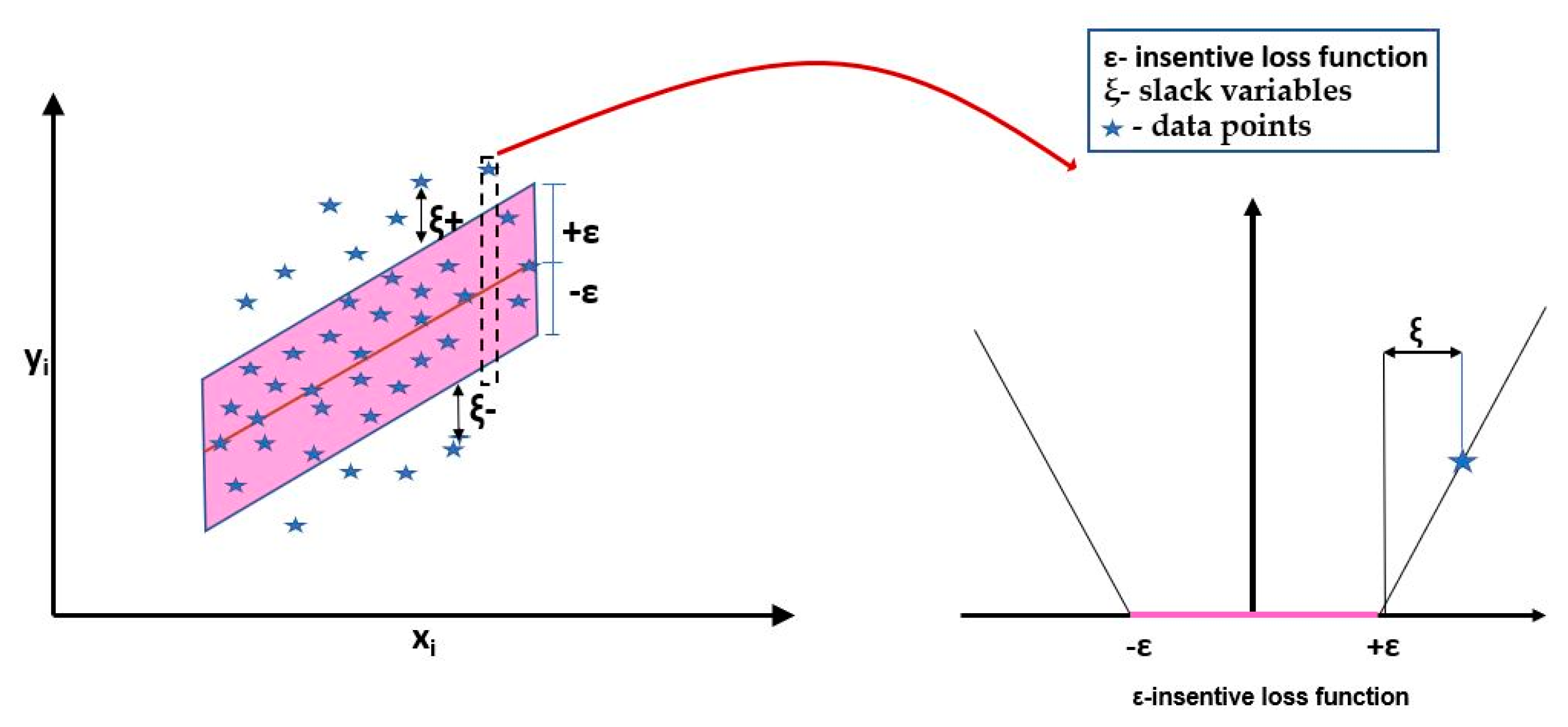
A modern universal learning machine proposed by Vapnik (1995) [
33] is the support vector machine (SVM), which is applied to both regression [
30,
34] and pattern recognition. An SVM uses a kernel mapping device to map the input space data to a high-dimensional feature space where the problem is linearly separable. An SVM’s decision function relates to the number of support vectors (S.V.s) and their weights and the kernel chosen a priori, called the kernel [
1,
21]. Several kinds of kernels are Gaussian and polynomial kernels that may be used [
10]. Moreover, artificial neural networks (ANN), wavelet-based artificial neural networks (WANN), support vector machine (SVM) were applied at different combinations of input variables by [
23]. Their results showed that ANN, which contains three variables of air temperatures and solar radiation, produces root mean square error (RMSE) of 0.701, mean absolute error (MAE) of 0.525, correlation coefficient (R) of 0.990, and Nash–Sutcliffe efficiency (NSE) of 0.977 had better performances in comparison with WANN and SVR.
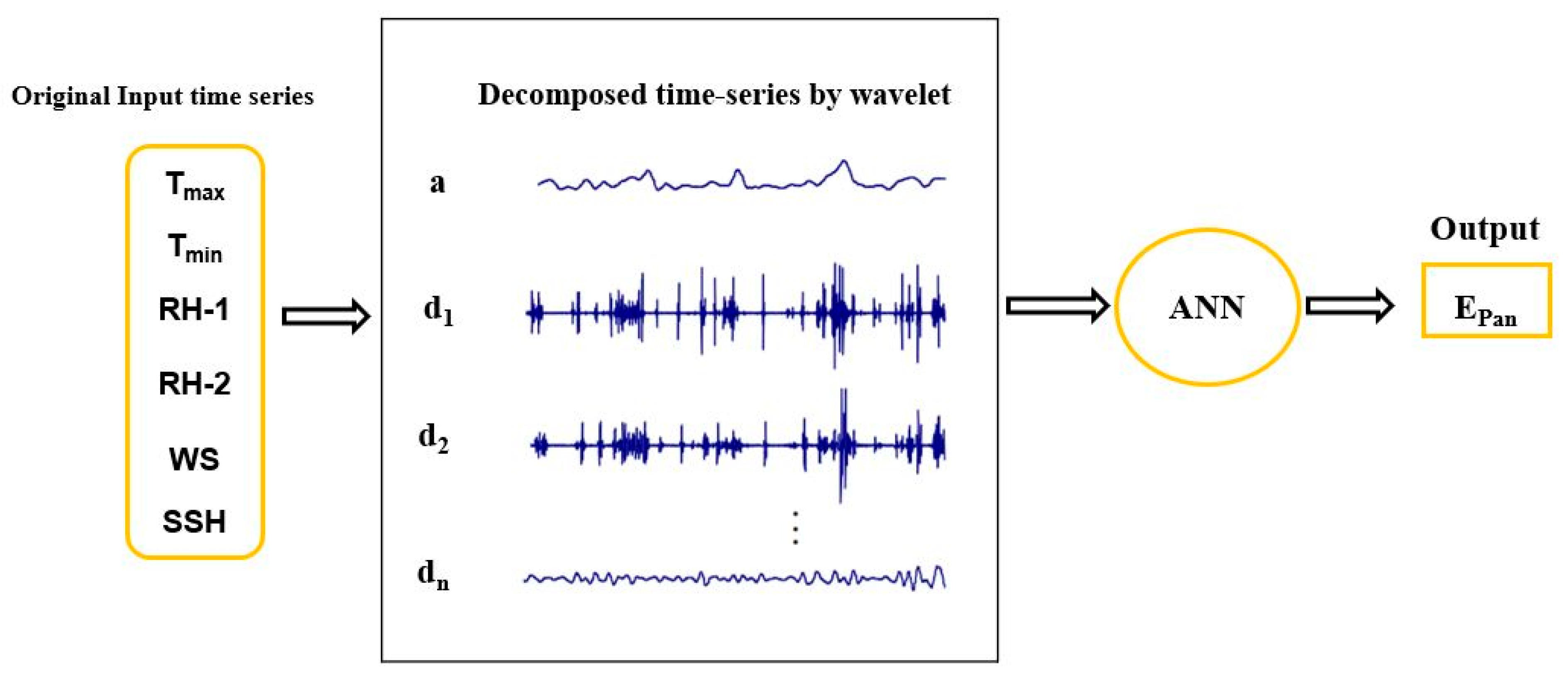
In principle, wavelet decomposition emerges as an efficient approximation instrument [
18]; that is to say, a set of bases can approximate the random wavelet functions. To approximate E
pan, researchers used ANN, WANN, radial function-based support vector machine (SVM-RF), linear function-based support vector machine (SVM-LF), and multi-linear regression (MLR) models of climatic variables.
There have been many studies on the estimation of E
pan based on weather variables using data-driven methods. However, the estimation of E
pan based on lag-time weather variables, which can be obtained easily, is not standard. After testing different acceptable combinations as input variables, the same inputs were used in artificial intelligence processes. In the proposed study, the main objective is to (1) model E
pan using ANN, WANN, SVM-RF, SVM-LF, and MLR models under different scenarios and (2) to select the best-developed model and scenario in E
pan estimation based on statistical metrics. The document’s format is as follows.
Section 2 contains the study’s materials and methods:
Section 3 gives the statistical indexes and methodological properties. The models’ applicability to evaporation prediction and the results are discussed in
Section 4. The conclusion is found in
Section 5.
3. Results
3.1. Quantitative and Qualitative Evaluation of Results
This section deals with quantitative and qualitative results obtained for the developed models. ANN and WANN trials were conducted depending on the different number of neurons in hidden layers. In contrast, SVM-LF and SVM-RF trials were performed by taking several values of SVM-g, SVM-c, and SVM-e parameters. These were represented in
Table 4,
Table 5 and
Table 6 as a structure for the model.
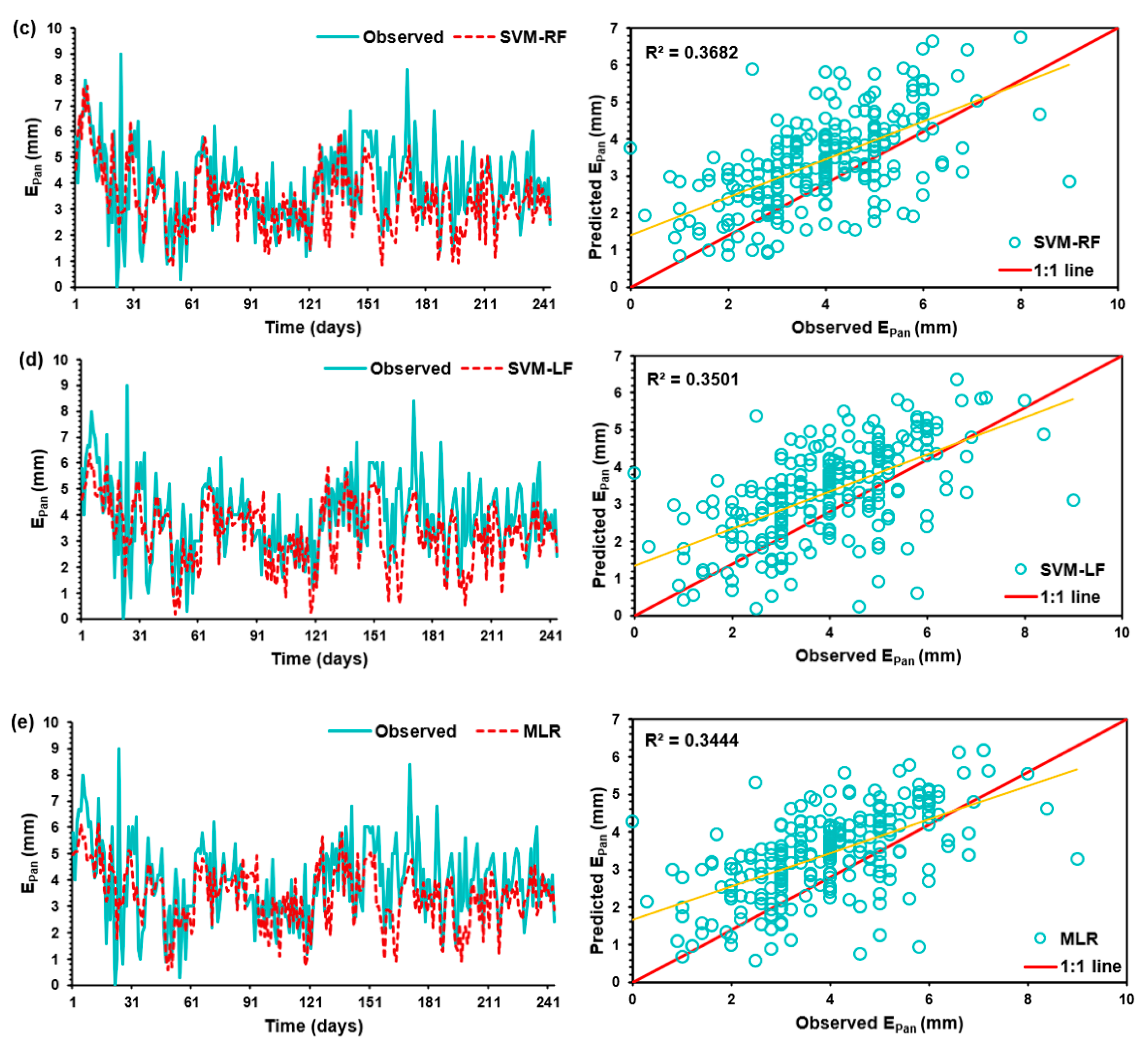
3.2. Comparison of Training and Testing Datasets for Scenario 1
The training results obtained by ANN, Wavelet, and SVM have been shown in
Table 4. As depicted in
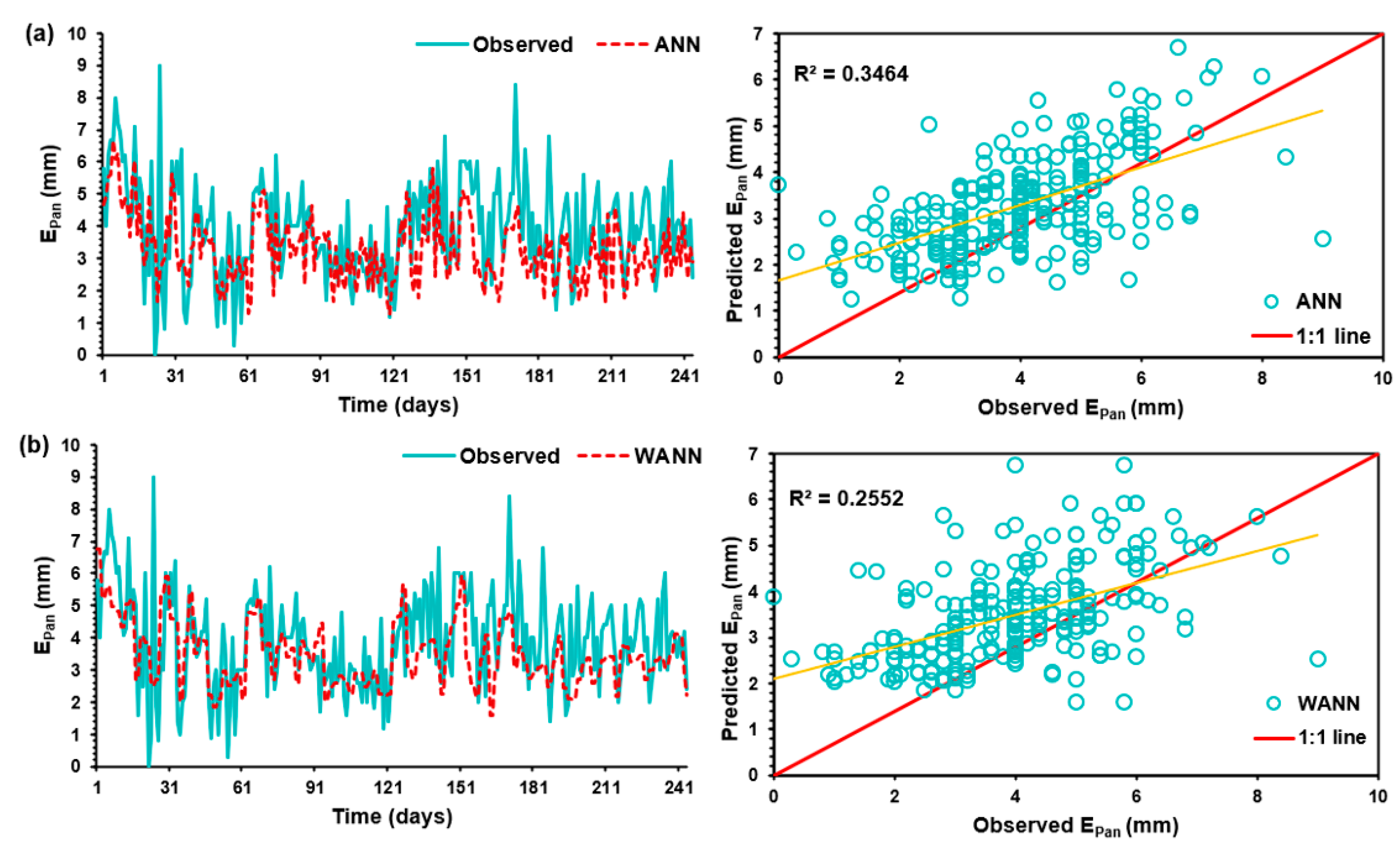
Table 4, for three developed ANN models, namely ANN-1, ANN-2, and ANN-3, ANN-1 has the highest PCC value of 0.832, the lowest RMSE value of 0.993, the highest NSE value of 0.685, and the highest WI value of 0.904.
Similarly, for the developed WANN model, WANN-1 has shown better performance, with a PCC value of 0.773. Furthermore, the WANN model also has the lowest RMSE value of 1.123, the highest NSE value of 0.597, and the highest WI value of 0.860. Furthermore, among developed SVM-RF and SVM-LF models, SVM-RF-3 has shown better performance than other developed models. The SVM-RF-3 model has the highest PCC value of 0.857; it has the lowest RMSE value of 0.956, the highest NSE value of 0.708, and the highest WI value of 0.895 during training datasets. The value of PCC, RMSE, NSE, and WI for MLR techniques was 0.695, 1.274, 0.483, and 0.800. Thus, it can be stated that SVM-RF has modeled the Epan most efficiently of all the machine learning algorithms developed for training.
Among developed ANN models, ANN-1 has the highest PCC value of 0.589; it has the lowest RMSE value of 1.387 and the highest NSE value of 0.136. Similarly, for the WANN model, WANN-1 has shown better performance with a PCC value of 0.505, the lowest RMSE value of 1.394, the highest NSE value of 0.129, and a WI value of 0.676.
Furthermore, among developed SVM-RF and SVM-LF models, SVM-RF-3 has shown better performance than other developed models. The SVM-RF-3 model has the highest PCC value of 0.607, RMSE value of 1.349, NSE value of 0.183, and the highest WI value of 0.749 training datasets. The values of PCC, RMSE, NSE, and WI for MLR techniques were 0.587, 1.345, 0.188, and 0.725, respectively. The scatter plot and line diagram for the testing data set has been shown in
Figure 6. From the line diagram, it can be observed that the obtained results were under-predicted for all models. The scatter plot shows that the highest value of the determination (R
2) coefficients was obtained for the SVM-RF model. Thus, it can be suggested that SVM-RF has modeled the E
pan most efficiently among all the machine learning algorithms developed for testing.
3.3. Comparison of Training and Testing Datasets for Scenario 2
In Scenario 2, 70% of the entire data set has been used for training, and the rest of the data has been used for testing the developed model. The training results obtained by ANN, Wavelet, and SVM have been shown in
Table 5.
As shown in
Table 5, among three developed ANN models, the ANN-1 has the highest PCC value of 0.760, the lowest RMSE value of 1.180, the highest NSE value of 0.577, and the highest WI value of 0.854. Similarly, for the WANN model, WANN-2 has shown better performance with a PCC value of 0.725, a lowest RMSE value of 1.264, a highest NSE value of 0.515, and a highest WI value of 0.831. Furthermore, among developed SVM-RF and SVM-LF models, SVM-RF-3 has shown better performance than other developed models. The SVM-RF-3 model has the highest PCC value of 0.812, the lowest RMSE value of 1.262, the highest NSE value of 0.650, and the highest WI value of 0.714 during training datasets. The values of PCC, RMSE, NSE, and WI for MLR techniques were 0.693, 1.308, 0.481, and 0.799, respectively, during training processes. Thus, it can be stated that SVM-RF has modeled the E
pan most efficiently among all the machine-learning algorithms developed for training.
For Scenario 2, where 30% of the data set has been used for testing, model ANN-1 has the highest PCC value of 0.547, the lowest RMSE value of 1.222, the highest NSE value of 0.046, and a WI value of 0.704 among ANN models. Similarly, WANN-1 has shown better performance, with a PCC value of 0.457, the lowest RMSE value of 1.252, the highest NSE value of −0.002, and the highest WI value of 0.639 WANN models. Furthermore, SVM-RF-3 has shown better performance as compared to other developed models among SVM-RF and SVM-LF models. The SVM-RF-3 model has the highest PCC value of 0.568, the lowest RMSE value of 1.262, and the highest WI value of 0.714 during training datasets. The values of PCC, RMSE, NSE, and WI for MLR techniques were 0.531, 1.262, −0.017, and 0.700, respectively. The scatter plot and line diagram for testing have been shown in
Figure 7. It can be seen from the line diagram that the obtained results were under-predicted for all models. The scatter plot showed that the highest value of the coefficient of determination (R
2) was obtained for SVM-RF models of 0.3221. Thus, it can be shown that SVM-RF has modeled the E
pan most efficiently among all the machine learning algorithms developed for testing.
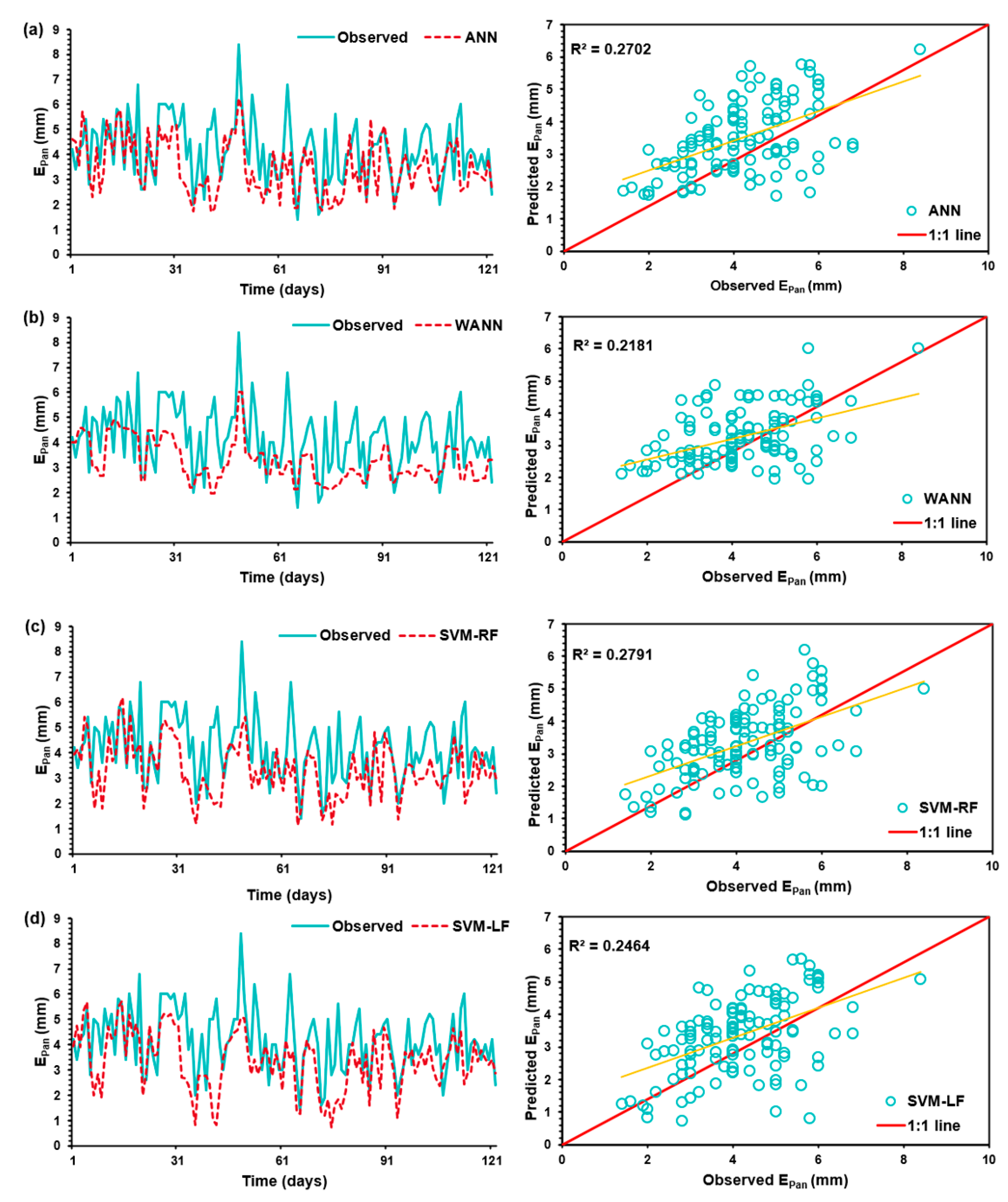
3.4. Comparison of Training and Testing Datasets for Scenario 3
In Scenario 3, 80% of the total dataset was used for training periods, while the rest, 20%, was used to test the models. The training results obtained by ANN, wavelet analysis, and SVM have been shown in
Table 6.
As depicted from
Table 6, for developed ANN models, model ANN-3 has the highest PCC value of 0.520; it has an RMSE value of 1.333 and a W.I. value of 0.688. Similarly, for the WANN model, WANN-1 has shown better performance with a PCC value of 0.725, the lowest RMSE value of 1.213, the highest NSE value of 0.519, and the highest WI value of 0.812. Further, SVM-RF-3 has shown better performance compared to other developed models. The SVM-RF-3 model has the highest PCC value of 0.893, the lowest RMSE value of 0.858, the highest NSE value of 0.760, and the highest WI value of 0.913 during training datasets. The values of PCC, RMSE, NSE, and WI for MLR techniques were 0.688, 1.269, 0.474, and 0.795, respectively. Thus, it can be depicted that SVM-RF has modeled the E
pan most efficiently among all the machine learning algorithms developed for training.
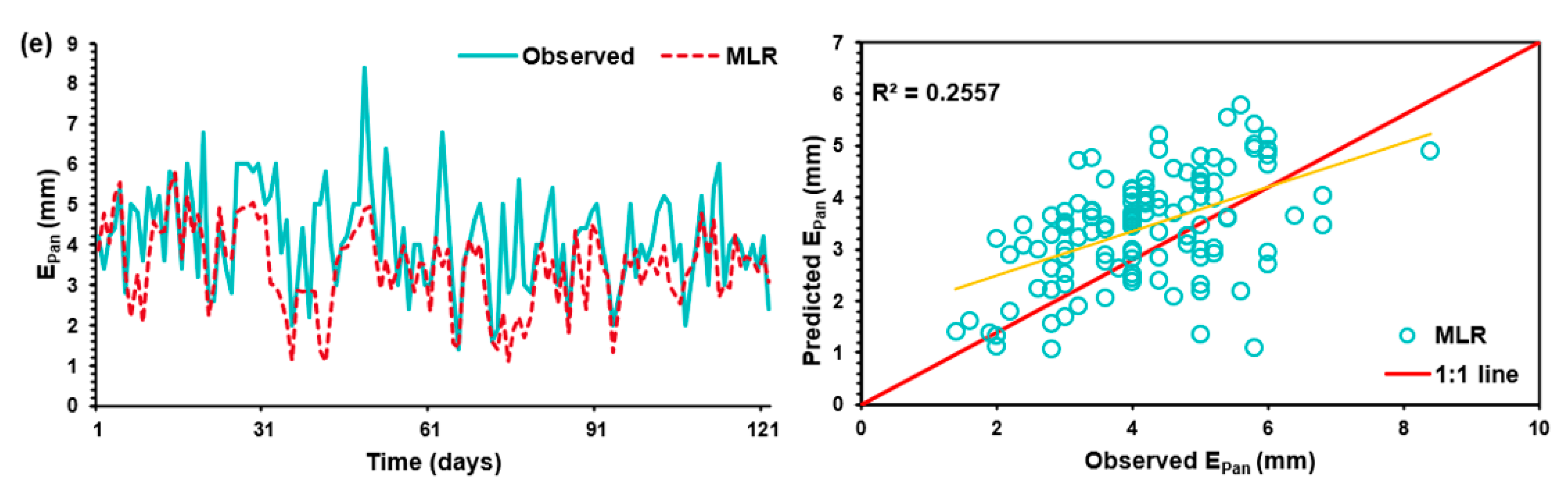
For testing datasets, for developed ANN models, ANN-3 has the highest PCC value of 0.520, an RMSE value of 1.333, and the highest W.I. value of 0.688. Similarly, for the WANN model, WANN-1 has shown better performance with a PCC value of 0.467, an RMSE value of 1.447, and WI value of 0.639. Furthermore, among developed SVM-RF and SVM-LF models, SVM-RF-1 has shown better performance than other developed models. The SVM-RF-1 model has the highest PCC value of 0.528, the lowest RMSE value of 1.411, and the highest WI value of 0.665 during the testing of datasets.
The values of PCC, RMSE, NSE, and WI for MLR techniques were 0.506, 1.363, −0.227, and 0.665. The scatter plot and line diagram for testing have been shown in
Figure 8. From the line diagram, it has been observed that obtained results were under-predicted and over-predicted for all models. The scatter plot showed that the highest value of the coefficient of determination (R
2) was obtained for SVM-RF models of 0.2791. Thus, it can be seen that SVM-RF has modeled the daily E
pan most efficiently among all the machine learning algorithms developed for testing.
The comparative results of training and testing data results have been shown in
Table 7. This table could suggest that training and testing data using the SVM-RF model, E
pan, can be modeled more accurately than ANN and WANN.
The performance of models from best to lowest is SVM > ANN > MLR > WANN for all three scenarios.
Table 7 also showed that the WANN model performed poorly compared to other models. This is because wavelet transformation does not reveal the hidden information present in the primary time-series data through different sub-series. It is also observed that, with an increase in the sample set for training, the testing data will show a less accurate modeled result.
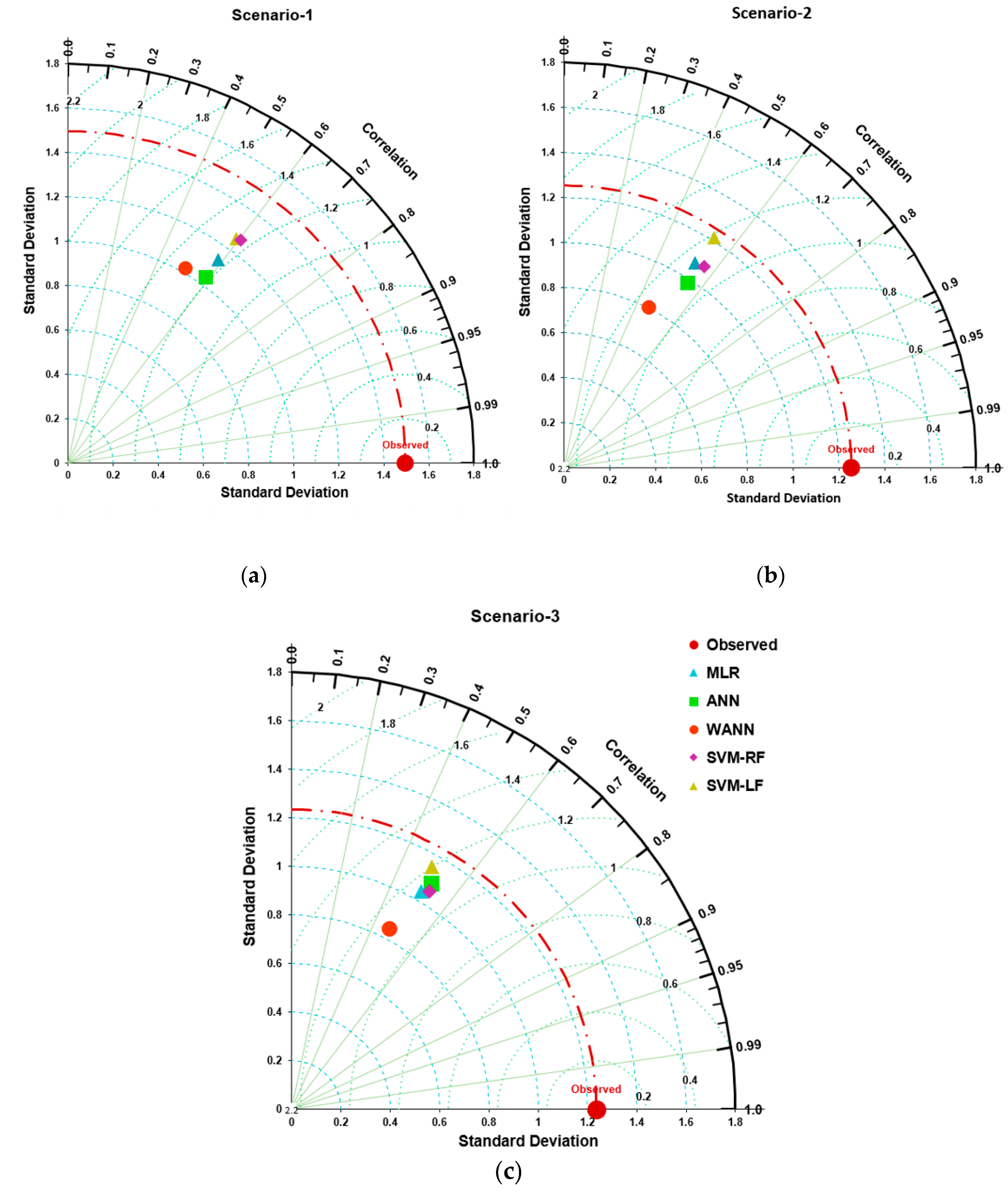
The comparative result of all three scenarios of all developed models has also been shown through Taylor’s diagram [
50] in
Figure 9a–c, which acquires information based on correlation coefficient, standard deviation, and root mean square difference [
27].
Figure 9a–c indicates that the SVM-RF model predictions in all three scenarios are very close to the daily values of E
pan, which are tending more toward observed point values at abscissa. The performance-based correlation coefficient, standard deviation, and root mean square difference are also superior compared to others. Therefore, the SVM-RF model with T
max, T
min, RH-1, RH-2, WS, and SSH climate variables can be used for daily E
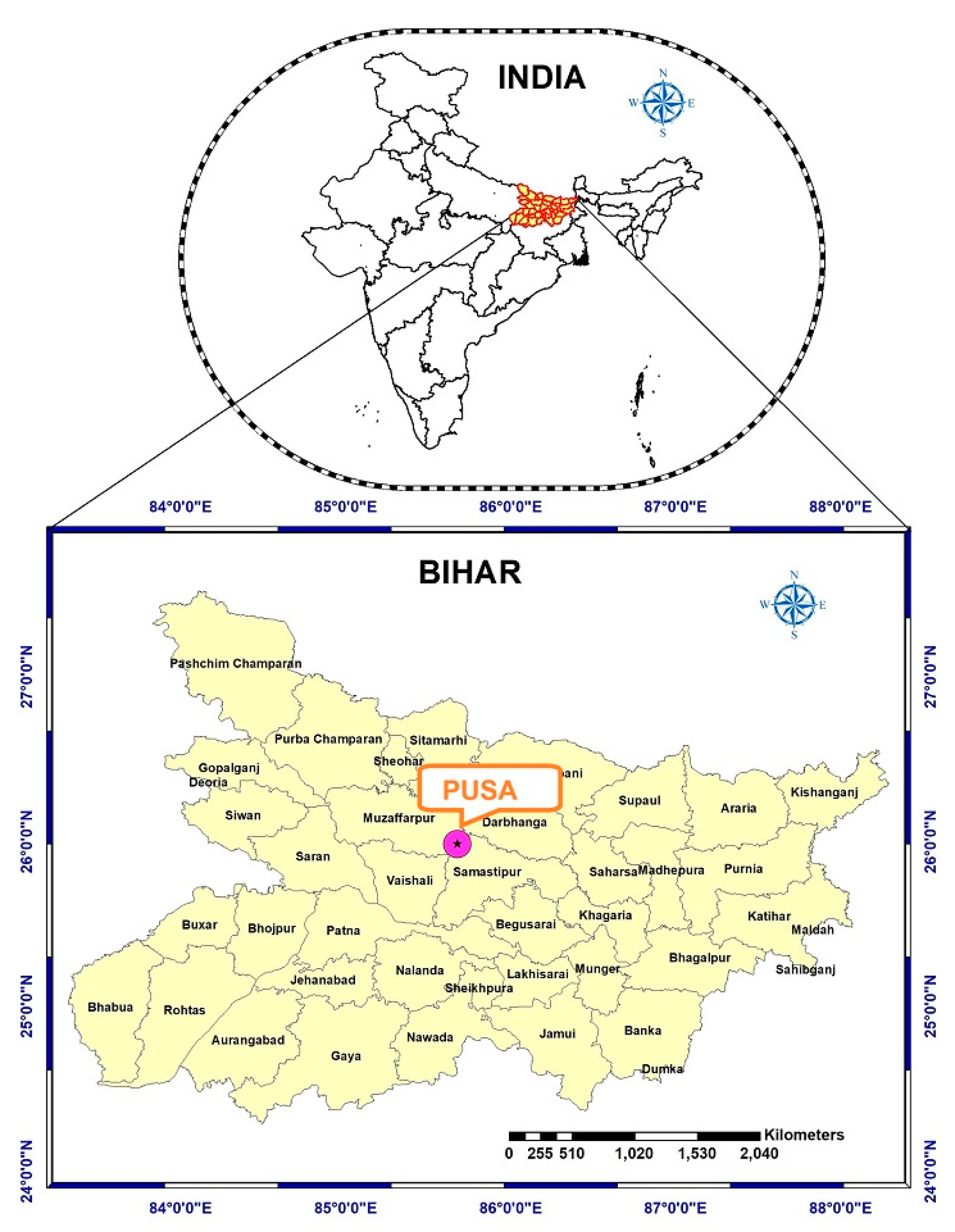
pan estimation at the Pusa station.
4. Discussion
Our results as obtained are similar to the results of [
17,
39]. They modeled pan evaporation and found that the ANN and SVR models achieved high correlation coefficients ranging from 0.81 to 0.90. In addition, our findings are in agreement with Cobaner [
15], who observed that the ANN model with Bayesian Regularization (BR) and algorithm during training, validation, and testing generated 0.76, 0.67, and 0.72, respectively. Applying Levenberg–Marquardt (LM) algorithm, the corresponding values were 0.77, 0.69, and 0.71, respectively. Furthermore, for SVR, this model’s findings are close to those of Tezel and Buyukyildiz [
51]. They concluded that the SVR gave high correlations, ranging from 0.86 to 0.90, for evaporation forecasting. Moreover, the results obtained with SVR are in line with Pammar and Deka [
52]. They stated that the correlation coefficients and RMSE ranged from 0.79 to 0.84 and from 0.90 to 1.03 under the different kernels. The values of RMSE conducted by Alizamir et al. [
17] were 0.836 and 0.882 for ANN 4-6-6-1 and 1.028 and 1.106 for MLR models through the training and testing period. Their results found that ANN’s evaporation estimation was better than the estimation through MLR and agreed with the present study results. The ANN model of pan evaporation, with all available variables as inputs, proposed by Rahimi Khoob [
21] was the most accurate, delivering an R
2 of 0.717 and an RMSE of 1.11 mm independent evaluation data set, which correlates with our outcomes. As reported by Keskin and Terzi [
25], the R
2 values of the ANN 3, 6, 1, ANN 6, 2, 1, and ANN 7, 2, 1 model equaling 0.770, 0.787, and 0.788 for modeling E
pan are also acceptable and agree with our results. These developed models produced a more acceptable outcome than Kim et al. [
53]. The latter stated that the ANN and MLR generated R
2 values ranging from 0.69 to 0.74 and from 0.61 to 0.64. The RMSE for these models varied from 1.38 to 1.48 and from 1.56 to 1.60, respectively. However, all developed models in this manuscript could not capture the variability of extreme values present in the input and output parameters at the given study location. The models’ efficiency might be improved if the extreme values are removed. This is one of the limitations of the study outlined in this paper.
5. Conclusions
Evaporation processes are strongly non-linear and stochastic phenomena affected by relative humidity, temperature, vapor pressure deficit, and wind speed. In the present study, daily pan evaporation (Epan) estimation was evaluated using ANN, WANN, SVM-RF, SVM-LF, and MLR models. The input climatic variables for the estimation of daily Epan were: maximum and minimum temperatures (Tmax and Tmin), relative humidity (RH-1 and RH-2), wind speed (W.S.), and bright sunshine hours (SSH). The free availability of these meteorological parameters for other stations in Bihar, India, is a significant concern and limitation of this research. The proposed models were trained and tested in three separate scenarios, i.e., Scenario 1, Scenario 2, and Scenario 3, utilizing different percentages of data points. The models above were evaluated using statistical tools, namely, PCC, RMSE, NSE, and WI, through visual inspection using a line diagram, scatter plot, and Taylor diagram. Research results evidenced the SVM-RF model’s ability to estimate daily Epan, integrating all weather details like Tmax, Tmin, RH-1, RH-2, WS, and SSH The SVM-RF model’s dominance was found at Pusa station for all scenarios investigated. It is also clear that, with an increase in the sample set for training, the testing data will show a less accurate modeled result. Since the Pusa dataset has many extreme values, the developed model could not capture extreme values very efficiently; this is one of the limitations of this paper. Overall, the current research outcome showed the SVM-RF model’s viability as a newly established data-intelligent method to simulate pan evaporation in the Indian area. It can be extended to many water resource engineering applications. It is also recommended that SVM-RF models can be applied under the same climatic conditions and the availability of the same meteorological parameters.