Multiscale Modeling of Convection and Pollutant Transport Associated with Volcanic Eruption and Lava Flow: Application to the April 2007 Eruption of the Piton de la Fournaise (Reunion Island)
Abstract
1. Introduction
2. Models and Method
Fluxes and Effusion Models
3. Flux Parameterizations for the 2017 Eruption
- The sensible heat flux zone: This zone covers the entire domain at 100 m resolution coupled with ForeFire. As a result, the sensible heat forcing will be triggered for any point in contact with lava.
- The CO flux zone: These zones correspond to the locations of the primary drillings (in green in Figure 3).
- The SO flux zone: This zone corresponds to the eruptive vent where all the estimated sulfur dioxide will be emitted.
- The HO and HCl flux zone: This zone corresponds to the entry of lava into the sea. The flow models of HCl and water vapor will be triggered simultaneously (in blue in the Figure 3).
3.1. Parameterization of CO Fluxes
3.2. Parameterization of Sensible Heat Fluxes
3.3. Parameterization of SO Fluxes
3.4. Water Va Pour Fluxes at the Vent
3.5. Water Vapour Fluxes for the Laze Plume over Seawater
3.6. HCl Fluxes
4. Simulation Results and Analysis
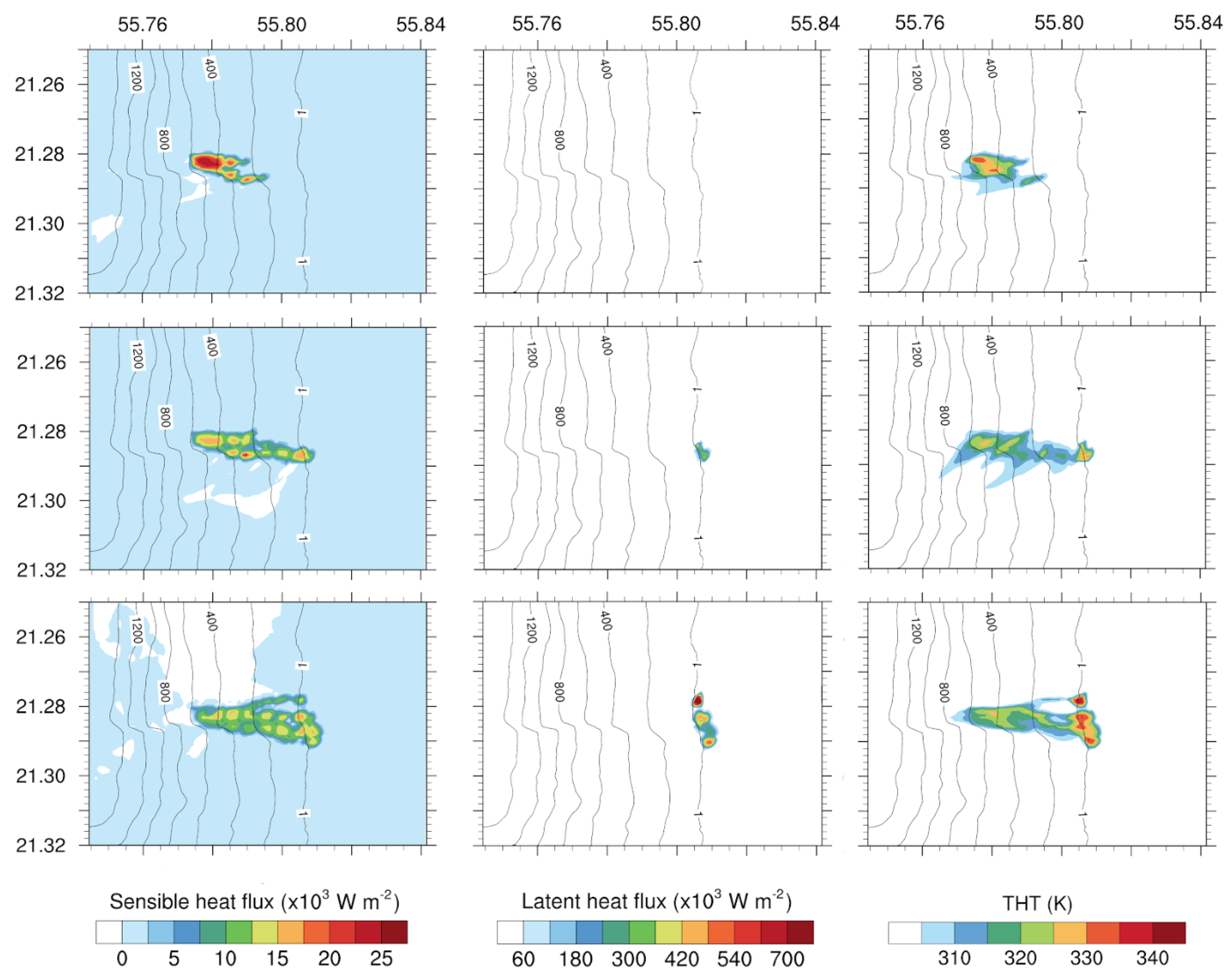
4.1. Evolution of Heat Flux at the Surface
4.2. CO Dilution
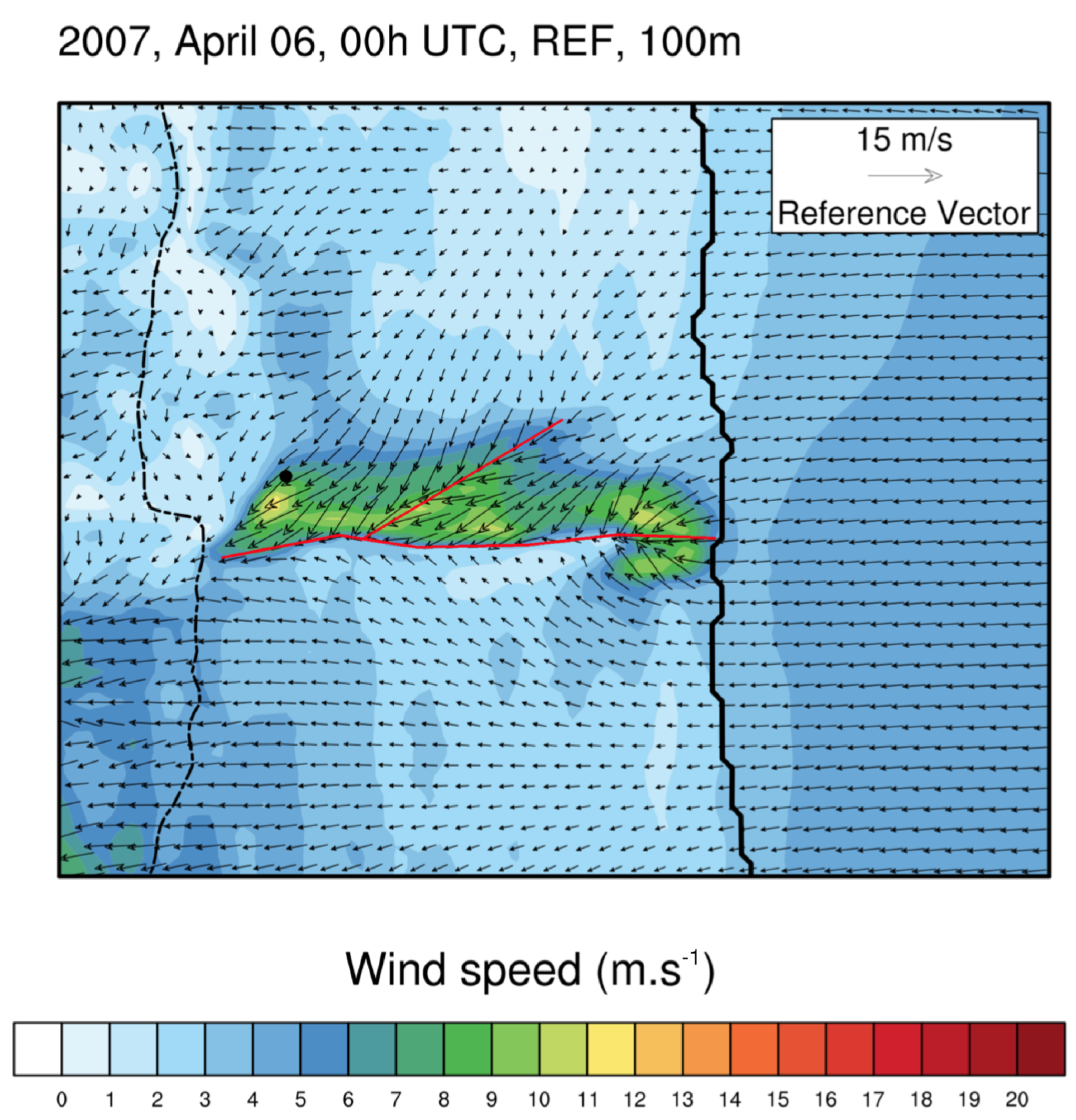
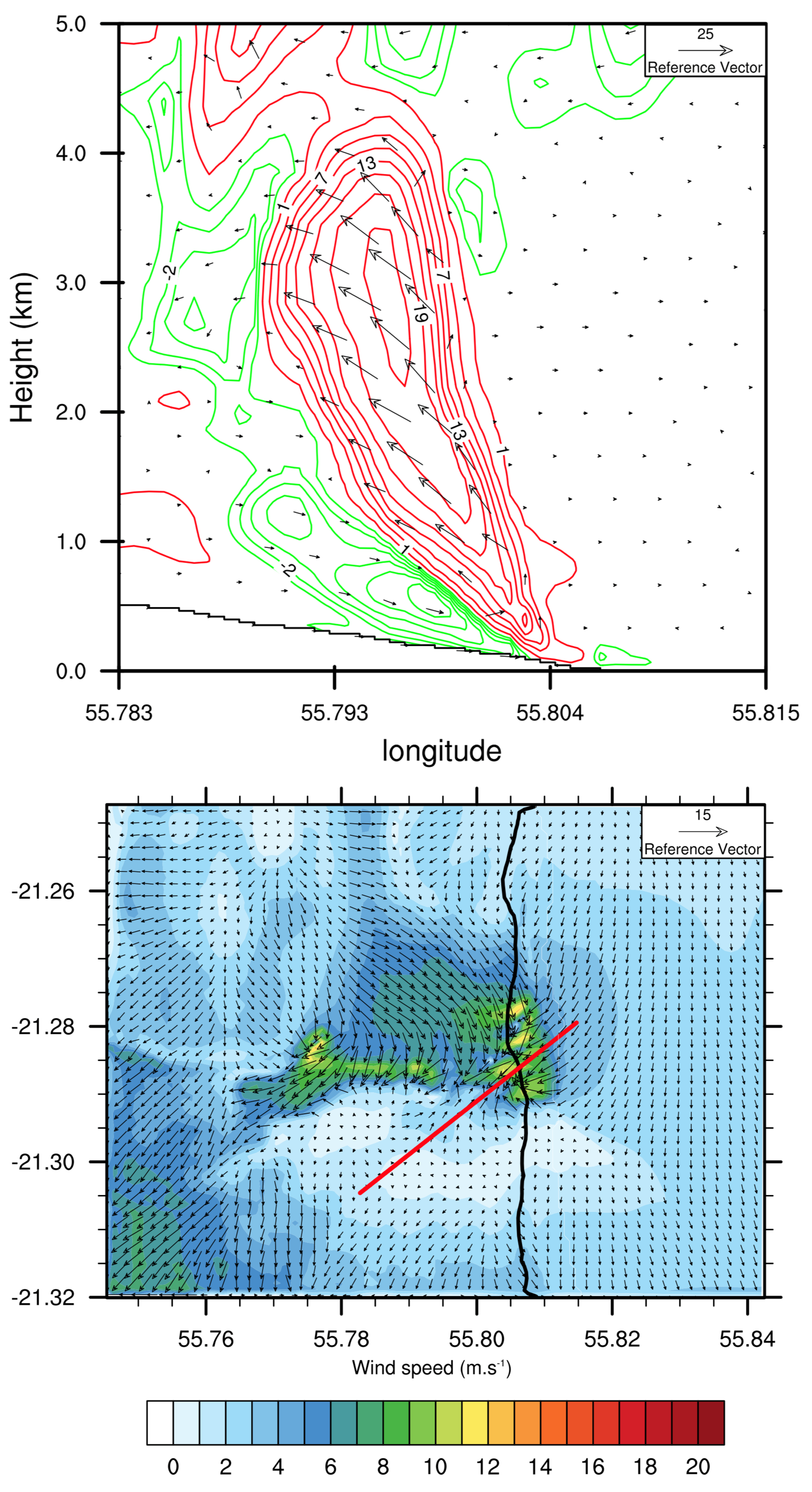
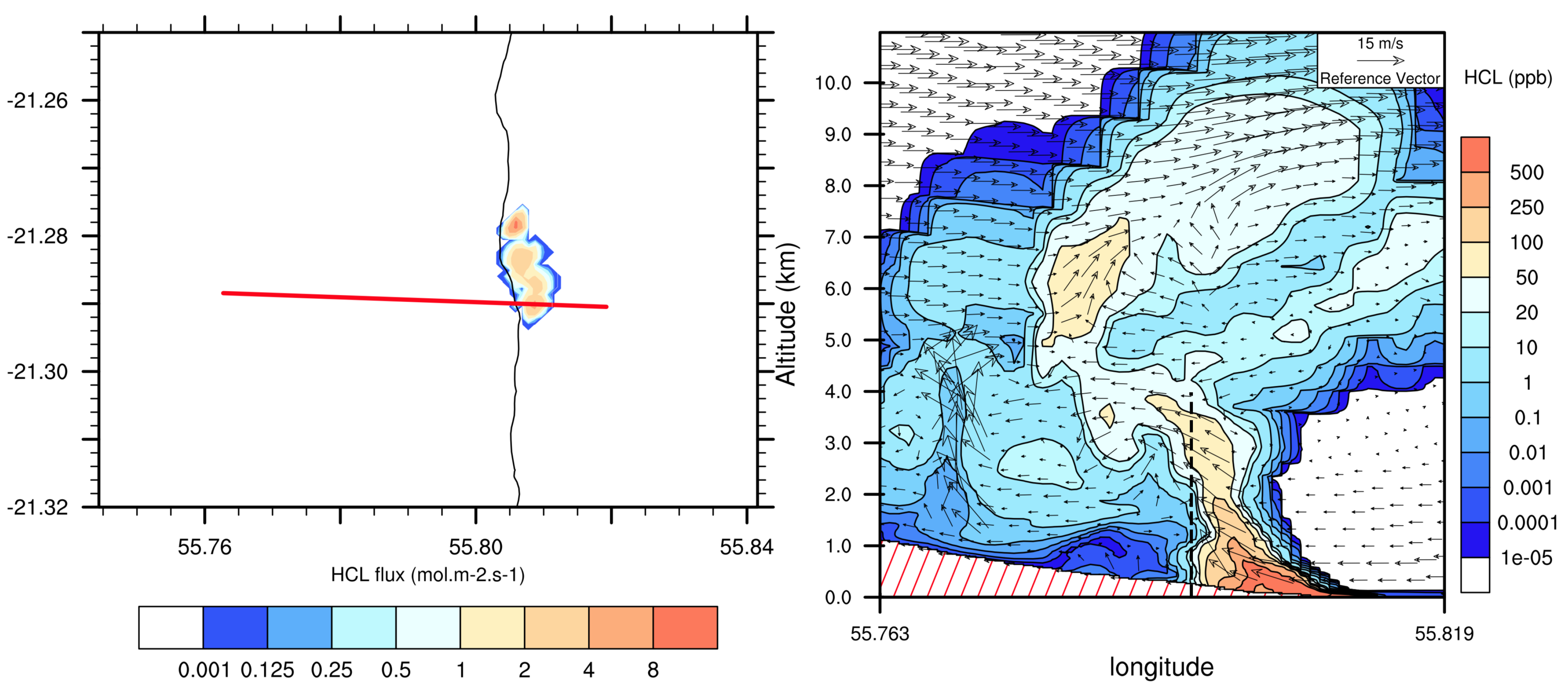
4.3. Lava Entering Sea Water
4.4. Transport of the SO over the Island
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oppenheimer, C. Climatic, environmental and human consequences of the largest known historic eruption: Tambora volcano (Indonesia) 1815. Prog. Phys. Geogr. 2003, 27, 230–259. [Google Scholar] [CrossRef]
- von Glasow, R.; Bobrowski, N.; Kern, C. The effects of volcanic eruptions on atmospheric chemistry. Chem. Geol. 2009, 263, 131–142. [Google Scholar] [CrossRef]
- Pollack, J.B.; Toon, O.B.; Danielsen, E.F.; Hofmann, D.J.; Rosen, J.M. The El Chichon volcanic cloud—An introduction. Geophys. Res. Lett. 1983, 10, 989–992. [Google Scholar] [CrossRef]
- Hoffman, D.J. Perturbations to the global atmosphere associated with the El Chichon volcanic eruption of 1982. Rev. Geophys. 1987, 25, 743–759. [Google Scholar] [CrossRef]
- McCornick, M.P.; Thomason, L.W.; Trepte, C.R. Atmospheric effects of the Mt Pinatubo eruption. Nature 1995, 373, 399–404. [Google Scholar] [CrossRef]
- Fiocco, G.; Fua, D.; Visconti, G. The Mount Pinatubo Eruption—Effects on the Atmosphere and Climate; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Robock, A. Pinatubo eruption—The climatic aftermath. Science 2002, 295, 1242–1244. [Google Scholar] [CrossRef] [PubMed]
- Solomon, S. Stratospheric ozone depletion: A review of concepts and history. Rev. Geophys. 1999, 37, 275–316. [Google Scholar] [CrossRef]
- Robock, A. Volcanic eruptions and climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Mather, T.A.; Pyle, D.M.; Oppenheimer, C. Tropospheric volcanic aerosol. In Volcanism and the Earth Atmosphere; American Geophysical Union: Washington, DC, USA, 2003; pp. 189–212. [Google Scholar] [CrossRef]
- Zambri, B.; Robock, A.; Mills, M.J.; Schmidt, A. Modeling the 1783–1784 Laki Eruption in Iceland: 1. Aerosol Evolution and Global Stratospheric Circulation Impacts. J. Geophys. Res. Atmos. 2019. [Google Scholar] [CrossRef]
- Rose, C.; Foucart, B.; Picard, D.; Colomb, A.; Metzger, J.M.; Tulet, P.; Sellegri, K. New particle formation in the volcanic eruption plume of the Piton de la Fournaise: Specific features from a long-term dataset. Atmos. Chem. Phys. 2019, 19, 13243–13265. [Google Scholar] [CrossRef]
- Pianezze, J.; Tulet, P.; Foucart, B.; Leriche, M.; Liuzzo, M.; Salerno, G.; Colomb, A.; Freney, E.; Sellegri, K. Volcanic Plume Aging During Passive Degassing and Low Eruptive Events of Etna and Stromboli Volcanoes. J. Geophys. Res. Atmos. 2019, 124, 11389–11405. [Google Scholar] [CrossRef]
- Bhugwant, C.; Siéja, B.; Bessafi, M.; Staudacher, T.; Ecormier, J. Atmospheric sulfur dioxide measurements during the 2005 and 2007 eruptions of the Piton de La Fournaise volcano: Implications for human health and environmental changes. J. Volcanol. Geotherm. Res. 2009, 184, 208–224. [Google Scholar] [CrossRef]
- Baxter, P.J.; Stoiber, R.; Williams, S.N. Volcanic gases and health: Masaya Volcano, Nicaragua. Lancet 1982, 2, 150–151. [Google Scholar] [CrossRef]
- Mannino, D.; Ruben, S.; Holschuh, F.; Holschuh, T.; Wilson, M.; Holschuh, T. Emergency department visits and hospitalizations for respiratory disease on the island of Hawaii. Hawaii Med. J. 1996, 55, 48–54. [Google Scholar] [PubMed]
- Allen, A.G.; Baxter, P.J.; Ottley, C.J. Gas and particle emissions from Soufrière Hills Volcano, Montserrat, West Indies: Characterization and health hazard assessment. Bull. Volcanol. 2000, 62, 8–19. [Google Scholar] [CrossRef]
- Delmelle, P.; Stix, J.; Bourque, C.A.; Baxter, P.; Garcia-Alvarez, J.; Barquero, J. Dry deposition and heavy acid loading in the vicinity of Masaya Volcano, a major sulfur and chlorine source in Nicaragua. Environ. Sci. Technol. 2001, 35, 1289–1293. [Google Scholar] [CrossRef] [PubMed]
- Seifert, P.; Ansmann, A.; Groß, S.; Freudenthaler, V.; Heinold, B.; Hiebsch, A.; Mattis, I.; Schmidt, J.; Schnell, F.; Tesche, M.; et al. Ice formation in ash-influenced clouds after the eruption of the Eyjafjallajökull volcano in April 2010. J. Geophys. Res. Atmos. 2011, 116, D00U04. [Google Scholar] [CrossRef]
- Prata, F.A.J.; Zehner, C.; Stebel, K. Earth observations and volcanic ash. A report from the ESA/Eumetsat Dublin workshop, 4–7 March 2013, April 2014. ESA/NILU 2014. [Google Scholar] [CrossRef]
- Durand, J.; Tulet, P.; Leriche, M.; Bielli, S.; Villeneuve, N.; Di Muro, A.; Fillipi, J. Modeling the lava heat flux during severe effusive volcanic eruption: An important impact on surface air quality. J. Geophys. Res. 2014. [Google Scholar] [CrossRef]
- Filippi, J.B.; Bosseur, F.; Mari, C.; Lac, C. Simulation of a Large Wildfire in a Coupled Fire-Atmosphere Model. Atmosphere 2018, 9, 218. [Google Scholar] [CrossRef]
- Lac, C.; Chaboureau, J.P.; Masson, V.; Pinty, J.P.; Tulet, P.; Escobar, J.; Leriche, M.; Barthe, C.; Aouizerats, B.; Augros, C.; et al. Overview of the Meso-NH model version 5.4 and its applications. Geosci. Model Dev. 2018, 11, 1929–1969. [Google Scholar] [CrossRef]
- Masson, V.; Moigne, P.L.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The {SURFEXv}7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef]
- Tulet, P.; Crassier, V.; Solmon, F.; Guedalia, D.; Rosset, R. Description of the MESOscale NonHydrostatic Chemistry model and application to a transboundary pollution episode between northern France and southern England. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Crassier, V.; Suhre, K.; Tulet, P.; Rosset, R. Development of a reduced chemical scheme for use in mesoscale meteorological models. Atmos. Environ. 2000, 34, 2633–2644. [Google Scholar] [CrossRef]
- Staudacher, T.; Ferrazzini, V.; Peltier, A.; Kowalski, P.; Boissier, P.; Catherinea, P.; Laureta, F.; Massin, F. The April 2007 eruption and the Dolomieu crater collapse, two major events at Piton de la Fournaise (La Reunion Island, Indian Ocean). J. Volcanol. Geotherm. Res. 2009, 184, 126–137. [Google Scholar] [CrossRef]
- Tulet, P.; Villeneuve, N. Large scale modeling of the transport, the chemical transformation and the mass budget of the sulfur emitted during the eruption of April 2007 by the Piton de la Fournaise. Atmos. Chem. Phys. Discuss. 2010, 10. [Google Scholar] [CrossRef]
- Servadio, Z.; Villeneuve, N.; Bachlery, P. Automatic Mapping of the Lava Flows at Piton de la Fournaise Volcano, by Combining Thermal Data in Near and Visible Infrared. In Remote Sensing—Applications; InTech: London, UK, 2012. [Google Scholar] [CrossRef]
- Brown, S.; Lugo, A.E. The Storage and Production of Organic Matter in Tropical Forests and Their Role in the Global Carbon Cycle. Biotropica 1982, 14, 161. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.; Lugo, A. Biomass Estimation Methods for Tropical Forests with Applications to Forest Inventory Data. For. Sci. 1989, 35, 881–902. [Google Scholar]
- Oppenheimer, C. Lava flow cooling estimated from Landsat Thematic Mapper infrared data: The Lonquimay eruption (Chile, 1989). J. Geophys. Res. 1991, 96, 21865–21878. [Google Scholar] [CrossRef]
- Klingelhofer, F.; Hort, M.; Kumpel, H.J.; Schemincke, H.U. Constraints on the formation of submarine lava flows from numerical model calculations. J. Volcanol. Geotherm. Res. 1999, 92, 215–229. [Google Scholar] [CrossRef]
- Quareni, F.; Tallarico, A.; Dragoni, M. Modeling of the steady state temperature field in lava flow levees. J. Volcanol. Geotherm. Res. 2004, 132, 241–251. [Google Scholar] [CrossRef]
- Harris, A.; Bailey, J.; Calvari, S.; Dehn, J. Heat loss measured at a lava channel and its implication for down-channel cooling and rheology. Geol. Soc. Am. 2005, 396, 125. [Google Scholar]
- Keszthelyi, L.; Harris, A.; Dehn, J. Observations of the effect of wind on the cooling of active lava flows. J. Geophys. Res. 2003, 30, SDE 4-1. [Google Scholar] [CrossRef]
- Bachèlery, P.; Saint-Ange, F.; Villeneuve, N.; Savoye, B.; Normand, A.; Le Drezen, E.; Barrère, A.; Quod, J.; Deplus, C. A’a Lava flows into the sea, April 2007, Piton de la Fournaise volcano, La Réunion Island. In Active Volcanoes of the Southwest Indian Ocean: Piton de la Fournaise and Karthala. Active Volcanoes of the World; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Di Muro, A.; Métrich, N.; Vergani, D.; Rosi, M.; Armienti, P.; Fougeroux, T.; Deloule, E.; Arienzo, I.; Civetta, L. The shallow plumbing system of Piton de la Fournaise Volcano (La Réunion Island, Indian Ocean) revealed by the major 2007 caldera forming eruption. J. Petrol. 2014, 55, 1287–1315. [Google Scholar] [CrossRef]
- Famin, V.; Welsch, B.; Okumura, S.; Bachelery, P.; Nakashima, S. Three differentiation stages of a single magma at Piton de la Fournaise volcano (Reunion hot spot). Geochem. Geophys. Geosyst. 2009, 10. [Google Scholar] [CrossRef]
- Coppola, D.; Piscopo, D.; Staudacher, T.; Cigolini, C. Lava discharge rate and effusive pattern at Piton de la Fournaise from MODIS data. J. Volcanol. Geotherm. Res. 2009, 184, 174–192. [Google Scholar] [CrossRef]
- Edmonds, M.; Gerlach, T.M. The airborne lava-seawater interaction plume at Kilauea Volcano, Hawaii. Earth Planet. Sci. Lett. 2014, 244. [Google Scholar] [CrossRef]
- Villeneuve, N.; Neuville, D.R.; Boivin, P.; Bachèlery, P.; Richet, P. Magma crystallization and viscosity: A study of molten basalts from the Piton de la Fournaise volcano (La Réunion island). Chem. Geol. 2008, 256, 242–251. [Google Scholar] [CrossRef]
- Saint-Ange, S. La Sedimentation Volcanoclastique en Contexte de Point Chaud (ile de La Renion, Océan Indien). Ph.D. Thesis, Université de La Réunion, La Réunion, France, 2009. [Google Scholar]
- Roberts, T.J.; Lurton, T.; Giudice, G.; Liuzzo, M.; Aiuppa, A.; Coltelli, M.; Vignelles, D.; Salerno, G.; Couté, B.; Chartier, M.; et al. Validation of a novel Multi-Gas sensor for volcanic HCl alongside H2S and SO2 at Mt. Etna. Bull. Volcanol. 2017, 79. [Google Scholar] [CrossRef]
- Galle, B.; Arellano, S.; Bobrowski, N.; Conde, V.; Fischer, T.P.; Gerdes, G.; Gutmann, A.; Hoffmann, T.; Itikarai, I.; Krejci, T.; et al. A multi-purpose, multi-rotor drone system for long range and high-altitude volcanic gas plume measurements. Atmos. Meas. Tech. Discuss. 2020. [Google Scholar] [CrossRef]
- Liu, E.J.; Aiuppa, A.; Alan, A.; Arellano, S.; Bitetto, M.; Bobrowski, N.; Carn, S.; Clarke, R.; Corrales, E.; de Moor, J.M.; et al. Aerial strategies advance volcanic gas measurements at inaccessible, strongly degassing volcanoes. Sci. Adv. 2020, 6, eabb9103. [Google Scholar] [CrossRef] [PubMed]

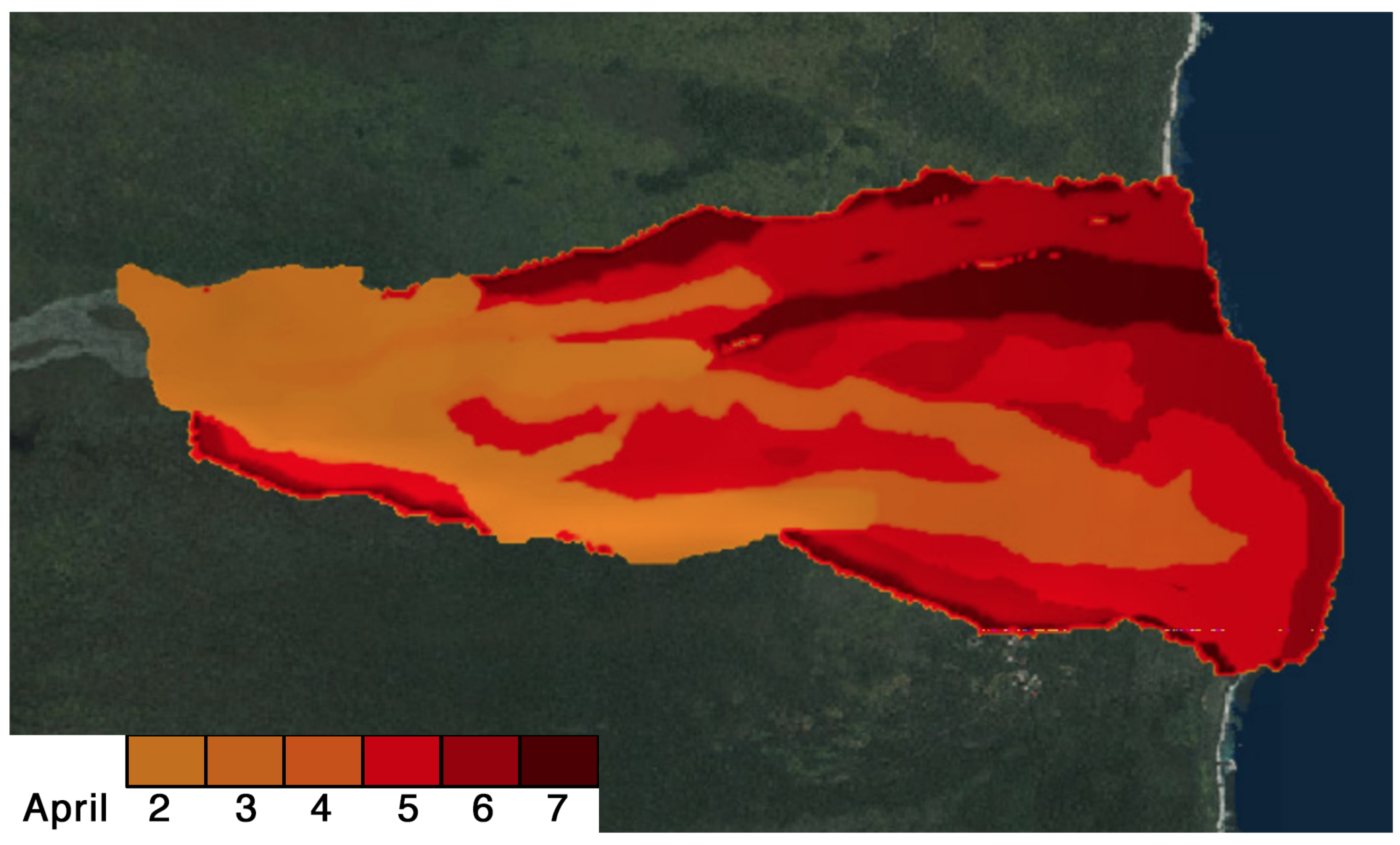
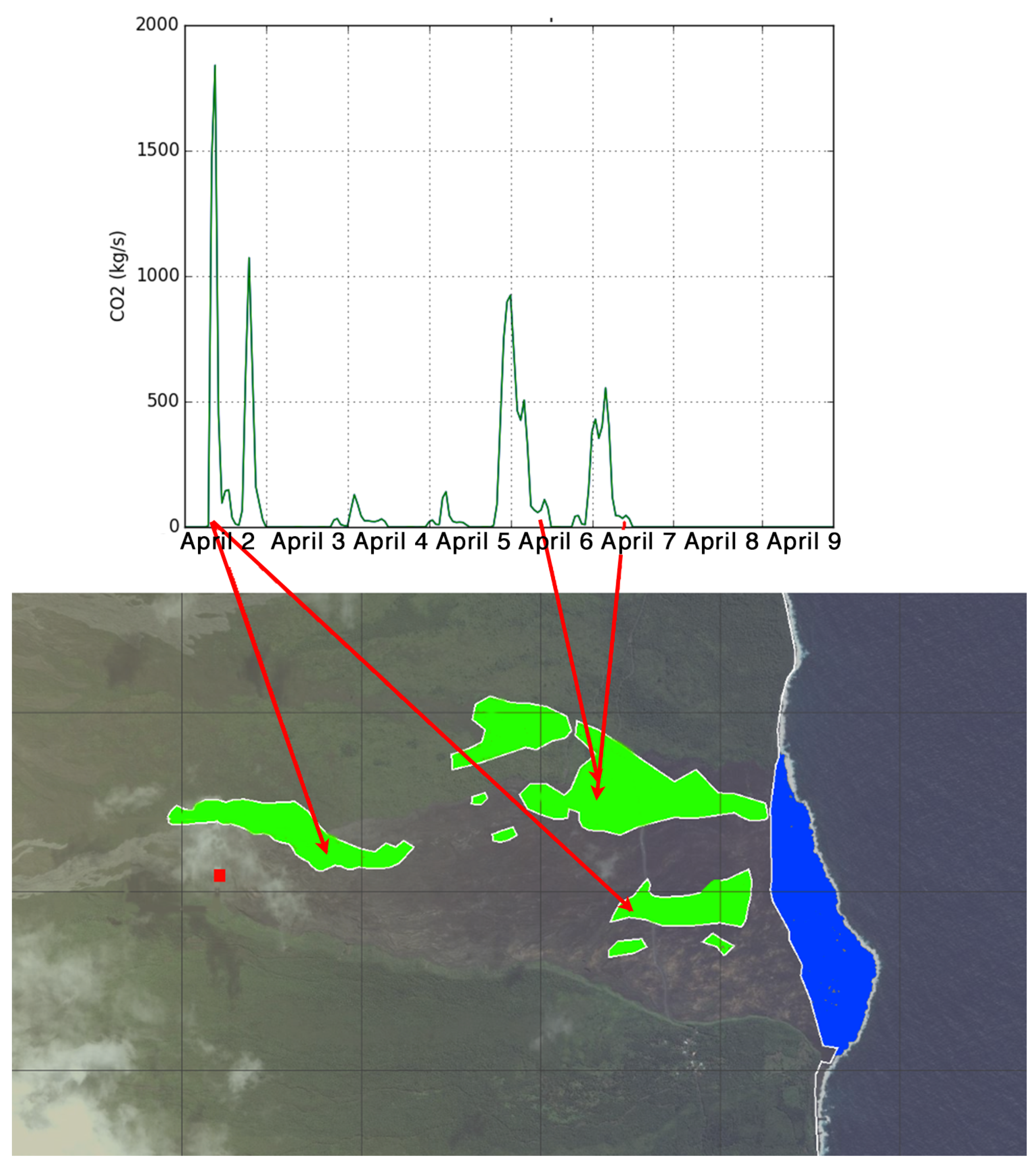
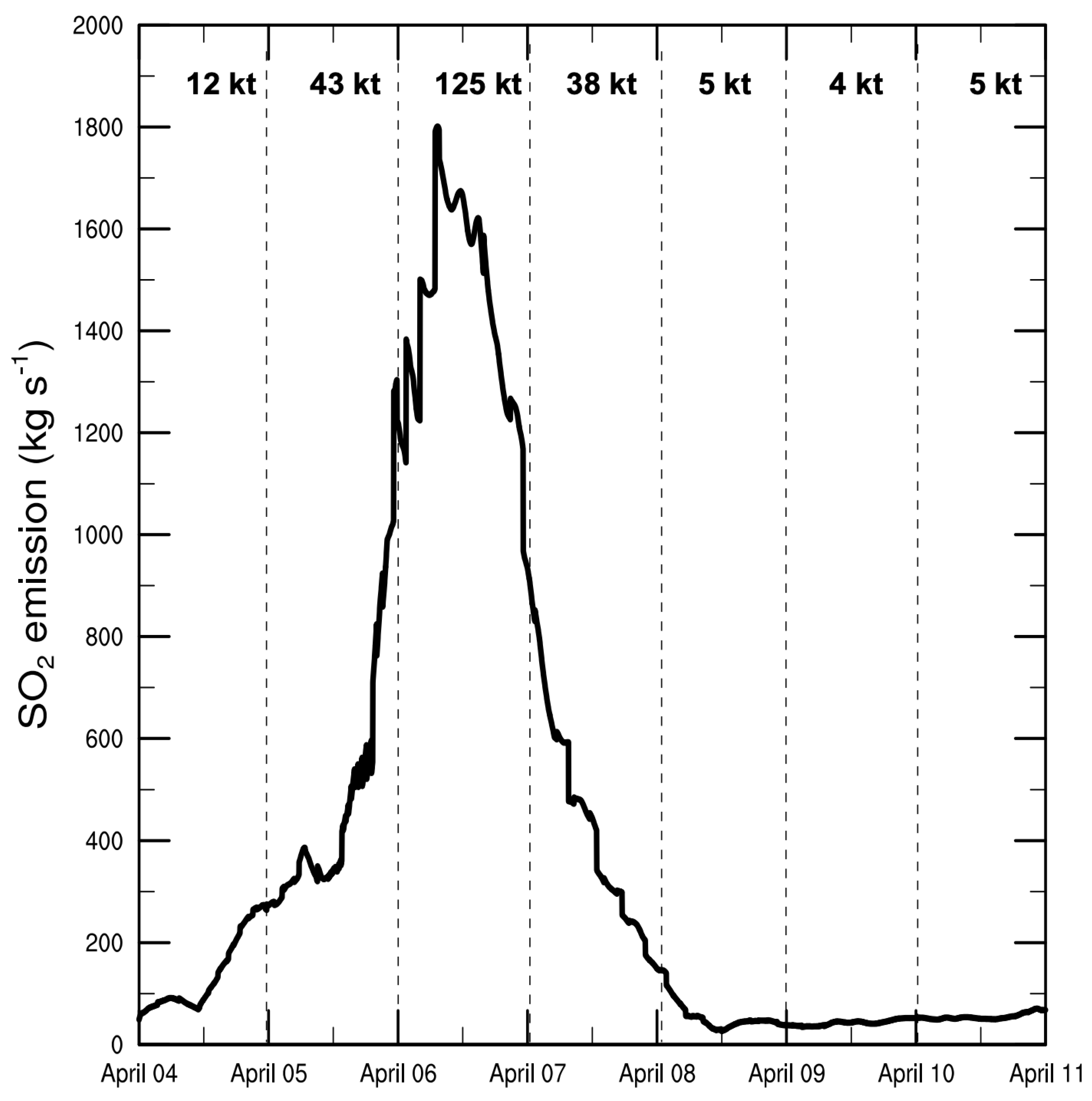
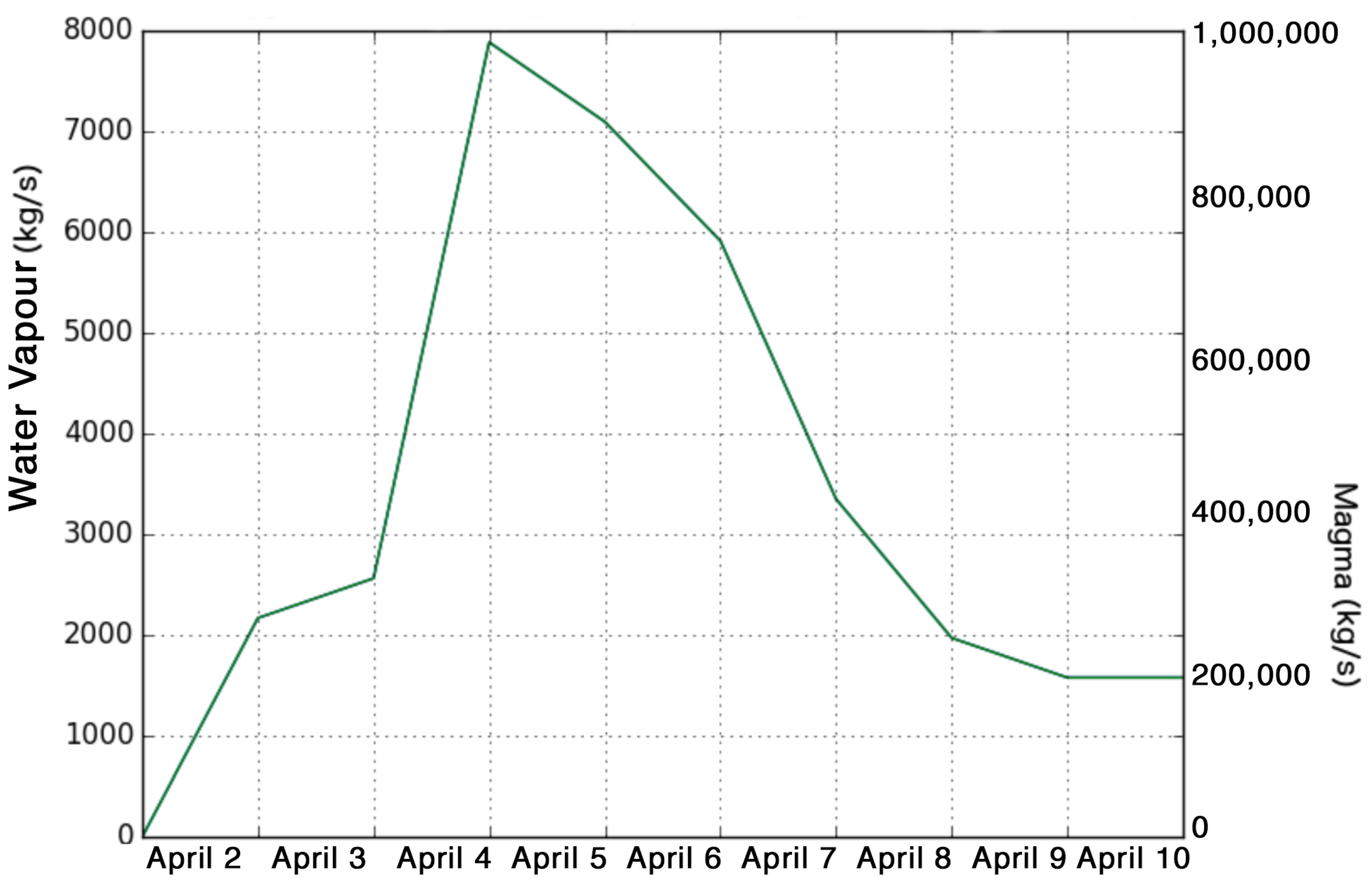


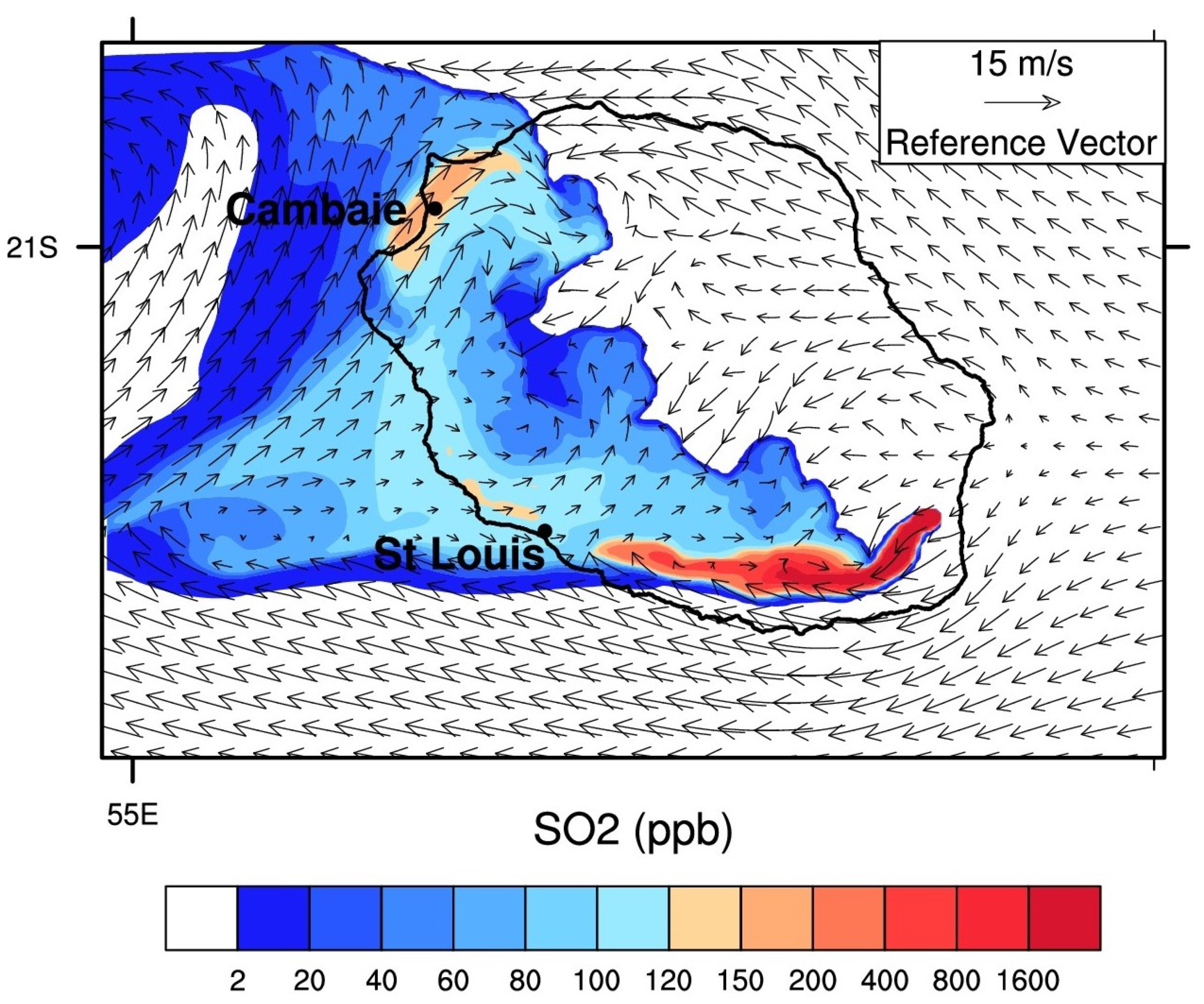
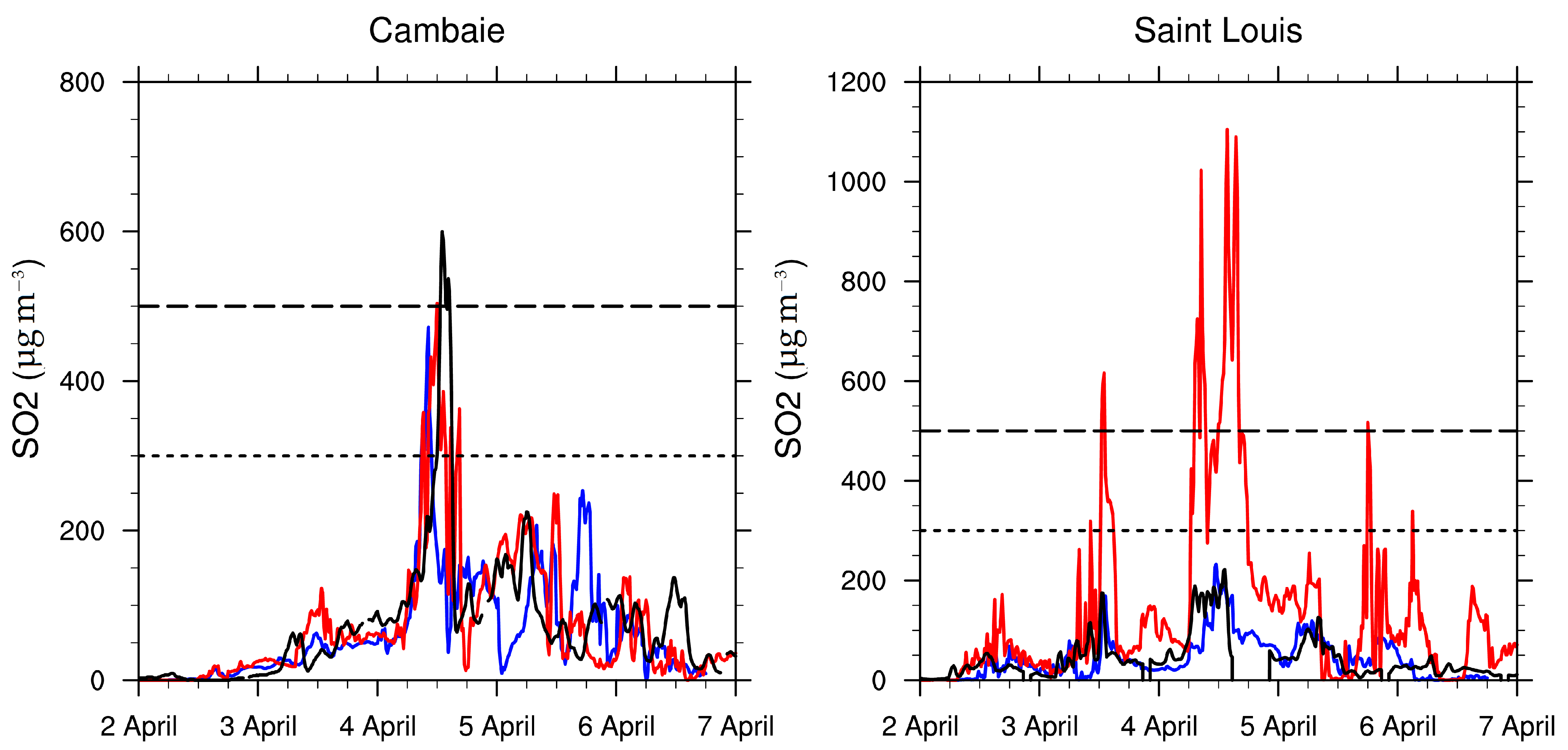
| Date | Apr 2 6UTC | Apr 2 10UTC | Apr 3 00UTC | Apr 4 00UTC | Apr 4 12UTC | Apr 5 12UTC | Apr 5 18UTC | Apr 6 6UTC | Apr 6 18UTC |
|---|---|---|---|---|---|---|---|---|---|
| Value (kg/s) | 40 | 70 | 180 | 400 | 462 | 605 | 1916 | 1650 | 345 |
| Date | Apr 2 17UTC | Apr 3 4UTC | Apr 4 4UTC | Apr 5 4UTC | Apr 6 4UTC | Apr 7 4UTC | Apr 8 4UTC |
|---|---|---|---|---|---|---|---|
| Values (kg s−1) | 0 | 20,800 | 24,200 | 38,700 | 35,400 | 20,000 | 5300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filippi, J.-B.; Durand, J.; Tulet, P.; Bielli, S. Multiscale Modeling of Convection and Pollutant Transport Associated with Volcanic Eruption and Lava Flow: Application to the April 2007 Eruption of the Piton de la Fournaise (Reunion Island). Atmosphere 2021, 12, 507. https://doi.org/10.3390/atmos12040507
Filippi J-B, Durand J, Tulet P, Bielli S. Multiscale Modeling of Convection and Pollutant Transport Associated with Volcanic Eruption and Lava Flow: Application to the April 2007 Eruption of the Piton de la Fournaise (Reunion Island). Atmosphere. 2021; 12(4):507. https://doi.org/10.3390/atmos12040507
Chicago/Turabian StyleFilippi, Jean-Baptiste, Jonathan Durand, Pierre Tulet, and Soline Bielli. 2021. "Multiscale Modeling of Convection and Pollutant Transport Associated with Volcanic Eruption and Lava Flow: Application to the April 2007 Eruption of the Piton de la Fournaise (Reunion Island)" Atmosphere 12, no. 4: 507. https://doi.org/10.3390/atmos12040507
APA StyleFilippi, J.-B., Durand, J., Tulet, P., & Bielli, S. (2021). Multiscale Modeling of Convection and Pollutant Transport Associated with Volcanic Eruption and Lava Flow: Application to the April 2007 Eruption of the Piton de la Fournaise (Reunion Island). Atmosphere, 12(4), 507. https://doi.org/10.3390/atmos12040507






