Properties of Hall-MHD Turbulence at Sub-Ion Scales: Spectral Transfer Analysis
Abstract
:1. Introduction
2. Methods
2.1. Hall-MHD Simulations of Plasma Turbulence: Numerical Setup
2.2. Spectral Transfer Equations
3. Results
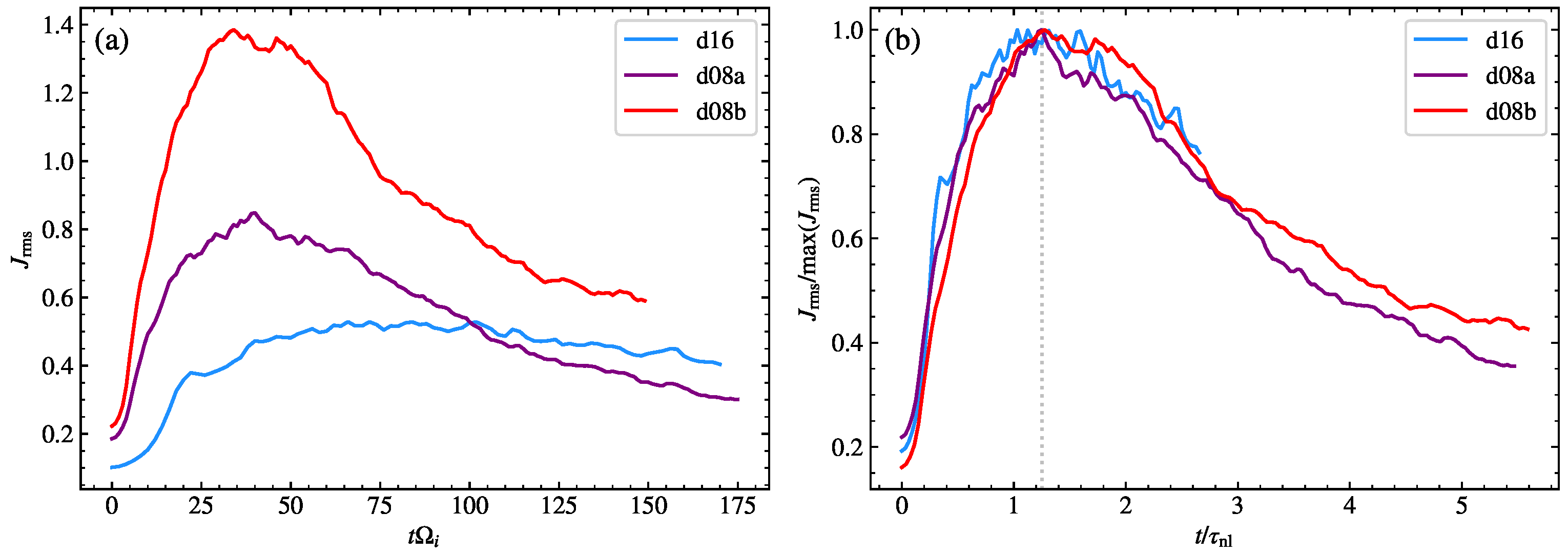
3.1. General Evolution
3.2. Spectral Properties and Cross-Scales Energy Transfer
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. LRSP 2013, 10. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. Dissipation of Energy in Locally Isotropic Turbulence. Akad. Nauk SSSR Dokl. 1941, 32, 16. [Google Scholar]
- Hellinger, P.; Verdini, A.; Landi, S.; Franci, L.; Matteini, L. von Kármán-Howarth Equation for Hall Magnetohydrodynamics: Hybrid Simulations. Astrophys. J. Lett. 2018, 857, L19. [Google Scholar] [CrossRef] [Green Version]
- Papini, E.; Franci, L.; Landi, S.; Verdini, A.; Matteini, L.; Hellinger, P. Can Hall Magnetohydrodynamics Explain Plasma Turbulence at Sub-ion Scales? Astrophys. J. 2019, 870, 52. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, R.; Sorriso-Valvo, L.; Chasapis, A.; Hellinger, P.; Matthaeus, W.H.; Verdini, A.; Landi, S.; Franci, L.; Matteini, L.; Giles, B.L.; et al. In-situ observation of Hall Magnetohydrodynamic Cascade in Space Plasma. Phys. Rev. Lett. 2020, 124. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Small-Scale Energy Cascade of the Solar Wind Turbulence. Astrophys. J. 2008, 674, 1153–1157. [Google Scholar] [CrossRef] [Green Version]
- Howes, G.G.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Quataert, E.; Schekochihin, A.A. A model of turbulence in magnetized plasmas: Implications for the dissipation range in the solar wind. J. Geophys. Res. Space Phys. 2008, 113, A05103. [Google Scholar] [CrossRef] [Green Version]
- Schekochihin, A.A.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Howes, G.G.; Quataert, E.; Tatsuno, T. Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. Astrophys. J. Suppl. 2009, 182, 310–377. [Google Scholar] [CrossRef] [Green Version]
- Sahraoui, F.; Goldstein, M.L.; Belmont, G.; Canu, P.; Rezeau, L. Three Dimensional Anisotropic k Spectra of Turbulence at Subproton Scales in the Solar Wind. Phys. Rev. Lett. 2010, 105, 131101. [Google Scholar] [CrossRef]
- Boldyrev, S.; Perez, J.C. Spectrum of Kinetic-Alfvén Turbulence. Astrophys. J. Lett. 2012, 758, L44. [Google Scholar] [CrossRef] [Green Version]
- Wan, M.; Matthaeus, W.H.; Karimabadi, H.; Roytershteyn, V.; Shay, M.; Wu, P.; Daughton, W.; Loring, B.; Chapman, S.C. Intermittent Dissipation at Kinetic Scales in Collisionless Plasma Turbulence. Phys. Rev. Lett. 2012, 109, 195001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, P.; Perri, S.; Osman, K.; Wan, M.; Matthaeus, W.H.; Shay, M.A.; Goldstein, M.L.; Karimabadi, H.; Chapman, S. Intermittent Heating in Solar Wind and Kinetic Simulations. Astrophys. J. Lett. 2013, 763, L30. [Google Scholar] [CrossRef] [Green Version]
- Franci, L.; Verdini, A.; Matteini, L.; Landi, S.; Hellinger, P. Solar Wind Turbulence from MHD to Sub-ion Scales: High-resolution Hybrid Simulations. Astrophys. J. Lett. 2015, 804, L39. [Google Scholar] [CrossRef]
- Franci, L.; Landi, S.; Matteini, L.; Verdini, A.; Hellinger, P. High-resolution Hybrid Simulations of Kinetic Plasma Turbulence at Proton Scales. Astrophys. J. 2015, 812, 21. [Google Scholar] [CrossRef] [Green Version]
- Sulem, P.L.; Passot, T.; Laveder, D.; Borgogno, D. Influence of the Nonlinearity Parameter on the Solar Wind Sub-ion Magnetic Energy Spectrum: FLR-Landau Fluid Simulations. Astrophys. J. 2016, 818, 66. [Google Scholar] [CrossRef] [Green Version]
- Franci, L.; Cerri, S.S.; Califano, F.; Landi, S.; Papini, E.; Verdini, A.; Matteini, L.; Jenko, F.; Hellinger, P. Magnetic Reconnection as a Driver for a Sub-ion-scale Cascade in Plasma Turbulence. Astrophys. J. Lett. 2017, 850, L16. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Matthaeus, W.H.; Parashar, T.N.; Haggerty, C.C.; Roytershteyn, V.; Daughton, W.; Wan, M.; Shi, Y.; Chen, S. Energy transfer, pressure tensor, and heating of kinetic plasma. Phys. Plasmas 2017, 24, 072306. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Siregar, E.; Roberts, D.A.; Goldstein, M.L. Simulation of high-frequency solar wind power spectra using Hall magnetohydrodynamics. J. Geophys. Res. 1996, 101, 2493–2504. [Google Scholar] [CrossRef]
- Biskamp, D.; Schwarz, E.; Zeiler, A.; Celani, A.; Drake, J.F. Electron magnetohydrodynamic turbulence. Phys. Plasmas 1999, 6, 751–758. [Google Scholar] [CrossRef] [Green Version]
- Galtier, S.; Buchlin, E. Multiscale Hall-Magnetohydrodynamic Turbulence in the Solar Wind. Astrophys. J. 2007, 656, 560–566. [Google Scholar] [CrossRef]
- Shaikh, D.; Shukla, P.K. 3D Simulations of Fluctuation Spectra in the Hall-MHD Plasma. Phys. Rev. Lett. 2009, 102, 045004. [Google Scholar] [CrossRef] [PubMed]
- Roberts, O.W.; Narita, Y.; Escoubet, C.P. Direct Measurement of Anisotropic and Asymmetric Wave Vector Spectrum in Ion-scale Solar Wind Turbulence. Astrophys. J. Lett. 2017, 851, L11. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Chasapis, A.; Chhiber, R.; Parashar, T.N.; Maruca, B.A.; Matthaeus, W.H.; Schwartz, S.J.; Eriksson, S.; Le Contel, O.; Breuillard, H.; et al. Solar Wind Turbulence Studies Using MMS Fast Plasma Investigation Data. Astrophys. J. 2018, 866, 81. [Google Scholar] [CrossRef] [Green Version]
- Pitňa, A.; Šafránková, J.; Němeček, Z.; Franci, L.; Pi, G. A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence. Atmosphere 2021, 12, 1547. [Google Scholar] [CrossRef]
- Alexandrova, O.; Saur, J.; Lacombe, C.; Mangeney, A.; Mitchell, J.; Schwartz, S.J.; Robert, P. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys. Rev. Lett. 2009, 103, 165003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.H.K.; Boldyrev, S. Nature of Kinetic Scale Turbulence in the Earth’s Magnetosheath. Astrophys. J. 2017, 842, 122. [Google Scholar] [CrossRef]
- Howes, G.G.; Tenbarge, J.M.; Dorland, W.; Quataert, E.; Schekochihin, A.A.; Numata, R.; Tatsuno, T. Gyrokinetic Simulations of Solar Wind Turbulence from Ion to Electron Scales. Phys. Rev. Lett. 2011, 107, 035004. [Google Scholar] [CrossRef] [Green Version]
- Franci, L.; Landi, S.; Matteini, L.; Verdini, A.; Hellinger, P. Plasma Beta Dependence of the Ion-scale Spectral Break of Solar Wind Turbulence: High-resolution 2D Hybrid Simulations. Astrophys. J. 2016, 833, 91. [Google Scholar] [CrossRef] [Green Version]
- Cerri, S.S.; Franci, L.; Califano, F.; Landi, S.; Hellinger, P. Plasma turbulence at ion scales: A comparison between particle in cell and Eulerian hybrid-kinetic approaches. J. Plasma Phys. 2017, 83, 705830202. [Google Scholar] [CrossRef] [Green Version]
- González, C.A.; Parashar, T.N.; Gomez, D.; Matthaeus, W.H.; Dmitruk, P. Turbulent electromagnetic fields at sub-proton scales: Two-fluid and full-kinetic plasma simulations. Phys. Plasmas 2019, 26, 012306. [Google Scholar] [CrossRef] [Green Version]
- Loureiro, N.F.; Boldyrev, S. Collisionless Reconnection in Magnetohydrodynamic and Kinetic Turbulence. Astrophys. J. 2017, 850, 182. [Google Scholar] [CrossRef] [Green Version]
- Mallet, A.; Schekochihin, A.A.; Chandran, B.D.G. Disruption of Alfvénic turbulence by magnetic reconnection in a collisionless plasma. J. Plasma Phys. 2017, 83, 905830609. [Google Scholar] [CrossRef] [Green Version]
- Parashar, T.N.; Matthaeus, W.H. Propinquity of Current and Vortex Structures: Effects on Collisionless Plasma Heating. Astrophys. J. 2016, 832, 57. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, R.; Matthaeus, W.H.; Parashar, T.N.; Yang, Y.; Chasapis, A.; Giles, B.L.; Gershman, D.J.; Pollock, C.J.; Russell, C.T.; Strangeway, R.J.; et al. Statistics of Kinetic Dissipation in the Earth’s Magnetosheath: MMS Observations. Phys. Rev. Lett. 2020, 124, 255101. [Google Scholar] [CrossRef] [PubMed]
- Hellinger, P.; Papini, E.; Verdini, A.; Landi, S.; Franci, L.; Matteini, L.; Montagud-Camps, V. Spectral transfer and Kármán-Howarth-Monin equations for compressible Hall magnetohydrodynamics. Astrophys. J. 2021, 917, 101. [Google Scholar] [CrossRef]
- Landi, S.; Del Zanna, L.; Papini, E.; Pucci, F.; Velli, M. Resistive Magnetohydrodynamics Simulations of the Ideal Tearing Mode. Astrophys. J. 2015, 806, 131. [Google Scholar] [CrossRef] [Green Version]
- Papini, E.; Landi, S.; Zanna, L.D. Fast magnetic reconnection: The ideal tearing instability in classic, Hall, and relativistic plasmas. J. Phys. Conf. Series 2018, 1031, 012020. [Google Scholar] [CrossRef]
- Papini, E.; Landi, S.; Del Zanna, L. Fast Magnetic Reconnection: Secondary Tearing Instability and Role of the Hall Term. Astrophys. J. 2019, 885, 56. [Google Scholar] [CrossRef]
- Papini, E.; Franci, L.; Landi, S.; Hellinger, P.; Verdini, A.; Matteini, L. Statistics of Magnetic Reconnection and Turbulence in Hall-MHD and Hybrid-PIC Simulations. Available online: https://www.sif.it/riviste/sif/ncc/econtents/2019/042/01/article/22 (accessed on 2 December 2017).
- Wray, A.A. Minimal Sstorage Time Aadvancement Schemes for Spectral Methods. Available online: https://www.researchgate.net/publication/246830945_Minimal_storage_time-advancement_schemes_for_spectral_methods (accessed on 2 December 2017).
- Orszag, S.A. On the Elimination of Aliasing in Finite-Difference Schemes by Filtering High-Wavenumber Components. J. Atmos. Sci. 1971, 28, 1074. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Hossain, M.; Matthaeus, W.H. The application of spectral methods in simulating compressible fluid and magnetofluid turbulence. Comp. Phys. Commun. 1993, 74, 18–40. [Google Scholar] [CrossRef]
- Schmidt, W.; Grete, P. Kinetic and internal energy transfer in implicit large-eddy simulations of forced compressible turbulence. Phys. Rev. E 2019, 100. [Google Scholar] [CrossRef] [Green Version]
- Praturi, D.S.; Girimaji, S.S. Effect of pressure-dilatation on energy spectrum evolution in compressible turbulence. Phys. Fluids 2019, 31. [Google Scholar] [CrossRef]
- Kida, S.; Orszag, S.A. Energy and spectral dynamics in forced compressible turbulence. J. Sci. Comput. 1990, 5, 85–125. [Google Scholar] [CrossRef]
- Wan, M.; Matthaeus, W.H.; Roytershteyn, V.; Parashar, T.N.; Wu, P.; Karimabadi, H. Intermittency, coherent structures and dissipation in plasma turbulence. Phys. Plasmas 2016, 23, 042307. [Google Scholar] [CrossRef]
- Yang, Y.; Matthaeus, W.H.; Parashar, T.N.; Wu, P.; Wan, M.; Shi, Y.; Chen, S.; Roytershteyn, V.; Daughton, W. Energy transfer channels and turbulence cascade in Vlasov-Maxwell turbulence. Phys. Rev. E 2017, 95, 061201. [Google Scholar] [CrossRef] [Green Version]
- Papini, E.; Cicone, A.; Piersanti, M.; Franci, L.; Hellinger, P.; Landi, S.; Verdini, A. Multidimensional Iterative Filtering: A new approach for investigating plasma turbulence in numerical simulations. J. Plasma Phys. 2020, 86, 871860501. [Google Scholar] [CrossRef]
- Uritsky, V.M.; Pouquet, A.; Rosenberg, D.; Mininni, P.D.; Donovan, E.F. Structures in magnetohydrodynamic turbulence: Detection and scaling. Phys. Rev. E 2010, 82, 056326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miura, H.; Araki, K. Structure transitions induced by the Hall term in homogeneous and isotropic magnetohydrodynamic turbulence. Phys. Plasmas 2014, 21, 072313. [Google Scholar] [CrossRef] [Green Version]
- Agudelo Rueda, J.A.; Verscharen, D.; Wicks, R.T.; Owen, C.J.; Nicolaou, G.; Walsh, A.P.; Zouganelis, I.; Germaschewski, K.; Vargas Domínguez, S. Three-dimensional magnetic reconnection in particle-in-cell simulations of anisotropic plasma turbulence. J. Plasma Phys. 2021, 87, 905870228. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Toward a Theory of Interstellar Turbulence. II. Strong Alfvenic Turbulence. Astrophys. J. 1995, 438, 763. [Google Scholar] [CrossRef]
- Parashar, T.N.; Gary, S.P. Dissipation of Kinetic Alfvénic Turbulence as a Function of Ion and Electron Temperature Ratios. Astrophys. J. 2019, 882, 29. [Google Scholar] [CrossRef]
- Gary, S.P.; Bandyopadhyay, R.; Qudsi, R.A.; Matthaeus, W.H.; Maruca, B.A.; Parashar, T.N.; Roytershteyn, V. Particle-in-cell Simulations of Decaying Plasma Turbulence: Linear Instabilities versus Nonlinear Processes in 3D and 2.5D Approximations. Astrophys. J. 2020, 901, 160. [Google Scholar] [CrossRef]
- Oughton, S.; Matthaeus, W.H.; Dmitruk, P. Reduced MHD in Astrophysical Applications: Two-dimensional or Three-dimensional? Astrophys. J. 2017, 839, 2. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, R.; Oughton, S.; Wan, M.; Matthaeus, W.H.; Chhiber, R.; Parashar, T.N. Finite Dissipation in Anisotropic Magnetohydrodynamic Turbulence. Phys. Rev. X 2018, 8, 041052. [Google Scholar] [CrossRef] [Green Version]
- Karimabadi, H.; Roytershteyn, V.; Wan, M.; Matthaeus, W.H.; Daughton, W.; Wu, P.; Shay, M.; Loring, B.; Borovsky, J.; Leonardis, E.; et al. Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys. Plasmas 2013, 20, 012303. [Google Scholar] [CrossRef]
- Franci, L.; Landi, S.; Verdini, A.; Matteini, L.; Hellinger, P. Solar Wind Turbulent Cascade from MHD to Sub-ion Scales: Large-size 3D Hybrid Particle-in-cell Simulations. Astrophys. J. 2018, 853, 26. [Google Scholar] [CrossRef]
- Franci, L.; Hellinger, P.; Guarrasi, M.; Chen, C.H.K.; Papini, E.; Verdini, A.; Matteini, L.; Landi, S. Three-dimensional simulations of solar wind turbulence with the hybrid code CAMELIA. JPhCS 2018, 1031, 012002. [Google Scholar] [CrossRef]
- Shay, M.A.; Drake, J.F.; Rogers, B.N.; Denton, R.E. Alfvénic Collisionless Magnetic Reconnection and the Hall Term. J. Geophys. Res. 2001, 106, 3759. [Google Scholar] [CrossRef]
- Bruno, R.; Trenchi, L.; Telloni, D. Spectral Slope Variation at Proton Scales from Fast to Slow Solar Wind. Astrophys. J. Lett. 2014, 793, L15. [Google Scholar] [CrossRef] [Green Version]
- Quijia, P.; Fraternale, F.; Stawarz, J.E.; Vásconez, C.L.; Perri, S.; Marino, R.; Yordanova, E.; Sorriso-Valvo, L. Comparing turbulence in a Kelvin-Helmholtz instability region across the terrestrial magnetopause. MNRAS 2021, 503, 4815–4827. [Google Scholar] [CrossRef]


| Run | Re (Rm) | |||||||
|---|---|---|---|---|---|---|---|---|
| d16 | 32 | 16 | 0.25 | 64 | 8000 | ∼ | ||
| d08a | 32 | 8 | 0.25 | 32 | 4000 | ∼ | ||
| d08b | 32 | 8 | 0.30 | 9600 | ∼ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papini, E.; Hellinger, P.; Verdini, A.; Landi, S.; Franci, L.; Montagud-Camps, V.; Matteini, L. Properties of Hall-MHD Turbulence at Sub-Ion Scales: Spectral Transfer Analysis. Atmosphere 2021, 12, 1632. https://doi.org/10.3390/atmos12121632
Papini E, Hellinger P, Verdini A, Landi S, Franci L, Montagud-Camps V, Matteini L. Properties of Hall-MHD Turbulence at Sub-Ion Scales: Spectral Transfer Analysis. Atmosphere. 2021; 12(12):1632. https://doi.org/10.3390/atmos12121632
Chicago/Turabian StylePapini, Emanuele, Petr Hellinger, Andrea Verdini, Simone Landi, Luca Franci, Victor Montagud-Camps, and Lorenzo Matteini. 2021. "Properties of Hall-MHD Turbulence at Sub-Ion Scales: Spectral Transfer Analysis" Atmosphere 12, no. 12: 1632. https://doi.org/10.3390/atmos12121632
APA StylePapini, E., Hellinger, P., Verdini, A., Landi, S., Franci, L., Montagud-Camps, V., & Matteini, L. (2021). Properties of Hall-MHD Turbulence at Sub-Ion Scales: Spectral Transfer Analysis. Atmosphere, 12(12), 1632. https://doi.org/10.3390/atmos12121632







