A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence
Abstract
1. Introduction
2. Methodology
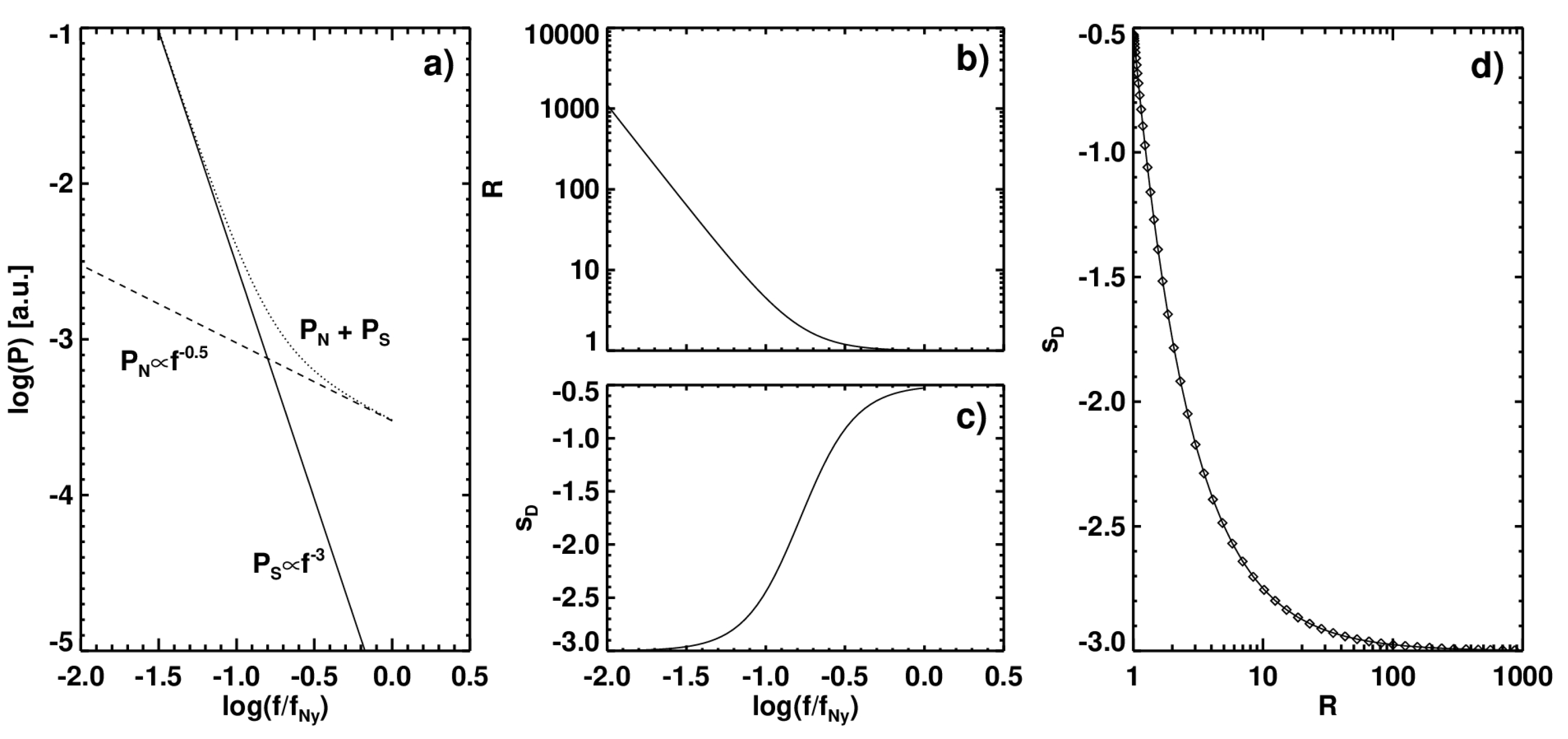
2.1. Signal-to-Noise Ratio
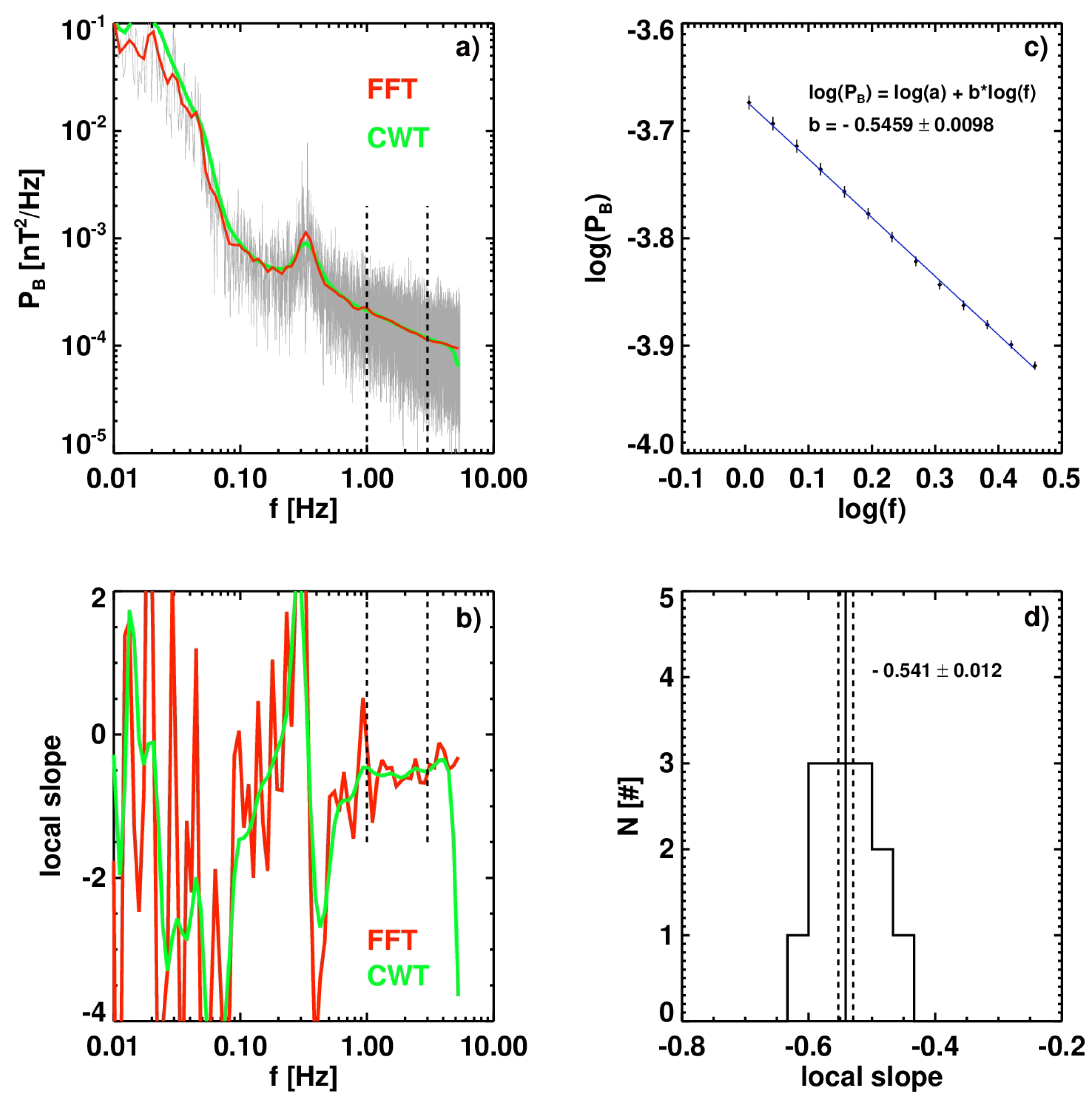
2.2. Continuous Wavelet Transform
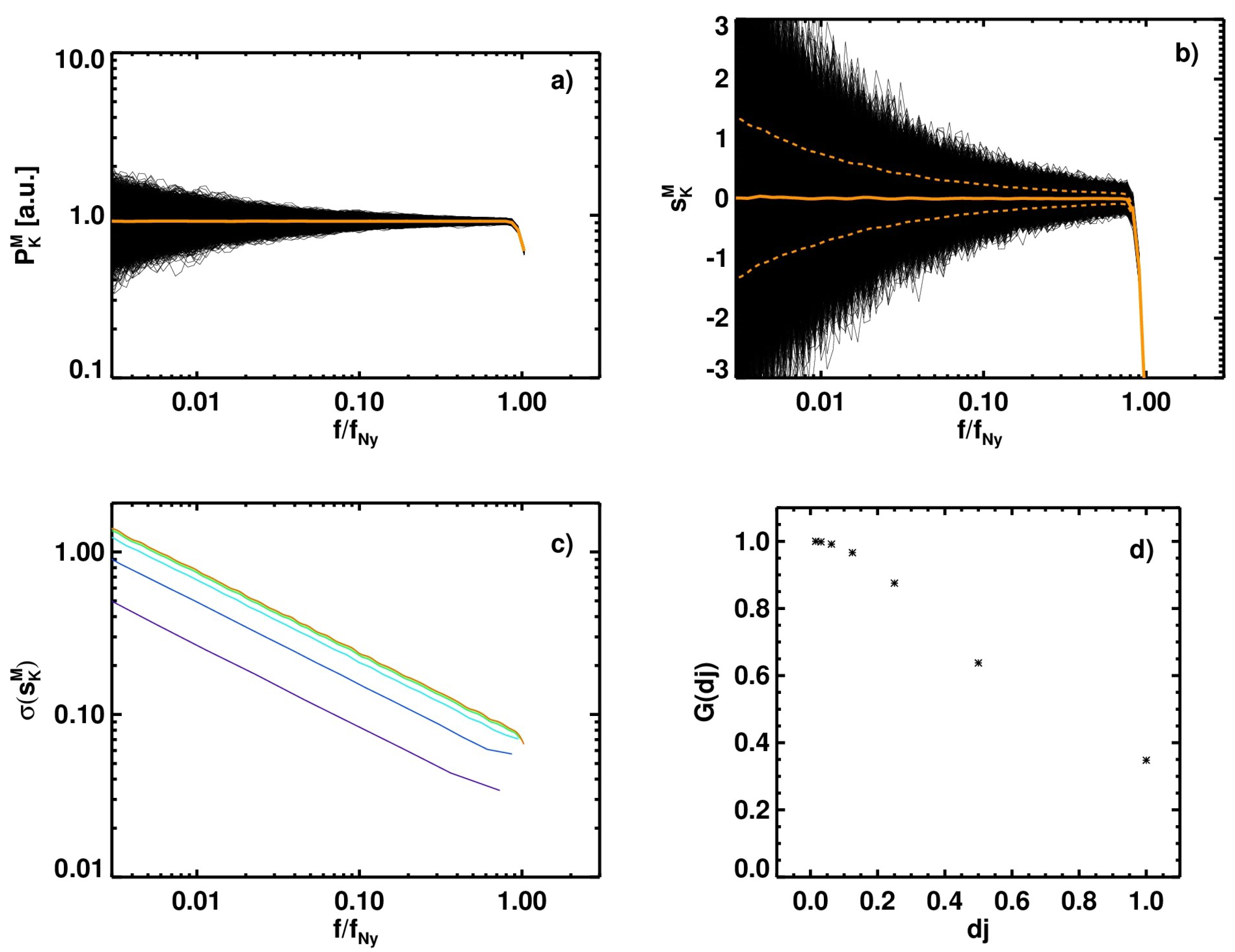
2.3. Local Slope and Monte Carlo Simulations of Its Error Distribution Function
- (1)
- We draw a set of N independent and identically distributed random K-dimensional vectors from (Multivariate normal distribution function with zero mean vector and diagonal covariance matrix with unit variances), denoted as ;
- (2)
- (3)
- (4)
- (5)
- We construct a probability distribution function of for each scale , and estimate its standard deviation , , where denotes the variance.
3. Statistics of Sub-ion Scale Power Spectra
3.1. Wind MFI and SWE Instruments
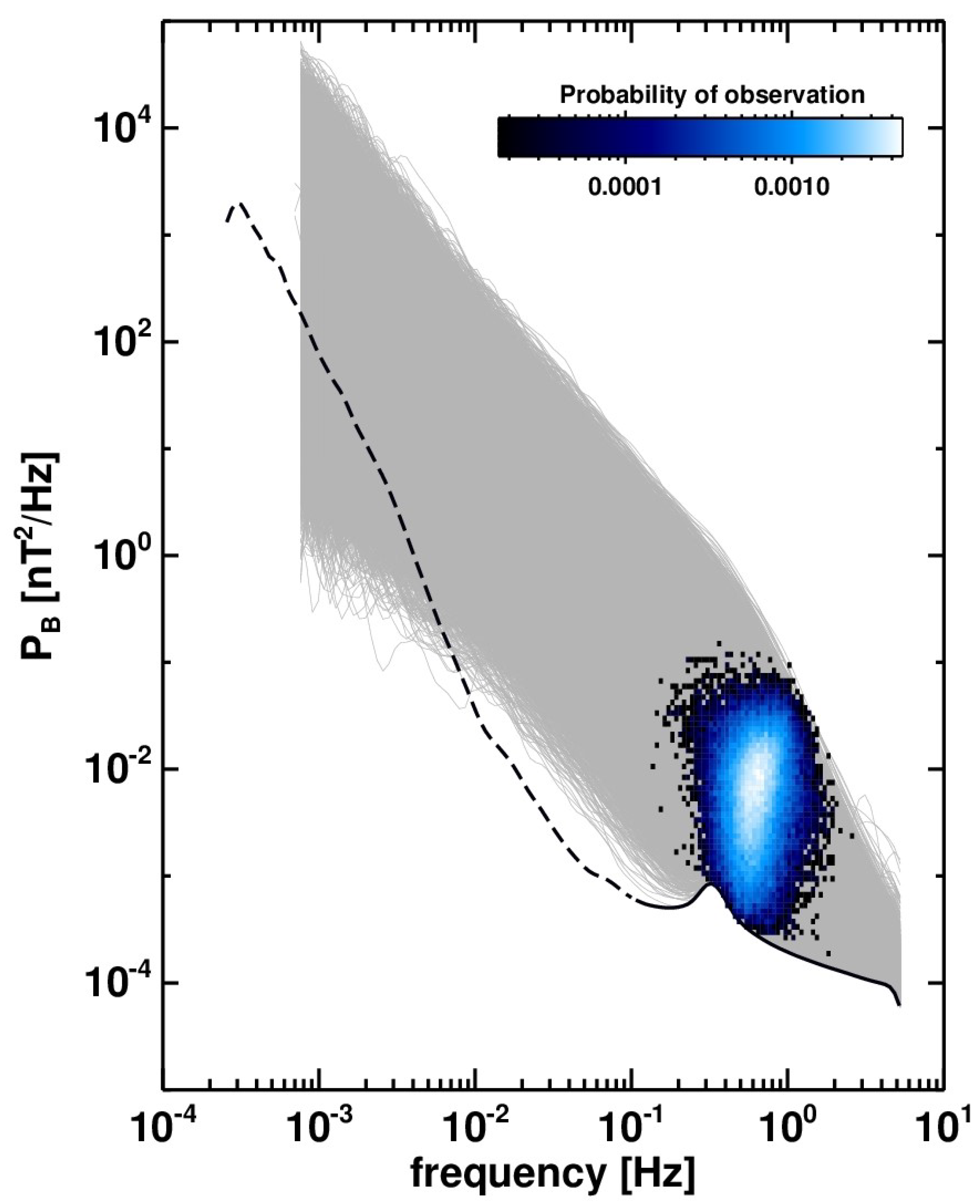
3.2. 11 Years of Wind MFI Data
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMWN | Correlated Multivariate White Noise |
| CWT | Continuous Wavelet Transform |
| FF | Fast Forward |
| FFT | Fast Fourier Transform |
| FR | Fast Reverse |
| IMF | Interplanetary Magnetic Field |
| IP | Interplanetary |
| KAW | Kinetic Alfvén Wave |
| MC | Monte Carlo |
| MFI | Magnetic Field Investigation |
| MHD | Magnetohydrodynamics |
| PSD | Power Spectral Density |
| SW | Solar Wind |
| UMWN | Uncorrelated Multivariate White Noise |
Appendix A
| Symbol | Description |
|---|---|
| R | Signal-to-noise ratio plus one |
| Ratio of the power spectrum of observed signal and empirical noise level | |
| s | Local slope |
| Derivative of a sum of two power law functions in a log-log coordinate system | |
| Standard deviation of local slope | |
| Standard deviation of local slope in the framework of simple Alfvénic turbulence model | |
| Standard deviation of distribution of local slopes of MFI Wind PSDs at particular spacecraft frame frequency | |
| Standard deviation of ‘intrinsic’ distribution of local slopes at any particular spacecraft frame frequency (estimated via Equation (12) employing ) | |
| Standard deviation of ‘intrinsic’ distribution of local slopes at any particular spacecraft frame frequency (estimated via Equation (12) employing ) | |
| ‘Intrinsic’ local slope; value that would have been measured in the absence of noise | |
| Measure of correlation between the power spectra of two components of magnetic field | |
| Measure of correlation between two components of magnetic field | |
| Measure of correlation between two consecutive values of trace power spectrum of B | |
| Measure of correlation between the trace power spectrum of B and power spectrum of noise |
Appendix B
Appendix C
Appendix D
Appendix E
References
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Astron. 1963, 40, 742. [Google Scholar]
- Kraichnan, R.H. Inertial Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef]
- Shebalin, J.V.; Matthaeus, W.H.; Montgomery, D. Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 1983, 29, 525–547. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. Astrophys. J. 1995, 438, 763–775. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Bale, S.D.; Salem, C.S.; Maruca, B.A. Residual Energy Spectrum of Solar Wind Turbulence. Astrophys. J. 2013, 770, 125. [Google Scholar] [CrossRef][Green Version]
- Bowen, T.A.; Mallet, A.; Bonnell, J.W.; Bale, S.D. Impact of Residual Energy on Solar Wind Turbulent Spectra. Astrophys. J. 2018, 865, 45. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Goldstein, M.L.; Roberts, D.A. Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. 1990, 95, 20673–20683. [Google Scholar] [CrossRef]
- Dasso, S.; Milano, L.J.; Matthaeus, W.H.; Smith, C.W. Anisotropy in Fast and Slow Solar Wind Fluctuations. Astrophys. J. Lett. 2005, 635, L181–L184. [Google Scholar] [CrossRef]
- Zank, G.P.; Nakanotani, M.; Zhao, L.L.; Adhikari, L.; Telloni, D. Spectral Anisotropy in 2D plus Slab Magnetohydrodynamic Turbulence in the Solar Wind and Upper Corona. Astrophys. J. 2020, 900, 115. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.; Guo, F.; Li, X.; Roytershteyn, V. Parametric Decay Instability and Dissipation of Low-frequency Alfvén Waves in Low-beta Turbulent Plasmas. Astrophys. J. 2018, 855, 139. [Google Scholar] [CrossRef]
- Bowen, T.A.; Badman, S.; Hellinger, P.; Bale, S.D. Parametric Decay of Alfven Waves in the Solar Wind. In Solar Heliospheric and INterplanetary Environment (SHINE 2018); SHINE: Cocoa Beach, FL, USA, 2018; p. 11. [Google Scholar]
- Chandran, B.D.G. Parametric instability, inverse cascade and the 1/f range of solar-wind turbulence. J. Plasma Phys. 2018, 84, 905840106. [Google Scholar] [CrossRef] [PubMed]
- Oughton, S.; Matthaeus, W.H. Critical Balance and the Physics of Magnetohydrodynamic Turbulence. Astrophys. J. 2020, 897, 37. [Google Scholar] [CrossRef]
- Hollweg, J.V. Kinetic Alfvén wave revisited. J. Geophys. Res. 1999, 104, 14811–14820. [Google Scholar] [CrossRef]
- Howes, G.G.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Quataert, E.; Schekochihin, A.A. Astrophysical Gyrokinetics: Basic Equations and Linear Theory. Astrophys. J. 2006, 651, 590–614. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Howes, G.G.; Quataert, E.; Tatsuno, T. Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. Astrophys. J. Suppl. Ser. 2009, 182, 310–377. [Google Scholar] [CrossRef]
- Boldyrev, S.; Horaites, K.; Xia, Q.; Perez, J.C. Toward a Theory of Astrophysical Plasma Turbulence at Subproton Scales. Astrophys. J. 2013, 777, 41. [Google Scholar] [CrossRef]
- Zhao, J.S.; Voitenko, Y.; Yu, M.Y.; Lu, J.Y.; Wu, D.J. Properties of Short-wavelength Oblique Alfvén and Slow Waves. Astrophys. J. 2014, 793, 107. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Leung, L.; Boldyrev, S.; Maruca, B.A.; Bale, S.D. Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys. Res. Lett. 2014, 41, 8081–8088. [Google Scholar] [CrossRef]
- Franci, L.; Landi, S.; Matteini, L.; Verdini, A.; Hellinger, P. Plasma Beta Dependence of the Ion-scale Spectral Break of Solar Wind Turbulence: High-resolution 2D Hybrid Simulations. Astrophys. J. 2016, 833, 91. [Google Scholar] [CrossRef]
- Safránková, J.; Němeček, Z.; Němec, F.; Přech, L.; Pitňa, A.; Chen, C.H.K.; Zastenker, G.N. Solar Wind Density Spectra around the Ion Spectral Break. Astrophys. J. 2015, 803, 107. [Google Scholar] [CrossRef][Green Version]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. London. Ser. A-Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Sahraoui, F.; Goldstein, M.L.; Belmont, G.; Canu, P.; Rezeau, L. Three Dimensional Anisotropic k Spectra of Turbulence at Subproton Scales in the Solar Wind. Phys. Rev. Lett. 2010, 105, 131101. [Google Scholar] [CrossRef]
- Bowen, T.A.; Mallet, A.; Bale, S.D.; Bonnell, J.W.; Case, A.W.; Chandran, B.D.G.; Chasapis, A.; Chen, C.H.K.; Duan, D.; Dudok de Wit, T.; et al. Constraining Ion-Scale Heating and Spectral Energy Transfer in Observations of Plasma Turbulence. Phys. Rev. Lett. 2020, 125, 025102. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; He, J.; Bowen, T.A.; Woodham, L.D.; Wang, T.; Chen, C.H.K.; Mallet, A.; Bale, S.D. Anisotropy of Solar Wind Turbulence in the Inner Heliosphere at Kinetic Scales: PSP Observations. Astrophys. J. Lett. 2021, 915, L8. [Google Scholar] [CrossRef]
- Huang, S.Y.; Sahraoui, F.; Andrés, N.; Hadid, L.Z.; Yuan, Z.G.; He, J.S.; Zhao, J.S.; Galtier, S.; Zhang, J.; Deng, X.H.; et al. The Ion Transition Range of Solar Wind Turbulence in the Inner Heliosphere: Parker Solar Probe Observations. Astrophys. J. Lett. 2021, 909, L7. [Google Scholar] [CrossRef]
- Borovsky, J.E. The velocity and magnetic field fluctuations of the solar wind at 1 AU: Statistical analysis of Fourier spectra and correlations with plasma properties. J. Geophys. Res. (Space Phys.) 2012, 117, A05104. [Google Scholar] [CrossRef]
- Alexandrova, O.; Lacombe, C.; Mangeney, A.; Grappin, R.; Maksimovic, M. Solar Wind Turbulent Spectrum at Plasma Kinetic Scales. Astrophys. J. 2012, 760, 121. [Google Scholar] [CrossRef]
- Sahraoui, F.; Huang, S.Y.; Belmont, G.; Goldstein, M.L.; Rétino, A.; Robert, P.; De Patoul, J. Scaling of the Electron Dissipation Range of Solar Wind Turbulence. Astrophys. J. 2013, 777, 15. [Google Scholar] [CrossRef]
- Roberts, O.W.; Alexandrova, O.; Kajdič, P.; Turc, L.; Perrone, D.; Escoubet, C.P.; Walsh, A. Variability of the Magnetic Field Power Spectrum in the Solar Wind at Electron Scales. Astrophys. J. 2017, 850, 120. [Google Scholar] [CrossRef]
- Alexandrova, O.; Jagarlamudi, V.K.; Hellinger, P.; Maksimovic, M.; Shprits, Y.; Mangeney, A. Spectrum of kinetic plasma turbulence at 0.3-0.9 astronomical units from the Sun. Phys. Rev. E 2021, 103, 063202. [Google Scholar] [CrossRef]
- Russell, C.T. Comments on the Measurement of Power Spectra of the Interplanetary Magnetic Field. In Scientific and Technical Information Office, National Aeronautics and Space Administration; NASA Special Publication: Washington, DC, USA, 1972; Volume 308, p. 365. [Google Scholar]
- Woodham, L.D.; Wicks, R.T.; Verscharen, D.; Owen, C.J. The Role of Proton Cyclotron Resonance as a Dissipation Mechanism in Solar Wind Turbulence: A Statistical Study at Ion-kinetic Scales. Astrophys. J. 2018, 856, 49. [Google Scholar] [CrossRef]
- Horbury, T.S.; Forman, M.; Oughton, S. Anisotropic Scaling of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2008, 101, 175005. [Google Scholar] [CrossRef] [PubMed]
- Podesta, J.J. Dependence of Solar-Wind Power Spectra on the Direction of the Local Mean Magnetic Field. Astrophys. J. 2009, 698, 986–999. [Google Scholar] [CrossRef]
- Dudok de Wit, T.; Alexandrova, O.; Furno, I.; Sorriso-Valvo, L.; Zimbardo, G. Methods for Characterising Microphysical Processes in Plasmas. Space Sci. Rev. 2013, 178, 665–693. [Google Scholar] [CrossRef]
- Lion, S.; Alexandrova, O.; Zaslavsky, A. Coherent Events and Spectral Shape at Ion Kinetic Scales in the Fast Solar Wind Turbulence. Astrophys. J. 2016, 824, 47. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bullet. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The Wind Magnetic Field Investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Koval, A.; Szabo, A. Magnetic field turbulence spectra observed by the wind spacecraft. In Solar Wind 13; American Institute of Physics Conference Series; Zank, G.P., Borovsky, J., Bruno, R., Cirtain, J., Cranmer, S., Elliott, H., Giacalone, J., Gonzalez, W., Li, G., Marsch, E., et al., Eds.; AIP: Melville, NY, USA, 2013; Volume 1539, pp. 211–214. [Google Scholar] [CrossRef]
- Ogilvie, K.W.; Chornay, D.J.; Fritzenreiter, R.J.; Hunsaker, F.; Keller, J.; Lobell, J.; Miller, G.; Scudder, J.D.; Sittler, E.C.J.; Torbert, R.B.; et al. SWE, A Comprehensive Plasma Instrument for the Wind Spacecraft. Space Sci. Rev. 1995, 71, 55–77. [Google Scholar] [CrossRef]
- Bruno, R.; Trenchi, L.; Telloni, D. Spectral Slope Variation at Proton Scales from Fast to Slow Solar Wind. Astrophys. J. Lett. 2014, 793, L15. [Google Scholar] [CrossRef]
- Franci, L.; Del Sarto, D.; Papini, E.; Giroul, A.; Stawarz, J.E.; Burgess, D.; Hellinger, P.; Landi, S.; Bale, S.D. Evidence of a “current-mediated” turbulent regime in space and astrophysical plasmas. arXiv 2020, arXiv:2010.05048. [Google Scholar]
- Matteini, L.; Franci, L.; Alexandrova, O.; Lacombe, C.; Landi, S.; Hellinger, P.; Papini, E.; Verdini, A. Magnetic Field Turbulence in the Solar Wind at Sub-ion Scales: In Situ Observations and Numerical Simulations. Front. Astron. Space Sci. 2020, 7, 83. [Google Scholar] [CrossRef]
- Smith, C.W.; Hamilton, K.; Vasquez, B.J.; Leamon, R.J. Dependence of the Dissipation Range Spectrum of Interplanetary Magnetic Fluctuationson the Rate of Energy Cascade. Astrophys. J. 2006, 645, L85–L88. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Weygand, J.M.; Chuychai, P.; Dasso, S.; Smith, C.W.; Kivelson, M.G. Interplanetary Magnetic Taylor Microscale and Implications for Plasma Dissipation. Astrophys. J. 2008, 678, L141–L144. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Parashar, T.N.; Wan, M.; Wu, P. Turbulence and Proton–Electron Heating in Kinetic Plasma. Astrophys. J. Lett. 2016, 827, L7. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Kawazura, Y.; Barnes, M.A. Constraints on ion versus electron heating by plasma turbulence at low beta. J. Plasma Phys. 2019, 85, 905850303. [Google Scholar] [CrossRef]
- Kawazura, Y.; Barnes, M.; Schekochihin, A.A. Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl. Acad. Sci. USA 2019, 116, 771–776. [Google Scholar] [CrossRef]
- Zhdankin, V.; Uzdensky, D.A.; Werner, G.R.; Begelman, M.C. Electron and Ion Energization in Relativistic Plasma Turbulence. Phys. Rev. Lett. 2019, 122, 055101. [Google Scholar] [CrossRef]
- Hughes, R.S.; Gary, S.P.; Wang, J. Electron and ion heating by whistler turbulence: Three-dimensional particle-in-cell simulations. Geophys. Res. Lett. 2014, 41, 8681–8687. [Google Scholar] [CrossRef]
- Pi, G.; Pitňa, A.; Němeček, Z.; Šafránková, J.; Shue, J.H.; Yang, Y.H. Long- and Short-Term Evolutions of Magnetic Field Fluctuations in High-Speed Streams. Solar Phys. 2020, 295, 84. [Google Scholar] [CrossRef]
- Podesta, J.J. Spectra that behave like power-laws are not necessarily power-laws. Adv. Space Res. 2016, 57, 1127–1132. [Google Scholar] [CrossRef]
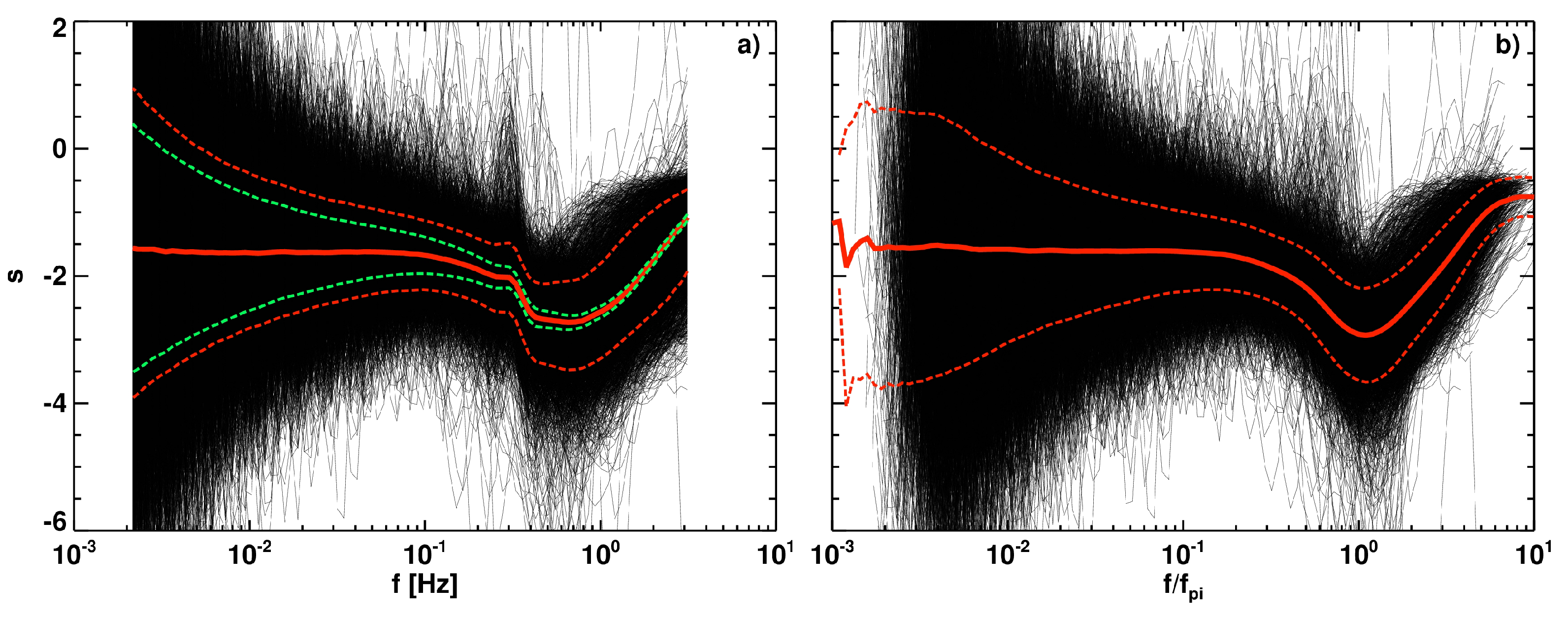
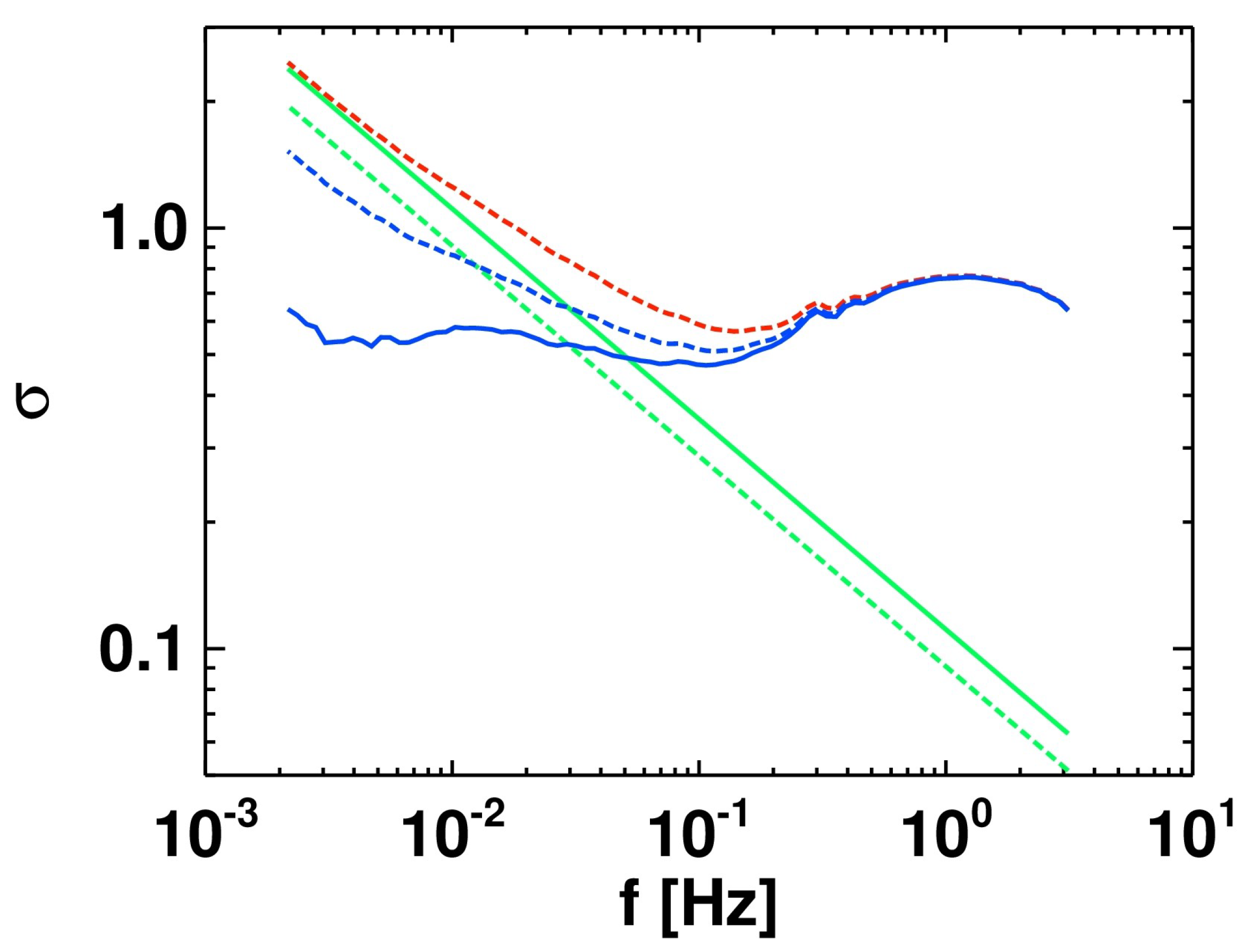

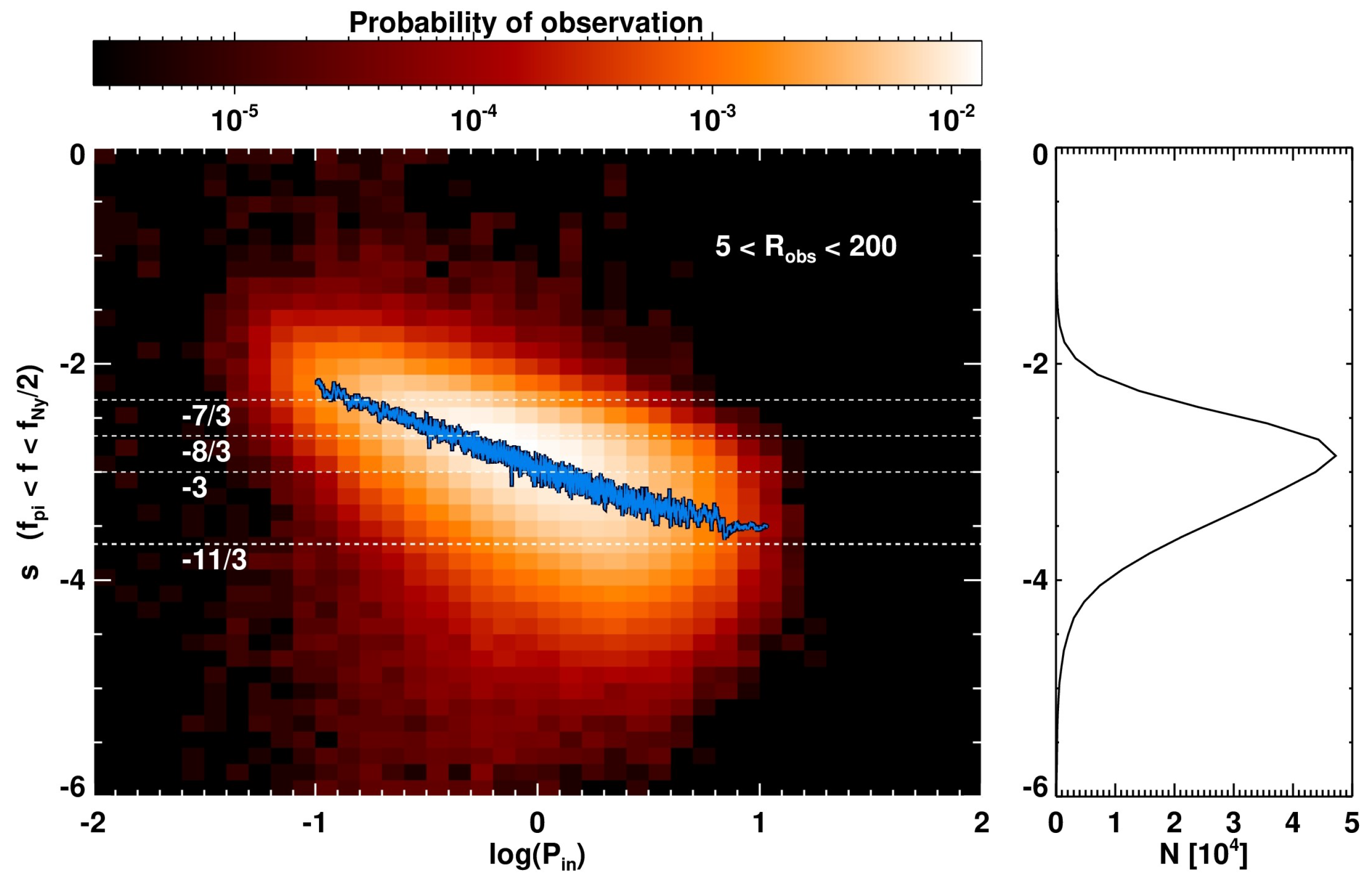
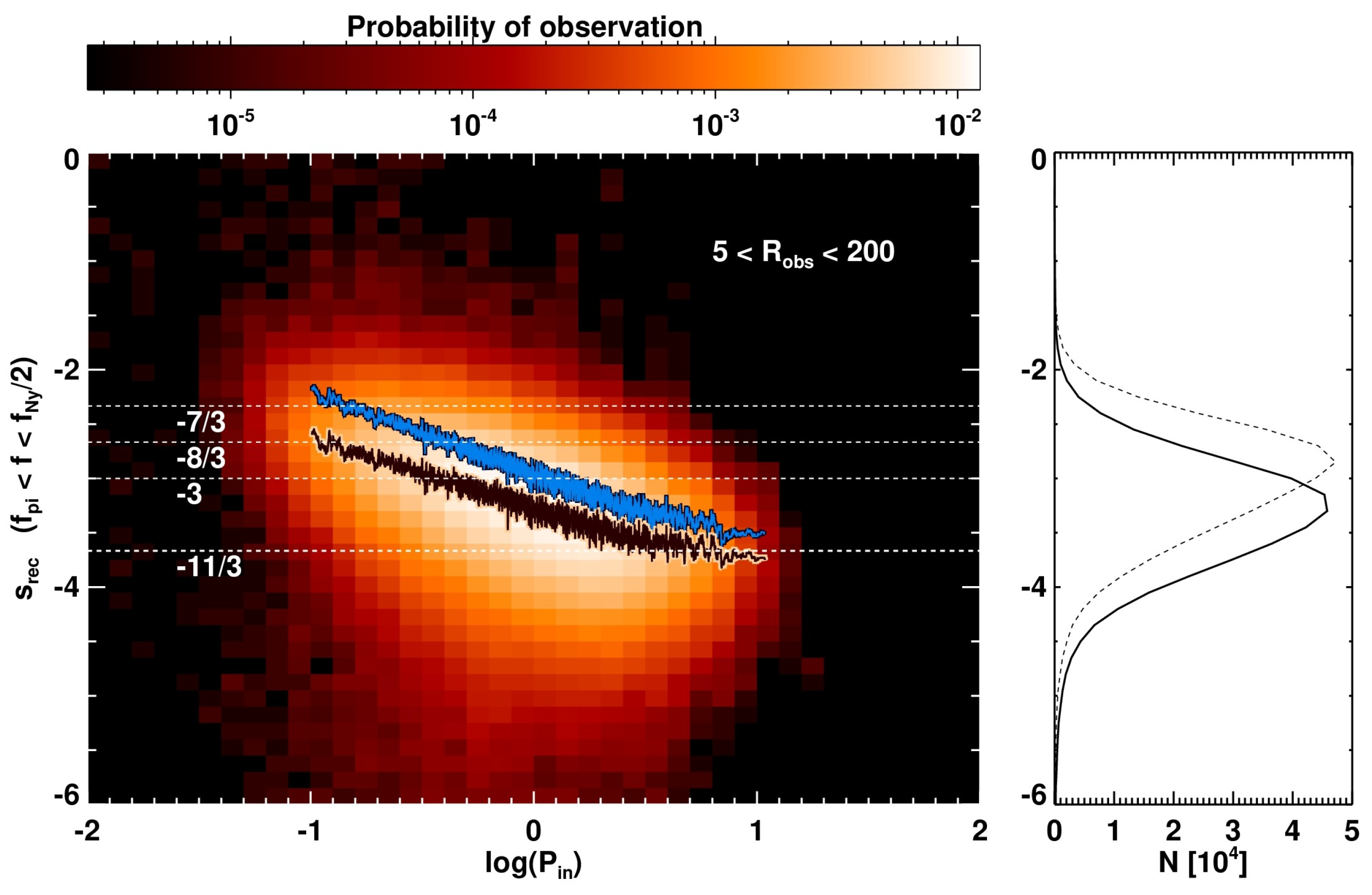
| 1/64 | 1 |
| 1/32 | 0.998 |
| 1/16 | 0.992 |
| 1/8 | 0.966 |
| 1/4 | 0.875 |
| 1/2 | 0.637 |
| 1 | 0.348 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitňa, A.; Šafránková, J.; Němeček, Z.; Franci, L.; Pi, G. A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence. Atmosphere 2021, 12, 1547. https://doi.org/10.3390/atmos12121547
Pitňa A, Šafránková J, Němeček Z, Franci L, Pi G. A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence. Atmosphere. 2021; 12(12):1547. https://doi.org/10.3390/atmos12121547
Chicago/Turabian StylePitňa, Alexander, Jana Šafránková, Zdeněk Němeček, Luca Franci, and Gilbert Pi. 2021. "A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence" Atmosphere 12, no. 12: 1547. https://doi.org/10.3390/atmos12121547
APA StylePitňa, A., Šafránková, J., Němeček, Z., Franci, L., & Pi, G. (2021). A Novel Method for Estimating the Intrinsic Magnetic Field Spectrum of Kinetic-Range Turbulence. Atmosphere, 12(12), 1547. https://doi.org/10.3390/atmos12121547







