Abstract
The high ambient ozone concentrations cause impairing effects on vegetation leading to plant injuries. The potential ozone uptake to vegetation through open stomata can be quantified using stomatal conductance measurements under the local environmental conditions. This study compares the ozone stomatal conductance to vegetation obtained with a modified Jarvis formula adopted from the Vegetation Manual of United Nations Economic Commission for Europe, and experimental field measurements’ data. The stomatal conductance was measured by a portable photosynthesis and gas exchange analyzer system LiCOR6400. The measurements were performed in the submontane environment of the High Tatra Mountains in Slovakia on Swiss pine (Pinus cembra), as a native species of the local flora. According to previous studies, Swiss pine is considered as an ozone-sensitive species. The modified Jarvis model for the ozone stomatal conductance is compared with the field measurements. The suitable parameterization of the modified Jarvis model for Swiss pine is obtained. The parameterization of stomatal conductance for Swiss pine in the local environment would help understand its specificity and similarity to other conifer species. In the case of using parameterization for a boreal coniferous from the Vegetation Manual of the International Cooperative Programme on Effects of Air Pollution on Natural Vegetation and Crops, validation of the model with the measurements without temperature adjustment of the conifer chamber achieved a coefficient of determination of . This result is not in contradiction with the previous researches. With the optimal set of parameters, obtained in this paper, the Jarvis model reaches . The data suggest that Jarvis-type models with appropriate parameterization are applicable for stomatal conductance estimation for Pinus cembra when the measurements do not modify the temperature regime.
1. Introduction
Ozone is a gas molecule present in the air and originated as a secondary pollutant from both biogenic and anthropogenic sources. The majority of the gas is located in the stratosphere, where it forms the ozone layer. The rest is situated in the troposphere. We were interested in ozone in the lower layer of the troposphere where ozone–biota interactions are acting. The ozone in this layer is called ground-level ozone. Even though the historical ozone measurements since the 1850s have been semi-quantitative, these and later measurements provide a rough estimate of the long-term ground-level ozone increase. The concentration growth from the 1950s till the 2000s and later [1,2] is caused mainly by increased levels of the ozone’s precursor, such as nitrogen oxides NOX and volatile organic compounds VOC [2,3].
The future ozone trend in the RCP8.5 scenario of representative concentration pathway (RCP) predicts the global increase of ground-level ozone compared to the early 2000s. The other RCP scenarios predictions are ambiguous and locality dependent [4,5,6]. The studies highlight the potential influence of CH4 emissions, global warming, and weakened NO titration [4] on ozone formation and decay in the future.
The interaction between ozone and vegetation has been investigated for several decades [7,8,9,10,11]. Those studies had provided the basis of ozone uptake into vegetation models [12,13,14]. In these models, the quantity of the specific gas entering the vegetation through stomata is represented by stomatal conductance.
Ozone stomatal conductance is an important element in ozone stomatal flux, and the ozone dose calculation which is used for the estimation of the vegetation’s injury.
The canopy-scale stomatal conductance of ozone might be calculated by the eddy covariance method. The method is based on the eddy covariance measurements of water vapor and sensible heat fluxes [15,16]. This method is demanding on the equipment. The more approachable way to obtain the stomatal conductance of ozone is the calculation from the stomatal conductance of water vapor, by comparing the molecular diffusivities of ozone and water [17].
The demand for the estimation of ozone flux gave rise to several models of stomatal conductance. Presumably, the most widely used model for ozone stomatal conductance in the European environment, promoted by the United Nations Economic Commission for Europe (UNECE), is the Jarvis-type multiplicative model [13] modified by Emberson [18,19]. This model is implemented in the European Monitoring and Evaluation Programme Meteorological Synthesizing Centre-West (EMEP MSC-W) chemical transport model, which predicts the formation, transportation, and deposition of pollutants in Europe [20,21].
The gas exchange between the environment and the vegetation is essential for water and carbon management [22]. This exchange is provided by stomatal pores in reaction to the number of environmental and inner plant conditions, such as CO2 concentration, light, humidity, and soil conditions. The Kaiser study [23] suggests that the opening of stomatal pores leads to a rapid increase in stomatal conductance. The later opening of pores does not induce a further significant stomatal conductance growth. Closing stomatas occurs after the sudden stressor exposition. The reaction time is approximately 5–10 min [24]. The overall closure happens after 10–60 min [22]. The time necessary for adaptation is known as stomatal or response lag.
The studies point to the effects of ozone on vegetation. The most manifested effects are a visible foliar injury [18,25], such as mottling or bronzing [26,27], reduction of carbon fixation via photosynthesis [28,29], reduced increase of the biomass [30,31], premature senescence [31], and reduction in the net photosynthesis followed by biomass reduction. The dynamics of ozone influence on vegetation is still under intensive study and the predominant suggestion connects plant damages with cumulative ozone uptake instead of external ozone exposure [32,33]. The vegetation sensitivity to ozone flux is influenced by different factors, such as developmental stage of the plant, ambient microclimate, phenology, compensation processes, antioxidant capacity, morphology, and the anatomy of genus or species variation [18,34]. The literature about the Swiss pine suggests that the species is sensitive to ozone and environmental stress [35]. Defoliation, chlorotic mottles, and microscopic changes of the mesophyll are considered as the effects of ozone impact on P. cembra species [36,37].
The purpose of the research was to find the most suitable parameterizations of the modified Jarvis model for stomatal conductance for P. cembra based on the measured data of stomatal conductance.
2. Materials and Methods
2.1. Location Characteristic
The study area took place in the research facility of Tatra National Park’s State Forest organization in Tatranská Lomnica (49.16646° N and 20.28437° E). The location is a submontane area at an altitude of 850 m asl, surrounded by the High Tatra Mountains from the northwest. In the vicinity of the study area, a meteorological observatory, Stará Lesná (approximately 1.7 km, 49.15199° N, 20.28810° E), is located. The time series from 1988 to 2013 describe the location by cold continental climate with air an temperature range from −26.5 to 34.2 °C and a mean annual air temperature 5.9 °C. The mean annual relative humidity varies from 74 to 81%. The majority of the precipitation is recorded during the summer half-year, and it is affected mainly by the atmospheric circulation and orography. The average annual precipitation is 744 mm. The prevalent winds in the locality are the southern winds from the open southern side, with the relative frequency at 36% and are followed by the northerly winds (30%). The average wind speed reaches 2.1 [38].
The basic descriptive information about 16 days of measurements is recorded in Table 1. The data were obtained during both cyclonal and anticyclonal situations. The mean temperature and vapor pressure deficit in the instrumental chamber with pine needles are also marked in the table. The mean temperature of the measurements varied from 2 to 38 °C. The mean vapor pressure deficit condition was in the range of 0.1 to 4.5 kPa.

Table 1.
List of days of measurements with the duration of measurement and the basic meteorological parameters.
The local vegetation is characterized by temperate coniferous and mixed forests. The Swiss pine (P. cembra) is a native conifer in the Alps and the Carpathian Mountains. Swiss pine forests in the Carpathians Mountains grow in the range from 1300 to 1700 m asl and the isolated individuals from 900 to 1985 m asl [39,40].
Human activity had influenced the distribution of P. cembra in mountain environments by direct impacts such as land use transformation or indirectly by changing the climate and the air composition. Recent chamber fumigation studies pointed out the impairing effects of ground ozone on pine trees [37] by both visible and microscopical injuries. According to Casalegno’s article [40], the future scenarios of P. cembra distribution might be endangered by potentially warmer and more xeric conditions considering the greater competitive abilities of the species Picea abies and Larix decidua. There is a prediction of P. cembra spreading to higher altitudes, preferably to abandoned agro-pastoral landscapes.
2.2. Field Measurements of Stomatal Conductance
The stomatal conductance of ozone was determined by the portable photosynthesis system LiCOR6400 (Li-Cor Inc., Inc, Lincoln, NE, USA). The instrument was equipped with a standard LiCOR 6400-22 Opaque Conifer Chamber. Component 6400-18 RGB Light Source was used as a source of photosynthetically active radiation (PAR). The measurements were executed on the terminal shoots of lateral branches from the middle part of the plants. The examined twig was located in the conifer chamber. The measurement was executed on terminal shoots of lateral branches on 8 solitary mature trees. The tree height ranged from 8 to 12 m, and measurement took place between 2 and 4 m on both sunny and shaded sides. Portable metal construction was used for regular access to the canopy. The stomatal conductance to water vapor was determined by the incoming and outgoing flow rates from the chamber and the incoming and outgoing water mole fractions [41]. The value of () was derived from () by the conversion factor represented by a value of 0.663 [17]. The factor is derived as the ratio between the molecular diffusivity of ozone to air and the molecular diffusivity of water vapor to the air. This factor is recommended by the guideline from the International Cooperative Programme on Effects of Air Pollution on Natural Vegetation and Crops (ICP Vegetation) [18]. Recently, the ozone molecular diffusivities to air were experimentally measured for the first time [42], and the uncertainty of this quantity was reduced substantially. The conversion factor should be updated in the future according to the results [42] to the value of 0.704 with 8% uncertainty. This new factor is in accordance with the currently used recommended value within the uncertainties.
The PAR value in the measurements was always adjusted, as the opaque conifer chamber was used. The experiment was divided into two sets according to the internal chamber temperature. The first group consists of measurements with the internal chamber temperature determined by the environment (“without temperature adjustment”, WoTA), as the instrument did not alter the temperature of the incoming air. This dataset consists of 191 individual measurements. Each measurement was preceded by gas exchange stabilization for approximately 4–10 min.
The second group consists of measurements with the adjusted internal chamber temperature by the executor (“with temperature adjustment”, WTA). This group of 757 measurements provided a greater range of measured temperature in the conifer chamber. The second setup was provided in a series of 2 to 9 individual measurements on the same twig. The gas exchange stabilization was executed after the twig change. The measurements within the series differ by the PAR parameter (achieving values from 120 to 2000 μmol m−2 s−1). The overall number of series was 140.
2.3. Modified Jarvis Model of Stomatal Conductance
From this time forward, the phrase stomatal conductance will refer to stomatal conductance to ozone. The multiplicative model based on Jarvis [13] and modified by Mills’s [18] and Emberson’s [43] article is a widely used model of stomatal conductance. The model is promoted by the United Nations Economic Commission for Europe (UNECE). The impact of the outer and the inner environment is considered within the model. Stomatal conductance is calculated by the multiplication of maximal stomatal conductance with the reducing factors or their combination. The reducing factors take into account the phenological , meteorological , , , and environmental limitations.
According to [43], stomatal conductance can be calculated as:
where represents the species-specific maximum value of stomatal conductance, which can be reached within the model. The value in the literature is defined either as the 95th percentile of stomatal conductance measured independently from the different water supply treatment [44], or as the averaged value above the 90th percentile of all of the valid stomatal conductance measurements [45], or by deriving from the values measured in the field under optimal condition for without outliers [19]. The model is described by unitless reducing factors of stomatal conductance. The reducing factors reach values within the interval from 0 to 1. The factor represents the minimum stomatal conductance during the daylight period under field conditions [46]. The reducing factor of air temperature is described in Equations (A1) and (A2) [19], and is determined by three parameters. and are limiting temperatures at which opening and closure of the stomata occur, respectively [19,47]. Optimum temperature is the temperature measured during the maximal [47]. The impact of solar radiation is represented by the factor . Solar radiation might be represented either by photosynthetically active radiation (mol m−2 s−1) or by global radiation (W m−2). The reducing factor is expressed by the exponential function (A3) or (A4) [19]. Reducing factor represents the stomatal response to the vapor pressure deficit. The response is described by the limiting values of stomatal opening corresponding to and , as described in Equation (A5) [19]. Fares [48] suggests setting and to 10th and 95th percentile of all of the measured values at the leaf level on sunlit leaves. Factor represents the phenology reducing factor. In this study its value equals one during the vegetation period, and otherwise, its value is zero. describes the impact of soil humidity (soil water potential (SWP) and plant available water (PAW)). Due to sufficient soil humidity repletion from the abundance of precipitation and local water management, we can omit this reduction factor.
Parameterization of Modified Jarvis Model
The crucial part of the modified Jarvis model of stomatal conductance of ozone is parameterization. Our measurements were not sufficient to estimate the parameters (, , , , , , , ) according to the methodology mentioned in Section 2.3. It means that due to the lack of the data, we were not able to find the values of these parameters from the first principles, i.e., we were not able to determine from the data the temperature in which stomata opening occurs and others. In order to find another way to estimate suitable parameters, two different approaches were examined. The two approaches differ in the selection of the model parameters. In the first approach, the modified Jarvis model with each of the nine en-block parameterizations adopted from the literature in Table 2 is validated against the measured values provided by the LiCOR measurements and the best en-block parameterization is selected. In the second approach, 1,764,000 unique sets of parameters from Table 3 are used in the validation of the Jarvis model and the optimal set of parameters is selected. The parameters in Table 3 are based on the parameters from Table 2. The value = 0.008 is excluded due to the similarity to values 0.0075 and 0.0083, and two different values of parameter 0.0 and 0.25 kPa were added.

Table 2.
Sets of parameterization of the modified Jarvis model for conifer species available in the literature.

Table 3.
Set of static parameters used in the Jarvis model based on the Table 2. The Jarvis model with each combination of parameters in this table was validated against measured stomatal conductance.
The performance of the modified Jarvis model was evaluated by the coefficient of determination , root mean square error , and [49]. The performance of the model was ranked primarily by the and secondarily by the . Parameter does not have an impact on performance, therefore the evaluation of the was crucial to distinguish the appropriate value.
The performance of the Jarvis model was evaluated separately on two types of measurements “without temperature adjustment, WoTA” and “with temperature adjustment WTA”.
3. Results
In order to find the parameters of the modified Jarvis model according to the first approach described in Section 2.3, the evaluation of the modified Jarvis models with en-block parameterizations from the literature is presented in Table 4. The model performs significantly better on the WoTA data than on the WTA data. In the case of the WTA data, the model performance is within the range from 0.01 to 0.20. For the WoTA data, the model reaches between the values 0.31 to 0.75. The for WTA ranges between 42.2 and 164.2 mol O3 m−2 PLA s−1 and for WoTA between 20.5 and 172.9 mol O3 m−2 PLA s−1.

Table 4.
Validation of the modified Jarvis model against WoTA and WTA measurements of stomatal conductance for each set of static parameters adopted from the literature in Table 2.
For the WoTA data, the Jarvis model with parameters for boreal coniferous species [18] based on the measurements of Norway spruce has the best performance according to the and ranked the third in the values. For the WTA data, the model with parameters for continental coniferous species has similarly as the WoTA achieved the best performance according to the and the third for the values. The model for temporal coniferous forests performs very similarly. Note, that the Jarvis model is not able to describe the WTA data satisfactorily with any set of the parameters from Table 2.
Because the model validation coefficient is insensitive to the parameter, we adjust the parameter in order to minimize the and of the model. The dependency of the and on the parameter for the boreal coniferous set of parameters is displayed on the left plot in Figure 1 for the WoTA data.
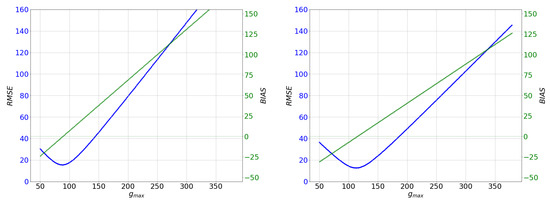
Figure 1.
The dependency of the and on the parameter for the boreal coniferous set of parameters (left figure) and for the optimal set of parameters from Table 5 (right figure). The WoTA data are assumed.
The best performance of model with = 15.6 and the corresponding = −0.21 has occurred for the = 88 mol O3 m−2 PLA s−1. This value is 30% lower than the original value of 125 mol O3 m−2 PLA s−1.
According to the second approach, in order to find the parameters of the Jarvis model, each combination of parameters from Table 3 was tested against the measured stomatal conductance and the performance of the modified Jarvis model was evaluated.
Figure 2 represents the achieved (in red) and (in blue) coefficients for the WoTA data. Each red or blue point represents one combination of parameters from Table 3 and its corresponding or , respectively. The dots in the figure have often visually merged into the form of a line. Maximal and minimal represent the favorable case scenarios for the model performance. The validation showed that the modified Jarvis model prefers the lower (0.0 and 0.25 kPa) and (2.5 kPa) in order to achieve a better model performance. The parameter achieved notable performances within the majority of the examined values. Parameter favours higher values (39 and 200 °C) but keeps a high performance of for all the examined values. The modified Jarvis model validation is more sensitive to the parameter and, in general, the model performs better for higher values of . As is seen in Figure 2, the coefficient does not depend on the value. However, the model reaches the lowest coefficient for values = 110, 125 and 130 mol O3 m−2 PLA s−1.
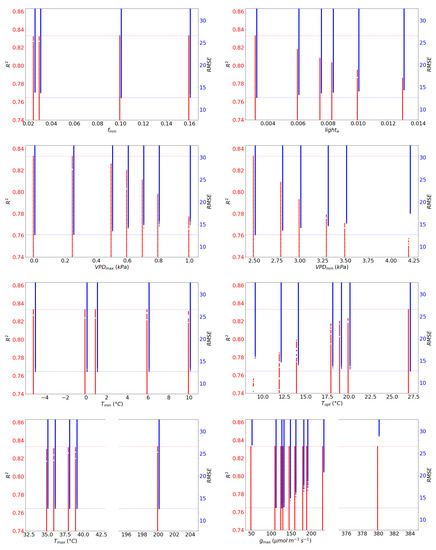
Figure 2.
The and coefficients from validation of the modified Jarvis model against the WoTA measurements for each set of static parameters in Table 3.
The selection of the optimal set of parameters of the modified Jarvis model for WoTA from all of the combinations of parameters from Table 3 was performed according to the following procedure. At first, 200 parameterizations of the modified Jarvis model with the best values were selected. Among all of the parameters in these 200 parameterizations, some parameters achieved a single unique value in these 200 best-performing models. These are the values of the parameters: kPa, °C, and . These values were unambiguously chosen to the optimal set of parameters. The predominant value of the parameter was the value 200 °C. On the contrary, the Jarvis model with several values parameters and performs equally well, therefore we selected the prevalent values of these parameters in the assumed 200 parameterizations to the optimal set of parameters. The occurrence of different values in the best-performing parameterizations was roughly equivalent. Therefore, the value of from the literature [18] was selected to the optimal set of parameters. The value with the lowest corresponding was selected according to an analysis demonstrated in Figure 1. For this optimal set of parameters, the validation of the modified Jarvis model with the WoTA data leads to , , , and 113 mol O3 m−2 PLA s−1. A similar process was executed for the WTA dataset. The optimal set of parameters is presented in Table 5, together with the best set of parameters adopted from the literature.

Table 5.
Selected parameterizations of the modified Jarvis model with the best evaluation of the model performance.
Comparison of stomatal conductances from LiCOR measurements and modeled conductance via the modified Jarvis models based on Table 5 are presented in Figure 3. The plots on the left side represent scattered plots between the measured and modeled data with the best parameterization selected from the literature. The scatter plots on the right side represent the Jarvis model with the optimal set of parameters. The equations of linear regression and coefficients of determination are shown in the plots. The purple line in the plot represents a 1:1 ideal line. The best performance of the model is in the case of WoTA dataset using the optimal set of parameters.
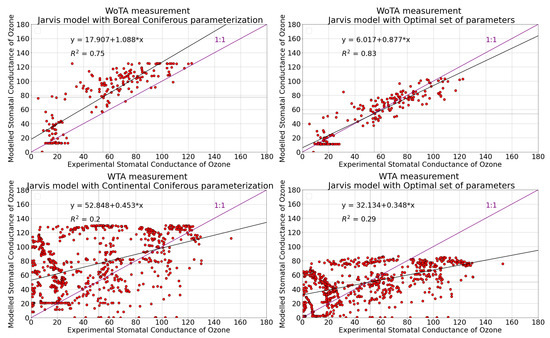
Figure 3.
Comparison of stomatal conductances from LiCOR measurements and modeled conductance via the modified Jarvis model. Dataset of WoTA is examined on the upper plots and dataset of WTA on the lower plots. On the left side, the parameterization of boreal coniferous for WoTA and continental coniferous for WTA are examined, respectively. On the right side, the Jarvis model with the optimal set of parameters is evaluated. The used unit of stomatal conductance is mol O3 m−2 PLA s−1.
The visualization of the parameters for relative stomatal conductance g is presented in Figure 4. The relative g is defined as the ratio .
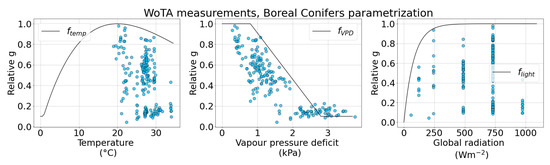
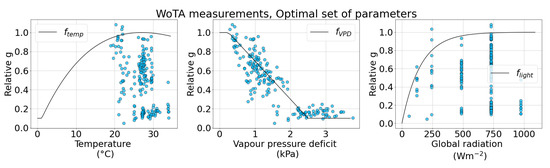
Figure 4.
Relative stomatal conductances for the WoTA dataset represents the ratio between the stomatal conductance and maximal stomatal conductance . In the upper plots = 125 mol O3 m−2 PLA s−1 and in the lower plots mol O3 m−2 PLA s−1. Blue dots represent the actual measurements and the black lines represent the modeled values of reduction factors , and .
4. Discussion
Explicit parameterization of the modified Jarvis model for ozone stomatal conductance for Pinus cembra species was absent in the scientific literature. In this paper, two types of measurements of the ozone stomatal conductance for P. cembra were taken. In the first type of measurements (WoTA), the internal chamber temperature was determined by the environment. In the second (WTA), this temperature was adjusted by the executor. Due to the lack of data describing lower temperatures and the vapor pressure deficit, the presented measurements were not suitable to determine the parameters of the Jarvis model from the physical and biological view, as is presented in Section 2.3. Two other approaches described in Section 2.3 were used for finding suitable parameters of the Jarvis model instead. It was found that the modified Jarvis model with suitable parameters describes the WoTA data well. In the case of the WTA data, we were not able to find a suitable parameterization of the Jarvis model that describes this data adequately. It is assumed that the temperature discrepancy between the external environment influencing the tree and the inner chamber temperature affecting the examined twig caused the low performance of the Jarvis model in the WTA data. For this reason, we will further discuss the results with just the WoTA dataset.
As described in Section 2.3, we first validated the Jarvis model with parameterizations available in the literature for various conifer species. Most of the nine selected parameterizations provided a reasonable performance within the interval from 0.59 to 0.75. These values are comparable with the results from other papers concerning pine species, e.g., for Pinus pinea [52] or for Pinus ponderosa [54]. The modified Jarvis model for ozone stomatal conductance for P. cembra achieved the best performance with the parameterization for boreal coniferous [18], reaching the highest and the third lowest value of . Two other Picea abies parameterizations [18,53] performed poorly with less than 0.4. Both parameterizations differ from the rest by the low value of the parameter (14 and 9 °C). As we can see in Figure 2, the model performance is better for higher values.
By the second approach of finding the suitable parameters for P. cembra, we found several better parameterizations than that adopted from the literature for different conifer species. The optimal set of parameters obtained by this approach is in Table 5, denoted as OP. Using this optimal set of parameters, the Jarvis model performs with and . We must note that the approach described in Section 2.3 diverges from the original design of the Jarvis model based on the descriptive parameters. This way of searching for suitable parameterization might change the descriptive parameters into the forcing parameters. This feature is also present in the official parameterization from the ICP Vegetation guideline [18]. For example, the value = 200 °C is not a realistic value of the parameter, but it is used for boreal coniferous species [18]. The best two models from both approaches selected = 200 °C. According to the ICP [18], this value simulates the weak response to high temperatures of trees growing under northern European conditions.
The best sets of parameters for the Jarvis model obtained from both approaches for WoTA differ from each other in all of the parameters except , , and . The most significant difference is in , , and values, the third one is considered to be the key parameter of the model. The 95th percentile of of the WoTA dataset is 106 mol O3 m−2 PLA s−1. However, the condition of independent measurements from the different water supply treatments was not accomplished. From the analysis of the model with boreal coniferous parameterization, we found out that the lowest is achieved with the parameter = 88 mol O3 m−2 PLA s−1. For the optimal set of parameters, = 113 mol O3 m−2 PLA s−1 reaches the lowest .
The soil water potential was not considered because the submontane environment does provide a plentitude of soil water to the environment. Therefore, this parameter in the referenced locality is relatively insignificant.
Since our measurements lacked the data during lower air temperature, lower vapor pressure deficit, and lower intensity of photosynthetically active radiation, future research covering that area of interest is needed. Further research should concern measurements in different locations, especially at different altitudes and during naturally changing external conditions and diurnal variation for an extended period of time.
5. Conclusions
Measurements of the ozone stomatal conductance for Pinus cembra indicate that the well-parameterized modified Jarvis model is able to describe the ozone stomatal conductance of this selected species in the field conditions. Assuming the parameterizations available in the literature for other conifer species, the most suitable parameterization for the P. cembra is the parameterization for boreal coniferous with coefficient of determination . In addition to this, the optimal set of parameters for the P. cembra with was selected. This model performance is comparable with the previous published studies for other conifer species. Therefore, the Jarvis model with the optimal set of parameters obtained in the present study or with parameterization for boreal coniferous provides a reliable estimations of the stomatal conductance of ozone and can be used as the basis for further ozone flux or phytotoxic ozone doses calculations for P. cembra. On the other hand, the Jarvis model is not able to estimate reasonably the stomatal conductance of ozone when the temperature conditions in the conifer chamber and the external conditions differ significantly.
Author Contributions
Conceptualization, A.B., P.F.J., D.Š., S.B. and V.L.; Data curation, P.F.J. and S.B.; Formal analysis, A.B. and D.Š.; Investigation, A.B., D.Š. and V.L.; Methodology, A.B., P.F.J., D.Š. and S.B.; Resources, P.F.J., A.B. and V.L.; Supervision, S.B. and V.L.; Validation, P.F.J.; Visualization, A.B., D.Š. and V.L.; Writing—original draft, A.B.; Writing—review & editing, P.F.J., D.Š., S.B. and V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by research grant of Comenius University no. G-21-206-00, grant of The Ministry of Education, Science, Research, and Sport of the Slovak Republic VEGA 02/0093/21 and by grants from Slovak Research and Development Agency no. APVV-18-0390, and APVV-17-0644.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank two anonymous reviewers for their valuable comments on this manuscript. We are also grateful to Lucia Čekovská for providing the measurements used in this research. Additional support was provided from the Stefan Schwarz fund for postdoctoral researchers awarded by the Slovak Academy of Sciences to Veronika Lukasová.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Equations for Reducing Factors
References
- Vingarzan, R. A review of surface ozone background levels and trends. Atmos. Environ. 2004, 38, 3431–3442. [Google Scholar] [CrossRef]
- Tarasick, D.; Galbally, I.E.; Cooper, O.R.; Schultz, M.G.; Ancellet, G.; Leblanc, T.; Wallington, T.J.; Ziemke, J.; Liu, X.; Steinbacher, M.; et al. Tropospheric ozone assessment report: Tropospheric ozone from 1877 to 2016, observed levels, trends and uncertainties. Elementa 2019, 7. [Google Scholar] [CrossRef]
- IPCC. IPCC 2014 Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Sicard, P.; Anav, A.; De Marco, A.; Paoletti, E. Projected global ground-level ozone impacts on vegetation under different emission and climate scenarios. Atmos. Chem. Phys. 2017, 17, 12177–12196. [Google Scholar] [CrossRef]
- Mills, G.; Pleijel, H.; Malley, C.S.; Sinha, B.; Cooper, O.R.; Schultz, M.G.; Neufeld, H.S.; Simpson, D.; Sharps, K.; Feng, Z.; et al. Tropospheric Ozone Assessment Report: Present-day ozone distribution and trends relevant to human health. Elementa 2018, 6. [Google Scholar] [CrossRef]
- Agathokleous, E.; Belz, R.B.; Calatayud, V.; De Marco, A.; Hoshika, Y.; Kitao, M.; Saitanis, C.J.; Sicard, P.; Paoletti, E.; Calabrese, E.J. Predicting the effect of ozone on vegetation via linear non-threshold (LNT), threshold and hormetic dose-response models. Sci. Total Environ. 2019, 649, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Kurpius, M.R.; Goldstein, A.H. Gas-phase chemistry dominates O-3 loss to a forest, implying a source of aerosols and hydroxyl radicals to the atmosphere. Geophys. Res. Lett. 2003, 30, 1371–1374. [Google Scholar] [CrossRef]
- Hogg, A.; Uddling, J.; Ellsworth, D.; Carroll, M.A.; Pressley, S.; Lamb, B.; Vogel, C. Stomatal and non-stomatal fluxes of ozone to a northern mixed hardwood forest. Tellus B Chem. Phys. Meteorol. 2007, 58, 514–525. [Google Scholar]
- Regener, V.H. The vertical flux of atmospheric ozone. J. Geophys. Res. 1957, 62, 221–228. [Google Scholar] [CrossRef]
- Lamaud, E.; Carrara, A.; Bruneta, Y.; Lopez, A.; Druilhet, A. Ozone fluxes above and within a pine forest canopy in dryand wet conditions. Atmos. Environ. 2002, 36, 77–88. [Google Scholar] [CrossRef]
- Mikkelsen, T.N.; Ro-Poulsen, H.; Hovm, M.F.; Jensen, N.O.; Pilegaard, K.; Egeløv, A.H. Five-year measurements of ozone fluxes to a Danish Norway spruce canopy. Atmos. Environ. 2004, 38, 2361–2371. [Google Scholar] [CrossRef]
- Wesely, M.L. Parameterization of surface resistances to gaseous dry deposition in regional-scale numerical models. Atmos. Environ. 1989, 23, 1293–1304. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B 1976, 273, 593–610. [Google Scholar]
- Zhang, L.; Moran, M.; Makar, P.; Brook, J.R.; Gong, S. Modelling gaseous dry deposition in AURAMS—A Unified Regional Air-quality Modelling System. Atmos. Environ. 2002, 36, 537–560. [Google Scholar] [CrossRef]
- Cieslik, S.; Tuovinen, J.P.; Baumgarten, M.; Matyssek, R.; Brito, P.; Wieser, G. Gaseous exchange between forests and the atmosphere. Dev. Environ. Sci. 2013, 13, 19–36. [Google Scholar]
- Conte, A.; Otu-Larbi, F.; Alivernini, A.; Hoshika, Y.; Paoletti, E.; Ashworth, K.; Fares, S. Exploring new strategies for ozone-risk assessment: A dynamic-threshold case study. Environ. Pollut. 2021, 287, 117620. [Google Scholar] [CrossRef] [PubMed]
- Massman, W.J. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
- Mills, G.; Harmens, H.; Hayes, F.; Pleijel, H.; Büker, P.; González, I.; Alonso, R.; Bender, J.; Bergmann, E.; Bermejo, V.; et al. Mapping Critical Levels for Vegetation Revised Chapter 3 of the Manual on Methodologies and Criteria for Modelling and Mapping Critical Loads and Levels and Air Pollution Effects, Risks and Trends. Available online: https://www.researchgate.net/publication/329101282 (accessed on 16 September 2019).
- Emberson, L.D.; Wieser, G.; Ashmore, M.R. Modelling of stomatal conductance and ozone flux of Norway spruce: Comparison with field data. Environ. Pollut. 2000, 109, 393–402. [Google Scholar] [CrossRef]
- Tuovinen, J.-P.; Simpson, D.; Fagerli, H.; Jonson, J.E.; Tsyro, S.; Wind, P. Transboundary Acidification, Eutrophication and Ground Level Ozone in Europe, PART 1, Unified EMEP Model Description; Norwegian Meteorological Institute: Oslo, Norway, 2003.
- Tuovinen, J.-P.; Ashmore, M.R.; Emberson, L.D.; Simpson, D. Testing and improving the EMEP ozone deposition module. Atmos. Environ. 2004, 38, 2373–2385. [Google Scholar] [CrossRef]
- Kaiser, H.; Paoletti, E. Trees in a Changing Environment. Chapter: Dynamic Stomatal Changes, 1st ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 61–82. [Google Scholar]
- Kaiser, H. Relat. Stomatal Aperture Gas Exch. Consid. Pore Geom. Diffus. Resist. Mesophyll. Plant, Cell Environ. 2009, 32, 1091–1098. [Google Scholar] [CrossRef] [PubMed]
- Pei, Z.; Kuchitsu, K. Early ABA Signal. Events Guard Cells. J. Plant Growth Regul. 2005, 24, 296–307. [Google Scholar] [CrossRef]
- Mills, G.; Hayes, F.; Simpson, D.; Emberson, L.; Norris, D.; Harmens, H.; Büker, P. Evid. Widespread Eff. Ozone Crop. (semi-)natural Veg. Eur. (1990–2006) Relat. AOT40- Flux-Based Risk Maps. Global Chang. Biol. 2011, 17, 592–613. [Google Scholar] [CrossRef]
- Novak, K.; Skelly, J.M.; Schaub, M.; Kräuchi, N.; Hug, C.; Landolt, W.; Bleuler, P. Ozone Air Pollut. Foliar Inj. Dev. Nativ. Plants Switzerland. Environ. Pollut. 2003, 125, 41–52. [Google Scholar] [CrossRef]
- Orendovici, T.; Skelly, J.M.; Ferdinand, J.A.; Savage, J.E.; Sanz, M.J.; Smith, G.C. Response Nativ. Plants Northeast. United States South. Spain Ozone Expo. Determ. Expo. Relationships. Environ. Pollut. 2003, 1, 31–40. [Google Scholar] [CrossRef]
- Bussotti, F.; Desotgiu, R.; Cascio, C.; Pollastrini, M.; Gravano, E.; Gerosa, G.; Marzuoli, R.; Nali, C.; Lorenzini, G.; Salvatori, E.; et al. Ozone Stress Woody Plants Assess. Chlorophyll A Fluorescence. A Crit. Reassess. Exist. Datall. Environ. Exp. Bot. 2011, 73, 19–308. [Google Scholar] [CrossRef]
- Wittig, V.E.; Ainsworth, E.A.; Naidu, S.L.; Karnosky, D.F.; Long, S.P. Quantifying the impact of current and future tropospheric ozone on tree biomass, growth, physiology and biochemistry: A quantitative meta-analysis. Glob. Chang. Biol. 2009, 15, 396–424. [Google Scholar] [CrossRef]
- Proietti, C.; Anav, A.; De Marco, A.; Sicard, P.; Vitale, M. Early ABA Signal. Events Guard Cells. Sci. Total Environ. 2016, 556, 1–11. [Google Scholar] [CrossRef]
- Matyssek, R.; Karnosky, D.F.; Wieser, G.; Percy, K.; Oksanen, E.; Grams, T.E.E.; Kubiske, M.; Hanke, D.; Pretzsch, H. Advances in understanding ozone impact on forest trees: Messages from novel phytotron and free-air fumigation studies. Environ. Pollut. 2010, 158, 1990–2006. [Google Scholar] [CrossRef]
- Massman, W.J.; Musselman, R.C.; Lefohn, A.S. A conceptual ozone dose-response model to develop a standard to protect vegetation. Atmos. Environ. 2000, 34, 745–759. [Google Scholar] [CrossRef]
- Wieser, G.; Häsler, R.; Götz, B.; Koch, W.; Havranek, W.M. Role of climate, crown position, tree age and altitude in calculated ozone flux into needles of Picea abies and Pinus cembra: A synthesis. Environ. Pollut. 2000, 109, 415–422. [Google Scholar] [CrossRef]
- Chappelka, A.H.; Samuelson, L.J. Ambient ozone effects on forest trees of the eastern United States: A review. New Phytol. 1998, 139, 91–108. [Google Scholar] [CrossRef]
- Bičárová, S.; Shashikumar, A.; Dalstein-Richier, L.; Lukasová, V.; Adamčíková, K.; Pavlendová, H.; Sitková, Z.; Buchholcerová, A.; Bilčík, D. The response of Pinus species to ozone uptake in different climate regions of Europe. Cent. Eur. For. J. 2020, 66, 255–268. [Google Scholar]
- Dalstein, N.; Vas, N. Ozone concentrations and ozone-induced symptoms on coastal and alpine mediterrnean pines in southern France. Water Air Soil Pollut. 2005, 160, 181–195. [Google Scholar] [CrossRef]
- Sicard, P.; Vas, N.; Calatayud, V.; García Breijo, F.J.; Reig-Armiñana, J.; Snaz, M.; Dalstein, L. Dommages forestiers et pollution à l’ozone dans les réserves naturelles: Le cas de l’arolle dans le sud-est de la France. Foręt Méditerranéenne 2010, 31, 273–286. [Google Scholar]
- Bičárová, S.; Mačutek, J.; Bilčík, D. Climate of submontane location Stará Lesná (1988-2013). Contrib. Geophys. Geod. 2014, 44, 95–113. [Google Scholar] [CrossRef][Green Version]
- Ulber, M.; Gugerli, F.; Bozic, G. Swiss stone pine (Pinus cembra). EUFORGEN Tech. Guidel. Genet. Conserv. Use 2004, 4. Available online: http://www.euforgen.org/fileadmin//templates/euforgen.org/upload/Publications/Technical_guidelines/Technical_Guidelines_Pinus_cembra.pdf (accessed on 28 July 2021).
- Casalegno, S.; Amatulli, G.; Camia, A.; Nelson, A.; Pekkarinen, A. Vulnerability of Pinus cembra L. in the Alps and the Carpathian mountains under present and future climates. For. Ecol. Manag. 2010, 259, 750–761. [Google Scholar] [CrossRef]
- LiCOR6400 Manual. Available online: https://www.licor.com/documents/b5e98kr2wbjuh8g8eo4r (accessed on 28 July 2021).
- Langenberg, S.; Carstens, T.; Hupperich, D.; Schweighoefer, S.; Schurath, U. Technical note: Determination of binary gas-phase diffusion coefficients of unstable and adsorbing atmospheric trace gases at low temperature—Arrested flow and twin tube method. Atmos. Chem. Phys. 2000, 20, 3669–3682. [Google Scholar] [CrossRef]
- Emberson, L.D.; Büker, P.; Ashmore, M.R. Assessing the risk caused by ground level ozone to European forest trees: A case study in pine, beech and oak across different climate regions. Environ. Pollut. 2007, 147, 454–466. [Google Scholar] [CrossRef]
- Gerosa, G.; Marzuoli, R.; Desotgiu, R.; Bussotti, F.; Ballarin-Denti, A. Validation of the stomatal flux approach for the assessment of ozone visible injury in young forest trees. Results from the TOP (transboundary ozone pollution) experiment at Curno, Italy. Environ. Pollut. 2009, 157, 1497–1505. [Google Scholar] [CrossRef]
- Goumenaki, E.; Fernandez, I.G.; Papanikolaou, A.; Papadopoulou, D.; Askianakis, C.; Kouvarakis, G.; Barnes, J. Derivation of ozone flux-yield relationships for lettuce: A key horticultural crop. Environ. Pollut. 2007, 146, 699–706. [Google Scholar] [CrossRef]
- Emberson, L.D.; Simpson, D.; Tuovinen, J.-P.; Ashmore, M.R.; Cambridge, H.M. Towards a Model of Ozone Deposition and Stomatal Uptake over Europe; EMEP/MSC-W 2000; Norwegian Meteorological Institute: Oslo, Norway, 2000.
- Op de Beeck, M.; Löw, M.; Deckmyn, G.; Ceulemans, R. A comparison of photosynthesis-dependent stomatal models using twig cuvette field data for adult beech (Fagus sylvatica L.). Agric. For. Meteorol. 2010, 150, 531–540. [Google Scholar] [CrossRef]
- Fares, S.; Matteucci, G.; Scarascia Mugnozza, G.; Morani, A.; Calfapietra, C.; Salvatori, E.; Fusaro, L.; Manes, F.; Loreto, F. Testing of models of stomatal ozone fluxes with field measurements in a mixed Mediterranean forest. Atmos. Environ. 2013, 67, 242–251. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Mills, G.; Harmens, H.; Hayes, F.; Pleijel, H.; Büker, P.; González, I.; Alonso, R.; Bender, J.; Bergmann, E.; Bermejo, V.; et al. Scientific Background Document B: Developing Areas of Research of Relevance to Chapter III (Mapping Critical Levels for Vegetation) of the Modelling and Mapping Manual of the LRTAP Convention. 2020. Available online: https://icpvegetation.ceh.ac.uk/sites/default/files/Scientific%20Background-%20document%20B%20June%202020.pdf (accessed on 30 November 2020).
- Bičárová, S.; Sitková, Z.; Pavlendová, H.; Fleischer, P.; Bytnerowicz, A.; Fleischer, P. The role of environmental factors in ozone uptake of Pinus mugo Turra. Atmos. Pollut. Res. 2019, 10, 283–293. [Google Scholar] [CrossRef]
- Hoshika, Y.; Fares, S.; Savi, F.; Gruening, C.; Goded, I.; De Marco, A.; Sicard, P.; Paoletti, E. Stomatal conductance models for ozone risk assessment at canopy level in two Mediterranean evergreen forests. Agric. For. Meteorol. 2017, 234–235, 212–221. [Google Scholar] [CrossRef]
- Wieser, G.; Emberson, L. Evaluation of the stomatal conductance formulation in the EMEP ozone deposition model for Picea abies. Atmos. Environ. 2004, 38, 2339–2348. [Google Scholar] [CrossRef]
- Misson, L.; Panek, J.A.; Goldstein, A.H. A comparison of three approaches to modeling leaf gas exchange in annually drought-stressed ponderosa pine forests. Tree Physiol. 2004, 24, 529–541. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).