A Non-Stationary Heat Spell Frequency, Intensity, and Duration Model for France, Integrating Teleconnection Patterns and Climate Change
Abstract
1. Introduction
2. Materials and Methods
2.1. Intensity, Frequency, and Duration Estimation
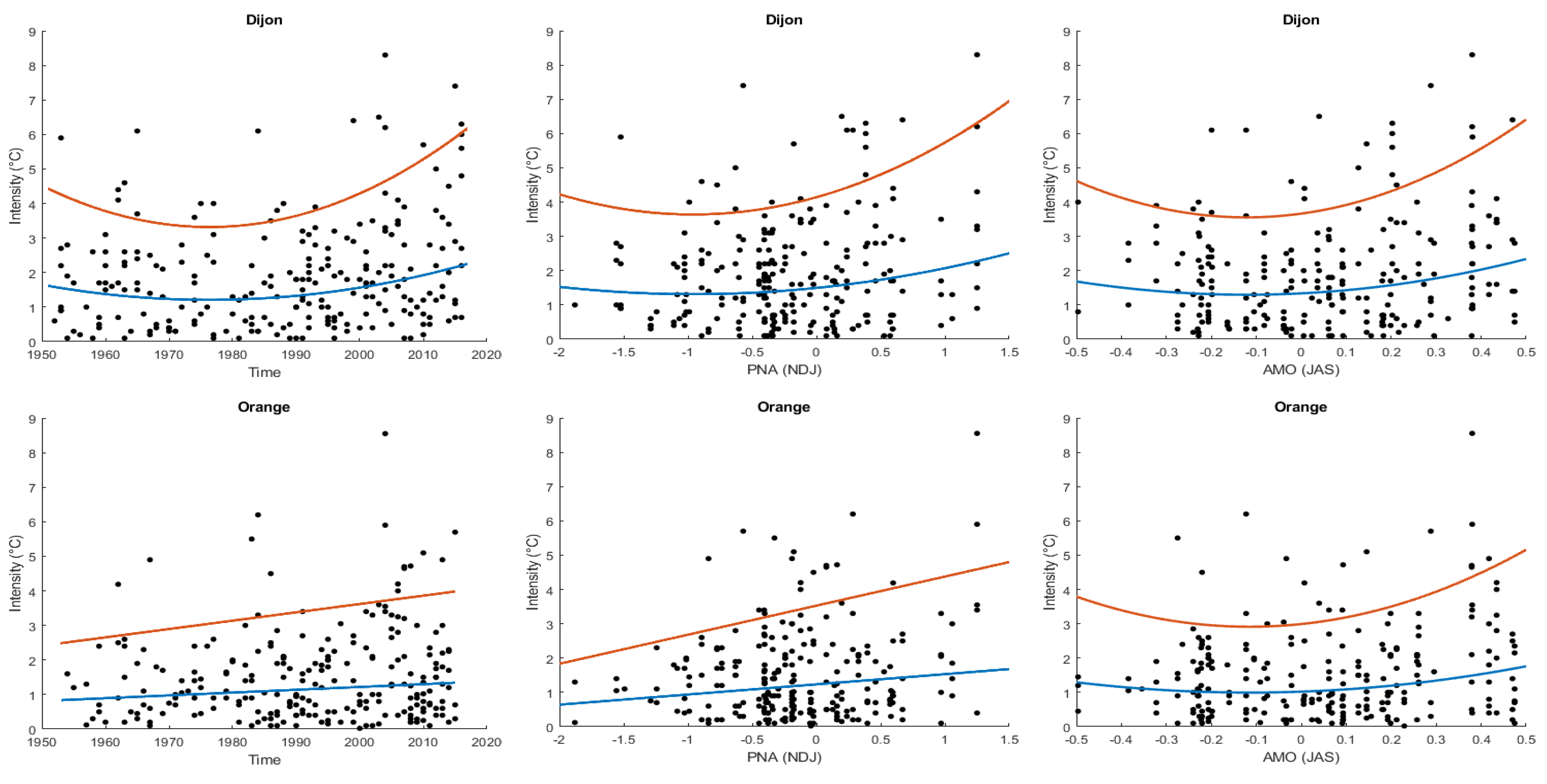
2.1.1. Modelling of the Intensity
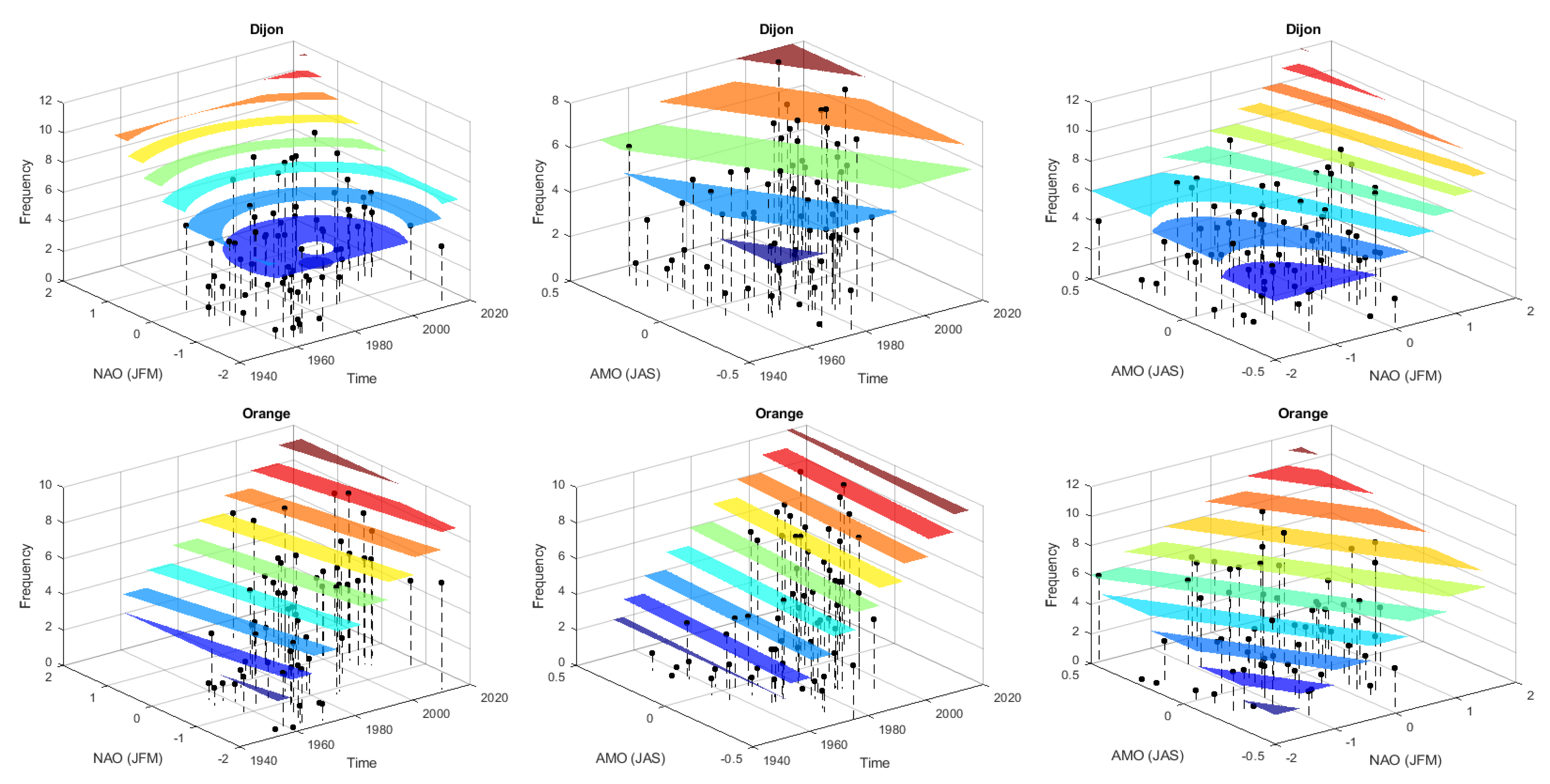
2.1.2. Modelling of the Frequency
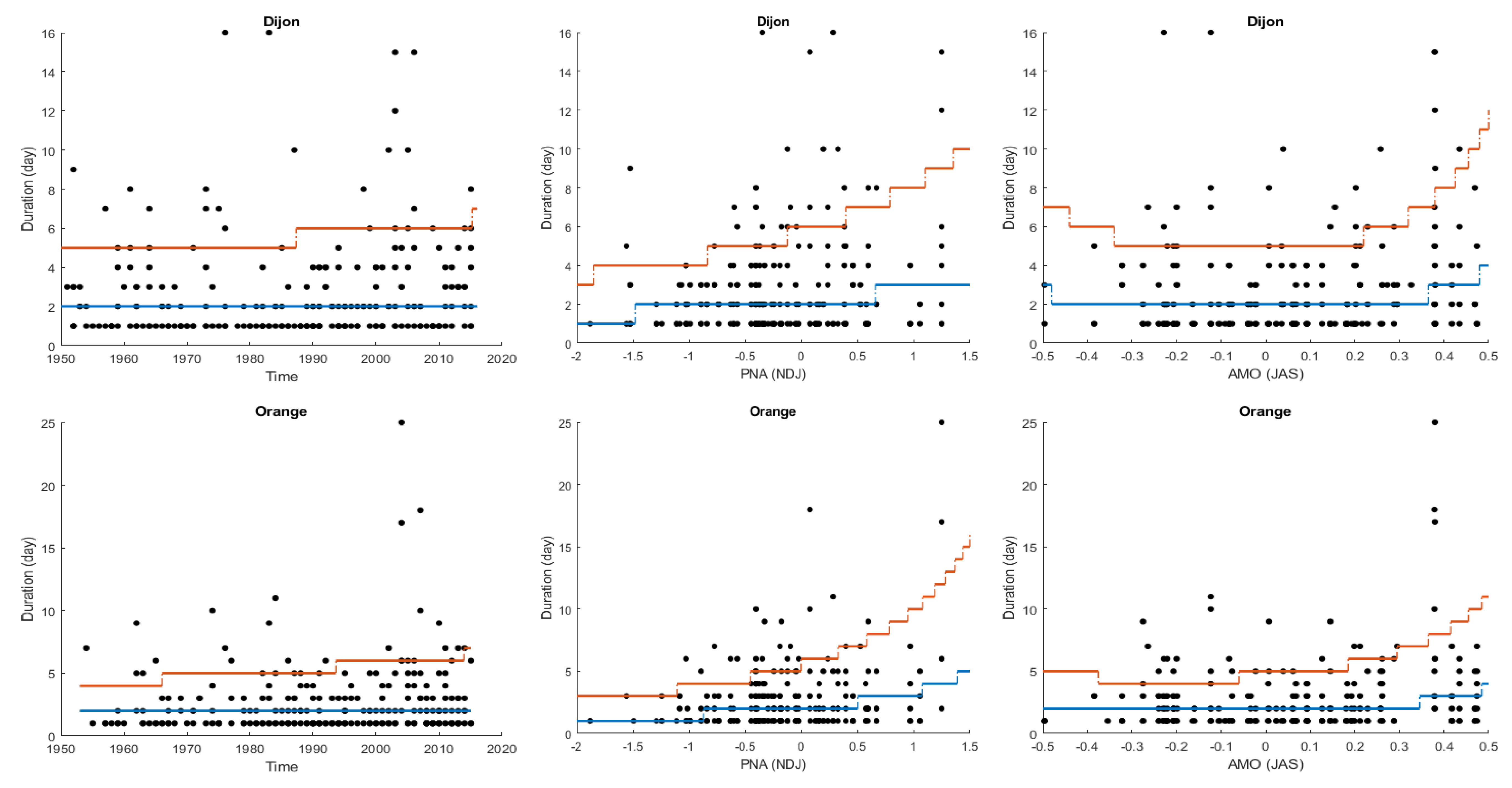
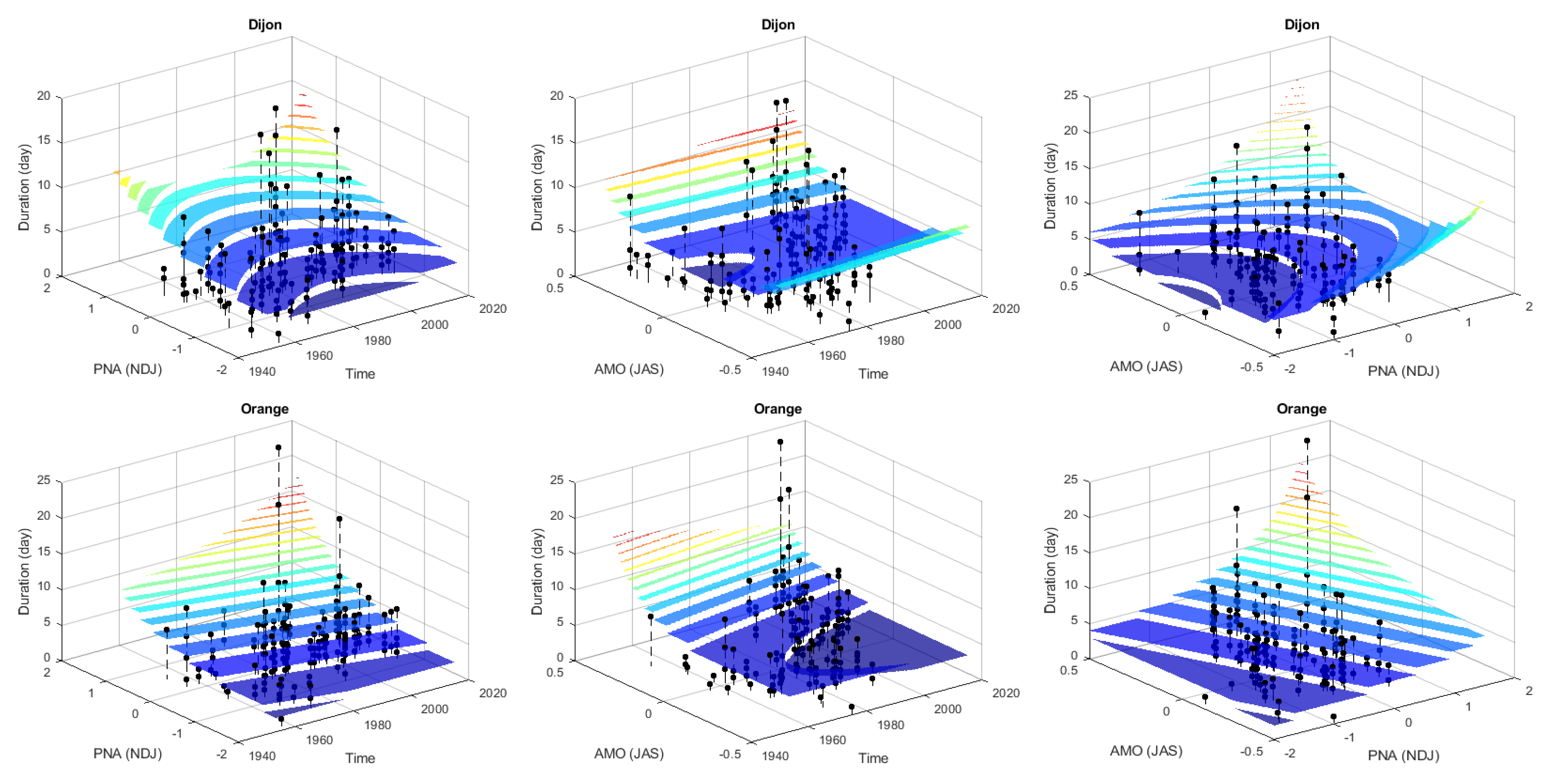
2.1.3. Modelling of the Duration
2.2. NS Models: Model Selection
2.2.1. Non-stationary Distribution Models
2.2.2. Model Selection and Comparison
2.3. Definition and Extraction of Heat Spells
3. Case Study and Data
3.1. Orange and Dijon
3.2. Teleconnection Patterns AMO, NAO and PNA
- -
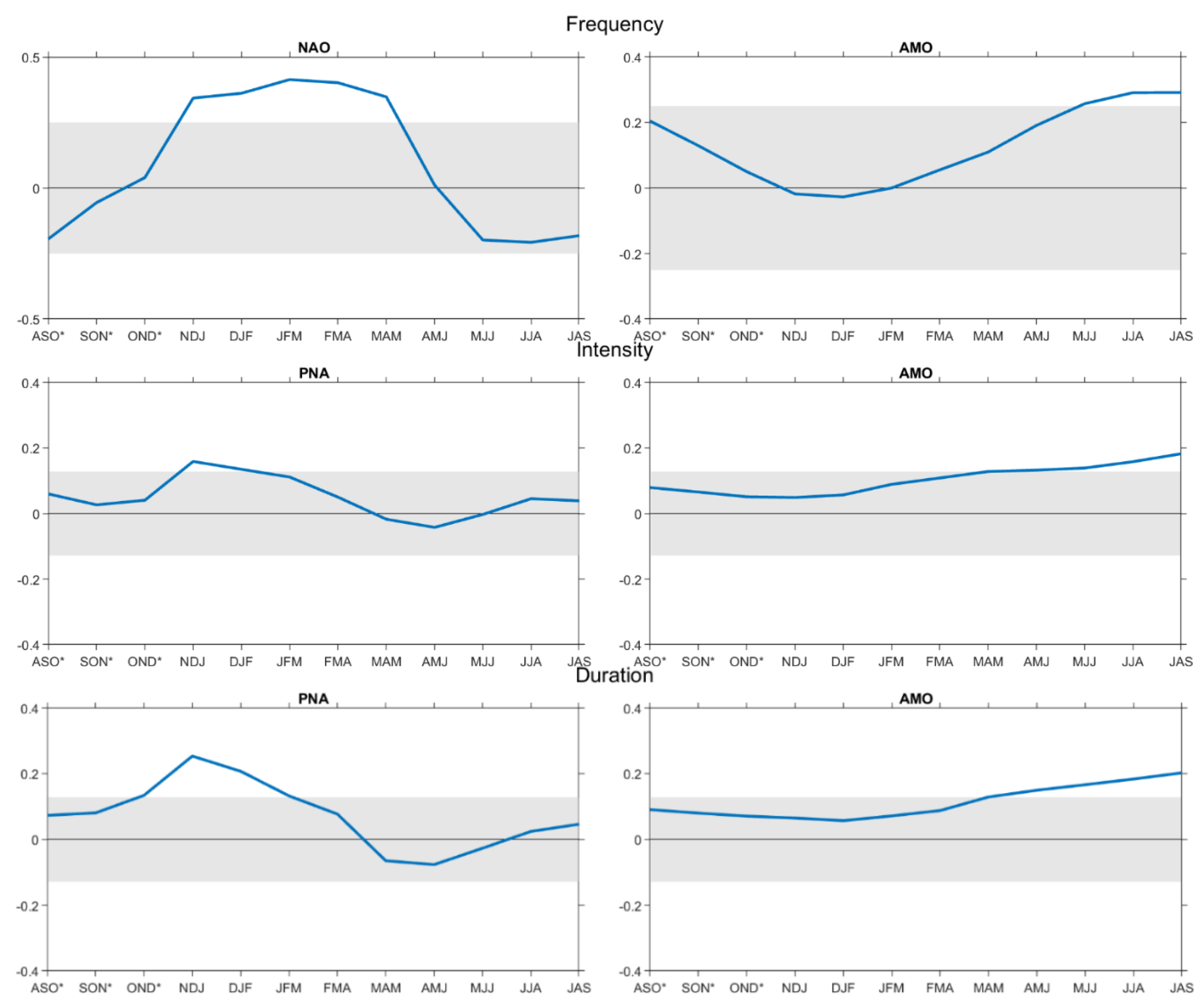
- It has been shown that the AMO can be linked to the warming in France during the last 15–20 years, which is due to the exchange of energy between the ocean and atmosphere, as well as the connection between the AMO and forest fires in France during the period of 1980–2014 that were established.
- -
- It has also been shown in the literature that the NAO and AMO (with other weather patterns associated with wet and dry conditions) have a significant influence on heat spells in France. It was stated that these patterns are responsible for the increase of drought severity in southern France.
4. Results
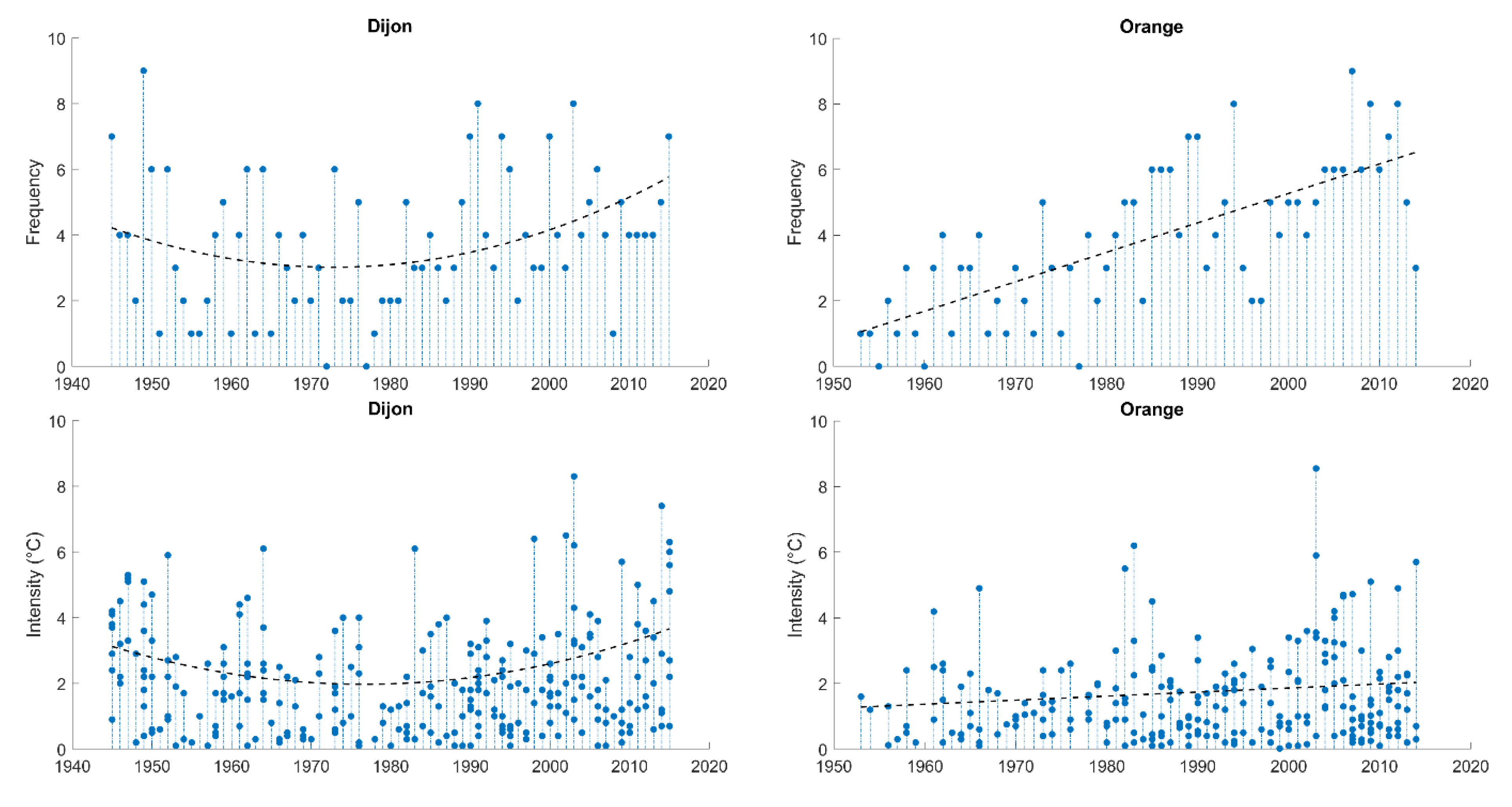
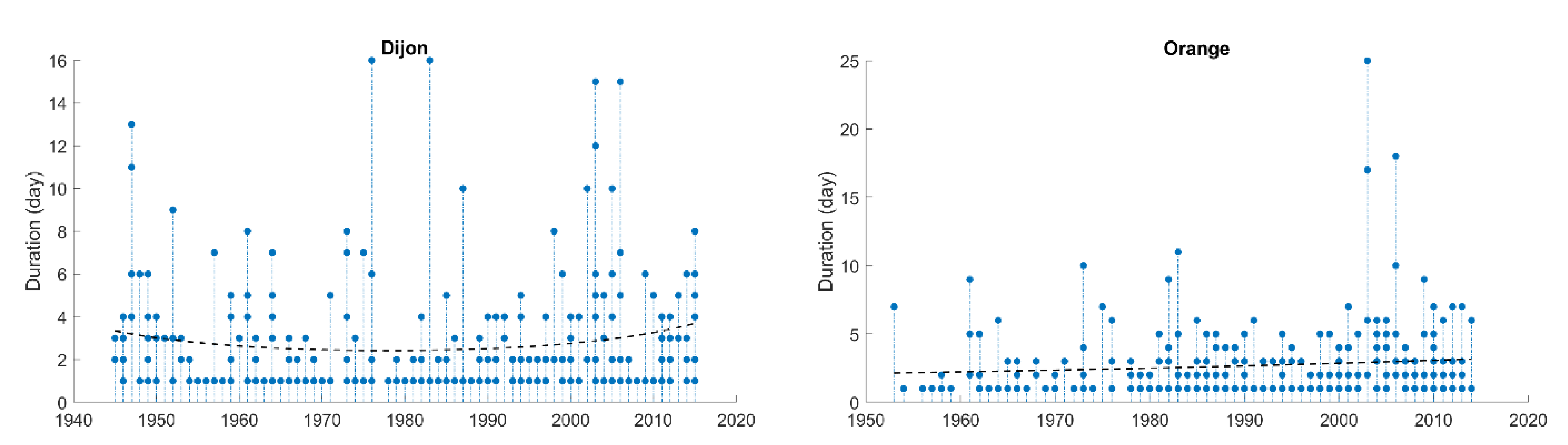
4.1. Computation of Heat Spell Events
4.2. Abrupt Changes and Trend Analysis of the Heat Spell Time Series
4.2.1. Change Point Dates
4.2.2. Trend Analysis
4.2.3. Correlations between CIs and Heat Spell Variables
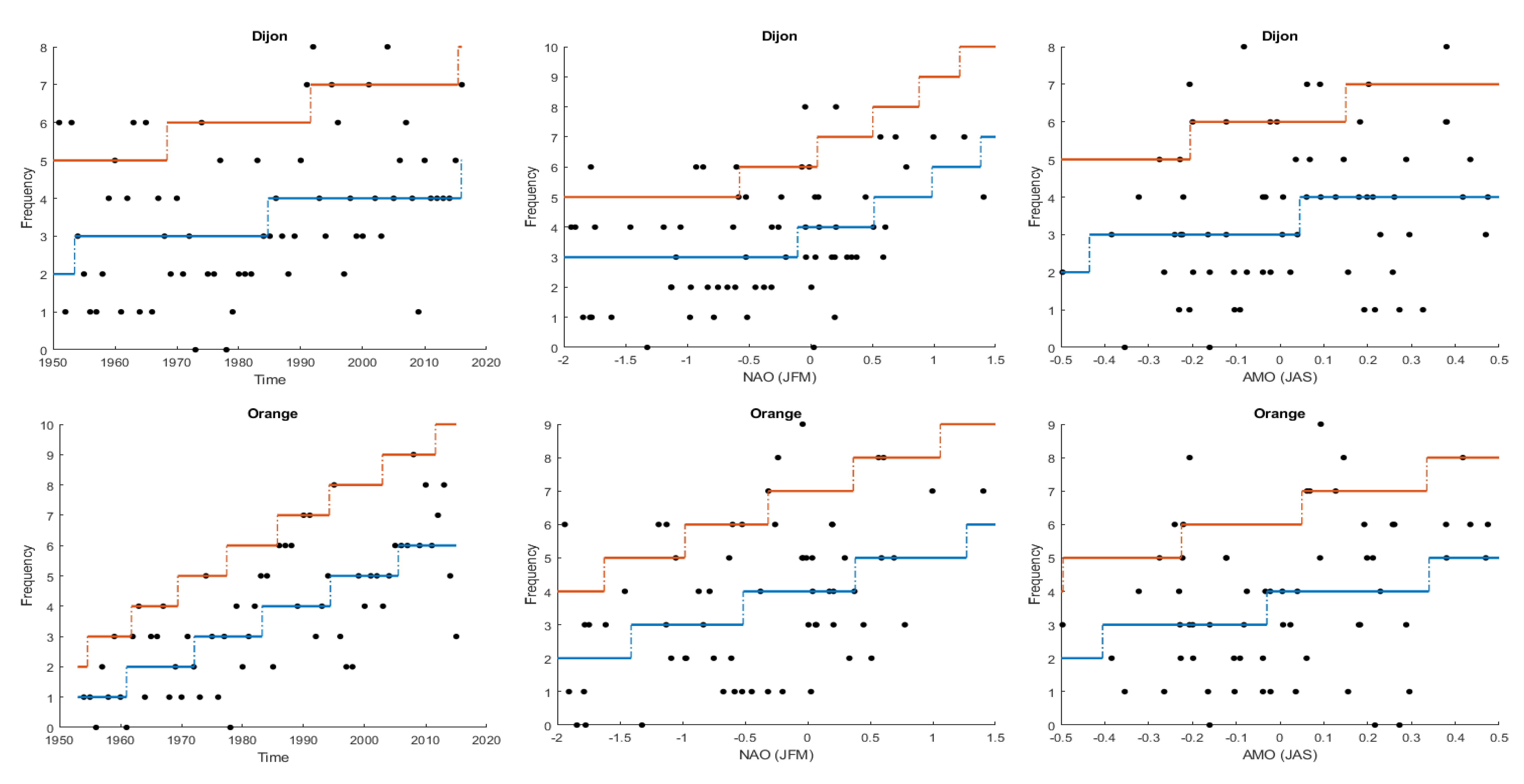
4.3. NS Frequency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cassou, C.; Terray, L.; Phillips, A.S. Tropical Atlantic influence on European heatwaves. J. Clim. 2005, 18, 2805–2811. [Google Scholar] [CrossRef]
- Jones, P.D.; Moberg, A. Hemispheric and large-scale surface air temperature variations: An extensive revision and an update to 2001. J. Clim. 2003, 16, 206–223. [Google Scholar] [CrossRef]
- Tank, A.M.G.K.; Können, G.P. Trends in indices of daily temperature and precipitation extremes in Europe, 1946–1999. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Beniston, M. The 2003 heat wave in Europe: A shape of things to come? An analysis based on Swiss climatological data and model simulations. Geophys. Res. Let. 2004, 31, 384. [Google Scholar] [CrossRef]
- Schär, C.; Vidale, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 333–336. [Google Scholar] [CrossRef]
- Poumadere, M.; Mays, C.; Mer, S.L.; Blong, R.J. The 2003 heat wave in France: Dangerous climate change here and now. Risk Anal. 2005, 25, 1483–1494. [Google Scholar] [CrossRef]
- Fouillet, A.; Ray, G.; Laurent, F.; Bellec, S.; Guihenneuc-Jouyaux, C.; Clavel, J.; Jougla, E.; Hémon, D. Excess mortality related to the August 2003 heat wave in France. Int. Arch. Occup. Environ. Health 2006, 80, 16–24. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Tank, A.M.G.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Brown, S.J.; Caesar, J.; Ferro, C.A.T. Global changes in extreme daily temperature since 1950. J. Geophys. Res. Atmos. 2008, 13. [Google Scholar] [CrossRef]
- Coumou, D.; Rahmstorf, S. A decade of weather extremes. Nat. Clim. Change 2012, 2, 491–496. [Google Scholar] [CrossRef]
- Coumou, D.; Robinson, A. Historic and future increase in the global land area affected by monthly heat extremes. Environ. Res. Lett. 2013, 8, 034018. [Google Scholar] [CrossRef]
- Parey, S.; Malek, F.; Laurent, C.; Dacunha-Castelle, D. Trends and climate evolution: Statistical approach for very high temperatures in France. Clim Change. 2007, 81, 331–352. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Basha, G.; Kishore, P.; Ratnam, M.V.; Jayaraman, A.; Agha Kouchak, A.; Ouarda, T.B.M.J.; Velicogna, I. Historical and Projected Surface Temperature over India during the 20th and 21st century. Sci. Rep. 2017, 7, 2987. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2012; p. 582. [Google Scholar]
- Ouarda, T.B.M.J.; Charron, C.; Kumar, K.N.; Phanikumar, D.V.; Molini, A.; Basha, G. Nonstationary warm spell frequency analysis integrating climate variability and change with application to the Middle East. Clim. Dyn. 2019, 53, 5329–5347. [Google Scholar] [CrossRef]
- Ouzeau, G.; Soubeyroux, J.M.; Schneider, M.; Vautard, R.; Planton, S. Heat waves analysis over France in present andfuture climate: Application of a new method on the EURO-CORDEX ensemble. Clim. Serv. 2016, 4, 1–12. [Google Scholar] [CrossRef]
- Pausader, M.; Bernie, D.; Parey, S.; Nogaj, M. Computing the distribution of return levels of extreme warm temperatures for future climate projections. Clim. Dyn. 2012, 38, 1003–1015. [Google Scholar] [CrossRef]
- Ouzeau, G.; Déqué, M.; Jouini, M.; Planton, S.; Vautard, R. Le Climat de la France au XXIe Siècle Volume 4-Scénarios Régionalisés: Édition 2014 Pour la Métropole et les Régions D’outre-mer. 2014. Available online: https://www.actu-environnement.com/media/pdf/news-22612-onerc-climat-france.pdf (accessed on 15 February 2021).
- Milenković, M.; Ducić, V.; Burić, D.; Lazić, B. The Atlantic Multidecadal Oscillation (AMO) and the forest fires in France in the period 1980–2014. J. Geogr. Inst. Jovan Cvijic SASA 2016, 66, 35–44. [Google Scholar] [CrossRef]
- Giuntoli, B.; Renard, J.P.; Vidal, A.B. Low Flows in France and their relationship to large scale climate indices. J. Hydrol. 2013, 482, 105–118. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Wea. Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field duringthe Northern Hemisphere winter. Mon. Weather. Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Cattiaux, J. Extrêmes de Température en Europe: Mécanismes et Réponses au Changement Climatique. Ph.D. Thesis, Pierre et Marie Curie University, Paris, France, 2010. [Google Scholar]
- Conte, M.; Giuffrida, S.; Tedesco, S. The Mediterranean oscillation: Impact on precipitation and hydrology in Italy. Dans Clim. Water 1989, 121–137. [Google Scholar]
- Efthymiadis, D.; Goodess, C.M.; Jones, P.D. Trends in Mediterranean gridded temperature extremes and large-scale circulation influences. Nat. Hazards Earth Syst. Sci. 2011, 11, 2199–2214. [Google Scholar] [CrossRef]
- Ouachani, R.; Bargaoui, Z.; Ouarda, T.B.M.J. Power of teleconnection patterns on precipitation and streamflow variability of upper Medjerda Basin. Int. J. Climatol. 2013, 33, 58–76. [Google Scholar] [CrossRef]
- Naizghi, M.S.; Ouarda, T.B.M.J. Teleconnections and analysis of long-term wind speed variability in the UAE. Int. J. Climatol. 2017, 37, 230–248. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C.; St-Hilaire, A. Uncertainty of stationary and nonstationary models for rainfall frequency analysis. Int. J. Climatol. 2020, 40, 2373–2392. [Google Scholar] [CrossRef]
- Keellings, D.; Waylen, P. Investigating teleconnection drivers of bivariate heat waves in Florida using extreme value analysis. Clim. Dyn. 2015, 44, 3383–3391. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarada, T.; Gachon, P.; Sushama, L. Stochastic modeling of hot weather spells and their characteristics. Clim. Res. 2011, 47, 187–199. [Google Scholar] [CrossRef][Green Version]
- Caroni, C.; Panagoulia, D. Non-stationary modelling of extreme temperatures in a mountainous area of Greece. REVSTAT 2016, 14, 217–228. [Google Scholar]
- Hamdi, Y.; Duluc, C.-M.; Rebour, V. Temperature Extremes: Estimation of Non-Stationary Return Levels and Associated Uncertainties. Atmosphere 2018, 9, 129. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; El-Adlouni, S. Bayesian nonstationary frequency analysis of hydrological variables. J. Am. Water Resour. Assoc. 2011, 47, 496–505. [Google Scholar] [CrossRef]
- Hundecha, Y.; St-Hilaire, A.; Ouarda, T.B.M.J.; El Adlouni, S.; Gachon, P. A nonstationary extreme value analysis for the assessment of changes in extreme annual wind speed over the gulf of St. Lawrence, Canada. J. Appl. Meteorol. Climatol. 2008, 47, 2745–2759. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water. Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar]
- Hamdi, Y.; Bardet, L.; Duluc, C.-M.; Rebour, V. Extreme storm surges: A comparative study of frequency analysis approaches. Nat. Hazards Earth Syst. Sci. 2014, 14, 2053–2067. [Google Scholar] [CrossRef]
- Pickands, J. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Ashkar, F.; Ouarda, T.B.M.J. On some methods of ftting the generalized Pareto distribution. J. Hydrol. 1996, 177, 117–141. [Google Scholar] [CrossRef]
- Whitaker, L. On the Poisson law of small numbers. Biometrika 1914, 10, 36–71. [Google Scholar] [CrossRef]
- Furrer, E.; Katz, R.W.; Walter, M.D.; Furrer, R. Statistical modeling of hot spells and heat waves. Clim. Res. 2010, 43, 191–205. [Google Scholar] [CrossRef]
- Keellings, D.; Waylen, P. Increased risk of heat waves in Florida: Characterizing changes in bivariate heat wave risk using extreme value analysis. Appl. Geogr. 2014, 46, 90–97. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, W.; Li, Y.; Wang, X.; Wang, D. Statistical modeling and CMIP5 simulations of hot spell changes in China. Clim. Dyn. 2015, 44, 2859–2872. [Google Scholar] [CrossRef]
- Beguería, S.; Angulo-Martínez, M.; Vicente-Serrano, S.M.; López-Moreno, J.I.; El-Kenawy, A. Assessing trends in extreme precipitation events intensity and magnitude using non-stationary peaks-over-threshold analysis: A case study in northeast Spain from 1930 to 2006. Int. J. Climatol. 2011, 31, 2102–2114. [Google Scholar] [CrossRef]
- Panagoulia, D.; Economou, P.; Caroni, C. Stationary and nonstationary generalized extreme value modelling of extreme precipitation over a mountainous area under climate change. Environmetrics 2014, 25, 29–43. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C. Changes in the distribution of hydro-climatic extremes in a non-stationary framework. Sci. Rep. 2019, 9, 8104. [Google Scholar] [CrossRef] [PubMed]
- Ouarda, T.B.M.J.; Charron, C. Non-stationary statistical modelling of wind speed: A case study in eastern Canada. Energy Convers. Manag. 2021, 236, 114028. [Google Scholar] [CrossRef]
- Robinson Peter, J. On the Definition of a Heat Wave. J. App. Meteor. 2001, 40, 762–775. [Google Scholar] [CrossRef]
- Russo, S.; Dosio, A.; Graversen, R.G.; Sillmann, J.; Carrao, H.; Dunbar, M.B.; Singleton, A.; Montagna, P.; Barbola, P.; Vogt, J.V. Magnitude of extreme heat waves in present climate and their projectionin a warming world. J. Geophys. Res.-Atmos. 2014, 119, 12500–12512. [Google Scholar] [CrossRef]
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Klein Tank, A.; Peterson, T. Global changes in climatic extremes during the 2nd half of the 20th century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Rafferty, J.P. Heat Wave. 5 December 2018. Available online: https://www.britannica.com/science/heat-wave-meteorology (accessed on 23 May 2021).
- Perkins, S.E.; Alexander, L.V. On the measurement of heat waves. J. Clim. 2012, 26, 4500–4517. [Google Scholar] [CrossRef]
- Della-Marta, P.M.; Haylock, M.R.; Luterbacher, J.; Wanner, H. Doubled length of western European summer heat waves since 1880. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Stefanon, M.; Fabio, D.; Drobinski, P. Heatwave classification over Europe and the Mediterranean region. Environ. Res. Lett. 2012, 7, 014023. [Google Scholar] [CrossRef]
- Bladé, I.; Fortuny, D.; Van Oldenborgh, G.J.; Liebmann, B. The summer North Atlantic Oscillation in CMIP3 models and related uncertainties in projected summer drying in Europe. J. Geophys. Res.-Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Folland, C.K.; Knight, J.; Linderholm, H.W.; Fereday, D.; Ineson, S.; Hurrell, J.W. The Summer North Atlantic Oscillation: Past, Present, and Future. J. Clim. 2009, 22, 1082–1103. [Google Scholar] [CrossRef]
- Fuentes-Franco, R.; Koenigk, T. Identifying remote sources of interannual variability for summer precipitation over Nordic European countries tied to global teleconnection wave patterns. Dyn. Meteorol. Oceanogr. 2020, 72, 1–15. [Google Scholar] [CrossRef]
- Kingston, D.G.; McGregor, G.R.; Hannah, D.M.; Lawler, D.M. River flow teleconnections across the northern North Atlantic region. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Knight, J.R.; Folland, C.K.; Scaife, A.A. Climate impacts of the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Lamb, P.; Peppler, R. North Atlantic oscillation: Concept and an application. Bull. Amer. Meteor. Soc. 1987, 68, 1218–1225. [Google Scholar] [CrossRef]
- Wanner, H.; Brönnimann, S.; Casty, C.; Gyalistras, D.; Luterbacher, J.; Schmutz, C.; Stephenson, D.B.; Xoplaki, E. North Atlantic Oscillation–Concepts And Studies. Surv. Geophys. 2001, 22, 321–381. [Google Scholar] [CrossRef]
- Seidou, O.; Asselin, J.J.; Ouarda, T.B.M.J. Bayesian multivariate linear regression with application to change point models in hydrometeorological variables. Water. Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Seidou, O.; Ouarda, T.B.M.J. Recursion-based multiple changepoint detection in multiple linear regression and application to river streamflows. Water. Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Green, J.S.A. The weather during July I976: Some dynamical considerations of the drought. Weather 1977, 32, 120–126. [Google Scholar] [CrossRef]



| Station | Variable | Covariate | |||
|---|---|---|---|---|---|
| Time | NAO (JFM) | PNA (NDJ) | AMO (JAS) | ||
| Dijon | Frequency | 0.19 | 0.41 * | 0.05 | 0.23 * |
| Duration | 0.04 | 0.11 | 0.18 * | 0.17 * | |
| Intensity | 0.03 | 0.03 | 0.18 * | 0.15 * | |
| Orange | Frequency | 0.71 * | 0.41 * | 0.15 | 0.29 * |
| Duration | 0.13 | <0.01 | 0.16 * | 0.18 * | |
| Intensity | 0.10 | −0.03 | 0.25 * | 0.20 * | |
| Variable | Covariate(s) | AIC | BIC | Model |
|---|---|---|---|---|
| Frequency | Stationary | 275.7 | 277.9 | |
| Time | 270.4 | 274.8 | ||
| NAO | 266.9 | 273.4 * | ||
| AMO | 273.8 | 278.1 | ||
| Time + NAO | 267.1 | 278.0 | ||
| Time + AMO | 270.9 | 277.4 | ||
| NAO + AMO | 265.1 * | 273.9 | ||
| Time + NAO + AMO | 266.7 | 275.5 | ||
| Intensity (°C) | Stationary | 765.7 | 772.7 | |
| Time | 755.5 | 769.3 | ||
| PNA | 759.8 | 773.6 | ||
| AMO | 758.5 | 772.3 | ||
| Time + PNA | 746.8 * | 767.6 * | ||
| Time + AMO | 754.4 | 775.1 | ||
| PNA + AMO | 753.2 | 770.4 | ||
| Time + PNA + AMO | 757.4 | 774.7 | ||
| Duration (Days) | Stationary | 840.6 | 844.1 | |
| Time | 839.5 | 846.4 | ||
| PNA | 831.4 | 838.3 * | ||
| AMO | 832.2 | 842.6 | ||
| Time + PNA | 832.6 | 846.4 | ||
| Time + AMO | 833.9 | 847.8 | ||
| PNA + AMO | 828.0 * | 841.9 | ||
| Time + PNA + AMO | 832.0 | 845.9 |
| Variable | Covariate(s) | AIC | BIC | Model |
|---|---|---|---|---|
| Frequency | Stationary | 277.5 | 279.7 | |
| Time | 235.4 * | 239.7 * | ||
| NAO | 265.6 | 269.9 | ||
| AMO | 273.0 | 277.3 | ||
| Time + NAO | 236.5 | 242.9 | ||
| Time + AMO | 237.3 | 243.7 | ||
| NAO + AMO | 260.5 | 266.9 | ||
| Time + NAO + AMO | 238.5 | 247.0 | ||
| Intensity (°C) | Stationary | 670.0 | 676.9 | |
| Time | 667.7 | 678.1 | ||
| PNA | 663.9 | 674.2 * | ||
| AMO | 664.3 | 678.1 | ||
| Time + PNA | 664.1 | 678.0 | ||
| Time + AMO | 666.3 | 683.6 | ||
| PNA + AMO | 662.8 * | 676.7 | ||
| Time + PNA + AMO | 664.7 | 682.0 | ||
| Duration (Days) | Stationary | 840.8 | 844.2 | |
| Time | 838.6 | 845.5 | ||
| PNA | 818.8 | 825.7 * | ||
| AMO | 826.6 | 837.0 | ||
| Time + PNA | 819.0 | 829.4 | ||
| Time + AMO | 828.2 | 842.0 | ||
| PNA + AMO | 815.5 * | 825.9 | ||
| Time + PNA + AMO | 817.5 | 831.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdi, Y.; Charron, C.; Ouarda, T.B.M.J. A Non-Stationary Heat Spell Frequency, Intensity, and Duration Model for France, Integrating Teleconnection Patterns and Climate Change. Atmosphere 2021, 12, 1387. https://doi.org/10.3390/atmos12111387
Hamdi Y, Charron C, Ouarda TBMJ. A Non-Stationary Heat Spell Frequency, Intensity, and Duration Model for France, Integrating Teleconnection Patterns and Climate Change. Atmosphere. 2021; 12(11):1387. https://doi.org/10.3390/atmos12111387
Chicago/Turabian StyleHamdi, Yasser, Christian Charron, and Taha B. M. J. Ouarda. 2021. "A Non-Stationary Heat Spell Frequency, Intensity, and Duration Model for France, Integrating Teleconnection Patterns and Climate Change" Atmosphere 12, no. 11: 1387. https://doi.org/10.3390/atmos12111387
APA StyleHamdi, Y., Charron, C., & Ouarda, T. B. M. J. (2021). A Non-Stationary Heat Spell Frequency, Intensity, and Duration Model for France, Integrating Teleconnection Patterns and Climate Change. Atmosphere, 12(11), 1387. https://doi.org/10.3390/atmos12111387







