Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI
Abstract
1. Introduction
1.1. Gravity Waves
1.2. Mesospheric Inversion Layers
1.3. Wind–Wave Interactions
1.4. Large-Scale Waves
2. Instruments and Data
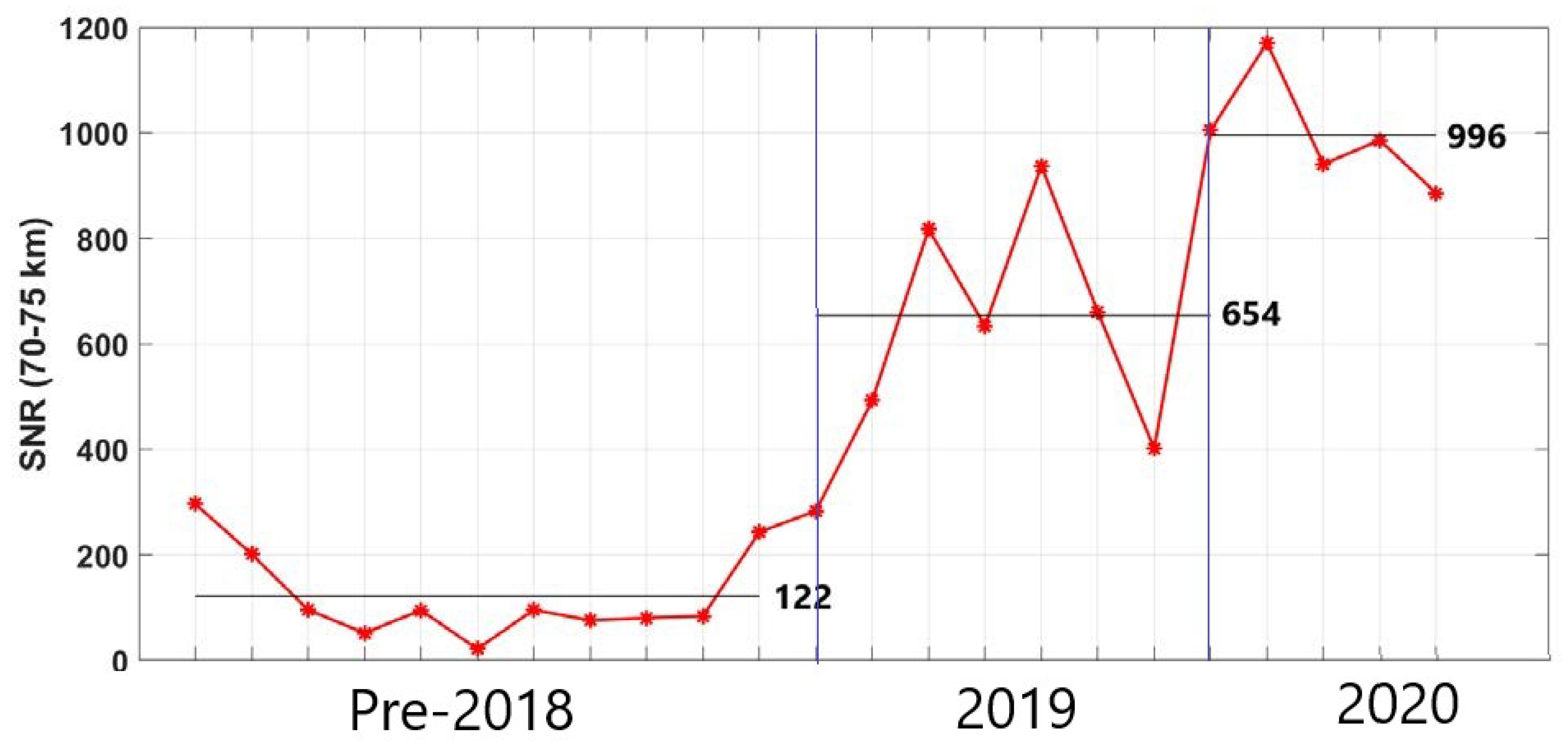
2.1. Monge Lidar and Experimental Improvements
2.2. ICON Satellite
2.3. Sounding of the Atmosphere Using Broadband Emission Radiometry (SABER)
2.4. Microwave Limb Sounder (MLS)
2.5. Radiosondes
2.6. ECMWF—ERA5 Reanalysis
3. Methods
3.1. Lidar Temperatures
3.2. Lidar Filtering
3.3. Wavelet Analysis
3.4. Lidar Gravity Wave Estimates
4. Data
4.1. Context of the Campaign
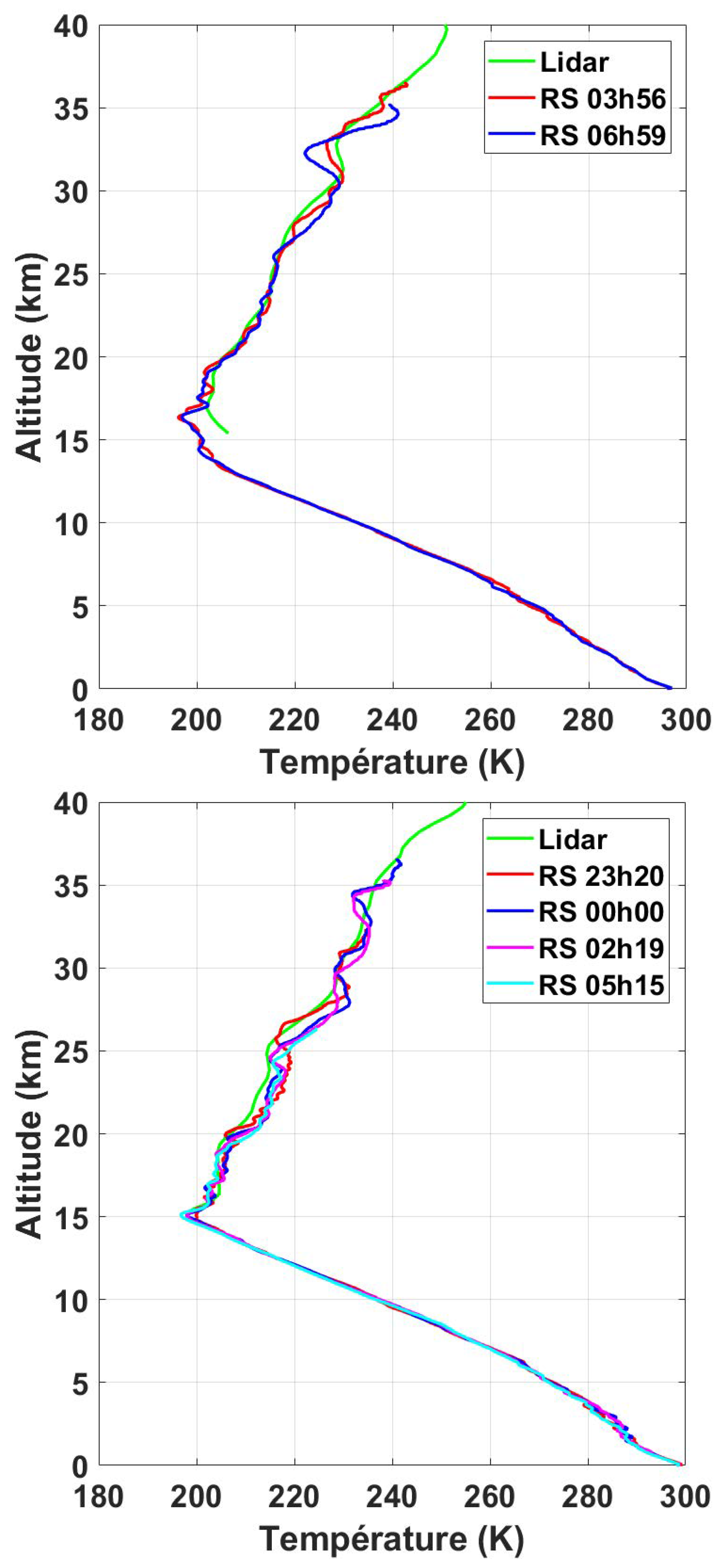
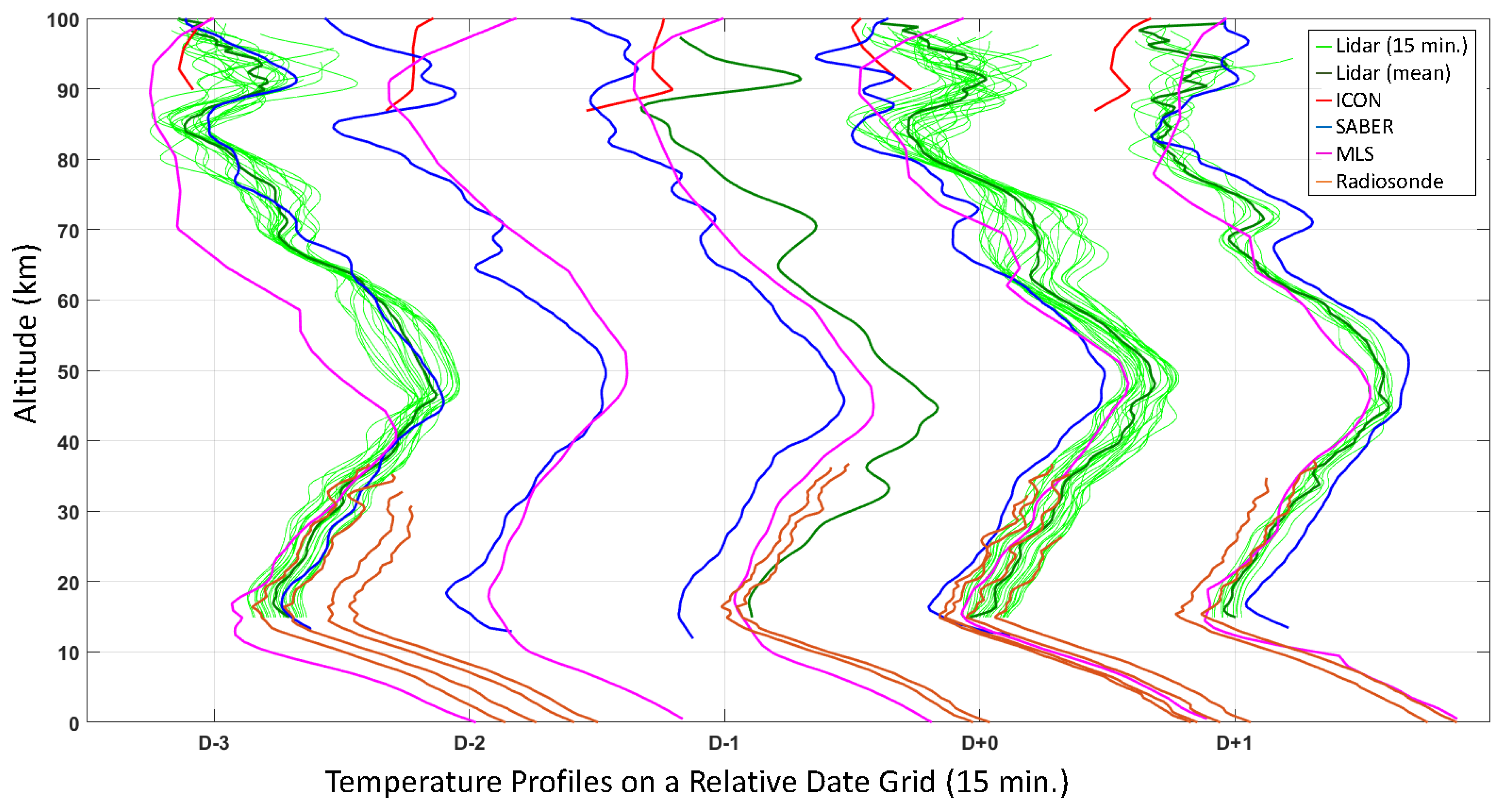
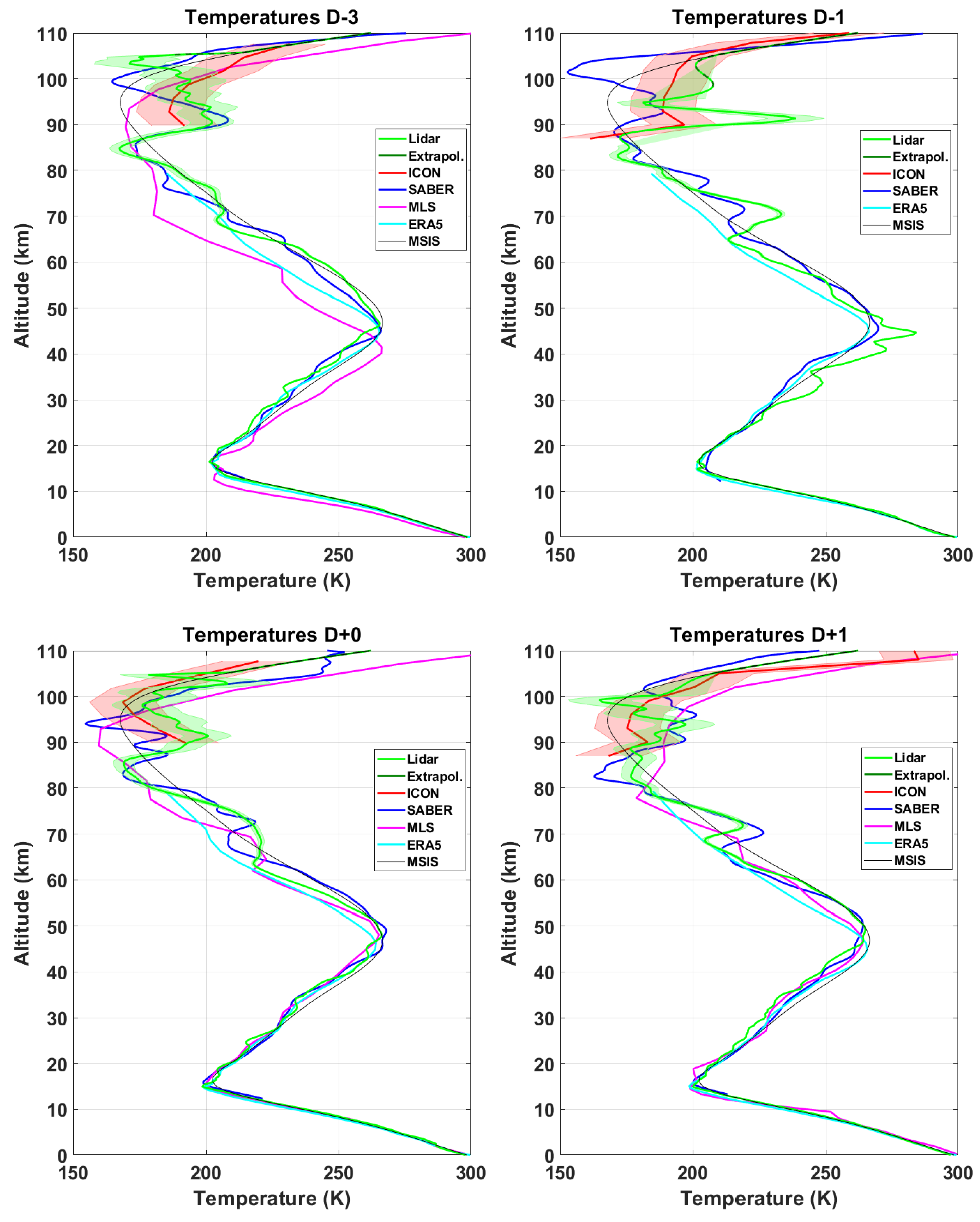
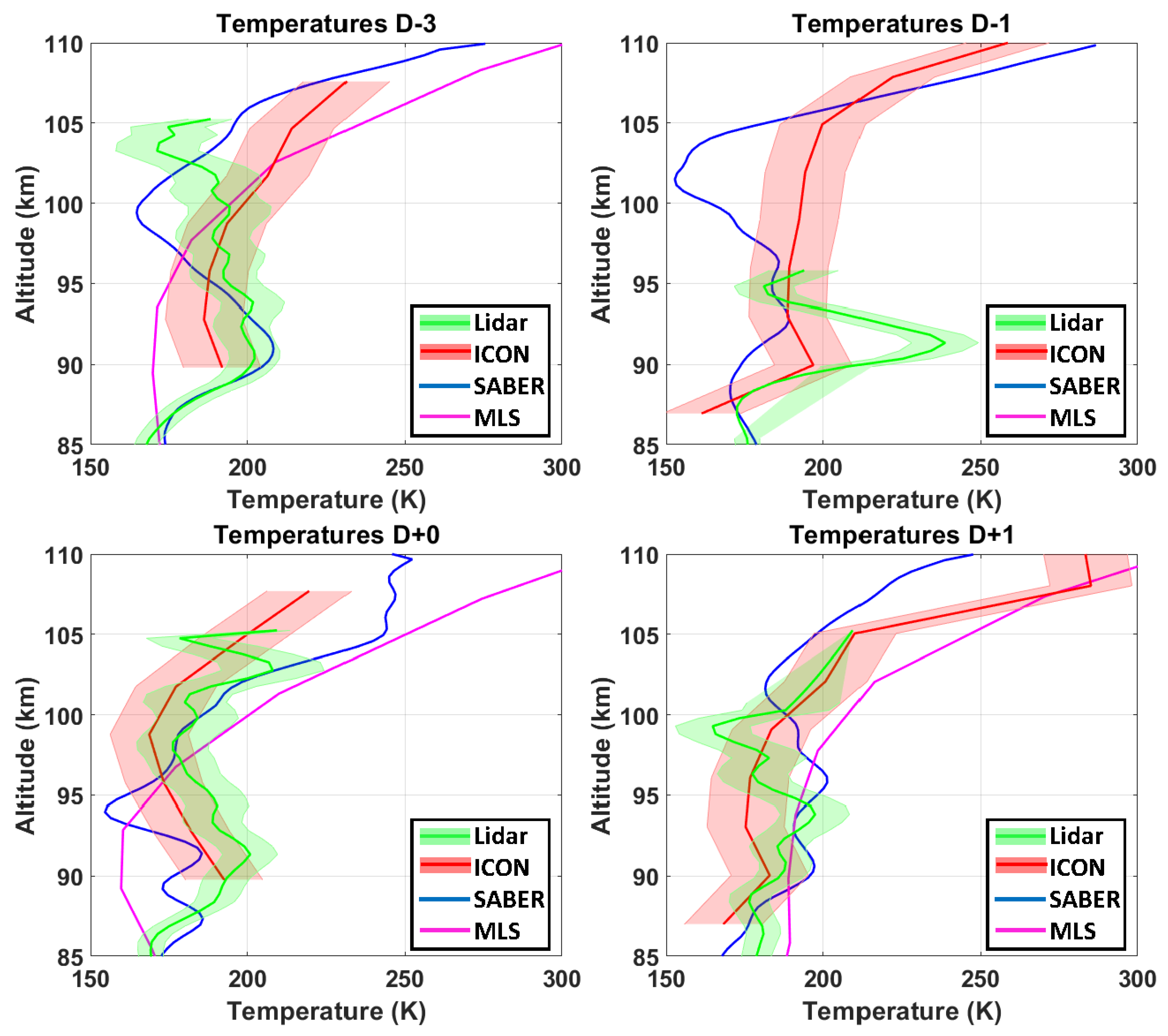
4.2. Atmospheric Temperature Profiles
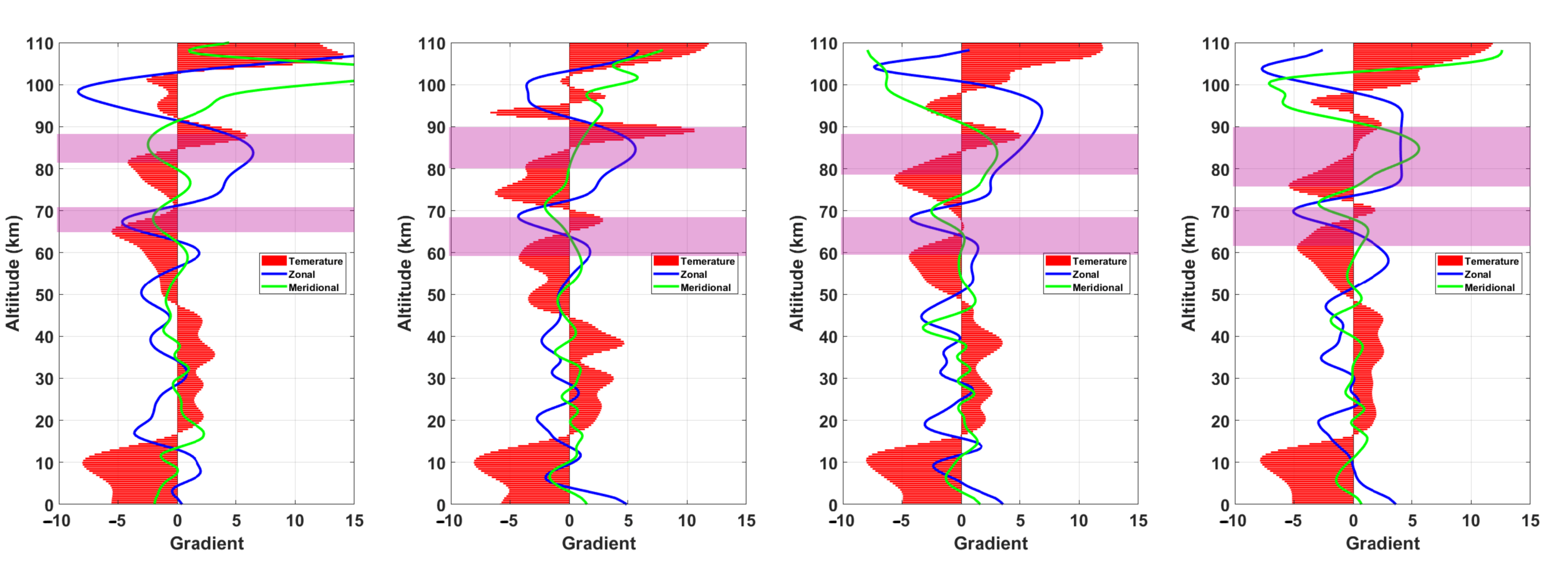
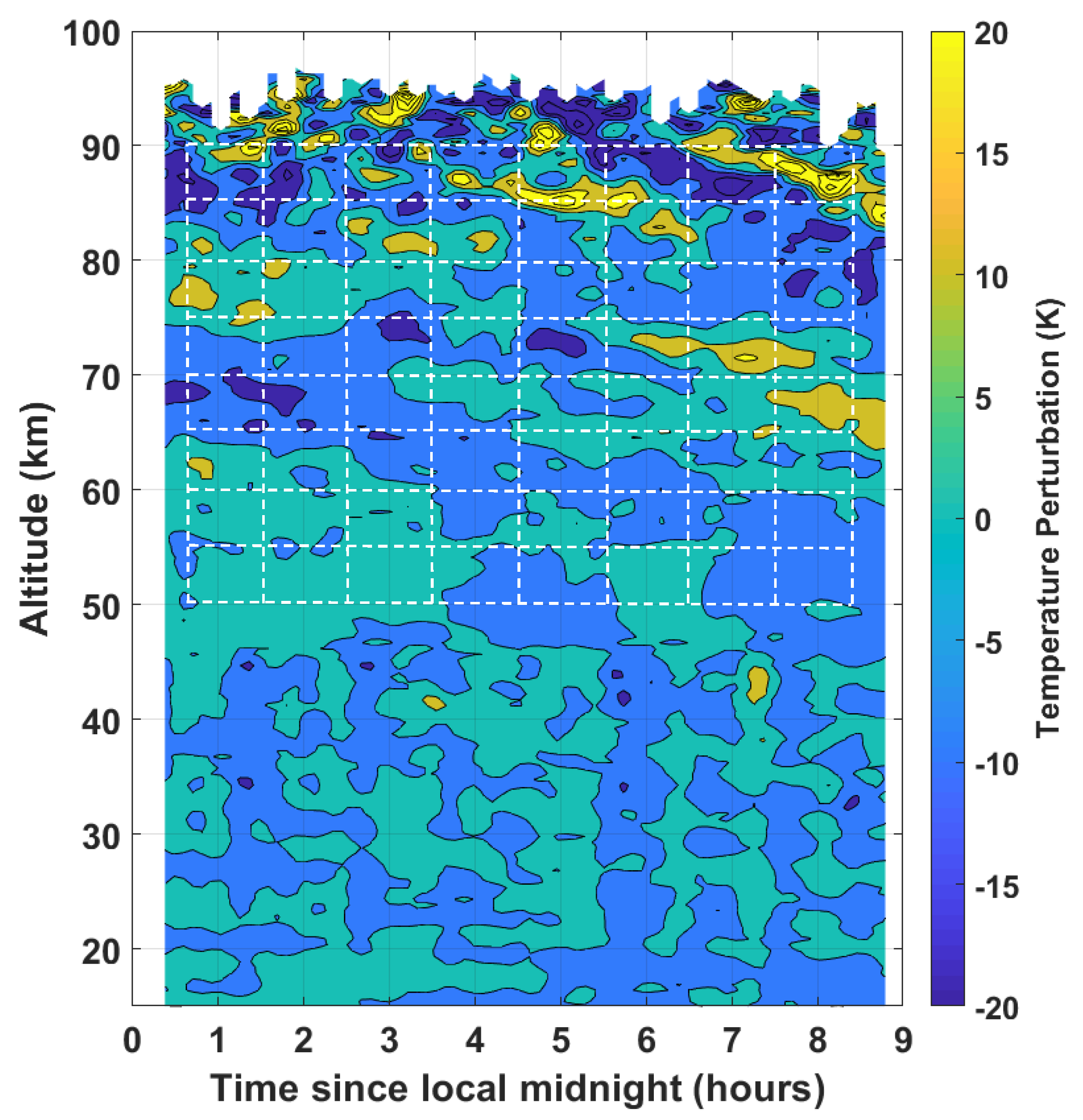
4.3. Lidar Temperature Perturbations
4.4. Validation of ICON Temperatures
4.5. Merged Temperatures and Winds
5. Results
Case Study Night of D+0
6. Discussion
7. Conclusions and Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bodilis, A. Le bâtiment d’essais et de mesures Monge. REE. Rev. L’électricité L’électronique 2001, 1, 84–89. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. Ocean. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Holton, J.R. The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere. J. Atmos. Sci. 1982, 39, 791–799. [Google Scholar] [CrossRef]
- Fritts, D.C. Gravity wave saturation in the middle atmosphere: A review of theory and observations. Rev. Geophys. 1984, 22, 275–308. [Google Scholar] [CrossRef]
- Garcia, R.R.; Solomon, S. The effect of breaking gravity waves on the dynamics and chemical composition of the mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 1985, 90, 3850–3868. [Google Scholar] [CrossRef]
- Snively, J.B.; Pasko, V.P. Breaking of thunderstorm-generated gravity waves as a source of short-period ducted waves at mesopause altitudes. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Isler, J.R.; Taylor, M.J.; Fritts, D.C. Observational evidence of wave ducting and evanescence in the mesosphere. J. Geophys. Res. Atmos. 1997, 102, 26301–26313. [Google Scholar] [CrossRef]
- Fritts, D.C.; Blanchard, R.C.; Coy, L. Gravity wave structure between 60 and 90 km inferred from space shuttle reentry data. J. Atmos. Sci. 1989, 46, 423–434. [Google Scholar] [CrossRef][Green Version]
- Hauchecorne, A.; Chanin, M.L.; Wilson, R. Mesospheric temperature inversion and gravity wave breaking. Geophys. Res. Lett. 1987, 14, 933–936. [Google Scholar] [CrossRef]
- Wilson, R.; Chanin, M.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar: 1. Case studies. J. Geophys. Res. Atmos. 1991, 96, 5153–5167. [Google Scholar] [CrossRef]
- Wilson, R.; Chanin, M.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar: 2. Climatology. J. Geophys. Res. Atmos. 1991, 96, 5169–5183. [Google Scholar] [CrossRef]
- Whiteway, J.; Duck, T.; Donovan, D.P.; Bird, J.; Pal, S.; Carswell, A. Measurements of gravity wave activity within and around the Arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef]
- Sica, R.; Thayaparan, T.; Argall, P.; Russell, A.; Hocking, W. Modulation of upper mesospheric temperature inversions due to tidal-gravity wave interactions. J. Atmos. Sol.-Terr. Phys. 2002, 64, 915–922. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Höffner, J.; Lübken, F.J. Lidar temperature measurements of gravity waves over Kühlungsborn (54° N) from 1 to 105 km: A winter-summer comparison. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Chu, X.; Yu, Z.; Gardner, C.S.; Chen, C.; Fong, W. Lidar observations of neutral Fe layers and fast gravity waves in the thermosphere (110–155 km) at McMurdo (77.8 S, 166.7 E), Antarctica. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Ehard, B.; Kaifler, B.; Kaifler, N.; Rapp, M. Evaluation of methods for gravity wave extraction from middle-atmospheric lidar temperature measurements. Atmos. Meas. Tech. 2015, 8, 4645–4655. [Google Scholar] [CrossRef]
- Baumgarten, K.; Gerding, M.; Lübken, F.J. Seasonal variation of gravity wave parameters using different filter methods with daylight lidar measurements at midlatitudes. J. Geophys. Res. Atmos. 2017, 122, 2683–2695. [Google Scholar] [CrossRef]
- Triplett, C.C.; Collins, R.L.; Nielsen, K.; Harvey, V.L.; Mizutani, K. Role of wind filtering and unbalanced flow generation in middle atmosphere gravity wave activity at Chatanika Alaska. Atmosphere 2017, 8, 27. [Google Scholar] [CrossRef]
- Triplett, C.C.; Li, J.; Collins, R.L.; Lehmacher, G.A.; Barjatya, A.; Fritts, D.C.; Strelnikov, B.; Lübken, F.J.; Thurairajah, B.; Harvey, V.L.; et al. Observations of reduced turbulence and wave activity in the Arctic middle atmosphere following the January 2015 sudden stratospheric warming. J. Geophys. Res. Atmos. 2018, 123, 13–259. [Google Scholar] [CrossRef]
- Taylor, M.J.; Turnbull, D.; Lowe, R. Spectrometric and imaging measurements of a spectacular gravity wave event observed during the ALOHA-93 campaign. Geophys. Res. Lett. 1995, 22, 2849–2852. [Google Scholar] [CrossRef]
- Sedlak, R.; Hannawald, P.; Schmidt, C.; Wüst, S.; Bittner, M.; Stanič, S. Gravity wave instability structures and turbulence from more than one and a half years of OH* airglow imager observations in Slovenia. Atmos. Meas. Tech. Discuss. 2021, 2021, 1–28. [Google Scholar] [CrossRef]
- Fritts, D.C.; Wang, L.; Werne, J.; Lund, T.; Wan, K. Gravity wave instability dynamics at high Reynolds numbers. Part I: Wave field evolution at large amplitudes and high frequencies. J. Atmos. Sci. 2009, 66, 1126–1148. [Google Scholar] [CrossRef]
- Fritts, D.C.; Wang, L.; Werne, J.; Lund, T.; Wan, K. Gravity wave instability dynamics at high Reynolds numbers. Part II: Turbulence evolution, structure, and anisotropy. J. Atmos. Sci. 2009, 66, 1149–1171. [Google Scholar] [CrossRef]
- Meriwether, J.W.; Gardner, C.S. A review of the mesosphere inversion layer phenomenon. J. Geophys. Res. Atmos. 2000, 105, 12405–12416. [Google Scholar] [CrossRef]
- Schmidlin, F. Temperature inversions near 75 km. Geophys. Res. Lett. 1976, 3, 173–176. [Google Scholar] [CrossRef]
- Salby, M.; Sassi, F.; Callaghan, P.; Wu, D.; Keckhut, P.; Hauchecorne, A. Mesospheric inversions and their relationship to planetary wave structure. J. Geophys. Res. Atmos. 2002, 107, ACL-4. [Google Scholar] [CrossRef]
- Mertens, C.J.; Mlynczak, M.G.; López-Puertas, M.; Wintersteiner, P.P.; Picard, R.H.; Winick, J.R.; Gordley, L.L.; Russell, J.M. Retrieval of mesospheric and lower thermospheric kinetic temperature from measurements of CO2 15 µm Earth Limb Emission under non-LTE conditions. Geophys. Res. Lett. 2001, 28, 1391–1394. [Google Scholar] [CrossRef]
- Ramesh, K.; Sridharan, S.; Vijaya Bhaskara Rao, S. Causative mechanisms for the occurrence of a triple layered mesospheric inversion event over low latitudes. J. Geophys. Res. Space Phys. 2014, 119, 3930–3943. [Google Scholar] [CrossRef]
- Lehmacher, G.; Croskey, C.; Mitchell, J.; Friedrich, M.; Lübken, F.J.; Rapp, M.; Kudeki, E.; Fritts, D. Intense turbulence observed above a mesospheric temperature inversion at equatorial latitude. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Fechine, J.; Wrasse, C.; Takahashi, H.; Mlynczak, M.; Russell, J. Lower-mesospheric inversion layers over Brazilian equatorial region using TIMED/SABER temperature profiles. Adv. Space Res. 2008, 41, 1447–1453. [Google Scholar] [CrossRef]
- Gan, Q.; Zhang, S.D.; Yi, F. TIMED/SABER observations of lower mesospheric inversion layers at low and middle latitudes. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Siva Kumar, V.; Bhavani Kumar, Y.; Raghunath, K.; Rao, P.; Krishnaiah, M.; Mizutani, K.; Aoki, T.; Yasui, M.; Itabe, T. Lidar measurements of mesospheric temperature inversion at a low latitude. Ann. Geophys. 2001, 19, 1039–1044. [Google Scholar] [CrossRef]
- Leblanc, T.; Hauchecorne, A. Recent observations of mesospheric temperature inversions. J. Geophys. Res. Atmos. 1997, 102, 19471–19482. [Google Scholar] [CrossRef]
- McLandress, C.; Ward, W. Tidal/gravity wave interactions and their influence on the large-scale dynamics of the middle atmosphere: Model results. J. Geophys. Res. Atmos. 1994, 99, 8139–8155. [Google Scholar] [CrossRef]
- Hedin, A.E.; Biondi, M.; Burnside, R.; Hernandez, G.; Johnson, R.; Killeen, T.; Mazaudier, C.; Meriwether, J.; Salah, J.; Sica, R.; et al. Revised global model of thermosphere winds using satellite and ground-based observations. J. Geophys. Res. Space Phys. 1991, 96, 7657–7688. [Google Scholar] [CrossRef]
- Smith, A.K. Longitudinal variations in mesospheric winds: Evidence for gravity wave filtering by planetary waves. J. Atmos. Sci. 1996, 53, 1156–1173. [Google Scholar] [CrossRef]
- Sassi, F.; Garcia, R.; Boville, B.; Liu, H. On temperature inversions and the mesospheric surf zone. J. Geophys. Res. Atmos. 2002, 107, ACL-8. [Google Scholar] [CrossRef]
- Baumgarten, K.; Gerding, M.; Baumgarten, G.; Lübken, F.J. Temporal variability of tidal and gravity waves during a record long 10-day continuous lidar sounding. Atmos. Chem. Phys. 2018, 18, 371–384. [Google Scholar] [CrossRef]
- Wing, R.; Martic, M.; Hauchecorne, A.; Porteneuve, J.; Keckhut, P.; Courcoux, Y.; Yung, L.; Retailleau, P.; Cocuron, D. Atmospheric Density and Temperature Vertical Profile Retrieval for Flight-Tests with a Rayleigh Lidar On-Board the French Advanced Test Range Ship Monge. Atmosphere 2020, 11, 75. [Google Scholar] [CrossRef]
- Keckhut, P.; Hauchecorne, A.; Chanin, M. A critical review of the database acquired for the long-term surveillance of the middle atmosphere by the French Rayleigh lidars. J. Atmos. Ocean. Technol. 1993, 10, 850–867. [Google Scholar] [CrossRef]
- Keckhut, P.; Chanin, M.L.; Hauchecorne, A. Stratosphere temperature measurement using Raman lidar. Appl. Opt. 1990, 29, 5182–5186. [Google Scholar] [CrossRef]
- Faduilhe, D.; Keckhut, P.; Bencherif, H.; Robert, L.; Baldy, S. Stratospheric temperature monitoring using a vibrational Raman lidar Part 1: Aerosols and ozone interferences. J. Environ. Monit. 2005, 7, 357–364. [Google Scholar] [CrossRef]
- Hauchecorne, A.; Chanin, M.; Keckhut, P.; Nedeljkovic, D. Lidar monitoring of the temperature in the middle and lower atmosphere. Appl. Phys. B 1992, 55, 29–34. [Google Scholar] [CrossRef]
- Immel, T.J.; England, S.; Mende, S.; Heelis, R.; Englert, C.; Edelstein, J.; Frey, H.; Korpela, E.; Taylor, E.; Craig, W.; et al. The ionospheric connection explorer mission: Mission goals and design. Space Sci. Rev. 2018, 214, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Englert, C.R.; Harlander, J.M.; Brown, C.M.; Marr, K.D. Spatial heterodyne spectroscopy at the Naval Research Laboratory. Appl. Opt. 2015, 54, F158–F163. [Google Scholar] [CrossRef] [PubMed]
- Englert, C.R.; Harlander, J.M.; Brown, C.M.; Marr, K.D.; Miller, I.J.; Stump, J.E.; Hancock, J.; Peterson, J.Q.; Kumler, J.; Morrow, W.H.; et al. Michelson interferometer for global high-resolution thermospheric imaging (MIGHTI): Instrument design and calibration. Space Sci. Rev. 2017, 212, 553–584. [Google Scholar] [CrossRef] [PubMed]
- Harding, B.J.; Makela, J.J.; Englert, C.R.; Marr, K.D.; Harlander, J.M.; England, S.L.; Immel, T.J. The MIGHTI wind retrieval algorithm: Description and verification. Space Sci. Rev. 2017, 212, 585–600. [Google Scholar] [CrossRef] [PubMed]
- Stevens, M.H.; Englert, C.R.; Harlander, J.M.; England, S.L.; Marr, K.D.; Brown, C.M.; Immel, T.J. Retrieval of lower thermospheric temperatures from O2 A band emission: The MIGHTI experiment on ICON. Space Sci. Rev. 2018, 214, 1–9. [Google Scholar] [CrossRef]
- Makela, J.J.; Baughman, M.; Navarro, L.A.; Harding, B.J.; Englert, C.R.; Harlander, J.M.; Marr, K.D.; Benkhaldoun, Z.; Kaab, M.; Immel, T.J. Validation of ICON-MIGHTI Thermospheric Wind Observations: 1. Nighttime Red-Line Ground-Based Fabry-Perot Interferometers. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028726. [Google Scholar] [CrossRef]
- Harding, B.J.; Chau, J.L.; He, M.; Englert, C.R.; Harlander, J.M.; Marr, K.D.; Makela, J.J.; Clahsen, M.; Li, G.; Ratnam, M.V.; et al. Validation of ICON-MIGHTI thermospheric wind observations: 2. Green-line comparisons to specular meteor radars. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028947. [Google Scholar] [CrossRef]
- Rezac, L.; Jian, Y.; Yue, J.; Russell, J.; Kutepov, A.; Garcia, R.; Walker, K.; Bernath, P. Validation of the global distribution of CO volume mixing ratio in the mesosphere and lower thermosphere from SABER. J. Geophys. Res. 2015, 120, 12067–12081. [Google Scholar] [CrossRef]
- Rezac, L.; Kutepov, A.; Russell, J.; Feofilov, A.; Yue, J.; Goldberg, R. Simultaneous retrieval of T(p) and CO; VMR from two-channel non-LTE limb radiances and application to daytime SABER/TIMED measurements. J. Atmos. Sol.-Terr. Phys. 2015, 130–131, 23–42. [Google Scholar] [CrossRef]
- Schwartz, M.J.; Lambert, A.; Manney, G.L.; Read, W.G.; Livesey, N.J.; Froidevaux, L.; Ao, C.O.; Bernath, P.F.; Boone, C.D.; Cofield, R.E.; et al. Validation of the Aura Microwave Limb Sounder temperature and geopotential height measurements. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Waters, J.W.; Froidevaux, L.; Harwood, R.S.; Jarnot, R.F.; Pickett, H.M.; Read, W.G.; Siegel, P.H.; Cofield, R.E.; Filipiak, M.J.; Flower, D.A.; et al. The Earth observing system microwave limb sounder (EOS MLS) on the aura Satellite. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1075–1092. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations. Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- Marlton, G.; Charlton-Perez, A.; Harrison, G.; Polichtchouk, I.; Hauchecorne, A.; Keckhut, P.; Wing, R.; Leblanc, T.; Steinbrecht, W. Using a network of temperature lidars to identify temperature biases in the upper stratosphere in ECMWF reanalyses. Atmos. Chem. Phys. 2021, 21, 6079–6092. [Google Scholar] [CrossRef]
- Wing, R.; Hauchecorne, A.; Keckhut, P.; Godin-Beekmann, S.; Khaykin, S.; McCullough, E.M.; Mariscal, J.F.; d’Almeida, E. Lidar temperature series in the middle atmosphere as a reference data set–Part 1: Improved retrievals and a 20-year cross-validation of two co-located French lidars. Atmos. Meas. Tech. 2018, 11, 5531–5547. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107. [Google Scholar] [CrossRef]
- Hauchecorne, A.; Chanin, M.L. Density and temperature profiles obtained by lidar between 35 and 70 km. Geophys. Res. Lett. 1980, 7, 565–568. [Google Scholar] [CrossRef]
- Khanna, J.; Bandoro, J.; Sica, R.J.; McElroy, C.T. New technique for retrieval of atmospheric temperature profiles from Rayleigh-scatter lidar measurements using nonlinear inversion. Appl. Opt. 2012, 51, 7945–7952. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, T.; Sica, R.J.; van Gijsel, J.A.E.; Godin-Beekmann, S.; Haefele, A.; Trickl, T.; Payen, G.; Gabarrot, F. Proposed standardized definitions for vertical resolution and uncertainty in the NDACC lidar ozone and temperature algorithms – Part 1: Vertical resolution. Atmos. Meas. Tech. 2016, 9, 4029–4049. [Google Scholar] [CrossRef]
- Leblanc, T.; Sica, R.J.; van Gijsel, J.A.E.; Haefele, A.; Payen, G.; Liberti, G. Proposed standardized definitions for vertical resolution and uncertainty in the NDACC lidar ozone and temperature algorithms—Part 3: Temperature uncertainty budget. Atmos. Meas. Tech. 2016, 9, 4079–4101. [Google Scholar] [CrossRef]
- Iarlori, M.; Madonna, F.; Rizi, V.; Trickl, T.; Amodeo, A. Effective resolution concepts for lidar observations. Atmos. Meas. Tech. 2015, 8, 5157–5176. [Google Scholar] [CrossRef]
- Godin, S.; Carswell, A.I.; Donovan, D.P.; Claude, H.; Steinbrecht, W.; McDermid, I.S.; McGee, T.J.; Gross, M.R.; Nakane, H.; Swart, D.P.; et al. Ozone differential absorption lidar algorithm intercomparison. Appl. Opt. 1999, 38, 6225–6236. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Carswell, A.I. Lidar observations of gravity wave activity in the upper stratosphere over Toronto. J. Geophys. Res. Atmos. 1995, 100, 14113–14124. [Google Scholar] [CrossRef]
- Hagan, M.; Forbes, J.M. Migrating and nonmigrating semidiurnal tides in the upper atmosphere excited by tropospheric latent heat release. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Sica, R.; Russell, A. How many waves are in the gravity wave spectrum? Geophys. Res. Lett. 1999, 26, 3617–3620. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wing, R.; Martic, M.; Triplett, C.; Hauchecorne, A.; Porteneuve, J.; Keckhut, P.; Courcoux, Y.; Yung, L.; Retailleau, P.; Cocuron, D. Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI. Atmosphere 2021, 12, 1386. https://doi.org/10.3390/atmos12111386
Wing R, Martic M, Triplett C, Hauchecorne A, Porteneuve J, Keckhut P, Courcoux Y, Yung L, Retailleau P, Cocuron D. Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI. Atmosphere. 2021; 12(11):1386. https://doi.org/10.3390/atmos12111386
Chicago/Turabian StyleWing, Robin, Milena Martic, Colin Triplett, Alain Hauchecorne, Jacques Porteneuve, Philippe Keckhut, Yann Courcoux, Laurent Yung, Patrick Retailleau, and Dorothee Cocuron. 2021. "Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI" Atmosphere 12, no. 11: 1386. https://doi.org/10.3390/atmos12111386
APA StyleWing, R., Martic, M., Triplett, C., Hauchecorne, A., Porteneuve, J., Keckhut, P., Courcoux, Y., Yung, L., Retailleau, P., & Cocuron, D. (2021). Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI. Atmosphere, 12(11), 1386. https://doi.org/10.3390/atmos12111386






