Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Agronomic Procedures
2.2. Weather, Crop and Soil Characteristics
2.3. ETR and Derived Variables for The Field
2.4. Statistical Analyses
3. Results and Discussion
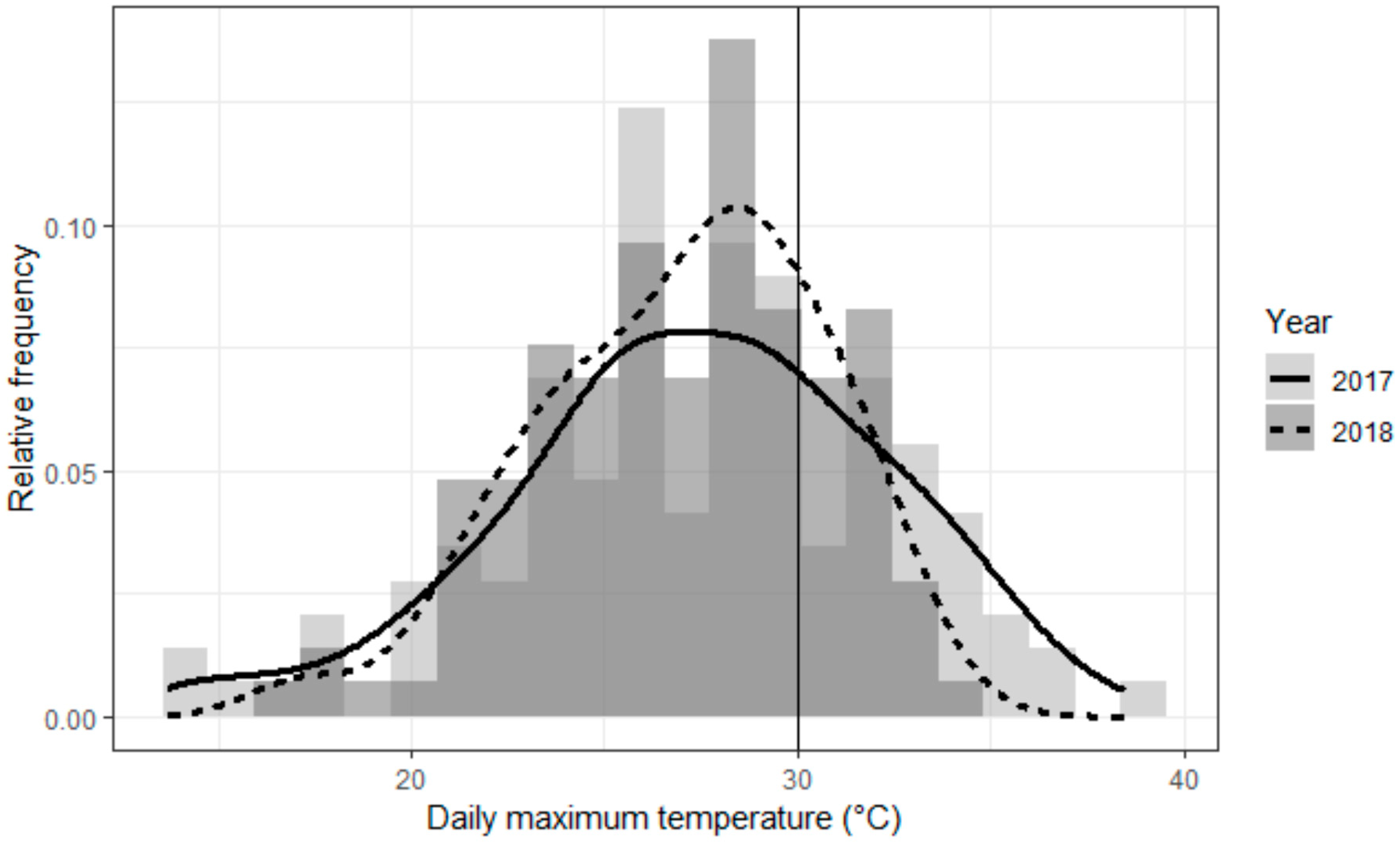
3.1. Weather Conditions of the Studied Growing Seasons
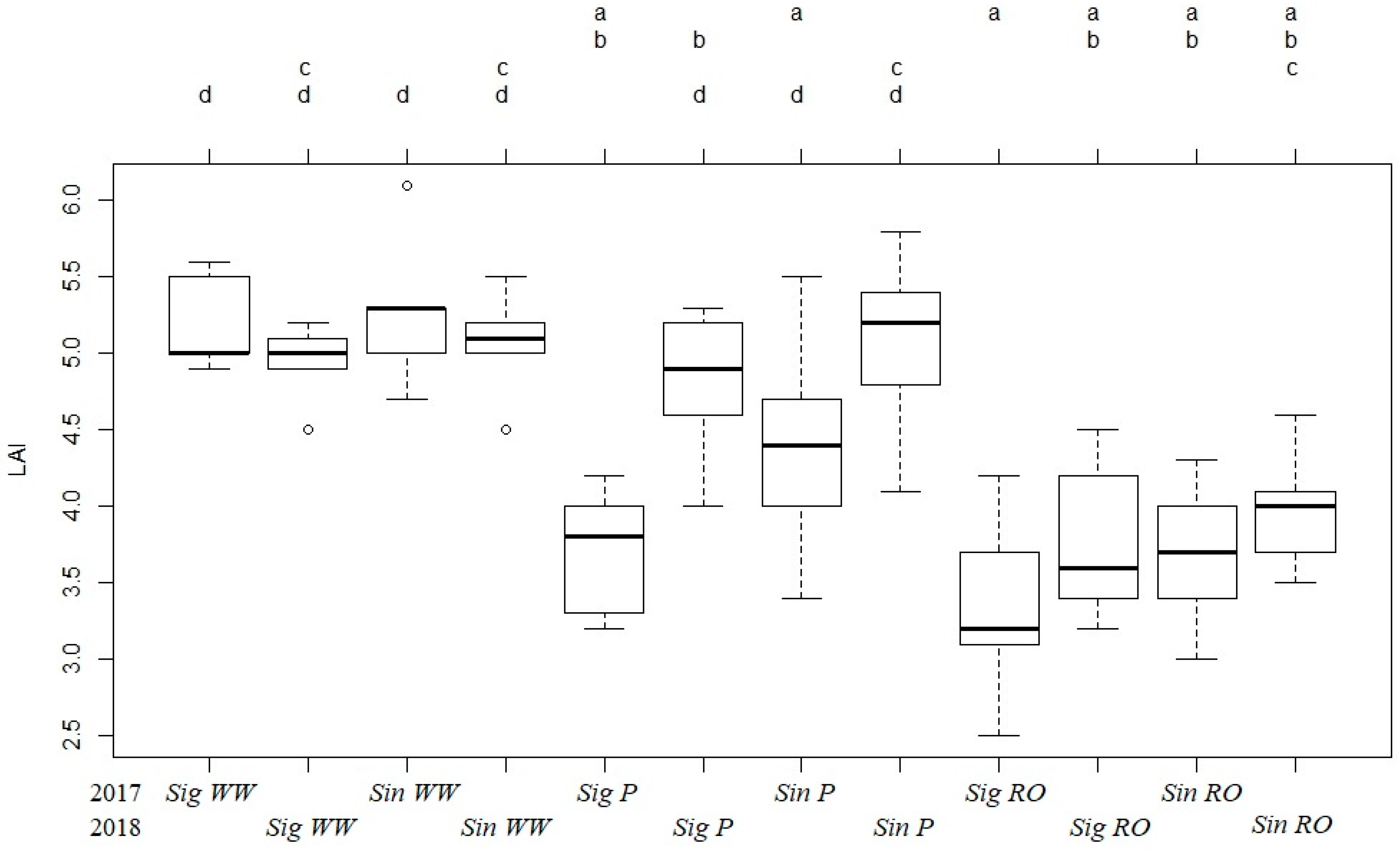
3.2. Soybean Development (Phenological Stages, LAI and SPAD)
3.2.1. Phenological Stages
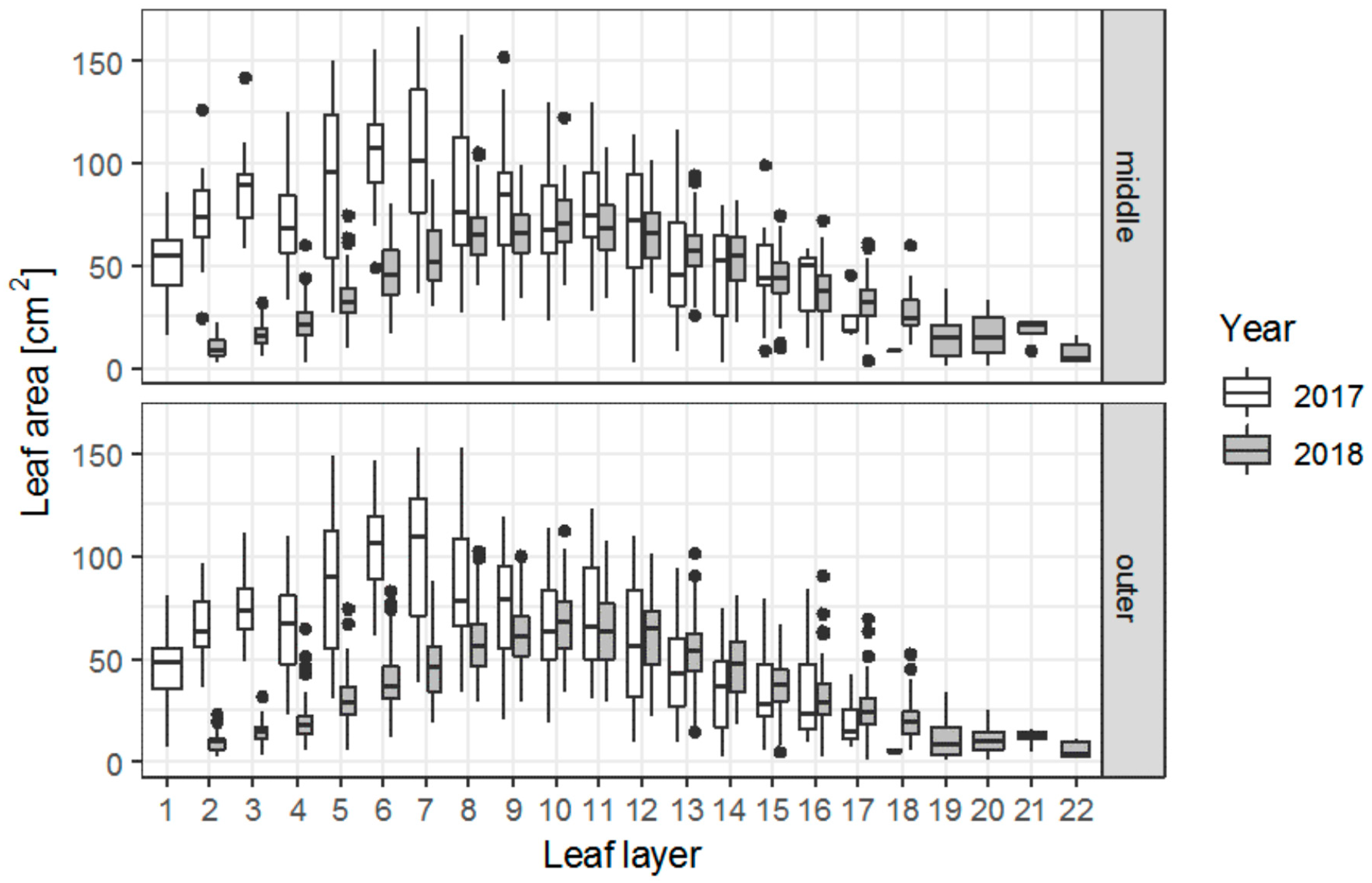
3.2.2. Leaf (Leaflet) Area of Soybean
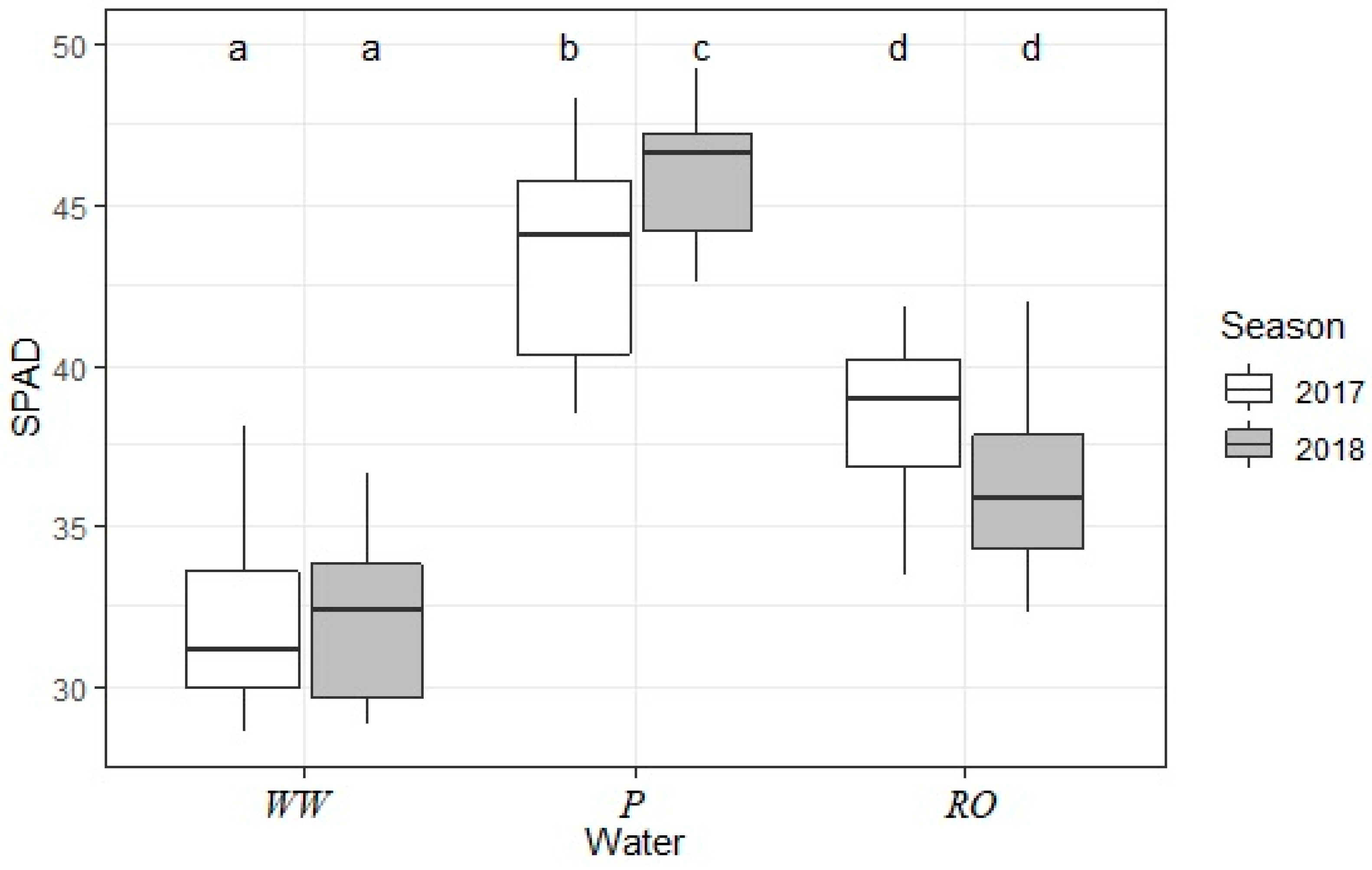
3.2.3. Chlorophyll Content of the Leaves (SPAD)
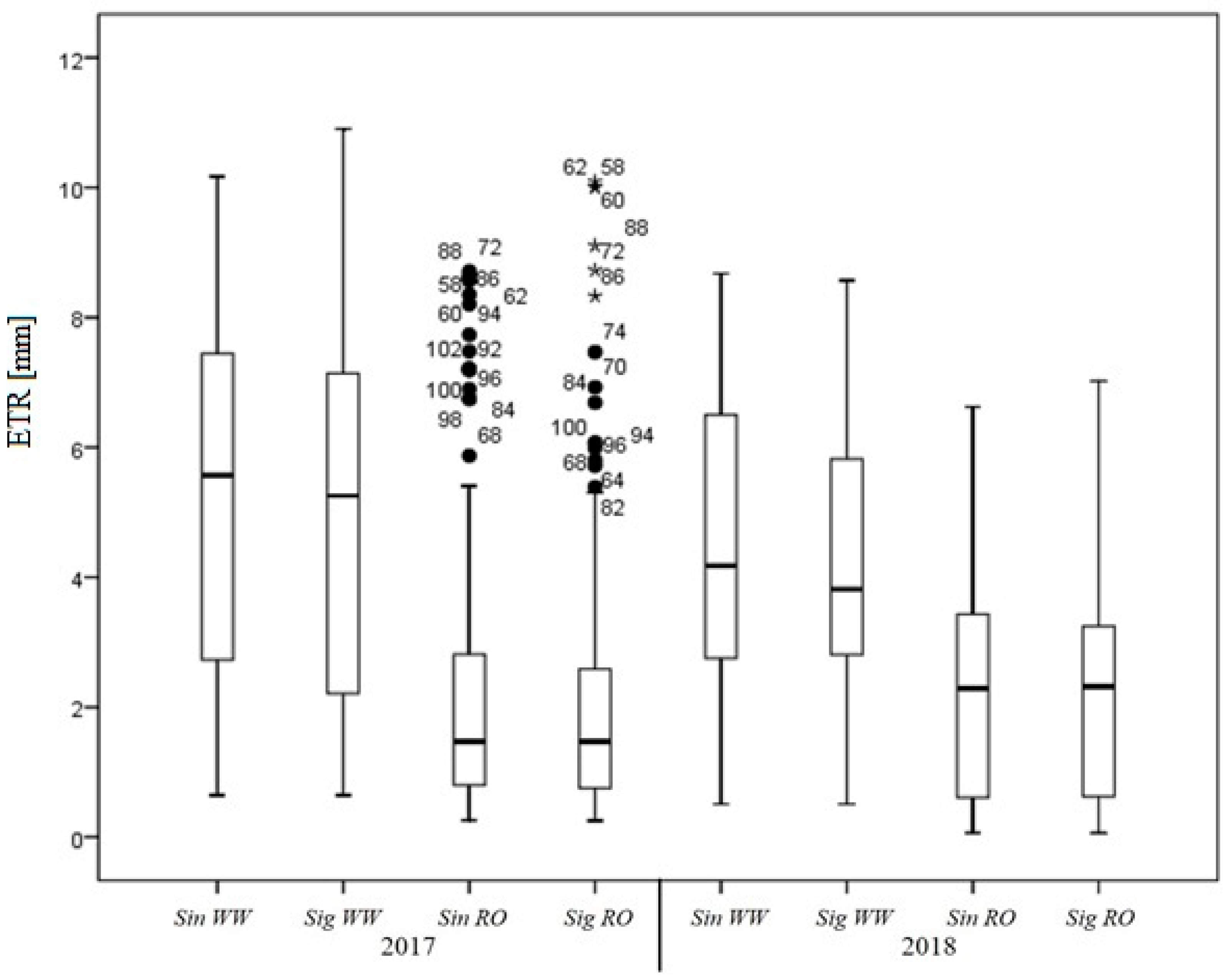
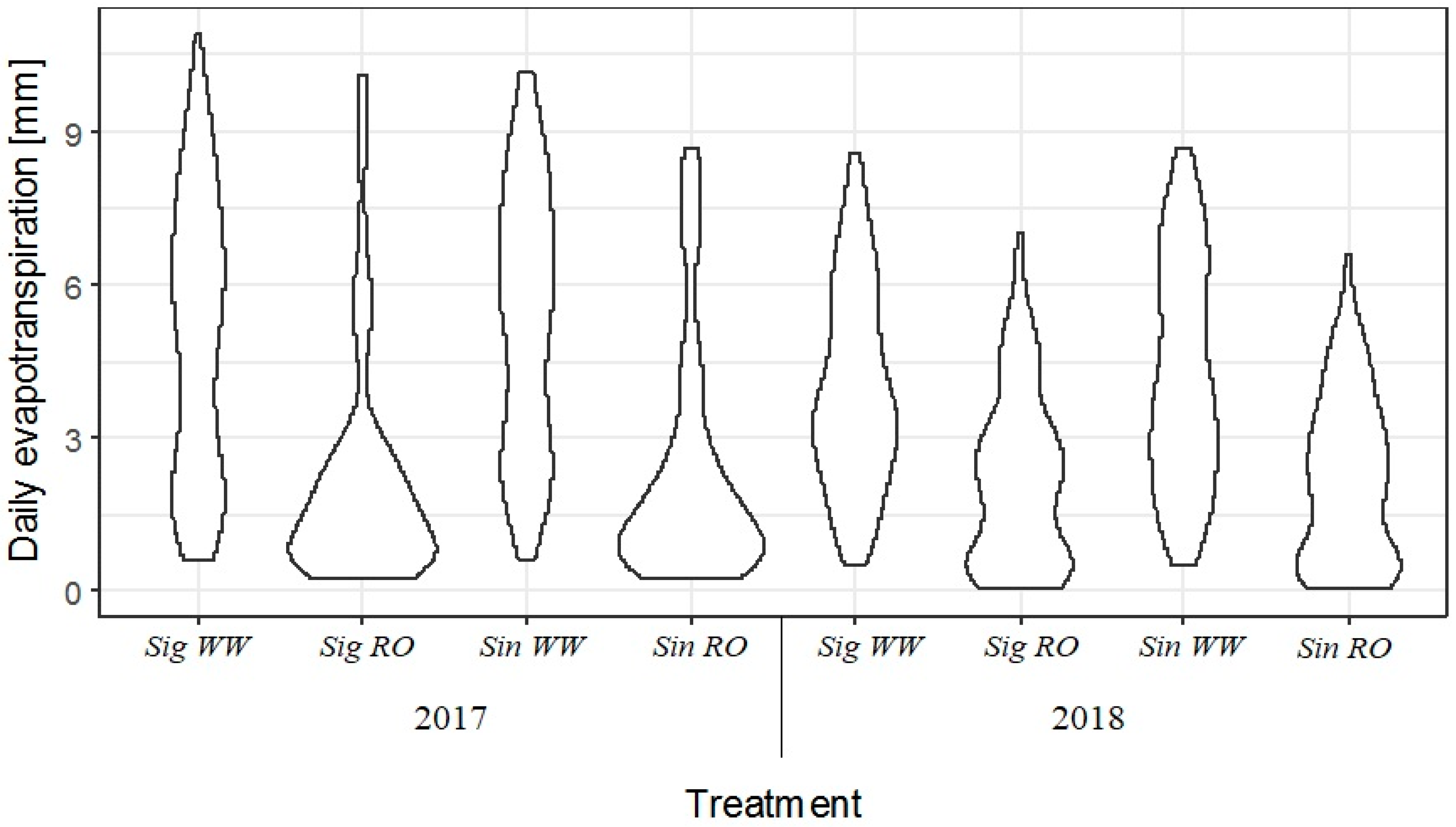
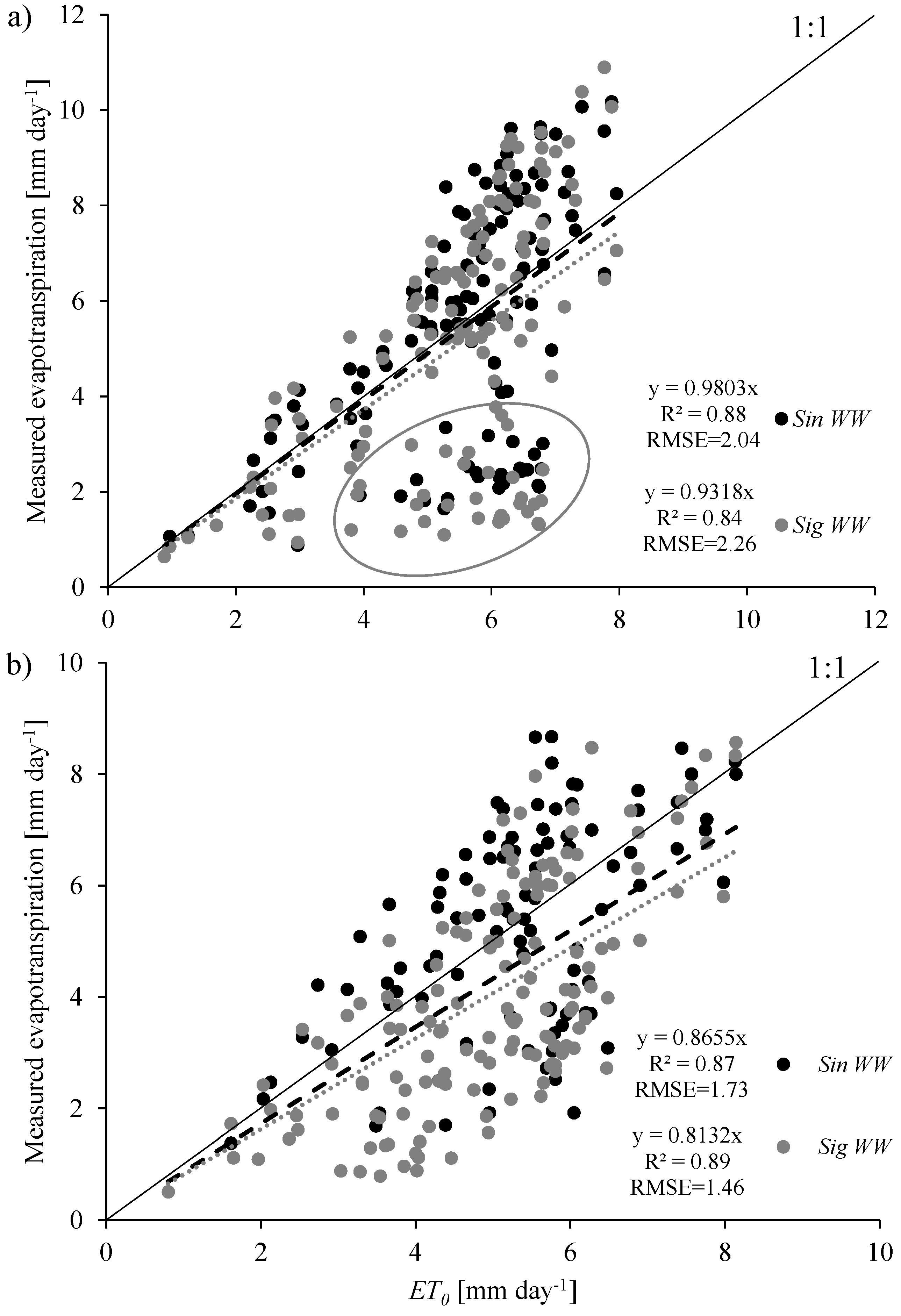
3.3. ETR in Soybean
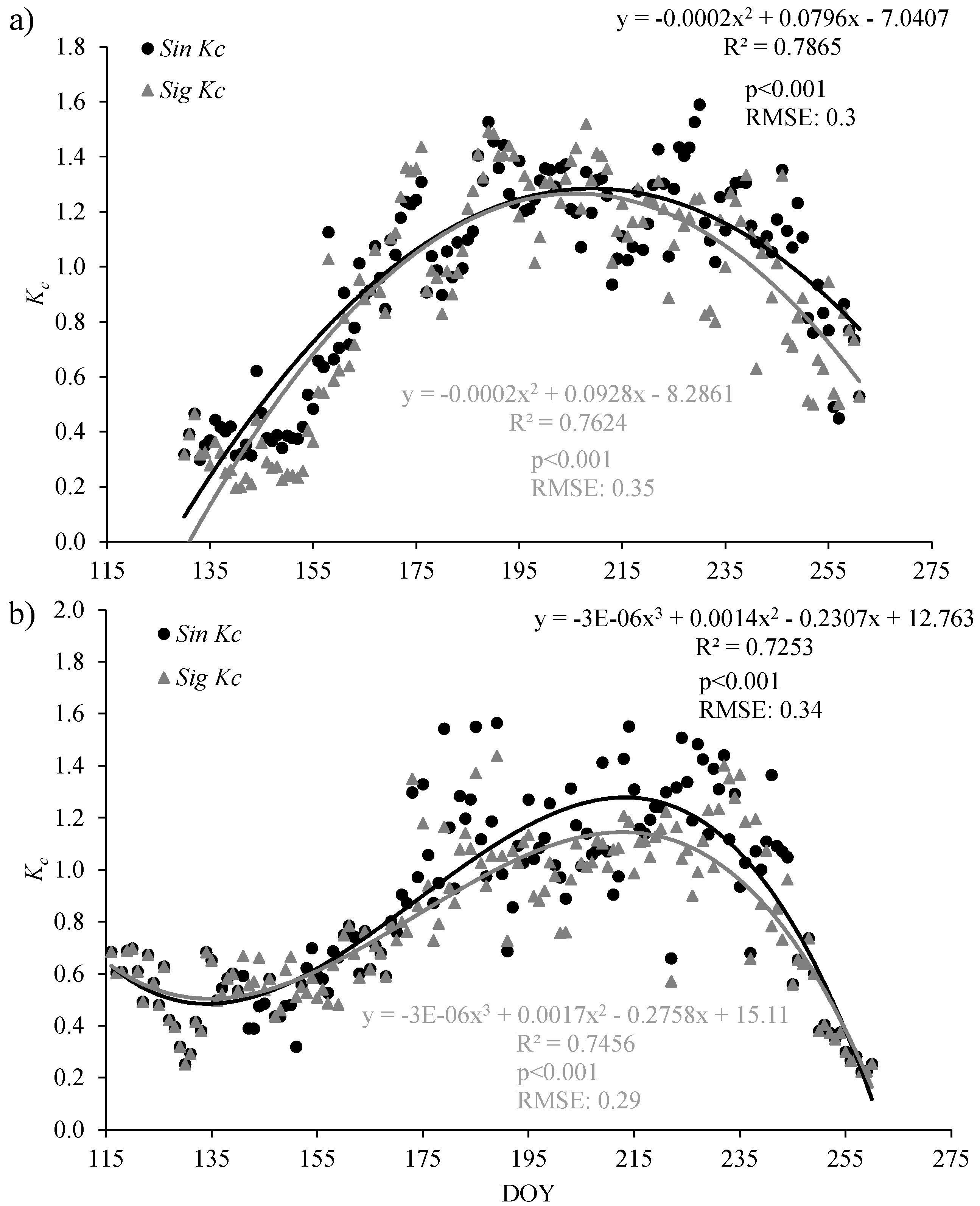
3.4. Crop Coefficients, Kc
3.5. The Impact of Weather Variables on Daily Mean ETR
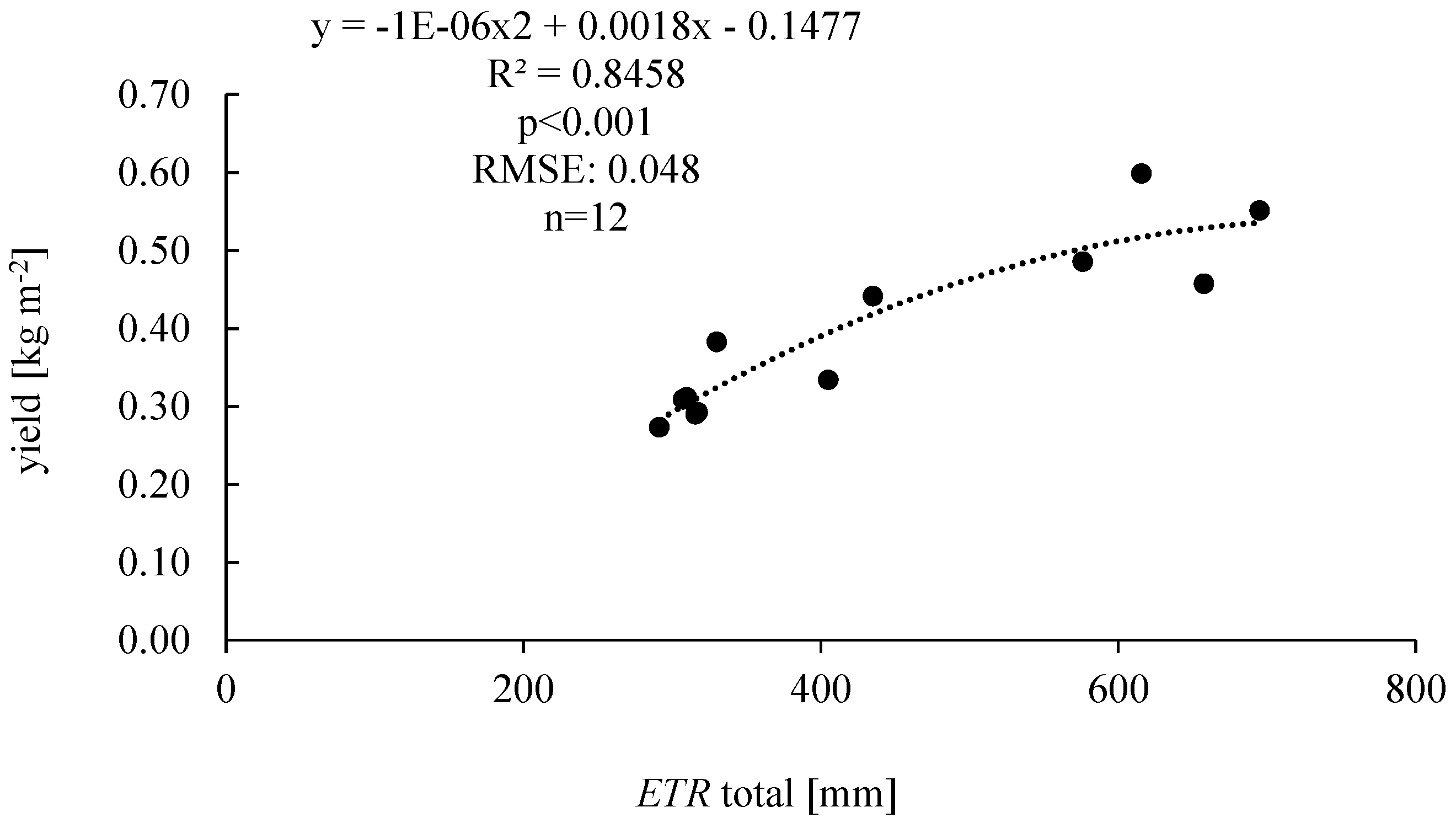
3.6. Relationship between Seed Yield and Seasonal Water Use
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Proházka, P.; Stranc, P.; Pazderu, K.; Stranc, J.; Vostrel, J. Effects of biologically active substances used in soybean seed treatment on oil, protein and fibre content of harvested seeds. Plant Soil Environ. 2017, 63, 564–568. [Google Scholar]
- Tyagi, S.D.; Khan, M.H.; Teixeira da Silva, J.A. Yield stability of some soybean genotypes across diverse environments. Int. J. Plant Breed. 2011, 5, 37–41. [Google Scholar]
- El Sabagh, A.; Hossain, A.; Islam, M.S.; Barutçular, C.; Ratnasekera, D.; Kumar, N.; Meena, R.S.; Gharib, H.S.; Saneoka, H.; Teixeira da Silva, J.A. Sustainable soybean production and abiotic stress management in saline environments: A critical review. Aust. J. Crop Sci. 2019, 13, 228–236. [Google Scholar] [CrossRef]
- KSH. Statisztikai Tükör (Statistical Mirror); Központi Statisztikai Hivatal: Budapest, Hungary; Available online: http://www.ksh.hu/docs/hun/xftp/gyor/vet/vet1806.pdf (accessed on 3 August 2018). (In Hungarian)
- Thuzar, M.; Puteh, A.; Abdullah, N.; Lassim, M.M.; Jusoff, K. The effects of temperature stress on the quality and yield of soya bean [(Glycine max L.) Merrill.]. J. Agric. Sci. 2010, 2, 172–179. [Google Scholar]
- Anda, A.; Soós, G. Some physiological responses of agricultural crops to global warming. Időjárás 2016, 120, 85–101. [Google Scholar]
- Wang, T.; Tang, X.; Zheng, C.; Gu, Q.; Wei, J.; Ma, M. Differences in ecosystem water-use efficiency among the typical croplands. Agric. Water Manag. 2018, 209, 142–150. [Google Scholar] [CrossRef]
- Karam, F.; Maasad, R.; Sfeir, T.; Mounzer, O.; Rouphael, Y. Evapotranspiration and seed yield of field grown soybean under deficit irrigation conditions. Agric. Water Manag. 2005, 75, 226–244. [Google Scholar] [CrossRef]
- Ergo, V.V.; Lascano, R.; Vega, C.R.C.; Parola, R. Heat and water stressed field-grown soybean: A multivariate study on the relationship between physiological-biochemical traits and yield. Environ. Exp. Bot. 2018, 148, 1–11. [Google Scholar] [CrossRef]
- Borhan, M.S.; Panigrahi, S.; Satter, M.A.; Gu, H. Evaluation of computer imaging technique for predicting the SPAD readings in potato leaves. Inform. Proc. Agric. 2017, 4, 275–282. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Pongrácz, R.; Bartholy, J.; Kis, A. Estimation of future precipitation conditions for Hungary with special focus on dry periods. Időjárás 2014, 118, 305–321. [Google Scholar]
- Anapalli, S.S.; Fisher, D.K.; Reddy, K.N.; Wagle, P. Quantifying soybean evapotranspiration using eddy covariance approach. Agric. Water Manag. 2018, 209, 228–239. [Google Scholar] [CrossRef]
- Gajić, B.; Kresović, B.; Tapanarova, A.; Životić, L.; Todorović, M. Effect of irrigation regime on yield, harvest index and water productivity of soybean grown under different precipitation conditions in a temperate environment. Agric. Water Manag. 2018, 210, 224–231. [Google Scholar] [CrossRef]
- Luo, C.; Wang, Z.; Sauer, T.J.; Helmers, M.J.; Horton, R. Portable canopy chamber measurements of evapotranspiration in corn, soybean, and reconstructed prairie. Agric. Water Manag. 2018, 198, 1–9. [Google Scholar] [CrossRef]
- Zhang, B.; Feng, G.; Ahuja, L.R.; Kong, X.; Ouyang, Y.; Adeli, A.; Jenkins, J.N. Soybean crop-water production function in a humid region across years and soils determined with APEX model. Agric. Water Manag. 2018, 204, 180–191. [Google Scholar] [CrossRef]
- Payero, J.O.; Irmak, S. Daily energy fluxes, evapotranspiration and crop coefficient of soybean. Agric. Water Manag. 2013, 129, 31–43. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D.; Irmak, A.; Arkebauer, T.J.; Weiss, A.; Martin, D.L.; Eisenhauer, D.E. On the scaling up leaf stomatal resistance to canopy resistance using photosynthetic photon flux density. Agric. For. Meteorol. 2008, 148, 1034–1044. [Google Scholar] [CrossRef]
- Singer, J.W.; Heitman, J.L.; Hernandez-Ramirez, G.; Sauer, T.J.; Prueger, J.F.; Hatfield, J.L. Contrasting methods for estimating evapotranspiration in soybean. Agric. Water Manag. 2010, 98, 157–163. [Google Scholar] [CrossRef]
- Mbangiwa, N.C.; Savage, M.J.; Mabhaudhi, T. Modelling and measurement of water productivity and total evaporation in a dryland soybean crop. Agric. For. Meteorol. 2019, 266–267, 65–72. [Google Scholar] [CrossRef]
- Wallace, J.S.; Lloyd, C.R.; Sivakumar, M.V.K. Measurements of soil, plant, and total evaporation from millet in Niger. Agric. For. Meteorol. 1993, 63, 149–169. [Google Scholar] [CrossRef]
- Suyker, A.E.; Verma, S.B. Interannual water vapor and energy exchange in an irrigated maize-based agroecosystem. Agric. For. Meteorol. 2008, 148, 417–427. [Google Scholar] [CrossRef]
- Baker, J.M.; van Bavel, C.H.M. Measurement of mass flow of water in the stems of herbaceous plants. Plant Cell Environ. 1987, 10, 777–782. [Google Scholar]
- Kamkar, B.; Langeroodi, A.R.S.; Teixeira da Silva, J.A.; Nodehi, D.A.; Lack, S.; Ghooshchi, F. Study on crop-water production functions for soybean in Mediterranean climatic conditions. Sci. J. Agron. Plant Breed. 2013, 1, 6–21. [Google Scholar]
- Anda, A.; Soós, G.; Menyhárt, L.; Kucserka, T.; Simon, B. Yield features of two soybean varieties under different water supplies and field conditions. Field Crop. Res. 2020, 245, 107673. [Google Scholar] [CrossRef]
- Fehr, W.R.; Caviness, C.E. Stages of Soybean Development; Special Report 80; Iowa State University: Ames, IA, USA, 1977. [Google Scholar]
- Vollmann, M.; Antoniw, K.; Hartung, F.-M.; Renner, B. Social support as mediator of the stress buffering effect of optimism: The importance of differentiating the recipients’ and providers’ perspective. Personal. Soc. Relat. 2011, 25, 146–154. [Google Scholar] [CrossRef]
- WRB. World Reference Base for Soil Resources 2015. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Food and Agriculture Organization of the United Nations, Viale delle Terme di Caracalla, 00100 Rome, Italy. 2006. Available online: http://www.fao.org/3/i3794en/I3794en.pdf (accessed on 6 May 2020).
- Ritchie, J. Water dynamics in the soil-plant-atmosphere system. Plant Soil 1981, 58, 81–96. [Google Scholar] [CrossRef]
- Anda, A.; Simon, B.; Soós, G.; Teixeira da Silva, J.A.; Kucserka, T. Crop-water relation and production of two soybean varieties under different water supplies. Theor. Appl. Climatol. 2019, 137, 1515–1528. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In The State and Movement of Water in Living Organism, Proceedings of the XIX. Symp. Soc. Exp. Biol.; Fogg, G.E., Ed.; Cambridge University Press: Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. Royal Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Allen, R.G.; Clemmens, A.J.; Burt, C.M.; Solomon, K.; O’Halloran, T. Prediction accuracy for project wide evapotranspiration using crop coefficients and reference evapotranspiration. J. Irrig. Drain. Eng. ASCE 2005, 131, 24–36. [Google Scholar] [CrossRef]
- Soós, G.; Anda, A. A methodological study on local application of the FAO-56 Penman-Monteith reference evapotranspiration equation. Georgikon For. Agric. 2014, 18, 71–85. [Google Scholar]
- Howell, T.A.; Evett, S.R.; Tolk, J.A.; Copeland, K.S.; Dusek, D.A.; Colaizzi, P.D. Crop coefficients developed at Bushland, Texas for corn, wheat, sorghum, soybean, cotton, and alfalfa. In Proceedings of the World Water and Environmental Resources Congress. Examining the Confluence of Environmental and Water Concerns, Omaha, NH, USA, 21–25 May 2006; CDROM: Omaha, NH, USA, 2006. [Google Scholar]
- SPSS Inc. SPSS for Windows User’s Guide Series, Release 7.0; SPSS Inc.: Chicago, IL, USA, 1996. [Google Scholar]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 20 December 2018).
- Montoya, F.; García, C.; Pintos, F.; Otero, A. Effects of irrigation regime on the growth and yield of irrigated soybean in temperate humid climatic conditions. Agric. Water Manag. 2017, 193, 30–45. [Google Scholar] [CrossRef]
- Kross, A.; Lapen, D.R.; McNairn, H.; Sunohara, M.; Champagne, C.; Wilkes, G. Satellite and in situ derived corn and soybean biomass and leaf area index: Response to controlled tile drainage under varying weather conditions. Agric. Water Manag. 2015, 160, 118–131. [Google Scholar] [CrossRef]
- Akhtar, K.; Wang, W.; Khan, A.; Ren, G.; Afridi, M.Z.; Feng, Y.; Yang, G. Wheat straw mulch offset soil moisture deficient for improving physiological and growth performance of summer sown soybean. Agric. Water Manag. 2019, 211, 16–25. [Google Scholar] [CrossRef]
- Matsuo, N.; Takahashi, M.; Yamada, T.; Takahashi, M.; Hajka, M.; Fukami, K.; Tsuchiya, S. Effects of water table management and row width on the growth and yield of three soybean cultivars in southwestern Japan. Agric. Water Manag. 2017, 192, 85–97. [Google Scholar] [CrossRef]
- Setiyono, T.D.; Weiss, A.; Specht, J.E.; Cassman, K.G.; Dobermann, A. Leaf area index simulation in soybean grown under near-optimal conditions. Field Crops Res. 2008, 108, 82–92. [Google Scholar] [CrossRef]
- Anda, A.; Simon, B.; Menyhárt, L.; Soós, G.; Kucserka, T. Investigation on soybean leaf area influenced by water supply. Időjárás 2019, 123, 73–87. [Google Scholar] [CrossRef]
- Bajgain, R.; Kawasaki, Y.; Akamatsu, Y.; Tanaka, Y.; Kawamura, H.; Katsura, K.; Shiraiwa, T. Biomass production and yield of soybean grown under converted paddy fields with excess water during the early growth stage. Field Crops Res. 2015, 180, 321–327. [Google Scholar] [CrossRef]
- Charles-Edwards, D.A.; Stutzel, H.; Ferraris, R.; Beech, D.F. An analysis of spatial variation in the nitrogen content of leaves from different horizons within a canopy. Ann. Bot. 1987, 60, 421–426. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Bagg, J.; Banks, S.; Baute, T.; Bohner, H.; Brown, C.; Cowbrough, M.; Hall, B.; Hayes, A.; Johnson, P.; Martin, H.; et al. Agronomy Guide for Field Crops: Publication 811; Brown, C., Ed.; Ministry of Agriculture, Food and Rural Affairs: Toronto, ON, Canada, 2009.
- Dornbos, D.L., Jr.; Mullen, R.E. Influence of stress during soybean seed fill on seed weight, germination, and seedling growth rate. Can. J. Plant Sci. 1991, 71, 373–383. [Google Scholar] [CrossRef]
- Wei, Z.; Paredes, P.; Liu, Y.; Chi, W.W.; Pereira, L.S. Modelling transpiration, soil evaporation and yield prediction of soybean in North China Plain. Agric. Water Manag. 2015, 147, 43–53. [Google Scholar] [CrossRef]
- Payero, J.O.; Melvin, S.; Irmak, S. Response of soybean to deficit irrigation in the semi-arid environment of west-central Nebraska. Trans. ASAE 2005, 48, 2189–2203. [Google Scholar] [CrossRef]
- Doorenbos, J.; Kassam, J.H. FAO Irrigation and Drainage Paper; No. 33; FAO: Rome, Italy, 1979; p. 193. [Google Scholar]
- Sincik, M.; Candogan, B.N.; Demirtas, C.; Büyükcangaz, H.; Yazgan, S.; Göksoy, A.T. Deficit irrigation of soybean [Glycine max (L.) Merr.] in a sub-humid climate. J. Agron. Crop Sci. 2008, 194, 200–205. [Google Scholar] [CrossRef]
- Candogan, B.N.; Sincik, M.; Buyukcangaz, H.; Demirtas, C.; Goksoy, A.T.; Yazgan, S. Yield, Quality and crop water stress index relationships for deficit-irrigated soybean [Glycine max (L.) Merr.] in sub-humid climatic conditions. Agric. Water Manag. 2018, 118, 113–121. [Google Scholar] [CrossRef]
- Patil, C.S.; Manickam, R. Crop evapotranspiration and crop coefficient of soybean (Glycine max L. Merrill) in Bengaluru, Karnataka. J. Agrometeorol. 2017, 19, 292–293. [Google Scholar]
- Kuo, S.F.; Ho, S.S.; Liu, C.W. Estimation irrigation water requirements with derived crop coefficients for upland and paddy crops in ChiaNan Irrigation Association, Taiwan. Agric. Water Manag. 2006, 82, 433–451. [Google Scholar] [CrossRef]
- Jagtap, S.S.; Jones, J.W. Stability of crop coefficients under different climate and irrigation management practices. Irrig. Sci. 1989, 10, 231–244. [Google Scholar] [CrossRef]
- Tabrizi, M.S.; Masoud, P.; Babazadeh, H. Efficacy of partial root drying technique for optimizing soybean crop production in semi-arid regions. Irrig. Drain. 2012, 61, 80–88. [Google Scholar] [CrossRef]
- Paredes, P.; Wie, Z.; Liu, Y.; Xu, D.; Xin, Y.; Zhang, B.; Pereira, L.S. Performance assessment of the FAO AquaCrop model for soil water, soil evaporation, biomass and yield of soybeans in North China Plain. Agric. Water Manag. 2015, 152, 57–71. [Google Scholar] [CrossRef]
- Irmak, S.; Odhiambo, L.O.; Specht, J.E.; Djaman, K. Hourly and daily single and basal evapotranspiration crop coefficients as a function of growing degree days, days after emergence, leaf area index, fractional green canopy cover, and plant phenology for soybean. Trans. ASABE 2013, 56, 1785–1803. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Liu, H.-Z.; Feng, J.-W. Seasonal and interannual variation of evapotranspiration and energy exchange over different land surfaces in a semi-arid area of China. J. Appl. Meteorol. Climatol. 2012, 51, 1875–1888. [Google Scholar]
- Sadok, W.; Sinclair, T.R. Genetic variability of transpiration response to vapor pressure deficit among soybean (Glycine max [L.] Merr.) genotypes selected from a recombinant inbred line population. Field Crops Res. 2009, 113, 156–160. [Google Scholar] [CrossRef]
- Gilbert, M.E.; Zwieniecki, M.A.; Holbrook, N.M. Independent variation in photosynthetic capacity and stomatal conductance leads to differences in intrinsic water use efficiency in 11 soybean genotypes before and during mild drought. J. Exp. Bot. 2011, 62, 2875–2887. [Google Scholar] [CrossRef]
- Rhine, M.D.; Stevens, G.; Shannon, G.; Wrather, A.; Sleper, D. Yield and nutritional responses of waterlogging of soybean cultivars. Irrig. Sci. 2010, 28, 135–142. [Google Scholar] [CrossRef]
- Katerji, N.; Mastrorilli, M.; Rana, G. Water use efficiency of crops cultivated in the Mediterranean region: Review and analysis. Eur. J. Agron. 2008, 28, 493–507. [Google Scholar] [CrossRef]
- Lathuillière, M.J.; Dalmagro, H.J.; Black, T.A.; de Arruda, P.H.Z.; Hawthorne, I.; Couto, E.G.; Johnson, M.S. Rain-fed and irrigated cropland-atmosphere water fluxes and their implications for agricultural production in Southern Amazonia. Agric. For. Meteorol. 2018, 256–257, 407–419. [Google Scholar] [CrossRef]
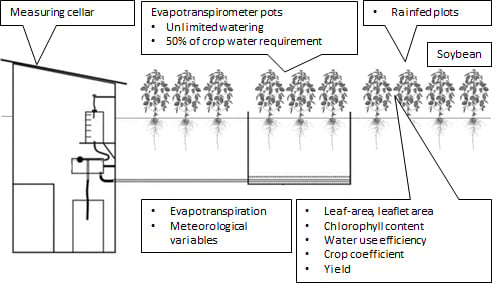
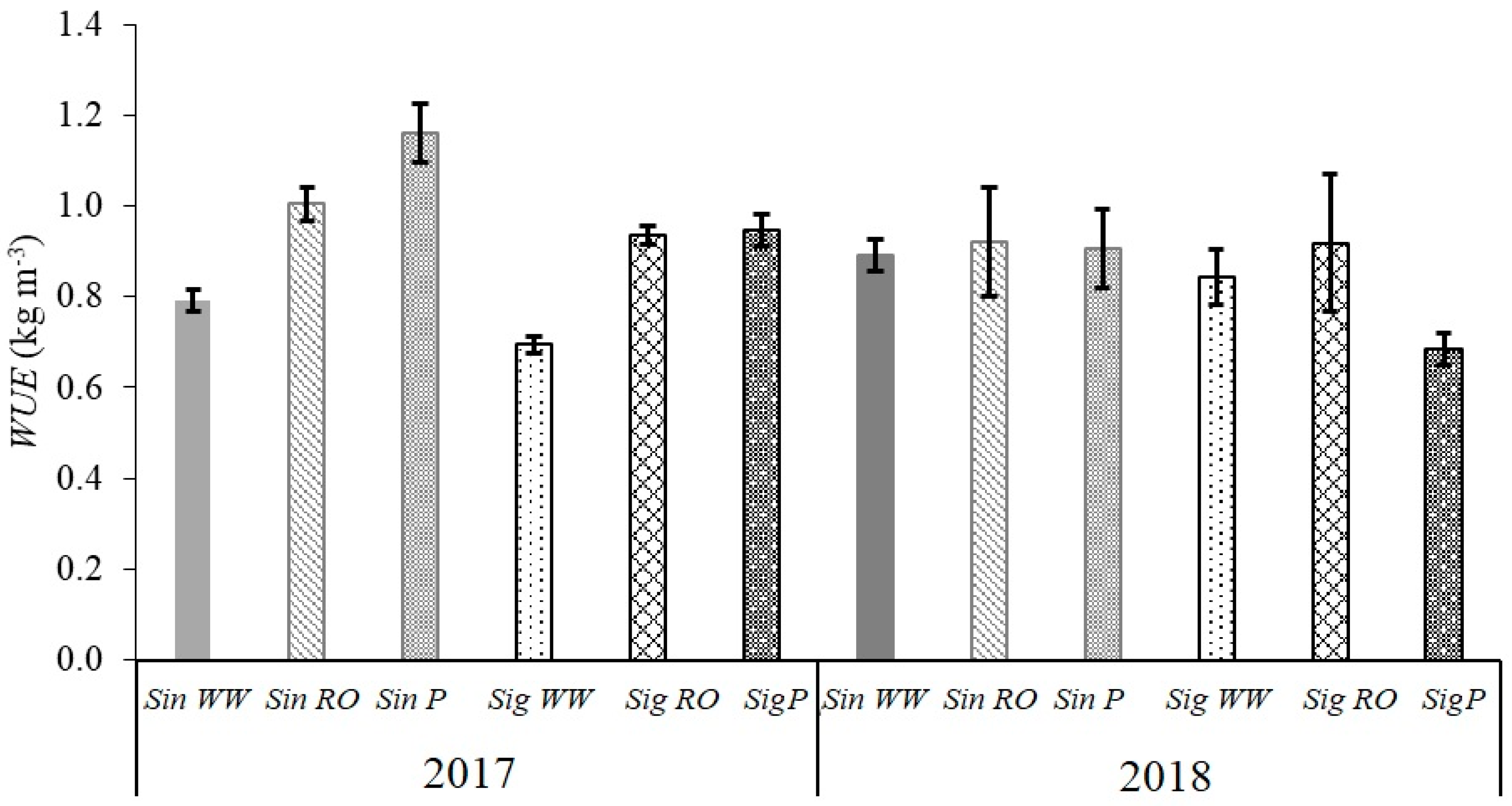
 , pots of water-stressed treatment with Sigalia (Sig RO). In (b) the following abbreviations were used: 2, measuring cellar; 3, US class “A” pan; 4, wind tower with a pyranometer; 5, QLC-50 automatic climate station; 6, evaporation pan with a surface area of 20 m2. The same experimental setup was used in both observation seasons (2017 and 2018). Several plant indicators (phenology, leaf and leaflet areas, chlorophyll index, yield, water use efficiency) were measured in all water and variety treatments (upper part (a): 1 and X). Daily evapotranspiration was measured in (a) 1, 1–12 evapotranspirometer pots. The crop coefficient was derived from these equipment pots. Evapotranspiration totals were also estimated from the field (a). All meteorological variables were derived from observational garden (b).
, pots of water-stressed treatment with Sigalia (Sig RO). In (b) the following abbreviations were used: 2, measuring cellar; 3, US class “A” pan; 4, wind tower with a pyranometer; 5, QLC-50 automatic climate station; 6, evaporation pan with a surface area of 20 m2. The same experimental setup was used in both observation seasons (2017 and 2018). Several plant indicators (phenology, leaf and leaflet areas, chlorophyll index, yield, water use efficiency) were measured in all water and variety treatments (upper part (a): 1 and X). Daily evapotranspiration was measured in (a) 1, 1–12 evapotranspirometer pots. The crop coefficient was derived from these equipment pots. Evapotranspiration totals were also estimated from the field (a). All meteorological variables were derived from observational garden (b).
 , pots of water-stressed treatment with Sigalia (Sig RO). In (b) the following abbreviations were used: 2, measuring cellar; 3, US class “A” pan; 4, wind tower with a pyranometer; 5, QLC-50 automatic climate station; 6, evaporation pan with a surface area of 20 m2. The same experimental setup was used in both observation seasons (2017 and 2018). Several plant indicators (phenology, leaf and leaflet areas, chlorophyll index, yield, water use efficiency) were measured in all water and variety treatments (upper part (a): 1 and X). Daily evapotranspiration was measured in (a) 1, 1–12 evapotranspirometer pots. The crop coefficient was derived from these equipment pots. Evapotranspiration totals were also estimated from the field (a). All meteorological variables were derived from observational garden (b).
, pots of water-stressed treatment with Sigalia (Sig RO). In (b) the following abbreviations were used: 2, measuring cellar; 3, US class “A” pan; 4, wind tower with a pyranometer; 5, QLC-50 automatic climate station; 6, evaporation pan with a surface area of 20 m2. The same experimental setup was used in both observation seasons (2017 and 2018). Several plant indicators (phenology, leaf and leaflet areas, chlorophyll index, yield, water use efficiency) were measured in all water and variety treatments (upper part (a): 1 and X). Daily evapotranspiration was measured in (a) 1, 1–12 evapotranspirometer pots. The crop coefficient was derived from these equipment pots. Evapotranspiration totals were also estimated from the field (a). All meteorological variables were derived from observational garden (b).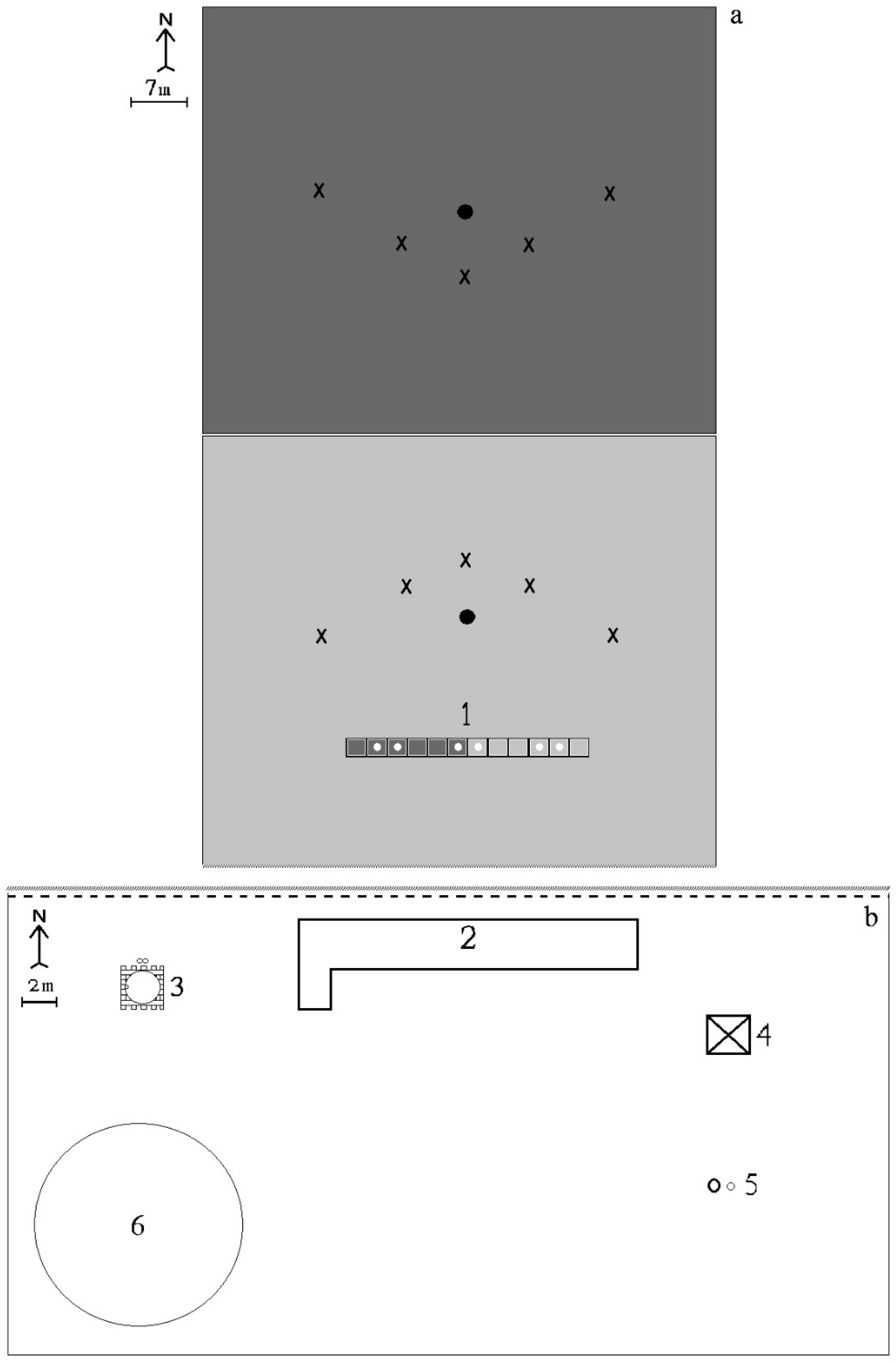


| April | May | June | July | August | September | ||
|---|---|---|---|---|---|---|---|
| Mean air temperature, Ta [°C] | Mean | ||||||
| Climate norm | 10.5 | 15.7 | 18.7 | 20.5 | 20.1 | 15.7 | 16.9 |
| 2017 | 10.8 | 16.6 | 21.2 | 22.3 | 22.8 | 15.1 | 18.1 |
| 2018 | 15.3 | 18.8 | 20.5 | 21.7 | 22.6 | 16.9 | 19.3 |
| Precipitation sum, PR [mm] | Sum | ||||||
| Climate norm | 50.5 | 59.6 | 78.5 | 73.5 | 65.1 | 57.1 | 384.4 |
| 2017 | 20.9 | 38.8 | 61.1 | 53.8 | 32.7 | 140.1 | 347.4 |
| 2018 | 13.4 | 68.4 | 101.2 | 78.9 | 87.1 | 128.7 | 477.7 |
| Vapor pressure deficit, VPD [kPa] | Mean | ||||||
| Climate norm | 3.9 | 5.3 | 6.1 | 7.1 | 6.4 | 3.7 | 5.4 |
| 2017 | 4.3 | 5.5 | 7.6 | 8.6 | 9.2 | 3.1 | 6.4 |
| 2018 | 5.4 | 5.6 | 6.3 | 7.3 | 7.1 | 3.9 | 5.9 |
| Source | Sum of Squares | df | Mean Square | F | p-Value |
|---|---|---|---|---|---|
| Season | 1.85 | 1 | 1.85 | 6.79 | 0.012 |
| Water | 20.41 | 2 | 10.21 | 37.49 | 0.000 |
| Season × water | 3.08 | 2 | 1.54 | 5.66 | 0.006 |
| Error | 14.70 | 54 | 0.27 |
| Kc for Soybean | Studied Seasons | Latitude | Study Site | Reference |
|---|---|---|---|---|
| Latitude below 15° | ||||
| 0.51–1.28 | 3 | 12° N | Bangalore, India | Patil and Manickam (2017) [56] |
| Latitude between 16° and 30° | ||||
| 0.35–1.10 | 1 | 23° N | Taiwan | Kuo et al. (2006) [57] |
| 0.73–1.30 | 1 | 29° N | Gainesville, FL, USA | Jagtap and Jones (1989) [58] |
| 0.19–1.12 | 1 | 30° S | KwaZulu-Natal, South Africa | Mbangiwa et al. (2019) [21] |
| 0.45–1.03 1 | 1 | 30° S | KwaZulu-Natal, South Africa | Mbangiwa et al. (2019) [21] |
| Latitude between 31° and 40° | ||||
| 0.40–1.00 | 2 | 31° S | Salto, Uruguay | Montoya et al. (2017) [38] |
| 0.48–1.02 | 1 | 33° N | Stoneville, MS, USA | Anapalli et al. (2018) [13] |
| 0.62–1.00 | 2 | 33° N | Bekaa Valley, Lebanon | Karam et al. (2005) [8] |
| 1.00 1 | 1 | 35° N | Karaj, Iran | Tabrizi et al. (2012) [59] |
| 0.18–1.18 2 | 3 | 35° N | Bushland, TX, USA | Howell et al. (2006) [35] |
| 0.18–1.00 2 | 4 | 39° N | Daxing, China | Paredes et al. (2015) [60] |
| 0.15–1.08 | 4 | 39° N | Daxin, China | Wei et al. (2015) [51] |
| 0.40–1.14 | 2 | 40° N | Bursa, Turkey | Candogan et al. (2013) [55] |
| Latitude above 41° | ||||
| 0.27–1.03 | 5 | 41° N | Mead, NE, USA | Suyker and Verma (2008) [23] |
| 0.27–1.47 | 3 | 41° N | Nebraska, USA | Irmak et al. (2013) [61] |
| 0.40–1.33 | 4 | 41° N | North Platte, Nebraska, USA | Payero and Irmak (2013) [17] |
| 0.15–1.15 3 | 40–45° N 4 | Central USA | Allen et al. (1998) [62] | |
| 0.19–1.56 | 2 | 46° N | Keszthely, Hungary | In the current study |
| 2017 | 2018 | |||||||
|---|---|---|---|---|---|---|---|---|
| V | R1–R6 | R7–R8 | Mean ± SD | V | R1–R6 | R7–R8 | Mean ± SD | |
| Sin WW | 0.54 ± 0.22 | 1.21 ± 0.16 | 1.08 ± 0.28 | 0.97 ± 0.36 | 0.53 ± 0.12 | 1.00 ± 0.32 | 0.98 ± 0.41 | 0.85 ± 0.36 |
| Sig WW | 0.45 ± 0.24 | 1.23 ± 0.19 | 0.92 ± 0.26 | 0.91 ± 0.39 | 0.54 ± 0.11 | 0.91 ± 0.27 | 0.90 ± 0.35 | 0.79 ± 0.30 |
| Seasons | ET0 (mm) | Ta (°C) | RH (%) | VPD (kPa) | u (m s−1) | Rs (MJ m−2 h−1) | |
|---|---|---|---|---|---|---|---|
| 2017 | Sin WW | 0.60 ** | 0.73 ** | −0.51 ** | 0.76 ** | −0.21 | 0.40 ** |
| Sig WW | 0.56 ** | 0.74 ** | −0.45 ** | 0.73 ** | −0.48 | 0.38 ** | |
| 2018 | Sin WW | 0.63 ** | 0.58 ** | −0.52 ** | 0.67 ** | 0.09 | 0.45 ** |
| Sig WW | 0.69 ** | 0.61 ** | −0.58 ** | 0.74 ** | 0.10 | 0.49 ** |
| Adjusted r2 | F | F sig. | SE of Coefficient | Regression Equation | |
|---|---|---|---|---|---|
| 2017 | |||||
| Sin WW Estimation 1 | 0.574 | 177.677 | 0.000 | Const. = 0.422 VPD = 0.523 | ETR = 6.968VPD-0.015 |
| Sin WW Estimation 2 | 0.615 | 105.712 | 0.000 | Const. = 0.889 VPD = 0.832 Ta = 0.063 | ETR = 4.396VPD + 0.243Ta-3.070 |
| Sig WW Estimation 1 | 0.541 | 155.683 | 0.000 | Const. = 0.922 Ta = 0.044 | ETR = 0.550Ta-6.348 |
| Sig WW Estimation 2 | 0.591 | 95.723 | 0.000 | Const. = 0.982 Ta = 0.070 VPD = 0.920 | ETR = 0.321Ta + 3.772VPD-4.483 |
| 2018 | |||||
| Sin WW Estimation 1 | 0.442 | 113.141 | 0.000 | Const. = 0.362 VPD = 0.523 | ETR = 5.563VPD + 0.687 |
| Sin WW Estimation 2 | 0.468 | 64.429 | 0.000 | Const. = 1.026 VPD = 0.678 Ta = 0.061 | ETR = 4.2VPD + 0.184Ta-2.239 |
| Sig WW Estimation 1 | 0.543 | 172.002 | 0.000 | Const. = 0.292 VPD = 0.423 | ETR = 5.545VPD + 0.426 |
| Sig WW Estimation 2 | 0.574 | 97.970 | 0.000 | Const. = 2.614 VPD = 0.915 RH = 0.028 | ETR = 8.312VPD + 0.094RH-8.354 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anda, A.; Simon, B.; Soos, G.; Teixeira da Silva, J.A.; Farkas, Z.; Menyhart, L. Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers. Atmosphere 2020, 11, 830. https://doi.org/10.3390/atmos11080830
Anda A, Simon B, Soos G, Teixeira da Silva JA, Farkas Z, Menyhart L. Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers. Atmosphere. 2020; 11(8):830. https://doi.org/10.3390/atmos11080830
Chicago/Turabian StyleAnda, Angela, Brigitta Simon, Gabor Soos, Jaime A. Teixeira da Silva, Zsuzsanna Farkas, and Laszlo Menyhart. 2020. "Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers" Atmosphere 11, no. 8: 830. https://doi.org/10.3390/atmos11080830
APA StyleAnda, A., Simon, B., Soos, G., Teixeira da Silva, J. A., Farkas, Z., & Menyhart, L. (2020). Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers. Atmosphere, 11(8), 830. https://doi.org/10.3390/atmos11080830