Next Article in Journal
Study on the Pollution Characteristics and Sources of Ozone in Typical Loess Plateau City
Next Article in Special Issue
Assessment of Soybean Evapotranspiration and Controlled Water Stress Using Traditional and Converted Evapotranspirometers
Previous Article in Journal
Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 11
Issue 6
10.3390/atmos11060554
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region

by
Nikolaos Proutsos
1 and
Dimitris Tigkas
2,*
1
Institute of Mediterranean Forest Ecosystems, Hellenic Agricultural Organisation “DEMETER”, 11528 Athens, Greece
2
Centre for the Assessment of Natural Hazards and Proactive Planning & Laboratory of Reclamation Works and Water Resources Management, National Technical University of Athens, 15780 Athens, Greece
*
Author to whom correspondence should be addressed.
Atmosphere 2020, 11(6), 554; https://doi.org/10.3390/atmos11060554
Submission received: 3 May 2020 / Revised: 20 May 2020 / Accepted: 23 May 2020 / Published: 27 May 2020
(This article belongs to the Special Issue Plant Ecosystems in a Changing World: Monitoring, Modelling and Risk Assessment)
Browse Figures
Versions Notes

Abstract

:
Weather variations affect natural ecosystems, while in regions where climate change is anticipated to intensify extreme events such as droughts, the vitality of vulnerable species may be reduced. The sensitivity of key-species to the climatic conditions may illustrate their adjustability in specific areas and assist decision making towards proper mitigation and adaptation measures. Pinus nigra, commonly known as black pine, is an endemic species, forming many protected habitats in the Mediterranean. In this study, black pine tree-ring data from Greece are used to assess the response of tree growth to specific temperature-related (mean, max. and min. temperature and diurnal temperature range) and water-related (precipitation, evapotranspiration, relative humidity and vapor pressure deficit) meteorological parameters. Additionally, the effect of drought episodes is estimated using indices, including the well-established standardised precipitation index (SPI) and reconnaissance drought index (RDI), as well as two recently proposed modifications, namely, the agricultural SPI (aSPI) and the effective RDI (eRDI). The outcomes reveal several seasonal patterns, emphasising the sensitivity of black pine principally to water-related meteorological parameters, with winter and early spring conditions having a primary role on annual tree growth. Black pine seems to be tolerant to drought in the study region, in terms of its resilience; however, there are indications that multiyear droughts may have prolonged effects on tree growth, which may last approximately three years after drought ends. Additionally, it is derived that both aSPI and eRDI illustrate more efficiently tree growth response to drought, indicating that these modifications provide increased accuracy regarding drought characterisation in the forest environment.

1. Introduction

The Mediterranean region is considered as a climate change and biodiversity hotspot and is expected to face increased challenges due to climate shifts [1,2]. The unique Mediterranean-type ecosystems and several species with distinctive Mediterranean features may be highly affected by extreme climatological events such as droughts, which are anticipated to be intensified in the forthcoming period [3]. The decreasing tree growth of specific species is associated with the warming climate and decreasing precipitation trends observed in the Mediterranean [4,5,6], while reduced water availability and drought have been identified as the main factors limiting tree growth in the region [7,8]. Understanding the response of ecosystems and specific forest species to meteorological factors and drought events may provide essential information regarding the anticipated stress that they may undergo due to adverse climatic conditions, while appropriate mitigation or adaptation measures may be taken.
Pine forests characterise the Mediterranean landscape. Precipitation is of major importance, with a positive effect on radial growth of pines, indicating specific species as dendroclimatically sensitive [9,10,11].
Pinus nigra, commonly known as black pine, is an endemic species, considered of high ecological importance for the Mediterranean. Its forests are dominated by various subspecies [12] presenting high genetic variety, protected by the European Union (priority habitat 9530*-“[Sub-] Mediterranean pine forests with endemic black pines” included in the Annex I of Directive 92/43/EEC). Specifically, in southern Europe, there are comparatively few (169) such forests, with a fragmented distribution area, most of them located in Spain (69), Italy (37) and Greece (35) [13].
Black pine forests have been greatly affected by climate change during the second half of the 20th century [14]. The specific species is considered suitable for studying the effect of climate on its growth, which is useful for several applications such as dendroclimatology assessment [15].
The response of black pine to droughts may vary, depending on the region, the climatic conditions and the altitude [16]. In a study at a low-elevation region, Lebourgeois [17] identified summer drought as a major factor limiting growth in western France, while Fkiri et al. [18] mention that spring droughts cause low annual tree growth in northern Tunisia. Eilmann and Rigling [19] state that black pine cope with drought better than other species, according to the results from a study in an area of Switzerland (650–700 m a.s.l.). Generally, although extreme drought episodes may have significant impacts on its growth [20], black pine is considered a drought tolerant species compared to other pines, especially in higher altitudes [21,22].
Many recent studies related to drought and tree growth of black pine employ drought indices combined with dendroclimatological series. The standardised precipitation index (SPI) and the standardised precipitation-evapotranspiration index (SPEI) have been used along with tree-ring data for long-term drought reconstruction [23], investigation of drought-induced tree vitality decline [22], assessment of drought effects on black pine morphological features [24] and examination of desynchronisation patterns in east and west parts of the Mediterranean [25]. Furthermore, the Palmer drought severity index (PDSI) and its self-calibrated form (sc-PDSI) have been used in studies that focus on soil moisture conditions, assessing drought effects on metabolic processes and tree growth [26,27].
Identifying the sensitivity of a forest species in certain conditions provides important information regarding its adjustability in a specific environment, which is an essential input in restoration and climate change adaptation plans. The main objective of this paper is to assess the growth response of black pine to monthly, seasonal and annual meteorological variations and under drought stress conditions. The evaluation is based on dendroclimatological data from a high-altitude Mediterranean forest located in Greece. The analysis is performed using a multiscalar approach, in order to examine significant seasonal patterns throughout the year. Temperature-related and water-related meteorological factors are employed, including parameters that have been studied to a limited extent for black pine, such as the diurnal temperature range (DTR), the reference evapotranspiration (ETo), the vapor pressure deficit (VPD) and the relative humidity (RH). Two widely known meteorological drought indices, the SPI and the reconnaissance drought index (RDI), are used for identifying meteorological conditions and drought events. The RDI, incorporating both precipitation and reference evapotranspiration, is used for the first time for drought analysis on a species of the genus Pinus. Furthermore, two recently proposed modifications of the aforementioned indices aiming at characterising vegetation-agricultural drought, which have never been applied in a forest environment, are also used and evaluated for their suitability in identifying drought effects on the specific species.

2. Material and Methods

2.1. Overview

The assessment of growth response of black pine to meteorological factors (temperature-related and water-related) and drought was based on tree-ring data acquired from a high-altitude area of southern Greece.
A multi-scalar approach is utilised, involving several timescales (1-month up to 12-month) to identify the role of each examined parameter in different periods of the year. Specifically, reference periods starting from different months are considered (e.g., 12-month period October to September, 6-month period January to June, 3-month period December to February, and 1-month period March), aiming at covering all periods of the year, up to the end-month of annual tree growth (September). For each reference period, the monthly values of the examined factor are either averaged (applies to temperature-related parameters, RH and VPD) or accumulated (applies to the rest of water-related parameters and drought indices), expressing, respectively, the average or total value of the parameter for the corresponding period.
For obtaining a straightforward conceptual association between each parameter and annual tree growth, the hydrological year (October–September) is used as the calculation base, referring to the period coinciding to the start of the rainy season and soil moisture recharge. This selection is further supported by findings of previous studies, demonstrating the association of meteorological conditions during the last months of the previous year with black pine annual growth (e.g., [16,24]).
The relationship between each factor and tree-ring data is assessed based on Pearson correlation coefficient (r), considering two significance levels (p < 0.01 and p < 0.05) along with r values. The parameters are separately correlated for each reference period (78 reference periods per parameter), while the outcomes are presented on a starting-month/timescale matrix. For instance, the matrix cell corresponding to the starting month O (October) and timescale 4 denotes the 4-month reference period October to January.
Several software tools were used in different parts of the analysis. Tree-ring data processing performed with COFECHA, ver. 6.06 (cross dating and quality control) [28] and ARSTAN software, ver. 6.05 (detrending and standardisation) [29]. The drought indices were calculated using the Drought Indices Calculator-DrinC software, ver. 1.7 [30], while the reference evapotranspiration (ETo) was estimated using FAO–ETo Calculator software, ver. 3.1 [31]. The IBM SPSS Statistics package, ver. 23, was used for conducting the statistical analysis [32].

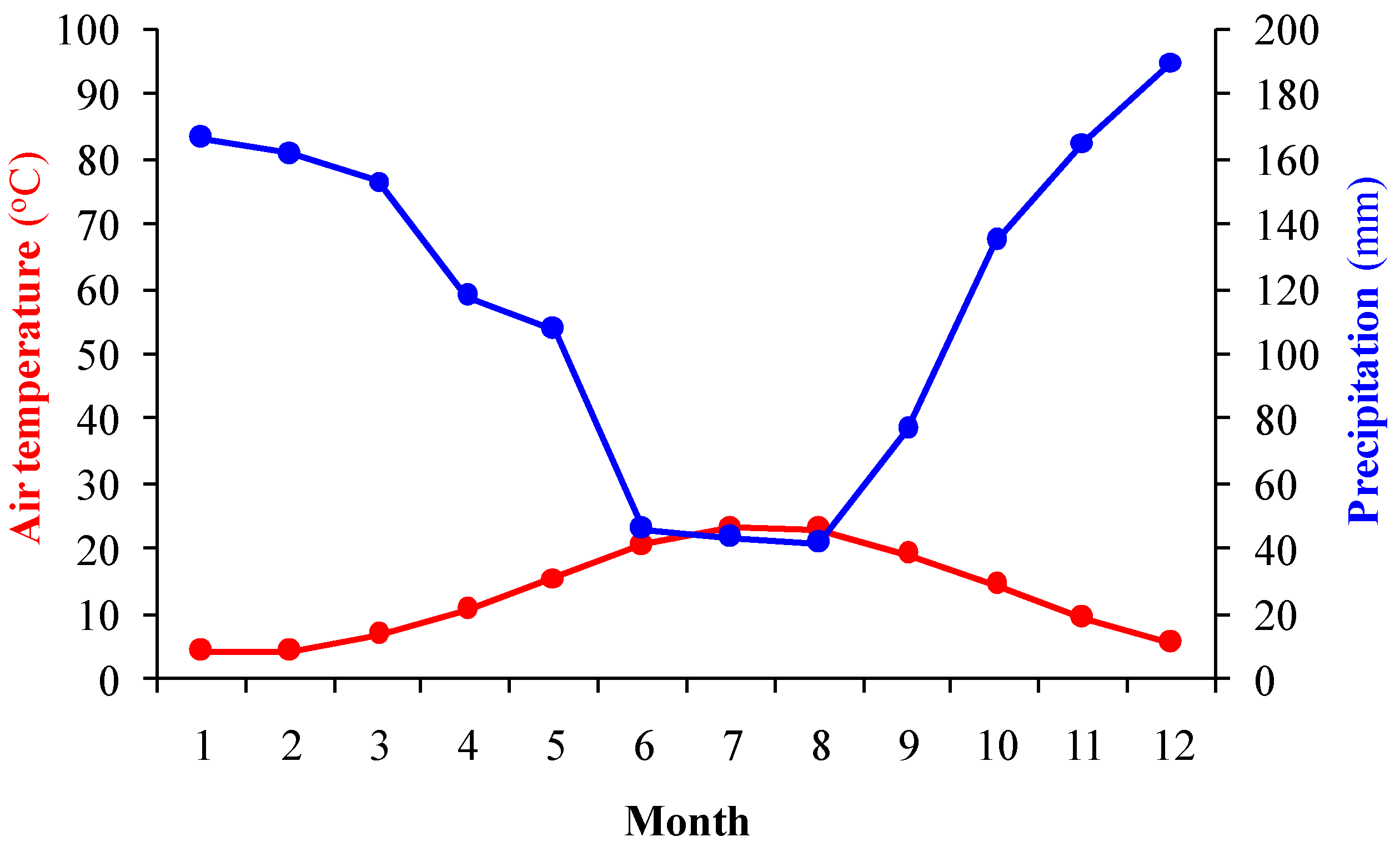
2.2. Study Area

The study site is located at Mt Parnonas in southeast Peloponnese (Greece), within a broader forest area of about 55,650 ha with coordinates 37.22° N–22.63° E and altitude of approximately 1400 m a.s.l. The area is characterised as a Site of Community Importance (SCI) of the NATURA 2000 Network “Oros Parnonas kai periochi Malevis” (code GR2520006) protected by European and Greek regulations [33].
The aridity index [34] for the study area is 1.32, indicating that the region is quite humid with respect to the Mediterranean climate, probably due to the altitudinal position of the site. The annual mean temperature is 13.0 °C, with respective average minimum and maximum values 7.0 and 18.9 °C. The average annual precipitation is 1403 mm, presenting seasonal variations from 131 mm in summer to 517 mm in winter. The average annual ETo is 1077 mm, while the average annual water balance is 326 mm. According to the pluviothermic diagram, the dry season is short (about 1.5 months) prevailing from July to mid-August (Figure 1).
The study area is characterised by high diversity of plant and animal species. It hosts mainly conifer forests of Abies cephalonica and Pinus nigra var. pallasiana and is the only European site for the Juniperus drupacea species. The main habitat types (in terms of the area they occupy, i.e., more than 1000 ha) are the 9530* “(Sub)-Mediterranean pine forests with endemic black pines” in 4201 ha, the 9340 “Querqus ilex and Quercus rotundifolia forests” in 3703 ha, the 9560* “Endemic forests with Juniperus spp” in 3039 ha., the 4090 “Endemic oro-Mediterranean heaths with gorce” in 2035 ha, and the 5420 “Sarcopoterium spinosum phryganas” in 1050 ha. Except for the 9560* and 9530*, which are priority habitat types, in Mt. Parnonas exists also the priority habitat type 6250* “Species-rich Nardus grasslands, on siliceous substrates in mountain areas in Continental Europe”, which occupies only 63 ha. The total area is characterised as a site of high ecological importance, since 85 of the taxa hosted in the area are rare and 12 very rare. Additionally, there are 12 species that are either recently discovered and are new (not yet included in red list, but vulnerable or endangered) or Balkan endemics or with small, scattered population characterised as in danger or under extinction.
In the past, black pine forests covered about 7.5% of Mt Parnonas total area, but a great percentage was destroyed due to extended forest fires in 2007. Restoration was supported by the European Union through the LIFE NATURE funding tool [35].

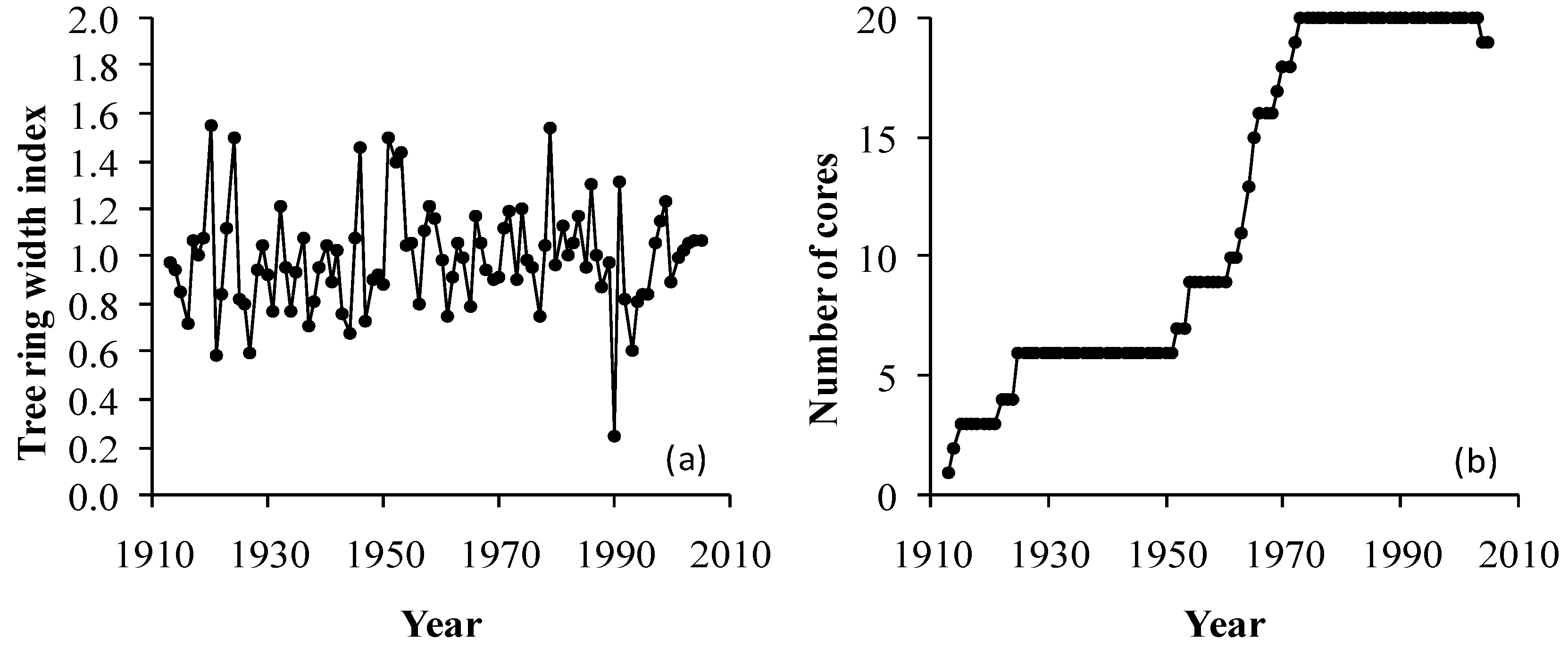
2.3. Tree-Ring Data and Analysis

Dendroclimatology using tree-ring data is a well-established approach for assessing the climatic impact on tree-growth in many species of the genus Pinus [9,36]. Tree sampling was conducted in the study area by extracting two cores from each black pine tree, vertical to each other. A total sample of 20 cores from 10 individual trees was collected. The selected trees were growing in areas with relatively low vegetation density, to minimise the effects due to competition with other individuals. The trees had no visible injuries or signs of phytopathological factors that could have affected their growth [36]. The cores were extracted from the trunk at a height of 1.3 m above ground level. The cores dried naturally in the laboratory for about one month and the ring width and dating were determined by using a Kutschenreiter-Lenz Digital Positiometer type II, with an accuracy of 0.01 mm.
Cross dating and quality control were performed on the produced data series [28]. A total of 1140 rings (from 20 cores) were analysed, covering the period from 1911 to 2005 (95 years). The mean length and intercorrelation of the series were 57.0 and 0.606, respectively, with an average mean sensitivity of 0.319. A double detrending and standardisation procedure was performed to the tree–tree ring width timeseries. The main objective of the process was to identify and remove the trend of the timeseries and part of the variance caused by nonclimatic factors (tree age, tree size, stand dynamics, etc.) [29,37]. Through this procedure, a robust mean tree-ring index standard chronology (tree-ring width index-TRWI) was produced and modelled as an autoregressive process [38]. The timeseries of TRWI and the available number of tree cores per year are presented in Figure 2.

2.4. Meteorological Data and Parameters

Daily meteorological data of the Climate Forecast System Reanalysis [39] were used, referring to the location of the study area (g.c. 37.3° N, 22.5° E). The available dataset includes precipitation, temperature (maximum and minimum), wind speed, relative humidity, and solar radiation parameters, for a period of 31 hydrological years (1979–1980 to 2010–2011). It is noted that the hydrological year in the area follows the typical pattern for the Mediterranean basin, in which the rainy season starts in October.
The FAO Penman–Monteith (FAO-56 PM) method was used to estimate the reference evapotranspiration (ETo), as it is the recommended approach for both RDI and eRDI calculation [40,41,42]. ETo is estimated from the following equation [43]:
E T o = 0.408 Δ ( R n − G ) + γ 900 T + 273 u 2 ( e s − e a ) Δ + γ ( 1 + 0.34 u 2 )
in which Rn is the net radiation at the crop surface (MJ/m2∙day), G is the soil heat flux density (MJ/m2∙day), T is the mean daily air temperature at 2 m height (°C), u2 is the wind speed at 2 m height (m/s), es is the saturation vapour pressure (kPa) estimated by Tetens [44] equation, ea is the actual vapour pressure (kPa), Δ is the slope of the vapour pressure curve (kPa/°C), and γ is the psychrometric constant (kPa/°C).
The diurnal temperature range (DTR) is also employed, expressing the daily changes of temperature and estimated by the difference between the maximum and minimum temperature. Additionally, the vapor pressure deficit (VPD) is used, indicating the atmospheric dryness, combining the effects of mean temperature and relative humidity.

2.5. Drought Indices

The use of drought indices is the typical approach for identifying drought episodes and assessing their main characteristics, i.e., the severity, the duration, and the areal extent [45,46]. Many meteorological drought indices are efficient for examining the temporal (monthly, seasonal, and annual) variation of meteorological parameters (e.g., precipitation, temperature, and evapotranspiration), while they may be also used as climatic indicators [47,48,49,50,51,52,53].
One of the most widely used drought indices worldwide is the SPI. The index is formed through a standardisation procedure, which involves the fitting of precipitation timeseries to the gamma function, defining the relationship of probability to precipitation [54]. According to the established relationship based on the available data, the probability of any precipitation value may be assessed. The latter, together with an estimate of the inverse normal, is used to calculate SPI, expressing the precipitation deviation for a normally distributed probability density. This process may be performed for different accumulation periods (timescales) of precipitation (e.g., 1-month, 3-month, 6-month). The average value of the produced SPI timeseries is zero, allowing the direct identification of wet periods (positive values) and dry periods (negative values). The calculation process of SPI is presented in detail by Edwards and McKee [55].
Another index that has been extensively used during the last decade is the RDI, which is based on the ratio of cumulative precipitation (P) to cumulative reference evapotranspiration (ETo), for specified reference periods [56]. Thus, the initial form of the index (α) for a reference period of k months is calculated as
α k = ∑ j = 1 j = k P j ∑ j = 1 j = k E T o j .
The standardised form of the index (RDIst) is derived from the initial form following a similar procedure to the one used for SPI calculation. More specifically, RDIst is typically calculated by fitting the gamma probability density function to the given frequency distribution of αk, which is then transformed into normal distribution. Therefore, RDIst represents the magnitude of drought in a specific location, based on the probability of occurrence of a drought event, as determined by its corresponding αk value. Details on the calculation approach of RDI may be found in Tsakiris et al. [56] and Tigkas [57].
The main advantages of the above indices are their simple structure and low data requirements, while they can be calculated for several timescales (e.g., 1-, 3-, 6-, 12-month periods). Additionally, their results regarding the magnitude of a drought event can be interpreted uniformly, for any location, according to the classification presented in Table 1. Although these indices have not been specifically designed for assessing the effects of drought on vegetation, there are several studies that have used them for such a purpose with satisfactory results (e.g., [58,59,60,61,62,63]).
Recently, two modifications of SPI and RDI were proposed, namely the agricultural standardised precipitation index (aSPI) [64] and the effective reconnaissance drought index (eRDI) [65]. The main adjustment introduced in both modifications was the substitution of precipitation by effective precipitation, i.e., the portion of total precipitation that can be used productively by the plants for their growth. The classification of Table 1 is also applied for aSPI and eRDI. The anticipated goal of the above modifications is to improve the accuracy in vegetation-agricultural drought characterisation. Additionally, to retain low data requirements, the use of precipitation-based empirical methods for assessing effective precipitation have been proposed [64]. In this study, effective precipitation is estimated by monthly precipitation values, according to percentages corresponding to precipitation classes (Table 2), based on the US Bureau of Reclamation method [64,66].

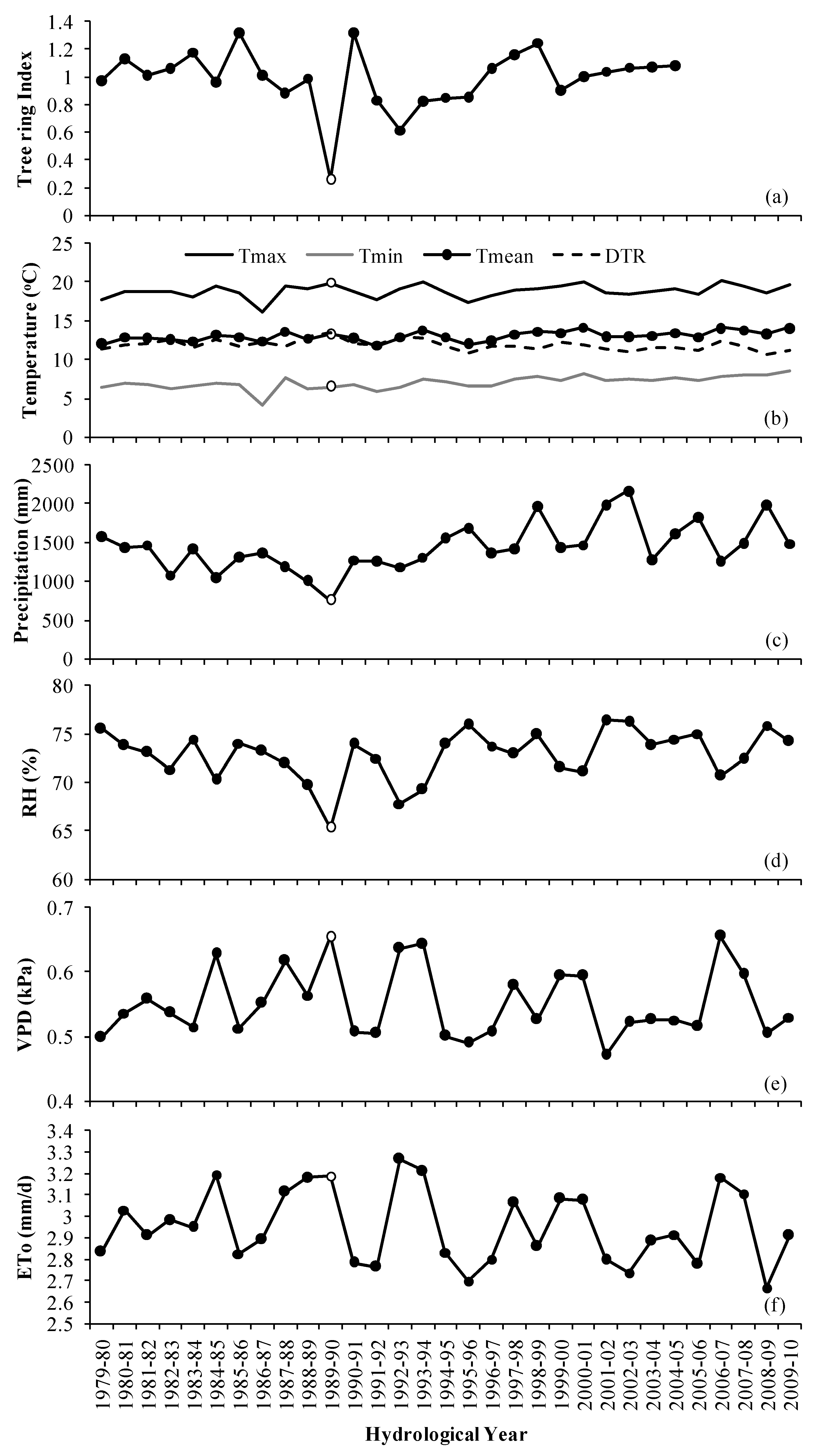
3. Results

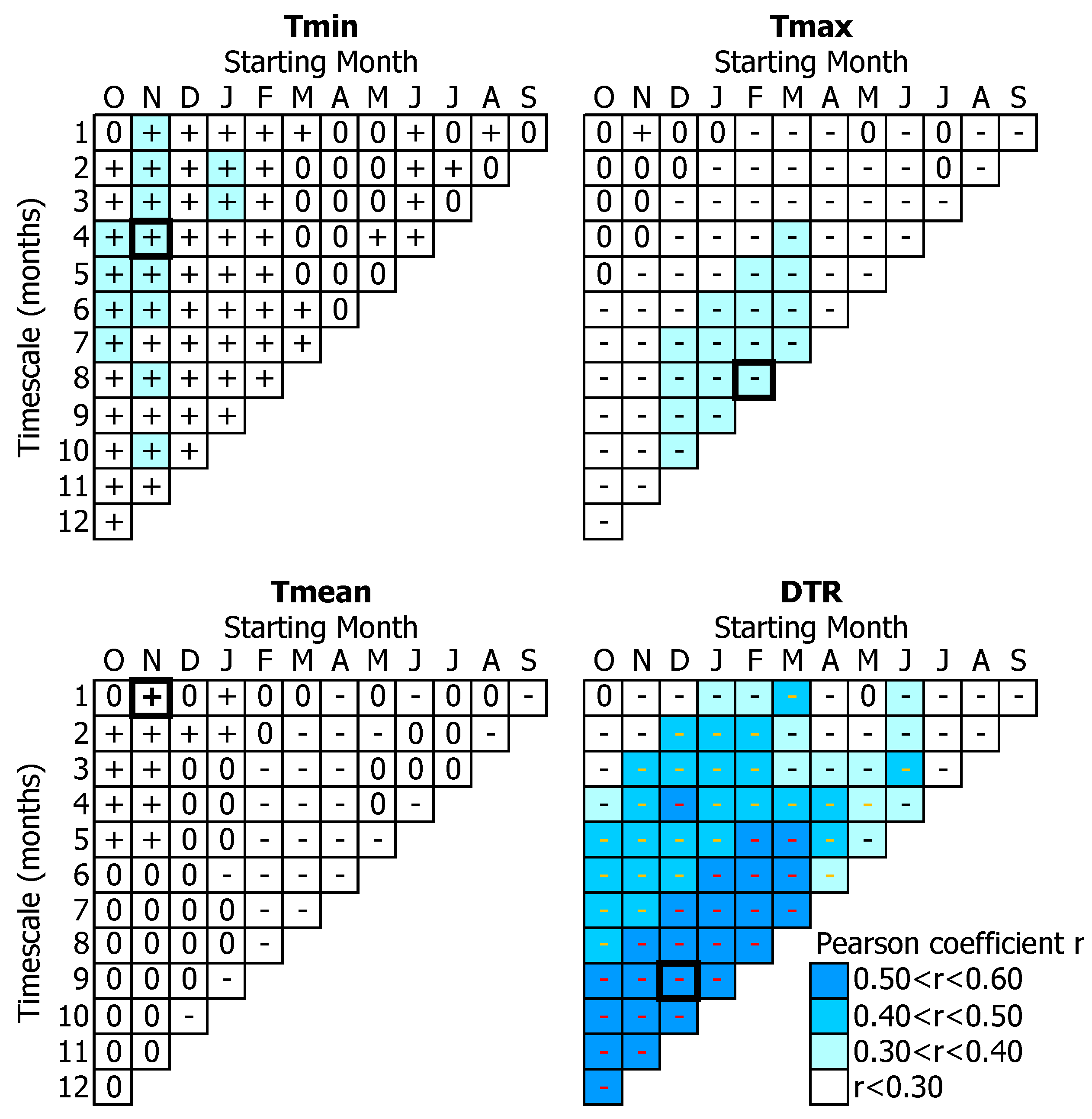
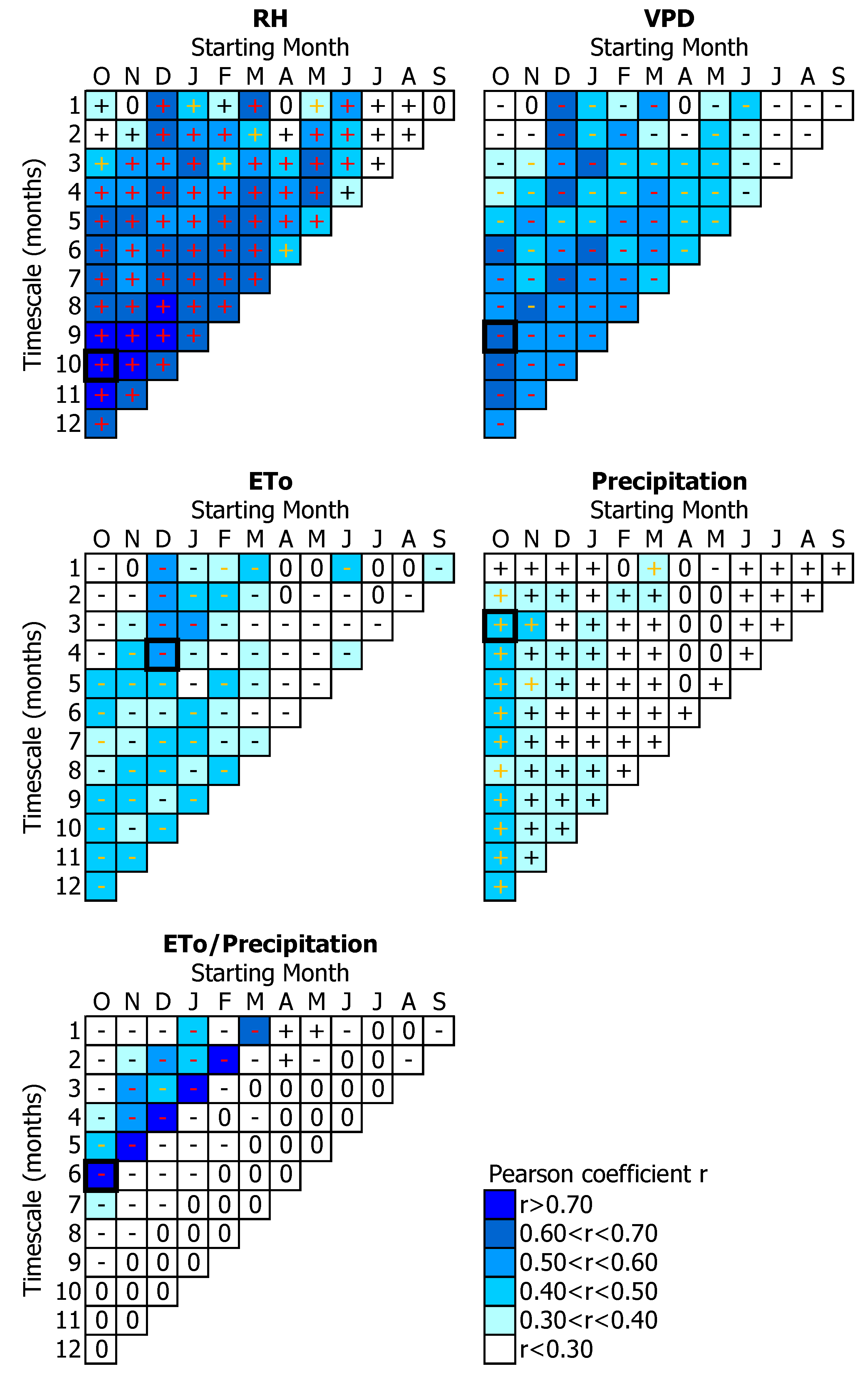
3.1. Tree-Growth Response to Meteorological Factors

The assessment of tree-growth response to the weather conditions prevailing during the study period (1979–2010) indicates that some meteorological parameters have evident effects on the annual growth of the trees, as presented in Figure 3. Precipitation and other water-related parameters, such as RH, VPD and ETo, seem to have a greater influence on tree-ring width, compared to temperature-related parameters. It is noteworthy the small value of TRWI during the year 1989–1990, which is characterised as a year of extreme drought, corresponding to a significantly low amount of precipitation. The impact of the meteorological parameters on annual tree growth is evaluated by examining a great number of correlations, for various reference periods at different timescales, while the results are analysed separately for each parameter.

3.1.1. Temperature-Related Parameters

The Pearson’s correlation coefficients (r) for all temperature-related parameters and TWRI are presented in Figure 4. Based on the results, temperature does not appear to have significant effects on black pine growth in the study area, regardless of the temperature attribute (Tmean, Tmax or Tmin). More specifically, temperature attributes (except DTR) do not present statistically significant correlations with TWRI (p > 0.05) for any reference period. Although no significant relationships have been established, higher Tmin appears to have an overall minor positive effect, while higher Tmax a minor negative effect on tree growth. Tmean presents also nonsignificant positive correlations during autumn and winter, and negative correlations during spring and summer.
In contrast to the other temperature attributes, the results of DTR denote significant negative correlations with TRWI, for several reference periods, especially between December and June. Overall, DTR seems to affect tree growth mostly during winter, spring and early summer. At 1-month timescale, March is the only month presenting significant correlation (r = −0.45, p < 0.05), while the strongest correlation (r = −0.60, p < 0.01) is found for the 9-month period December–August.

3.1.2. Water-Related Parameters

Regarding the effect of water-related parameters on tree growth, the correlations of the annual TRWI with the values of RH, VPD, precipitation, ETo and ETo/P ratio were analysed (Figure 5).
Water-related parameters present a stronger correlation with tree radial growth compared to temperature parameters. RH presents the strongest correlations, with the highest value (r = 0.74, p < 0.01) identified at the 10-month period October–July. Additionally, the respective r values of the average RH for the reference periods November–July, October–May, November–June, December–August, December–July and October–August are also high (r > 0.7, p < 0.01). In general, the effect of RH on TRWI is positive. Based on 1-month timescale analysis, it is derived that RH presents significant positive correlations with TRWI in December, January, March, May and June. The highest correlations are recorded in December and March, with r values 0.61 (p < 0.01) and 0.63 (p < 0.01), respectively.
The VPD effect on tree growth is, in general, negative, regardless of the reference period. All months also present negative correlations with TRWI. The strongest monthly correlation is identified for December (r = −0.60, p < 0.01). The VPD values are also significantly correlated for several reference periods. The strongest correlation (r = −0.66, p < 0.01) between VPD and TRWI is recorded for the 10-month period October–June.
Similar to the VPD, tree growth response to ETo is also negative. The relevant patterns of ETo show significant correlations of the parameter with TRWI at specific reference periods, with the highest r value being identified for the 4-month period December–March (r = −0.55, p < 0.01). The 1-month timescale analysis indicates December as the most influential month for tree radial growth (r = −0.51, p < 0.01).
Precipitation correlates generally positively with TWRI, with the highest r identified for the 3-month period October–December (r = 0.48, p < 0.05). The 1-month timescale analysis indicates that March is the only month with significant correlation between precipitation and TWRI (r = 0.40, p < 0.05).
The combined ratio of reference evapotranspiration to precipitation (ETo/P) shows significant correlations with TWRI, presenting r values greater than 0.7 in specific reference periods. The tree response to increasing ETo/P is generally negative. From the 1-month timescale analysis, March ratio has the greatest influence on tree-growth (r = −0.69, p < 0.01), while January also presents a significant correlation (r = −0.50, p < 0.01). The strongest correlation is identified for the 6-month period October–March (r = −0.75, p < 0.01). It is also noted that the average ETo/P of the 5-month period November–March, the 4-month period December–March, the 3-month period January–March and the 2-month period February–March are also significantly correlated with TRWI, presenting absolute r values greater than 0.7 (p < 0.01).

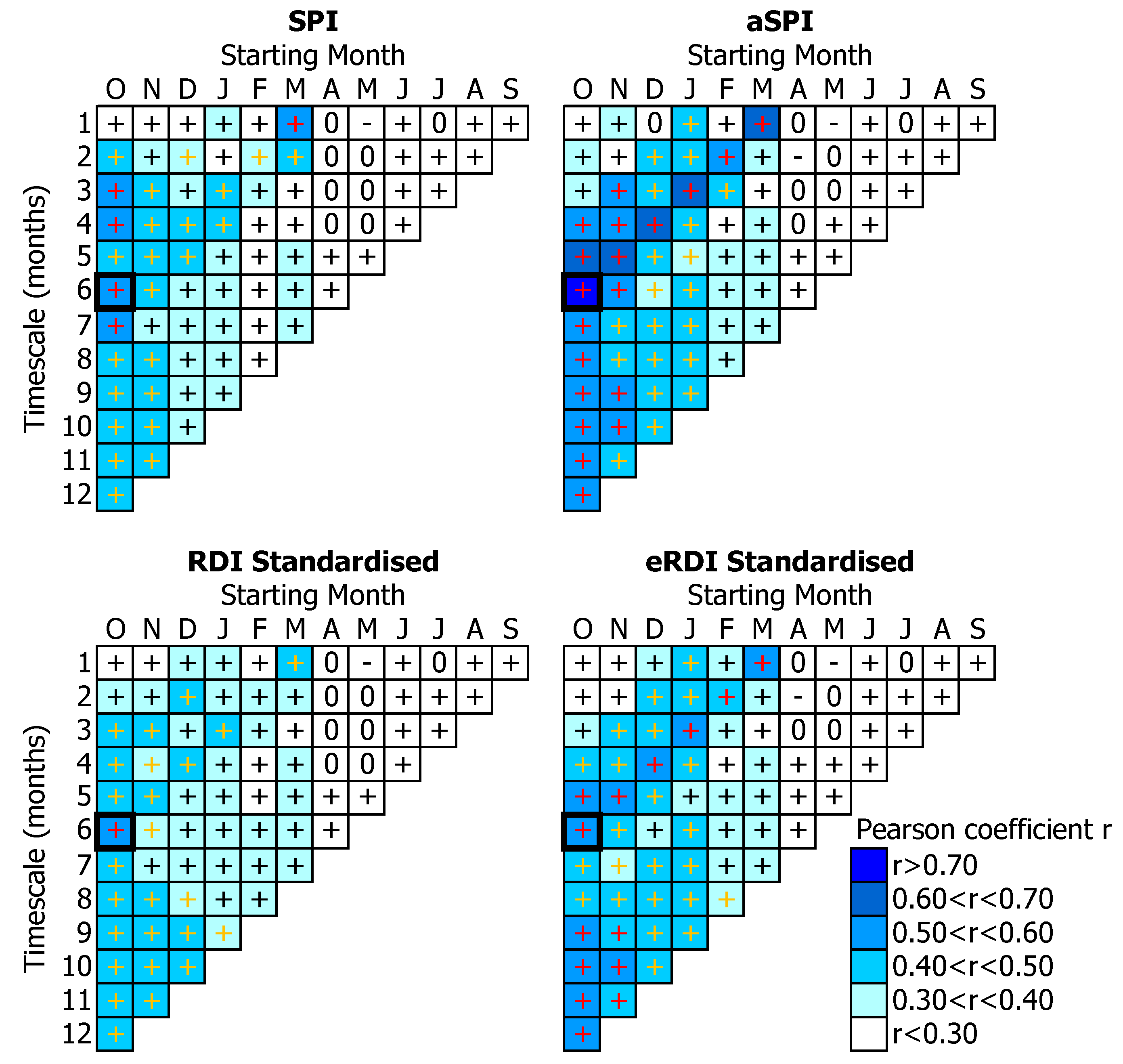
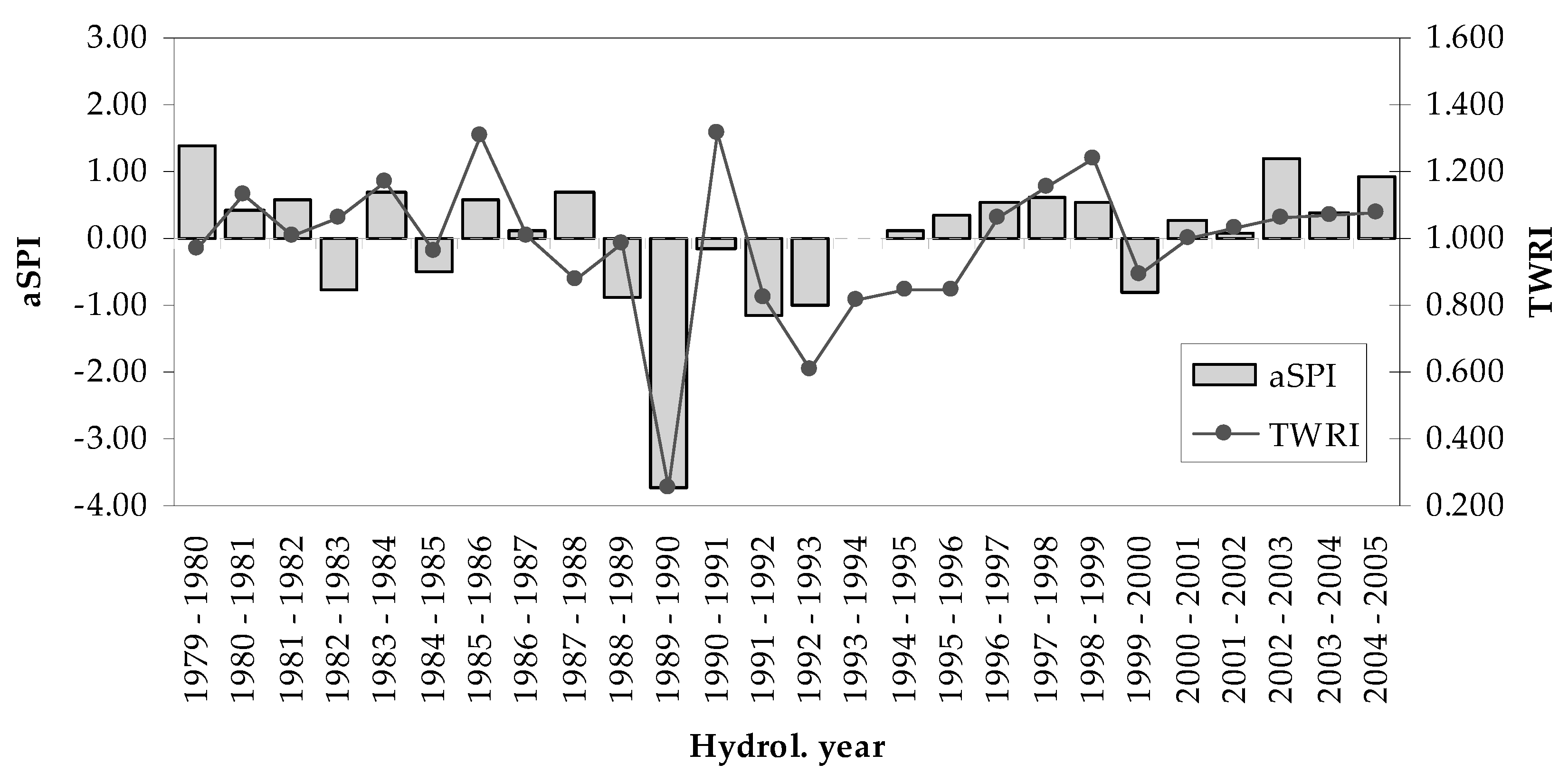
3.2. Tree-Growth Response to Drought

The correlation outcomes between each drought index (SPI, RDI, aSPI and eRDI) and TWRI are shown in Figure 6. Based on the results, all indices appear to have significant correlations with TWRI, for various reference periods. It seems that the conditions during the wet period, from the beginning of the hydrological year (October) until March, have the most direct effects on tree growth. More specifically, the 6-month period October–March presents the highest correlations with annual tree growth, as indicated by all drought indices. The strongest correlation is recorded for aSPI (r = 0.72, p < 0.01) and eRDI (r = 0.58, p < 0.01), whereas SPI and RDI present also high r values (r = 0.53, p < 0.01 and r = 0.51, p < 0.01, respectively). Both aSPI and eRDI appear to be more sensitive in identifying the impact on the annual tree growth compared to SPI and RDI.
The 1-month timescale analysis shows significant effects on tree growth during March and, to a lesser extent, in January. In general, all indices present positive correlations with tree growth, indicating that the trees present increased growth rates as the indices values decrease, i.e., more intense droughts prevailing.
In Figure 7, an indicative comparison of TRWI and drought index values is presented (aSPI, 6-month period October–March), in which the effect of wet-period conditions on tree growth is shown. It is interesting to note that, although there is no clear evidence that single drought episodes have significant effects on tree-growth during the succeeding years, there are indications that multiyear droughts may have a cumulative impact on tree development. For instance, the extreme drought conditions during 1989–1990 caused a significantly low TWRI value during the same year, but in the next year (near-normal drought conditions) tree growth presented a fast recovery. However, during the 2-year drought event in the succeeding years (moderate drought conditions), there was a decline of TWRI that remained in relatively low levels for three more years (near normal drought conditions).

4. Discussion

4.1. Temperature Effects on Tree-Growth

The temperature influence on tree growth is dependent on the local climate. In cool regions, where low temperature is the main limiting factor, the temperature influence is positive [67,68,69], while in regions where high temperatures limit tree growth, the effect of temperature is negative [5,6,70]. Additionally, increased summer temperatures affect mostly the development of the trees growing faster compared to others [71]. In the region of this study, no significant influence of temperature attributes (Tmean, Tmax and Tmin) on tree growth has been shown. However, there seems to be a minor (not significant) positive correlation for Tmin and negative for Tmax, while the correlation for Tmean is positive for winter and autumn and negative for spring and summer. The negative effect of high spring and summer temperatures on black pine has been also identified in other studies [72,73].
In western Mediterranean mountains, Martín-Benito et al. [74] studied black pine growth variations and concluded that higher August–October temperature suppressed tree growth, while December–February temperature enhanced it. In our region, the temperature effect is more evident in specific months or time periods. More specifically, Tmean of November and September appears to be the most influencing on tree annual growth, presenting the highest positive and negative r values, respectively. This indicates that an increase of Tmean in November or a decrease in September may enhance tree growth. Especially, for November, the positive influence is identified also for Tmin and Tmax. However, the greatest influence of Tmin concerns its average value from November to December and it is positive, whereas for Tmax the average value of the period from February to September appears to have a higher negative effect on tree growth. For winter temperatures, a positive influence has also been found [74], suggesting that this is attributed to the higher photosynthetic rates and carbohydrates accumulation [17] favoured by warmer winters, resulting finally in an increase in earlywood width [75]. Such responses to winter temperatures are also identified in other Mediterranean plant species (Erica multiflora and Globularia alypum) [76].
The influence of temperature for specific months or periods is also site dependent, mainly determined by the latitudinal position and altitude. Summer temperatures have been found to have a negative effect on black pine tree growth in western Mediterranean mountains; however, the specific month influence is depended by the latitude [25,74]. June temperature seems to affect the growth in the southernmost regions, June–August temperatures the central ones and July–August temperatures have greater influence at the northern sites, suggesting that significant temperatures in southern sites present a lag on the order of 1–2 months ahead of the northern sites [74].
The temperature-related factor that has a significant impact on black pine in the study area is DTR. Wide daily temperature ranges (high DTR values) seem to stress black pine mostly during late winter, spring and early summer. Although, to the best of our knowledge, the effect of DTR on black pine has not been previously studied, high DTR values, especially during spring and early summer, are also linked to vigour levels of other pines in the Mediterranean [77]. DTR can be related to cloudiness and radiation factors that control photosynthetic activity [78,79,80]. Furthermore, cloudiness (lower DTR values) can be associated with higher precipitation probability and lower evapotranspiration rate [81], which affect water availability. Therefore, low DTR values, especially after the season of the year that precipitation amount typically declines (late winter–spring), may indicate favourable hydroclimatic conditions that enhance tree growth.

4.2. Water Availability Effects on Tree-Growth

Many studies for black pine indicate a negative summer–temperature effect and a positive influence of September–June precipitation on tree radial growth in the Mediterranean [6,14,70,74] and in other European sites [17,82]. Leal et al. [82] also reported a strong positive correlation of black pine ring width with spring-summer precipitation in Austria, while similar results were extracted from studies conducted in Turkey [83], Bosnia and Herzegovina [84] and Albania [85]. Shishkova and Panayotov [86] analysed black pine tree rings from Rhodope mountain in Bulgaria, reporting also a positive effect of precipitation. In the current study, the positive effect of precipitation on tree growth is also identified. The cumulative October to December precipitation appears to have the strongest positive influence on tree growth. Spring precipitation has also a positive impact, with the most significant effects to be related with precipitation during March.
The effect of monthly precipitation on tree growth seems to differ, according to the period under examination. For instance, Martín-Benito et al. [74] mention that the most influential month for black pine trees (in terms of monthly precipitation) was July in the 1900’s but gradually displaced to June around the 1950’s, while changing later to May, with respect to the latitudinal positions of the study sites in the western Mediterranean mountains. Specifically, May–June precipitation had greater influence on tree growth at the southern and central sites and June–July precipitation at the northern sites.
Several studies indicate spring and summer water availability as the main driver of black pine growth in the Mediterranean [18,20,22,75,87,88,89,90,91]. In the present study, the water availability impact was assessed by employing, beyond precipitation, the meteorological parameters RH, VPD, ETo and ETo/P ratio. According to the results, it is indicated that March is the most influential month for black pine growth, with significant correlations and high absolute r values for all the aforementioned parameters. The average ETo/P ratio of the 6-month period October–March has the stronger negative effect on tree growth, indicating that, as the ratio increases (i.e., water availability decreases) the tree growth is suppressed. Although many studies suggest that water availability in summer appears to limit the annual growth of black pine [72,73,92], in our study only June appears to have a significantly strong effect, as identified by RH, VPD and ETo correlations with TWRI.

4.3. Drought Effects on Tree-Growth

Tree-growth response to single-year droughts and, more characteristically, the extreme drought event that occurred during the hydrological year 1989–1990, is in line with other studies regarding the resistance and resilience levels, showing a significant impact during the drought year, but a fast recovery to the previous growth state in the next year. Although a major effect on tree development is anticipated at the time of an extreme event [20], the position of the study site at a relatively high altitude (1400 m) compared to the low-elevation threshold of black pine in the region, provides favourable conditions for such a resilience response [16,21]. On the contrary, studies from low-elevation sites show reduced resilience level, especially after extreme drought episodes (e.g., [17,22]).
The cumulative effect of multiyear droughts, which is indicated by the decreased resilience level after the 1991–1993 drought period, agrees with other studies describing a “legacy effect” for a period of 2 to 3 years after the drought episode [16,20,22]. However, if multiyear drought magnitude remains within a moderate level, this effect does not seem to threaten tree vitality, as it is also discussed by Eilmann et al. [19].
Many studies indicate as a major limiting tree growth factor the summer droughts [16,17,20,75,93], especially affecting low-elevation areas, while others suggest spring droughts as a limiting factor, mainly in western parts of the Mediterranean [18,75]. In the area of the current study, it is interesting to note that winter and early spring conditions play also an important role on tree growth, with a strong correlation between all examined drought indices for the first 6 months of the hydrological year and a higher influence of March conditions.

4.4. Suitability of Drought Indices

All drought indices used in the study identified reasonably well the most important periods that determine the sensitivity of black pine to weather variations and drought conditions. However, the outcomes show that tree-growth response is represented more accurately, when the modified versions of the drought indices (aSPI and eRDI), incorporating effective precipitation, are employed. According to Huxman et al. [94], the water use efficiency of biomes, i.e., the aboveground net primary production to precipitation ratio, decreases as the mean annual precipitation increases; though, during drought years, water use efficiency convergences to a maximum value, which is typical to arid environments. Therefore, the implementation of effective precipitation in the drought indices seems to capture successfully the water use efficiency variations in the forest environment under study.

5. Conclusions

Black pine is an important tree species, endemic in many parts of the Mediterranean. In this study, several meteorological factors for various timescales were examined to determine their influence on black pine tree growth in a high-altitude region of Greece, identifying periods of the year during which the trees are more sensitive to specific factors.
Temperature attributes (Tmin, Tmax and Tmean) do not show any significant correlation with tree growth at the study area. Although not significantly associated, warmer conditions during autumn and winter and cooler conditions during spring and summer seem favourable for tree growth. On the other hand, significant correlations are derived by DTR analysis, revealing that high daily temperature range during winter, spring (mostly in March) and early summer can be associated with negative impacts on tree development.
Precipitation has an anticipated positive impact on tree growth, especially during the first months of the hydrological year (October–December). Spring precipitation has also a positive effect, mainly early in the season. The significance of water availability during the first semester of the hydrological year (especially March) is also indicated by several other parameters (RH, VPD, ETo and ETo/P ratio).
Drought conditions were assessed using two well-established drought indices (SPI and RDI), along with two recent modifications (aSPI and eRDI) that employ effective precipitation, instead of total precipitation, as input parameter. The outcomes show that black pine tree growth may be highly affected during an extreme drought episode, though the resilience of the trees is fast during the next year, which can be attributed to the relatively high altitude. However, multiyear droughts may have prolonged effects, with impacts on tree-growth during the successive years.
Regarding the suitability of the selected drought indices, all had a satisfactory performance in identifying critical periods related to drought effects on tree growth. However, both modified versions performed better than the original indices, with aSPI presenting the best response. This can be associated with the use of effective precipitation that may represent more adequately the efficiency of water use by the trees, thus providing increased accuracy on vegetation-agricultural drought characterisation in the forest ecosystem.
Based on the above, black pine tree growth in the study region present a more direct response to meteorological conditions during winter, early spring and early summer. Water availability during these periods is of high importance, while temperature, apart from daily temperature range, does not seem to be a significant limiting factor. Even though tree growth may be considerably affected during a major drought event, the trees are tolerant in terms of fast recovery within the next growing period. However, possible climate shifts, leading to more intense and prolonged droughts, are anticipated to increase the cumulative effects and endanger the vitality of the species in the region.

Author Contributions

Conceptualization, N.P. and D.T.; methodology, N.P. and D.T.; formal analysis, N.P. and D.T.; investigation, N.P. and D.T.; writing—original draft preparation, N.P. and D.T.; writing—review and editing, N.P. and D.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors wish to acknowledge the contribution of the researchers of the Institute of Mediterranean Forest Ecosystems, K. Tsagari, G. Karetsos and Th. Kritikos, for the collection of tree cores, used for the dendrochronological analysis conducted in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Diffenbaugh, N.S.; Giorgi, F. Climate change hotspots in the CMIP5 global climate model ensemble. Clim. Chang. 2012, 114, 813–822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; Da Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar] [CrossRef] [PubMed]
  3. Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
  4. Tsiros, I.X.; Nastos, P.; Proutsos, N.D.; Tsaousidis, A. Variability of the aridity index and related drought parameters in Greece using climatological data over the last century (1900–1997). Atmos. Res. 2020, 240, 104914. [Google Scholar] [CrossRef]
  5. Penuelas, J.; Hunt, J.M.; Ogaya, R.; Jump, A.S. Twentieth century changes of tree-ring δ13C at the southern range-edge of Fagus sylvatica: Increasing water-use efficiency does not avoid the growth decline induced by warming at low altitudes. Glob. Chang. Biol. 2008, 14, 1076–1088. [Google Scholar] [CrossRef] [Green Version]
  6. Sarris, D.; Christodoulakis, D.; Körner, C. Recent decline in precipitation and tree growth in the eastern Mediterranean. Glob. Chang. Biol. 2007, 13, 1187–1200. [Google Scholar] [CrossRef]
  7. Proutsos, N.; Liakatas, A.; Alexandris, S.; Tsiros, I. Carbon fluxes above a deciduous forest in Greece. Atmósfera 2017, 30, 311–322. [Google Scholar] [CrossRef] [Green Version]
  8. Specht, R. Primary Production in Mediterranean-Climate Ecosystems Regenerating after Fire; Ecosystems of the World; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
  9. Akkemik, Ü. Dendroclimatology of umbrella pine (Pinus pinea L.) in Istanbul, Turkey. Tree-Ring Bull. 2000, 56, 17–20. [Google Scholar]
  10. Cherubini, P. Studio dendroecologico su Pinus pinea L. in due differenti stazioni sulla costa mediterranea in Toscana (Italia). Dendrochronologia 1993, 11, 87–99. [Google Scholar]
  11. Perez-Antelo, A.; Fernandez-Cancio, A. A dendrochronology of Pines pinea in Central Spain. In Proceedings of the Tree Rings and Environment: Proceedings of the International Dendrochronological Symposium, Ystad, Sweden, 3–9 September 1990; pp. 254–255. [Google Scholar]
  12. European Commission. Interpretation Manual of European Union Habitats–EUR28; European Commission, DG Environment: Brussels, Belgium, 2013; Volume 144. [Google Scholar]
  13. Zaghi, D. Management of Natura 2000 Habitats. In 9530*(Sub)-Mediterranean Pine Forests with Endemic Black Pines; European Commission: Brussels, Belgium, 2008; Volume 27. [Google Scholar]
  14. Andreu-Hayles, L.; Merino, E.G.; Macias, M.; Ribas, M.; Bosch, O.; Camarero, J.J. Climate increases regional tree-growth variability in Iberian pine forests. Glob. Chang. Biol. 2007, 13, 804–815. [Google Scholar] [CrossRef]
  15. Szymczak, S.; Joachimski, M.M.; Bräuning, A.; Hetzer, T.; Kuhlemann, J. Are pooled tree ring δ13C and δ18O series reliable climate archives—A case study of Pinus nigra spp. laricio (Corsica/France). Chem. Geol. 2012, 308, 40–49. [Google Scholar] [CrossRef]
  16. Marqués, L.; Camarero, J.J.; Gazol, A.; Zavala, M.A. Drought impacts on tree growth of two pine species along an altitudinal gradient and their use as early-warning signals of potential shifts in tree species distributions. For. Ecol. Manag. 2016, 381, 157–167. [Google Scholar] [CrossRef]
  17. LeBourgeois, F. Climatic signals in earlywood, latewood and total ring width of Corsican pine from western France. Ann. For. Sci. 2000, 57, 155–164. [Google Scholar] [CrossRef] [Green Version]
  18. Fkiri, S.; Guibal, F.; Fady, B.; El Khorchani, A.; Khaldi, A.; Khouja, M.L.; Nasr, Z. Tree-rings to climate relationships in nineteen provenances of four black pines sub-species (Pinus nigra Arn.) growing in a common garden from Northwest Tunisia. Dendrochronologia 2018, 50, 44–51. [Google Scholar] [CrossRef]
  19. Eilmann, B.; Rigling, A. Tree-growth analyses to estimate tree species’ drought tolerance. Tree Physiol. 2012, 32, 178–187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Granda, E.; Camarero, J.J.; Gimeno, T.E.; Martínez-Fernández, J.; Valladares, F. Intensity and timing of warming and drought differentially affect growth patterns of co-occurring Mediterranean tree species. Eur. J. For. Res. 2013, 132, 469–480. [Google Scholar] [CrossRef]
  21. Herrero, A.; Zamora, R. Plant Responses to Extreme Climatic Events: A Field Test of Resilience Capacity at the Southern Range Edge. PLoS ONE 2014, 9, e87842. [Google Scholar] [CrossRef] [PubMed]
  22. Móricz, N.; Garamszegi, B.; Rasztovits, E.; Bidló, A.; Horváth, A.; Jagicza, A.; Illés, G.; Vekerdy, Z.; Somogyi, Z.; Gálos, B. Recent Drought-Induced Vitality Decline of Black Pine (Pinus nigra Arn.) in South-West Hungary—Is This Drought-Resistant Species under Threat by Climate Change? Forests 2018, 9, 414. [Google Scholar] [CrossRef] [Green Version]
  23. Levanič, T.; Popa, I.; Poljanšek, S.; Nechita, C. A 323-year long reconstruction of drought for SW Romania based on black pine (Pinus nigra) tree-ring widths. Int. J. Biometeorol. 2013, 57, 703–714. [Google Scholar] [CrossRef]
  24. Martin-Benito, D.; Beeckman, H.; Cañellas, I. Influence of drought on tree rings and tracheid features of Pinus nigra and Pinus sylvestris in a mesic Mediterranean forest. Eur. J. For. Res. 2013, 132, 33–45. [Google Scholar] [CrossRef]
  25. Sangüesa-Barreda, G.; Camarero, J.J.; Sánchez-Salguero, R.; Gutiérrez, E.; Linares, J.C.; Génova, M.; Ribas, M.; Tíscar, P.A.; López-Sáez, J.A. Droughts and climate warming desynchronize Black pine growth across the Mediterranean Basin. Sci. Total Environ. 2019, 697, 133989. [Google Scholar] [CrossRef]
  26. Shishkova, V.; Panayotov, M. Climate-growth relationship of Pinus nigra tree-ring width chronology from the Rhodope Mountains, Bulgaria. Bulg. J. Agric. Sci. 2013, 19, 225–228. [Google Scholar]
  27. Szymczak, S.; Joachimski, M.M.; Bräuning, A.; Hetzer, T.; Kuhlemann, J. Comparison of whole wood and cellulose carbon and oxygen isotope series from Pinus nigra ssp. laricio (Corsica/France). Dendrochronologia 2011, 29, 219–226. [Google Scholar] [CrossRef]
  28. Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
  29. Cook, E.; Holmes, R. Users Manual for Program ARSTAN; Laboratory of Tree–Ring Research; University of Arizona: Tucson, AZ, USA, 1986. [Google Scholar]
  30. Tigkas, D.; Vangelis, H.; Tsakiris, G. DrinC: A software for drought analysis based on drought indices. Earth Sci. Inform. 2015, 8, 697–709. [Google Scholar] [CrossRef]
  31. FAO. ETo calculator. In Land and Water Digital Media Series No 36; FAO: Rome, Italy, 2009; Available online: http://www.fao.org/land-water/databases-and-software/eto-calculator (accessed on 6 April 2020).
  32. IBM Corp. IBM SPSS Statistics for Windows; Version 23.0; IBM Corp.: Armonk, NY, USA, 2015; Available online: https://www.ibm.com/analytics/spss-statistics-software (accessed on 6 April 2020).
  33. NATURA 2000—Standard Data Forms, Site GR2520006. Available online: http://natura2000.eea.europa.eu/Natura2000/SDF.aspx?site=GR2520006 (accessed on 2 April 2020).
  34. Cherlet, M.; Hutchinson, C.; Reynolds, J.; Hill, J.; Sommer, S.; Von Maltitz, G. World Atlas of Desertification: Rethinking Land Degradation and Sustainable Land Management; Publications Office of the European Union: Brussels, Belgium, 2018. [Google Scholar]
  35. LIFE+ Project PINUS: Restoration of Pinus Nigra Forests on Mount Parnonas (GR2520006) through a Structured Approach. Available online: http://www.parnonaslife.gr/en (accessed on 2 April 2020).
  36. Kuang, Y.-W.; Sun, F.F.; Wen, D.; Zhou, G.; Zhao, P. Tree-ring growth patterns of Masson pine (Pinus massoniana L.) during the recent decades in the acidification Pearl River Delta of China. For. Ecol. Manag. 2008, 255, 3534–3540. [Google Scholar] [CrossRef]
  37. Fritts, H. Tree Rings and Climate; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
  38. Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Springer: Berlin, Germany, 1990. [Google Scholar] [CrossRef]
  39. Fuka, D.R.; Walter, M.T.; MacAlister, C.; DeGaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
  40. Tigkas, D.; Vangelis, H.; Tsakiris, G. Introducing a Modified Reconnaissance Drought Index (RDIe) Incorporating Effective Precipitation. Procedia Eng. 2016, 162, 332–339. [Google Scholar] [CrossRef] [Green Version]
  41. Vangelis, H.; Tigkas, D.; Tsakiris, G. The effect of PET method on Reconnaissance Drought Index (RDI) calculation. J. Arid Environ. 2013, 88, 130–140. [Google Scholar] [CrossRef]
  42. Zarei, A.R.; Mahmoudi, M.R. Evaluation of changes in RDIst index effected by different Potential Evapotranspiration calculation methods. Water Resour. Manag. 2017, 31, 4981–4999. [Google Scholar] [CrossRef]
  43. Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements, FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
  44. Tetens, O. Uber einige meteorologische Begriffe. Z. Geophys. 1930, 6, 297–309. [Google Scholar]
  45. Mishra, A.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
  46. Tsakiris, G.; Loukas, A.; Pangalou, D.; Vangelis, H.; Tigkas, D.; Rossi, G.; Cancelliere, A. Drought characterization. In Drought Management Guidelines Technical Annex; Iglesias, A., Moneo, M., López-Francos, A., Eds.; CIHEAM/EC MEDA Water: Zaragoza, Spain, 2007; pp. 85–102. [Google Scholar]
  47. Al-Faraj, F.A.M.; Scholz, M.; Tigkas, D.; Boni, M. Drought indices supporting drought management in transboundary watersheds subject to climate alterations. Water Policy 2015, 17, 865–886. [Google Scholar] [CrossRef]
  48. Lee, S.; Yoo, S.-H.; Choi, J.-Y.; Bae, S. Assessment of the Impact of Climate Change on Drought Characteristics in the Hwanghae Plain, North Korea Using Time Series SPI and SPEI: 1981–2100. Water 2017, 9, 579. [Google Scholar] [CrossRef] [Green Version]
  49. Li, R.; Tsunekawa, A.; Tsubo, M. Assessment of agricultural drought in rainfed cereal production areas of northern China. Theor. Appl. Clim. 2017, 127, 597–609. [Google Scholar] [CrossRef]
  50. Shokoohi, A.; Morovati, R. Basinwide Comparison of RDI and SPI Within an IWRM Framework. Water Resour. Manag. 2015, 29, 2011–2026. [Google Scholar] [CrossRef]
  51. Tigkas, D.; Vangelis, H.; Tsakiris, G. The RDI as a composite climatic index. Eur. Water 2013, 41, 17–22. [Google Scholar]
  52. Zarch, M.A.A.; Sivakumar, B.; Sharma, A. Droughts in a warming climate: A global assessment of Standardized precipitation index (SPI) and Reconnaissance drought index (RDI). J. Hydrol. 2015, 526, 183–195. [Google Scholar] [CrossRef]
  53. Karavitis, C.; Tsesmelis, D.; Skondras, N.A.; Stamatakos, D.; Alexandris, S.; Fassouli, V.; Vasilakou, C.G.; Oikonomou, P.D.; Gregorič, G.; Grigg, N.S.; et al. Linking drought characteristics to impacts on a spatial and temporal scale. Water Policy 2014, 16, 1172–1197. [Google Scholar] [CrossRef]
  54. McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
  55. Edwards, D.; McKee, T. Characteristics of 20th Century Droughts in the United States at Multiple Time Scales; Climatology Report, 97–2; Department of Atmospheric Sciences, Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
  56. Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional Drought Assessment Based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
  57. Tigkas, D. Drought characterisation and monitoring in regions of Greece. Eur. Water 2008, 23, 29–39. [Google Scholar]
  58. Al-Faraj, F.A.M.; Tigkas, D. Impacts of Multi-year Droughts and Upstream Human-Induced Activities on the Development of a Semi-arid Transboundary Basin. Water Resour. Manag. 2016, 30, 5131–5143. [Google Scholar] [CrossRef]
  59. Bautista-Capetillo, C.; Carrillo, B.; Picazo, G.; Júnez-Ferreira, H. Drought Assessment in Zacatecas, Mexico. Water 2016, 8, 416. [Google Scholar] [CrossRef] [Green Version]
  60. Liberato, M.L.R.; Ramos, A.M.; Gouveia, C.M.; Sousa, P.M.; Russo, A.; Trigo, R.M.; Santo, F.E. Exceptionally extreme drought in Madeira Archipelago in 2012: Vegetation impacts and driving conditions. Agric. For. Meteorol. 2017, 232, 195–209. [Google Scholar] [CrossRef]
  61. Sabau, N.C.; Man, T.E.; Armas, A.; Balaj, C.; Giru, M. Characterization of agricultural droughts using standardized precipitation index (SPI) and bhalme-mooley drought index (BDMI). Environ. Eng. Manag. J. 2015, 14, 1441–1454. [Google Scholar] [CrossRef]
  62. Tigkas, D.; Tsakiris, G. Early Estimation of Drought Impacts on Rainfed Wheat Yield in Mediterranean Climate. Environ. Process. 2015, 2, 97–114. [Google Scholar] [CrossRef] [Green Version]
  63. Zarei, A.R.; Moghimi, M.M.; Bahrami, M. Comparison of reconnaissance drought index (RDI) and effective reconnaissance drought index (eRDI) to evaluate drought severity. Sustain. Water Resour. Manag. 2019, 5, 1345–1356. [Google Scholar] [CrossRef]
  64. Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought characterisation based on an agriculture-oriented standardised precipitation index. Theor. Appl. Clim. 2019, 135, 1435–1447. [Google Scholar] [CrossRef]
  65. Tigkas, D.; Vangelis, H.; Tsakiris, G. An Enhanced Effective Reconnaissance Drought Index for the Characterisation of Agricultural Drought. Environ. Process. 2017, 4, 137–148. [Google Scholar] [CrossRef]
  66. Stamm, G.G. Problems and Procedures in Determining Water Supply Requirements for Irrigation Projects. In Irrigation of Agricultural Lands; Hagan, R.M., Haise, H.R., Edminster, T.W., Eds.; American Society of Agronomy: Madison, WI, USA, 1967; pp. 769–785. [Google Scholar]
  67. D’Arrigo, R.D.; Kaufmann, R.K.; Davi, N.; Jacoby, G.C.; Laskowski, C.; Myneni, R.; Cherubini, P. Thresholds for warming-induced growth decline at elevational tree line in the Yukon Territory, Canada. Glob. Biogeochem. Cycles 2004, 18, GB3021. [Google Scholar] [CrossRef]
  68. Pisaric, M.; Carey, S.K.; Kokelj, S.V.; Youngblut, D. Anomalous 20th century tree growth, Mackenzie Delta, Northwest Territories, Canada. Geophys. Res. Lett. 2007, 34, L05714. [Google Scholar] [CrossRef]
  69. Wilmking, M.; Juday, G.P.; Barber, V.A.; Zald, H.S.J. Recent climate warming forces contrasting growth responses of white spruce at treeline in Alaska through temperature thresholds. Glob. Chang. Biol. 2004, 10, 1724–1736. [Google Scholar] [CrossRef]
  70. Macias, M.; Andreu, L.; Bosch, O.; Camarero, J.J.; Gutiérrez, E. Increasing Aridity is Enhancing Silver Fir Abies Alba Mill.) Water Stress in its South-Western Distribution Limit. Clim. Chang. 2006, 79, 289–313. [Google Scholar] [CrossRef]
  71. Barber, V.A.; Juday, G.P.; Finney, B.P. Reduced growth of Alaskan white spruce in the twentieth century from temperature-induced drought stress. Nature 2000, 405, 668–673. [Google Scholar] [CrossRef] [PubMed]
  72. Klesse, S.; Ziehmer, M.M.; Rousakis, G.; Trouet, V.; Frank, D. Synoptic drivers of 400 years of summer temperature and precipitation variability on Mt. Olympus, Greece. Clim. Dyn. 2015, 45, 807–824. [Google Scholar] [CrossRef]
  73. Martin-Benito, D.; Kint, V.; Del Río, M.; Muys, B.; Cañellas, I. Growth responses of West-Mediterranean Pinus nigra to climate change are modulated by competition and productivity: Past trends and future perspectives. For. Ecol. Manag. 2011, 262, 1030–1040. [Google Scholar] [CrossRef]
  74. Martin-Benito, D.; Del Río, M.; Cañellas, I. Black pine (Pinus nigra Arn.) growth divergence along a latitudinal gradient in Western Mediterranean mountains. Ann. For. Sci. 2010, 67, 401. [Google Scholar] [CrossRef]
  75. Martin-Benito, D.; Cherubini, P.; Del Río, M.; Cañellas, I. Growth response to climate and drought in Pinus nigra Arn. trees of different crown classes. Trees 2008, 22, 363–373. [Google Scholar] [CrossRef]
  76. Penuelas, J.; Gordon, C.; Llorens, L.; Nielsen, T.; Tietema, A.; Beier, C.; Bruna, P.; Emmett, B.; Estiarte, M.; Gorissen, A. Nonintrusive Field Experiments Show Different Plant Responses to Warming and Drought Among Sites, Seasons, and Species in a North-South European Gradient. Ecosystems 2004, 7, 598–612. [Google Scholar] [CrossRef]
  77. Büntgen, U.; Martínez-Peña, F.; Aldea, J.; Rigling, A.; Fischer, E.M.; Camarero, J.J.; Hayes, M.J.; Fatton, V.; Egli, S. Declining pine growth in Central Spain coincides with increasing diurnal temperature range since the 1970s. Glob. Planet. Chang. 2013, 107, 177–185. [Google Scholar] [CrossRef]
  78. Gimeno, T.E.; Camarero, J.J.; Granda, E.; Pías, B.; Valladares, F. Enhanced growth of Juniperus thurifera under a warmer climate is explained by a positive carbon gain under cold and drought. Tree Physiol. 2012, 32, 326–336. [Google Scholar] [CrossRef] [Green Version]
  79. Gu, L.; Baldocchi, D.D.; Wofsy, S.C.; Munger, J.W.; Michalsky, J.J.; Urbanski, S.P.; Boden, T.A. Response of a Deciduous Forest to the Mount Pinatubo Eruption: Enhanced Photosynthesis. Science 2003, 299, 2035–2038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  80. Proutsos, N.; Liakatas, A.; Alexandris, S. Ratio of photosynthetically active to total incoming radiation above a Mediterranean deciduous oak forest. Theor. Appl. Clim. 2019, 137, 2927–2939. [Google Scholar] [CrossRef]
  81. Easterling, D.R.; Kang, S.M.; Hofmann, A.; Le, D.; Springer, M.L.; Stock, P.; Blau, H.M. Maximum and Minimum Temperature Trends for the Globe. Science 1997, 277, 364–367. [Google Scholar] [CrossRef] [Green Version]
  82. Leal, S.; Eamus, D.; Grabner, M.; Wimmer, R.; Cherubini, P. Tree rings of Pinus nigra from the Vienna basin region (Austria) show evidence of change in climatic sensitivity in the late 20th century. Can. J. For. Res. 2008, 38, 744–759. [Google Scholar] [CrossRef]
  83. Akkemik, Ü.; Aras, A. Reconstruction (1689–1994 AD) of April–August precipitation in the southern part of central Turkey. Int. J. Climatol. J. R. Meteorol. Soc. 2005, 25, 537–548. [Google Scholar] [CrossRef]
  84. Poljanšek, S.; Ceglar, A.; Levanič, T. Long term January–March and May–August temperature reconstructions from tree-ring records from Bosnia and Herzegovina. Clim. Past Discuss. 2012, 8, 4401–4442. [Google Scholar] [CrossRef]
  85. Levanič, T.; Toromani, E. Austrian pine (Pinus nigra Arnold.) tree-ring width chronology from northeast Albania–preliminary results. In Proceedings of the Conference: TRACE–Tree rings in Archaeology, Climatology and Ecology, Otočec, Slovenija, 22–25 April 2010; pp. 104–109. [Google Scholar]
  86. Panayotov, M.P.; Zafirov, N.; Cherubini, P. Fingerprints of extreme climate events in Pinus sylvestris tree rings from Bulgaria. Trees 2013, 27, 211–227. [Google Scholar] [CrossRef] [Green Version]
  87. Guada, G.; Camarero, J.J.; Sánchez-Salguero, R.; Cerrillo, R.M.N. Limited Growth Recovery after Drought-Induced Forest Dieback in Very Defoliated Trees of Two Pine Species. Front. Plant Sci. 2016, 7, 859. [Google Scholar] [CrossRef]
  88. Herguido, E.; Granda, E.; Benavides, R.; García-Cervigón, A.I.; Camarero, J.J.; Valladares, F.; Sevillano, E.H. Contrasting growth and mortality responses to climate warming of two pine species in a continental Mediterranean ecosystem. For. Ecol. Manag. 2016, 363, 149–158. [Google Scholar] [CrossRef]
  89. Janssen, E.; Kint, V.; Bontemps, J.-D.; Ozkan, K.; Mert, A.; Köse, N.; Içel, B.; Muys, B. Recent growth trends of black pine (Pinus nigra J.F. Arnold) in the eastern mediterranean. For. Ecol. Manag. 2018, 412, 21–28. [Google Scholar] [CrossRef]
  90. Martin-Benito, D.; Del Río, M.; Heinrich, I.; Helle, G.; Cañellas, I. Response of climate-growth relationships and water use efficiency to thinning in a Pinus nigra afforestation. For. Ecol. Manag. 2010, 259, 967–975. [Google Scholar] [CrossRef]
  91. Sánchez-Salguero, R.; Navarro-Cerrillo, R.M.; Camarero, J.J.; Fernández-Cancio, Á. Selective drought-induced decline of pine species in southeastern Spain. Clim. Chang. 2012, 113, 767–785. [Google Scholar] [CrossRef]
  92. LeBourgeois, F.; Mérian, P.; Courdier, F.; Ladier, J.; Dreyfus, P. Instability of climate signal in tree-ring width in Mediterranean mountains: A multi-species analysis. Trees 2012, 26, 715–729. [Google Scholar] [CrossRef]
  93. Doğan, M.; Köse, N. Influence of Climate on Radial Growth of Black Pine on the Mountain Regions of Southwestern Turkey. Plants 2019, 8, 276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  94. Huxman, T.E.; Smith, M.D.; Fay, P.A.; Knapp, A.K.; Shaw, M.R.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Zak, J.C.; Weltzin, J.F.; et al. Convergence across biomes to a common rain-use efficiency. Nature 2004, 429, 651–654. [Google Scholar] [CrossRef] [PubMed]
Atmosphere 11 00554 g001 550
Figure 1. Pluviothermic diagram of the study area.
Figure 1. Pluviothermic diagram of the study area.
Atmosphere 11 00554 g001
Atmosphere 11 00554 g002 550
Figure 2. Timeseries of tree-ring width index (TRWI) (a) and available number of tree cores per year (b).
Figure 2. Timeseries of tree-ring width index (TRWI) (a) and available number of tree cores per year (b).
Atmosphere 11 00554 g002
Atmosphere 11 00554 g003 550
Figure 3. Interannual changes of (a) TRWI, (b) Tmin, Tmean, Tmax and diurnal temperature range (DTR), (c) precipitation, (d) RH, (e) VPD and (f) ETo for the hydrological years from 1979–1980 to 2009–2010.
Figure 3. Interannual changes of (a) TRWI, (b) Tmin, Tmean, Tmax and diurnal temperature range (DTR), (c) precipitation, (d) RH, (e) VPD and (f) ETo for the hydrological years from 1979–1980 to 2009–2010.
Atmosphere 11 00554 g003
Atmosphere 11 00554 g004 550
Figure 4. Pearson coefficients (r) derived from the correlation of annual TRWI with Tmin, Tmean, Tmax and DTR at different timescales. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Figure 4. Pearson coefficients (r) derived from the correlation of annual TRWI with Tmin, Tmean, Tmax and DTR at different timescales. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Atmosphere 11 00554 g004
Atmosphere 11 00554 g005 550
Figure 5. Pearson coefficients (r) derived from the correlation of annual TRWI with relative humidity (RH), vapour pressure deficit (VPD), evapotranspiration (ETo), precipitation (P) and ETo/P. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Figure 5. Pearson coefficients (r) derived from the correlation of annual TRWI with relative humidity (RH), vapour pressure deficit (VPD), evapotranspiration (ETo), precipitation (P) and ETo/P. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Atmosphere 11 00554 g005
Atmosphere 11 00554 g006 550
Figure 6. Pearson coefficients (r) derived from the correlation of annual TRWI with SPI, aSPI, RDI and eRDI drought indices. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Figure 6. Pearson coefficients (r) derived from the correlation of annual TRWI with SPI, aSPI, RDI and eRDI drought indices. The positive correlations are indicated with “+”, the negative with “-” and the negligible (−0.1 < r < 0.1) with “0”. The significance level is indicated with red (p < 0.01), orange (p < 0.05) or black (not significant) signs, while the strongest correlation (highest absolute r value) per parameter is marked with broader line.
Atmosphere 11 00554 g006
Atmosphere 11 00554 g007 550
Figure 7. Comparison between TWRI and 6-month (October–March) aSPI for the period 1979–2005.
Figure 7. Comparison between TWRI and 6-month (October–March) aSPI for the period 1979–2005.
Atmosphere 11 00554 g007
Table
Table 1. Classification of drought conditions according to standardised precipitation index (SPI), agricultural SPI (aSPI) and standardised forms of reconnaissance drought index (RDIst) and effective RDI (eRDIst).
Table 1. Classification of drought conditions according to standardised precipitation index (SPI), agricultural SPI (aSPI) and standardised forms of reconnaissance drought index (RDIst) and effective RDI (eRDIst).
Drought Index ValueCategory
≥2.00Extremely wet
1.50 to 1.99Severely wet
1.00 to 1.49Moderately wet
0 to 0.99Near normal (mildly wet)
0 to −0.99Near normal (mild drought)
−1.00 to −1.49Moderate drought
−1.50 to −1.99Severe drought
≤−2Extreme drought
Table
Table 2. Monthly precipitation classes and corresponding percentage for estimating effective precipitation based on US Bureau of Reclamation method.
Table 2. Monthly precipitation classes and corresponding percentage for estimating effective precipitation based on US Bureau of Reclamation method.
Monthly Precipitation Class (mm)Effective Precipitation (% of Precipitation)
0.0–25.490–100
25.4–50.885–95
50.8–76.275–90
76.2–101.650–80
101.6–127.030–60
127.0–152.410–40
>152.40–10

Share and Cite

MDPI and ACS Style

Proutsos, N.; Tigkas, D. Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region. Atmosphere 2020, 11, 554. https://doi.org/10.3390/atmos11060554

AMA Style

Proutsos N, Tigkas D. Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region. Atmosphere. 2020; 11(6):554. https://doi.org/10.3390/atmos11060554

Chicago/Turabian Style

Proutsos, Nikolaos, and Dimitris Tigkas. 2020. "Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region" Atmosphere 11, no. 6: 554. https://doi.org/10.3390/atmos11060554

APA Style

Proutsos, N., & Tigkas, D. (2020). Growth Response of Endemic Black Pine Trees to Meteorological Variations and Drought Episodes in a Mediterranean Region. Atmosphere, 11(6), 554. https://doi.org/10.3390/atmos11060554

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop