Disdrometer, Polarimetric Radar, and Condensation Nuclei Observations of Supercell and Multicell Storms on 11 June 2018 in Eastern Nebraska
Abstract
1. Introduction
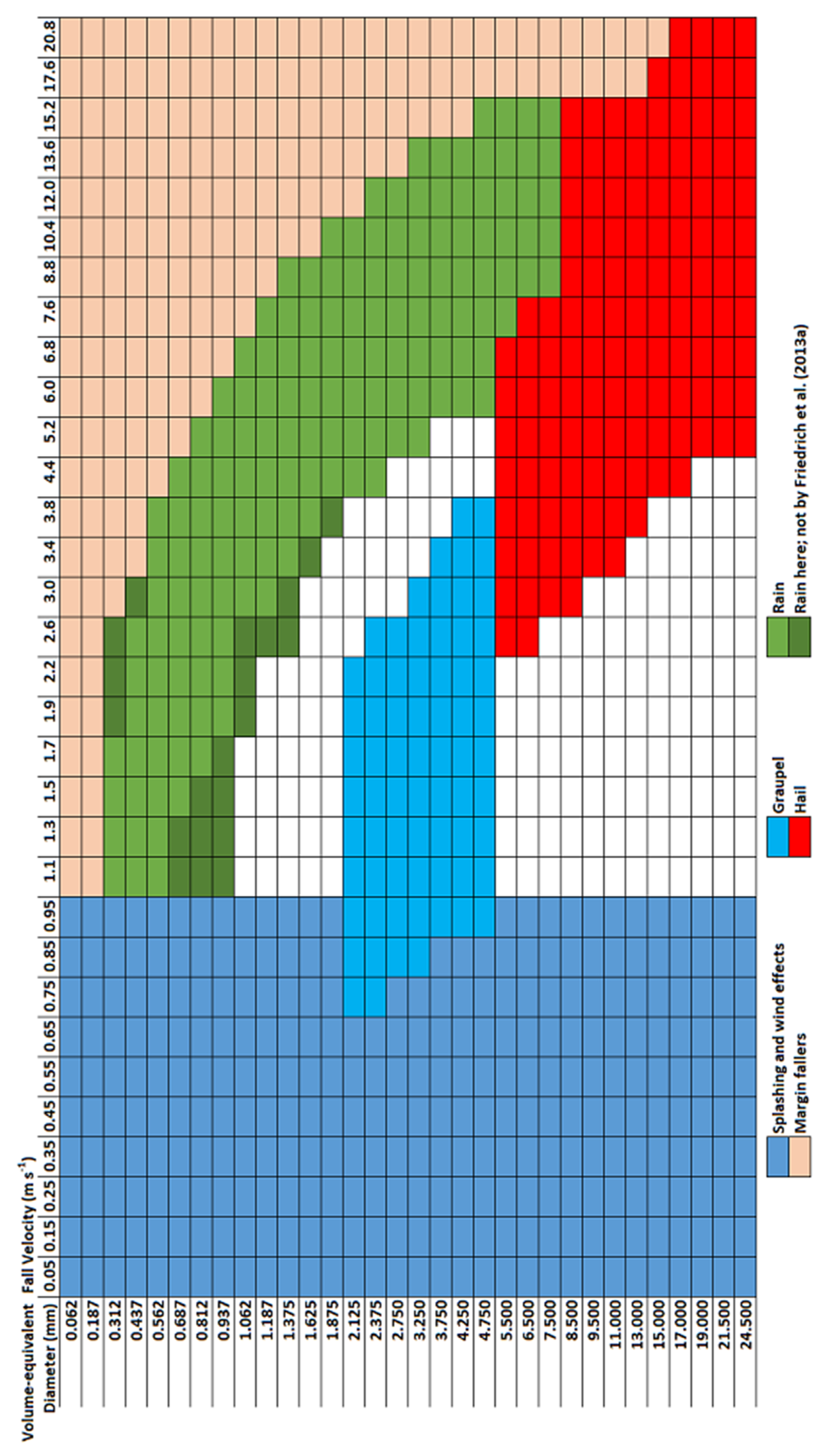
2. Data and Methods
3. Results
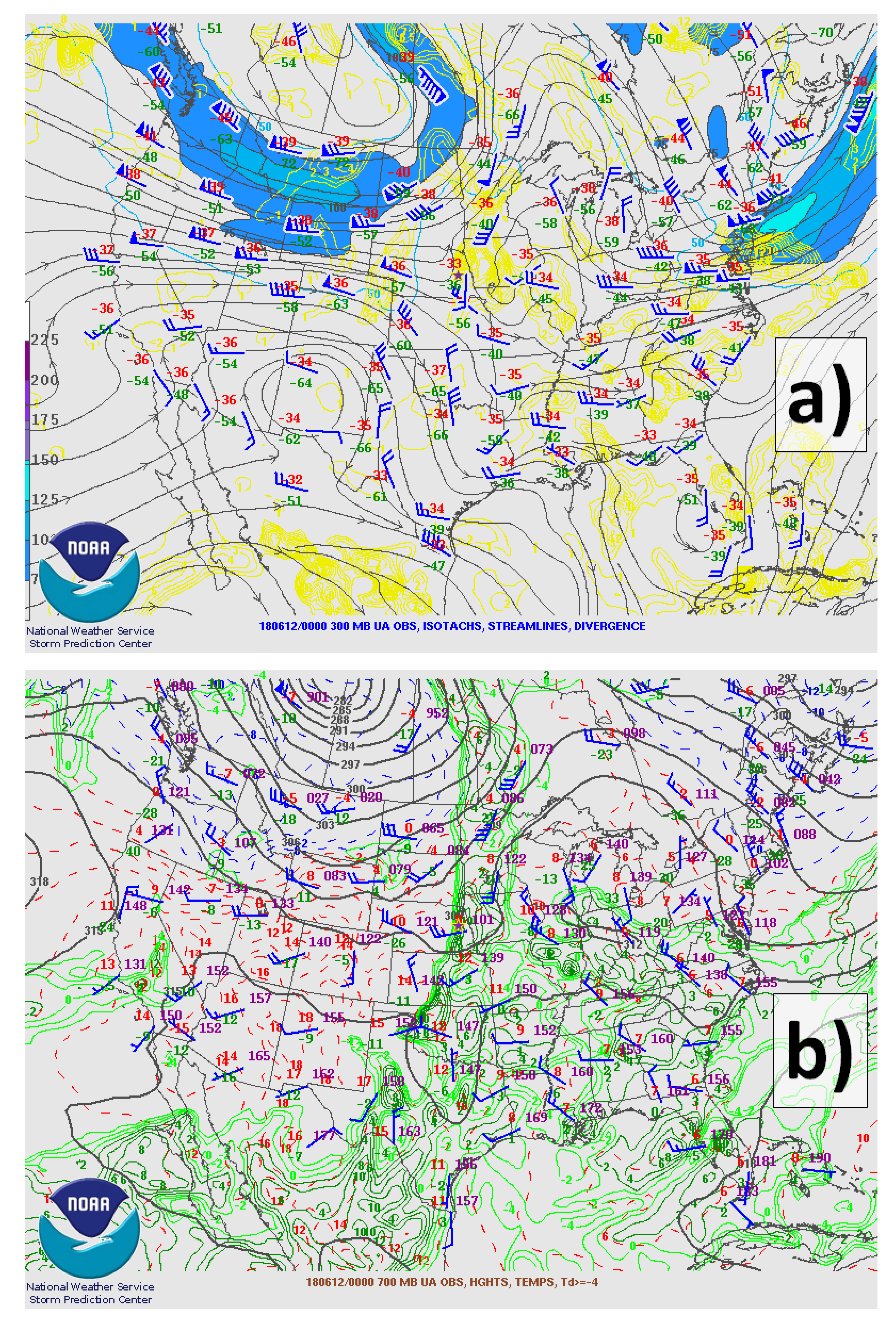
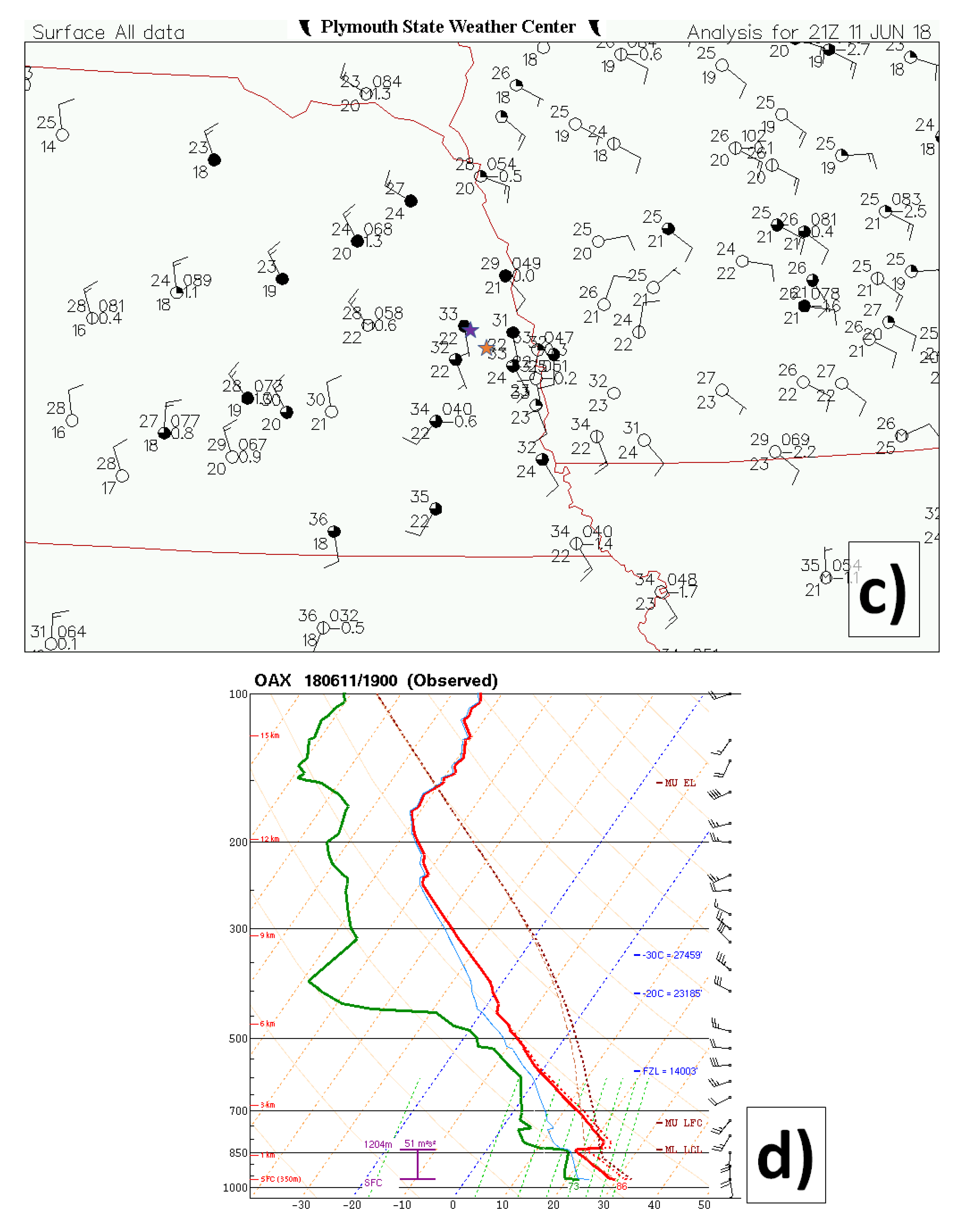
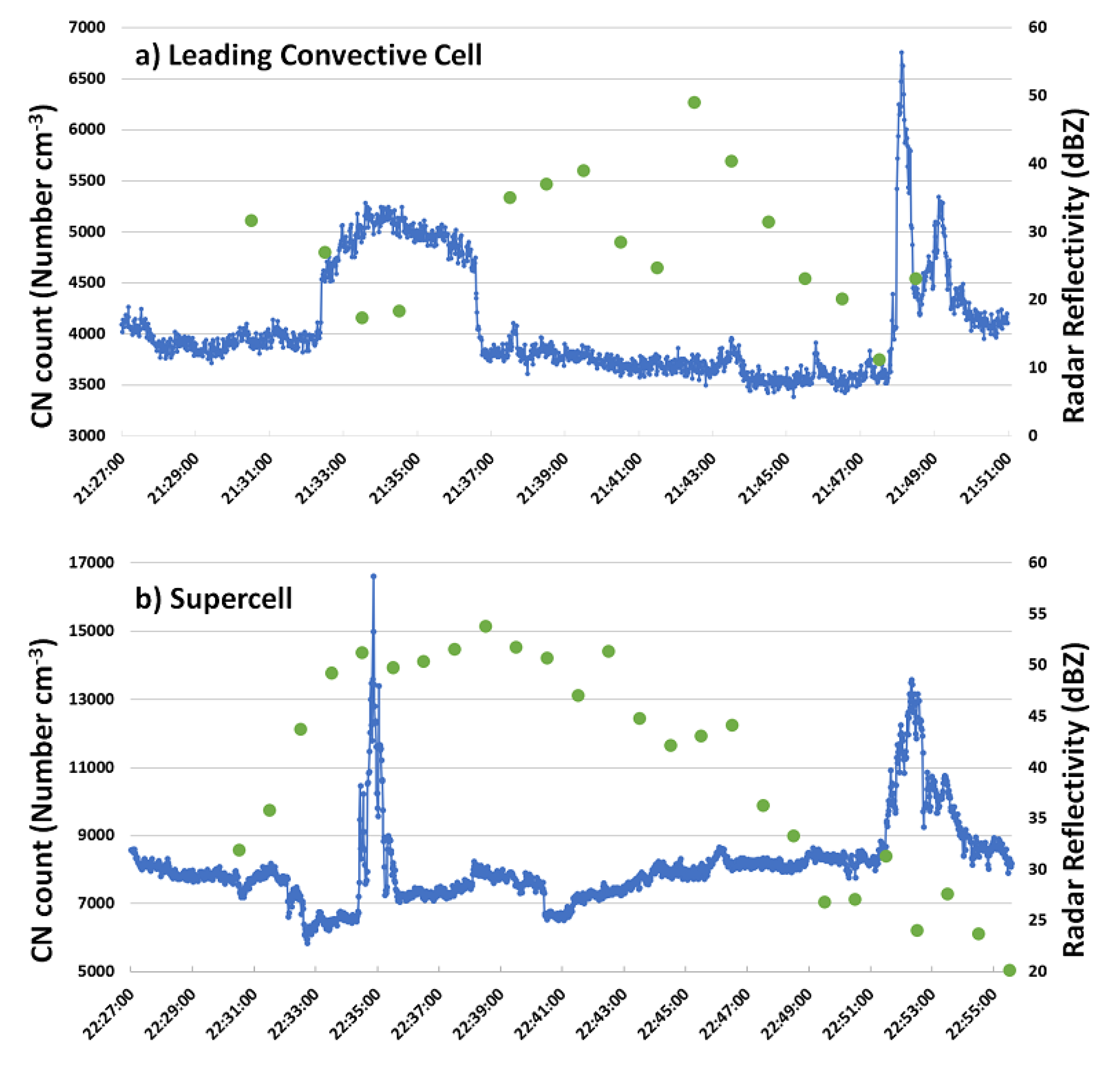
3.1. Supercell Storm Overview
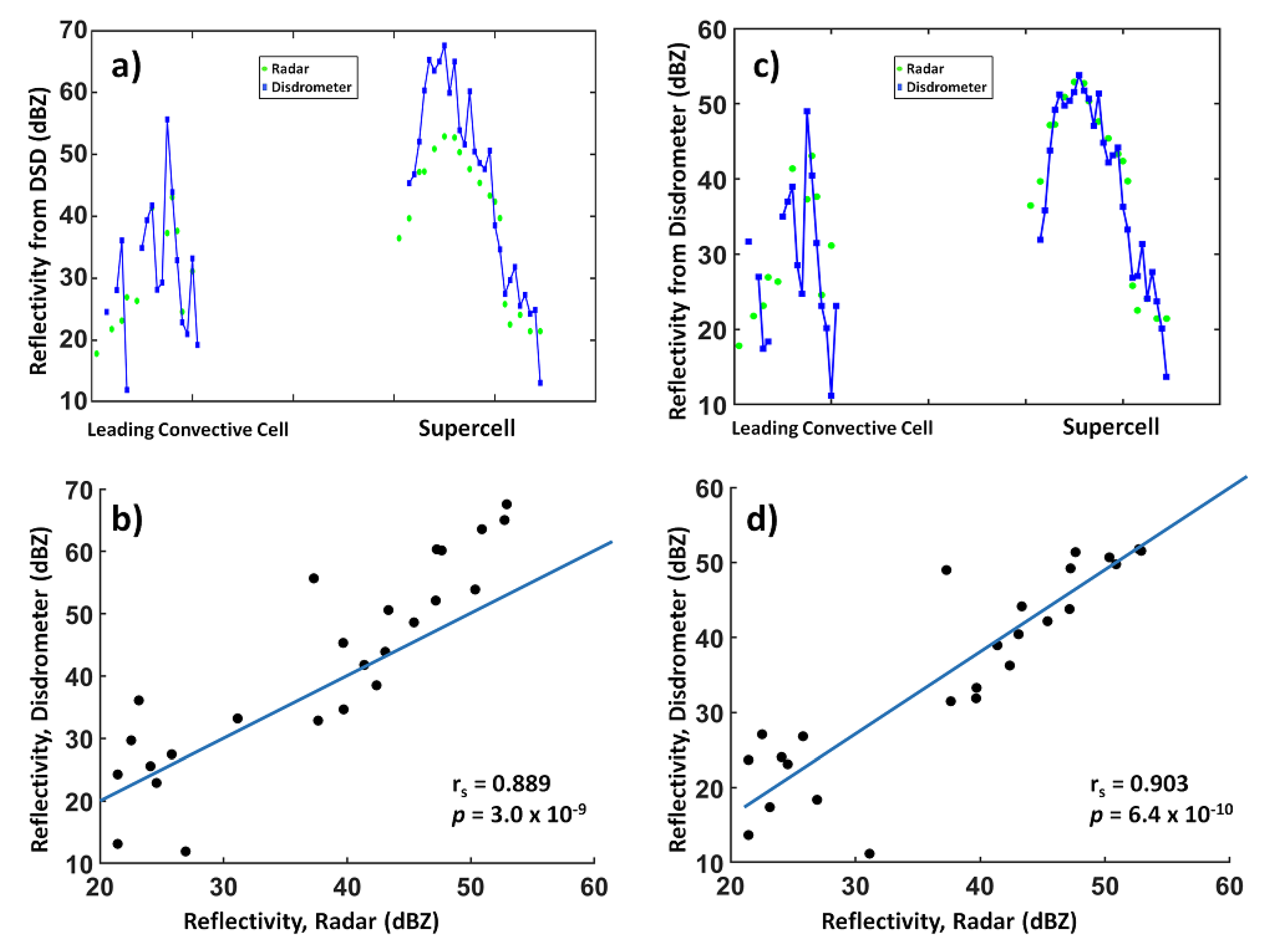
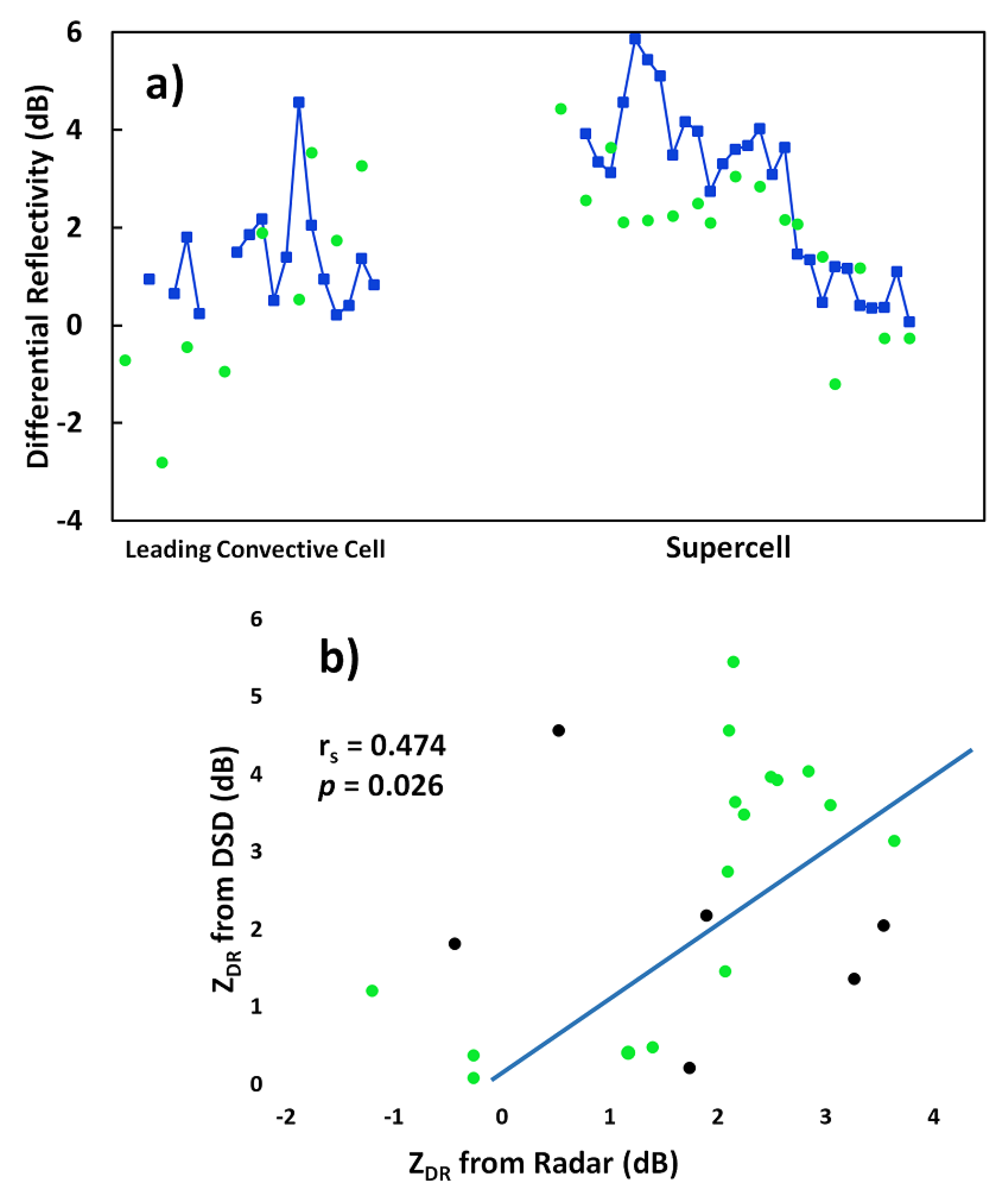
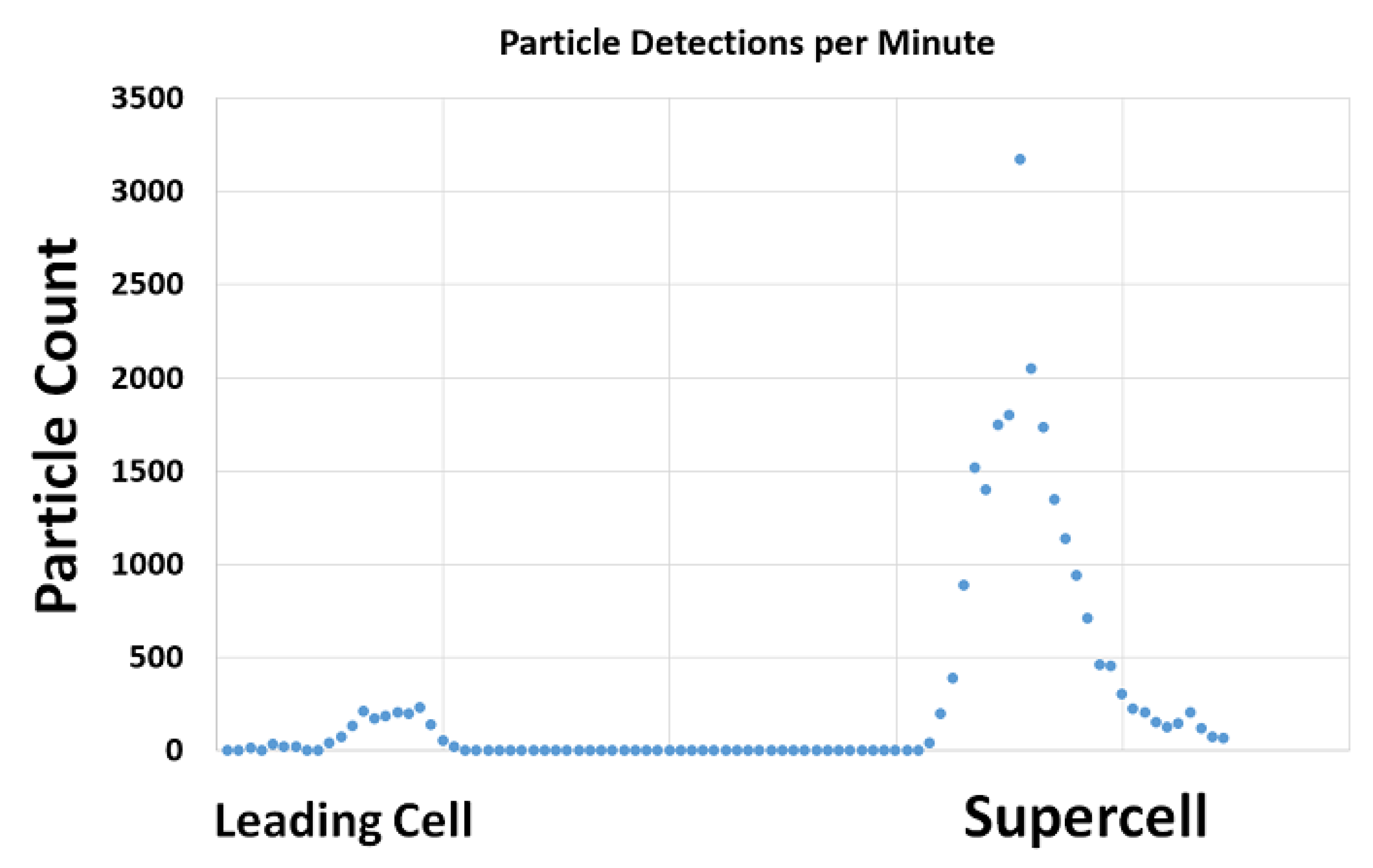
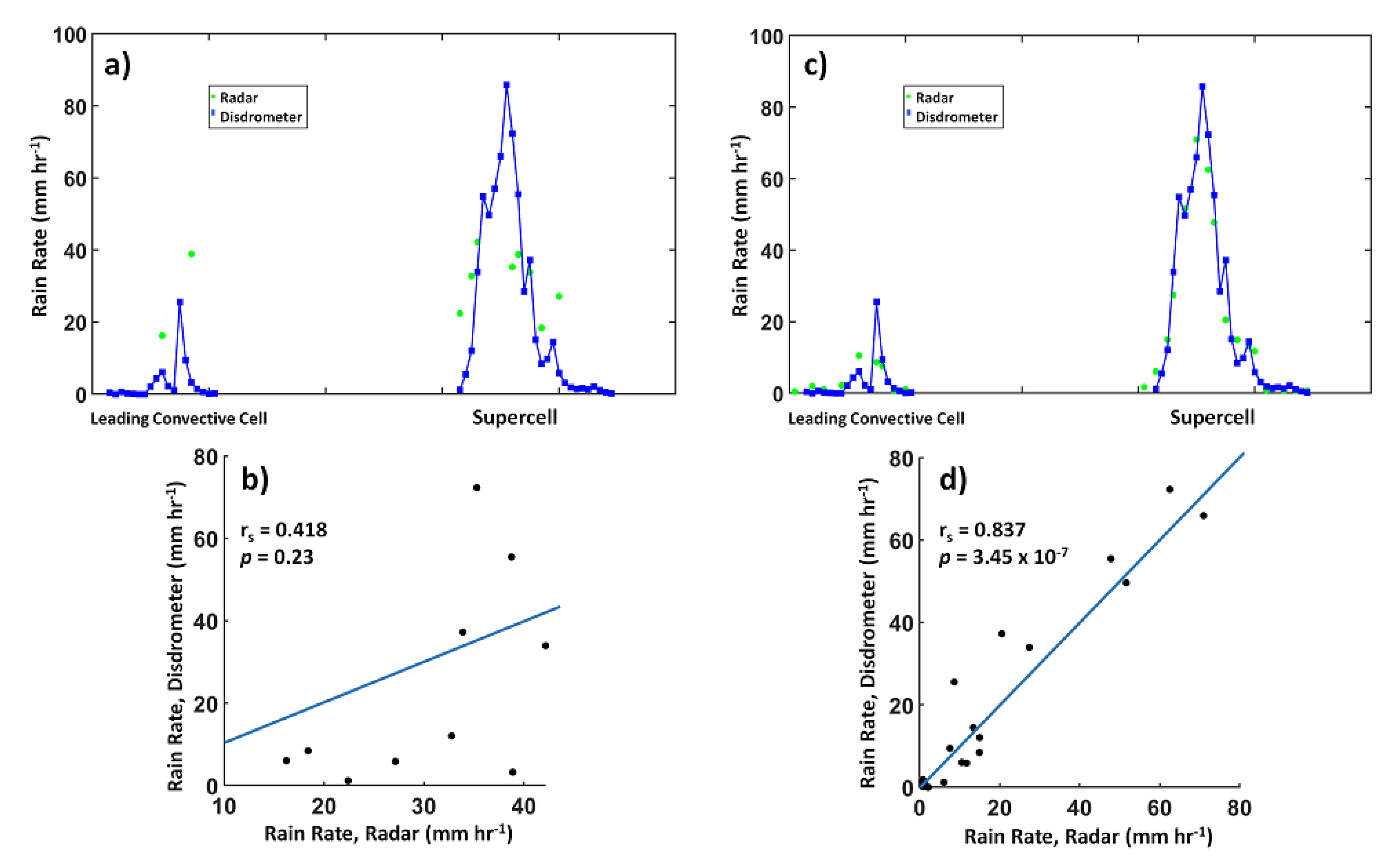
3.2. Comparison of Disdrometer, Polarimetric Radar, and CN Datasets
4. Conclusions and Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Duda, J.D.; Gallus, W.A. Spring and summer Midwestern severe weather reports in supercells compared to other morphologies. Weather Forecast. 2010, 25, 190–206. [Google Scholar] [CrossRef]
- Smith, B.T.; Thompson, R.L.; Grams, J.S.; Broyles, C.; Brooks, H.E. Convective modes for significant severe thunderstorms in the contiguous United States. Part I: Storm classification and climatology. Weather Forecast. 2012, 27, 1114–1135. [Google Scholar] [CrossRef]
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- French, M.M.; Burgess, D.W.; Mansell, E.R.; Wicker, L.J. Bulk hook echo raindrop sizes retrieved using mobile, polarimetric Doppler radar observations. J. Appl. Meteorol. Clim. 2015, 54, 423–450. [Google Scholar] [CrossRef]
- Lerach, D.G.; Cotton, W.R. Comparing aerosol and low-level moisture influences on supercell tornadogenesis: Three-dimensional idealized simulations. J. Atmos. Sci. 2012, 69, 969–987. [Google Scholar] [CrossRef]
- Kalina, E.A.; Friedrich, K.; Morrison, H.; Bryan, G.H. Aerosol effects on idealized supercell thunderstorms in different environments. J. Atmos. Sci. 2014, 71, 4558–4580. [Google Scholar] [CrossRef]
- Kumjian, M.R. Principles and applications of dual-polarization weather radar. Part II: Warm- and cold-season applications. J. Oper. Meteorol. 2013, 1, 243–264. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. Polarimetric signatures in supercell thunderstorms. J. Appl. Meteorol. Clim. 2008, 47, 1940–1961. [Google Scholar] [CrossRef]
- Romine, G.S.; Burgess, D.W.; Wilhelmson, R.B. A dual-polarization-radar-based assessment of the 8 May 2003 Oklahoma City area tornadic supercell. Mon. Weather Rev. 2008, 136, 2849–2870. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Straka, J.M.; Rasmussen, E.N. Polarimetric radar observations at low levels during tornado life cycles in a small sample of classic Southern Plains supercells. J. Appl. Meteorol. Clim. 2008, 47, 1232–1247. [Google Scholar] [CrossRef][Green Version]
- Kumjian, M.R.; Ryzhkov, A.V.; Melnikov, V.M.; Schuur, T.J. Rapid-scan super-resolution observations of a cyclic supercell with a dual-polarization WSR-88D. Mon. Weather Rev. 2010, 138, 3762–3786. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. Storm-relative helicity revealed from polarimetric radar measurements. J. Atmos. Sci. 2009, 66, 667–685. [Google Scholar] [CrossRef]
- Dawson, D.T.; Mansell, E.R.; Jung, Y.; Wicker, L.J.; Kumjian, M.R.; Xue, M. Low-level ZDR signatures in supercell forward flanks: The role of size sorting and melting of hail. J. Atmos. Sci. 2014, 71, 276–299. [Google Scholar] [CrossRef]
- Palmer, R.D.; Bodine, D.; Kumjian, M.; Cheong, B.; Zhang, G.; Cao, Q.; Bluestein, H.B.; Ryzhkov, A.; Yu, T.; Wang, Y. Observations of the 10 May 2010 tornado outbreak using OU-PRIME: Potential for new science with high-resolution polarimetric radar. Bull. Am. Meteorol. Soc. 2011, 92, 871–891. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. Polarimetric variability of classic supercell storms as a function of environment. J. Appl. Meteorol. Clim. 2016, 55, 1907–1925. [Google Scholar] [CrossRef]
- Crowe, C.; Schultz, C.; Kumjian, M.; Carey, L.; Petersen, W. Use of dual-polarization signatures in diagnosing tornadic potential. Elec. J. Oper. Meteorol. 2012, 13, 57–78. [Google Scholar]
- Van Den Broeke, M.S. Polarimetric radar metrics related to tornado life cycles and intensity in supercell storms. Mon. Weather Rev. 2017, 145, 3671–3686. [Google Scholar] [CrossRef]
- Ward, A.; Kumjian, M.; Bunkers, M.J.; Bieda III, S.W.; Simpson, R.J. Using polarimetric radar to identify potentially hazardous hail accumulations. In Proceedings of the 34th Conference on Environmental Information Processing Technologies, Austin, TX, USA, 7–11 January 2018. [Google Scholar]
- Ogden, F.L.; Sharif, H.O.; Senarath, S.U.S.; Smith, J.A.; Baeck, M.L.; Richardson, J.R. Hydrologic analysis of the Fort Collins, Colorado, flash flood of 1997. J. Hydrol. 2000, 228, 82–100. [Google Scholar] [CrossRef]
- Schuur, T.J.; Ryzhkov, A.V.; Zrnić, D.S.; Schönhuber, M. Drop size distributions measured by a 2D video disdrometer: Comparison with dual-polarization radar data. J. Appl. Meteorol. Clim. 2001, 40, 1019–1034. [Google Scholar] [CrossRef]
- Bringi, V.; Thurai, M.; Baumgardner, D. Raindrop fall velocities from an optical array probe and 2-D video disdrometer. Atmos. Meas. Tech. 2018, 11, 1377–1384. [Google Scholar] [CrossRef]
- Carey, L.D.; Petersen, W.A.; Thurai, M.; Anderson, M.E.; Schultz, E.V.; Schultz, C.J.; Knupp, K.K. Precipitation properties of a cool-season tornadic storm inferred from C-band dual-polarimetric radar and 2D-video disdrometer observations. In Proceedings of the 25th Conference Severe Local Storms, Denver, CO, USA, 11–14 October 2010. [Google Scholar]
- Thurai, M.; Gatlin, P.; Bringi, V.N.; Carey, L. Very large rain drops from 2D video disdrometers and concomitant polarimetric radar observations. In Proceedings of the 8th European Conference on Radar in Meteorology and Hydrology, Garmisch-Partenkirchen, Germany, 1–5 September 2014. [Google Scholar]
- Waugh, S.M.; Ziegler, C.L.; MacGorman, D.R. In situ microphysical observations of the 29-30 May 2012 Kingfisher, OK, supercell with a balloon-borne video disdrometer. J. Geophys. Res. Atmos. 2018, 123, 5618–5640. [Google Scholar] [CrossRef]
- Friedrich, K.; Higgins, S.; Masters, F.J.; Lopez, C.R. Articulating and stationary PARSIVEL disdrometer measurements in conditions with strong winds and heavy rainfall. J. Atmos. Ocean. Technol. 2013, 30, 2063–2080. [Google Scholar] [CrossRef]
- Kalina, E.A.; Friedrich, K.; Ellis, S.; Burgess, D. Comparison of disdrometer and X-band mobile radar observations in convective precipitation. Mon. Weather Rev. 2014, 142, 2414–2435. [Google Scholar] [CrossRef]
- Office of the Federal Coordinator for Meteorological Services and Supporting Research (OFCM). Federal Meteorological Handbook No. 11: WSR-88D Meteorological Observations. Part A: System Concepts, Responsiblities, and Procedures. 2012; FCM-H11A-2016; 25p. Available online: https://www.ofcm.gov/publications/fmh/FMH11/2016FMH11PTA.pdf (accessed on 2 June 2020).
- Kumjian, M.R. Principles and applications of dual-polarization weather radar. Part I: Description of the polarimetric radar variables. J. Oper. Meteorol. 2013, 1, 226–242. [Google Scholar] [CrossRef]
- Picca, J.; Ryzhkov, A. A dual-wavelength polarimetric analysis of the 16 May 2010 Oklahoma City extreme hailstorm. Mon. Weather Rev. 2012, 140, 1385–1403. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. A preliminary polarimetric radar comparison of pretornadic and nontornadic supercell storms. Mon. Weather Rev. 2020, 148, 1567–1584. [Google Scholar] [CrossRef]
- Andsager, K.; Beard, K.V.; Laird, N.F. Laboratory measurements of axis ratios for large raindrops. J. Atmos. Sci. 1999, 56, 2673–2683. [Google Scholar] [CrossRef]
- Jameson, A.R. Microphysical interpretation of multi-parameter radar measurements in rain. Part I: Interpretation of polarization measurements and estimation of raindrop shapes. J. Atmos. Sci. 1983, 40, 1792–1802. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL snow observations: A critical assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Ryzhkov, A.V. Estimation of rainfall based on the results of polarimetric echo classification. J. Appl. Meteorol. Clim. 2008, 47, 2445–2462. [Google Scholar] [CrossRef]
- Bringi, V.N.; Tolstoy, L.; Thurai, M.; Petersen, W.A. Estimation of spatial correlation of drop size distribution parameters and rain rate using NASA’s S-band polarimetric radar and 2D video disdrometer network: Two case studies from MC3E. J. Hydrometeorol. 2015, 16, 1207–1221. [Google Scholar] [CrossRef]
- Mordas, G.; Manninen, H.E.; Petäjä, T.; Aalto, P.P.; Hämeri, K.; Kulmala, M. On operation of the ultra-fine water-based CPC TSI 3786 and comparison with other TSI models (TSI 3776, TSI 3772, TSI 3025, TSI 3010, TSI 3007). Aerosol Sci. Technol. 2008, 42, 152–158. [Google Scholar] [CrossRef]
- King, A.T.; Kennedy, A.D. North American supercell environments in atmospheric reanalyses and RUC-2. J. Appl. Meteorol. Clim. 2019, 58, 71–92. [Google Scholar] [CrossRef]
- Thompson, R.L.; Mead, C.M.; Edwards, R. Effective storm-relative helicity and bulk shear in supercell thunderstorm environments. Weather Forecast. 2007, 22, 102–115. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Lebo, Z.J.; Morrison, H.C. On the mechanisms of rain formation in an idealized supercell storm. Mon. Weather Rev. 2015, 143, 2754–2773. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. The impact of size sorting on the polarimetric radar variables. J. Atmos. Sci. 2012, 69, 2042–2060. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Melnikov, V.M.; Schuur, T.J. Calibration issues of dual-polarization radar measurements. J. Atmos. Ocean. Technol. 2005, 22, 1138–1155. [Google Scholar] [CrossRef]
- Seigel, R.B.; van den Heever, S.C. Dust lofting and ingestion by supercell storms. J. Atmos. Sci. 2012, 69, 1453–1473. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Alsarraf, H. Polarimetric radar observations of dust storms at C- and S-band. J. Oper. Meteorol. 2016, 4, 123–131. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Den Broeke, M. Disdrometer, Polarimetric Radar, and Condensation Nuclei Observations of Supercell and Multicell Storms on 11 June 2018 in Eastern Nebraska. Atmosphere 2020, 11, 770. https://doi.org/10.3390/atmos11070770
Van Den Broeke M. Disdrometer, Polarimetric Radar, and Condensation Nuclei Observations of Supercell and Multicell Storms on 11 June 2018 in Eastern Nebraska. Atmosphere. 2020; 11(7):770. https://doi.org/10.3390/atmos11070770
Chicago/Turabian StyleVan Den Broeke, Matthew. 2020. "Disdrometer, Polarimetric Radar, and Condensation Nuclei Observations of Supercell and Multicell Storms on 11 June 2018 in Eastern Nebraska" Atmosphere 11, no. 7: 770. https://doi.org/10.3390/atmos11070770
APA StyleVan Den Broeke, M. (2020). Disdrometer, Polarimetric Radar, and Condensation Nuclei Observations of Supercell and Multicell Storms on 11 June 2018 in Eastern Nebraska. Atmosphere, 11(7), 770. https://doi.org/10.3390/atmos11070770




