Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia
Abstract
1. Introduction
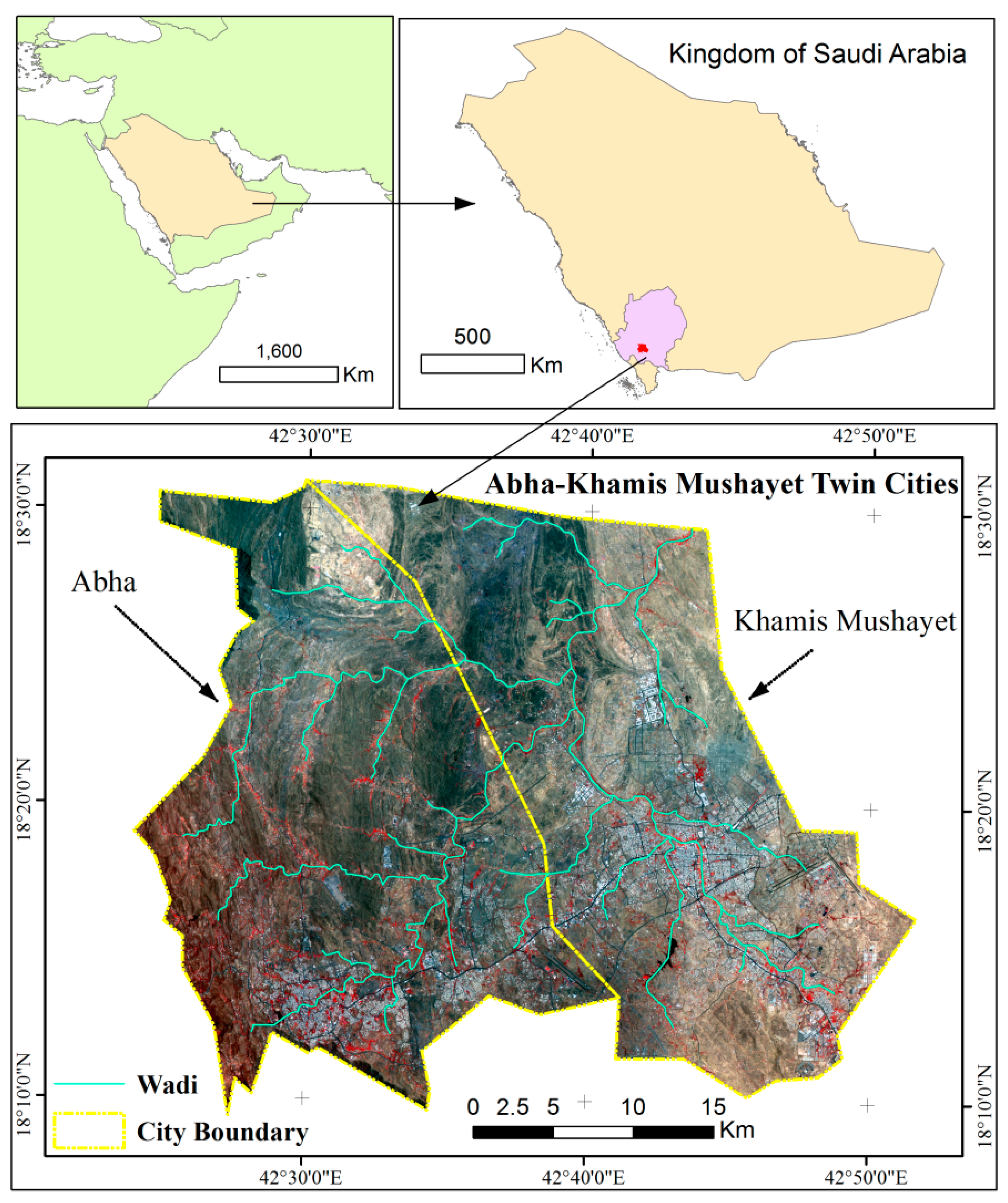
2. Study Area
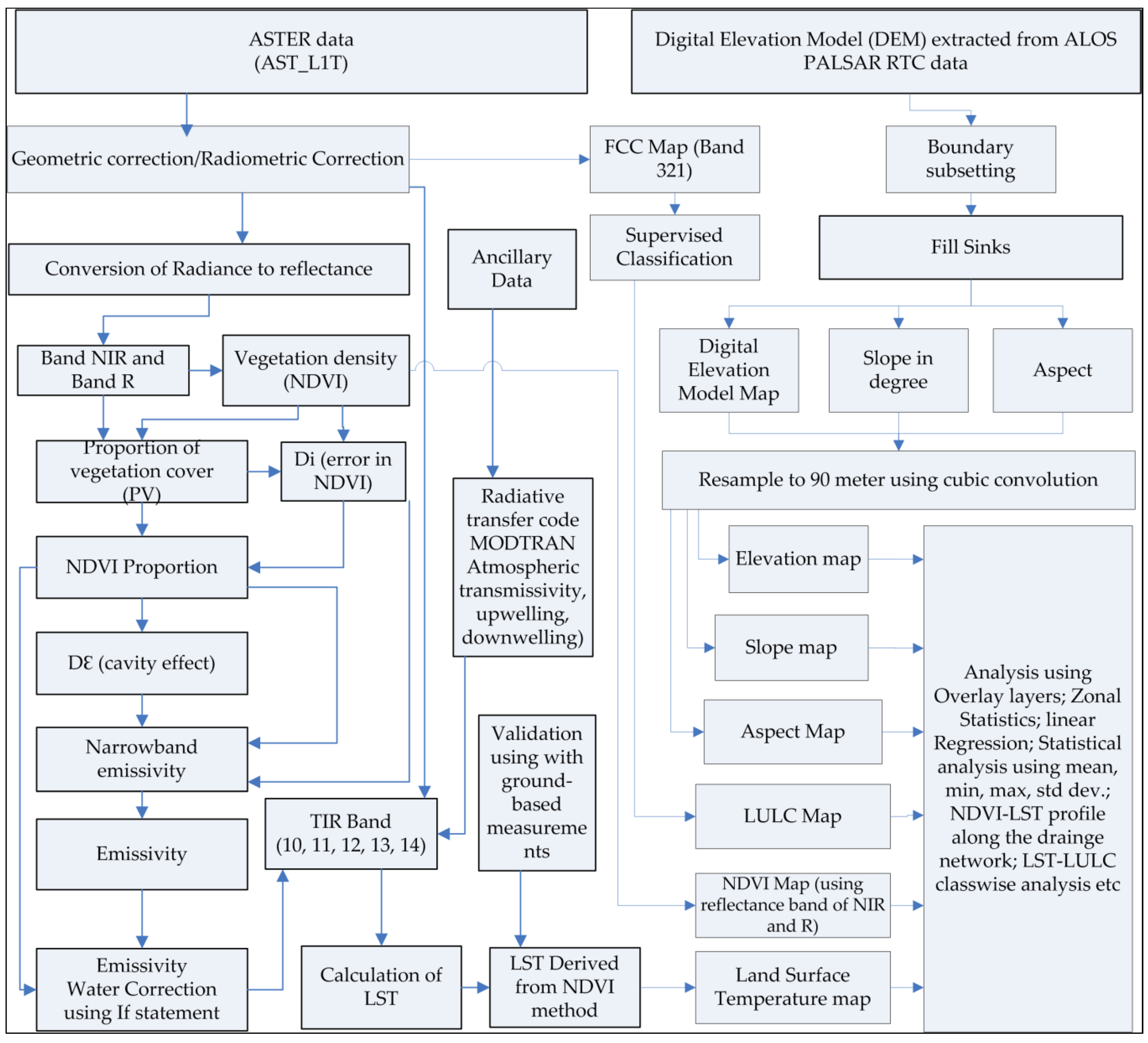
3. Methodology
3.1. ASTER Sensor
3.2. Radiometric Calibration
3.3. Atmospheric Correction for the ASTER Channel
3.4. Retrieval of Emissivity and LST
- = “spectral radiance observed by the sensor”,
- = “surface emissivity at wavelength j”,
- = “spectral radiance from a blackbody at surface temperature T”,
- = “spectral radiance incident upon the surface from the atmosphere (downwelling), from MODTRAN”,
- = “spectral radiance emitted by the atmosphere (upwelling), from MODTRAN”
- = “spectral atmospheric transmission, from MODTRAN”.
- = “First radiation constant = 3.74151 × 10−16 (W m2)”
- = “Second radiation constant = 1.44 × 104 (μm K)”
- = “wavelength of channel j, (m)”
- = “temperature”
4. Results
4.1. LST Result from Emissivity Derived from the Proportion of Vegetation Cover in Conjunction with NDVI
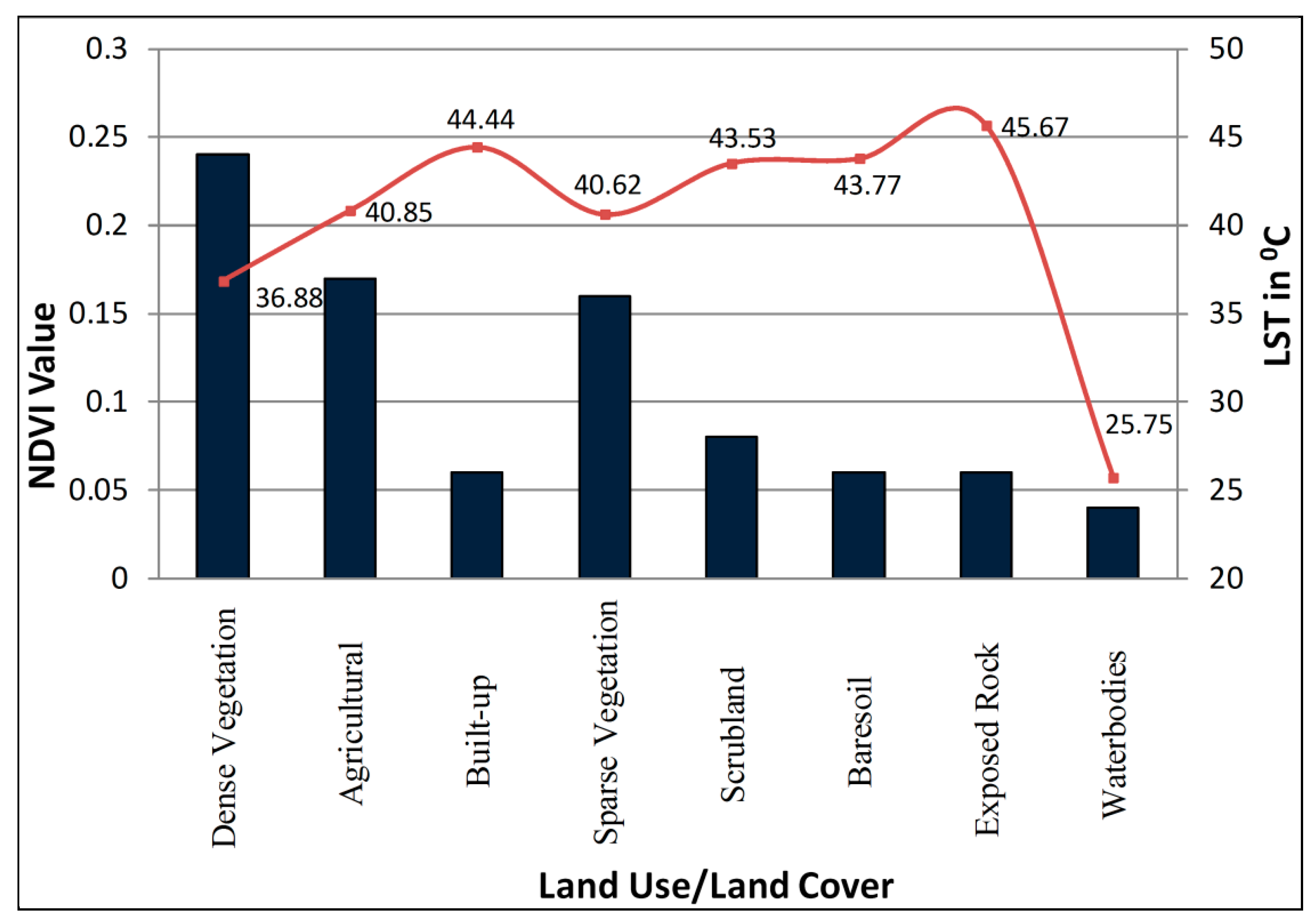
4.2. Relationship between LST and LULC
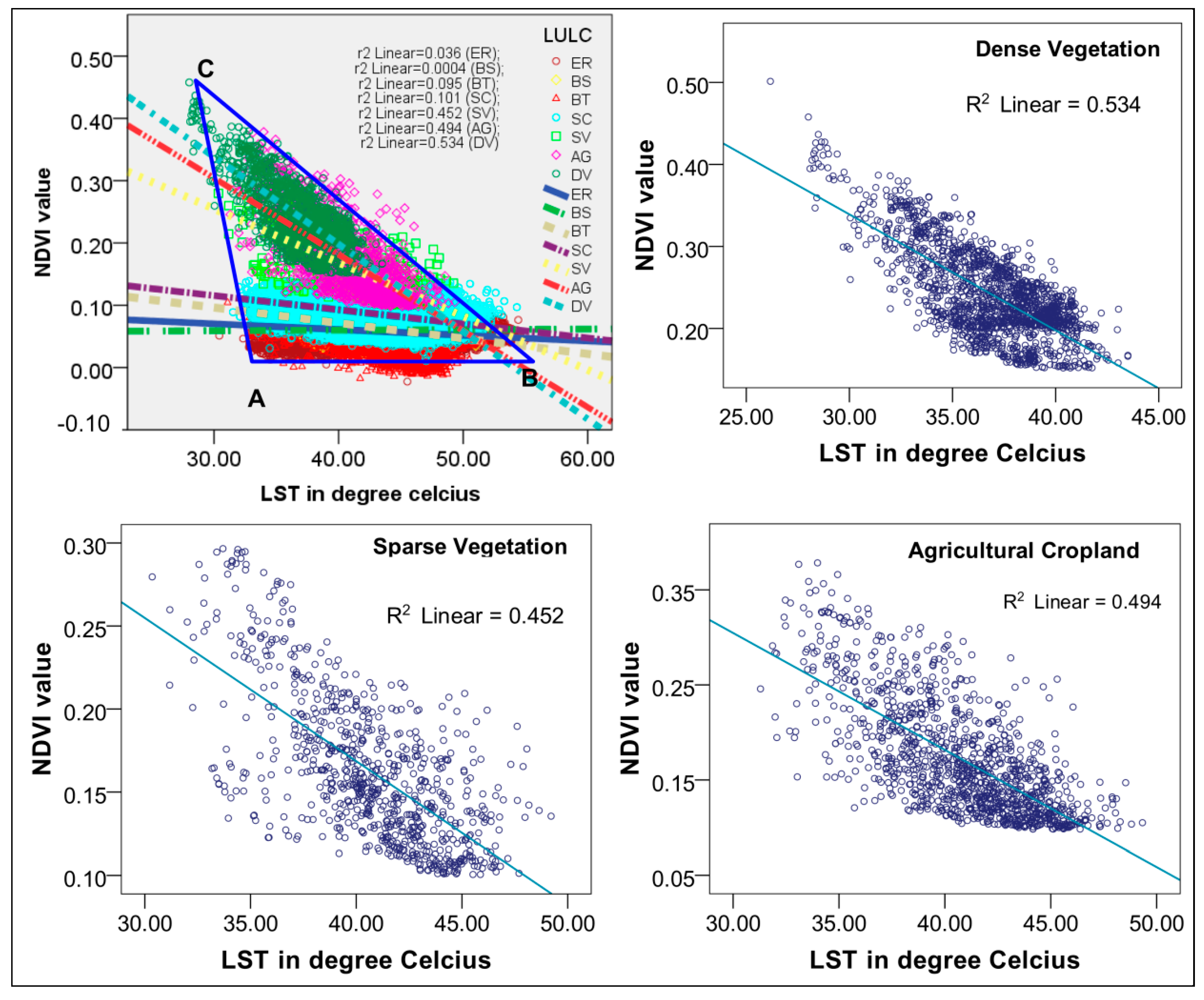
4.3. LST and NDVI Relationship
Characteristics LST and NDVI Distribution
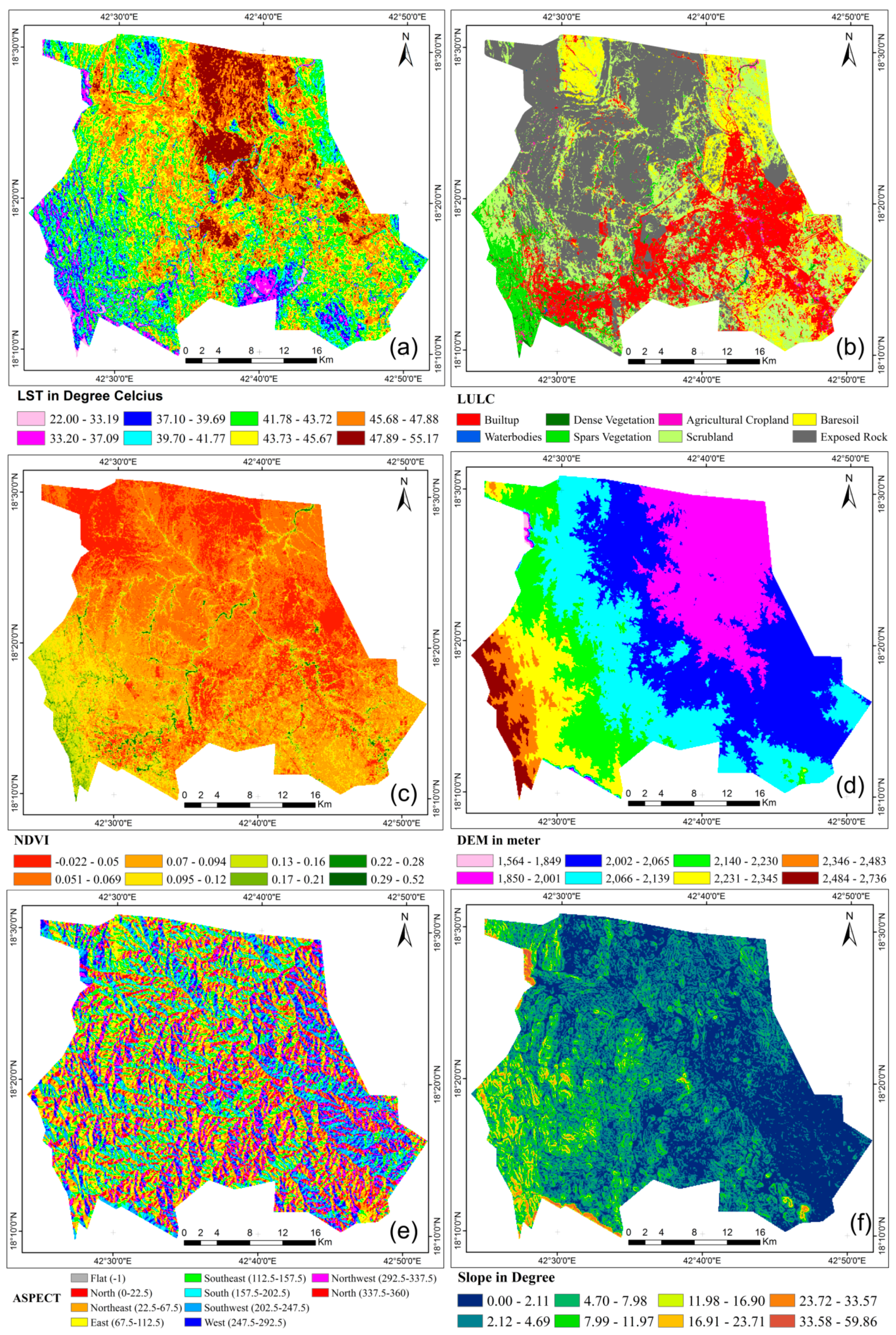
4.4. Spatial Structure of LST and LULC Relationship
4.5. Relationship between LST and Topographical Parameters
4.5.1. Effect of Elevation on the LST
4.5.2. Effect of Aspect on the LST
4.5.3. Effect of Slope on the LST
4.5.4. Effect of Vegetation on the LST
4.6. Spatial Characteristics of NDVI and LST Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van De Kerchove, R.; Lhermitte, S.; Veraverbeke, S.; Goossens, R. Spatio-temporal variability in remotely sensed land surface temperature, and its relationship with physiographic variables in the Russian Altay Mountains. Int. J. Appl. Earth Obs. Geoinf. 2012. [Google Scholar] [CrossRef]
- Aguilar, C.; Herrero, J.; Polo, M.J. Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale. Hydrol. Earth Syst. Sci. 2010. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Vivoni, E.R. Vegetation-hydrology dynamics in complex terrain of semiarid areas: A mechanistic approach to modeling dynamic feedbacks. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Rolland, C. Spatial and seasonal variations of air temperature lapse rates in alpine regions. J. Clim. 2003. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Wald, A.E.; Remer, L.A.; Gao, B.C.; Li, R.R.; Flynn, L. MODIS 2.1-μm channel—Correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998. [Google Scholar] [CrossRef]
- Guillevic, P.; Göttsche, F.; Nickeson, J.; Hulley, G.; Ghent, D.; Yu, Y.; Trigo, I.; Hook, S.; Sobrino, J.A.; Remedios, J.; et al. Land surface temperature product validation best practice protocol version 1.1. Best Pract. Satell.-Deriv. Land Prod. Valid. 2018. [Google Scholar] [CrossRef]
- McMillin, L.M. Estimation of sea surface temperatures from two infrared window measurements with different absorption. J. Geophys. Res. 1975. [Google Scholar] [CrossRef]
- Wan, Z. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996. [Google Scholar] [CrossRef]
- Prata, A.J.; Casellescoll, C.V.; Sobrino, J.A.; Ottle, C. Thermal remote sensing of land surface temperature from satellites: Current status and future prospects. Remote Sens. Rev. 1995. [Google Scholar] [CrossRef]
- Li, Z.L.; Becker, F. Feasibility of land surface temperature and emissivity determination from AVHRR data. Remote Sens. Environ. 1993. [Google Scholar] [CrossRef]
- Hook, S.J.; Gabell, A.R.; Green, A.A.; Kealy, P.S. A comparison of techniques for extracting emissivity information from thermal infrared data for geologic studies. Remote Sens. Environ. 1992. [Google Scholar] [CrossRef]
- Kealy, P.S.; Hook, S.J. Separating temperature and emissivity in thermal infrared multispectral scanner data: Implications for recovering land surface temperatures. IEEE Trans. Geosci. Remote Sens. 1993. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996. [Google Scholar] [CrossRef]
- Vázquez, D.P.; Reyes, F.J.O.; Arboledas, L.A. A comparative study of algorithms for estimating land surface temperature from AVHRR data. Remote Sens. Environ. 1997. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001. [Google Scholar] [CrossRef]
- Jiménez-Munoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009. [Google Scholar] [CrossRef]
- Mallick, J.; Rahman, A.; Singh, C.K. Modeling urban heat islands in heterogeneous land surface and its correlation with impervious surface area by using night-time ASTER satellite data in highly urbanizing city, Delhi-India. Adv. Space Res. 2013. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013. [Google Scholar] [CrossRef]
- Vostikolaei, F.S.; Akhoondzadeh, M. A comparison of four methods for extracting land surface emissivity and temperature in the thermal infrared hyperspectral data. Earth Obs. Geomat. Eng. 2018, 2, 56–63. [Google Scholar] [CrossRef]
- Mallick, J. Land characterization analysis of surface temperature of semi-arid mountainous city Abha, Saudi Arabia using remote sensing and GIS. J. Geogr. Inf. Syst. 2014. [Google Scholar] [CrossRef]
- El-Nahry, A.H.; Rashash, A. Impact of industrial areas on surface temperature using thermal infrared remote sensing and GIS techniques: A case study of Jubail City, KSA. In Proceedings of the 8th National GIS Symposium in Saudi Arabia, Dammam, Saudi Arabia, 8 June 2013. [Google Scholar]
- Rashash, A.A.; Mohammed, E.S. Impact of industrial activities on land surface temperature using remote sensing and GIS techniques—A case study in Jubail, Saudi Arabia. J. Geogr. Nat. Disasters 2016. [Google Scholar] [CrossRef]
- Mujabar, S.; Rao, V. Estimation and analysis of land surface temperature of Jubail Industrial City, Saudi Arabia, by using remote sensing and GIS technologies. Arab. J. Geosci. 2018. [Google Scholar] [CrossRef]
- Mujabar, P.S. Spatial-temporal variation of land surface temperature of Jubail Industrial City, Saudi Arabia due to seasonal effect by using Thermal Infrared Remote Sensor (TIRS) satellite data. J. Afr. Earth Sci. 2019. [Google Scholar] [CrossRef]
- Berg, A.; Lintner, B.R.; Findell, K.L.; Malyshev, S.; Loikith, P.C.; Gentine, P. Impact of soil moisture-atmosphere interactions on surface temperature distribution. J. Clim. 2014. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013. [Google Scholar] [CrossRef]
- Dickinson, R.E. Satellite systems and models for future climate change. In Future Climates of the World: A Modelling Perspective, 16th ed.; Henderson-Sellers, A., Ed.; World Survey of Climatology Elsevier: Amsterdam, The Netherlands, 1994; p. 27. [Google Scholar]
- Becker, F.; Li, Z.L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995. [Google Scholar] [CrossRef]
- Zareie, S.; Khosravi, H.; Nasiri, A.; Dastorani, M. Using Landsat Thematic Mapper (TM) sensor to detect change in land surface temperature in relation to land use change in Yazd, Iran. Solid Earth 2016. [Google Scholar] [CrossRef]
- Vlassova, L.; Perez-Cabello, F.; Nieto, H.; Martín, P.; Riaño, D.; Riva, J.D. Assessment of methods for land surface temperature retrieval from Landsat-5 TM images applicable to multiscale tree-grass ecosystem modeling. Remote Sens. 2014, 6, 4345–4368. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Luvall, J.C. Thermal Remote Sensing in Land Surface Processing; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Jia, L.; Menenti, M.; Su, Z.; Li, Z.-L.; Djepa, V.; Wang, J. Modeling sensible heat flux using estimates of soil and vegetation temperatures: The HEIFE and IMGRASS experiments. In Remote Sensing and Climate Modeling: Synergies and Limitations; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008. [Google Scholar] [CrossRef]
- Linh, N.T.; Huy, T.Q.; Jungwon, H.; Dongyeob, H. Land Surface temperatures of industrial complexes in Jeonnam using Landsat 7 ETM+ satellite images. J. KRSA 2015, 15, 87–95. [Google Scholar]
- Xu, T.; Bateni, S.M.; Margulis, S.A.; Song, L.; Liu, S.; Xu, Z. Partitioning evapotranspiration into soil evaporation and canopy transpiration via a two-source variational data assimilation system. J. Hydrometeorol. 2016. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Chen, X.; Ma, Y.; Su, Z. Comparison of satellite-based evapotranspiration estimates over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2016. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional Evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Amiri, R.; Weng, Q.; Alimohammadi, A.; Alavipanah, S.K. Spatial–temporal dynamics of land surface temperature in relation to fractional vegetation cover and land use/cover in the Tabriz urban area, Iran. Remote Sens. Environ. 2009, 113, 2606–2617. [Google Scholar] [CrossRef]
- Leng, P.; Song, X.; Duan, S.B.; Li, Z.L. A practical algorithm for estimating surface soil moisture using combined optical and thermal infrared data. Int. J. Appl. Earth Obs. Geoinf. 2016. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2014. [Google Scholar] [CrossRef]
- Rahimzadeh-Bajgiran, P.; Berg, A.A.; Champagne, C.; Omasa, K. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian Prairies. ISPRS J. Photogramm. Remote Sens. 2013, 83, 94–103. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Y.; Zhang, X.; Zhan, W. Modelling the diurnal variations of urban heat islands with multi-source satellite data. Int. J. Remote Sens. 2013. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010. [Google Scholar] [CrossRef]
- Li, Z.; Jia, L.; Lu, J. On uncertainties of the Priestley-Taylor/LST-Fc feature space method to estimate evapotranspiration: Case study in an arid/semiarid region in northwest China. Remote Sens. 2015, 7, 447–466. [Google Scholar] [CrossRef]
- Stroppiana, D.; Antoninetti, M.; Brivio, P.A. Seasonality of MODIS LST over Southern Italy and correlation with land cover, topography and solar radiation. Eur. J. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Munoz, J.C.; El-Kharraz, J.; Gómez, M.; Romaguera, M.; Sòria, G. Single-channel and two-channel methods for land surface temperature retrieval from DAIS data and its application to the Barrax site. Int. J. Remote Sens. 2004. [Google Scholar] [CrossRef]
- Li, Z.; Deng, X.; Shi, Q.; Ke, X.; Liu, Y. Modeling the impacts of boreal deforestation on the near-surface temperature in european Russia. Adv. Meteorol. 2013. [Google Scholar] [CrossRef]
- Emmanuel, M.R. An Urban Approach to Climate-Sensitive Design: Stategies for the Tropics; Taylor & Francis: London, UK, 2012; ISBN 9780203414644. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011. [Google Scholar] [CrossRef]
- Chen, Y.; Wong, N.H. Thermal benefits of city parks. Energy Build. 2006. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Mallick, J.; Kant, Y.; Bharath, B.D. Estimation of land surface temperature over Delhi using Landsat-7 ETM+. J. Ind. Geophys. Union 2008, 12, 131–140. [Google Scholar]
- Weng, Q. A remote sensing? GIS evaluation of urban expansion and its impact on surface temperature in the Zhujiang Delta, China. Int. J. Remote Sens. 2001. [Google Scholar] [CrossRef]
- Vincent, P. Saudi Arabia: An Environmental Overview; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Bindajam, A.A.; Mallick, J. Impact of the spatial configuration of streets networks on urban growth: A case study of Abha City, Saudi Arabia. Sustainability 2020, 12, 1856. [Google Scholar] [CrossRef]
- Mallick, J.; Khan, R.A.; Ahmed, M.; Alqadhi, S.D.; Alsubih, M.; Falqi, I.; Hasan, M.A. Modeling groundwater potential zone in a semi-arid region of aseer using Fuzzy-AHP and geoinformation techniques. Water 2019, 11, 2656. [Google Scholar] [CrossRef]
- Laurencelle, J.; Logan, T.; Gens, R. ASF Radiometrically Terrain Corrected ALOS PALSAR Productsi; Product Guide, Revision 1.2; Alaska Satellite Facility: Fairbanks, AK, USA, 2015. [Google Scholar]
- Abrams, M. The advanced spaceborne thermal emission and reflection radiometer (ASTER): Data products for the high spatial resolution imager on NASA’s Terra platform. Int. J. Remote Sens. 2000. [Google Scholar] [CrossRef]
- Roy, D.P.; Lewis, P.E.; Justice, C.O. Burned area mapping using multi-temporal moderate spatial resolution data-a bi-directional reflectance model-based expectation approach. Remote Sens. Environ. 2002. [Google Scholar] [CrossRef]
- Palluconi, F.; Hoover, G.; Alley, R.; Jentoft-Nilsen, M.; Thompson, T. An Atmospheric Correction Method for ASTER Thermal Radiometry over Land. Jet Propuls Lab Pasadena, California Institute of Technology. 1999. Available online: http://www.science.aster.ersdac.or.jp/en/documnts/pdf/2b01t.pdf (accessed on 10 July 2020).
- Jin, M.; Liang, S. An improved land surface emissivity parameter for land surface models using global remote sensing observations. J. Clim. 2006. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000. [Google Scholar] [CrossRef]
- Jacob, F.; Lesaignoux, A.; Olioso, A.; Weiss, M.; Caillault, K.; Jacquemoud, S.; Nerry, F.; French, A.; Schmugge, T.; Briottet, X.; et al. Reassessment of the temperature-emissivity separation from multispectral thermal infrared data: Introducing the impact of vegetation canopy by simulating the cavity effect with the SAIL-Thermique model. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Caselles, V.; Sobrino, J.A. Determination of frosts in orange groves from NOAA-9 AVHRR data. Remote Sens. Environ. 1989. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Chen, Z. Comparison of broad-band and narrow-band red and near-infrared vegetation indices. Remote Sens. Environ. 1995. [Google Scholar] [CrossRef]
- Sutherland, R.A. Broadband and spectral emissivities (2–18 μm) of some natural soils and vegetation. J. Atmos. Ocean. Technol. 1986. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Gillespie, A.; Sabol, D.; Gustafson, W.T. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006. [Google Scholar] [CrossRef]
- Caselles, V.; Coll, C.; Valor, E. Land surface emissivity and temperature determination in the whole HAPEX-sahel area from AVHRR data. Int. J. Remote Sens. 1997. [Google Scholar] [CrossRef]
- Mallick, J.; Singh, C.K.; Shashtri, S.; Rahman, A.; Mukherjee, S. Land surface emissivity retrieval based on moisture index from Landsat TM satellite data over heterogeneous surfaces of Delhi city. Int. J. Appl. Earth Obs. Geoinf. 2012. [Google Scholar] [CrossRef]
- Lo, C.P.; Quattrochi, D.A.; Luvall, J.C. Application of high-resolution thermal infrared remote sensing and GIS to assess the urban heat island effect. Int. J. Remote Sens. 1997. [Google Scholar] [CrossRef]
- Khandelwal, S.; Goyal, R.; Kaul, N.; Mathew, A. Assessment of land surface temperature variation due to change in elevation of area surrounding Jaipur, India. Egypt. J. Remote Sens. Space Sci. 2018. [Google Scholar] [CrossRef]
- Warrag, E.I.; Mallick, J.; Singh, R.K.; Khan, R.A. Status of dieback of Juniperus Procera (African pencil cedar) in natural stands and plantation in Alsouda highlands, Saudi Arabia. Appl. Ecol. Environ. Res. 2019. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature /vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Mallick, J.; Bindajam, A.A.; AlQadhi, S.; Ahmed, M.; Hang, H.T.; Thanh, N.V. A comparison of four land surface temperature retrieval method using TERRA-ASTER satellite images in the semi-arid region of Saudi Arabia. Geocarto Int. 2020. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997. [Google Scholar] [CrossRef]
- Tian, Y.; Bai, X.; Wang, S.; Qin, L.; Li, Y. Spatial-temporal changes of vegetation cover in Guizhou Province, Southern China. Chin. Geogr. Sci. 2017. [Google Scholar] [CrossRef]
- Qin, L.; Bai, X.; Wang, S.; Zhou, D.; Li, Y.; Peng, T.; Tian, Y.; Luo, G. Major problems and solutions on surface water resource utilisation in karst mountainous areas. Agric. Water Manag. 2015. [Google Scholar] [CrossRef]
- Mallick, J.; Al-Wadi, H.; Rahman, A.; Ahmed, M. Landscape dynamic characteristics using satellite data for a mountainous watershed of Abha, Kingdom of Saudi Arabia. Environ. Earth Sci. 2014. [Google Scholar] [CrossRef]
- Wen, L.; Yang, H.; Wang, H.; Dong, L.; Shang, X. An analysis of land surface temperature (LST) and its influencing factors in summer in western Sichuan Plateau: A case study of Xichang City. Remote Sens. Land Resour. 2017, 29, 207–214. [Google Scholar]
- Zhou, Y.; Shi, T.M.; Hu, Y.M.; Liu, M. Relationships between land surface temperature and normalized difference vegetation index based on urban land use type. Chin. J. Ecol. 2011, 30, 1504–1512. [Google Scholar]
- Ghobadi, Y.; Pradhan, B.; Shafri, H.Z.M.; Kabiri, K. Assessment of spatial relationship between land surface temperature and landuse/cover retrieval from multi-temporal remote sensing data in South Karkheh Sub-basin, Iran. Arab. J. Geosci. 2015, 8, 525–537. [Google Scholar] [CrossRef]
- Liang, B.P.; Li, Y.; Chen, K.Z. A research on land features and correlation between NDVI and land surface temperature in Guilin City. Remote Sens. Technol. Appl. 2012, 27, 429–435. [Google Scholar]
- Deng, Y.; Wang, S.; Bai, X.; Tian, Y.; Wu, L.; Xiao, J.; Chen, F.; Qian, Q. Relationship among land surface temperature and LUCC, NDVI in typical karst area. Sci. Rep. 2018. [Google Scholar] [CrossRef] [PubMed]

| Features | Ground Based Measurements on 24–27 June 2019 (10.00–11.30 Local time) in °C | Satellite Observation ASTER 26 June 2019 °C | GCS Coordinates WGS 84 Decimal Degrees |
|---|---|---|---|
| Dense Vegetation | 29.46 °C | 31.26 °C | 42.587765 E 18.251733 N |
| Concrete (built-up) | 41.12 °C | 43.29 °C | 42.724764 E 18.302471 N |
| Asphalt (Parking) | 50.42 °C | 48.77 °C | 42.560936 E 18.252881 N |
| Exposed Rocky area | 52.45 °C | 50.52 °C | 42.617576 E 18.389468 N |
| LULC Class Name | NDVI | LST in °C | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | Min | Max | Mean | Std.dev. | |
| Built up | −0.02 | 0.12 | 0.0605 | 0.021 | 25.40 | 52.69 | 44.44 | 3.339 |
| Waterbodies | 0.02 | 0.11 | 0.0441 | 0.022 | 22.00 | 37.17 | 25.75 | 2.568 |
| Dense Vegetation | 0.15 | 0.50 | 0.242 | 0.054 | 26.17 | 43.50 | 36.88 | 2.783 |
| Sparse Vegetation | 0.10 | 0.30 | 0.1633 | 0.044 | 30.35 | 49.21 | 40.62 | 3.255 |
| Agricultural | 0.10 | 0.38 | 0.1712 | 0.054 | 31.29 | 49.33 | 40.85 | 3.202 |
| Scrubland | 0.01 | 0.16 | 0.0848 | 0.0217 | 24.68 | 54.31 | 43.53 | 3.061 |
| Baresoil | 0.01 | 0.09 | 0.0603 | 0.0111 | 33.59 | 51.54 | 43.77 | 2.569 |
| Exposed Rock | −0.02 | 0.08 | 0.0558 | 0.0132 | 28.60 | 55.17 | 45.67 | 3.238 |
| LULC | 1564–2000 | 2001–2100 | 2101–2300 | 2301–2500 | 2501–2736 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | |
| Built-up | 43.34 | 0.061 | 46.14 | 166.22 | 0.067 | 44.44 | 62.82 | 0.082 | 42.46 | 12.44 | 0.104 | 41.33 | 1.18 | 0.123 | 39.29 |
| Waterbodies | -- | -- | -- | 0.39 | 0.072 | 28.55 | 0.162 | 0.076 | 28.02 | 0.02 | 0.176 | 27.01 | -- | -- | -- |
| Dense Vegetation | 0.92 | 0.166 | 41.15 | 1.39 | 0.152 | 38.37 | 3.39 | 0.162 | 38.10 | 1.94 | 0.157 | 37.71 | 0.49 | 0.176 | 33.95 |
| Sparse Vegetation | 2.92 | 0.130 | 43.81 | 10.91 | 0.119 | 42.59 | 15.70 | 0.133 | 40.96 | 22.38 | 0.136 | 39.73 | 18.83 | 0.146 | 38.46 |
| Agricultural Cropland | 3.37 | 0.132 | 42.96 | 5.40 | 0.117 | 42.91 | 2.02 | 0.141 | 41.03 | 0.65 | 0.129 | 40.57 | 0.42 | 0.142 | 39.23 |
| Scrubland | 66.59 | 0.072 | 45.40 | 162.19 | 0.080 | 43.72 | 73.77 | 0.093 | 42.87 | 24.85 | 0.110 | 41.12 | 8.69 | 0.128 | 40.02 |
| Baresoil | 43.79 | 0.059 | 44.93 | 56.95 | 0.067 | 42.91 | 4.55 | 0.072 | 42.52 | 0.02 | 0.066 | 41.47 | 0.11 | 0.116 | 38.76 |
| Exposed Rocks | 85.48 | 0.055 | 47.71 | 165.10 | 0.061 | 45.70 | 183.38 | 0.068 | 43.74 | 18.19 | 0.092 | 40.91 | 0.02 | 0.102 | 35.25 |
| Aspect | 1564–2000 | 2001–2100 | 2101–2300 | 2301–2500 | 2501–2736 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | |
| Flat | 3 | 0.072 | 46.34 | 6.4 | 0.077 | 43.93 | 1.6 | 0.100 | 42.84 | 0.18 | 0.110 | 40.06 | 0.09 | 0.161 | 38.74 |
| North (0–22.5 and 337.5–360) | 29 | 0.065 | 46.22 | 71.6 | 0.074 | 44.35 | 39.2 | 0.086 | 42.82 | 8 | 0.120 | 39.92 | 2.67 | 0.144 | 38.15 |
| Northeast (22.5–67.5) | 41 | 0.062 | 46.58 | 92.5 | 0.071 | 44.72 | 581 | 0.082 | 43.73 | 14.7 | 0.112 | 41.15 | 6.25 | 0.137 | 39.57 |
| East (67.5–112.5) | 34 | 0.062 | 47.05 | 83.6 | 0.068 | 44.89 | 65.6 | 0.077 | 44.07 | 19.1 | 0.107 | 42.26 | 6.82 | 0.135 | 40.81 |
| Southeast (112.5–157.5) | 26 | 0.061 | 47.11 | 60.1 | 0.066 | 44.82 | 43.4 | 0.072 | 43.80 | 9.5 | 0.108 | 41.25 | 3.0 | 0.132 | 39.69 |
| South (157.5–202.5) | 23 | 0.065 | 46.40 | 56.4 | 0.066 | 44.43 | 31.9 | 0.079 | 42.78 | 5.8 | 0.110 | 39.86 | 2.34 | 0.135 | 38.30 |
| Southwest (202.5–247.5) | 31 | 0.064 | 45.23 | 62.8 | 0.069 | 43.86 | 33.9 | 0.079 | 42.09 | 8.3 | 0.120 | 38.64 | 3.53 | 0.138 | 35.93 |
| West (247.5–292.5) | 32 | 0.065 | 45.03 | 68.8 | 0.073 | 43.69 | 38.6 | 0.082 | 41.89 | 9.4 | 0.120 | 38.51 | 3.08 | 0.147 | 35.84 |
| Northwest (292.5–337.5) | 27 | 0.067 | 45.66 | 68.9 | 0.077 | 43.90 | 35.6 | 0.085 | 42.32 | 6.0 | 0.126 | 38.97 | 2.16 | 0.151 | 36.57 |
| Slope in Degree | 1564–2000 | 2001–2100 | 2101–2300 | 2301–2500 | 2501–2736 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | Area | Mean NDVI | Mean LST | |
| 0.00–3.00 | 178.66 | 0.066 | 46.45 | 395.4 | 0.073 | 44.43 | 107.58 | 0.086 | 43.13 | 6.86 | 0.121 | 40.74 | 1.59 | 0.136 | 39.56 |
| 3.01–7.00 | 60.24 | 0.059 | 45.97 | 150.4 | 0.067 | 44.37 | 150.60 | 0.078 | 43.44 | 22.25 | 0.115 | 40.85 | 6.47 | 0.141 | 39.22 |
| 7.01–13.00 | 5.20 | 0.064 | 43.82 | 22.10 | 0.067 | 43.85 | 70.10 | 0.075 | 43.01 | 30.34 | 0.112 | 40.65 | 11.28 | 0.140 | 38.88 |
| 13.01–23.00 | 0.79 | 0.057 | 39.08 | 1.80 | 0.066 | 42.79 | 15.72 | 0.074 | 41.66 | 19.54 | 0.111 | 40.46 | 9.23 | 0.141 | 38.70 |
| 23.01–59.86 | 2.12 | 0.032 | 36.67 | 1.52 | 0.066 | 36.21 | 3.75 | 0.087 | 36.78 | 1.99 | 0.120 | 39.70 | 1.39 | 0.150 | 37.48 |
| Data | Study Area | Authors | Results |
|---|---|---|---|
| Landsat−7 | Delhi, India | [58] | LST-NDVI showed a negative correlation |
| ASTER | Delhi, India | [20] | Day-Night LST with impervious surface, positive correlation |
| Landsat-5 & Landsat-7 | South Karkheh, Iran | [88] | LST-NDVI showed a negative correlation |
| Landsat-5 | Shenyang, China | [87] | “LST and NDVI scatter plots showed triangle relation, the three directions represent water area, green land and cultivated land, construction land, respectively” |
| Landsat-5 | Guilin, China | [89] | LST-NDVI showed a negative correlation |
| Landsat-8 | Guizhou, China | [90] | “LST and NDVI scatter plots showed an obtuse-angled triangle distribution” |
| ASTER | Abha, Saudi Arabia | Current research | LST-NDVI showed a negative correlation and NDVI scatter plots showed an “obtuse-angled triangle” distribution |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bindajam, A.A.; Mallick, J.; AlQadhi, S.; Singh, C.K.; Hang, H.T. Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia. Atmosphere 2020, 11, 762. https://doi.org/10.3390/atmos11070762
Bindajam AA, Mallick J, AlQadhi S, Singh CK, Hang HT. Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia. Atmosphere. 2020; 11(7):762. https://doi.org/10.3390/atmos11070762
Chicago/Turabian StyleBindajam, Ahmed Ali, Javed Mallick, Saeed AlQadhi, Chander Kumar Singh, and Hoang Thi Hang. 2020. "Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia" Atmosphere 11, no. 7: 762. https://doi.org/10.3390/atmos11070762
APA StyleBindajam, A. A., Mallick, J., AlQadhi, S., Singh, C. K., & Hang, H. T. (2020). Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia. Atmosphere, 11(7), 762. https://doi.org/10.3390/atmos11070762





