High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model
Abstract
1. Introduction
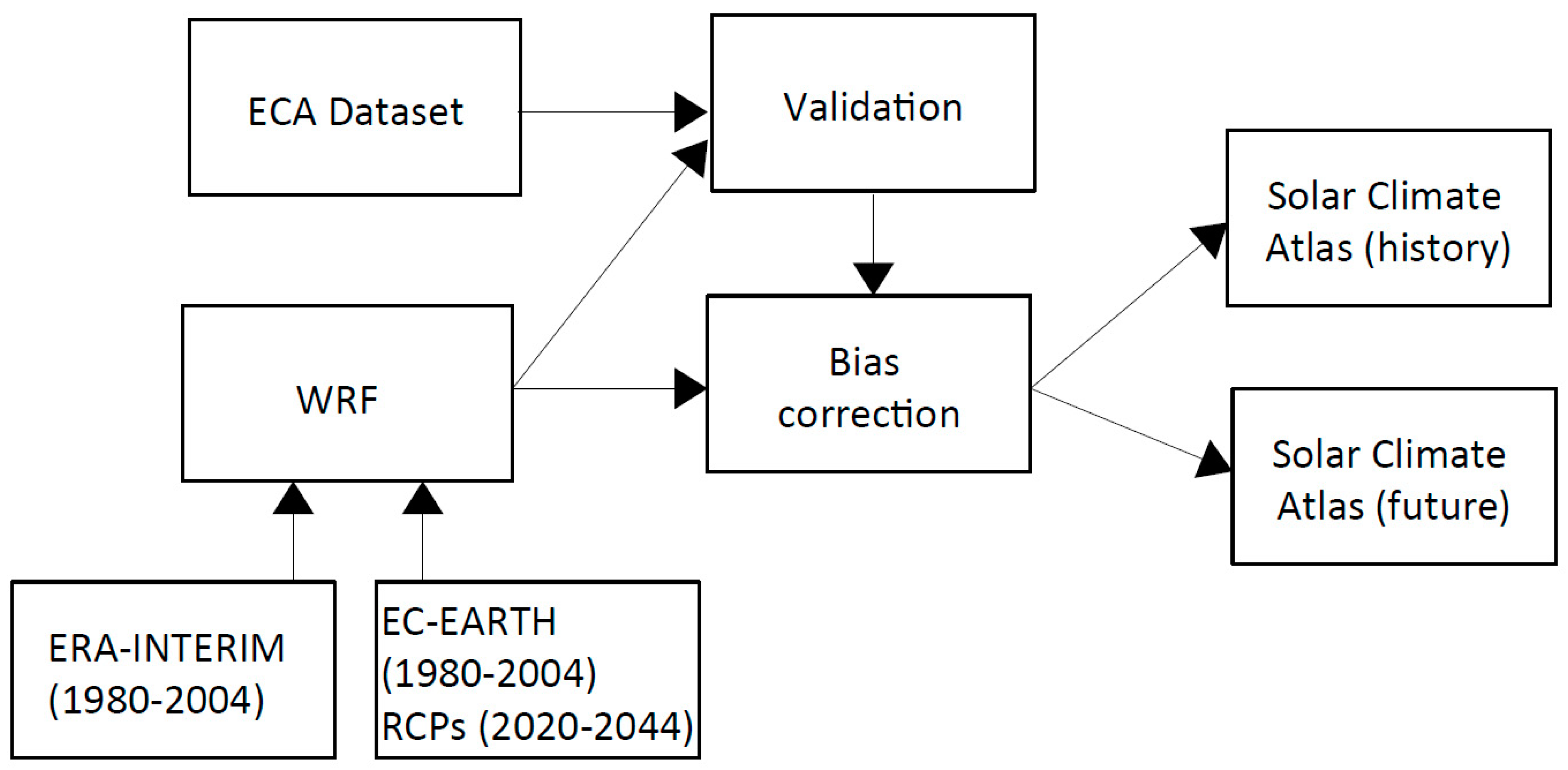
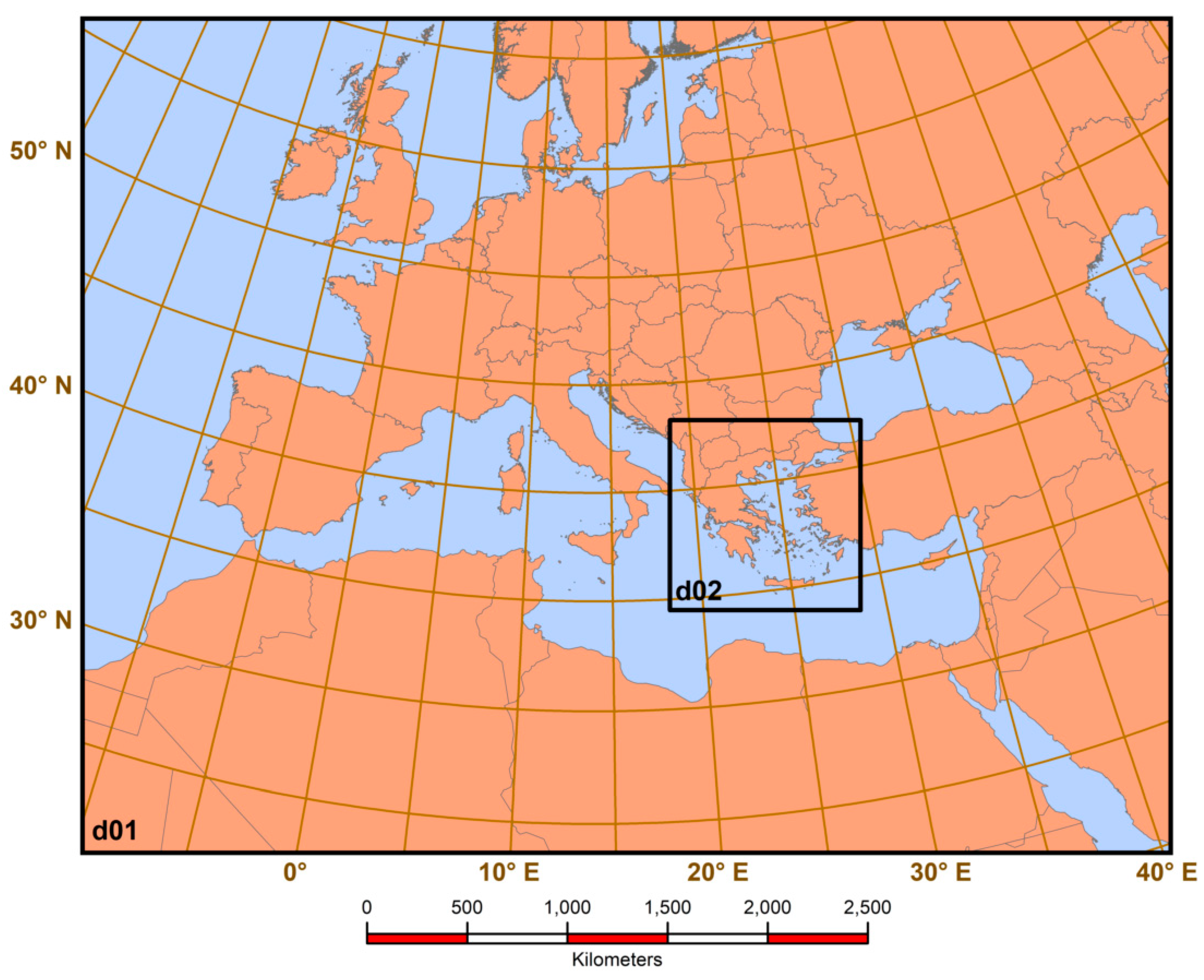
2. Data and Methodology
2.1. Data Sources
2.2. Derived Solar Climatology Parameters
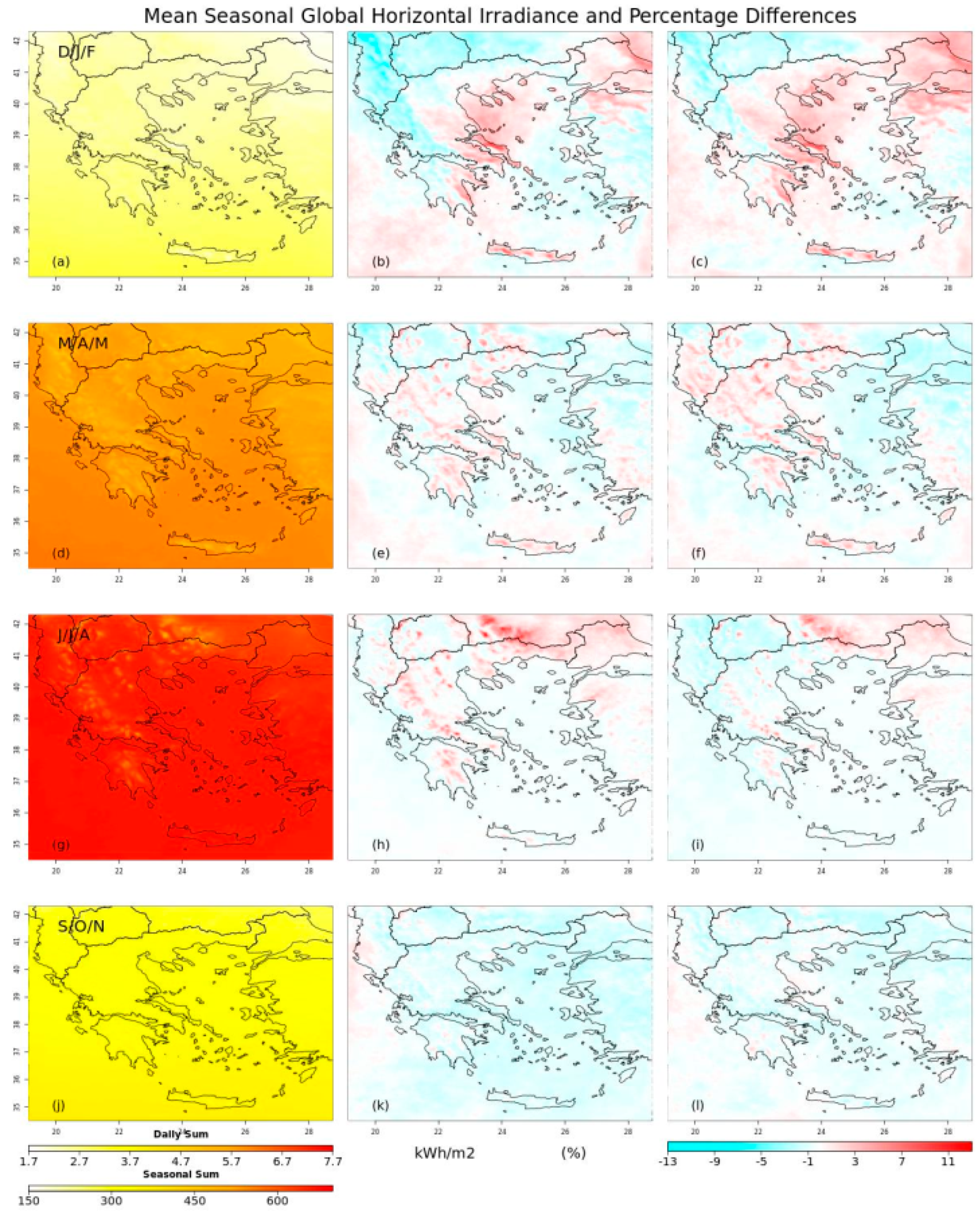
2.2.1. Mean Daily Global Horizontal and Direct Normal Irradiation
2.2.2. Sunshine Duration
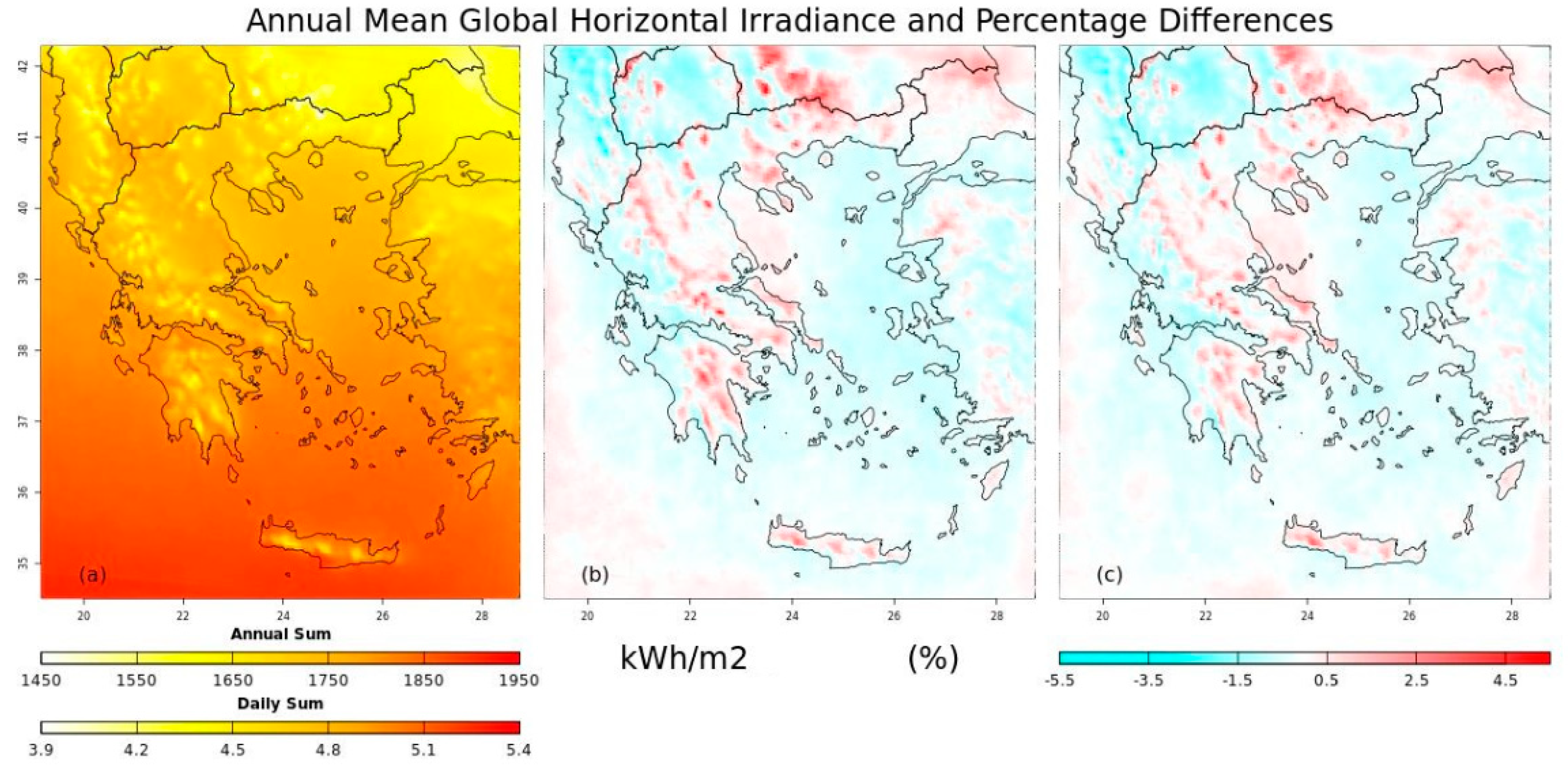
2.2.3. Annual GHI Estimation (kWh/m2)
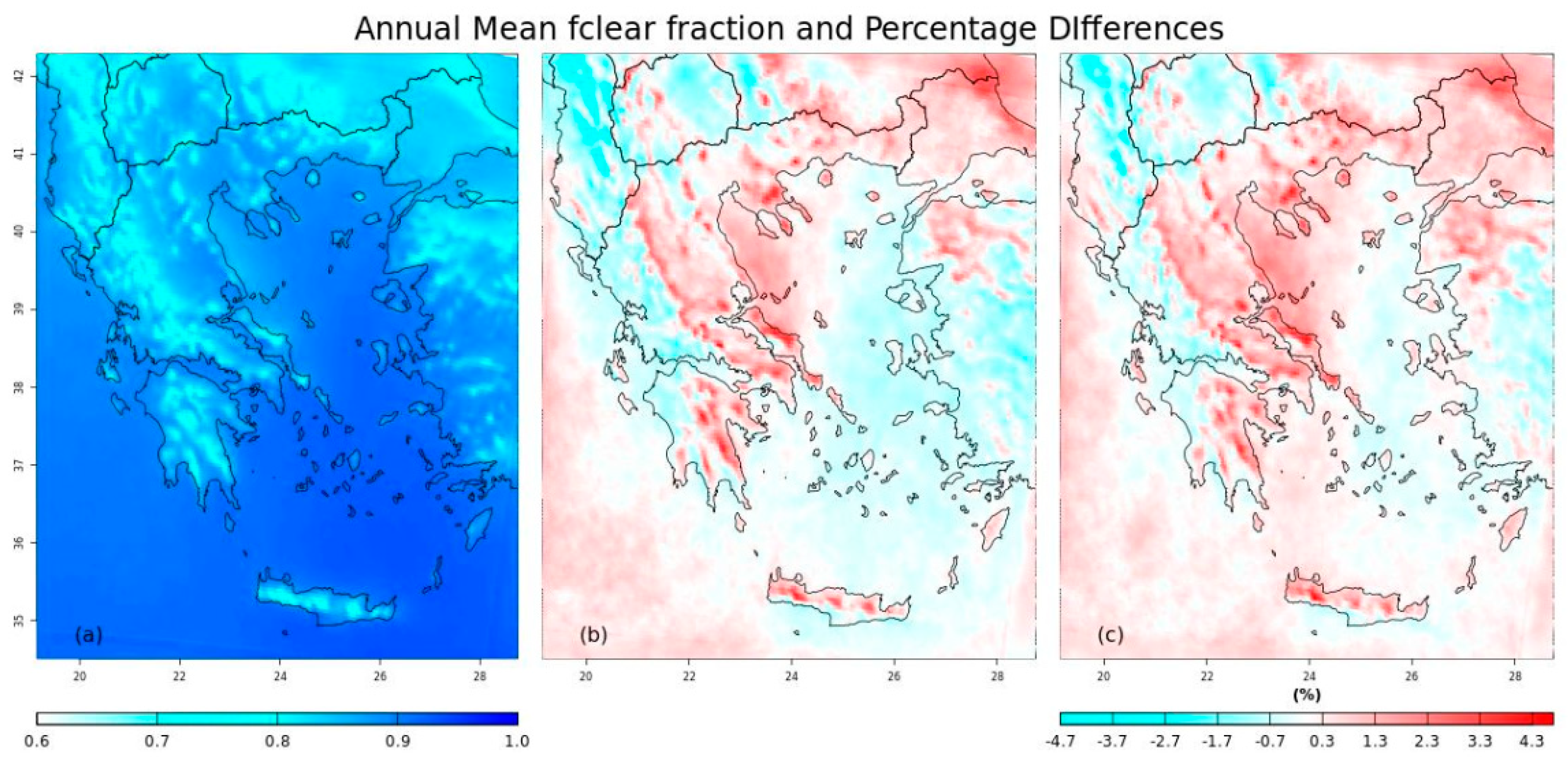
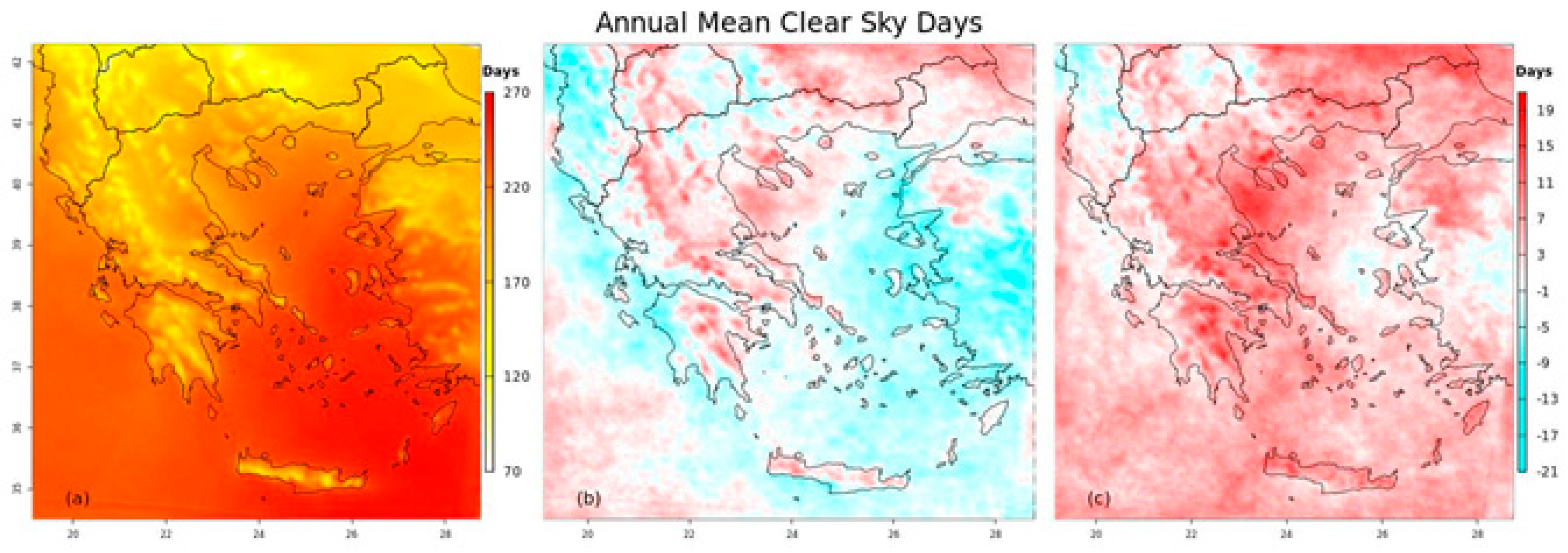
2.2.4. Clear-Sky Days and fclear
3. WRF Solar Climatology Performance Validation
3.1. ECA Dataset
3.2. Qualitative Comparison
4. Reconstructing a Very High-Resolution Solar Climate Atlas for Greece
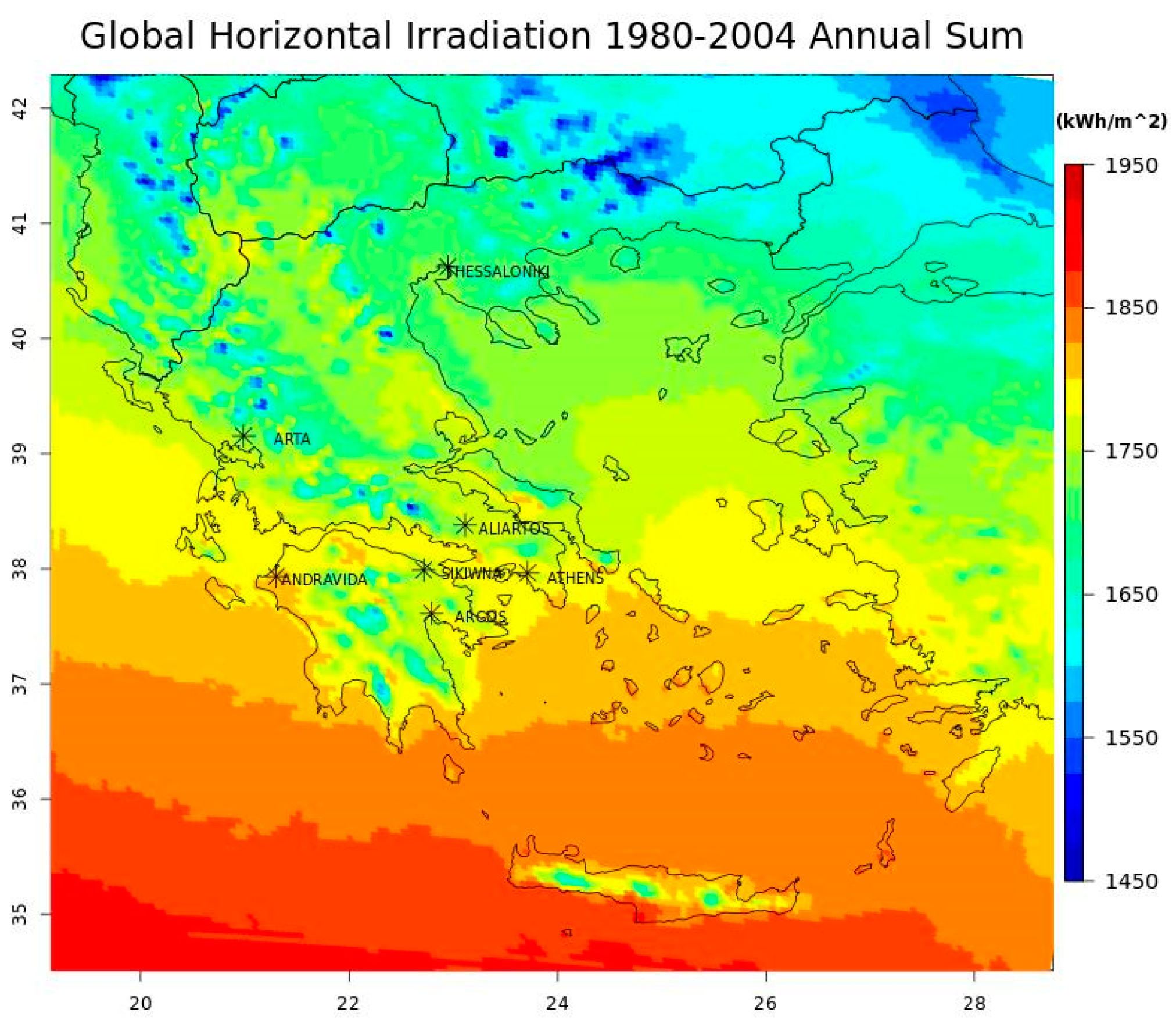
4.1. Mean Annual GHI Analysis
4.2. Mean Seasonal GHI Analysis
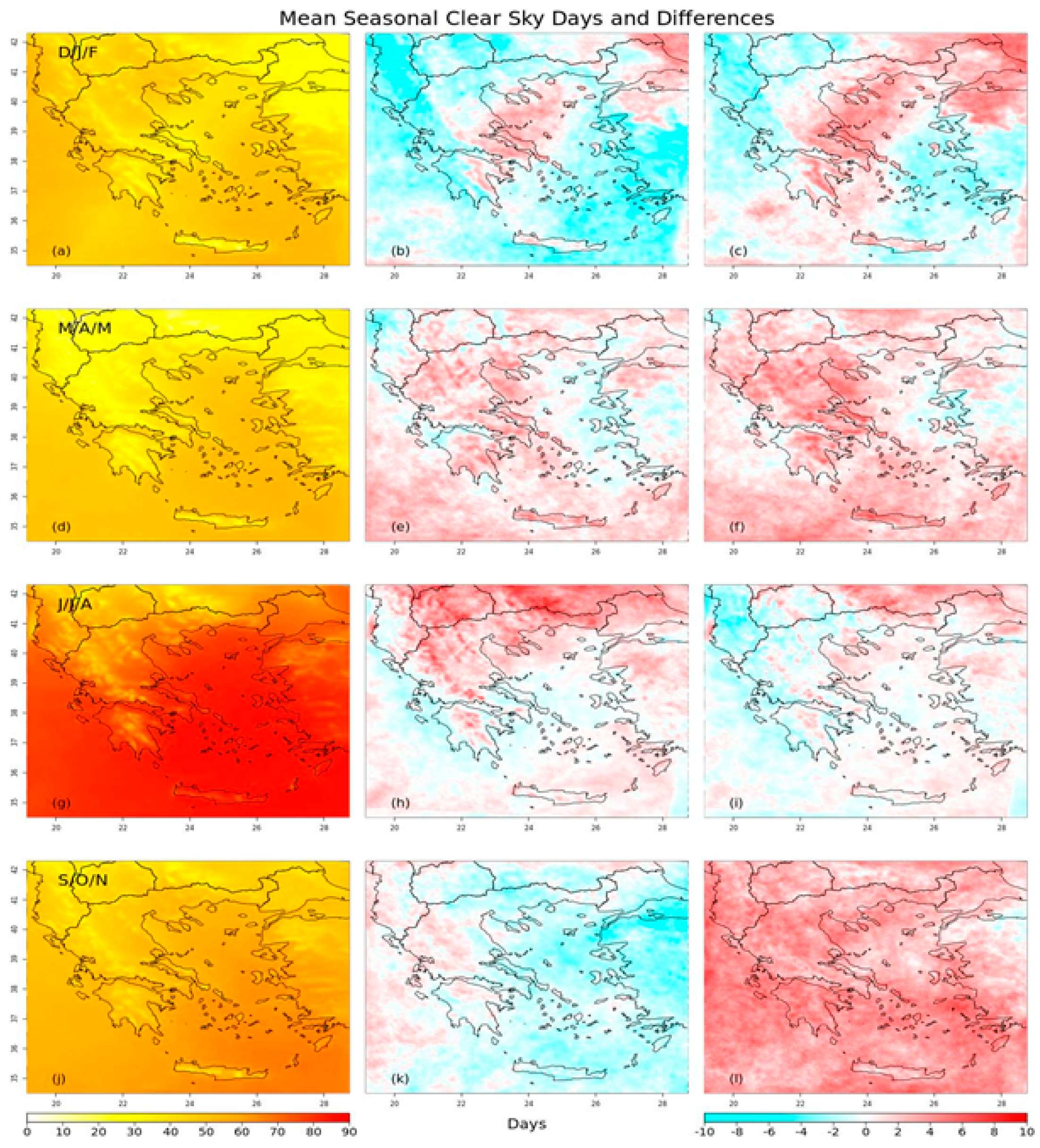
4.3. Clear-Sky Fraction- fclear -and Number of Clear-Sky Days
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- REN21. Renewables 2019—Global Status Report; REN21 Secretariat: Paris, France, 2019. [Google Scholar]
- Chowdhury, M.S.; Rahman, K.S.; Chowdhury, T.; Nuthammachot, N.; Techato, K.; Akhtaruzzaman, M.; Tiong, S.K.; Sopian, K.; Amin, N. An overview of solar photovoltaic panels’ end-of-life material recycling. Energy Strategy Rev. 2020, 27, 100431. [Google Scholar] [CrossRef]
- Huang, W.-H.; Shin, W.J.; Wang, L.; Sun, W.-C.; Tao, M. Strategy and technology to recycle wafer-silicon solar modules. Sol. Energy 2017, 144, 22–31. [Google Scholar] [CrossRef]
- Schaeffer, R.; Szklo, A.S.; Pereira de Lucena, A.F.; Moreira Cesar Borba, B.S.; Pinheiro Pupo Nogueira, L.; Pereira Fleming, F.; Troccoli, A.; Harrison, M.; Sadeck Boulahya, M. Energy sector vulnerability to climate change: A review. Energy 2012, 38, 1–12. [Google Scholar] [CrossRef]
- Liu, D.L.; Scott, B.J. Estimation of solar radiation in Australia from rainfall and temperature observations. Agric. For. Meteorol. 2001, 106, 41–59. [Google Scholar] [CrossRef]
- Martín, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Sol. Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Mathiesen, P.; Kleissl, J. Evaluation of numerical weather prediction for intra-day solar forecasting in the continental United States. Sol. Energy 2011, 85, 967–977. [Google Scholar] [CrossRef]
- Ma, W.W.; Rasul, M.G.; Liu, G.; Li, M.; Tan, X.H. Climate change impacts on techno-economic performance of roof PV solar system in Australia. Renew. Energy 2016, 88, 430–438. [Google Scholar] [CrossRef]
- Pan, Z.; Segal, M.; Arritt, R.W.; Takle, E.S. On the potential change in solar radiation over the US due to increases of atmospheric greenhouse gases. Renew. Energy 2004, 29, 1923–1928. [Google Scholar] [CrossRef]
- Crook, J.A.; Jones, L.A.; Forster, P.M.; Crook, R. Climate change impacts on future photovoltaic and concentrated solar power energy output. Energy Environ. Sci. 2011, 4, 3101. [Google Scholar] [CrossRef]
- Müller, J.; Mitra, I.; Mieslinger, T.; Meyer, R.; Chhatbar, K.; Gomathinayagam, S.; Giridhar, G. Towards building solar in India—A combined mapping and monitoring approach for creating a new solar atlas. Energy Sustain. Dev. 2017, 40, 31–40. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.A.; Dunlop, E.D.; Ossenbrink, H.A. Potential of solar electricity generation in the European Union member states and candidate countries. Sol. Energy 2007, 81, 1295–1305. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Burnett, D.; Barbour, E.; Harrison, G.P. The UK solar energy resource and the impact of climate change. Renew. Energy 2014, 71, 333–343. [Google Scholar] [CrossRef]
- Kazadzis, S.; Founda, D.; Psiloglou, B.E.; Kambezidis, H.; Mihalopoulos, N.; Sanchez-Lorenzo, A.; Meleti, C.; Raptis, P.I.; Pierros, F.; Nabat, P. Long-term series and trends in surface solar radiation in Athens, Greece. Atmos. Chem. Phys. 2018, 18, 2395–2411. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Nikitidou, E.; Salamalikis, V.; Tzoumanikas, P.; Zagouras, A. New challenges in solar energy resource and forecasting in Greece. Int. J. Sustain. Energy 2018, 37, 428–435. [Google Scholar] [CrossRef]
- Panagea, I.S.; Tsanis, I.K.; Koutroulis, A.G.; Grillakis, M.G. Climate Change Impact on Photovoltaic Energy Output: The Case of Greece. Adv. Meteorol. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Politi, N.; Sfetsos, A.; Vlachogiannis, D.; Nastos, P.T.; Karozis, S. A Sensitivity Study of High-Resolution Climate Simulations for Greece. Climate 2020, 8, 44. [Google Scholar] [CrossRef]
- Politi, N.; Nastos, P.T.; Sfetsos, A.; Vlachogiannis, D.; Dalezios, N.R. Evaluation of the AWR-WRF model configuration at high resolution over the domain of Greece. Atmos. Res. 2018, 208, 229–245. [Google Scholar] [CrossRef]
- ECA&D Daily Data. Available online: https://www.ecad.eu/dailydata/index.php (accessed on 5 February 2020).
- Klein Tank, A.M.G.; Wijngaard, J.B.; Können, G.P.; Böhm, R.; Demarée, G.; Gocheva, A.; Mileta, M.; Pashiardis, S.; Hejkrlik, L.; Kern-Hansen, C.; et al. Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment: EUROPEAN TEMPERATURE AND PRECIPITATION SERIES. Int. J. Climatol. 2002, 22, 1441–1453. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Navarro, J.C.; Batté, L.; Volpi, D.; Acosta, M.; Bellprat, O.; Bilbao, R.; Castrillo, M.; Fučkar, N.; Guemas, V.; et al. Using EC-Earth for climate prediction research. ECMWF Newsl. 2018. [Google Scholar] [CrossRef]
- SolarGIS. Solar Data behind the Maps. Available online: https://solargis.com/maps-and-gis-data/tech-specs (accessed on 15 April 2020).
- Dai, A.; Trenberth, K.E.; Karl, T.R. Effects of Clouds, Soil Moisture, Precipitation, and Water Vapor on Diurnal Temperature Range. J. Clim. 1999, 12, 23. [Google Scholar] [CrossRef]
- Suehrcke, H. On the relationship between duration of sunshine and solar radiation on the earth’s surface: Ångström’s equation revisited. Sol. Energy 2000, 68, 417–425. [Google Scholar] [CrossRef]
- The World Bank. Source: Global Solar Atlas 2.0-Solar Resource Data: Solargis; The World Bank: Washington, DC, USA, 2020; Available online: https://solargis.com/maps-and-gis-data/download/greece (accessed on 6 February 2020).
- Arima, Y.; Ooka, R.; Kikumoto, H. Bias correction method for solar radiation based on quantile mapping to provide weather data for building energy simulations. J. Environ. Eng. Trans. AIJ 2016, 81, 1047–1054. [Google Scholar] [CrossRef]
- Frank, C.W.; Wahl, S.; Keller, J.D.; Pospichal, B.; Hense, A.; Crewell, S. Bias correction of a novel European reanalysis data set for solar energy applications. Sol. Energy 2018, 164, 12–24. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Boland, J.; Schmutz, N.; Lauret, P. Post-processing of solar irradiance forecasts from WRF model at Reunion Island. Sol. Energy 2014, 105, 99–108. [Google Scholar] [CrossRef]
- GEO-CRADLE Project. The Solar Atlas of Greece (1999–2013). Available online: http://datahub.geocradle.eu/solar/ (accessed on 7 February 2020).
- Matzarakis, A.P.; Katsoulis, V.D. Sunshine duration hours over the Greek region. Theor. Appl. Climatol. 2006, 83, 107–120. [Google Scholar] [CrossRef]
- Martinopoulos, G.; Tsalikis, G. Diffusion and adoption of solar energy conversion systems—The case of Greece. Energy 2018, 144, 800–807. [Google Scholar] [CrossRef]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. 2008, 113, D20119. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. Global warming due to increasing absorbed solar radiation: Global warming by solar radiation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- HNMS Climate Atlas of Greece (1971–2000). Available online: http://climatlas.hnms.gr/sdi/ (accessed on 25 February 2020).
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
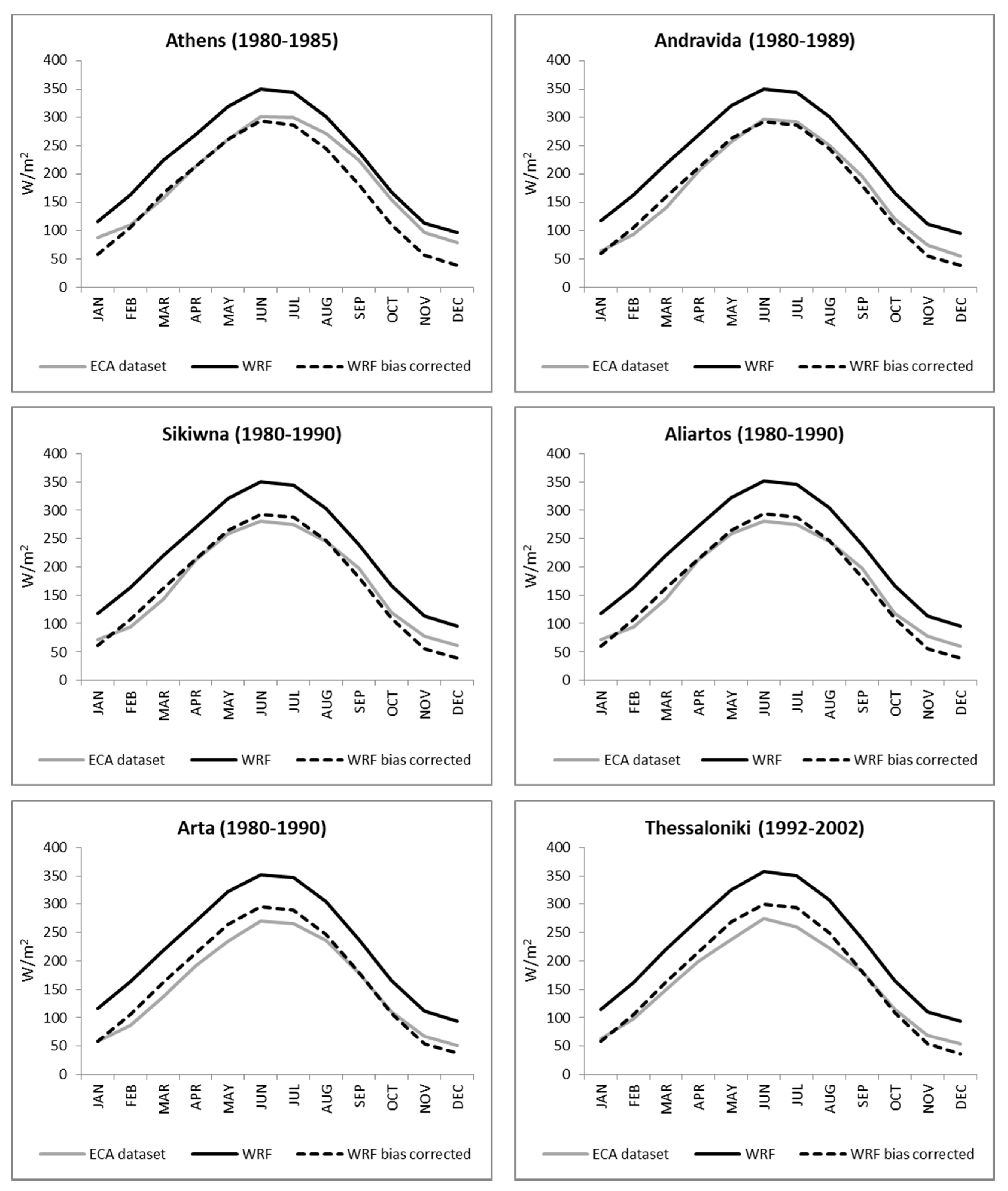
| Locations | LAT | LON | Time Period of Valid Measurements | COR | BIAS (W/m2) | MAPE (%) | RMSE (W/m2) | COR * | BIAS * (W/m2) | MAPE * (%) | RMSE * (W/m2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WRF direct output | WRF bias corrected output | ||||||||||
| Athens | 37.58 | 23.43 | (1980–1985) | 0.98 | 37.42 | 22.40 | 41.72 | 0.98 | −19.72 | 16.51 | 27.00 |
| Arta | 39.10 | 21.00 | (1980–1990) | 0.99 | 67.64 | 53.70 | 69.24 | 0.99 | 10.51 | 11.39 | 18.14 |
| Aliartos | 38.23 | 23.06 | (1980–1990) | 0.99 | 56.45 | 40.73 | 58.13 | 0.99 | −0.68 | 11.27 | 13.90 |
| Sikiwna | 37.59 | 22.44 | (1980–1990) | 0.99 | 55.74 | 39.94 | 57.49 | 0.99 | −1.39 | 11.44 | 14.13 |
| Andravida | 37.55 | 21.17 | (1980–1989) | 0.99 | 53.78 | 42.03 | 55.04 | 0.99 | −3.35 | 9.92 | 12.17 |
| Argos | 37.36 | 22.47 | (1983–1990) | 0.99 | 62.74 | 41.99 | 66.21 | 0.99 | 5.60 | 15.25 | 21.91 |
| Thessaloniki | 40.38 | 22.58 | (1992–2002) | 1.00 | 66.16 | 48.55 | 68.29 | 1.00 | 9.03 | 11.55 | 19.17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katopodis, T.; Markantonis, I.; Politi, N.; Vlachogiannis, D.; Sfetsos, A. High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model. Atmosphere 2020, 11, 761. https://doi.org/10.3390/atmos11070761
Katopodis T, Markantonis I, Politi N, Vlachogiannis D, Sfetsos A. High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model. Atmosphere. 2020; 11(7):761. https://doi.org/10.3390/atmos11070761
Chicago/Turabian StyleKatopodis, Theodoros, Iason Markantonis, Nadia Politi, Diamando Vlachogiannis, and Athanasios Sfetsos. 2020. "High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model" Atmosphere 11, no. 7: 761. https://doi.org/10.3390/atmos11070761
APA StyleKatopodis, T., Markantonis, I., Politi, N., Vlachogiannis, D., & Sfetsos, A. (2020). High-Resolution Solar Climate Atlas for Greece under Climate Change Using the Weather Research and Forecasting (WRF) Model. Atmosphere, 11(7), 761. https://doi.org/10.3390/atmos11070761








