Abstract
We analyzed 28-year-long monthly oxygen isotope composition of precipitation (δ18Op) data from Punta Arenas (Chile) on the leeward side of the Andes to understand how different synoptic weather types and moisture transport pathways influence δ18Op variability in this region. Combining weather station 6 h precipitation data and atmospheric back trajectories, we found that in such a region where the atmospheric circulation pattern is dominated by very strong westerlies, an increased monthly proportion of easterly-delivered precipitation—with the air-mass trajectory path evading the influence of Andean “isotopic rain shadow” and having less rainout en route—would increase δ18Op. These synoptic easterlies are a result of quasi-stationary blocking-like flow that are an important but underappreciated part of regional circulation patterns and climate. In addition, synoptic easterlies are more often associated with heavy precipitation events as shown by weather station data and higher deuterium excess that indicates weaker post-condensation raindrop re-evaporation. Therefore, our analysis demonstrated the process link between the frequency of synoptic weather types characterized by blocking-like flow and temporal variations in δ18Op in Southern Patagonia. We conclude that isotope proxy paleo-records in this region could provide unique insights into the behaviors and dynamics of the large-scale Southern Hemisphere Westerly Winds over long timescales.
1. Introduction
Stable isotopes in water (δ18O and δ2H) have been widely used as geochemical tracers for the hydrological cycle. Isotopic fractionation occurs in water molecules during phase transitions modulated by transport and also biotic processes, leading to distinct variations in isotopic compositions across the hydrosphere [1]. Of particular importance is the isotopic composition in precipitation (most of studies focus on oxygen isotopes in precipitation, δ18Op) with a large number of data collected since the 1950s [2]. The δ18Op data showed empirical relationships with climatic variables such as air temperature in the high-latitude regions and precipitation amount in the tropical regions [3]. The Rayleigh distillation model that depicts isotopic fractionations in air mass rainout processes could explain much of δ18Op variability at various temporal and spatial scales in both observations and models [3,4,5]. These well-established relationships between δ18Op and climatic variables led to applying stable isotope proxies in terrestrial climate archives to reconstruct past hydrological and climatic conditions (e.g., [6,7,8,9,10]). Over geological timescales, because of the strong connections among topography, climate, and atmospheric circulations, stable isotopes have also been used as proxies for terrain elevation to reconstruct landscape evolution (e.g., [11,12]). However, studies also revealed that the drivers controlling δ18Op variations are more complex and that air mass origin and history (e.g., [13,14,15]), in-cloud and below-cloud processes (e.g., [16,17,18]), as well as moisture recycling (e.g., [19,20,21]), are also important in some regions. It is particularly relevant in regions with complex terrain, where regional topographic features can additionally influence air mass transport, water vapor condensation, and consequently, the isotopic composition of precipitation [14,22,23,24,25,26].
Monitoring temporal variations in δ18Op provides an excellent opportunity to elucidate the confounding factors that influence δ18Op for a specific location or region. For many studies of this kind, precipitation samples were collected for individual events or at daily intervals. Rather than simply analyzing the relationships between δ18Op and local meteorological parameters, event-based studies usually link the δ18Op signal in each individual sample with the origin and history of an air mass preceding that event or a specific synoptic weather type [14,15,19,27,28,29,30], using tools such as the U.S. National Oceanic and Atmospheric Administration (NOAA) Air Resources Laboratory (ARL) Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model [31]. The rationale behind this practice is that the δ18Op signal reflects isotopic fractionation that occurs in evaporative source and during moisture transport more than local meteorology [32], although precipitation type (convective vs. stratiform) is also an important local factor affecting δ18Op in the tropical and mid-latitude regions [18,33]. Another important precipitation isotope database is the Global Network of Isotopes in Precipitation (GNIP) that archives isotope data from monthly-composited precipitation [34]. Because isotope data from monthly-composited precipitation have mixed isotopic signals from multiple precipitation events during that month, studies using GNIP data usually focus on precipitation isotope seasonality, long-term trends, empirical relationships with climatic variables, and statistics of meteoric water lines inferred from each individual GNIP station [4]. The influence of moisture sources and transport pathways on individual GNIP monthly δ18Op observations is rarely explored [35] due to the mixed signals from multiple precipitation events that make identifying process-based mechanisms difficult [14]. In fact, some of the GNIP stations have observational data over several decades. These observational data encompass longer-term δ18Op variability originated from changes in prevailing synoptic-scale circulation patterns than event-based data that usually only span one or a few years.
Here, we developed a new framework to leverage the value of GNIP monthly-composited δ18Op data in identifying process-based synoptic mechanisms that control δ18Op variability. We analyzed 28-year-long GNIP monthly δ18Op data from Punta Arenas (Chile) in Southern Patagonia, a region surrounded by ocean and with complex terrain. Southern Patagonia is in the core belt of the Southern Hemisphere Westerly Winds (SHWWs) that exert strong and year-round influence on regional climate [36]. Previous isotope-based paleoclimate and paleoaltimetry studies in this region (and Northern Patagonia) assumed that the westerlies—that pass over the Andes—are the only major moisture transport path for the eastern side of Patagonia [12,37,38] but did not consider the role of synoptic-scale circulation patterns within the SHWW belt such as the quasi-stationary easterlies and northerlies [39,40]. We combined weather station precipitation data and the HYSPLIT back-trajectory model to quantify the proportions of precipitation attributed to different trajectory clusters that represent distinct synoptic weather types in this region for each month. This would allow us to extract the effect of synoptic weather types and moisture transport pathways on monthly-composited δ18Op. We discussed how isotope proxy paleo-records in this region could reflect the changes in the frequency of these synoptic weather types that in turn elucidate the SHWW behaviors and dynamics.
2. Regional Setting
Punta Arenas is the capital city of Chile’s southernmost Magallanes Region, and one of the southernmost cities in the world. The city is situated with the Strait of Magellan to the east and low-lying hills and plateaus to the west. The GNIP Punta Arenas station (53.00° S, 70.83° W, 38 m above sea level (asl)) is located at Punta Arenas airport (PUQ), ~20 km north of the main city. The local terrain to the west is flat at the airport without low-lying hills and plateaus, unlike the main city.
Punta Arenas is in the unique topographic context of Southern Patagonia where climate is strongly influenced by the interaction between the strong SHWWs and the north-to-south oriented Andean mountain ranges (Figure 1). A large precipitation gradient occurs from the Pacific to Atlantic coasts as a result of uplift and downslope subsidence of westerlies and their embedded disturbances [36,41]. Therefore, Punta Arenas (including its airport) is clearly in the Andean rain shadow [42], although the Andean topographic barrier in the west is lower, with most terrain elevations less than 1000 m asl, than the rest of Patagonia (Figure 1). The mean annual precipitation amount in Punta Arenas airport was 402 mm, based on data from the Global Historical Climatology Network (GHCN) Version 2 [43] during the period 1990–2017. It is an order of magnitude less than Andean locations in the same latitude where mean annual precipitation amounts are more than 3000 mm [44,45]. Our analysis of combined wind sensor and precipitation data from airport weather station indicates that “local” westerlies (NW, WNW, W, WSW, and SW) account for 72% of total hours but only 41% of total precipitation amount during the period 1990–2017 (Figure A1a,b). In terms of the quotient between precipitation and frequency of the respective “local” wind direction [46], however, “local” non-westerlies are over three times more effective in bringing precipitation to Punta Arenas (Figure A1c). This reinforces the prevailing rain shadow effect on the leeward side of the Andes, while westerlies are still able, although less effectively, to deliver a large proportion of moisture to Punta Arenas.
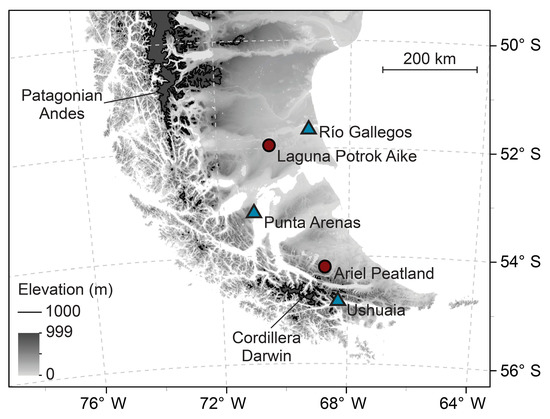
Figure 1.
Digital elevation map of Southern Patagonia. Also shown are major cities (cyan triangles) and field sites (red dots) discussed in this paper, and the elevation contour of 1000 m asl. The digital elevation model is from the Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010) at 30-arc-second resolution [47].
The influence of the SHWWs on Punta Arenas is year-round. During austral summer, the SHWWs form a condensed and strong belt between 45° S and 55° S and maximum wind speeds are reached in Punta Arenas. During austral winter, the SHWW belt expands northward as far as 30° S while the wind speed only relatively weakens in the south, including at Punta Arenas [48]. Despite the seasonal variations in the SHWWs, the seasonality of precipitation in Punta Arenas is very weak with only slightly more precipitation during austral autumn [49]. The mean annual air temperature in Punta Arenas airport was 6.2 °C, while the mean warmest month (January) air temperature was 10.8 °C and the mean coldest month (July) air temperature was 1.6 °C during the period 1990–2017 based on data from GHCN Version 3 [43]. Based on the Köppen−Geiger climate classification map [50], Punta Arenas is located at the boundary between Tundra climate (ET) and Subpolar oceanic climate (Cfc) zone.
Inter-annual or long-term climate variability in Southern Patagonia has been tied to the large-scale Southern Annular Mode (SAM), which is defined as the difference in zonal mean sea level pressure (SLP) between 40° S and 65° S [51]. This pressure gradient controls hemisphere-wide strength and latitudinal position of the SHWWs, and consequently, their associated storm tracks. Instrumental and reanalysis data suggest the leading role of the SAM on both temperature and precipitation patterns in broad regions of the extratropical Southern Hemisphere, including Southern Patagonia [48,52]. Specifically, a positive phase of the SAM, through the stronger and southwardly positioned SHWWs, increases air temperature but only marginally decreases precipitation in the domain of Punta Arenas, and vice versa [48,52,53]. The weak influence of the SAM on precipitation in Southern Patagonia is partly due to the fact that the SAM is a hemisphere-wide climate mode, while regional precipitation variability is mainly controlled by synoptic-scale processes.
3. Data
3.1. GNIP Isotope Data
Monthly precipitation isotope data from the GNIP Punta Arenas (airport) station are available from 1990 to 2017 with some short data gaps (Table S1) [34]. In total, there are 298 individual δ18Op measurements. The dataset contains some very high or even positive δ18Op values after 2002 (Figure 2b), which have been pointed out previously [49]. These samples likely experienced evaporation for unknown reasons, and the reason why these very high δ18Op values only appeared after 2002 is unknown. Since 2010, GNIP Punta Arenas station has started to label isotope data that showed a hint of sample evaporation if the calculated deuterium excess (d-excess, defined as δ2H − 8 × δ18O) value was below zero, although some of these potential problematic data were not necessarily impacted by sample evaporation, as d-excess usually has a relatively large scatter, and a value lower than zero is not unusual in maritime climates [1] such as in Punta Arenas. For the following HYSPLIT analysis, we filtered out GNIP data by removing those δ18Op data that were above −3‰ or that had corresponding d-excess below −10‰ (Figure 2a). These criteria were subjectively chosen but reasonable as δ18Op and d-excess values falling in these ranges are indeed too extreme to occur in monthly-composited precipitation at this latitude. Another GNIP station in Ushuaia (Argentina), located ~250 km southeast of Punta Arenas (see Figure 1), does not have any δ18Op data above −6.8‰ during its monitoring period 1981–2002. These two stations have a similar climate, yet Punta Arenas has a weighted mean annual δ18Op value 2‰–3‰ higher than Ushuaia; the exact value depends on how the potential outliers in both datasets were treated [49]. Considering this 2‰–3‰ offset would justify our conservative cut-off value (−3‰) for δ18Op. There are a few data with d-excess below −10‰ in Ushuaia likely due to sample evaporation as well, but these data only occurred before 1988 and were not an intermittent and common feature. This observation would also justify our cut-off value (−10‰) for d-excess. Nonetheless, we cannot rule out the small possibility that a few of these anomalously high δ18Op or low d-excess values are naturally occurring. If they were, the collected precipitation samples might be caused by a dominant contribution of local convective precipitation [18,33] or by a significant role of raindrop post-condensation re-evaporation [16,28]. Both mechanisms would underplay the role of moisture transport pathway in shaping the δ18Op value, thus removing a few of such values does not affect our analysis on robust data. We also removed two very low monthly δ18Op values. These two data points appear out of bound of typical observations (Figure 2a) and likely suggest additional factors that are not considered in our HYSPLIT framework; otherwise, these two extremes would have skewed the analysis. After the step of data filtering (all filtered out data are listed in Table S1), we obtained a final dataset with 265 δ18Op measurements. Each δ18Op datum has a corresponding d-excess value calculated from its paired δ2Hp (hydrogen isotope composition of precipitation) datum.
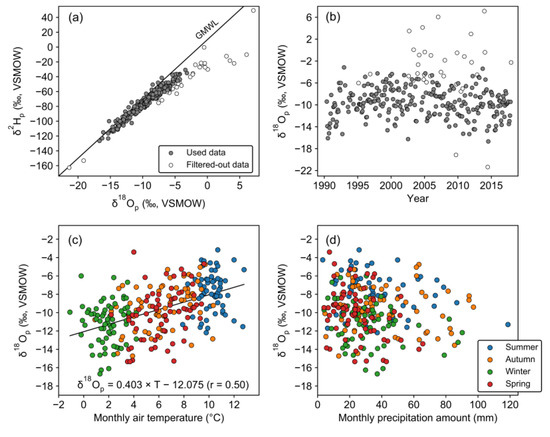
Figure 2.
Summary of Global Network of Isotopes in Precipitation (GNIP) precipitation isotope data from Punta Arenas [34]. (a) Scatter plot between monthly δ2Hp and δ18Op and the Global Meteoric Water Line (GMWL). (b) Long-term variations in monthly δ18Op during the period 1990–2017. Open dots in (a) and (b) are the raw data points that were excluded from the analysis hereafter (see Section 3.1 and Table S1 for details). (c) Scatter plot between monthly δ18Op and Global Historical Climatology Network (GHCN) monthly air temperature and their linear regression line. The use of GHCN monthly air temperature data [43] rather than GNIP monthly air temperature data is due to several potential erroneous data recordings in the GNIP database (see Figure A2d for details). One data gap in GHCN (February 2011) is filled by GNIP data. (d) Scatter plot between monthly δ18Op and Punta Arenas airport monthly cumulative precipitation (calculated from the sum of all 6 h precipitation data for each month; see Section 3.2 for details). There are 6 individual months during which precipitation data have temporal gaps, and these data are replaced by GHCN monthly precipitation amount data (see Figure A2a). In (c) and (d), symbols are color-coded to represent different austral seasons: summer (December–February), autumn (March–May), winter (June–August), and spring (September–November).
Among the selected data, it is clear that the monthly δ18Op value has a significant, though weak, linear correlation (p < 0.001) with monthly air temperature (Figure 2c), but not monthly precipitation amount (Figure 2d). A linear regression yields the relationship between monthly δ18Op and monthly air temperature (T) as:
where data for T are from GHCN version 3 [43] (Figure 2c). The observed seasonality in δ18Op is a prevalent phenomenon across the mid- and high-latitude regions even in maritime climate [1]. This δ18Op seasonality is driven by multiple processes, including changing moisture source region and condition as well as changing transport path and condensation history of water vapor among different seasons via the Rayleigh mechanism [1,4,32]. These net effects on δ18Op can be simply summarized by the empirical correlation with local air temperature. However, monthly air temperature is no more strongly correlated with δ18Op for summer (December–February; DJF) (p = 0.52) and winter (June–August; JJA) (p = 0.67), and explains less variance in δ18Op for autumn (March–May; MAM) (r = 0.38, p < 0.01) and spring (September–November; SON) (r = 0.38, p < 0.01). We thus define the δ18Op residual () as the observed δ18Op value () minus the regressed δ18Op value () obtained in Equation (1) as:
which allows us to explore other drivers controlling monthly δ18Op variability that are unrelated to δ18Op seasonality and/or air temperature. This approach is similar to but not the same as the multivariate regression approach by Krklec and Domínguez-Villar [54], who included both air temperature and monthly percentages of different moisture sources into their multivariate models.
δ18Op = 0.40 (±0.04) × T − 12.08 (±0.30) (r = 0.50),
3.2. Weather Station Precipitation Data
Punta Arenas airport cumulative precipitation amount data at 6 h intervals (at UTC time 00:00, 06:00, 12:00, and 18:00) are provided by the Dirección Meteorológica de Chile and are available for public download on [55]. The data were collected by Punta Arenas airport weather station. This same weather station also reports monthly climatology data to the GHCN (as presented in Section 3.1) and operates isotope sample collection for the GNIP [56]. The quality of 6 h cumulative precipitation data is robust as we find the monthly cumulative precipitation amount data, calculated from the sum of all 6 h precipitation data for each month, are clustering on the 1:1 line when plotted against either reported GHCN or GNIP monthly precipitation amount data (Figure A2a,b). Precipitation events (at least 0.1 mm) were recorded during 17% of all 6 h intervals. With 6 h cumulative precipitation data, we can explicitly know the time and precipitation amount of each precipitation event that together constitute the monthly precipitation sample that GNIP measured for isotopic composition.
4. Methods
We ran the HYSPLIT back-trajectory model to reconstruct the origin and path of air mass that resulted in precipitation event recorded by the weather station described above. We employed a Python-based package for HYSPLIT (PySPLIT) [57] to achieve a fast and flexible workflow in trajectory generation and analysis. Five-day (120 h) air mass backward trajectory was generated four times (at UTC time 00:00, 06:00, 12:00, and 18:00) at initial back-trajectory heights at 500, 1000, 1500, and 2000 m above ground level (agl) for each day from 1990 to 2017 to match with the 6 h cumulative precipitation data from the weather station. The duration of 120 h of back-trajectory modeling was chosen as it was long enough to allow trajectory clustering as introduced below and short enough to save computation capacity. For gridded meteorological datasets, we used the Global Data Assimilation System (GDAS) reanalysis dataset (1.0° spatial resolution) for the period 2005–2017. For the period 1990–2004 during which the GDAS dataset was not available, we used the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) reanalysis dataset (2.5° spatial resolution) [58]. Both datasets are archived on [59]. Based on the 6 h cumulative precipitation data from the weather station, trajectory files that are not associated with precipitation events were deleted. Then, all remaining trajectory files are associated with documented precipitation events. There are four trajectories with different initial back-trajectory heights for each event. For GDAS-based trajectories, only one trajectory at the height level that has the highest initial relative humidity was chosen for each event to better capture the level of precipitating air mass. Overall, 16%, 26%, 24%, and 34% of precipitation events have the highest relative humidity at the level of 500 m, 1000 m, 1500 m, and 2000 m, respectively. For NCEP/NCAR-based trajectories, this selection criterion was not reliable, as 64% of all events have the highest relative humidity at 500 m due to the limitation of the coarser-resolution reanalysis dataset; thus, we considered all cases of different initial back-trajectory heights specifically in the following analysis. We employed this simple but still realistic representation of precipitating air masses widely employed in literature [16,27,54,60,61], while a more complex approach has been applied using remote sensing data [32] or in an idealized framework [62]. To visualize the general trajectory pathway, we generated trajectory frequency contours by binning all precipitation-producing trajectory end point data in each 1.0° grid.
We grouped all generated trajectories into four clusters based on where trajectories entered into Southern Patagonian landmass. Although HYSPLIT GUI has provided a k-means clustering algorithm, it suggests that only a large number of clusters are appropriate to represent all trajectories in an acceptably low total spatial variance. To simplify the solution, we grouped trajectories based on the locations of back-trajectory end points when trajectories came across the eastern, northern, western, and southern boundaries of Southern Patagonian landmass (Figure A3). These trajectories were then clustered as the distal easterlies, northerlies, westerlies, and southerlies, respectively (Figure 3). These four trajectory pathway clusters represent major synoptic weather types in this region (see [45]). Here the word “distal” is to discern our definition of air mass transport direction that is based on modeling its back-trajectory over a course of time from transport direction defined based on “local” weather station wind direction (e.g., Figure A1 introduced in Section 2 and [14]). Using four simplified distal trajectory clusters reflects our goal that we are mainly interested in how Patagonian “upwind” terrains influence δ18Op in relatively inland Punta Arenas. Costal terrains on western (the Andes) and southern (the Cordillera Darwin) boundaries would produce the isotopic rain shadow effect [11,63] on their leeward side—air masses would have to experience orographic uplift, condensation, and rainout before reaching Punta Arenas (Figure 1). By contrast, terrains on northern and eastern boundaries are relatively flat without main topographic barriers; thus, air masses would experience different degrees of fractionation [28].
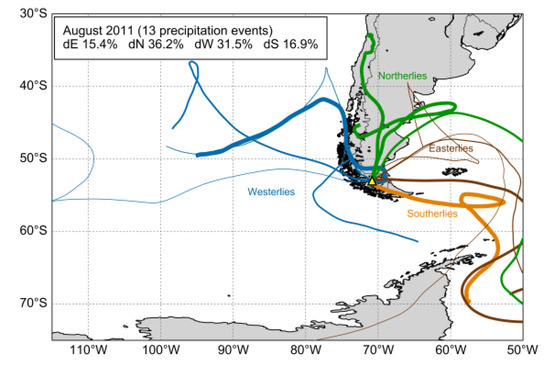
Figure 3.
Visualization of GDAS-based precipitation-producing back-trajectories for an example month (August 2011). There are 13 precipitation events based on the 6 h precipitation data in this month. The total monthly precipitation amount is 26 mm. Trajectory paths that enter eastern, northern, western, and southern boundaries of Southern Patagonian landmass are grouped into clusters of distal easterlies (brown), northerlies (green), westerlies (blue), and southerlies (orange), respectively. The trajectory line width is proportional to the 6 h precipitation amount associated with each trajectory. For reference, the thickest and thinnest paths on this graph represent 4.6 mm and 0.2 mm precipitation, respectively. Yellow triangle marks Punta Arenas. The proportions of precipitation contributed by different trajectory clusters (easterly-derived—dE, northerly-derived—dN, westerly-derived—dW, and southerly-derived—dS) in that month can be calculated. This provides an additional metric that allows us to investigate if the proportion of precipitation derived from a certain trajectory cluster could influence monthly-composited δ18Op and d-excess in GNIP data.
Because each trajectory is corresponding to a 6 h precipitation event, then the fraction of each trajectory cluster contributing to monthly total precipitation is calculated as (using the cluster of distal easterlies as an example):
where dE is the monthly percentage of distal easterly-derived precipitation, is the sum of all distal easterly-derived 6 h precipitation, and P is the sum of all 6 h precipitation for a particular month. Following Equation (3), the percentages of distal northerly-derived (dN), westerly-derived (dW), and southerly-derived (dS) precipitation can be also calculated (Figure 3). As such, we could quantify the contributions of major synoptic weather types to total monthly precipitation.
To extract the influence of synoptic weather types and moisture transport pathways on δ18Op in Punta Arenas, we directly looked into whether the metric is significantly correlated with dE, dN, dW, and dS, using the Pearson correlation coefficient. The statistical analysis was run for four different austral seasons. Correlation is considered significant if p-value is less than 0.1. If so, it would indicate that precipitation derived from that trajectory cluster has on average a distinct high or low δ18Op value relative to others, leading to statistical correlation between its proportion and monthly in our framework. Here a less conservative p-value is chosen because as presented below, the monthly proportions of precipitation contributed by different trajectory clusters have skewed distributions towards 100% or 0%. If skewed data were input into bivariate correlation, it often causes an “attenuation bias” [64] in the Pearson correlation coefficient, weakening its p-value. If significant correlation was found between dW and within a specific season, we calculated the regression coefficient to determine the sensitivity of δ18Op to the proportion of westerly-derived precipitation.
To investigate the cause for the distinct δ18Op value in a certain trajectory cluster, we calculated median, lower quartile, and upper quartile values for specific humidity (normalized to the initial air mass value) and precipitation rate (both are meteorological output variables in HYSPLIT) in each hour along modeled trajectories to characterize the rainout processes for different trajectory clusters. The meteorological output variables have been used to characterize air mass rainout history in some event-based studies (e.g., [16,30]). In reality, each trajectory has its own air mass history, not only in terms of trajectory path but also along-trajectory meteorological data. Thus, the aim of this analysis is to characterize the general evolutions of air masses in different trajectory clusters rather than to quantitively model the degree of rainout and isotopic fractionation in air masses. We also analyzed the correlation between d-excess data and the proportion of precipitation derived from different trajectory clusters to diagnose if moisture recycling or post-condensation raindrop re-evaporation affected precipitation isotopes for different moisture transport pathways.
5. Results and Discussion
5.1. Precipitation Origin from the HYSPLIT Framework
Mean monthly proportions of precipitation derived from the HYSPLIT framework (Table 1) and precipitation-producing trajectory frequency contour plots (Figure 4) are consistent with empirical observations that the strong SHWW belt dominates over Punta Arenas all year long. The distal westerlies on average contributed 82% (GDAS-based) or at least 85% (NCEP/NCAR-based) of precipitation despite the fact that Punta Arenas is on the leeward side of the Andes under the influence of the SHWWs. In general, the dW histogram is highly skewed towards the range of 95%–100% (Figure A4), meaning that for around half of all months the dW are higher than 95% while other trajectory cluster proportions are less than 5%. The dW have clear seasonal variations that are also consistent with the observed SHWW seasonal migration (see Section 2). The dW are higher and lower during summer and winter, respectively, while the shoulder seasons (autumn and spring) have intermediate dW (Table 1).

Table 1.
Mean monthly proportions of precipitation in Punta Arenas derived from different trajectory clusters in the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) framework for different seasons. Results from the NCEP/NCAR reanalysis dataset are shown for different initial back-trajectory heights (IBTH).
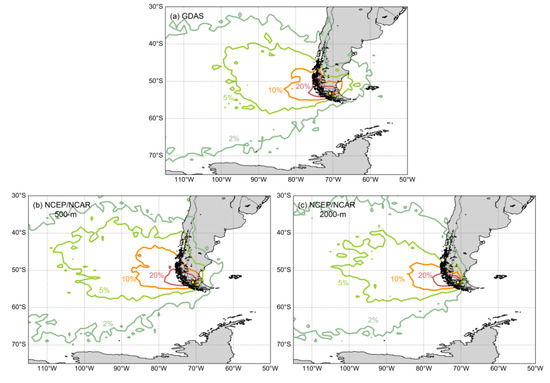
Figure 4.
Trajectory frequency contours for precipitation-producing back-trajectories generated from (a) the GDAS reanalysis dataset (2005–2017) and from (b,c) the NCEP/NCAR reanalysis dataset (1990–2004) with an initial back-trajectory height of 500 m (b) and 2000 m (c), respectively.
The derived monthly proportions of precipitation for each trajectory cluster are sensitive to the meteorological reanalysis dataset used for modeling back-trajectories. Although back-trajectories were modeled over different periods, using the GDAS reanalysis dataset would generate lower dW than using the NCEP/NCAR reanalysis dataset, especially during winter by at least 10%, but not for summer (Table 1). In addition, using GDAS would also generate higher dE than dN, while using NCEP/NCAR would generate the opposite (Table 1). Considering that the NCEP/NCAR reanalysis dataset has a lower resolution, some of their modeled back-trajectory paths likely would be deflected compared to the GDAS-based back-trajectory paths, leading to biased mean estimates on the origin of precipitation. Therefore, back-trajectory clustering results for periods 1990–2004 and 2005–2017 should be treated separately in the following discussion because these were derived from different meteorological reanalysis datasets.
Furthermore, the derived monthly proportions of precipitation for each trajectory cluster are also sensitive to the choice of initial back-trajectory height for the NCEP/NCAR dataset. Although the four selected initial back-trajectory heights represent the levels at which most of atmospheric moisture is entrained [65], higher initial back-trajectory heights would generate higher dW (Table 1). These results demonstrate the role of boundary-layer wind shear on modifying back-trajectory path, although many studies have suggested that different initial back-trajectory heights would not affect the general path of back-trajectory [54,60,65,66]. The influence of initial back-trajectory height is also illustrated in the plots of precipitation-producing trajectory frequency contours that encompassed the Atlantic Ocean and Northern Patagonia underscoring distal easterlies and northerlies when back-trajectories were initiated at 500 m agl (Figure 4b), but not when back-trajectories were initiated at higher levels (Figure 4c).
5.2. The Effect of Synoptic Weather Types on δ18Op
In the correlation coefficient heat map between the monthly proportions of precipitation derived from different trajectory clusters and monthly δ18Op (Figure 5a), the dW and dE are negatively and positively correlated with for the shoulder seasons from the GDAS reanalysis dataset at 0.1 level. From the NCEP/NCAR reanalysis dataset, the dW and dN are negatively and positively correlated with in autumn and winter while the significance level depends on the initial back-trajectory height. No correlation was found if the initial back-trajectory height was 500 m. This suggests this level might to be too low to represent the precipitating air masses, consistent with the GDAS-based initial relative humidity data (see Section 4).
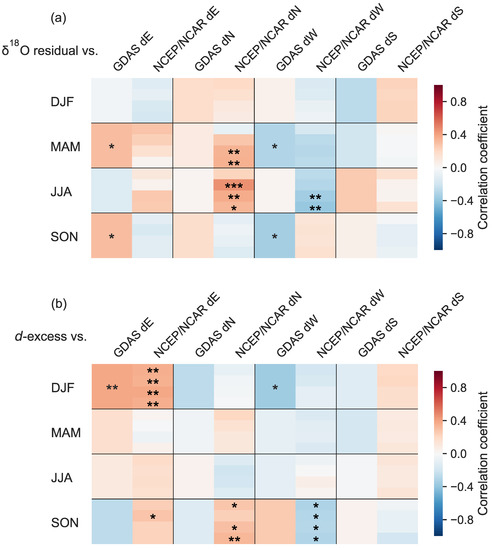
Figure 5.
The seasonal correlation coefficient heat map for monthly proportions of precipitation derived from different trajectory clusters (dE, dN, dW, and dS) with (a) monthly and with (b) monthly d-excess. For the NCEP/NCAR reanalysis dataset, the grid is segmented into four parts that from top to bottom represent the result with an initial back-trajectory height of 500 m, 1000 m, 1500 m, and 2000 m, respectively. Significance levels are noted by the following: * p < 0.1, ** p < 0.05, *** p < 0.01. The numbers of data for correlation analysis are listed in Table S2.
The above results present evidence that an increasing proportion of distal westerly-derived precipitation decreases δ18Op in Punta Arenas, although this moisture transport pathway effect is not manifested for summer during which the SHWW strength reaches maximum at this latitude and causes the distal westerlies almost the sole moisture transport pathway (Table 1). These findings are consistent with the Rayleigh distillation model that predicts lower δ18Op on the leeward side of the Andes due to the “upwind” orographic and rainout effects of westerlies [63]. This Andean isotopic rain shadow effect may not be as strong as in other parts of Patagonia due to the lower Andean elevation at the latitude of Punta Arenas (Figure 1), but our analysis mining the monthly δ18Op data still demonstrated this dynamical link. Along-trajectory meteorological data in GDAS-based distal westerlies indeed show orographic rainout during air mass transport. The specific humidity starts to slightly decrease about 5 h prior to reaching Punta Arenas (Figure 6e). The precipitation rate increases and decreases about 12 h and 2 h before reaching Punta Arenas, respectively, consistent with the orographic effect as “wet windward and dry leeward” conditions (Figure 6f). The similar process mechanism should also apply to distal southerlies, whereas in general distal southerlies contribute very little to total precipitation (Table 1) and the along-trajectory data do not show similar changes in meteorological data as distal westerlies (Figure 6g,h).
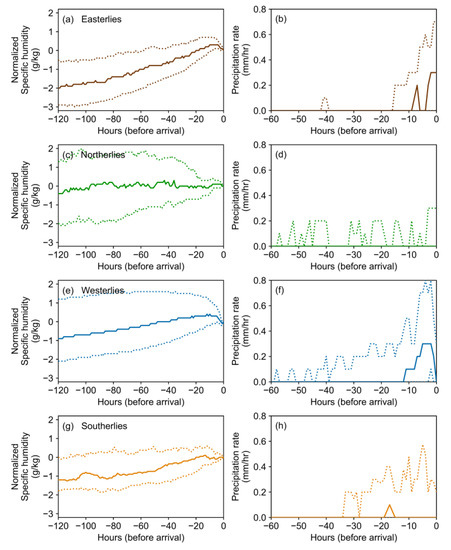
Figure 6.
Rainout characteristics in GDAS-modeled trajectories. Median (solid lines) and lower/upper quartile (dotted lines) values of specific humidity (normalized to initial back-trajectory value) (a,c,e,g) and precipitation rate (b,d,f,h) in each hour along trajectories in the clusters of distal easterlies (a,b), northerlies (c,d), westerlies (e,f), and southerlies (g,h).
The decrease in the proportion of distal westerly-derived precipitation implies that precipitation derived from secondary transport pathways become more important, in particular, the distal easterlies and northerlies (Table 1). However, because the NCEP/NCAR and GDAS reanalysis datasets have discrepancy in resolving the trajectory paths for distal easterlies and northerlies, caution should be taken in our interpretations. For the higher-resolution GDAS dataset, an increasing proportion of distal easterly-derived precipitation would increase the δ18Op. Indeed, distal easterlies have a less orographic rainout during moisture transport due to the relatively flat and lower-elevation terrain in the eastern side of Patagonia (Figure 1). The along-trajectory meteorological data show that distal easterlies have a strong moisture uptake from the Atlantic Ocean with increasing specific humidity until 4 h before reaching Punta Arenas (Figure 6a), after which the specific humidity decreases and precipitation rate increases (Figure 6a,b). Precipitation mainly occurs on site rather than en route for distal easterlies, unlike distal westerlies that show clear “up-and-down” pattern in precipitation rate. As a result, distal easterly-derived precipitation attains a higher δ18Op signal relative to the distal westerlies. The distal northerlies, by contrast, show no appreciable change in specific humidity, and the along-trajectory rainout is very low (Figure 6c,d). In reality, the distal northerlies in our HYSPLIT framework have a longer transport length on continent (Figure 3), similar to the setting with a stronger isotopic “continental effect” that should have increased the degree of rainout and decreased δ18Op [3,4]. However, the flat along-trajectory specific humidity profile might indicate an efficient moisture recycling, likely from plant transpiration flux from Patagonian grasslands (rather than evaporation), which could return water vapor efficiently [67,68,69] without kinetic fractionation and lead to relatively higher δ18Op [61]. Nevertheless, distal northerlies also contribute little to total precipitation (Table 1) and do not play a large enough role in modifying the δ18Op.
However, from the NCEP/NCAR reanalysis dataset, the dN are positively correlated with . It seems inconsistent with the GDAS-based results described above and requires some explanations. As mentioned in Section 5.1, the trajectory paths modeled from the NCEP/NCAR dataset might be deflected, particularly for distal northerlies that seemed overrepresented at the cost of distal easterlies. Instead, we examined the spatial relationships between dN and the independent European Center for Medium-Range Weather Forecasts (ECMWF) ERA5 reanalysis fields to focus on the general synoptic-scale atmospheric circulation patterns that have caused high dN. We found that the NCEP/NCAR-based dN are correlated with cyclonic anomalies (negative SLP anomalies) over Northwestern Patagonia and its adjacent Pacific Ocean, and anticyclonic anomalies (positive SLP anomalies) centered over the Eastern Antarctic Peninsula (Figure 7a). Such the blocking-like flow dynamically favor the occurrence of quasi-stationary synoptic easterlies [39,40,71], resulting in an overall reduced average zonal wind speed of prevailing westerlies (Figure 7b). In addition, the NCEP/NCAR-based dE also show similar patterns in spatial correlations with SLP and zonal wind speed fields (Figure 7c,d). Therefore, although the trajectory paths for distal easterlies and northerlies modeled from the NCEP/NCAR reanalysis dataset are uncertain compared to the GDAS, their synoptic-scale features are robust. We propose that a majority of distal northerlies modeled from the NCEP/NCAR reanalysis dataset were essentially distal easterlies if modeled from the higher-resolution GDAS reanalysis dataset, which was however not available before 2005. This could explain why the dN were overestimated over the dE from the NCEP/NCAR dataset. As such, the significantly positive correlation between dN and is still consistent with our previous finding from the GDAS-based results above.
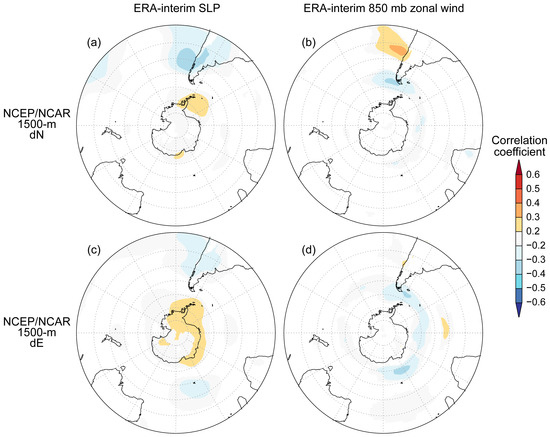
Figure 7.
Spatial correlation between NCEP/NCAR-based monthly proportion of precipitation related to northerly (a,b) and easterly (c,d) trajectory clusters and ERA5 (a,c) sea level pressure (SLP) and (b,d) 850 mb zonal wind speed fields. The results from an initial back-trajectory height of 1500 m were used because this level is close to 850 mb and likely represents the average level of main precipitating air masses (see Section 4). The dN and dE data from all months during the corresponding periods are used, including those months during which δ18Op data were missing or filtered out (see Section 3.1). Areas with p-value higher than 0.1 were masked out. The plots were generated on [70].
5.3. The Effect of Synoptic Weather Types on Deuterium Excess
There are multiple factors that could control the d-excess in precipitation, while major studies suggest evaporative source conditions, including sea surface temperature and boundary layer relative humidity, are the drivers of precipitation d-excess on global scale and have controlled the d-excess variations preserved in polar ice cores over millennial and orbital timescales [72,73]. However, at a specific location or region on continents, the short-term (monthly and seasonal) variations in precipitation d-excess are additionally modified by a multitude of processes unrelated to oceanic conditions, including moisture recycling (evaporation and transpiration) [20,69,74] and post-condensation raindrop re-evaporation [16,20,75].
From the similar correlation coefficient heat map analysis, we found that the dW and dE are negatively and positively correlated with d-excess, respectively (Figure 5b). We speculate that the degree of raindrop post-condensation re-evaporation is the main mechanism controlling monthly d-excess variability in Punta Arenas. From the 6 h weather station data, distal westerlies have much higher frequency of precipitation amount less than 1.2 mm (for the GDAS) and 1.5 mm (for the NCEP/NCAR) in 6 h (Figure 8a,c). As a result, distal westerly-derived precipitation consists of ~25% of this “drizzle” precipitation, which is more than double that of distal easterlies (Figure 8b,d). By contrast, distal easterlies have at least 50% of precipitation that has a precipitation rate of more than 5 mm within 6 h. Therefore, distal westerlies have such as higher proportion of drizzle precipitation component in which raindrop re-evaporation is significant in decreasing d-excess [28] but not for distal easterlies. Precipitation event samples collected at Río Gallegos and Laguna Potrok Aike in Eastern Patagonia (see Figure 1 for locations) [28] and other semi-arid regions such as Southeast Australia [16] also showed that drizzle precipitation is subjective to a higher degree of raindrop re-evaporation and support our speculation.
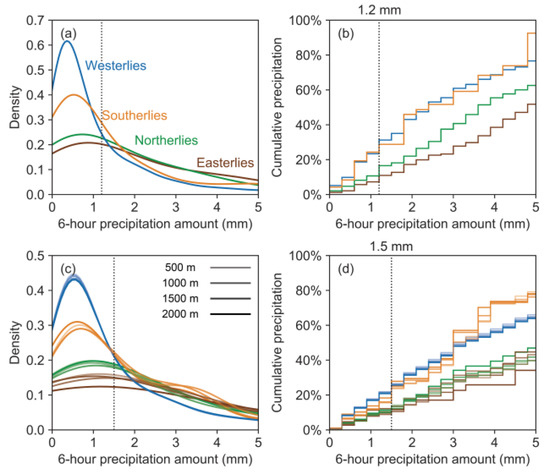
Figure 8.
Kernel density estimation plots for 6 h cumulative precipitation data (a,c) and amount-weighted cumulative 6 h precipitation histogram (with a bin size of 0.3 mm) (b,d) related to different trajectory clusters. Results are separated for the GDAS (a,b) and the NCEP/NCAR (c,d) reanalysis datasets. The color coding follows Figure 6. The transparency of lines in (c,d) is coded to represent results derived from different initial back-trajectory heights. The results derived from an initial back-trajectory height of 2000 m agl have zero transparency. The transparency increases (showing lighter color) with a decreasing initial back-trajectory height from 1500 m to 500 m agl. Distal westerlies have much higher frequency of precipitation amount less than 1.2 mm (for the GDAS) and 1.5 mm (for the NCEP/NCAR) in 6 h than distal easterlies marked by vertical dotted lines.
5.4. Implications for SHWW Reconstruction
The response of to dW in Punta Arenas demonstrated in our analysis indicates that δ18Op variations preserved in terrestrial climate archives on the leeward side of the Andes have the potential to reconstruct the long-term SHWW dynamics. When the SHWWs were strengthened at this latitude, regional precipitation was more governed by the prevailing westerlies and their associated storm tracks [36,76]. When the SHWWs were weakened with an overall reduced SLP gradient over the Drake Passage similar to the regional negative phase of the SAM, other synoptic weather types such as easterly flows that are a result of quasi-stationary blocking of the prevailing westerlies [40,71] might become more frequent in regional climate. A progressively positive shift in the SAM and an overall strengthening and poleward shift in the SHWWs during recent decades have been observed and was driven by ozone depletion and CO2 concentration rise [51,77]. The current dominance of the SHWWs is, however, not always the case in the past. For instance, temperature proxy data have shown that the SAM was in an extreme negative phase during the fifteenth century, meaning that the SHWW strength was much reduced during that time [77]. Therefore, the increasing frequency of synoptic weather types in which moisture is transported by non-westerlies during the waning of SHWWs is important for understanding the connection between δ18Op and SHWW behaviors in the past (Figure 9). Furthermore, the frequency and strength of blocking-like episodes in Patagonia have been linked with the El Niño-Southern Oscillation (ENSO) and would increase during the El Niño phase through the Rossby wave train [39,71]. We propose that δ18Op variations reflect the synoptic-scale processes related to the interactions between ENSO and SHWWs/SAM more than the simplistic strength of the SHWWs (Figure 9). Long-term temperature changes could also affect δ18Op in this region, in particular over orbital timescales (e.g., before the Holocene), but their roles are less prominent on multi-decadal and centennial timescales over which temperature variations are not likely to cause large shifts in δ18Op that if observed would instead imply a dynamical driver in the circulation pattern [39]. In addition, temperature effect might be also small during the Holocene. Synthesis data and models show that temperature variations were less than 0.8 °C over the past 8000 years [78].
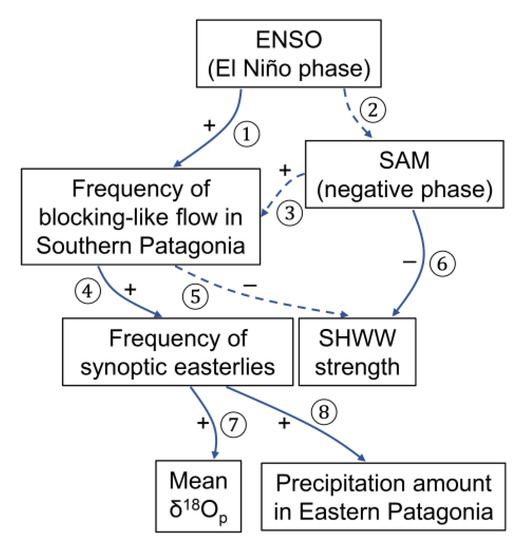
Figure 9.
The process-based interpretive diagram to link the large-scale climate mode with regional climate and δ18Op in Southern Patagonia in a paleoclimate setting. The plus and minus symbols show the direction of changes (strengthening or weakening, respectively). The solid and dashed arrows show the direct and indirect connections, respectively. The tropical Pacific Ocean (ENSO) could generate Rossby wave train propagating the tropospheric mass divergence anomalies to mid- and high-latitude of the Southern Hemisphere. Under the El Niño phase, the frequency of blocking-like flow in Southern Patagonia would increase (①) [39,71]. This Rossby wave train is responsible for the apparent ENSO–SAM phase teleconnection (②) [77,80], as the circulation anomalies of blocking-like flow is similar to the negative phase of the SAM (reduced mean SLP gradient across the Drake Passage) (③). The increased occurrence of quasi-stationary blocking-like flow would increase the occurrence of synoptic easterlies in Southern Patagonia (④). As a result, the overall strength of the prevailing westerlies would be reduced (⑤), although the strength of the hemisphere-wide SHWWs is directly related to the SLP gradient between mid- and high-latitude characterized by the phase of the SAM (⑥). As the synoptic easterlies became more frequent, their representation in regional precipitation in Eastern Patagonia would he higher, increasing the mean δ18Op over long timescales (⑦). In addition, the synoptic easterlies are more often associated with larger precipitation events that would increase the overall precipitation amount and weaken the Andean rain shadow in Eastern Patagonia (⑧) [46].
Sensitivity analysis indicates that a 20% less westerly-derived precipitation could cause a 0.6–1.3‰ higher δ18Op in Punta Arenas (Table 2). A previous study close to the Atlantic coast (Río Gallegos and Laguna Potrok Aike; see Figure 1) showed that precipitation event samples associated with westerlies have δ18Op signals ~7‰ higher than easterlies and northerlies [28], which from a simple isotopic and mass balance calculation could be converted to an effect of 1.4‰ in δ18Op for their sites was there 20% less westerly-derived precipitation. The different sensitivities may reflect the fact that Punta Arenas is in a central locus of Patagonian landmass, ~170 km away from the Atlantic coast, thus easterlies experience a higher degree of rainout during moisture transport compared to the sites in the Atlantic coast. In addition, the Andean divide at the latitude of Punta Arenas is not as high as other parts of Patagonia. This may further reduce the “upwind” orographic and rainout-related fractionation that has occurred in air masses delivered by westerlies. Therefore, terrestrial climate archives such as lakes and peat bogs closer to the Atlantic Ocean would be more sensitive in detecting the long-term variability in the frequency of synoptic easterlies and the SHWW dynamics from the δ18Op paleo-records. For example, peat moss cellulose data from Ariel Peatland (see Figure 1), which was close to the Atlantic coast (~80 km), showed that the δ18Op was ~2‰ higher than during the early twentieth century than the current period [39]. Taking the sensitivity into consideration, this shift might indicate that westerly-derived precipitation was ~30% less during the early twentieth century compared to today as a recent analogue for the period of weakened SHWWs.

Table 2.
Effect of a 20% less westerly-derived precipitation on δ18Op based on regression coefficients between and dW if within a specific season they are statistically significant from Figure 5a. Results are compared with another study [28] in which the authors based on event-based precipitation samples concluded that precipitation derived from westerlies are on average 7‰ lower than easterlies and northerlies at Río Gallegos and Laguna Potrok Aike (Figure 1). From a simple isotopic and mass balance calculation, it could be converted that a 20% less westerly-derived precipitation would have an effect of +1.4‰ in δ18Op for their sites.
The SHWW dynamics also regulate hydrological regimes in Southern Patagonia. Although today, the SHWWs are delivering a large amount of precipitation even to the leeward side of Southern Patagonia, they are not as efficient as other wind directions (Figure 8 and Figure A1). Some historic extreme precipitation events along the Atlantic coast of Patagonia have been linked with enhanced moisture flux derived from easterlies [40]. Our HYSPLIT back-trajectory modeling also showed that the extreme precipitation event on 11–12 March 2012, which caused historic flooding of river Río Las Minas in the main city of Punta Arenas [79], occurred under bursts of easterlies (Figure 10a). This event was caused by a transient migratory weather system with an anomalous anticyclonic center over the Antarctic Peninsula resulting in a blocking-like flow (Figure 10b). For this month, the dE is as high as 76%. The monthly precipitation amount is 63 mm (102 mm from conventional weather station Jorge C. Schythe in the main city of Punta Arenas [79]), which is around twice as high as the monthly average (Figure 2d). The GNIP δ18Op value for this month is −4.75‰, which corresponds to a +3.4‰ of . The d-excess for this month is 1.6‰, suggesting that the high δ18Op value is not an artifact from sample evaporation. This month is a good example showing that changes in synoptic-scale patterns in the past were able to influence both δ18Op and hydroclimate. If the proportion of precipitation derived from easterlies increased, it might also indicate an increase in moisture availability for grasslands and desserts in Eastern Patagonia [46]. Therefore, from terrestrial climate archives, the δ18Op paleo-records can be tied to other hydrological proxies to understand the coupled evolution of the synoptic-scale patterns and hydrological regimes in Southern Patagonia over long timescales (Figure 9).
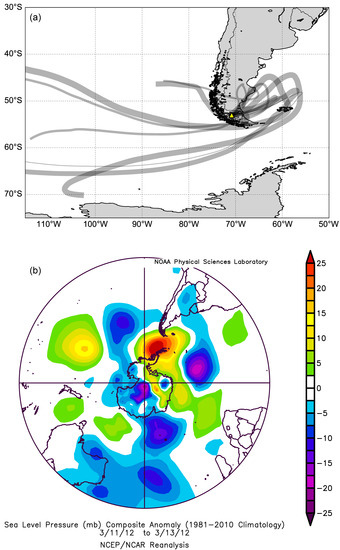
Figure 10.
The synoptic condition for the historic extreme precipitation event occurred on 11–12 March 2012. (a) Modeled back-trajectories (n = 8) with their UTC time starting from 12:00 on 11 March 2012 to 06:00 on 13 March 2012. The trajectory line width is proportional to the 6 h precipitation amount associated with each trajectory. For reference, the thickest and thinnest paths on this graph represent 11.4 mm and 0.8 mm precipitation, respectively. Yellow triangle marks Punta Arenas. (b) Three-day SLP anomaly for this event relative to the 1981–2010 mean climatology in NCEP/NCAR reanalysis. The plot was generated on [85].
5.5. Implications for Paleoaltimetry Reconstruction
Our results also have implications for isotope-based paleoaltimetry reconstruction in Southern Patagonia and, by extension, Northern Patagonia and other regions with similar settings such as the South Island in New Zealand (leeward side with a single dominant moisture transport pathway) [11,81]. Traditionally, these studies have assumed that a single dominant moisture transport pathway such as the strong SHWWs in Patagonia has also persisted throughout geological timescales. Under this assumption, any negative temporal shift in δ18Op in the modern leeward side could be interpreted as the development of isotopic rain shadow and used to estimate the surface elevation in upwind locations using an empirical isotopic lapse rate [12,37].
This study, however, shows that an additional complexity is involved in properly interpreting the signal of surface uplift from leeward isotope data. Specifically, the shifts in δ18Op can be alternatively caused by changes in moisture transport pathways under different atmospheric circulation patterns even in a region where today there seems to only have a single dominant moisture transport pathway. As such, shifts in Antarctic sea ice extent, Southern Hemisphere meridional sea surface temperature gradient, and tropical ocean-atmosphere system can also impose changes in SHWW strength and position [82,83,84] and, consequently, the synoptic-scale patterns and δ18Op signals preserved in terrestrial climate archives in the leeward side of Patagonia. Therefore, any leeward isotope-based paleoaltimetry studies should consider how atmospheric circulation was operated in the past under different paleogeography and climate boundary conditions. Because our sensitivity analysis (Table 2) indicated that δ18Op at sites farther away from the Atlantic coast is less sensitive to the SHWW variability, we would expect that sites from the nearest leeward locations are most suitable for detecting the major uplift signal of the Patagonian Andes from the δ18Op proxy data. Although the effect of changing moisture transport pathway on δ18Op might be not as large as the effect of mountain uplift, it could result in a biased estimate on uplift history if proxy data are collected from sites close to the Atlantic coast where a larger fraction of moisture could be advected from easterlies that break the rule of leeward paleoaltimetry.
6. Conclusions
Other than air temperature and precipitation amount, it has been well recognized that moisture source and transport pathway could also influence δ18Op for individual precipitation event on a regional scale. However, only a few paleoclimate studies are able to link δ18Op variations over time with synoptic-scale shifts in atmospheric circulation patterns. We here provide a new framework for extracting the relationship between the synoptic conditions and δ18Op hidden in decades-long GNIP monthly δ18Op record at a specific station. In such framework, weather station precipitation data and back-trajectory modeling are combined to quantify the proportions of precipitation delivered from different trajectory clusters that are characterized by different synoptic weather types on monthly basis. We apply this framework to GNIP monthly δ18Op record in Punta Arenas located in Southern Patagonia that today is under year-round influence of the strong SHWWs. We show that distal westerlies indeed contribute to a majority of precipitation in Punta Arena even though it is located in the Andean rain shadow, but not all of the precipitation. Instead, there is a considerable amount of precipitation originated from the distal easterlies, particularly during non-summer seasons. We further show that a decreasing proportion of distal westerly-derived precipitation would increase δ18Op, caused by a concurrently increasing proportion of distal easterly-derived precipitation that has a relatively higher δ18Op signal. We then link the proportions of precipitation origin with synoptic-scale atmospheric circulation patterns to provide an observational basis and a process-based mechanism for reconstructing the long-term SHWW dynamics from δ18Op paleo-records preserved in terrestrial climate archives. Our analysis highlights the importance of site location in preserving the most sensitive SHWW record inferred from δ18Op data, as sensitivity analysis indicates that the Atlantic coast might have the largest contrast in δ18Op between the westerly and easterly flows. Our results have implications for isotope-based leeward paleoaltimetry not only in Patagonia but also for other similar regions. Leeward paleoaltimetry studies often assume a single moisture transport pathway or source region has persisted throughout geological timescales, while our study suggests that different atmospheric circulation patterns in the past were also able to cause shifts in δ18Op, which sometimes were, however, interpreted as the sign of surface uplift or evaporative enrichment in soil water.
Finally, the framework introduced in this study provides new opportunities in linking large dataset of GNIP monthly precipitation isotopes with synoptic-scale patterns of moisture transport. Such framework utilizes station-based hourly or daily precipitation data to quantify the contributions of different synoptic weather types on each monthly-composited δ18Op as well as d-excess datum. These monthly-composited δ18Op and d-excess data readily available from multiple sites and over a long monitoring period, if put in a reasonable context of moisture transport, could provide insights into hydrological processes on terrestrial landscape, with implications for partitioning terrestrial water fluxes and reconstructing atmospheric circulation patterns using isotope data.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/5/514/s1, Table S1: Summary of all missing data or filtered dataset from GNIP Punta Arenas, Table S2: The number of δ18Op and d-excess data that are used in correlation heat map analysis.
Author Contributions
Conceptualization, Z.X. and Z.Y.; methodology, Z.X.; software, Z.X.; validation, Z.X.; formal analysis, Z.X.; investigation, Z.X.; resources, Z.X. and N.B.; data curation, Z.X. and N.B.; writing—original draft preparation, Z.X.; writing—review and editing, N.B. and Z.Y.; visualization, Z.X.; supervision, Z.Y.; project administration, Z.Y.; funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by a U.S. National Science Foundation grant, EAR-1502891.
Acknowledgments
The PySPLIT package is available on GitHub contributed by M.S.C. Warner at https://github.com/mscross/Pysplit/. The codes for reproducing the results of this study is hosted on a GitHub repository at https://github.com/zhx215/Patagonia_HYSPLIT/. We thank Hannah Bailey, Stephan Pfahl, and reviewers for comments that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
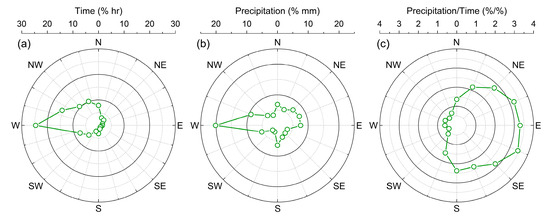
Figure A1.
Wind sensor (every 1 h) and rain gauge (every 6 h) data from weather station in Punta Arenas airport during the period 1990–2017 plotted on the 16-point compass rose. (a) Frequency percentage of hourly wind direction observations (n = 232,277). There are 13,177 observational gaps (5.4% of all hours). (b) Precipitation percentage from each wind direction. Six-hour cumulative precipitation amount (n = 40,769) was divided by 6 to match with each hourly wind direction data prior to each precipitation measurement, assuming that wind in each of that 6 h contributes to that 6 h cumulative precipitation equally. There are 140 observational gaps (0.3% of all hours). (c) The quotient between precipitation percentage and time percentage for each respective wind direction. The weather station data are available for public download on [55].
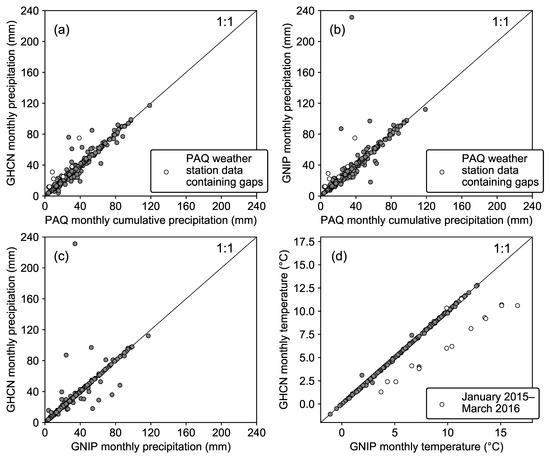
Figure A2.
Comparisons between different weather station databases of Punta Arenas airport. Solid lines in all plots indicate a 1:1 relationship. (a) Scatter plot between GHCN Version 2 reported monthly precipitation amount and monthly cumulative precipitation amount (calculated from the sum of all 6 h precipitation data for each month). The open dots indicate 6 individual months (March–June 2011, December 2011, and May 2012) during which 6 h precipitation data have temporal gaps (27%, 16%, 22%, 14%, 11%, and 6% of all 6 h intervals, respectively), which are responsible for their monthly cumulative precipitations amount underestimated compared to GHCN monthly precipitation amount data. It is still likely that a few GHCN monthly precipitation amount data are erroneous as well, which might explain the deviations from the monthly cumulative precipitation amount. (b) Scatter plot between reported GNIP monthly precipitation amount and Punta Arenas monthly cumulative precipitation amount similar as (a). (c) Scatter plot between GHCN Version 2 monthly precipitation amount and GNIP monthly precipitation amount. Clearly there are also several important erroneous data recordings in GNIP database. (d) Scatter plot between GHCN Version 3 monthly air temperature and GNIP monthly air temperature. Most data are plotted along the 1:1 line, but there are still several important erroneous GNIP data recordings. These data are mainly found from January 2015 to March 2016 (shown as open dots). These GNIP monthly air temperature values are much higher than normal, while weather station data from nearby city do not show any corresponding high air temperature, confirming that these GNIP data are erroneous.
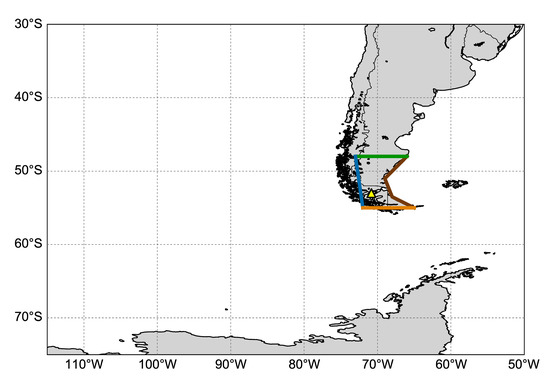
Figure A3.
Map showing the delineations of eastern (brown), northern (green), western (blue), and southern (orange) moisture transport boundaries of Southern Patagonia landmass used in this study. If a back-trajectory came across one of the above boundaries, that trajectory was clustered into distal easterlies, northerlies, westerlies, and southerly trajectories, respectively. Here the western boundary of Southern Patagonia landmass is set on the east of the Andes so that any back-trajectory crossing over the Andes will be classified as the distal westerlies.
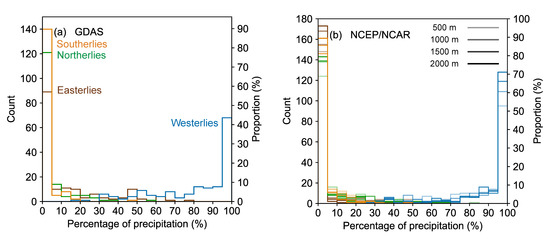
Figure A4.
Histogram of monthly dE (brown), dN (green), dW (blue), and dS (orange) derived from (a) the GDAS and (b) the NCEP/NCAR reanalysis datasets with a bin size of 5%. The transparency of histogram plots in (b) is coded to represent results derived from different initial back-trajectory heights. The results derived from an initial back-trajectory height of 2000 m agl have zero transparency. The transparency increases (showing lighter color) with a decreasing initial back-trajectory height from 1500 m to 500 m agl.
References
- Gat, J.R. Isotope Hydrology: A Study of the Water Cycle; Imperial College Press: London, UK, 2010. [Google Scholar]
- Dansgaard, W. The abundance of O18 in atmospheric water and water vapour. Tellus 1953, 5, 461–469. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Rozanski, K.; Araguás-Araguás, L.; Gonfiantini, R. Isotopic patterns in modern global precipitation. In Climate Change in Continental Isotopic Records; Swart, P.K., Lohmann, K.C., Mckenzie, J., Savin, S., Eds.; American Geophysical Union: Washingtong, DC, USA, 1993; pp. 1–36. [Google Scholar]
- Jouzel, J.; Hoffmann, G.; Koster, R.D.; Masson, V. Water isotopes in precipitation:: Data/model comparison for present-day and past climates. Quat. Sci. Rev. 2000, 19, 363–379. [Google Scholar] [CrossRef]
- Libby, L.M.; Pandolfi, L.J.; Payton, P.H.; Marshall, J.; Becker, B.; Giertz-Sienbenlist, V. Isotopic tree thermometers. Nature 1976, 261, 284–288. [Google Scholar] [CrossRef]
- Jouzel, J.; Lorius, C.; Petit, J.R.; Genthon, C.; Barkov, N.I.; Kotlyakov, V.M.; Petrov, V.M. Vostok ice core: A continuous isotope temperature record over the last climatic cycle (160,000 years). Nature 1987, 329, 403–408. [Google Scholar] [CrossRef]
- von Grafenstein, U.; Erlenkeuser, H.; Brauer, A.; Jouzel, J.; Johnsen, S.J. A mid-European decadal isotope-climate record from 15,500 to 5000 years B.P. Science 1999, 284, 1654–1657. [Google Scholar] [CrossRef]
- Wang, Y.J.; Cheng, H.; Edwards, R.L.; An, Z.S.; Wu, J.Y.; Shen, C.-C.; Dorale, J.A. A high-resolution absolute-dated late Pleistocene monsoon record from Hulu Cave, China. Science 2001, 294, 2345–2348. [Google Scholar] [CrossRef]
- Xia, Z.; Yu, Z. Applications of stable isotopes to studies of paleohydrology and paleoclimatology. In Encyclopedia of Water: Science, Technology, and Society; Maurice, P.A., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 1–17. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Poage, M.A. Reconstructing the paleotopography of mountain belts from the isotopic composition of authigenic minerals. Geology 2000, 28, 115–118. [Google Scholar] [CrossRef]
- Blisniuk, P.M.; Stern, L.A.; Chamberlain, C.P.; Idleman, B.; Zeitler, P.K. Climatic and ecologic changes during Miocene surface uplift in the Southern Patagonian Andes. Earth Planet. Sci. Lett. 2005, 230, 125–142. [Google Scholar] [CrossRef]
- Rindsberger, M.; Magaritz, M.; Carmi, I.; Gilad, D. The relation between air mass trajectories and the water isotope composition of rain in the Mediterranean Sea area. Geophys. Res. Lett. 1983, 10, 43–46. [Google Scholar] [CrossRef]
- Bailey, H.L.; Klein, E.S.; Welker, J.M. Synoptic and mesoscale mechanisms drive winter precipitation δ18O/δ2H in south-central Alaska. J. Geophys. Res. Atmos. 2019, 124, 4252–4266. [Google Scholar] [CrossRef]
- Sjostrom, D.J.; Welker, J.M. The influence of air mass source on the seasonal isotopic composition of precipitation, eastern USA. J. Geochem. Explor. 2009, 102, 103–112. [Google Scholar] [CrossRef]
- Crawford, J.; Hollins, S.E.; Meredith, K.T.; Hughes, C.E. Precipitation stable isotope variability and subcloud evaporation processes in a semi-arid region. Hydrol. Process. 2017, 31, 20–34. [Google Scholar] [CrossRef]
- Risi, C.; Bony, S.; Vimeux, F. Influence of convective processes on the isotopic composition (δ18O and δD) of precipitation and water vapor in the tropics: 2. Physical interpretation of the amount effect. J. Geophys. Res. Atmos. 2008, 113, D19306. [Google Scholar] [CrossRef]
- Aggarwal, P.K.; Romatschke, U.; Araguas-Araguas, L.; Belachew, D.; Longstaffe, F.J.; Berg, P.; Schumacher, C.; Funk, A. Proportions of convective and stratiform precipitation revealed in water isotope ratios. Nat. Geosci. 2016, 9, 624–629. [Google Scholar] [CrossRef]
- Friedman, I.; Harris, J.M.; Smith, G.I.; Johnson, C.A. Stable isotope composition of waters in the Great Basin, United States 1. Air-mass trajectories. J. Geophys. Res. Atmos. 2002, 107, ACL-14. [Google Scholar] [CrossRef]
- Kong, Y.; Pang, Z. A positive altitude gradient of isotopes in the precipitation over the Tianshan Mountains: Effects of moisture recycling and sub-cloud evaporation. J. Hydrol. 2016, 542, 222–230. [Google Scholar] [CrossRef]
- Winnick, M.J.; Chamberlain, C.P.; Caves, J.K.; Welker, J.M. Quantifying the isotopic ‘continental effect’. Earth Planet. Sci. Lett. 2014, 406, 123–133. [Google Scholar] [CrossRef]
- Galewsky, J. Orographic precipitation isotopic ratios in stratified atmospheric flows: Implications for paleoelevation studies. Geology 2009, 37, 791–794. [Google Scholar] [CrossRef]
- Lechler, A.R.; Galewsky, J. Refining paleoaltimetry reconstructions of the Sierra Nevada, California, using air parcel trajectories. Geology 2013, 41, 259–262. [Google Scholar] [CrossRef]
- Guan, H.; Simmons, C.T.; Love, A.J. Orographic controls on rain water isotope distribution in the Mount Lofty Ranges of South Australia. J. Hydrol. 2009, 374, 255–264. [Google Scholar] [CrossRef]
- Sinclair, K.E.; Marshall, S.J.; Moran, T.A. A Lagrangian approach to modelling stable isotopes in precipitation over mountainous terrain. Hydrol. Process. 2011, 25, 2481–2491. [Google Scholar] [CrossRef]
- Callow, N.; McGowan, H.; Warren, L.; Speirs, J. Drivers of precipitation stable oxygen isotope variability in an alpine setting, Snowy Mountains, Australia. J. Geophys. Res. Atmos. 2014, 119, 3016–3031. [Google Scholar] [CrossRef]
- Crawford, J.; Hughes, C.E.; Parkes, S.D. Is the isotopic composition of event based precipitation driven by moisture source or synoptic scale weather in the Sydney Basin, Australia? J. Hydrol. 2013, 507, 213–226. [Google Scholar] [CrossRef]
- Mayr, C.; Lücke, A.; Stichler, W.; Trimborn, P.; Ercolano, B.; Oliva, G.; Ohlendorf, C.; Soto, J.; Fey, M.; Haberzettl, T.; et al. Precipitation origin and evaporation of lakes in semi-arid Patagonia (Argentina) inferred from stable isotopes (δ18O, δ2H). J. Hydrol. 2007, 334, 53–63. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Crawford, J.; Hughes, C.E.; Du, M.; Liu, X. The effect of moisture source and synoptic conditions on precipitation isotopes in arid central Asia. J. Geophys. Res. Atmos. 2017, 122, 2667–2682. [Google Scholar] [CrossRef]
- Barras, V.J.I.; Simmonds, I. Synoptic controls upon δ18O in southern Tasmanian precipitation. Geophys. Res. Lett. 2008, 35, L02707. [Google Scholar] [CrossRef]
- Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.B.; Cohen, M.D.; Ngan, F. NOAA’s HYSPLIT Atmospheric Transport and Dispersion Modeling System. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Putman, A.L.; Feng, X.; Sonder, L.J.; Posmentier, E.S. Annual variation in event-scale precipitation δ2H at Barrow, AK, reflects vapor source region. Atmos. Chem. Phys. 2017, 17, 4627–4639. [Google Scholar] [CrossRef]
- Sun, C.; Shanahan, T.M.; Partin, J. Controls on the isotopic composition of precipitation in the south-central United States. J. Geophys. Res. Atmos. 2019, 124, 8320–8335. [Google Scholar] [CrossRef]
- IAEA/WMO. The Global Network of Isotopes in Precipitation Database. Available online: https://nucleus.iaea.org/wiser/ (accessed on 22 April 2020).
- Bailey, H.L.; Kaufman, D.S.; Henderson, A.C.G.; Leng, M.J. Synoptic scale controls on the δ18O in precipitation across Beringia. Geophys. Res. Lett. 2015, 42, 4608–4616. [Google Scholar] [CrossRef]
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-scale control on the Patagonian climate. J. Clim. 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Colwyn, D.A.; Brandon, M.T.; Hren, M.T.; Hourigan, J.; Pacini, A.; Cosgrove, M.G.; Midzik, M.; Garreaud, R.D.; Metzger, C. Growth and steady state of the Patagonian Andes. Am. J. Sci. 2019, 319, 431–472. [Google Scholar] [CrossRef]
- Colwyn, D.A.; Hren, M.T. An abrupt decrease in Southern Hemisphere terrestrial temperature during the Eocene–Oligocene transition. Earth Planet. Sci. Lett. 2019, 512, 227–235. [Google Scholar] [CrossRef]
- Xia, Z.; Yu, Z.; Loisel, J. Centennial-scale dynamics of the Southern Hemisphere Westerly Winds across the Drake Passage over the past two millennia. Geology 2018, 46, 855–858. [Google Scholar] [CrossRef]
- Agosta, E.; Compagnucci, R.; Ariztegui, D. Precipitation linked to Atlantic moisture transport: Clues to interpret Patagonian palaeoclimate. Clim. Res. 2015, 62, 219–240. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; Van den Broeke, M.R.; Van Wessem, J.M.; Van de Berg, W.J.; Van Meijgaard, E.; Van Ulft, L.H.; Schaefer, M. Extreme precipitation and climate gradients in Patagonia revealed by high-resolution regional atmospheric climate modeling. J. Clim. 2014, 27, 4607–4621. [Google Scholar] [CrossRef]
- Berman, A.L.; Silvestri, G.; Compagnucci, R. Eastern Patagonia seasonal precipitation: Influence of Southern Hemisphere circulation and links with subtropical South American precipitation. J. Clim. 2012, 25, 6781–6795. [Google Scholar] [CrossRef]
- NOAA. National Centers for Environmental Information: Global Historical Climatology Network (GHCN). Available online: https://www.ncdc.noaa.gov/data-access/land-based-station-data/land-based-datasets/global-historical-climatology-network-ghcn/ (accessed on 22 April 2020).
- Weidemann, S.S.; Sauter, T.; Kilian, R.; Steger, D.; Butorovic, N.; Schneider, C. A 17-year record of meteorological observations across the Gran Campo Nevado Ice Cap in southern Patagonia, Chile, related to synoptic weather types and climate modes. Front. Earth Sci. 2018, 6, 53. [Google Scholar] [CrossRef]
- Schneider, C.; Glaser, M.; Kilian, R.; Santana, A.; Butorovic, N.; Casassa, G. Weather observations across the southern Andes at 53° S. Phys. Geogr. 2003, 24, 97–119. [Google Scholar] [CrossRef]
- Mayr, C.; Wille, M.; Haberzettl, T.; Fey, M.; Janssen, S.; Lücke, A.; Ohlendorf, C.; Oliva, G.; Schäbitz, F.; Schleser, G.H.; et al. Holocene variability of the Southern Hemisphere westerlies in Argentinean Patagonia (52° S). Quat. Sci. Rev. 2007, 26, 579–584. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); Open File Rep. 2011-1073; U.S. Geological Survey: Reston, VA, USA, 2011; 26p.
- Garreaud, R.D.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Daley, T.J.; Mauquoy, D.; Chambers, F.M.; Street-Perrott, F.A.; Hughes, P.D.M.; Loader, N.J.; Roland, T.P.; van Bellen, S.; Garcia-Meneses, P.; Lewin, S. Investigating late Holocene variations in hydroclimate and the stable isotope composition of precipitation using southern South American peatlands: An hypothesis. Clim. Past 2012, 8, 1457–1471. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Gillett, N.P.; Kell, T.D.; Jones, P.D. Regional climate impacts of the Southern Annular Mode. Geophys. Res. Lett. 2006, 33, L23704. [Google Scholar] [CrossRef]
- Moreno, P.I.; Vilanova, I.; Villa-Martínez, R.; Garreaud, R.D.; Rojas, M.; De Pol-Holz, R. Southern Annular Mode-like changes in southwestern Patagonia at centennial timescales over the last three millennia. Nat. Commun. 2014, 5, 4375. [Google Scholar] [CrossRef]
- Krklec, K.; Domínguez-Villar, D. Quantification of the impact of moisture source regions on the oxygen isotope composition of precipitation over Eagle Cave, central Spain. Geochim. Cosmochim. Acta 2014, 134, 39–54. [Google Scholar] [CrossRef]
- Meteorological Direction of Chile—Cimate Services. Available online: https://climatologia.meteochile.gob.cl/ (accessed on 30 November 2019).
- Terzer-Wassmuth, S. International Atomic Energy Agency; Vienna International Centre: Vienna, Austria, 2019. [Google Scholar]
- Cross, M. PySPLIT: A Package for the Generation, Analysis, and Visualization of HYSPLIT Air Parcel Trajectories. In Proceedings of the 14th Python in Science Conference (SciPy 2015), Austin, TX, USA, 6–12 July 2015. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- NOAA. Air Resources Laboratory Gridded Meteorological Data Archives. Available online: https://www.ready.noaa.gov/archives.php/ (accessed on 22 April 2020).
- Fiorella, R.P.; Poulsen, C.J.; Pillco Zolá, R.S.; Barnes, J.B.; Tabor, C.R.; Ehlers, T.A. Spatiotemporal variability of modern precipitation δ18O in the central Andes and implications for paleoclimate and paleoaltimetry estimates. J. Geophys. Res. Atmos. 2015, 120, 4630–4656. [Google Scholar] [CrossRef]
- Krklec, K.; Domínguez-Villar, D.; Lojen, S. The impact of moisture sources on the oxygen isotope composition of precipitation at a continental site in central Europe. J. Hydrol. 2018, 561, 810–821. [Google Scholar] [CrossRef]
- Sodemann, H.; Schwierz, C.; Wernli, H. Interannual variability of Greenland winter precipitation sources: Lagrangian moisture diagnostic and North Atlantic Oscillation influence. J. Geophys. Res. Atmos. 2008, 113, D03107. [Google Scholar] [CrossRef]
- Stern, L.A.; Blisniuk, P.M. Stable isotope composition of precipitation across the southern Patagonian Andes. J. Geophys. Res. Atmos. 2002, 107, ACL-3. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Hafner: New York, NY, USA, 1958. [Google Scholar]
- Bershaw, J.; Penny, S.M.; Garzione, C.N. Stable isotopes of modern water across the Himalaya and eastern Tibetan Plateau: Implications for estimates of paleoelevation and paleoclimate. J. Geophys. Res. Atmos. 2012, 117, D02110. [Google Scholar] [CrossRef]
- Brittingham, A.; Petrosyan, Z.; Hepburn, J.C.; Richards, M.P.; Hren, M.T.; Hartman, G. Influence of the North Atlantic Oscillation on δD and δ18O in meteoric water in the Armenian Highland. J. Hydrol. 2019, 575, 513–522. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Winnick, M.J.; Mix, H.T.; Chamberlain, S.D.; Maher, K. The impact of Neogene grassland expansion and aridification on the isotopic composition of continental precipitation. Glob. Biogeochem. Cycles 2014, 28, 992–1004. [Google Scholar] [CrossRef]
- Mix, H.T.; Winnick, M.J.; Mulch, A.; Page Chamberlain, C. Grassland expansion as an instrument of hydrologic change in Neogene western North America. Earth Planet. Sci. Lett. 2013, 377–378, 73–83. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef]
- KNMI Climate Explorer. Available online: https://climexp.knmi.nl/ (accessed on 22 April 2020).
- Agosta, E.A.; Martin, P.B.; Serio, L.A. Persistent easterly winds leading to precipitation in the Atlantic Coast of Patagonia. Int. J Climatol. 2019, 39, 5063–5090. [Google Scholar] [CrossRef]
- Pfahl, S.; Sodemann, H. What controls deuterium excess in global precipitation? Clim. Past 2014, 10, 771–781. [Google Scholar] [CrossRef]
- Vimeux, F.; Masson, V.; Jouzel, J.; Stievenard, M.; Petit, J.R. Glacial–interglacial changes in ocean surface conditions in the Southern Hemisphere. Nature 1999, 398, 410–413. [Google Scholar] [CrossRef]
- Gat, J.R.; Bowser, C.J.; Kendall, C. The contribution of evaporation from the Great Lakes to the continental atmosphere: Estimate based on stable isotope data. Geophys. Res. Lett. 1994, 21, 557–560. [Google Scholar] [CrossRef]
- Froehlich, K.; Kralik, M.; Papesch, W.; Rank, D.; Scheifinger, H.; Stichler, W. Deuterium excess in precipitation of Alpine regions—Moisture recycling. Isot. Environ. Health Stud. 2008, 44, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Garreaud, R. Precipitation and circulation covariability in the extratropics. J. Clim. 2007, 20, 4789–4797. [Google Scholar] [CrossRef]
- Abram, N.J.; Mulvaney, R.; Vimeux, F.; Phipps, S.J.; Turner, J.; England, M.H. Evolution of the Southern Annular Mode during the past millennium. Nat. Clim. Chang. 2014, 4, 564–569. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, J.; Rosenthal, Y.; Zhang, X.; Otto-Bliesner, B.L.; Timmermann, A.; Smith, R.S.; Lohmann, G.; Zheng, W.; Elison Timm, O. The Holocene temperature conundrum. Proc. Natl. Acad. Sci. USA 2014, 111, E3501–E3505. [Google Scholar] [CrossRef]
- Butorovic, N. Resumen Metereológico año 2012 Estación “Jorge C. Schythe” (53°08′ S; 70°53′ W; 6m.s.n.m). Anal. Inst. Patag. 2013, 41, 153–162. [Google Scholar] [CrossRef][Green Version]
- Fogt, R.L.; Bromwich, D.H.; Hines, K.M. Understanding the SAM influence on the South Pacific ENSO teleconnection. Clim. Dynam. 2011, 36, 1555–1576. [Google Scholar] [CrossRef]
- Wheeler, L.B.; Galewsky, J. Atmospheric flow patterns around the Southern Alps of New Zealand and implications for paleoaltimetry. Geophys. Res. Lett. 2017, 44, 11601–11605. [Google Scholar] [CrossRef]
- Sime, L.C.; Kohfeld, K.E.; Le Quéré, C.; Wolff, E.W.; de Boer, A.M.; Graham, R.M.; Bopp, L. Southern Hemisphere westerly wind changes during the Last Glacial Maximum: Model-data comparison. Quat. Sci. Rev. 2013, 64, 104–120. [Google Scholar] [CrossRef]
- Lamy, F.; Kilian, R.; Arz, H.W.; Francois, J.-P.; Kaiser, J.; Prange, M.; Steinke, T. Holocene changes in the position and intensity of the southern westerly wind belt. Nat. Geosci. 2010, 3, 695–699. [Google Scholar] [CrossRef]
- Groeneveld, J.; Henderiks, J.; Renema, W.; McHugh, C.M.; De Vleeschouwer, D.; Christensen, B.A.; Fulthorpe, C.S.; Reuning, L.; Gallagher, S.J.; Bogus, K.; et al. Australian shelf sediments reveal shifts in Miocene Southern Hemisphere westerlies. Sci. Adv. 2017, 3, e1602567. [Google Scholar] [CrossRef] [PubMed]
- NOAA. Physical Sciences Laboratory (PSL) Daily Mean Composites. Available online: https://psl.noaa.gov/data/composites/day/ (accessed on 22 April 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).