Impact of Fake Below-Ground Meridional Wind on Hadley Circulation: Climatology, Interannual Variability, and Long-Term Trends
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Three Methods for Calculating the MSF
2.3. Definition of the Intensity, Rising, and Sinking Branches and Width of HC
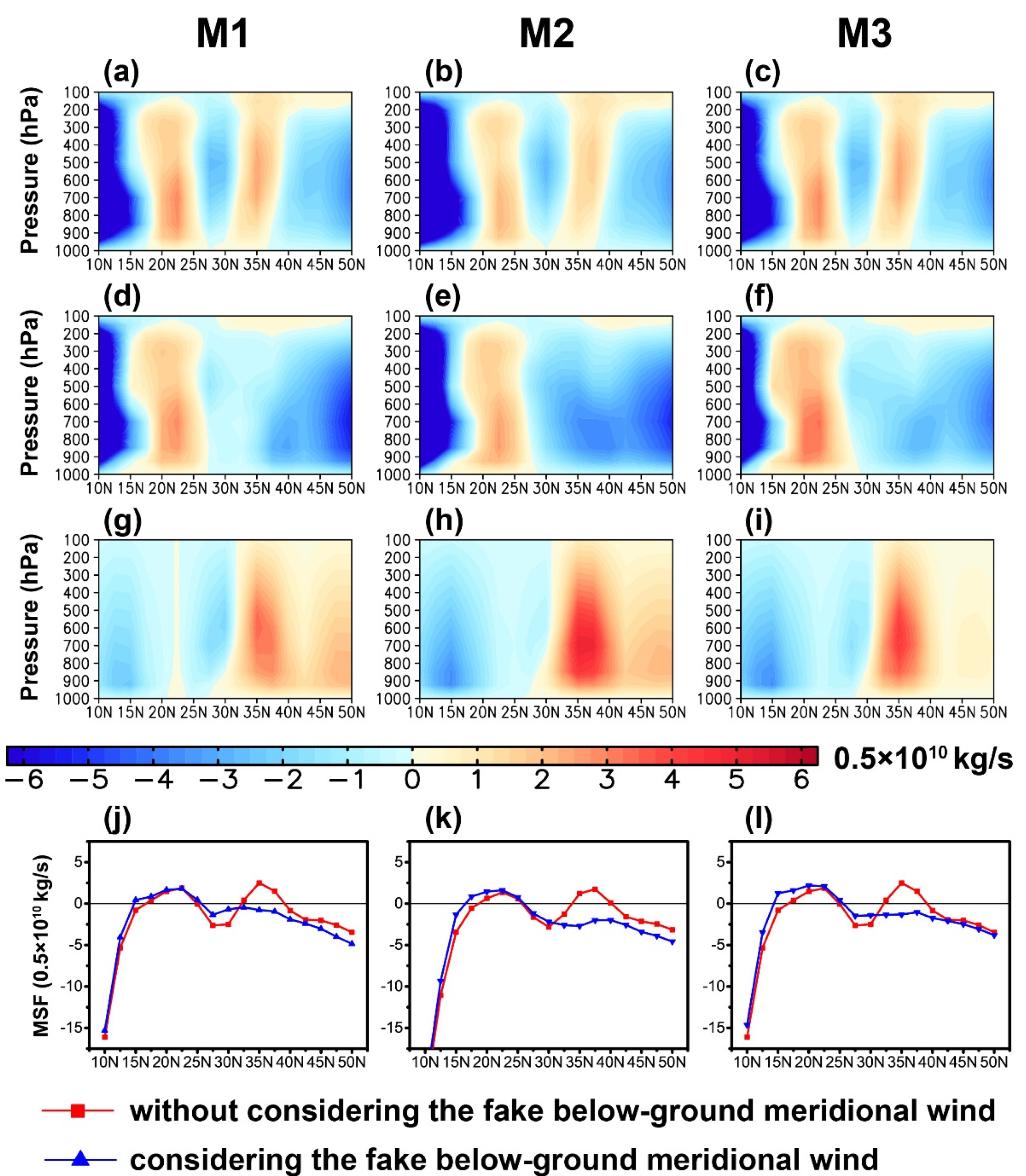
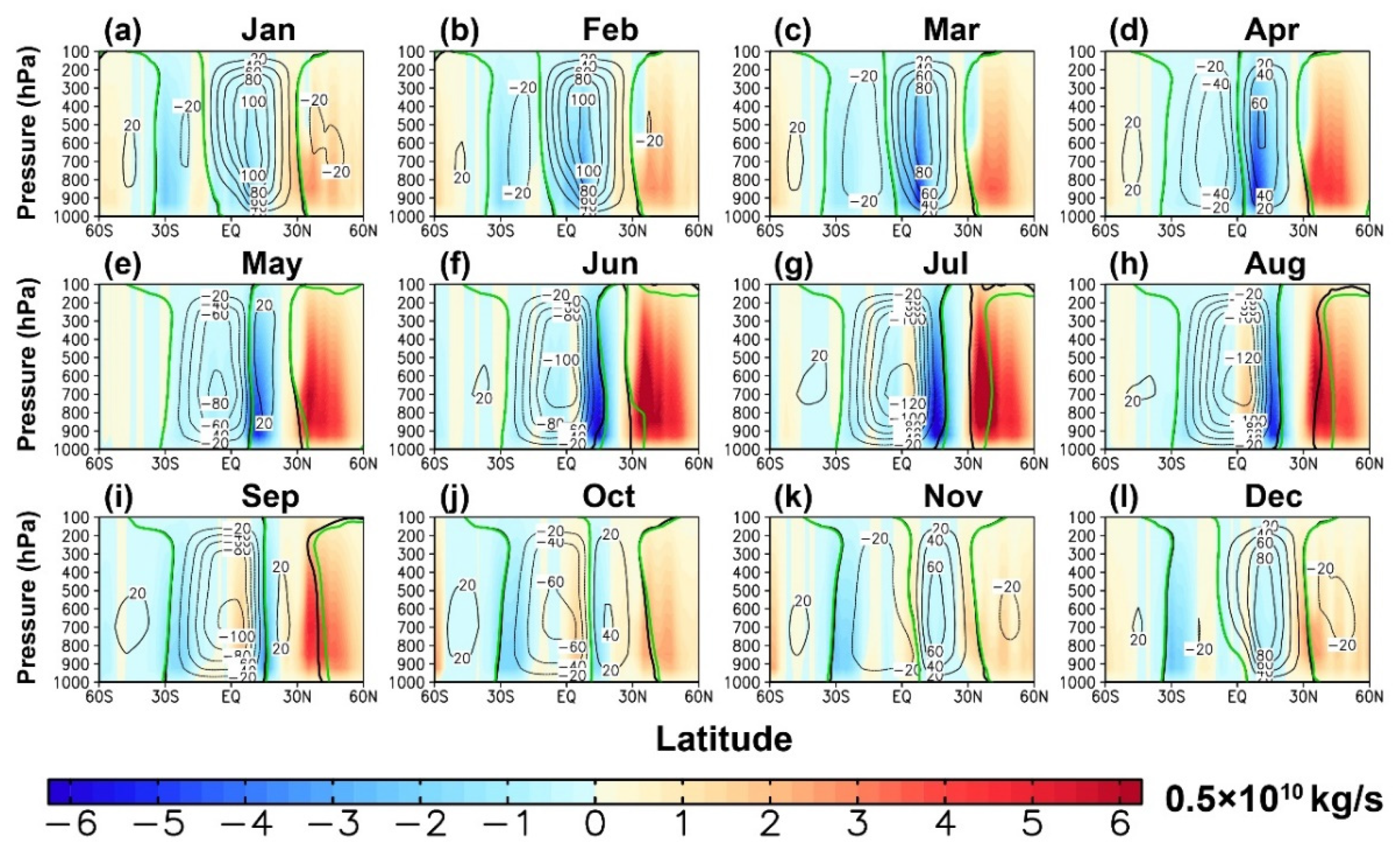
3. Impact of the Fake Below-Ground Meridional Wind on HC
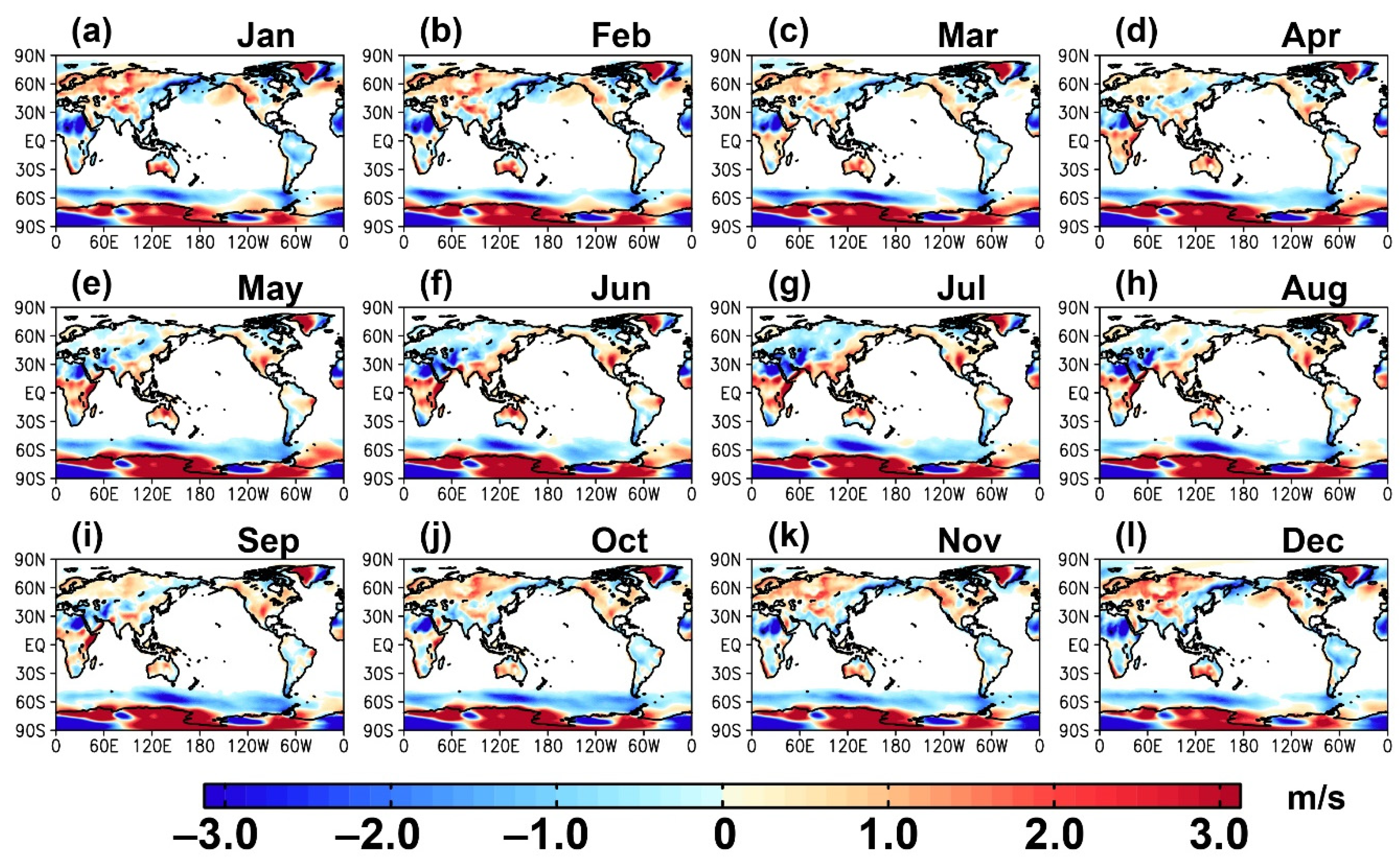
3.1. Climatology
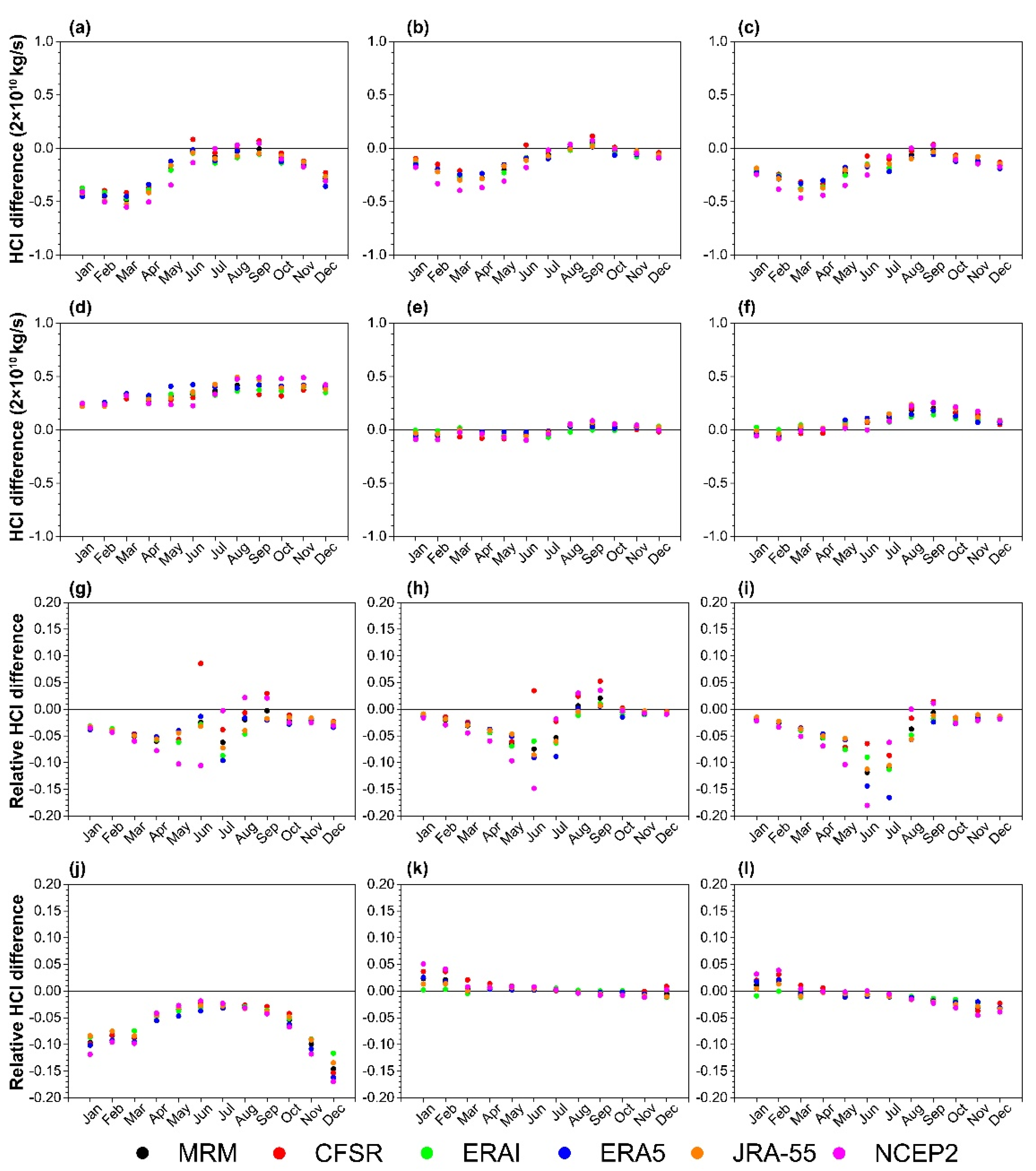
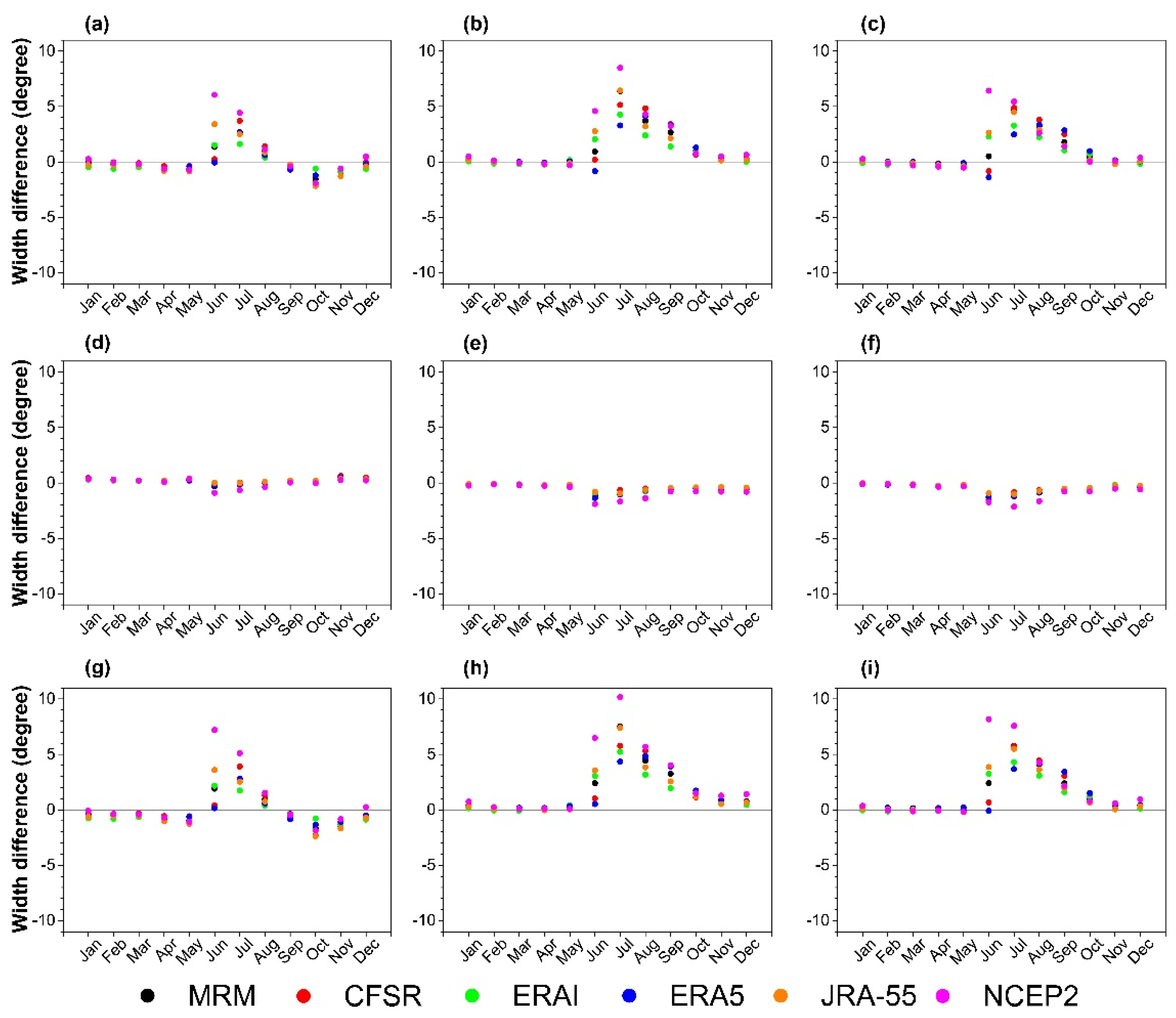
3.2. Interannual Variability
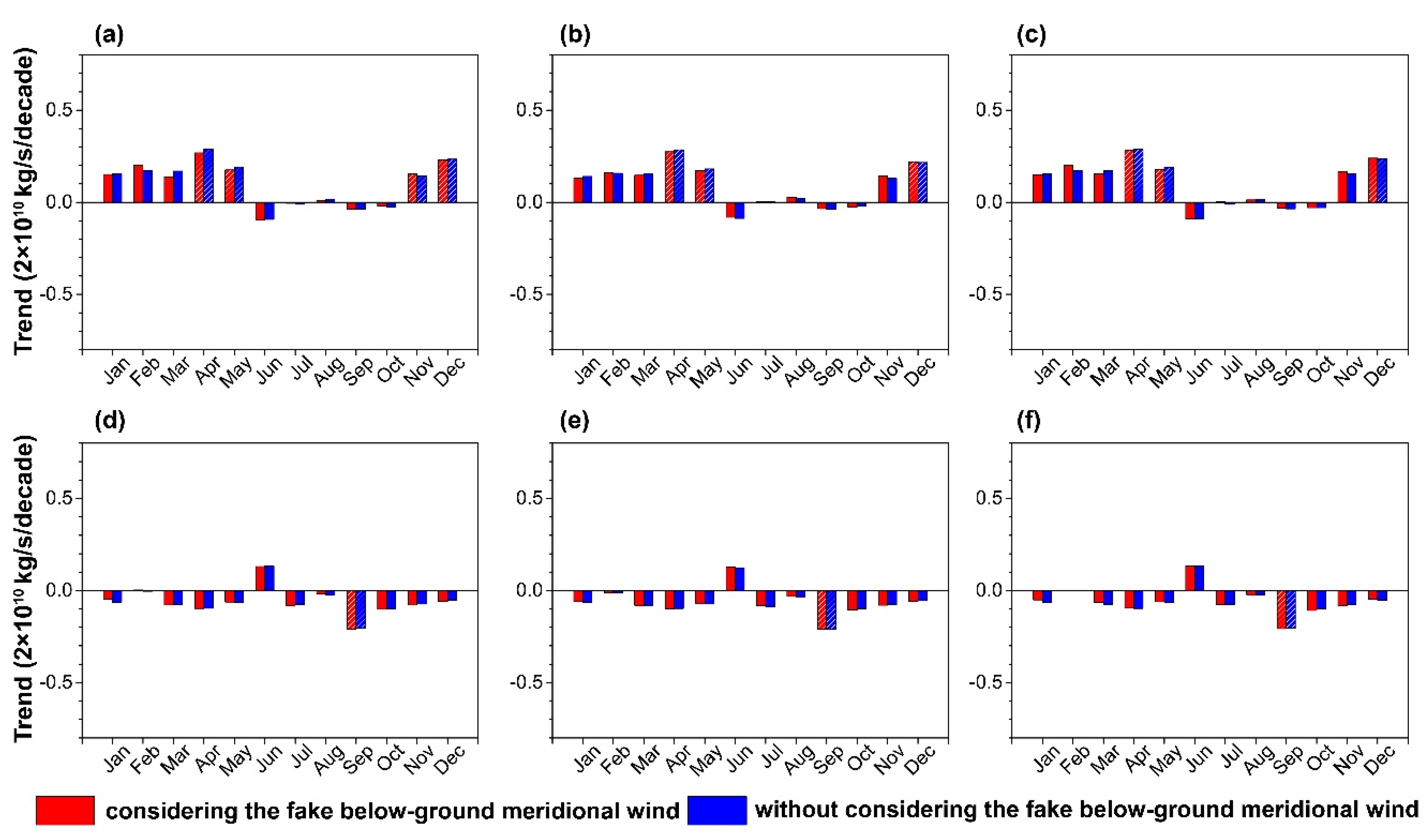
3.3. Long-Term Trends
4. Conclusions and Discussion
4.1. Conclusions
4.2. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hadley, G. Concerning the cause of the general trade-winds. Philos Trans. 1735, 39, 58–62. [Google Scholar]
- Bjerknes, J. A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature. Tellus 1966, 18, 820–829. [Google Scholar] [CrossRef]
- Oort, A.H.; Yienger, J.J. Observed interannual variability in the Hadley circulation and its connection to ENSO. J. Clim. 1996, 9, 2751–2767. [Google Scholar] [CrossRef]
- Diaz, H.F.; Bradley, R.S. The Hadley Circulation: Present, Past and Future; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Seidel, D.J.; Fu, Q.; Randel, W.J.; Reichler, T.J. Widening of the tropical belt in a changing climate. Nat. Geosci. 2008, 1, 21–24. [Google Scholar] [CrossRef]
- Chen, J.; Carlson, B.E.; Del Genio, A.D. Evidence for strengthening of the tropical general circulation in the 1990s. Science 2002, 295, 838–841. [Google Scholar] [CrossRef] [PubMed]
- Mitas, C.M.; Clement, A. Has the Hadley cell been strengthening in recent decades? Geophys. Res. Lett. 2005, 32, L03809. [Google Scholar] [CrossRef]
- Sohn, B.; Park, S.C. Strengthened tropical circulations in past three decades inferred from water vapor transport. J. Geophys. Res. Atmos. 2010, 115, D15112. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Hu, Y.; Ren, X. Changes in the strength and width of the Hadley circulation since 1871. Clim. Past. 2012, 8, 1169–1175. [Google Scholar] [CrossRef]
- Chen, S.; Wei, K.; Chen, W.; Song, L. Regional changes in the annual mean Hadley circulation in recent decades. J. Geophys. Res. Atmos. 2014, 119, 7815–7832. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Wong, T.; Allan, R.P.; Slingo, A.; Kiehl, J.T.; Soden, B.J.; Gordon, C.T.; Miller, A.J.; Yang, S.K.; Randall, D.A.; et al. Evidence for large decadal variability in the tropical mean radiative energy budget. Science 2002, 295, 841–844. [Google Scholar] [CrossRef]
- Ma, J.; Li, J. Strengthening of the boreal winter Hadley circulation and its connection with ENSO. Prog. Nat. Sci. 2007, 17, 1327–1333. [Google Scholar]
- Ma, J.; Li, J. The principal modes of variability of the boreal winter Hadley cell. Geophys. Res. Lett. 2008, 35, L01808. [Google Scholar]
- Tanaka, H.L.; Ishizaki, N.; Kitoh, A. Trend and interannual variability of Walker, monsoon and Hadley circulations defined by velocity potential in the upper troposphere. Tellus A 2004, 56, 250–269. [Google Scholar] [CrossRef]
- Mitas, C.M.; Clement, A. Recent behavior of the Hadley cell and tropical thermodynamics in climate models and reanalyses. Geophys. Res. Lett. 2006, 33, L01810. [Google Scholar] [CrossRef]
- Freitas, A.C.V.; Aímola, L.; Ambrizzi, T.; de Oliveira, C.P. Changes in intensity of the regional Hadley cell in Indian Ocean and its impacts on surrounding regions. Meteorol. Atmos. Phys. 2017, 129, 229–246. [Google Scholar] [CrossRef]
- Huang, R.; Chen, S.; Chen, W.; Hu, P.; Yu, B. Recent strengthening of the regional Hadley circulation over the western Pacific during boreal spring. Adv. Atmos. Sci. 2019, 36, 1251–1264. [Google Scholar] [CrossRef]
- Staten, P.W.; Lu, J.; Grise, K.M.; Davis, S.M.; Birner, T. Re-examining tropical expansion. Nat. Clim. Chang. 2018, 8, 768–775. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, Q. Observed poleward expansion of the Hadley circulation since 1979. Atmos. Chem. Phys. 2007, 7, 5229–5236. [Google Scholar] [CrossRef]
- Mathew, S.S.; Kumar, K.K.; Subrahmanyam, K.V. Hadley cell dynamics in Japanese Reanalysis-55 dataset: Evaluation using other reanalysis datasets and global radiosonde network observations. Clim. Dyn. 2016, 12, 3917–3930. [Google Scholar] [CrossRef]
- Huang, R.; Chen, S.; Chen, W.; Hu, P. Interannual variability of regional Hadley circulation intensity over western Pacific during boreal winter and its climatic impact over Asia-Australia region. J. Geophys. Res. Atmos. 2018, 123, 344–366. [Google Scholar] [CrossRef]
- Seidel, D.J.; Randel, W.J. Recent widening of the tropical belt: Evidence from tropopause observations. J. Geophys. Res. Atmos. 2007, 112, D20113. [Google Scholar] [CrossRef]
- Lucas, C.; Nguyen, H.; Timbal, B. An observational analysis of Southern Hemisphere tropical expansion. J. Geophys. Res. Atmos. 2012, 117, D17112. [Google Scholar] [CrossRef]
- Hudson, R.D.; Andrade, M.F.; Follette, M.B.; Frolov, A.D. The total ozone field separated into meteorological regimes—Part II: Northern Hemisphere mid-latitude total ozone trends. Atmos. Chem. Phys. 2006, 6, 5183–5191. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, C.; Liu, J. Observational evidence for poleward expansion of the Hadley circulation. Adv. Atmos. Sci. 2011, 28, 33–44. [Google Scholar] [CrossRef]
- Archer, C.L.; Caldeira, K. Historical trends in the jet streams. Geophys. Res. Lett. 2008, 35, L08803. [Google Scholar] [CrossRef]
- Kang, S.M.; Polvani, L.M.; Fyfe, J.C.; Sigmond, M. Impact of polar ozone depletion on subtropical precipitation. Science 2011, 332, 951–954. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Xu, K.M.; Sud, Y.C.; Betts, A.K. Recent trends of the tropical hydrological cycle inferred from global precipitation climatology project and international satellite cloud climatology project data. J. Geophys. Res. Atmos. 2011, 116, D09101. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, Z.; Hu, P.; Hou, X.; Gao, C.; Hu, S.; Feng, G. Significant role of orography in shaping the northern Hadley circulation and its poleward expansion during boreal summer. Geophys. Res. Lett. 2018, 45, 6619–6627. [Google Scholar] [CrossRef]
- Schwendike, J.; Govekar, P.; Reeder, M.J.; Wardle, R.; Berry, G.J.; Jakob, C. Local partitioning of the overturning circulation in the tropics and the connection to the Hadley and Walker circulations. J. Geophys. Res. Atmos. 2014, 119, 1322–1339. [Google Scholar] [CrossRef]
- Schwendike, J.; Berry, G.J.; Reeder, M.J.; Jakob, C.; Govekar, P.; Wardle, R. Trends in the local Hadley and local Walker circulations. J. Geophys. Res. Atmos. 2015, 120, 7599–7618. [Google Scholar] [CrossRef]
- Hu, S.; Cheng, J.; Chou, J. Novel three-pattern decomposition of global atmospheric circulation: Generalization of traditional two-dimensional decomposition. Clim. Dyn. 2017, 49, 3573–3586. [Google Scholar] [CrossRef]
- Hu, S.; Chou, J.; Cheng, J. Three-pattern decomposition of global atmospheric circulation: Part I—Decomposition model and theorems. Clim. Dyn. 2018, 50, 2355–2368. [Google Scholar] [CrossRef]
- Hu, S.; Cheng, J.; Xu, M.; Chou, J. Three-pattern decomposition of global atmospheric circulation: Part II—Dynamical equations of horizontal, meridional and zonal circulations. Clim. Dyn. 2018, 50, 2673–2686. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; Bechtold, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsl. 2016, 147, 7. [Google Scholar]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Staten, P.W.; Grise, K.M.; Davis, S.M.; Karnauskas, K.; Davis, N. Regional widening of tropical overturning: Forced change, natural variability, and recent trends. J. Geophys. Res. Atmos. 2019, 124, 6104–6119. [Google Scholar] [CrossRef]











| List | Acronyms |
|---|---|
| Hadley circulation | HC |
| Mass stream function | MSF |
| Fake below-ground meridional wind | FBGMW |
| Northern Hemisphere | NH |
| Southern Hemisphere | SH |
| HC intensity | HCI |
| Common inner edge | CE |
| Northern edge | NE |
| Southern edge | SE |
| HC width | HCW |
| Total HC width | TOT HCW |
| Multi-re-analyses mean | MRM |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Xu, Z.; Hou, X. Impact of Fake Below-Ground Meridional Wind on Hadley Circulation: Climatology, Interannual Variability, and Long-Term Trends. Atmosphere 2020, 11, 446. https://doi.org/10.3390/atmos11050446
Cheng J, Xu Z, Hou X. Impact of Fake Below-Ground Meridional Wind on Hadley Circulation: Climatology, Interannual Variability, and Long-Term Trends. Atmosphere. 2020; 11(5):446. https://doi.org/10.3390/atmos11050446
Chicago/Turabian StyleCheng, Jianbo, Zhihang Xu, and Xiaoya Hou. 2020. "Impact of Fake Below-Ground Meridional Wind on Hadley Circulation: Climatology, Interannual Variability, and Long-Term Trends" Atmosphere 11, no. 5: 446. https://doi.org/10.3390/atmos11050446
APA StyleCheng, J., Xu, Z., & Hou, X. (2020). Impact of Fake Below-Ground Meridional Wind on Hadley Circulation: Climatology, Interannual Variability, and Long-Term Trends. Atmosphere, 11(5), 446. https://doi.org/10.3390/atmos11050446




