Partitioning Waves and Eddies in Stably Stratified Turbulence
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations and Dispersion Relation
2.2. Numerical Method
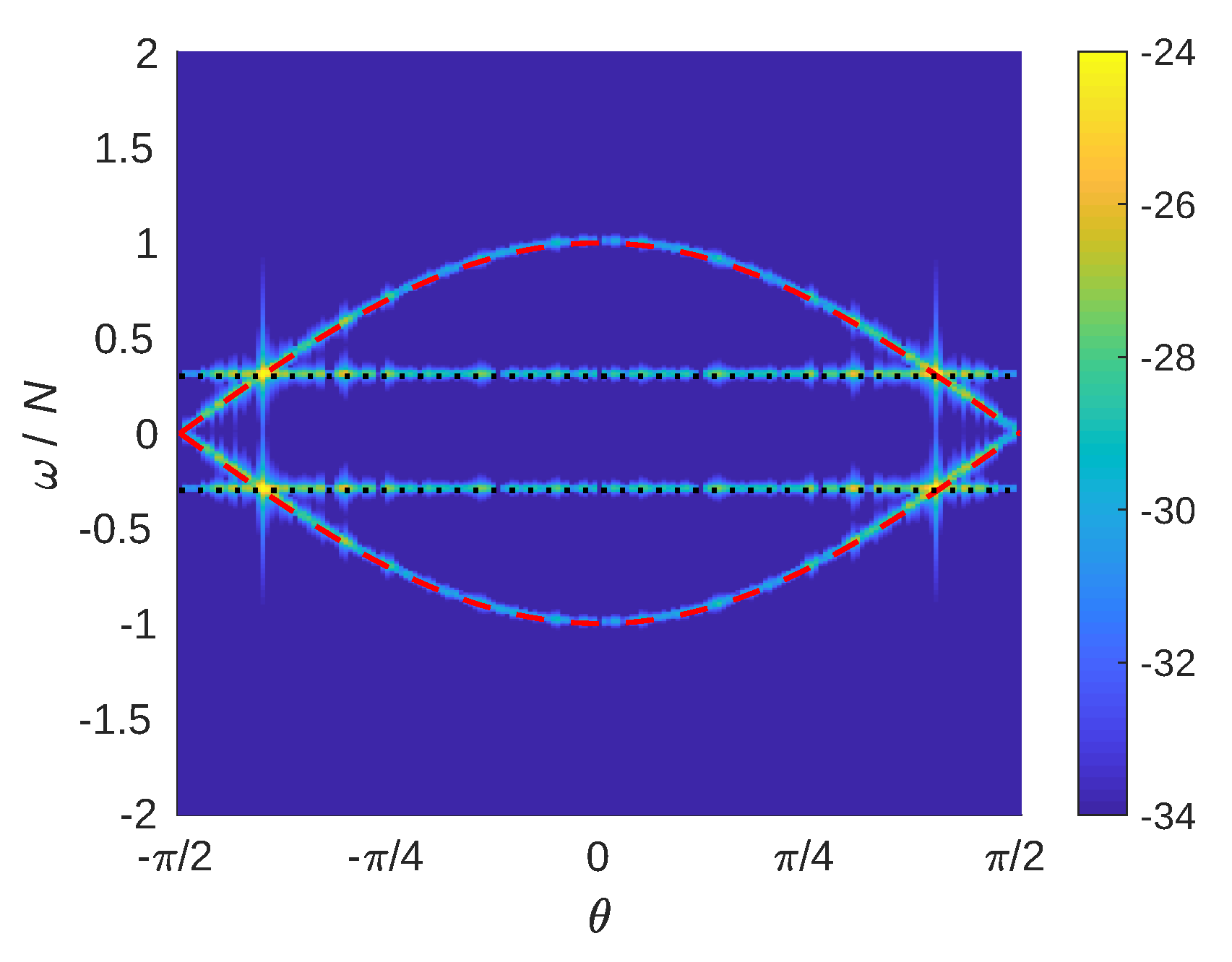
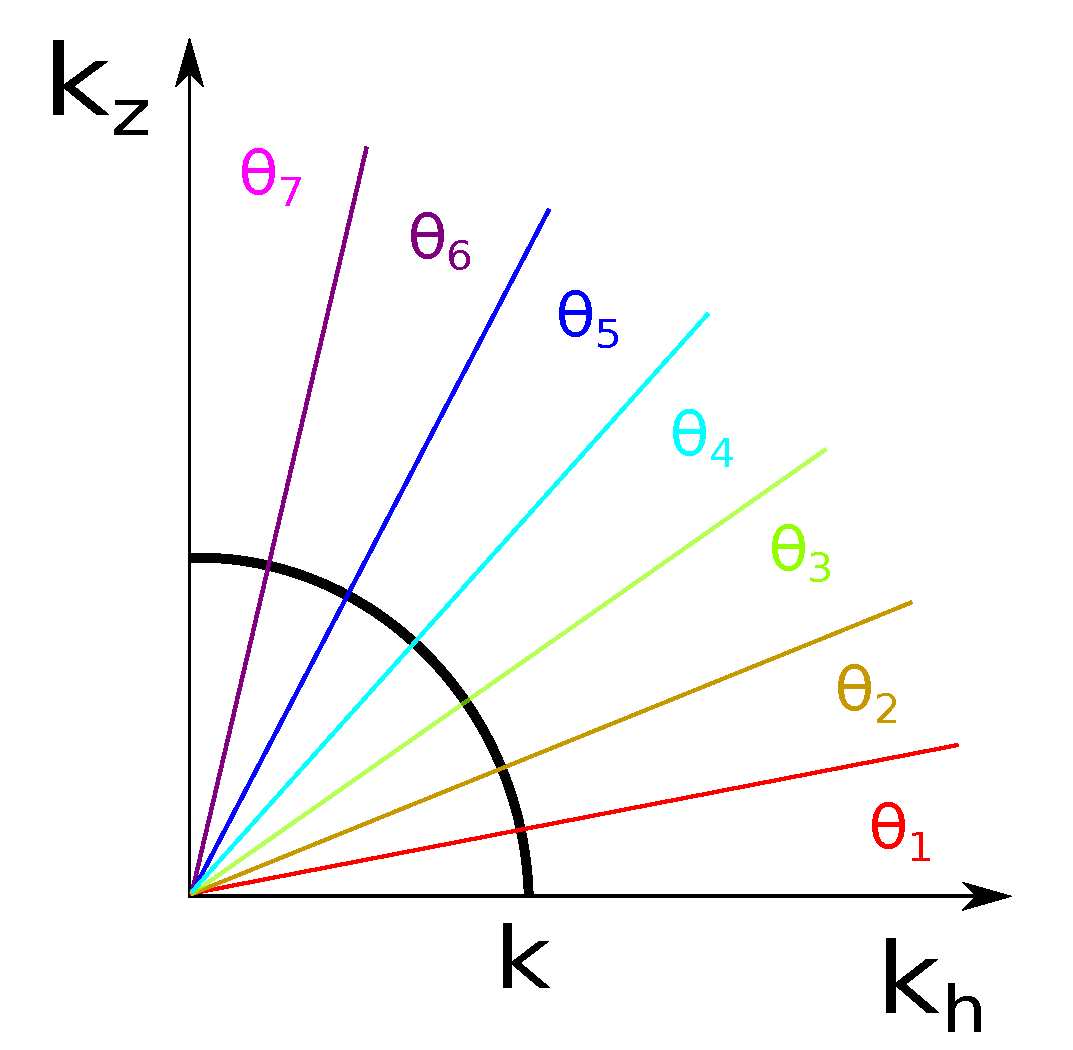
2.3. Space-Time Analysis of the Flow
- Each elementary cone, which contains wavevector with an angle , is divided into sub-volumes by selecting the scale . Then, all the velocity vectors are summed onto the sub-volume in a new variable .
- The Fourier transform in time of that new variable is computed as .
- The spectral density of kinetic energy is recovered in a plane for a range of scales between and that is a set of sub-volumes:
- The total spectral density of kinetic energy into an elementary cone, regardless of scale k, can be computed as a summation over all sub-volumes:
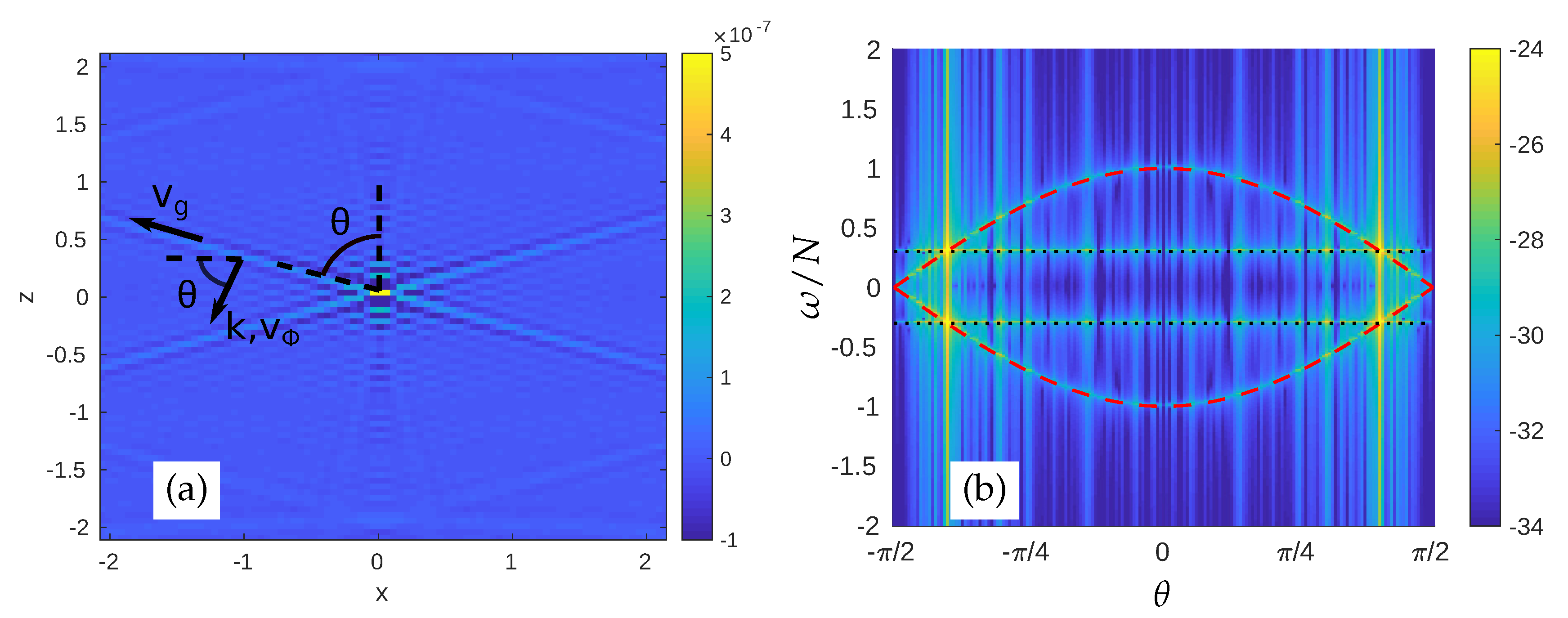
2.4. Saint Andrews cross Wave Propagation Benchmark
3. Sweeping and Doppler Effects on Internal Gravity Waves Propagation
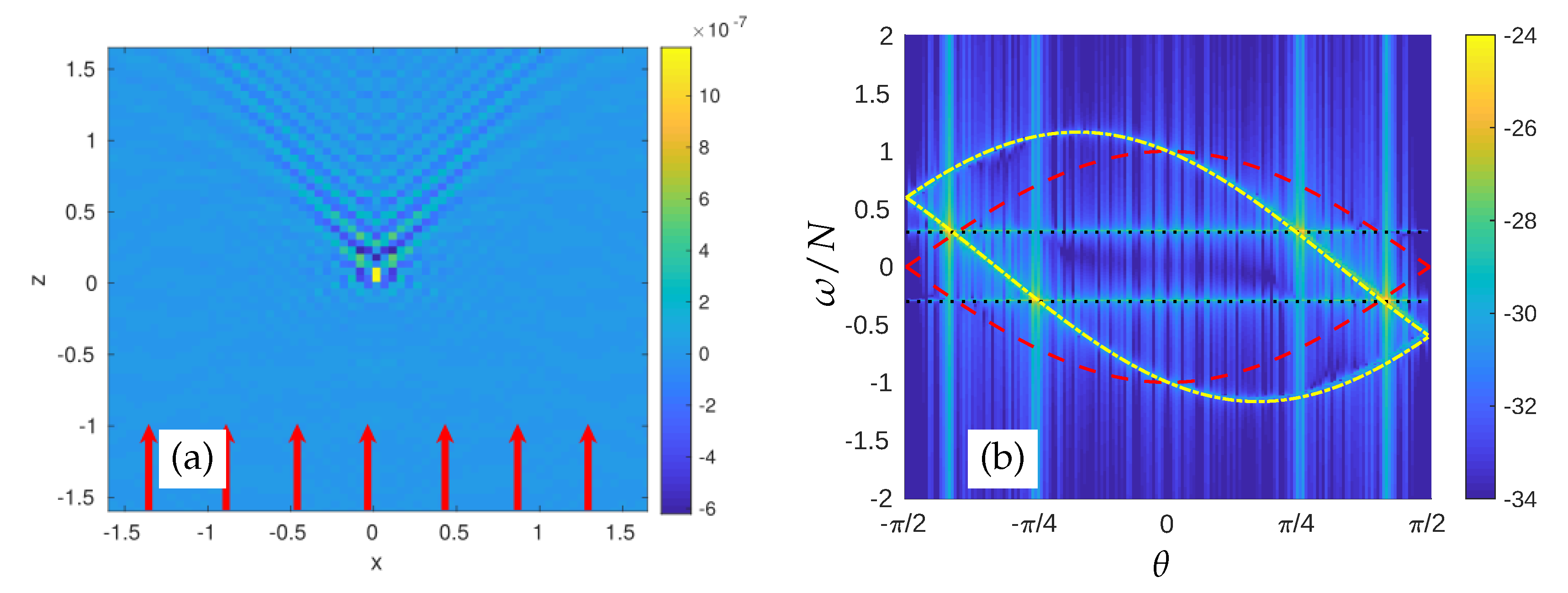
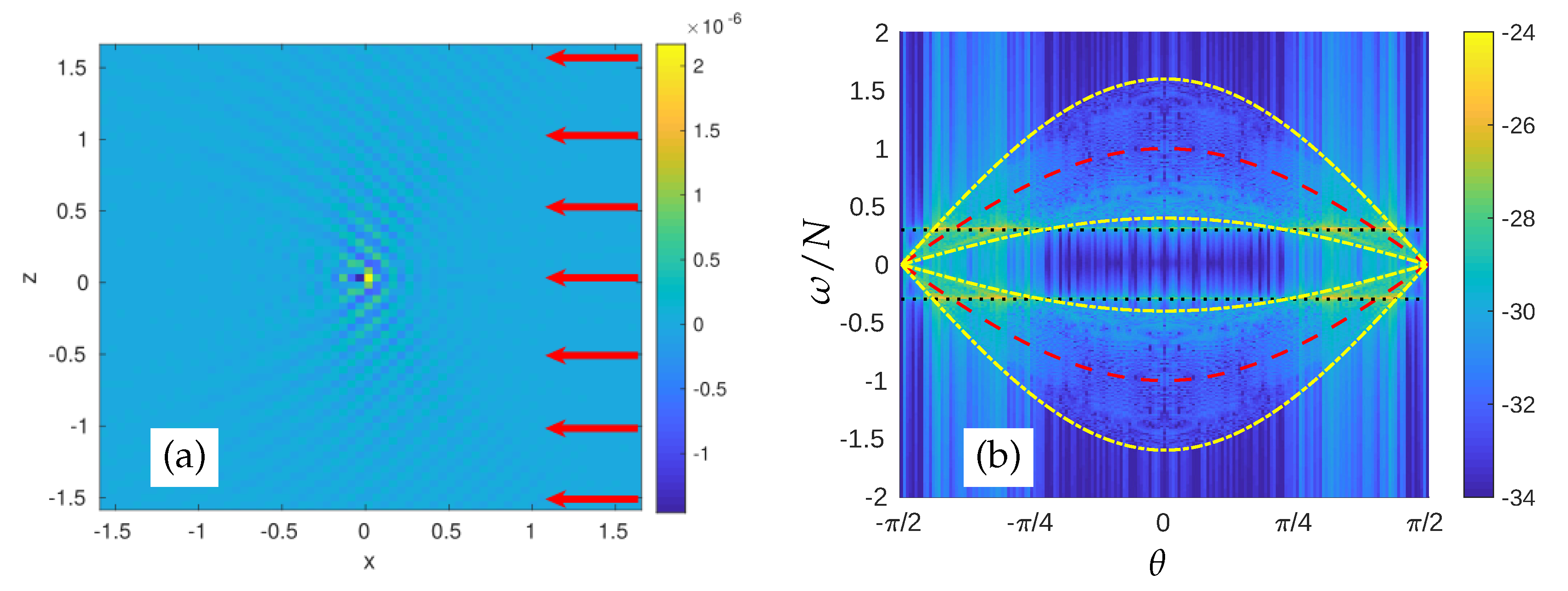
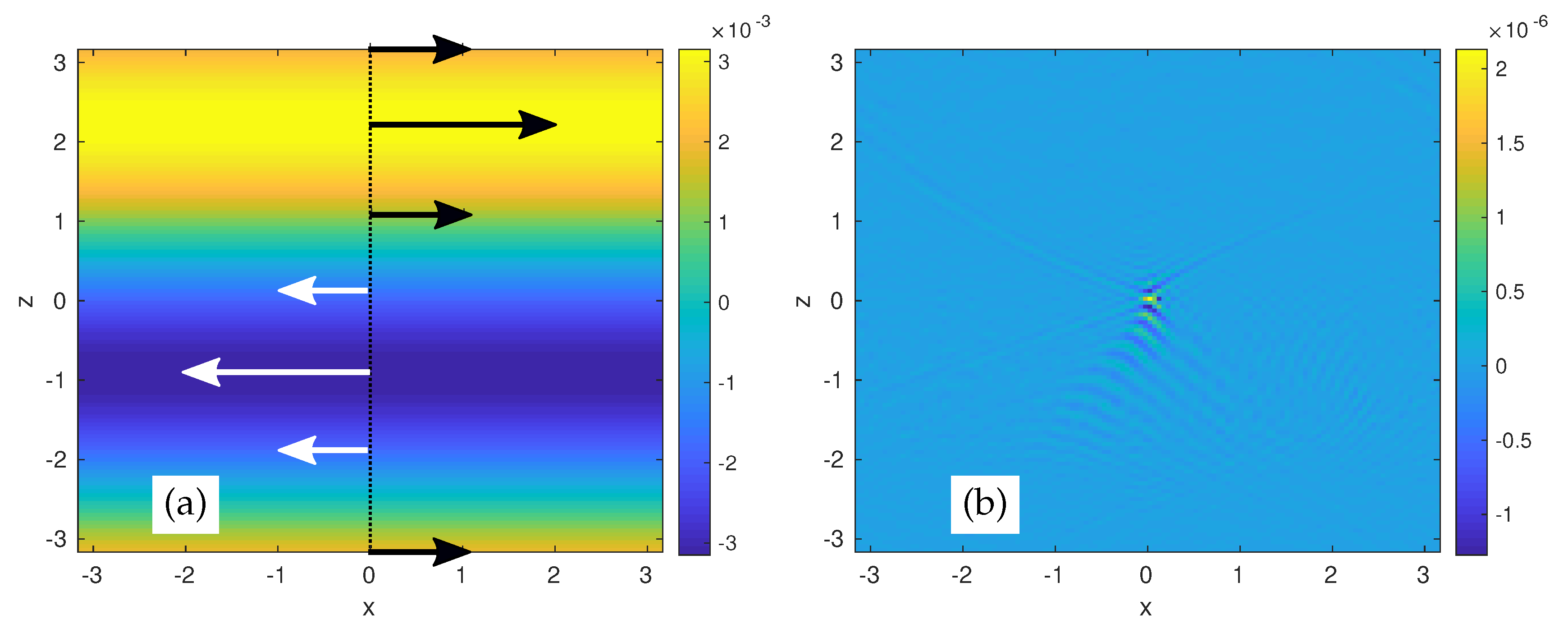
3.1. Sweeping by a Uniform Convective Flow
3.1.1. Theoretical Modified Dispersion Relation
3.1.2. Sweeping by Vertical Velocity
3.1.3. Sweeping by Horizontal Velocity
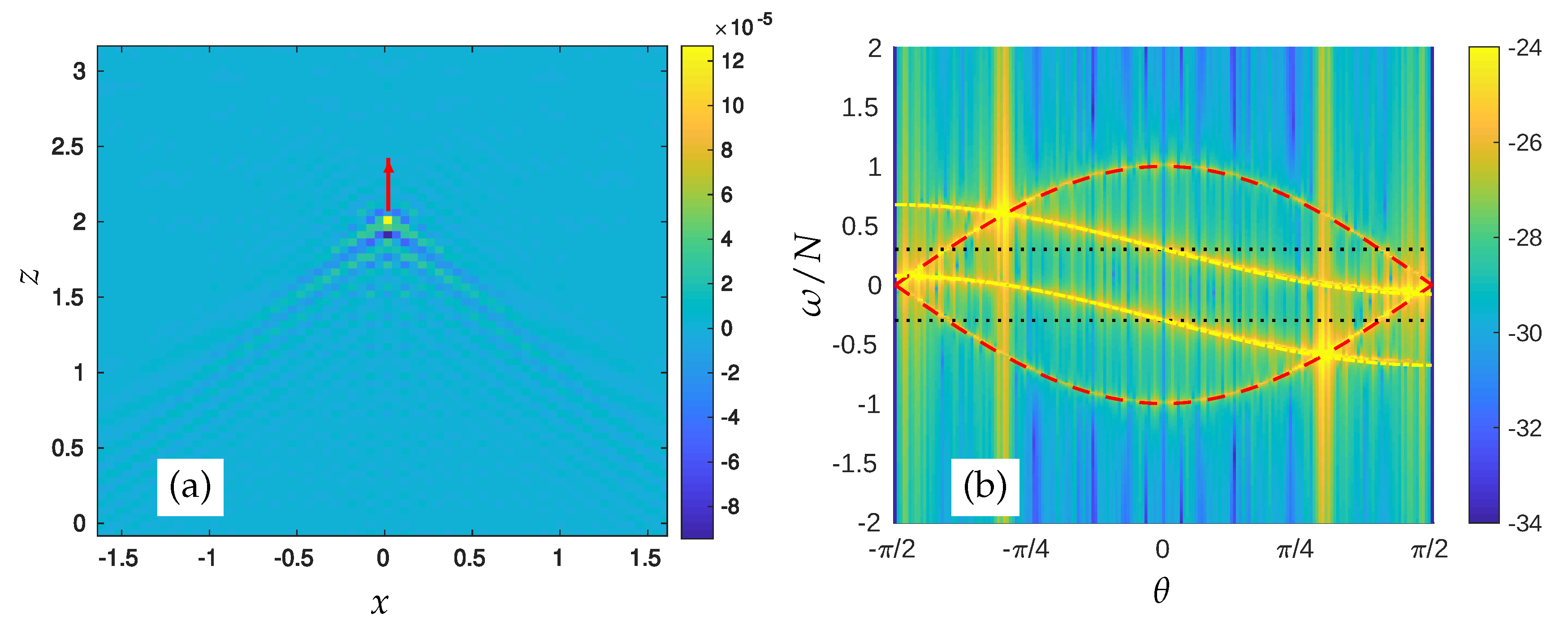
3.2. Doppler Shift Due to the Motion of the Wave Source
3.3. Sweeping by a Sheared Convective Mean Flow
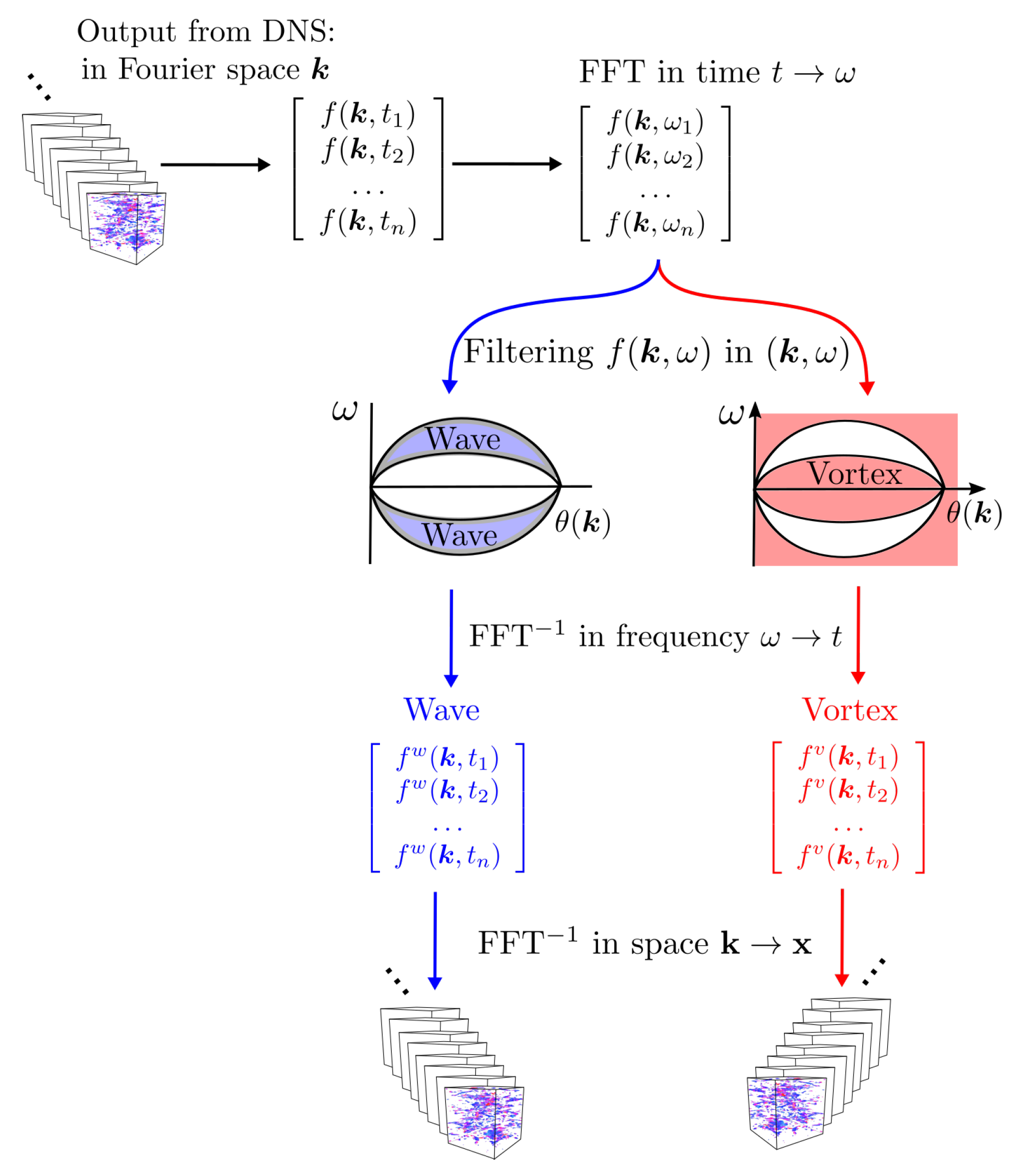
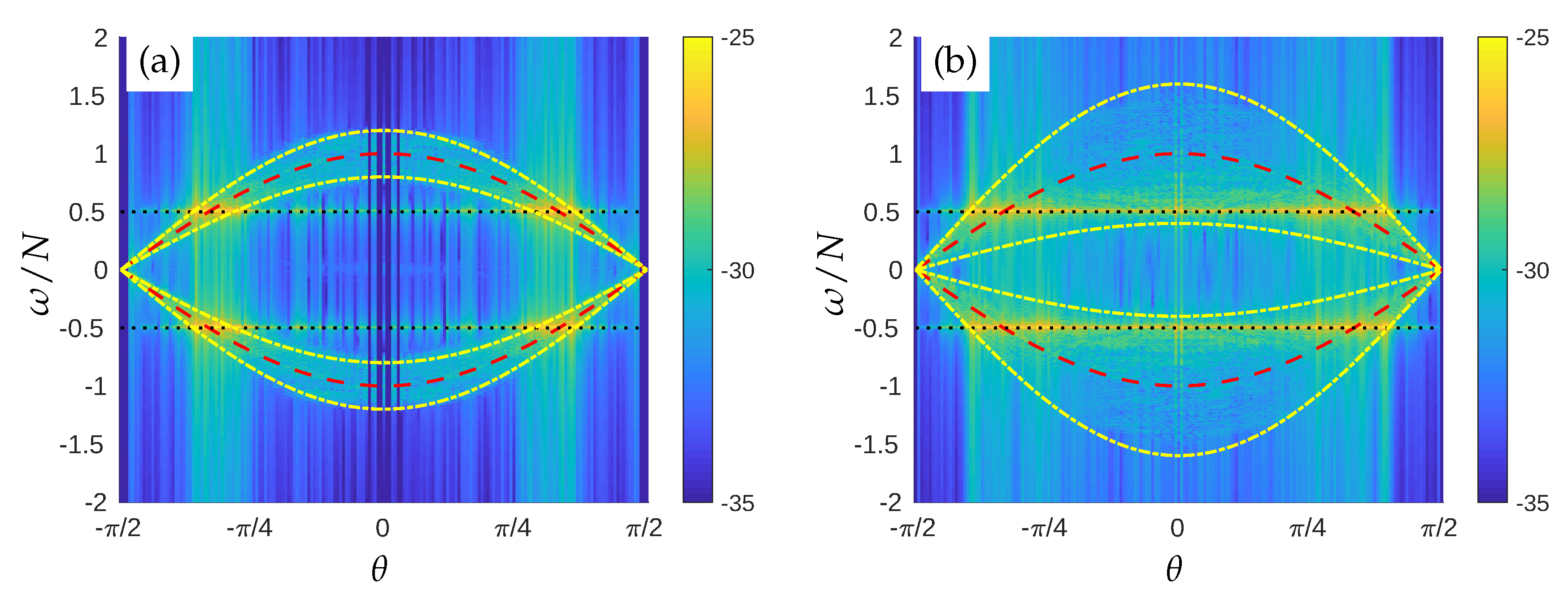
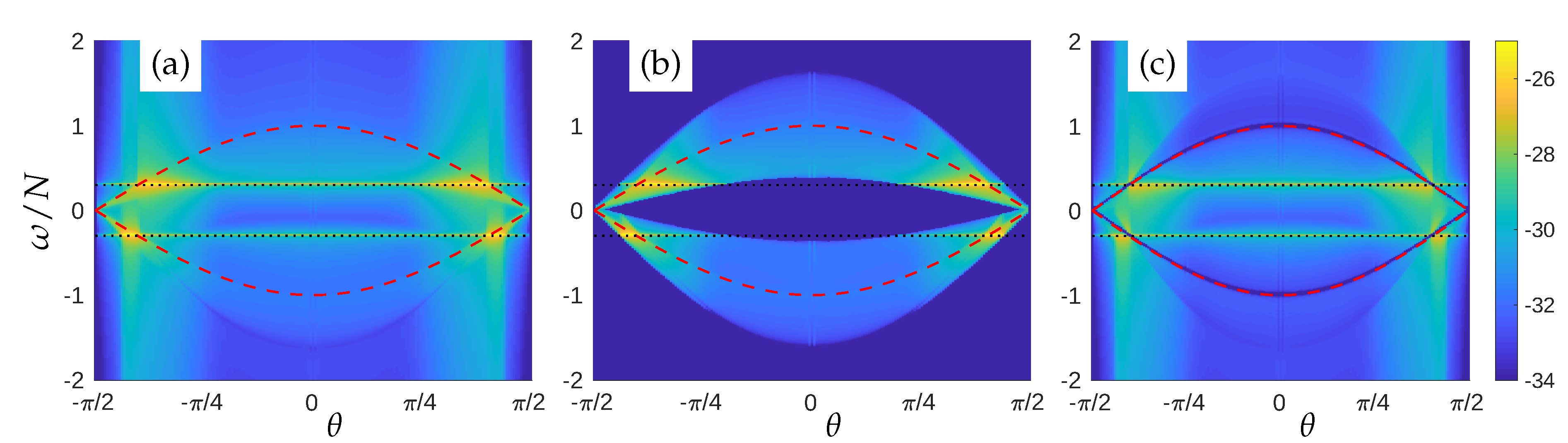
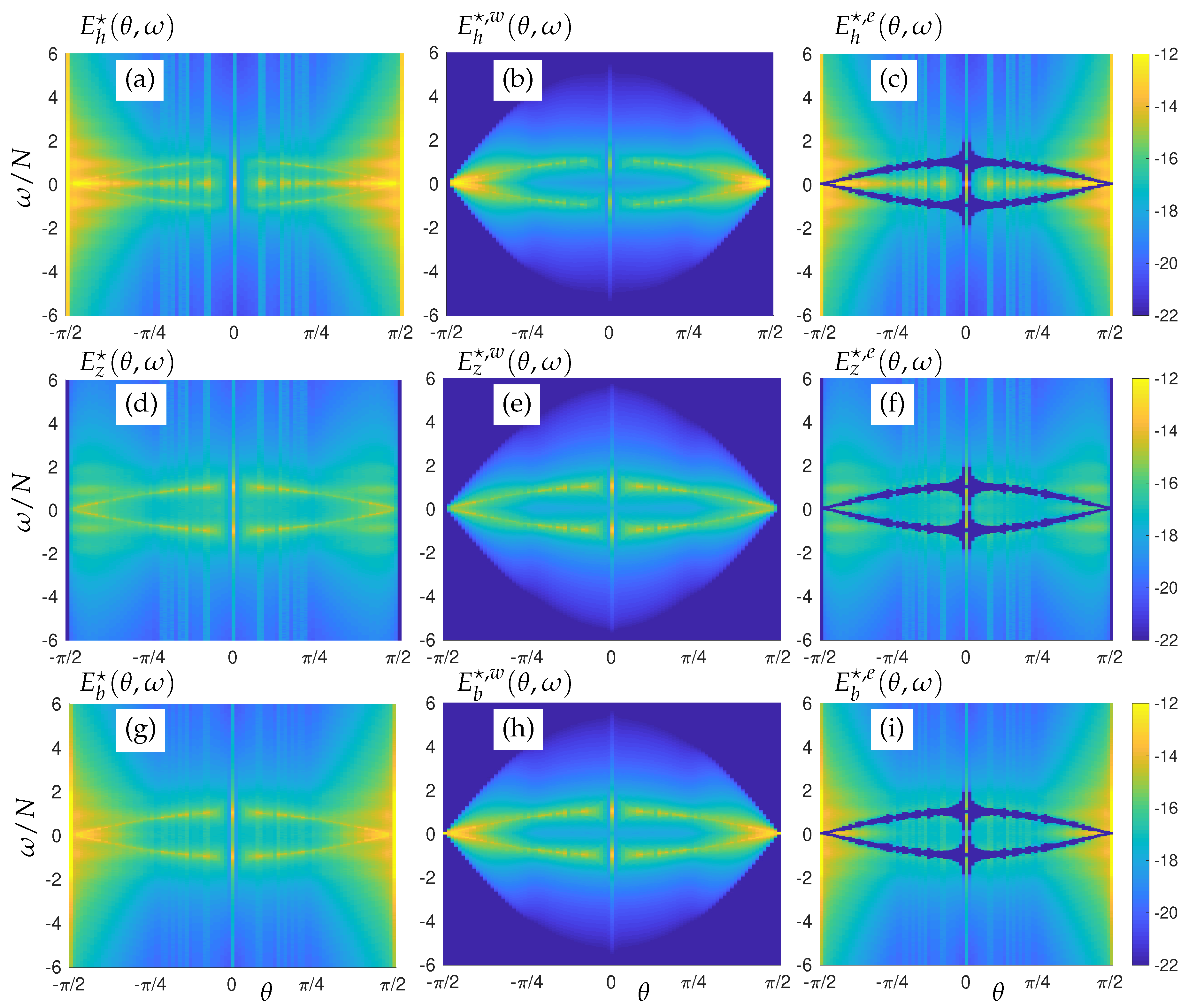
4. Explicit Space-Time Decomposition for Disentangling Waves and Eddies
4.1. Four-Dimensional Filtering
- Direct Numerical Simulation (DNS) provides time-dependent velocity–buoyancy spectral coefficients in 3D Fourier space in terms of the wavevector . In the following, we denote by f either the velocity or buoyancy coefficient, as .
- We compute the 1D time-Fourier transform as .
- For each point in the 4D space, the “waves” contribution to the flow field is denoted , and is obtained by filtering the Fourier modes matching the modified dispersion relation, i.e., lying in the region defined by:where the range of advective velocities is characterized by a single is obtained from DNS. The “eddy” part is denoted and obtained as the difference between f and . For the horizontal velocity field, the VSHF mode ( and ) is removed from the wave component. It corresponds to the point (, ) in the plane.
- We compute the 1D inverse Fourier transforms and to return to physical time for the wave and eddy coefficients.
- Compute the 3D inverse Fourier transform in physical space, which permits recovering the wave and eddy fields in physical space and to visualize them.
4.2. Application to the Sweeping by Horizontal Velocity of Saint-Andrews cross Wave Propagation
4.3. DNS and Numerical Parameters
4.4. Estimation of the Sweeping Velocity
4.5. Time-Windowing for the Time Fourier Transform
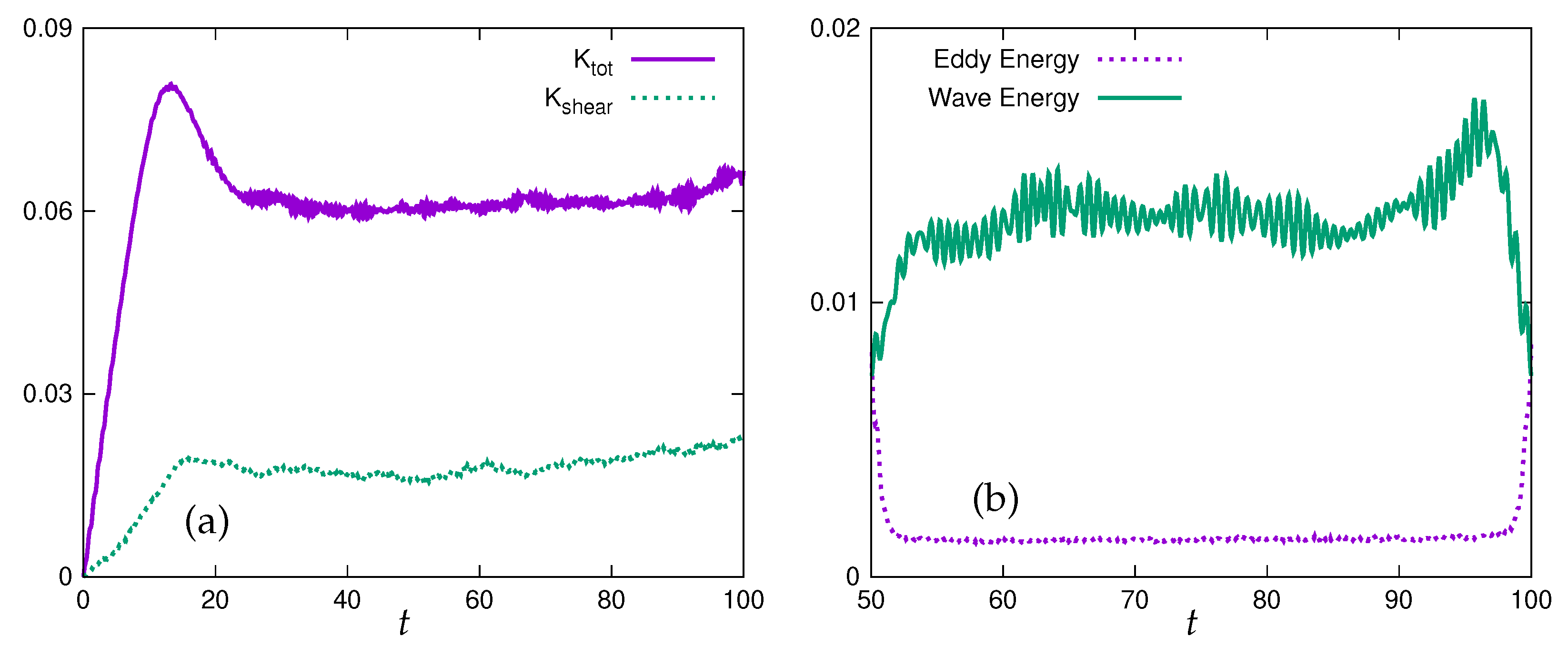
4.6. Energy Distribution in the Plane
- For horizontal and potential energy density, we define the wave part of the energies, respectively noted , , based on ,, and .
- Similarly, we define the eddy part of energy, with energies noted , , based on , , .
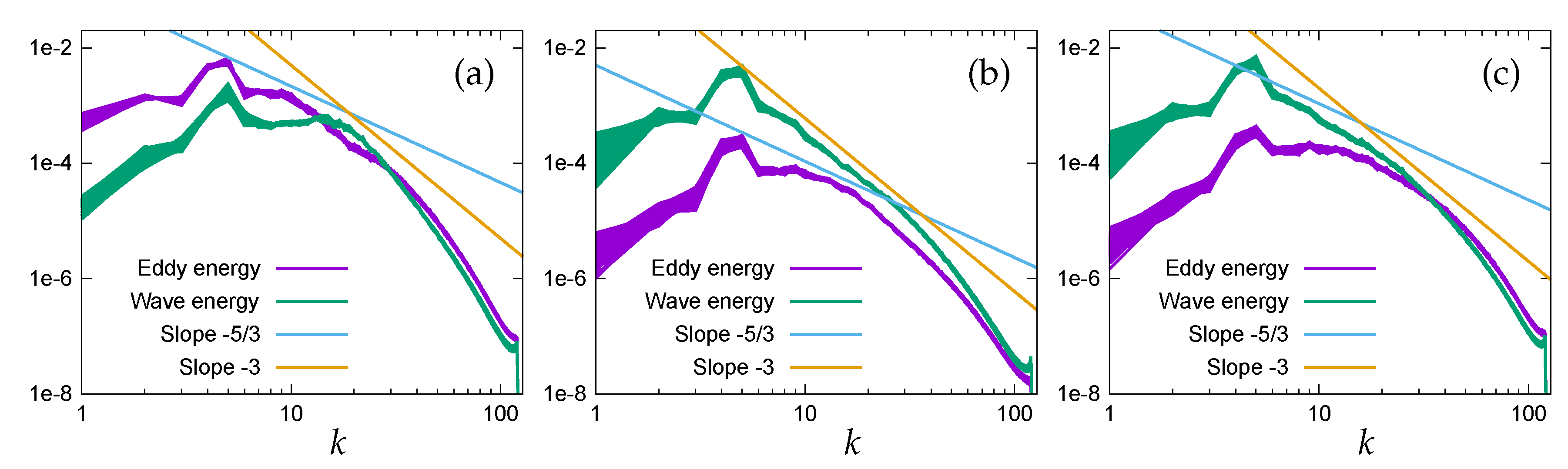
4.7. Energy Spectra
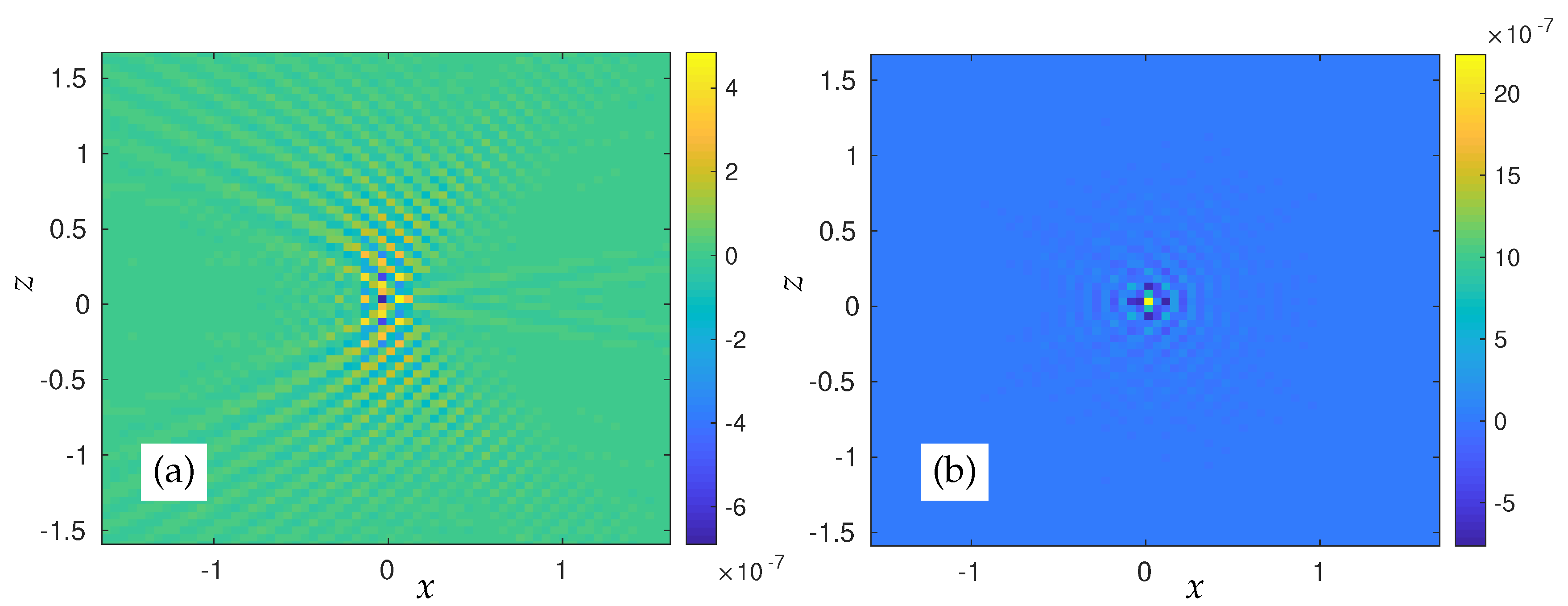
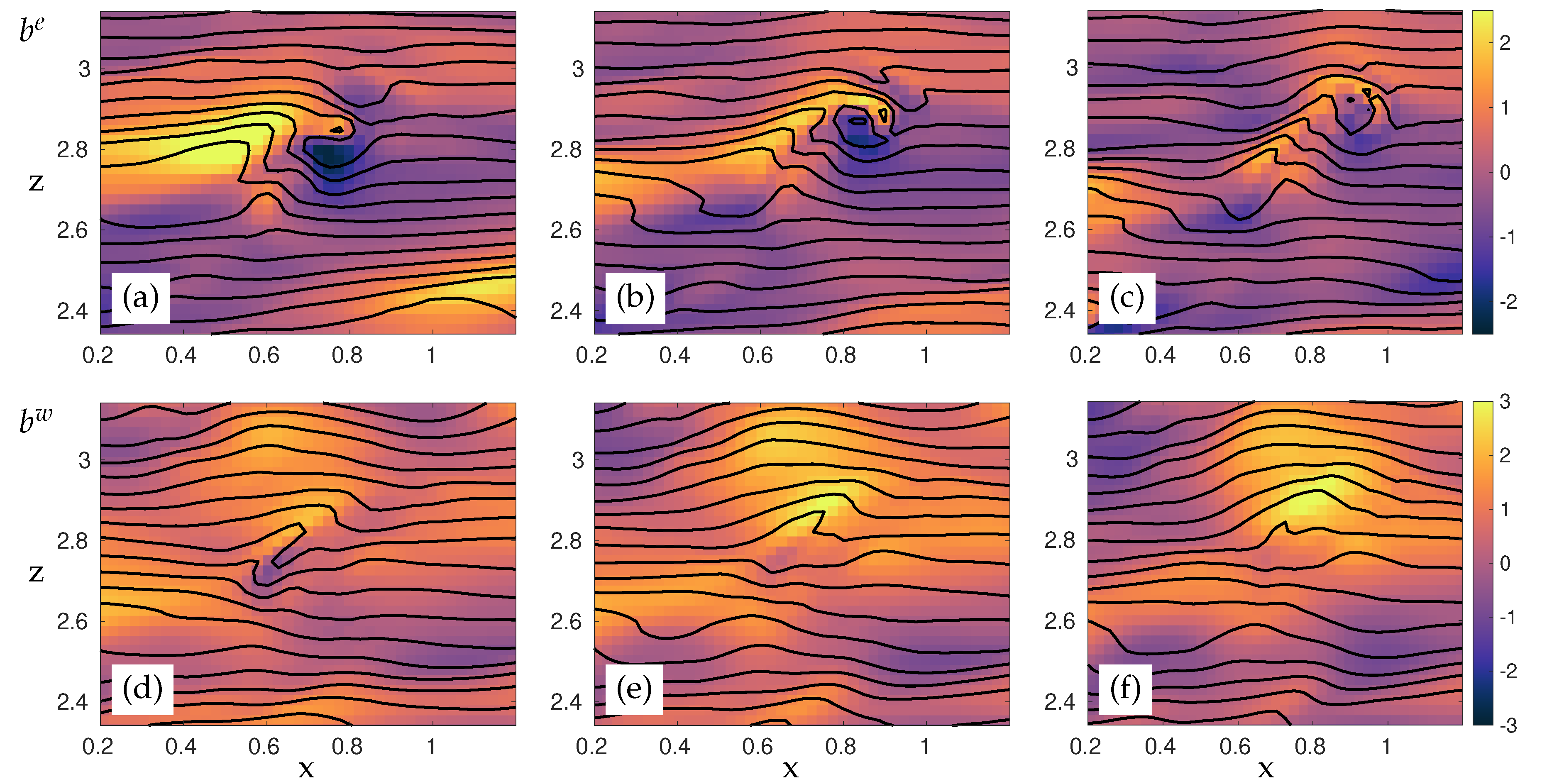
4.8. Physical Space Distribution of Wave and Eddy Fields
5. Conclusions and Perspectives
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Hann Window for Saint Andrews Cross
Appendix B. Analytical Solution for a Local Oscillating Buoyancy Forcing
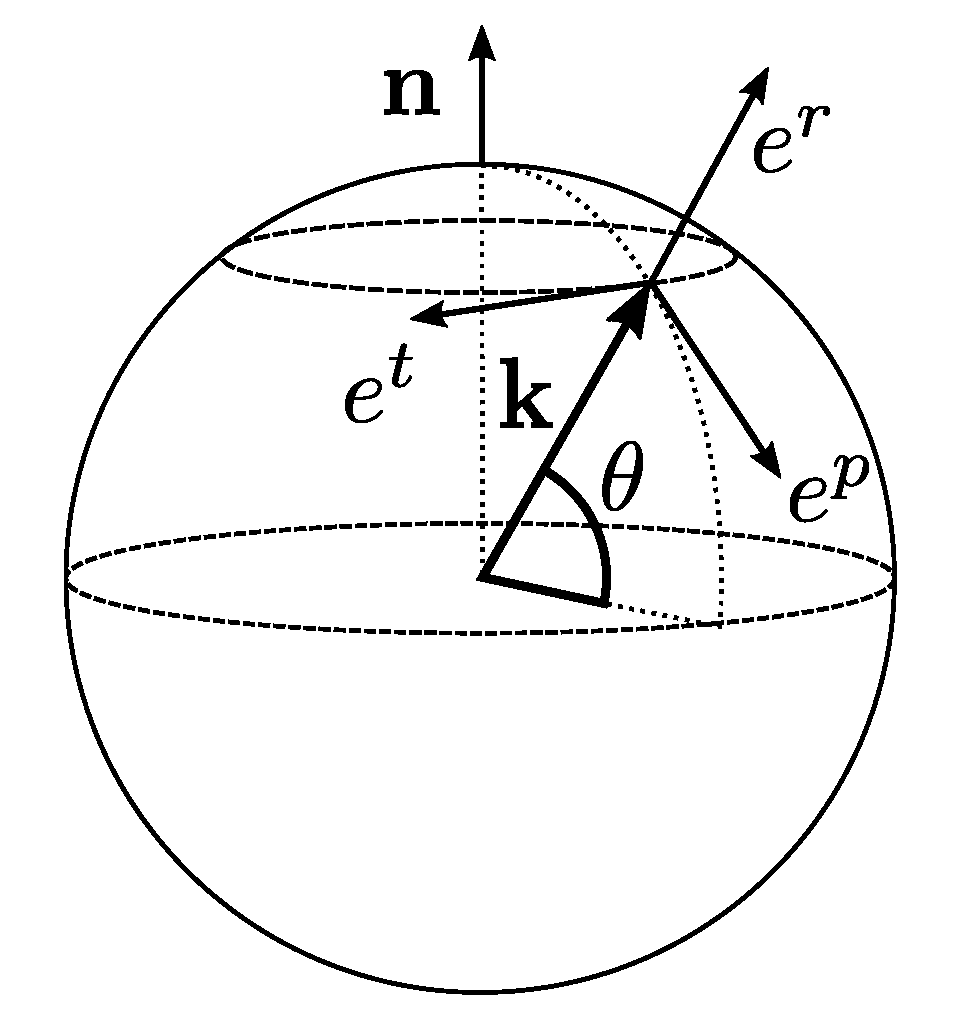
Appendix C. Algorithm for Time-Space Filtering of the Fields
References
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- MacKinnon, J. Oceanography: Mountain waves in the deep ocean. Nature 2013, 501, 321. [Google Scholar] [CrossRef] [PubMed]
- MacKinnon, J.A.; Zhao, Z.; Whalen, C.B.; Waterhouse, A.F.; Trossman, D.S.; Sun, O.M.; St. Laurent, L.C.; Simmons, H.L.; Polzin, K.; Pinkel, R.; et al. Climate Process Team on Internal Wave-Driven Ocean Mixing. Bull. Am. Meteorol. Soc. 2017, 98, 2429–2454. [Google Scholar] [CrossRef] [PubMed]
- Bretherton, F.P. Momentum transport by gravity waves. Q. J. R. Meteorol. Soc. 1969, 95, 213–243. [Google Scholar] [CrossRef]
- Lighthill, M.J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nazarenko, S. Wave Turbulence; Springer: Berlin/Heidelberg, Germany, 2011; Volume 825. [Google Scholar]
- Dyachenko, A.; Lvov, Y.; Zakharov, V.E. Five-wave interaction on the surface of deep fluid. Phys. D Nonlinear Phenom. 1995, 87, 233–261. [Google Scholar] [CrossRef]
- Yarom, E.; Sharon, E. Experimental observation of steady inertial wave turbulence in deep rotating flows. Nat. Phys. 2014, 10, 510–514. [Google Scholar] [CrossRef]
- Le Reun, T.; Favier, B.; Barker, A.J.; Le Bars, M. Inertial Wave Turbulence Driven by Elliptical Instability. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef]
- Clark di Leoni, P.; Mininni, P.D. Absorption of waves by large-scale winds in stratified turbulence. Phys. Rev. E 2015, 91. [Google Scholar] [CrossRef]
- Davidson, P.A.; Staplehurst, P.J.; Dalziel, S.B. On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 2006, 557, 135. [Google Scholar] [CrossRef]
- Fitzgerald, J.G.; Farrell, B.F. Statistical state dynamics of vertically sheared horizontal flows in two-dimensional stratified turbulence. J. Fluid Mech. 2018, 854, 544–590. [Google Scholar] [CrossRef]
- Alford, M.H.; MacKinnon, J.A.; Pinkel, R.; Klymak, J.M. Space–Time Scales of Shear in the North Pacific. J. Phys. Oceanogr. 2017, 47, 2455–2478. [Google Scholar] [CrossRef]
- Grimshaw, R. Nonlinear Internal Gravity Waves and Their Interaction with the Mean Wind. J. Atmos. Sci. 1975, 32, 1779–1793. [Google Scholar] [CrossRef]
- Gerkema, T.; Maas, L.R.M.; van Haren, H. A Note on the Role of Mean Flows in Doppler-Shifted Frequencies. J. Phys. Oceanogr. 2013, 43, 432–441. [Google Scholar] [CrossRef]
- Pinkel, R. Vortical and Internal Wave Shear and Strain. J. Phys. Oceanogr. 2014, 44, 2070–2092. [Google Scholar] [CrossRef]
- Riley, J.J.; Metcalfe, R.W.; Weissman, M.A. Direct numerical simulations of homogeneous turbulence in density-stratified fluids. AIP Conf. Proc. 1981, 76, 79–112. [Google Scholar] [CrossRef]
- Gibson, C.H. Internal waves, fossil turbulence, and composite ocean microstructure spectra. J. Fluid Mech. 1986, 168, 89–117. [Google Scholar] [CrossRef]
- Staquet, C.; Riley, J.J. On the velocity field associated with potential vorticity. Dyn. Atmos. Oceans 1989, 14, 93–123. [Google Scholar] [CrossRef]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 10. [Google Scholar]
- Godeferd, F.S.; Cambon, C. Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 1994, 6, 2084–2100. [Google Scholar] [CrossRef]
- Herbert, C.; Marino, R.; Rosenberg, D.; Pouquet, A. Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation. J. Fluid Mech. 2016, 806, 165–204. [Google Scholar] [CrossRef][Green Version]
- Maffioli, A.; Delache, A.; Godeferd, F. Signature and energetics of internal gravity waves in stratified turbulence. Phys. Rev. Fluids 2020, 2, 104802, submitted. [Google Scholar] [CrossRef]
- Pedlosky, J. Waves in the Ocean and Atmosphere: Introduction to Wave Dynamics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; National Aeronautics and Space Administration: Washington, DC, USA, 1981; Volume 81315.
- Pekurovsky, D. P3DFFT: A framework for parallel computations of Fourier transforms in three dimensions. SIAM J. Sci. Comput. 2012, 34, C192–C209. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Maffioli, A. Vertical spectra of stratified turbulence at large horizontal scales. Phys. Rev. Fluids 2017, 2. [Google Scholar] [CrossRef]
- Campagne, A.; Gallet, B.; Moisy, F.; Cortet, P.P. Disentangling inertial waves from eddy turbulence in a forced rotating-turbulence experiment. Phys. Rev. E 2015, 91, 043016. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.M.; Waleffe, F. Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 2002, 451, 145–168. [Google Scholar] [CrossRef]
- Herring, J.R.; Métais, O. Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 1989, 202, 97–115. [Google Scholar] [CrossRef]
- Smith, L.M. Numerical study of two-dimensional stratified turbulence. Contemp. Math. 2001, 283, 91–106. [Google Scholar]
- Godeferd, F.S.; Staquet, C. Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 2. Large-scale and small-scale anisotropy. J. Fluid Mech. 2003, 486, 115–159. [Google Scholar] [CrossRef]
- Kumar, A.; Verma, M.K.; Sukhatme, J. Phenomenology of two-dimensional stably stratified turbulence under large-scale forcing. J. Turbul. 2017, 18, 219–239. [Google Scholar] [CrossRef]
- Ascani, F.; Firing, E.; McCreary, J.P.; Brandt, P.; Greatbatch, R.J. The deep equatorial ocean circulation in wind-forced numerical solutions. J. Phys. Oceanogr. 2015, 45, 1709–1734. [Google Scholar] [CrossRef]
- Galmiche, M.; Hunt, J. The formation of shear and density layers in stably stratified turbulent flows: Linear processes. J. Fluid Mech. 2002, 455, 243–262. [Google Scholar] [CrossRef]
- Fincham, A.M.; Maxworthy, T.; Spedding, G.R. Energy dissipation and vortex structurein freely decaying stratified grid turbulence. Dyn. Atmos. Oceans 1996, 23, 155–169. [Google Scholar] [CrossRef]
- Yakovenko, S.N. Development of instability and turbulence in overturning lee waves: The map of different scenarios in Re–Pr space. J. Phys. Conf. Ser. 2016, 722, 012048. [Google Scholar] [CrossRef]
- Alexakis, A.; Mininni, P.D.; Pouquet, A. Shell-to-shell energy transfer in magnetohydrodynamics. I. Steady state turbulence. Phys. Rev. E 2005, 72. [Google Scholar] [CrossRef] [PubMed]
- Herring, J.R. Approach of axisymmetric turbulence to isotropy. Phys. Fluids 1974, 17, 859–872. [Google Scholar] [CrossRef]


| Section | Dispersion Relation | Forcing Frequency | Advective Velocity | N | |
|---|---|---|---|---|---|
| Section 2.4 | none | 1 | |||
| Section 3.1.2 | 1 | ||||
| Section 3.1.3 and Section 4.2 | 1 | ||||
| Section 3.2 | 1 | ||||
| Section 3.3 | 1 | ||||
| Section 4.3, Section 4.4, Section 4.5, Section 4.6, Section 4.7 and Section 4.8 | none | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, H.; Delache, A.; Godeferd, F.S. Partitioning Waves and Eddies in Stably Stratified Turbulence. Atmosphere 2020, 11, 420. https://doi.org/10.3390/atmos11040420
Lam H, Delache A, Godeferd FS. Partitioning Waves and Eddies in Stably Stratified Turbulence. Atmosphere. 2020; 11(4):420. https://doi.org/10.3390/atmos11040420
Chicago/Turabian StyleLam, Henri, Alexandre Delache, and Fabien S Godeferd. 2020. "Partitioning Waves and Eddies in Stably Stratified Turbulence" Atmosphere 11, no. 4: 420. https://doi.org/10.3390/atmos11040420
APA StyleLam, H., Delache, A., & Godeferd, F. S. (2020). Partitioning Waves and Eddies in Stably Stratified Turbulence. Atmosphere, 11(4), 420. https://doi.org/10.3390/atmos11040420





