1. Introduction
The solar corona is the most external, rarefied and hottest part of the Sun’s atmosphere, which is formed by a plasma at an average temperature of the order of or larger than
K. It is permeated by a strongly inhomogeneous magnetic field which is generated by the dynamo mechanism [
1,
2,
3,
4,
5,
6,
7] operating in the solar convection zone. Among coronal magnetic structures, coronal loops represent a common configuration. The problem of elucidating the physical mechanisms which are responsible for the energization of the solar corona and its consequent heating has been widely studied from a theoretical point of view. One of the possible sources of energy for the corona is represented by mechanical motions in the photosphere, which is the lowest and most dense part of the solar atmosphere. The energy associated with these motions, after crossing the chromosphere [
8], would be partially transferred to the rarefied corona through the magnetic field which is rooted in the photosphere and ubiquitously fills the corona. Two important issues still under debate are the following: (i) in which form and at which timescales does the energy of photospheric motions reaches the corona? (ii) How is this energy moved to the very small scales where it can be dissipated? This paper aims to give a contribution to both points.
Concerning the first question, models of coronal heating have been traditionally classified into two groups: “direct current” (DC) or “alternating current” (AC). In the former case, slow photospheric motions are considered, with timescales longer than the Alfvén crossing time
, which is the time a perturbation takes to cross a closed magnetic structure propagating at the Alfvén velocity. In that case, coronal structures continuously re-arrange through a sequence of quasi-equilibrium states. Magnetic energy increases in time until reaching a threshold when it is suddenly dissipated, while the kinetic energy remains at a much lower level. In contrast, AC heating models consider perturbations at timescales comparable to or shorter than
, essentially belonging to the Alfvén branch, where kinetic energy is of the order of magnetic energy. Indeed, quasi-periodic plasma velocity fluctuations have been ubiquitously detected in corona, propagating along the magnetic field with velocities compatible with the Alfvén speed [
9,
10,
11]. The frequency
f of such fluctuations spans a wide range, going from
Hz
to
Hz
. The frequency range of detected photospheric motions is as much as wide [
12,
13]. Observations also suggest the existence of velocity fluctuations in the corona at much higher frequencies, based on measurements of non-thermal broadenings of coronal lines [
14]. Therefore, the distinction between AC or DC mechanisms appears to be quite artificial, since both kind of processes are probably at work at the same time [
15]. In the present paper we will consider a situation where the frequency range of excited fluctuations covers both kind of phenomena.
Energy injected in the corona needs to be transferred to small dissipative scales in order to be converted into heat. Concerning this second question, different possibilities have been studied about the involved mechanism. Some of them are related to spatial inhomogeneities of the coronal structures that generate small scales in the perturbations propagating inside them, both within a fluid approach [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26] and taking into account kinetic effects [
27,
28]. These models consider the coupling between perturbations and a nonuniform background. In contrast, nonlinear couplings among perturbations are at the base of turbulence models, which describe the formation of an energy cascade that transfers fluctuation energy to small dissipative scales [
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]. Evaluations of energy balance between injected flux and spectral transfer has also been carried out in direct simulations [
40,
41,
42]. More recently, models taking into account both turbulence and inhomogeneities have been proposed [
43]. Related to the heating problem, other aspects have also been considered in the dynamics of a coronal loop, such as the complexity of magnetic topology induced by motions at its ends [
44], or kink and Alfvénic torsional mode interactions [
45,
46,
47].
Some of the above-cited papers are concerned with direct numerical simulation of magnetohydrodynamic (MHD) equations, and based on first principles. However, due to numerical limitations, the wide range of spatial scales of coronal turbulence is not adequately described. This problem can be circumvented using “reduced” models of turbulence, like the so-called shell models [
30,
31,
48], in which the dynamics of turbulence is represented in a simplified Fourier space. In a coronal context, hybrid shell models have been developed [
33,
37], based on Reduced MHD (RMHD) [
49,
50]. In such models the spatial dependence on the coordinate along the background magnetic field is retained, which allows one to impose boundary conditions at the coronal base. This approach is more appropriate with respect to classical shell models, since it is believed that the energization of the coronal structures is due to motions at the coronal base. Hybrid shell models have successfully reproduced statistical properties of coronal energy release events [
33], as well as the energy flux [
38,
39] necessary to maintain the corona at the observed temperature [
51]. Moreover, they predict fluctuating velocity enhancements associated with loop resonance [
38,
39], which can be related to increases of the spectral energy flux [
39] and to triggering of solar flares [
34,
35].
In references [
33,
35] a time dependent velocity has been imposed at the loop bases at the largest transverse scales, with a correlation time of the order of
s, corresponding to the typical time of photospheric
p-modes. In the present study we perform numerical simulations of turbulence in a coronal loop, by means of the same hybrid shell model as in [
33,
35], but using different boundary conditions. In particular, the presently adopted boundary conditions try to give a more realistic representation of the spatial and temporal dependence of photospheric motions. They are based on detailed space-time measurement of the photospheric velocity field [
12,
13]. Beside
p-modes, the corresponding frequency spectra display also oscillations at much lower frequencies, with different contributions at different spatial scales. The aim of the present study is to elucidate to which extent a more realistic representation of photospheric motions driving coronal loop oscillations can affect the results, in terms of loop frequency spectra, resonance triggering, level of oscillations and incoming energy flux. These results are relevant in the perspective of obtaining a more realistic modeling of the turbulence dynamics in a coronal loop.
3. Results
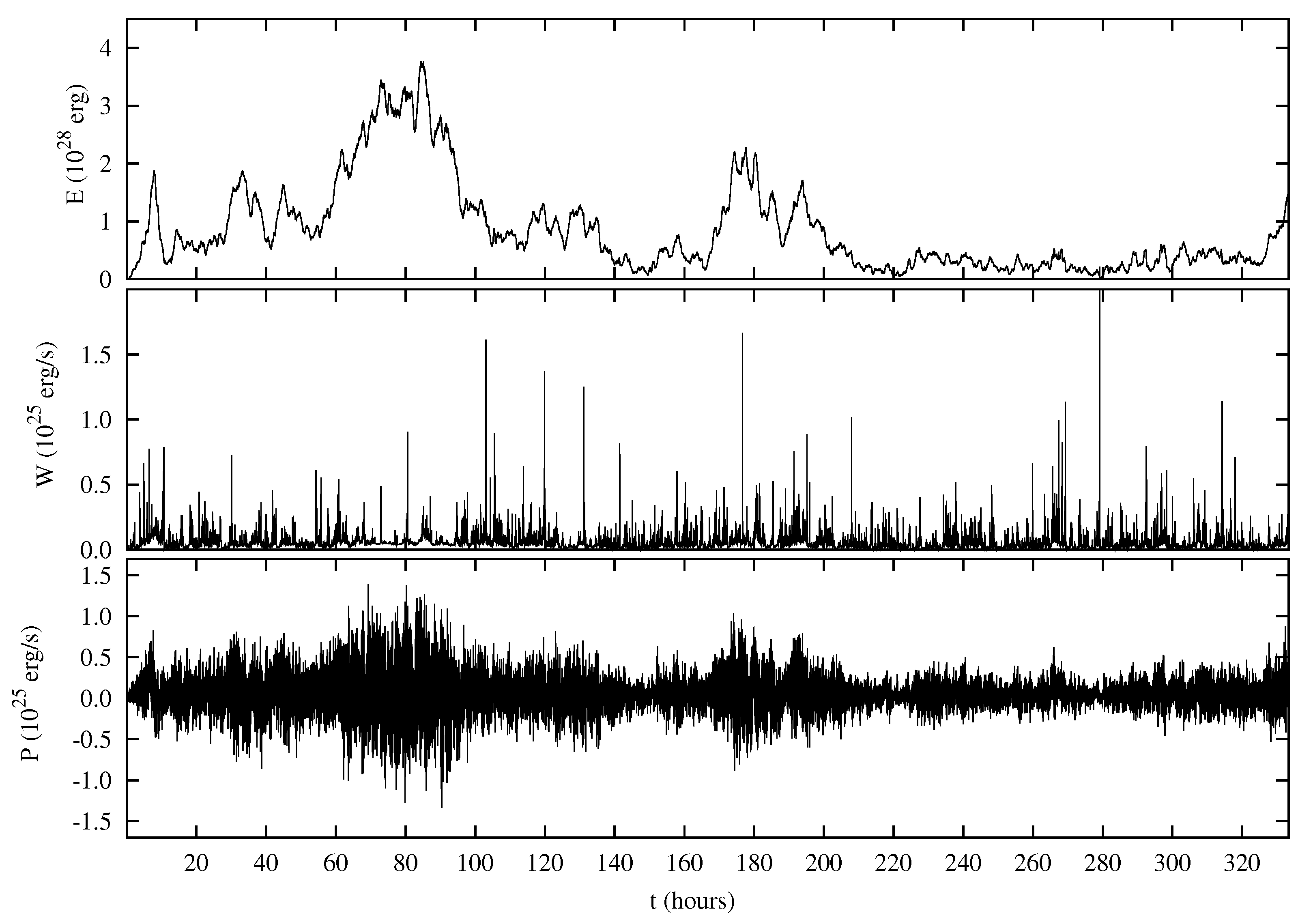
Due to the velocity imposed at the boundaries, energy is continuously injected into the domain in form of velocity and magnetic field fluctuations. The dynamics of such fluctuations is also determined by their propagation along the loop and by nonlinear interactions which move energy towards small scales, where it can be dissipated. In the top panel of
Figure 3 the time dependence of the total energy
E is plotted. It can be seen that the model does not predict a stationary level for the total energy
E of the fluctuating fields inside the loop. On the contrary,
E erratically varies during the time, reaching higher values
erg in the time interval 60 h
h, and a much lower level, roughly
erg, during the interval 220 h
h. This is due to the fact that the system is characterized by different dynamical regimes, that we will describe later in this section.
In consequence of intermittency—a peculiar feature of this system [
53]—the dissipated power
W displays abrupt bursts during the time (
Figure 3) which are a signature of the fragmentation of dissipative structures taking place at small scales. The average value of the dissipated power is
erg/s. Bursts of
W can be identified as energy release events taking place in the solar corona. Indeed, it has been shown that some statistical properties of dissipative events in the hybrid shell model, namely, the distributions of peak intensity, duration time, released energy and waiting times between subsequent events, positively compare with the same distributions found for coronal energy release events [
33].
The incoming power
P varies on a very short time scale, assuming both positive and negative signs. In fact, the value of
P depends on both inward and outward propagating modes (Equation (
8)), i.e.,
P is determined not only by the boundary conditions but also by the internal dynamics. However, the average value
erg/s is positive, indicating that, on average, motions imposed at the loop boundary have introduced energy inside the loop. We notice that
, indicating that the incoming power is almost balanced by the dissipated power. A perfect balance is not reached because the energy
E contained inside the loop is not stationary in time.
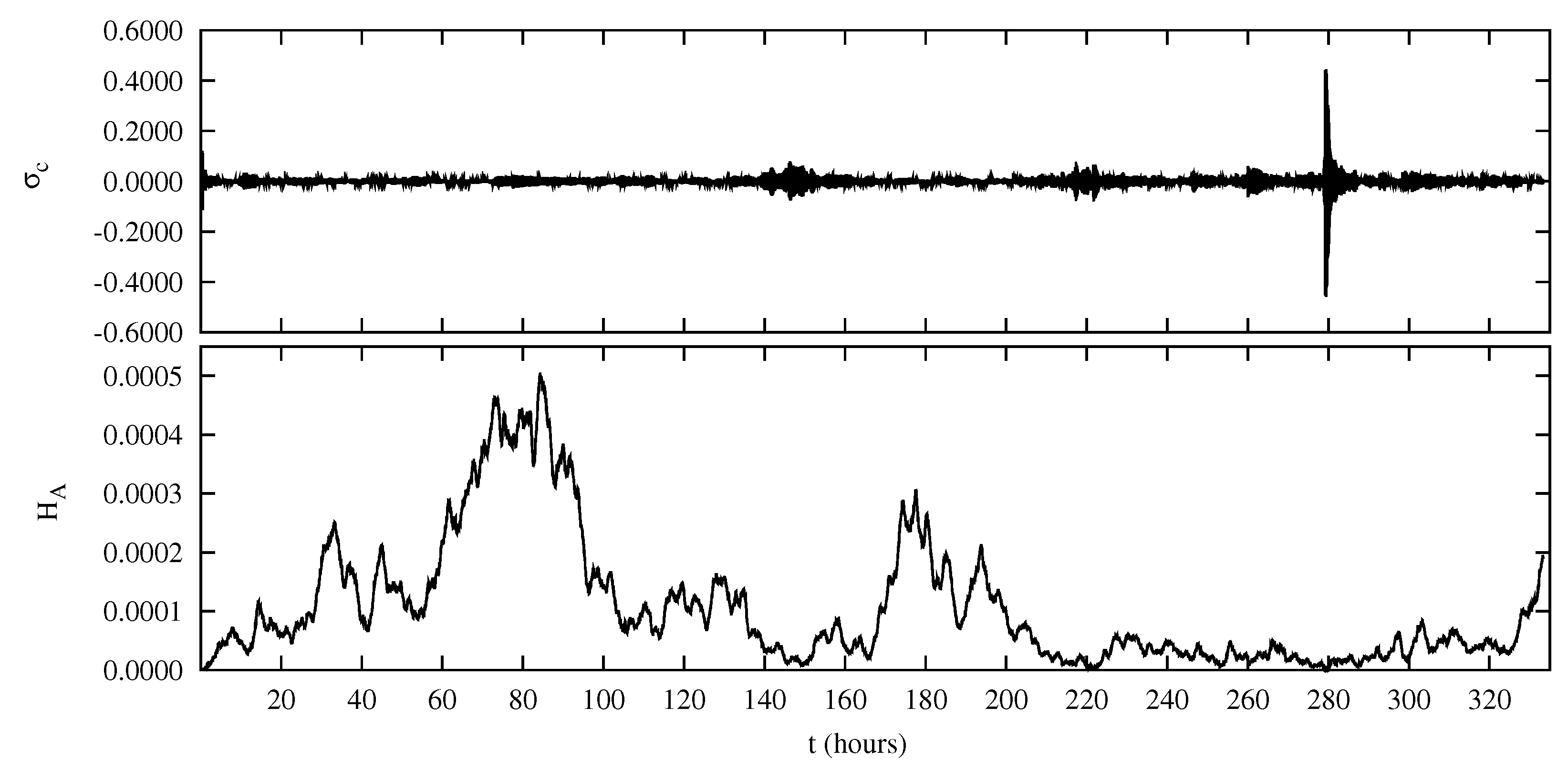
We calculated the normalized cross-helicity
, where the pseudo-energies are defined by
. The normalized cross-helicity satisfies the condition
; in particular, it is
(
) when
(
) fluctuations dominate on
(
) fluctuations. In
Figure 4 (upper panel) the normalized cross-helicity is plotted as a function of time. It can be seen that
is quite close to zero during almost all the simulation time, indicating that the level of
fluctuations is comparable with that of
fluctuations. Indeed, we will show that the most energetic fluctuations are low-frequency magnetic fluctuations, where
(in dimensionless units), this latter condition corresponding to
. Therefore, the dominance of magnetic fluctuations is compatible with low
values. During a short interval around
h,
displays fast oscillations where it changes sign on a short time scale, reaching values sensibly different form zero. During this phase of the time evolution the dominance of magnetic perturbations is temporarily suppressed, as testified by the particularly low value of the total energy
E (
Figure 3).
The squared magnetic potential, defined as
, is plotted as a function of time in the lower panel of
Figure 4. Comparing with the total energy plotted in
Figure 3 we see that
H and
E have a very similar time behaviour. This is again due to the dominance of large-scale magnetic fluctuations in determining
E and to the fact that the major contribution to
H comes from magnetic fluctuations at low
values. We notice that both cross-helicity
and squared magnetic potential
H are ideal invariants of 2D shell models, i.e., they are exactly conserved by nonlinear terms in Equation (
3). However, in the hybrid shell model
H and
are not conserved, both because of the driving imposed at boundaries
and
, and in consequence of dissipation.
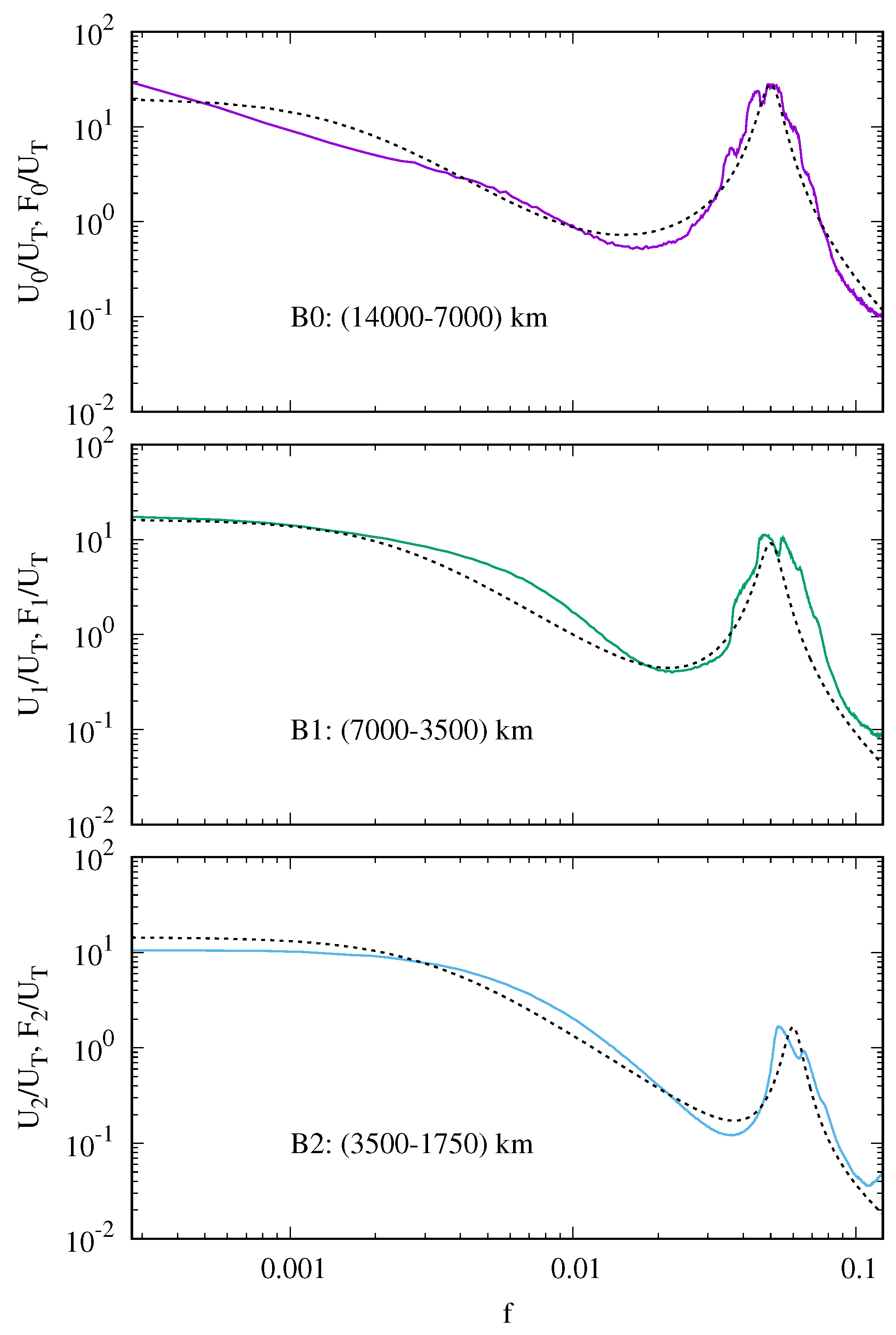
In order to see how velocity and magnetic field fluctuations are on average distributed along the longitudinal extension
x of the loop, we calculated the RMS of the velocity and magnetic field fluctuations as function of
x, as in the following:
where
and
. These quantities are plotted in
Figure 5, where time average has been performed over different intervals of time. In particular, we consider the RMS of both velocity and magnetic field fluctuations computed by considering the whole simulation time (black solid lines in
Figure 5), for the interval
h (grey dot-dashed lines) and for the interval 58 h
h (magenta dashed lines), respectively.
From
Figure 5 we see that the velocity and magnetic field fluctuation levels averaged over the whole simulation are
cm s
and
G, respectively. We notice that
, which is sufficiently consistent with the assumptions of RMHD. The RMS values corresponds to fluctuating kinetic and magnetic energy densities:
erg cm
and
erg cm
. Therefore, the fluctuating magnetic energy is much larger than the kinetic one. This property is peculiar to models describing the DC coronal heating. Comparing the profiles in the two time intervals
h, 54 h] and
h, 116 h], we see that velocity fluctuations are larger when the total energy
E is lower. Indeed, it has been shown [
34,
38] that a higher level of velocity fluctuations corresponds to a more efficient energy transfer from larger to smaller transverse scales. Therefore, the higher energy level in the interval
h, 116 h] can be interpreted as due to a lower velocity fluctuation level that partially inhibits the nonlinear cascade, allowing the energy—mostly magnetic energy—to accumulate at large scales. It is interesting to note that the velocity fluctuations in time interval
h, 116 h] are slightly lower than the average value computed on the whole simulation but certainly lower than those calculated in time interval
h, 54 h]. This highlights the high sensitivity of this system with respect to the velocity field fluctuations as regards the development of the nonlinear cascade and, consequently, of the intermittency. Moreover, since most of the energy
E is of magnetic origin, it is not surprising that larger
E corresponds to higher
values. Finally, we observe that the spatial profile
is essentially flat, with small-amplitude modulations along x, while the
profile starts from values of the order of a few km/s at the two boundaries
km and
km, rapidly reaching
50–60 km/s inside the loop. The latter values are compatible with velocity measurements deduced by the nonthermal broadening of coronal spectral lines [
14].
Analyzing the system in terms of input—embodied by the forcing velocity—and of output, i.e., the response of the system embodied by dynamically developed energy features, we examine the spectral kinetic and magnetic energies with their properties. These quantities are defined by
where
and
. They have been computed in two dynamically different time intervals, namely 0 h
54 h and 58 h
116 h.
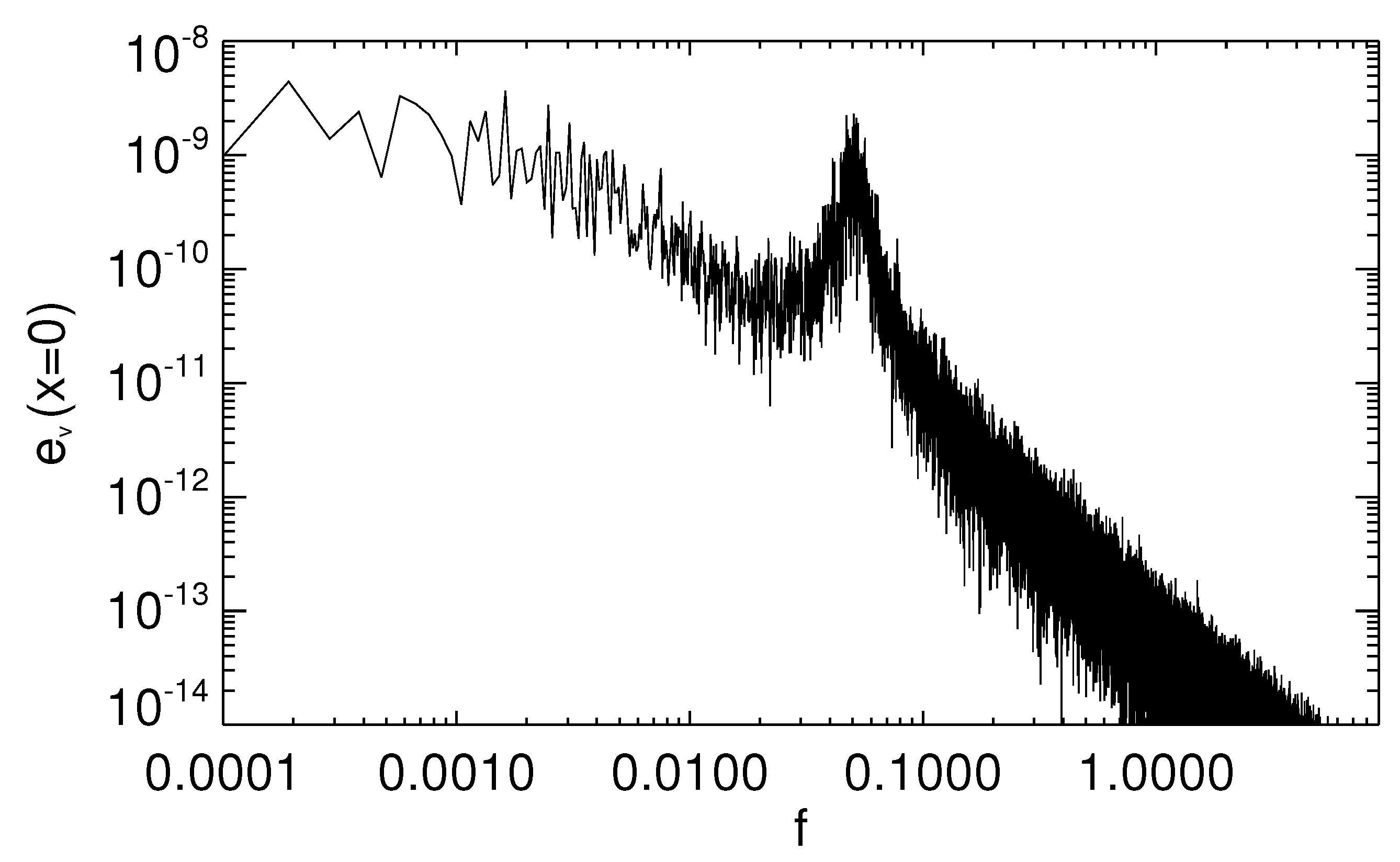
The kinetic energy imposed at the boundaries through the forcing velocity displays the same features as observed in the data of the photospheric velocity (input of the system). In particular, a bump centered at frequency
, corresponding to (300 s)
, is reproduced in the frequency spectrum (see
Figure 2). Correspondingly, the system responds by forming energy spectra with peculiar characteristics (see
Figure 6 and
Figure 7): a well-defined spike is present both in kinetic and magnetic spectra, centered at the fundamental resonant frequency
, i.e., inverse of the Alfvén crossing time
, as well as subsequent spikes corresponding to the higher harmonics, at frequencies multiples of the fundamental one (
). Resonant modes are standing Alfvénic fluctuations which are excited by the broad-band spectrum of the boundary velocity [
38,
39]. All these spikes are very sharp and slender. The resonance phenomenon is related to partial reflection of fluctuations taking place at both boundaries
and
. Of course, since the net incoming flux
P takes both positive and negative signs in time (
Figure 3), the reflection is not total, otherwise no energy could enter or leave the spatial domain.
Another feature which is present both in kinetic and magnetic spectra is a broader peak centered at frequency
, corresponding to the analogous peak in the forcing velocity spectrum (
Figure 2), which represents the contribution of
p-modes. Therefore, the model predicts that a clear signature of this particular photospheric frequency should be found in the spectrum of plasma velocity up in the corona. We also verified that such frequency is present in the body of the loop, far from the boundaries: indeed, even including only the central part of the loop in the integration domain (see Equation (
13), the peak at
in the resulting spectra is still present.
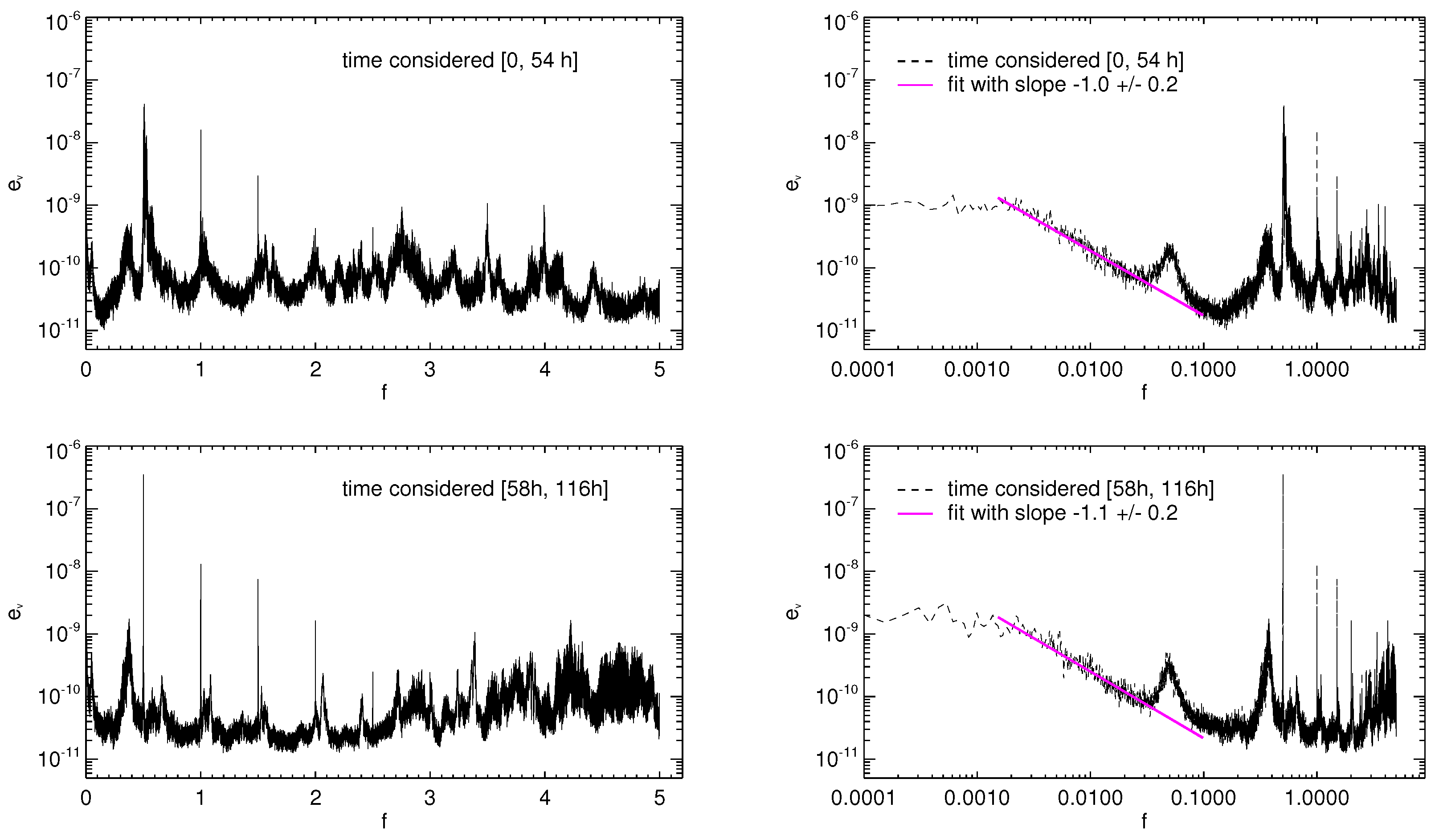
A relevant feature of kinetic and magnetic frequency spectra is the existence of power-law ranges at low frequencies. Considering the kinetic spectrum, we find a power law dependence in the interval of frequencies
, corresponding to
Hz
Hz, in physical units. A fitting procedure gives a spectral index
when the spectrum is calculated in the time interval
h, 54 h]. The index value slightly increases in absolute value when the time series considered for computing the spectrum is in the interval
h, 116 h], though this variation remains within the error bar. The existence of a power-law ranges in spectra of velocity measured in corona has been pointed out by [
9,
10,
11], in the frequency range
Hz
Hz. The spectral index varies according to the considered region within the corona, but it is around
in quiet-Sun regions [
11]. Therefore, the power-law range found in our result is in good accordance with measures of velocity fluctuations in quiet-Sun regions.
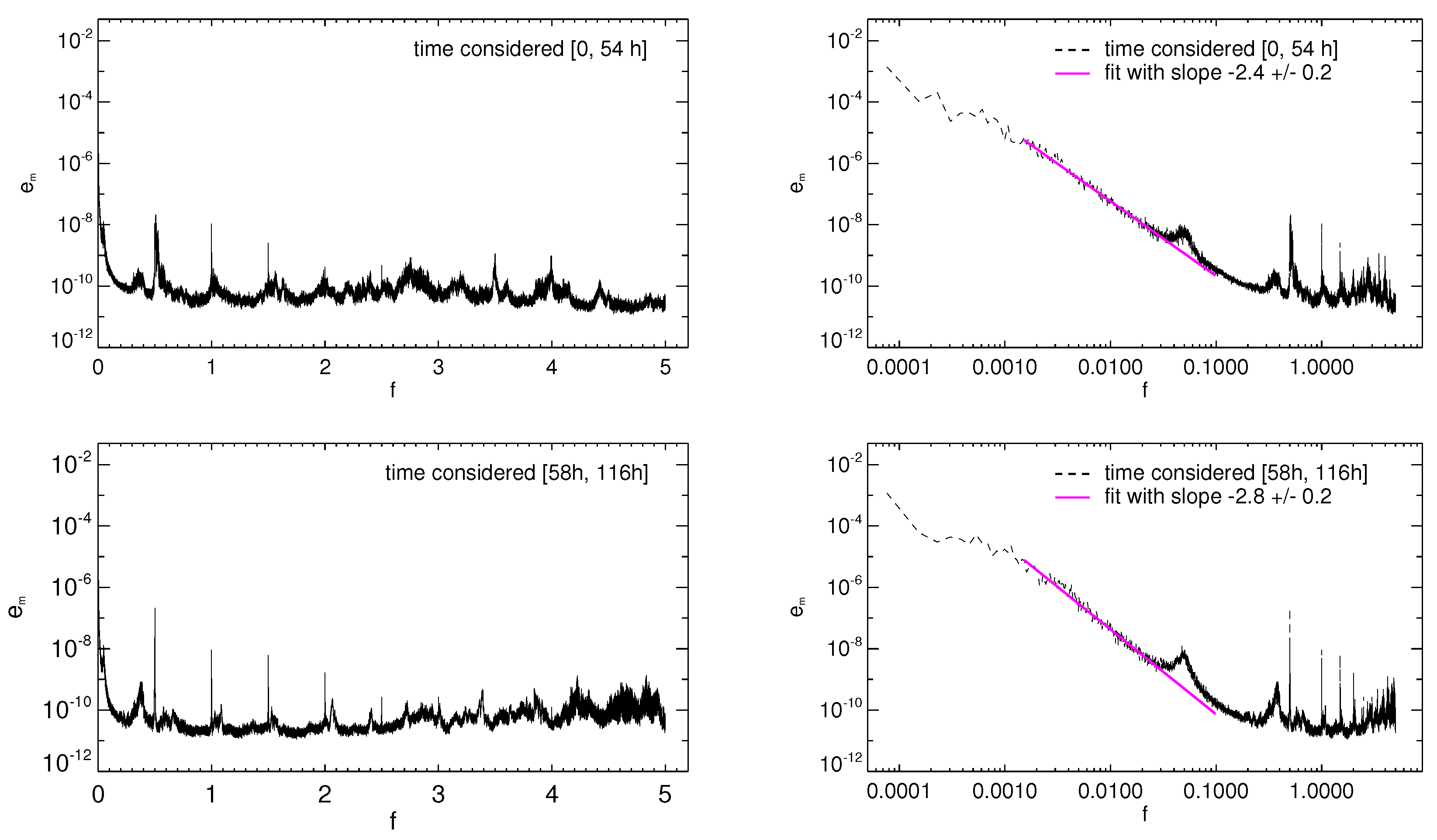
Considering magnetic spectra (
Figure 7), the power law is steeper and much more energy is accumulated mostly at low frequencies with respect to kinetic spectra. Moreover, the difference in the spectral index is significant (out of the error bar) when the spectrum is computed for the time series considered in time interval
(
) and the time interval
(
). This actually indicates that in the latter time interval, where the velocity fluctuation level is lower, nonlinear interactions are significantly less efficient than in the former. In conclusion, our results indicate that a higher level of velocity fluctuations corresponds to a lower level of fluctuating energy (mainly magnetic), a higher value of dissipation and a shallower magnetic spectrum. All these features are related with a larger spectral energy flux associated with the nonlinear cascade.
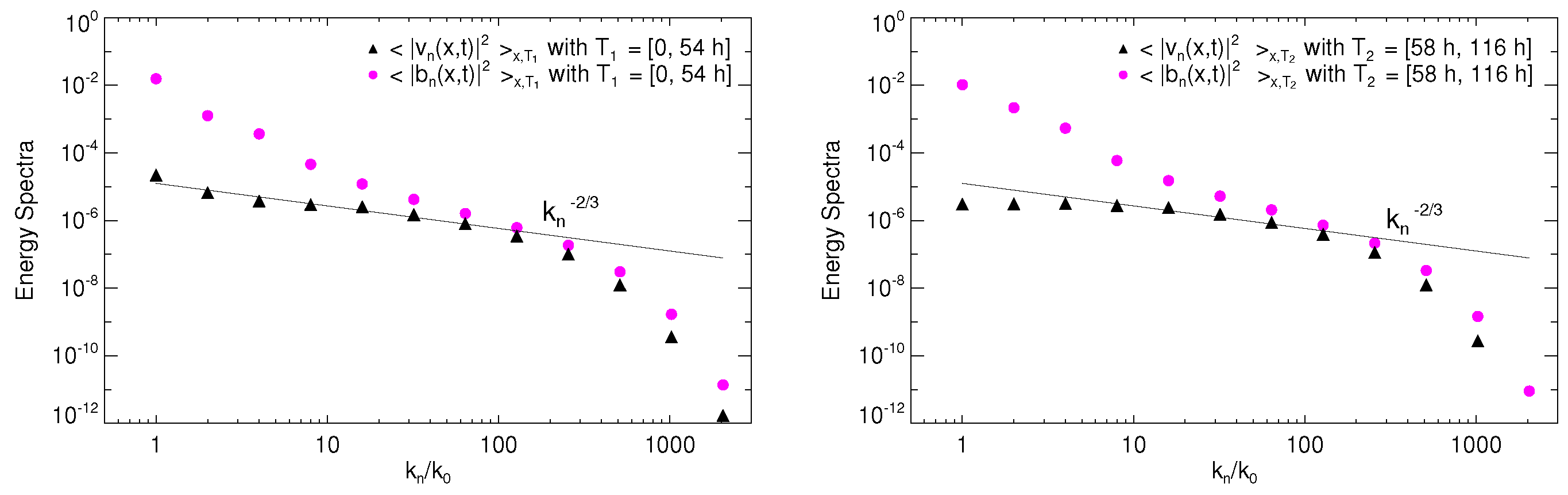
In
Figure 8 the transverse kinetic and magnetic spectra, defined by
and
, respectively, are plotted as functions of the transverse wavenumber
. Angular parentheses indicate space average in the domain
and time average over a given interval
T. The left and right panel refer to the time intervals
and
, respectively. At large transverse scales magnetic energy largely dominates over kinetic energy. However, there the magnetic spectrum is steeper and reaches the level of kinetic spectrum at intermediate wavenumbers, where a short range is present, with a kinetic-magnetic energy quasi-equipartition. The kinetic spectrum have a power-law range with a spectral index quite close to the Kolmogorov value (full line). Comparing the spectra in the two periods, we see that the of level of magnetic energy is larger in
than in
, consistently with larger total energy
E (
Figure 3); kinetic energy shows the opposite trend in the two periods.
4. Conclusions
In this paper we have presented a numerical simulation describing the long-term behaviour of turbulence in a coronal loop, which is continuously solicited at its bases by photospheric motions. The simulation covers a time interval of few thousand hours, which is much longer than any involved dynamical time. The possibility of representing such a long interval of the time evolution with an acceptable computational effort is due to the employment of the Hybrid Shell Model [
33]. On the other hand, in order to avoid exceedingly longer computational times, a smaller spectral width has been used than, for instance, in [
38]. This has given a less detailed description of the perpendicular kinetic and magnetic spectra. An important feature of the model is the possibility to implement boundary conditions at the loop bases, which represent a key aspect of the present work. In contrast, no boundary conditions can be specified in other kinds of shell models [
30] which have been applied to represent the turbulence dynamics in the solar corona [
31].
With respect to previous works [
33,
34,
35], the present simulation includes a more realistic representation of plasma motion soliciting the loop. In particular, we have considered frequency spectra of photospheric motions, calculated at different spatial scales from a dataset of the SOHO/MDI instrument [
12,
13]. Such spectra show two different contributions: a peak at frequency
s
, corresponding to global
p-mode oscillations, and a continuum at lower frequencies. The latter can be interpreted as due to the interaction between global gravity modes and the velocity pattern associated with convection. Indeed, numerical simulations have shown that the presence of the convective layer allows gravity modes, otherwise vanishing, to reach the photosphere and to appear as low-frequency oscillations at a spatial scale comparable with that of convection [
52]. The relative contribution of
p-modes and of low-frequency continuum is different at the various spatial scales.
In our model we have set up boundary conditions which emulate the above properties of photospheric motions. We have built up a numerical procedure which generates random motions at the loop bases at three different spatial scales. The associated velocity has multiple-Lorentzian spectra, whose parameters have been chosen in a way to fit the observed photospheric spectra. Such boundary conditions allow energy to enter the loop at different spatial and temporal scales, though the incoming power is determined by the interplay between boundary motions and internal dynamics [
38,
39]. For the considered parameters, we have found a net average incoming power
erg s
, corresponding to a incoming energy flux
erg s
cm
. Such a value compares well with the energy flux required to keep the quiet-Sun corona at the observed temperature against radiative and conductive losses [
51]. In the model we have assumed that the spectral properties of photospheric motions can be directly used to define boundary conditions at the loop bases. This assumption neglects the presence of the chromosphere and of the transition region, located between the photosphere and the corona. Those strongly inhomogeneous layers can affect the transmission of motions from the photosphere to the corona; modelling in a realistic way their effects represents a difficult task, even if steps in that direction have been done (e.g., [
54,
55]). On the other hand, one can expect that motions at the coronal base are somehow related to motions in the photosphere. In this line of ideas, our model represents a step toward increasing realism with respect to a series of previous similar models [
33,
34,
35,
36,
37,
38,
39], always bearing in mind its own limitations. In particular, the above estimation of the incoming energy flux
could be affected by the lack of the atmospheric layers between the photosphere and the corona.
Concerning the boundary condition, it might be interesting to compare the dynamics here described with that obtained using “open” boundary conditions, which have been considered in another model [
55] based on the same equations as the hybrid shell model. In open boundary conditions the incoming Elsässer variable is specified at boundaries, instead of velocity. In that model is has been found that an energy leakage is present for open boundary conditions, which modifies the dynamics, e.g., sensibly lowering the level of turbulent fluctuations [
55]. In our case, the choice of imposing the velocity at the boundaries (“line-tying” boundary conditions) is based on the consideration that, due to the much larger density of lower atmospheric layers, the inertia of the fluid underlying the corona is much higher than that of the coronal plasma. As a consequence, the velocity in low layers drives motions at the coronal base. We also notice that a certain level of energy leakage is also present in our model. In fact, we have found an amount of outcoming power which is of the same order as the incoming power (
Figure 3).
The fluctuating energy inside the loop is mainly magnetic, indicating that frequencies lower than
are mainly responsible for the loop energization, similar to what happens in classical DC heating mechanims. However, though the kinetic energy level is much lower than magnetic energy, velocity fluctuations play an important role in controlling the turbulent cascade, and consequently dissipation and heating. In fact, in our simulation we observed that a higher level of velocity fluctuations corresponds to a larger dissipated power and a lower level of fluctuating energy. This is in accordance with previous numerical results [
34], as well as analytical predictions [
38,
39] showing that the energy flux along the spectrum is larger for higher levels of fluctuating velocity. Therefore, in our model both DC and AC phenomena are important: while DC phenomena seem to regulate the net energy input and determine the predominance of magnetic with respect to kinetic energy, AC phenomena regulate the energy flux along the spectrum and, indirectly, dissipation and heating. The model results indicate a time-averaged velocity fluctation inside the loop ranging between ∼45 and ∼60 km/s. These values are of the order of typical fluctuating velocities of coronal plasma deduced from measures of nonthermal broadenings of coronal lines [
14].
The fluctuating velocity inside the loop is one order of magnitude larger that the velocity imposed at the loop bases. This growth of velocity amplitude in the loop body indicates kinetic energy storage, due to a resonance effect. The phenomenon of loop resonance is confirmed by the presence of well-defined resonance lines in the higher frequency part of both kinetic and magnetic energy spectra. A signature of the peak at frequency
Hz in the spectrum of boundary condition is found both in the kinetic and magnetic spectrum. Another relevant feature is localized in the lower frequency part of the kinetic energy spectrum, namely, a power-law range, with spectral index
in the frequency range
Hz
Hz. It compares well with frequency spectra of velocity measured in coronal structures [
9,
11]. Indeed, in such spectra power-law ranges are found for
Hz
Hz, with a spectral index which is
in quiet-Sun regions [
11]. Magnetic reconnection in complex magnetic configurations, like in the quiet-Sun corona, has been considered as an additional source of Alfvén waves [
56]. However, magnetic reconnection cannot be described by our model, due to the lack of spatial dependence on transverse coordinates.
In conclusion, our numerical model, with the implementation of more realistic boundary conditions, is able to reproduce several observational features of coronal structures in quiet-Sun regions, with particular regard to velocity spectra. In the next future we plan to improve the realism of the model by including a longitudinal stratification of the density, in order to reproduce possible effects of gravity, such as partial reflection of parallel-propagating perturbations.