The Rise of Climate-Driven Sediment Discharge in the Amazonian River Basin
Abstract
1. Introduction
2. Materials and Methods
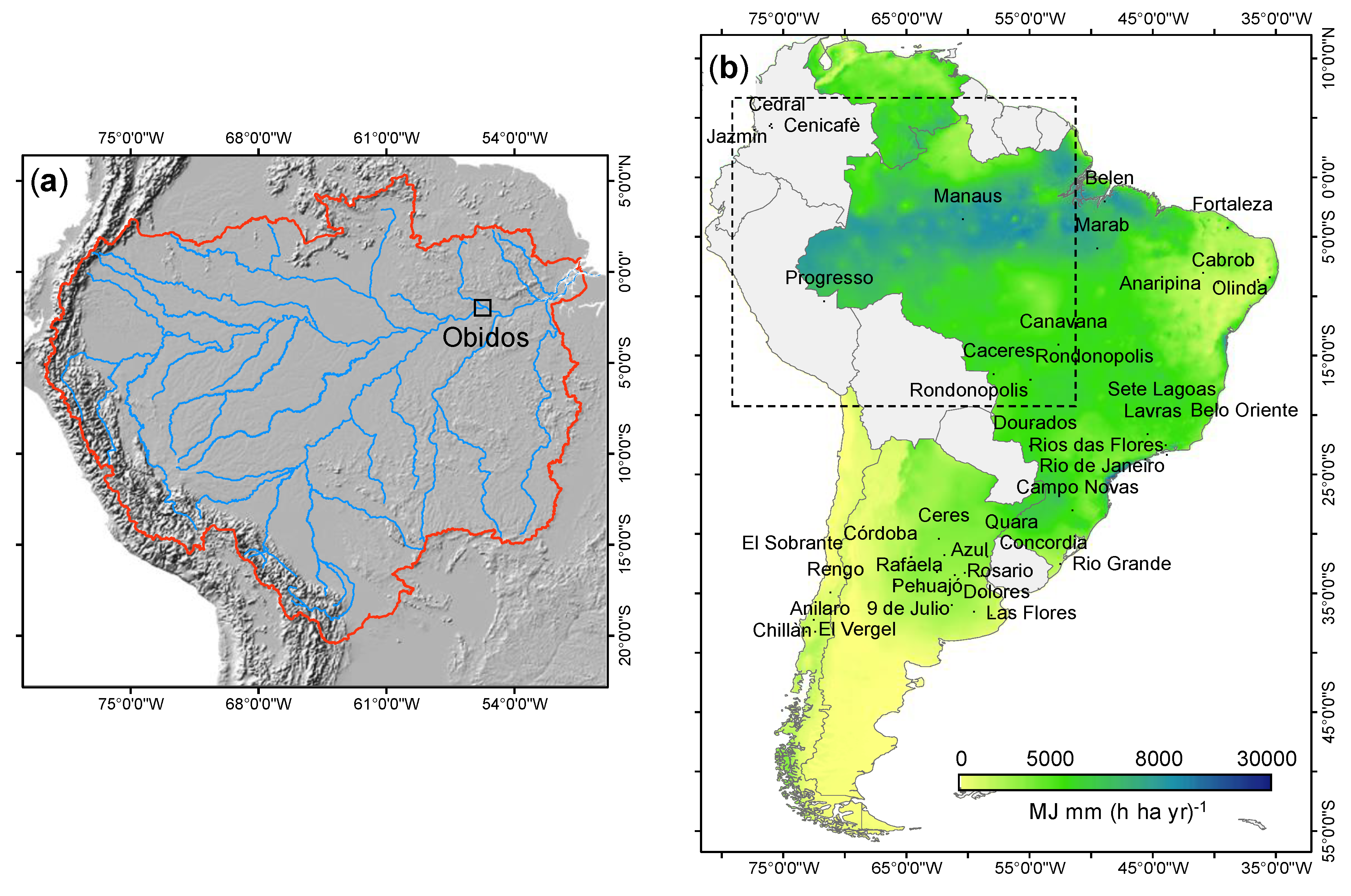
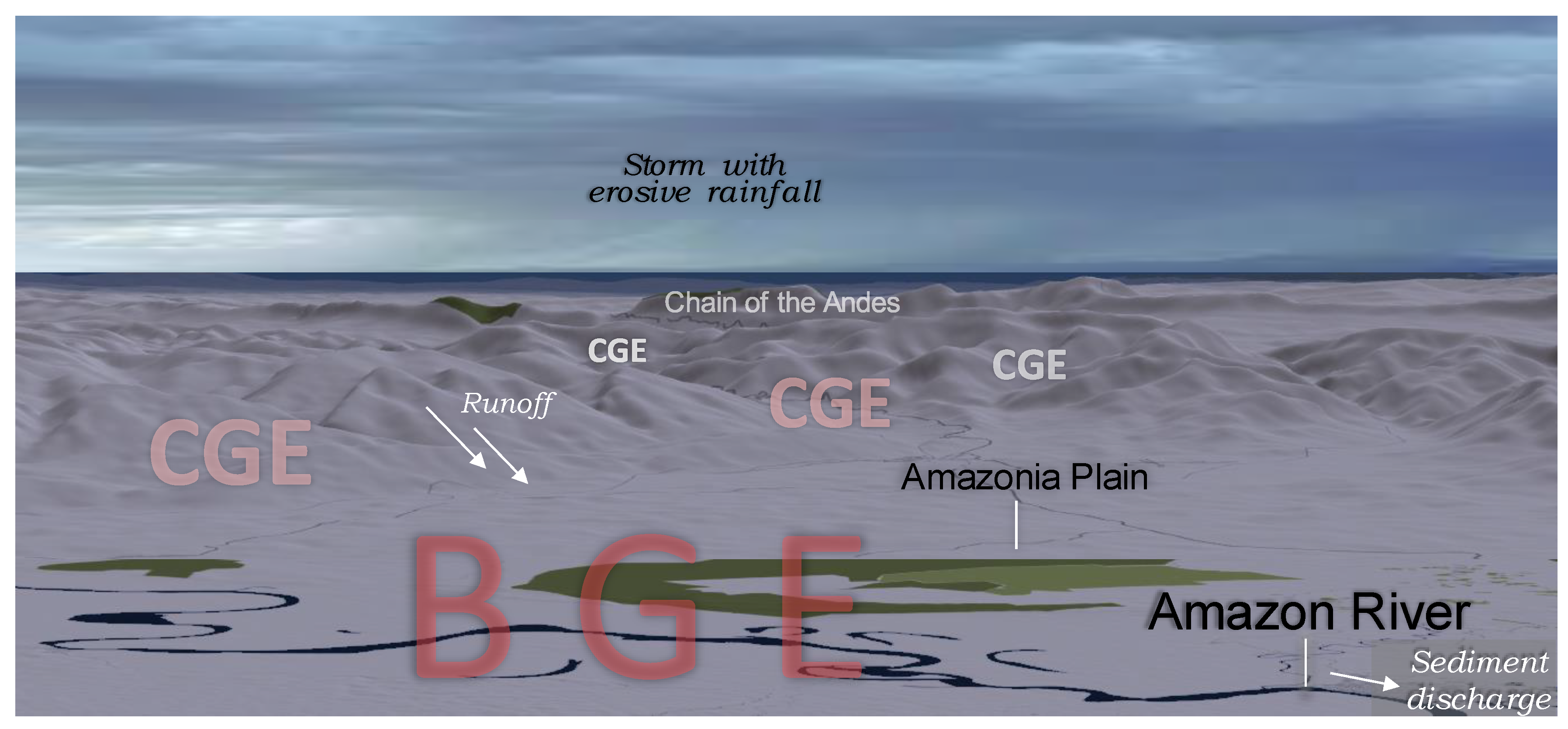
2.1. Environmental Setting
2.2. Data Sources
2.3. Modelling Approach
2.4. Model Assumptions
2.5. Model Calibration
3. Results and Discussion
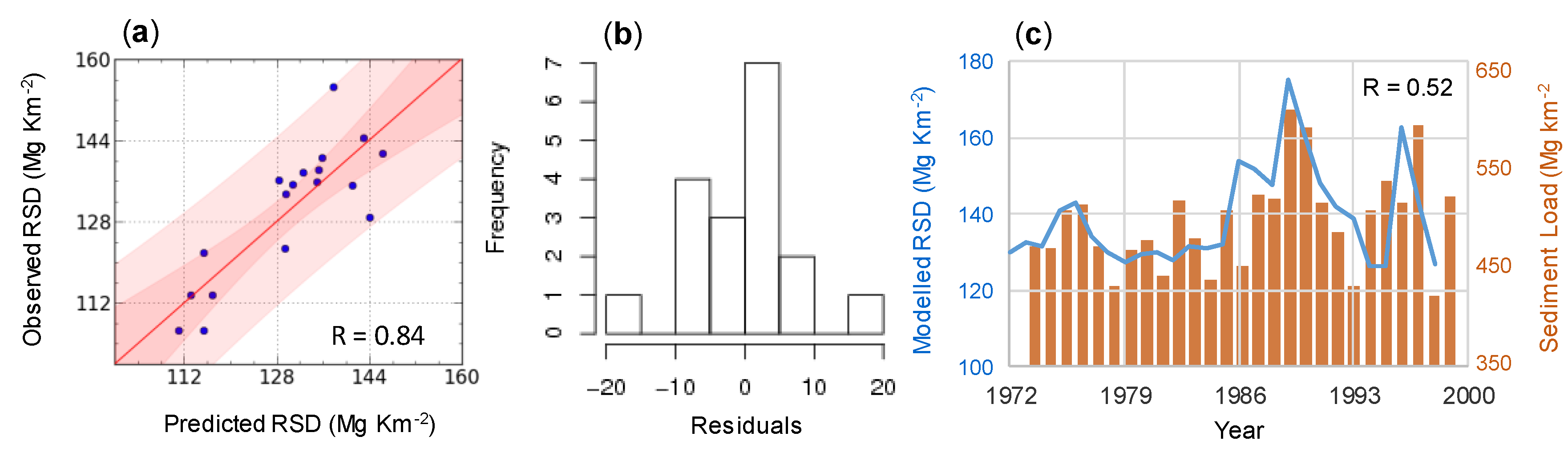
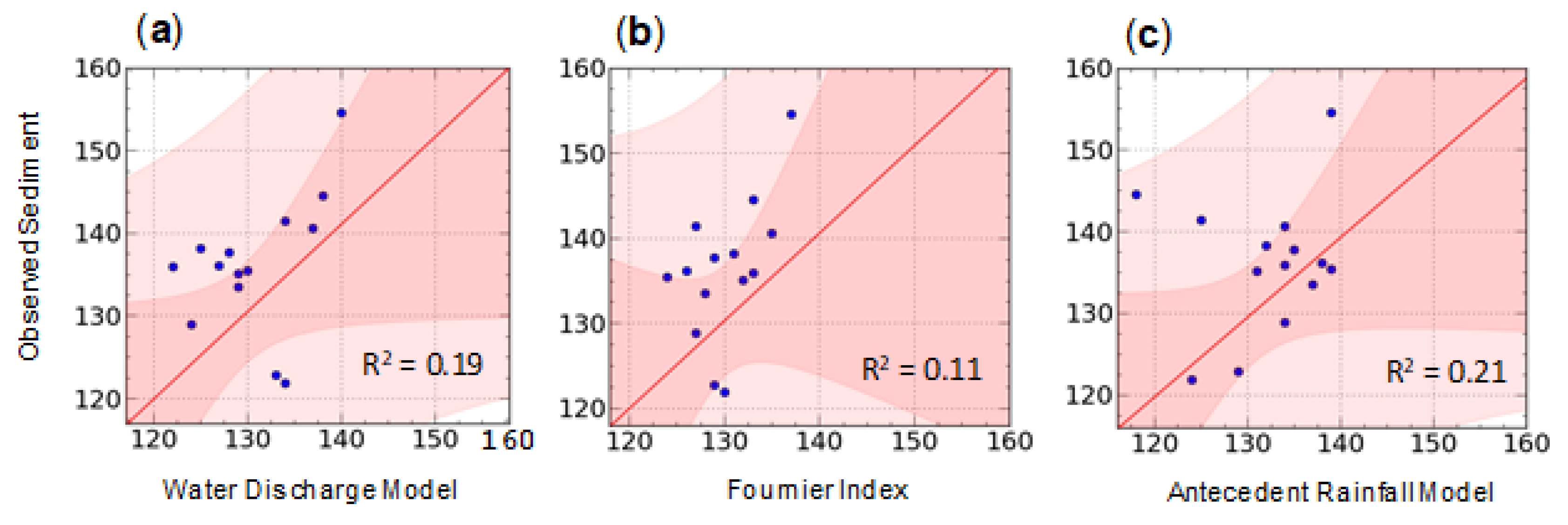
3.1. Model Parameterization and Evaluation
3.2. Discussion on the RSDA Model
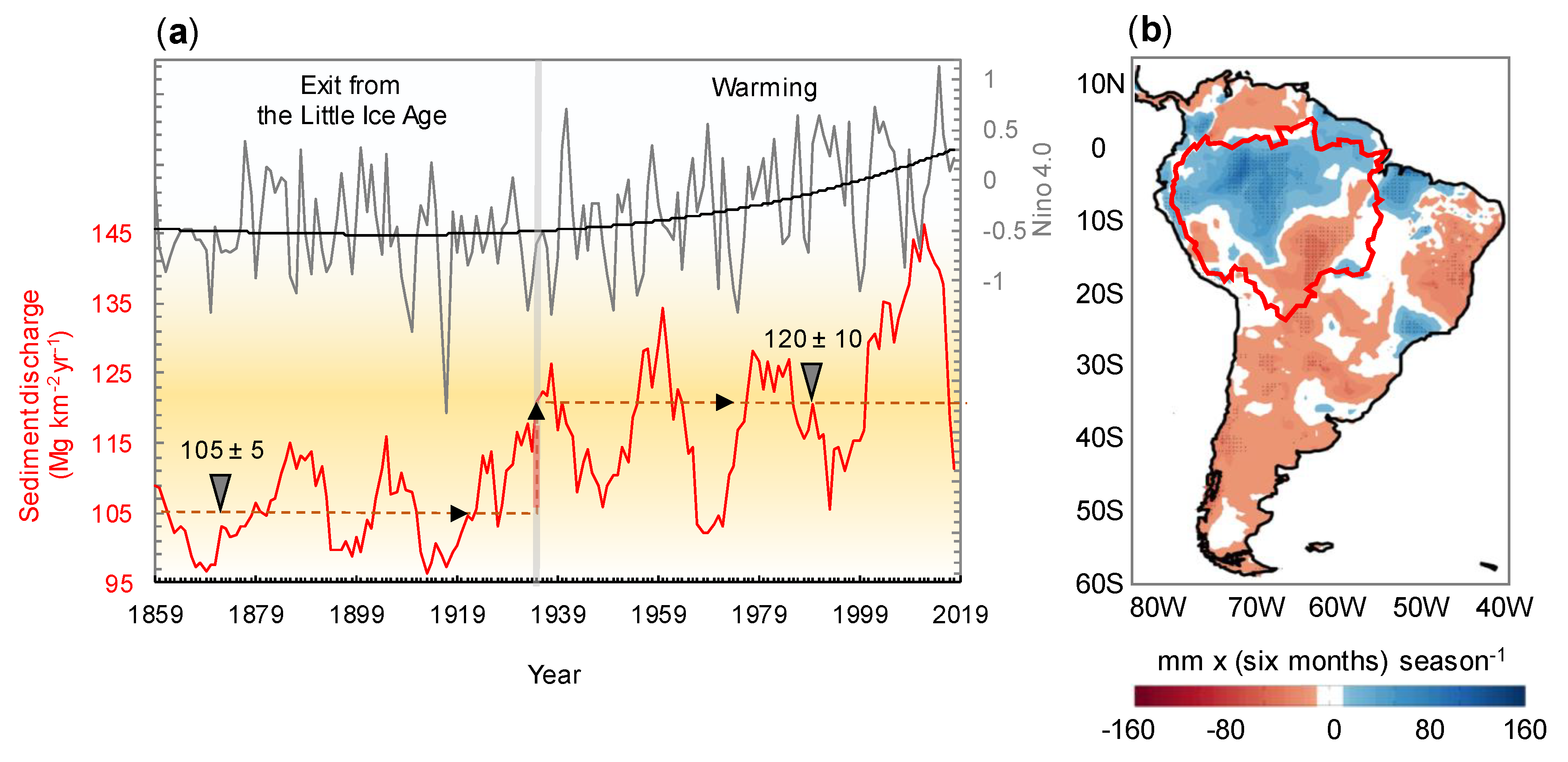
3.3. River Sediment Discharge Historical Reconstruction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef] [PubMed]
- Galy, V.; Peucker-Ehrenbrink, B.; Eglinton, T. Global carbon export from the terrestrial biosphere controlled by erosion. Nature 2015, 521, 204–207. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, P.; Panagos, P.; Lugato, E.; Alewell, C.; Ballabio, C.; Montanarella, L.; Robinson, D.A. Lateral carbon transfer from erosion in noncroplands matters. Glob. Chang. Biol. 2018, 24, 3283–3284. [Google Scholar] [CrossRef] [PubMed]
- Hilton, R.G.; Galy, A.; Hovius, N.; Chen, M.C.; Horng, M.-J.; Chen, H. Tropical-cyclone-driven erosion of the terrestrial biosphere from mountains. Nat. Geosci. 2008, 1, 759–762. [Google Scholar] [CrossRef]
- Ferrier, K.L.; Huppert, K.L.; Perron, J.T. Climatic control of bedrock river incision. Nature 2013, 496, 206–209. [Google Scholar] [CrossRef]
- Paytan, A. Mountains, weathering, and climate. Science 2012, 335, 810–811. [Google Scholar] [CrossRef]
- Cheng, H.; Sinha, A.; Cruz, F.W.; Wang, X.; Lawrence Edwards, R.; d’Horta, F.M.; Ribas, C.C.; Vuille, M.; Stott, L.D.; Auler, A.S. Climate change patterns in Amazonia and biodiversity. Nat. Commun. 2013, 4, 1411. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.-F.; Barbosa, H.M.J.; Hirota, M.; Montade, V.; Sampaio, G.; Staal, A.; Wang-Erlandsson, L.; Rammig, A. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat. Commun. 2017, 8, 14681. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Bofu, Y.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabiao, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef]
- Nam, P.T.; Yang, D.; Kanae, S.; Oki, T.; Musiake, K. Global soil loss estimate using Rusle model: The use of global spatial datasets on estimating erosive parameters. Geoinformatics 2003, 14, 49–53. [Google Scholar] [CrossRef]
- Frank, D.; Reichstein, M.; Bahn, M.; Thonicke, K.; Frank, D.; Mahecha, M.D.; Smith, P.; van der Welde, M.; Vicca, S.; Babst, F.; et al. Effects of climate extremes on the terrestrial carbon cycle: Concepts, processes and potential future impacts. Glob. Chang. Biol. 2015, 21, 2861–2880. [Google Scholar] [CrossRef] [PubMed]
- Higgins, A.; Restropo, J.C.; Ortiz, J.C.; Pierini, J.; Otero, L. Suspended sediment transport in the Magdalena River (Colombia, South America): Hydrologic regime, rating parameters and effective discharge variability. Int. J. Sediment Res. 2016, 31, 25–35. [Google Scholar] [CrossRef]
- Marchant, R.; Hooghiemstra, H. Rapid environmental change in African and South American tropics around 4000 years before present: A review. Earth-Sci. Rev. 2004, 66, 217–260. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G. Introduction. In Storminess and Environmental Change: Climate Forcing and Response in the Mediterranean Region; Diodato, N., Bellocchi, G., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 1–14. [Google Scholar]
- Dudgeon, D.; Arthington, A.H.; Gessner, M.O. Freshwater biodiversity: Importance, threats, status and conservation challenges. Biol. Rev. 2006, 81, 163–182. [Google Scholar] [CrossRef]
- Alho, C.J.R.; Reis, R.E.; Aquino, P.P.U. Amazonian freshwater habitats experiencing environmental and socioeconomic threats affecting subsistence fisheries. AMBIO 2015, 44, 412–425. [Google Scholar] [CrossRef]
- Constantine, J.A.; Dunne, T.; Ahmed, J.; Legleiter, C.; Lazarus, E.D. Sediment supply as a driver of river meandering and floodplain evolution in the Amazon Basin. Nat. Geosci. 2014, 7, 1–5. [Google Scholar] [CrossRef]
- Cherry, K.A.; Shepherd, M.; Withers, P.J.A.; Mooney, S.J. Assessing the effectiveness of actions to mitigate nutrient loss from agriculture: A review of methods. Sci. Total Environ. 2008, 406, 1–23. [Google Scholar] [CrossRef]
- Saavedra, C.P. Estimating Spatial Patterns of Soil Erosion and Deposition in the Andean Region Using Geo-Information Techniques: A Case Study in Cochabamba, Bolivia; ITC Dissertation; International Institute for Geo-Information Science and Earth Observation: Enschede, The Netherlands, 2005; p. 244. [Google Scholar]
- Merten, G.H.; Minella, P.G. The expansion of Brazilian agriculture: Soil erosion scenarios. Int. Soil Water Conserv. Res. 2013, 1, 37–48. [Google Scholar] [CrossRef]
- Locatelli, B.; Imbach, P.; Wunder, S. Synergies and trade-offs between ecosystem services in Costa Rica. Environ. Conserv. 2014, 41, 27–36. [Google Scholar] [CrossRef]
- Zimmerer, K.S. Soil erosion and labour shortages in the Andes with special reference to Bolivia, 1953–1991: Implications for Conservation with Development. World Dev. 1993, 21, 1659–1675. [Google Scholar] [CrossRef]
- Lal, R. Soil degradation by erosion. Land Degrad. Dev. 2011, 12, 519–539. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Diaz, H.F. Global climatic anomalies associated with extremes in the Southern Oscillation. J. Clim. 1989, 2, 1069–1090. [Google Scholar] [CrossRef]
- Aalto, R.; Nittrouer, C.A. 210Pb geochronology of flood events in large tropical river systems. Philos. Trans. R. Soc. A 2012, 370, 2040–2074. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Muñoz, J.C.; Mattar, C.; Barichivich, J.; Santamaría-Artigas, A.; Takahashi, K.; Malhi, Y.; Sobrino, J.A.; van der Schrier, G. Record-breaking warming and extreme drought in the Amazon rainforest during the course of El Niño 2015–2016. Sci. Rep. 2016, 6, 33130. [Google Scholar] [CrossRef] [PubMed]
- Labrière, N.; Locatelli, B.; Laumonier, Y.; Freycon, V.; Bernoux, M. Soil erosion in the humid tropics: A systematic quantitative review. Agric. Ecosyst. Environ. 2015, 203, 127–139. [Google Scholar] [CrossRef]
- Langbein, W.B.; Schumm, S.A. Yield of sediment in relation to mean annual precipitation. Eos 1958, 39, 1076–1084. [Google Scholar] [CrossRef]
- Fournier, F. Climat et érosion; la relation entre l’érosion du sol par l’eau et les précipitations atmosphériques; Presses Universitaires de France: Paris, France, 1960; p. 203. (In French) [Google Scholar]
- Douglas, I. Man, vegetation and the sediment yield of rivers. Nature 1967, 215, 925–928. [Google Scholar] [CrossRef]
- Wilson, L. Variations in mean annual sediment yield as a function of mean annual precipitation. Am. J. Sci. 1973, 273, 335–349. [Google Scholar] [CrossRef]
- Walling, D.E.; Webb, B.W. Patterns of Sediment Yield. In Background to Paleohydrology; Gregory, K.J., Ed.; Wiley & Sons: Hoboken, NJ, USA, 1983; pp. 69–100. [Google Scholar]
- Paiva, R.C.D.; Buarque, D.C.; Collischonn, W.; Bonnet, M.-P.; Frappart, F.; Calmant, S. Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef]
- Lewis, S.L.; Brando, P.M.; Phillips, O.L.; van der Heijden, G.M.F.; Nepstad, D. The 2010 Amazon drought. Science 2011, 331, 554. [Google Scholar] [CrossRef] [PubMed]
- Marengo, J.A.; Espinoza Villar, J.C. Extreme seasonal droughts and floods in Amazonia: Causes, trends and impacts. Int. J. Climatol. 2016, 36, 1033–1050. [Google Scholar] [CrossRef]
- Barichivich, J.; Gloor, E.; Peylin, P.; Brienen, R.J.W.; Schöngart, J.; Espinoza, J.C.; Pattnayak, K.C. Recent intensification of Amazon flooding extremes driven by strengthened Walker circulation. Sci. Adv. 2018, 4, eaat8785. [Google Scholar] [CrossRef] [PubMed]
- Marengo, J.A.; Souza, C.M., Jr.; Thonicke, K.; Burton, C.; Halladay, K.; Betts, R.A.; Alves, L.M.; Soares, W.R. Changes in climate and land use over the Amazon region: Current and future variability and trends. Front. Earth Sci. 2018, 6, 228. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Guntner, A.; Werth, S.; Santos da Silva, J.; Tomasella, J.; Seyler, F.; Prigent, C.; Rossow, W.B.; Calmant, S.; et al. Satellite-based estimates of groundwater storage variations in large drainage basins with extensive floodplains. Remote Sens. Environ. 2011, 115, 1588–1594. [Google Scholar] [CrossRef]
- Costa, M.H.; Foley, J.A. The water balance of the Amazon basin: Dependence on vegetation cover and canopy conductance. J. Geophys. Res. 1997, 102, 973–990. [Google Scholar] [CrossRef]
- Gautier, E.; Brunstein, D.; Vauchel, P.; Jouanneau, J.-M.; Roulet, M.; Garcia, C.; Guyot, J.-L.; Castro, M. Channel and floodplain sediment dynamics in a reach of the tropical meandering Rio Beni (Bolivian Amazonia). Earth Surf. Process. Landf. 2010, 35, 1838–1853. [Google Scholar] [CrossRef]
- Tao, W.; Wu, J.; Wang, Q. Mathematical model of sediment and solute transport along slope land in different rainfall pattern conditions. Sci. Rep. 2017, 7, 44082. [Google Scholar] [CrossRef]
- Sebestyen, S.D.; Boyer, E.W.; Shanley, J.B. Responses of stream nitrate and dissolved organic carbon loadings to hydrological forcing and climate change in an upland forest of the northeast USA. J. Geophys. Res. 2009, 114, G02002. [Google Scholar] [CrossRef]
- Mahmoodabadi, M. Sediment yield estimation using a semi-quantitative model and GIS-remote sensing data. Int. Agrophys. 2011, 25, 241–247. [Google Scholar]
- Van der Fels-Klerx, H.J.; Van Asselt, E.D.; Raley, M.; Poulsen, M.; Korsgaard, H.; Bredsdorff, L.; Nauta, M.; D’agostino, M.; Coles, D.; Marvin, H.J.; et al. Critical review of methods for risk ranking of food-related hazards, based on risks for human health. Crit. Rev. Food Sci. 2018, 58, 178–193. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, J.D. A spatially distributed model for the long-term suspended sediment discharge and delivery ratio of drainage basins. J. Geophys. Res. 2012, 117, F02028. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J. The current status of global river discharge monitoring and potential new technologies complementing traditional discharge measurements. Predictions in ungauged basins. IAHS Publication 2007, 309, 129–136. [Google Scholar]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef]
- Callède, J.; Guyot, J.L.; Ronchail, J.; L’hote, Y.; Niel, H.; De Oliveira, E. Evolution du débit de l’Amazone á Óbidos de 1903 á 1999. Hydrol. Sci. J. 2004, 49, 85–97. (In French) [Google Scholar] [CrossRef]
- Available online: http://www.ore-hybam.org (accessed on 15 February 2020).
- Martinez, J.M.; Guyot, J.L.; Filizola, N.; Sondag, F. Increase in suspended sediment discharge of the Amazon River assessed by monitoring network and satellite data. Catena 2009, 79, 257–264. [Google Scholar] [CrossRef]
- Toy, T.J.; Foster, G.R.; Renard, K.J. Soil Erosion: Processes, Prediction, Measurement, and Contro; John Wiley & Sons: New York, NY, USA, 2002; p. 352. [Google Scholar]
- Garstang, M.; Massie, L., Jr.; Halverson, J.; Greco, S.; Scala, J. Amazon coastal squall lines, Part I, Structure and kinematics. Mon. Weather Rev. 1994, 122, 608–622. [Google Scholar] [CrossRef]
- Melo, D.d.C.D.; Wendland, E. Hydrological system time lag responses to meteorological shifts. Braz. J. Water Resour. 2016, 21, 766–776. [Google Scholar] [CrossRef][Green Version]
- Available online: https://www.esri.com (accessed on 15 February 2020).
- Espinoza Villar, J.C.; Ronchail, J.; Guyot, J.L.; Junquas, C.; Vauchel, P.; Lavado, W.; Drapeau, G.; Pombosa, R. Climate variability and extreme drought in the upper Solimões River (western Amazon Basin): Understanding the exceptional 2010 drought. Geophys. Res. Lett. 2011, 38, L13406. [Google Scholar] [CrossRef]
- Marengo, J.A.; Tomasella, J.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A. The drought of 2010 in the context of historical droughts in the Amazon region. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Guyot, J.L.; Bazan, H.; Fraizy, P.; Ordonez, J.J.; Armijos, E.; Crave, A. Suspended sediment yields in the Amazon basin of Peru: A first estimation. Int. Assoc. Hydrol. Sci. Publ. 2007, 314, 1–8. [Google Scholar]
- Available online: http://climexp.knmi.nl/start.cgi (accessed on 15 February 2020).
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The twentieth century reanalysis project. Quart. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
- Espinoza Villar, J.C. Impact de la variabilitè climatique sur l’hydrologie du bassin amazonien; Diplôme, Université de Paris 6: Paris, France, 2009; p. 202. (In French) [Google Scholar]
- Da Silva, A.M. Rainfall erosivity map for Brazil. Catena 2004, 57, 251–259. [Google Scholar] [CrossRef]
- Aronica, G.; Ferro, V. Rainfall erosivity over the Calabria region. Hydrol. Sci. J. 1997, 42, 35–48. [Google Scholar] [CrossRef]
- Diodato, N.; Borrelli, P.; Fiener, P.; Bellocchi, G.; Romano, N. Discovering historical rainfall erosivity with a parsimonious approach: A case study in Western Germany. J. Hydrol. 2017, 544, 1–9. [Google Scholar] [CrossRef]
- Pelacani, S.; Märker, M.; Rodolfi, G. Simulation of soil erosion and deposition in a changing land use: A modelling approach to implement the support practice factor. Geomorphology 2008, 99, 329–340. [Google Scholar] [CrossRef]
- Diodato, N.; Higgins, S.; Bellocchi, G.; Fiorillo, F.; Romano, N.; Guadagno, F.M. Hydro-climatic forcing of dissolved organic carbon in two boreal lakes of Canada. Sci. Total Environ. 2016, 571, 50–58. [Google Scholar] [CrossRef]
- Marengo, J.A.; Tomasella, J.; Uvo, C. Trends in streamflow and rainfall in tropical South America: Amazonia, eastern Brazil, and northwestern Peru. J. Geophys. Res. 1998, 103, 1775–1783. [Google Scholar] [CrossRef]
- Available online: https://demo.f4map.com/#camera.theta=0.9 (accessed on 15 February 2020).
- Callède, J.; Ronchail, J.; Guyot, J.-L.; De Oliveiraet, E. Deboisement Amazonien: Son influence sur le débit de l’Amazone à Óbidos (Bresil). Revue des Sciences de l’Eau 2008, 21, 59–72. (In French) [Google Scholar] [CrossRef][Green Version]
- Espinoza Villar, J.C.; Ronchail, J.; Guyot, J.-L.; Cochonneau, G.; Naziano, F.; Lavado, W.; De Oliveira, E.; Pombosa, R.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. [Google Scholar] [CrossRef]
- Diodato, N.; Grauso, S. An improved correlation model for sediment delivery ratio assessment. Environ. Earth Sci. 2009, 59, 223–231. [Google Scholar] [CrossRef]
- Quinton, J.N.; Catt, J.A.; Wood, G.A.; Steer, J. Soil carbon losses by water erosion: Experimentation and modeling at field and national scales in the UK. Agric. Ecosyst. Environ. 2006, 112, 87–102. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression. II. Biometrika 1951, 38, 159–177. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Hyung, N.; Jeon, Y. Spurious regressions with stationary series. Appl. Econ. 2001, 33, 899–904. [Google Scholar] [CrossRef]
- Nau, R. STATGRAPHICS V.5: Overview & Tutorial Guide. 2005. Available online: http://www.duke.edu/~rnau/sgwin5.pdf (accessed on 15 February 2020).
- Wessa, P. A framework for statistical software development, maintenance, and publishing within an open-access business model. Comput. Stat. 2009, 24, 183–193. [Google Scholar] [CrossRef]
- Walling, D.E. The Impact of Global Change on Erosion and Sediment transport by Rivers: Current Progress and Future Challenges; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2009; p. 26. [Google Scholar]
- Syvitski, J.P.; Morehead, M.D.; Bahr, D.B.; Mulder, T. Estimating fluvial sediment transport: The rating parameters. Water Resour. Res. 2000, 36, 2747–2760. [Google Scholar] [CrossRef]
- Castillo, V.M.; Gómez-Plata, A.; Martínez-Mena, M. The role of antecedent soil water content in the runoff response of semiarid catchments: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Deriving stage–discharge–sediment concentration relationships using fuzzy logic. Hydrol. Sci. J. 2007, 52, 793–807. [Google Scholar] [CrossRef]
- Mattikalli, N.M.; Devereux, B.J.; Rchards, K.S. Prediction of river discharge and surface water quality using an integrated geographical information system approach. Int. J. Remote Sens. 1996, 17, 683–701. [Google Scholar] [CrossRef]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Surface flow measurements from drones. J. Hydrol. 2016, 540, 240–245. [Google Scholar] [CrossRef]
- Thomas, M.F. Landscape sensitivity in time and space—An introduction. Catena 2001, 42, 83–98. [Google Scholar] [CrossRef]
- Diodato, N.; Gericke, A.; Bellocchi, G. Modelling the inter-annual variability of sediment yields: A case study for the upper Lech River. Catena 2012, 97, 12–19. [Google Scholar] [CrossRef]
- Diodato, N.; de Vente, J.; Bellocchi, G.; Guerriero, L.; Soriano, M.; Fiorillo, F.; Revellino, P.; Guadagno, F.M. Estimating long-term sediment export using a seasonal rainfall-dependent hydrological model in the Glonn River basin, Germany. Geomorphology 2015, 228, 628–636. [Google Scholar] [CrossRef]
- Diodato, N.; Mao, L.; Borrelli, P.; Panagos, P.; Fiorillo, F.; Bellocchi, G. Climate-scale modelling of suspended sediment load in an Alpine catchment debris flow (Rio Cordon-northeastern Italy). Geomorphology 2018, 309, 20–28. [Google Scholar] [CrossRef]
- Braga, B.; Varella, P.; Gonçalves, H. Transboundary water management of the Amazon Basin. Int. J. Water Resour. Dev. 2011, 27, 477–496. [Google Scholar] [CrossRef]
- Keen, C. Greatest Places Physical Geography, Amazon Basin. 1997. Available online: http://www.greatestplaces.org/notes/amazon.htm (accessed on 15 February 2020).
- Liu, W.; Huang, B.; Thorne, P.W.; Banzon, V.F.; Zhang, H.-M.; Freeman, E.; Lawrimore, J.; Peterson, T.C.; Smith, T.M.; Woodruff, S.D. Extended reconstructed sea surface temperature version 4 (ERSST.v4): Part II. Parametric and structural uncertainty estimations. J. Clim. 2014, 28, 931–951. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Li, X.; Zhu, J.; Tanajura, C.A.S. The strengthening of Amazonian precipitation during the wet season driven by tropical sea surface temperature forcing. Environ. Res. Lett. 2018, 13, 094015. [Google Scholar] [CrossRef]
- Jadhav, J.; Panickal, S.; Marathe, S.; Ashok, K. On the possible cause of distinct El Niño types in the recent decades. Sci. Rep. 2015, 5, 17009. [Google Scholar] [CrossRef]
- Li, X.; Xie, S.-P.; Gille, S.T.; Yoo, C. Atlantic-induced pan-tropical climate change over the past three decades. Nat. Clim. Chang. 2016, 6, 275–279. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 1968, 97, 163–172. [Google Scholar] [CrossRef]
- Li, W.; Zhang, P.; Ye, J.; Li, L.; Baker, P.A. Impact of two different types of El Niño events on the Amazon climate and ecosystem productivity. J. Plant Ecol. 2011, 4, 91–99. [Google Scholar] [CrossRef]
- Foley, J.A.; Botta, A.; Coe, M.T. El Niño–Southern oscillation and the climate, ecosystems and rivers of Amazonia. Glob. Biogeochem. Cycles 2002, 16, 1132. [Google Scholar] [CrossRef]
- Aalto, R.; Maurice-Bourgoin, L.; Dunne, T.; Montgomery, D.R.; Nittrouer, C.A.; Guyot, J.L. Episodic sediment accumulation on Amazonian flood plains influenced by El Niño/Southern Oscillation. Nature 2003, 425, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Apaéstegui, J.; Cruz, F.W.; Sifeddine, A.; Espinoza Villar, J.C.; Guyot, J.-L.; Khodri, M.; Strikis, N.; Santos, R.V.; Cheng, H.; Edwards, L.; et al. Hydroclimate variability of the South American Monsoon System during the last 1600 year inferred from speleothem isotope records of the north-eastern Andes foothills in Peru. Clim Past Discuss. 2014, 10, 533–561. [Google Scholar] [CrossRef]
- Mello, C.R.; Norton, L.D.; Curi, N.; Yanagi, S.N.M.; Silva, A.M. El-Niño southern oscillation and rainfall erosivity in the headwater region of the Grande River Basin, Southeast Brazil. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 10707–10738. [Google Scholar] [CrossRef]
- Jahfer, S.; Vinayachandran, P.N.; Nanjundiah, R.S. Long-term impact of Amazon river runoff on northern hemispheric climate. Sci. Rep. 2017, 7, 10989. [Google Scholar] [CrossRef]
- Cohen, S.; Kettner, A.J.; James, J.; Syvitski, P.M. Global suspended sediment and water discharge dynamics between 1960 and 2010: Continental trends and intra-basin sensitivity. Glob. Planet. Chang. 2014, 115, 44–58. [Google Scholar] [CrossRef]
- Davidson, E.A.; de Araújo, A.C.; Artaxo, P.; Balch, J.K.; Brown, I.F.; Bustamante, M.M.C.; Coe, M.T.; DeFries, R.S.; Keller, M.; Longo, M.; et al. The Amazon basin in transition. Nature 2012, 481, 321. [Google Scholar] [CrossRef]
- Diodato, N.; Esposito, L.; Bellocchi, G. A first regional-scale estimate of climate-driven terrestrial carbon export in boreal catchments. Climate 2018, 6, 22. [Google Scholar] [CrossRef]
- Diodato, N.; Verstraeten, G.; Bellocchi, G. Decadal modelling of rainfall erosivity in Belgium. Land Degrad. Dev. 2014, 25, 511–519. [Google Scholar] [CrossRef]
- Lal, R. Soil erosion and sediment transport research in tropical Africa. Hydrol. Sci. J. 1985, 30, 239–256. [Google Scholar] [CrossRef]
- Verstraeten, G.; Poesen, J. Factors controlling sediment yield from small intensively cultivated catchments in a temperate humid climate. Geomorphology 2001, 40, 123–144. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diodato, N.; Filizola, N.; Borrelli, P.; Panagos, P.; Bellocchi, G. The Rise of Climate-Driven Sediment Discharge in the Amazonian River Basin. Atmosphere 2020, 11, 208. https://doi.org/10.3390/atmos11020208
Diodato N, Filizola N, Borrelli P, Panagos P, Bellocchi G. The Rise of Climate-Driven Sediment Discharge in the Amazonian River Basin. Atmosphere. 2020; 11(2):208. https://doi.org/10.3390/atmos11020208
Chicago/Turabian StyleDiodato, Nazzareno, Naziano Filizola, Pasquale Borrelli, Panos Panagos, and Gianni Bellocchi. 2020. "The Rise of Climate-Driven Sediment Discharge in the Amazonian River Basin" Atmosphere 11, no. 2: 208. https://doi.org/10.3390/atmos11020208
APA StyleDiodato, N., Filizola, N., Borrelli, P., Panagos, P., & Bellocchi, G. (2020). The Rise of Climate-Driven Sediment Discharge in the Amazonian River Basin. Atmosphere, 11(2), 208. https://doi.org/10.3390/atmos11020208






