Abstract
The goals of our study were to evaluate the historical aspects of maize (Zea mays L.) production in Hungary, and to provide a prognosis for the yield for 2050 based on the trends of temperature, precipitation, and climatic water balance changes. Different climate zones for the period of 1970–2019 were investigated by means of correlation analyses, normality tests, time series analysis, and multiple linear regression analysis. Two well-distinguishable linear trends in the yields were found, the first representing large-scale farming, and the second starting with the change of the socio-economic system in 1989. The annual amount of precipitation showed high variations both spatially and temporally, although no significant change was identified for the last five decades. In the period 1990–2019, not only were higher temperatures characteristic, but the frequency of extreme high temperature values (Tmax > 30 °C) also increased. We quantified the heat stress, expressing it in heat stress units (HSU, °C) derived from the heat-sum of the daily maximum air temperature values above 30 °C. By 2050, the average increase in HSUs may reach 35 °C. Increasing HSU causes yield depression; according to our estimations, a 1 °C increase in HSU results in a 23 kg ha−1 yield depression of maize. Taking the unfavorable effect of heat stress and technological development into consideration, the average domestic yield of maize will be 8.2 t ha−1. Our study revealed that without taking technological development into consideration, prediction models may overestimate the adverse effect of climate change on crop production.
1. Introduction
Changes in the yields of the different crops generally show an increase over time worldwide. In the long term, changes in the trend lines can occur when major improvements result in significant changes in productivity, as for example, Nielsen [1] demonstrated for maize in the USA. The effect of the changes in environmental conditions are assumed to be continuous variables and they are incorporated into the overall effect of the development [2]. A sharp change in the slope clearly indicates the introduction of a new technology, for example, new hybrids with increased genetic yield potential [1,3,4,5], or a sudden socio-economic change, such as the land use reform in the former communist countries in the 1990s [6,7]. However, if the variation in the environmental factors increases, its contribution results in a larger deviation from the trend line. This may become increasingly dominant with spatial downscaling.
As summarized by Amanullah and Fahad [8], climate change projections are the following: (1) the global temperature will increase but the changes will not be uniform across regions; (2) there will be more hot extremes and fewer cold extremes both daily and seasonally; (3) precipitation will increase globally, but with substantial spatial variation; (4) atmospheric water holding capacity will increase, resulting in a higher intensity of precipitation and a greater amount per rain event; and (5) annual surface evaporation will increase as the temperature increases, but evaporation is linked to precipitation. Almost two decades ago, Olesen and Bindi [9] emphasized that in Europe a possible increase in water shortages and extreme weather events would cause lower harvestable yields, higher yield variability and a reduction in suitable areas for traditional crops. More specifically, they predicted that these effects would reinforce the trends of extensification in the southeastern parts of Europe.
Today, one of the major challenges in crop production is still how the potential adverse effects of global climate change in a given region can be handled in a socially, economically and environmentally sustainable way. There is a need for proper alternatives to keep variation in both the quantity and quality of products low, and at the same time maintain a continuous increase in production, ideally governed by the commercial market [10].
There are numerous low-scale spatial and temporal projections based on trend analyses of historical datasets; however, due to the sensitivity of the models developed or adapted, the outputs are often contradictory, even if the inputs are rather similar. Furthermore, different models can give non-comparable results, while earlier projections are frequently found to be invalid later [11,12].
In the case of mathematical modeling, at least two aspects are sources of uncertainty. On the one hand, algorithms for soil, crop and weather parameters are combined, where the first two are deterministic, while the third is a stochastic element. Weather is assumed to behave according to a chaotic model and shows scale-independent distribution, considerably increasing the uncertainty in the predictions; and even if a relationship is found between weather variability and crop yield variation as a response, crop yield cannot be estimated since weather cannot be predicted in advance [13]. For example, Roudier et al. [14] predicted for West Africa that rainfall changes, still uncertain in climate projections, have the potential to either exacerbate or mitigate the impact of climate change, depending on whether rainfall decreases or increases. On the other hand, assessments should also include economic and technological aspects, such as the relocation of maize (Zea mays L.) producing regions [15,16], technical adaptation to weather conditions, such as changes in sowing date [17,18], seeding density [19], crop rotation [20], and fertilization [21], or increasing genetic potential via the introduction of new hybrids [22]. However, using transgenic seeds may be recommended on a small-scale, from both social and biological perspectives [23].
Mathematically described trends for weather or yield parameters based on biophysical modeling are not necessarily realistic or even meaningful, and thus may be misleading when used for predictions. Taking into account the degree of the socio-economic contributions to overall crop production may have potential in providing a realistic prediction, as they may not only reduce the adverse climatic effects but may even explain a continuous increase in yield [24]. As Döös and Show [25] concluded, one cannot say with any certainty whether or not the food supply will meet the expected demand in the future.
Of all agricultural crops, maize is produced in the highest quantity worldwide. When estimating the global yields of grain maize using different methods, Bassu et al. [26] predicted that rising temperatures would have a strong negative effect on maize yield. According to that study, even a conservative target of 2 °C average global warming would cause a reduction of 8–14% in global maize production. Zhao et al. [27] predicted that, at the global scale, among the major crops the loss in yield would be the highest for maize, with a range of −7.4 ± 4.5% per °C increase in global mean temperature, with magnitudes varying by region. In Africa and Latin America, Jones and Thornton [28] calculated a 10% of loss in maize production by 2055, with high variability, while as part of a further assessment for the East African region, Thornton et al. [29] also predicted considerable spatial and temporal variations in crop response, arguing against spatially contiguous development domains for identifying and implementing adaptation options. For a spring maize zone in China, Ma and Maystadt [30] predicted that one standard deviation in temperature and drought conditions would decrease maize yields by 1.4% and 2.5%, respectively. Lobell and Burke [31] simulated the impact of temperature and precipitation changes on maize yield in Sub-Saharan Africa for a period of 40 years using the CERES-Maize model. They found that a 2 °C warming was three times more important than a 20% decline in precipitation, with projected yield losses of 5.8% and 14.4%, respectively.
As the climatic stratification provided by, for example, Metzger et al. [32] shows, Europe is highly variable in terms of climatic zonation. In a study of maize production, Olesen et al. [2] predicted that higher temperatures would positively influence the length of the growing season in the boreal and Atlantic northern zones, but shorten the growth duration in the continental, Lusitanian, Mediterranean mountain zones and the Mediterranean southern zones, also highlighting that maize is expected to be more vulnerable to drought and heat stress in the Pannonian (including Hungary), Lusitanian and Mediterranean southern zones. In accordance with these data, Durdu [33] predicted negative trends in maize yields in western Turkey with the climate change resulting from the expected moisture deficit in the growing seasons, while Vanuytrecht et al. [34] concluded that maize would not suffer from temperature extremes in Western Europe. Supit et al. [35], however, came to the conclusion that maize could benefit from the higher temperatures in summer in northern Europe, and the potential maize yields would decrease only in a limited number of European regions. Similarly, Parent et al. [22] concluded that European maize production for 2050 could be stable even with current practices, and would increase when adjusting sowing date and crop cycle duration to the local environment. For Hungary during the period of 2022–2050, Fogarasi et al. [12], for example, calculated a slight decrease in maize yield without risk mitigation, and the stabilization of production in the case of adjusted technologies, due to the expected changes in the climatic conditions.
Despite its relatively small geographic size compared to other main exporters, Hungary was among the top 8 maize-exporting countries in 2019. As reported by Wu and Guclu [36], in the period of 2000–2009 the total amount exported was close to 28.6 billion tons, about half of the amount exported by Brazil, and 18% of the USA export, which was ranked first. After joining the European Union in 2004, Hungarian maize exports increased considerably due to the new economic environment, initially showing a strong fluctuation [37], after which it became economically successful within a short period of time [38]. According to the data summarized by the Hungarian Central Statistical Office, in 2014 a record volume of maize was produced in the country, reaching 15% of the total production in the European Union [10]. In 2019, Hungary imported maize with a value close to 143.7 million USD and exported maize with a value of more than 871.6 million USD trade value in the world market. For comparison, the USA imported 371.1 million USD of maize, and exported 8013.0 million USD trade value [39].
As the reliability of projections for maize production in Hungary is of special interest, and to avoid either over- or underestimations, models as well as methods and databases should be carefully chosen, the findings should be critically assessed, and the available projections should be periodically reassessed. Based on the above, our objectives were the following: (1) to evaluate the historical socio-political aspects of maize production in Hungary as a post-communist country; (2) to assess the contribution of changes in weather conditions to the variation of maize yield by climate zone; (3) to estimate the trends in temperature changes and water shortages as the potentially critical issues in balanced maize production; and (4) to provide a prognosis for the Hungarian maize yield for the year 2050.
2. Experiments
2.1. Crop Yield and Meteorological Databases
The yearly average and total yield, and the harvest area data of maize for each county of Hungary for the period 1970–2019 were provided by the Hungarian Central Statistical Office [40]. The databases were homogenized and validated with no data gaps.
According to the climatic classification of the Intergovernmental Panel on Climate Change (IPCC), two climate zones are distinguished for Hungary [41]; (a) Cold Temperate Dry (CTED) covering approximately 3540 thousand hectares and making up 40% of the territory of the country, where the mean annual temperature is below 10 °C and the annual precipitation is less than evapotranspiration, and (b) Warm Temperate Dry (WTED) covering 5762 thousand hectares, where the mean annual temperature is above 10 °C and the annual precipitation is less than evapotranspiration (Figure 1).
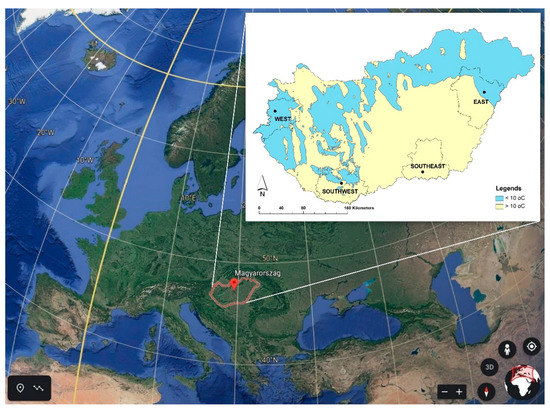
Figure 1.
Location of the investigated regions in the two Intergovernmental Panel on Climate Change (IPCC) climate zones (mean annual temperature below and above 10 °C) of Hungary.
In this study we selected four different geographical regions. The meteorological data recorded in Szombathely (7.231384, 21.624262) were applied to the West (W) region of 145,000 ha, the data recorded in Debrecen (47.532229, 21.624289) to the East (E) region of 329,800 ha, the data recorded in Pécs (46.077251, 16.621671) to the Southwest (SW) region of 225,600 ha, while the data recorded in Szeged (46.251462, 20.148701) were applied to the Southeast (SE) region of 255,200 ha (Figure 1). The source of the spatial data is the Research Institute of Agricultural Economics of the National Agricultural and Innovation Centre [42]. Here we note that the area of the regions and the grid size of the E-OBS dataset are quite comparable; furthermore, spatial interpolation has a considerable impact on the magnitudes of the extremes, where the largest smoothing of the extremes occurs in the interpolation of the daily anomalies [43].
According to the IPCC classification, only the Southeast region fits in its entirety into one category, namely the WTED. The majority of the area of the West region is covered by the CTED category. The Southwest and the East regions mostly fall into the WTED category with some CTED in the north.
For the assessment, the meteorological database of the National Meteorological Service of Hungary was used. Daily data of a 120-year long time series were analyzed for minimum temperature (Tmin) maximum temperature (Tmax), precipitation, global radiation, and the number of sunshine hours. The wind velocity and relative air humidity data were estimated from the monthly recorded data. In Hungary, the grain maize has not been irrigated in the investigated period of time.
2.2. Statistical Analyses
For correlation analyses, normality was tested with the Shapiro–Wilk normality test (α = 0.05) [44,45,46]. The time series used for the analyses involved historical crop yield and weather data from the past 50 years. Since the magnitude of the seasonal fluctuations for both maize yield and weather data did not vary with the level of the time series, the additive model was appropriate to determine the composition model, where trend, seasonal and irregular components are added together to give the observed series, as described by Equation (1).
where Y[t] is the time series value at period t, T is the trend, S is the seasonality and e is the residual component [47].
Y[t] = T[t] + S[t] + e[t]
Seasonal meteorological parameters characteristic of the vegetation period (May–August) of maize were generated: mean air temperature (°C), growing degree days (°C days), extremely high temperatures (Tmax > 30 °C), total amount of precipitation (mm), potential evapotranspiration (PET, mm), and climatic water balance (CWB, mm). These were considered the independent variables in the modeling. Extreme temperature values cause heat stress in maize. We quantified the heat stress, expressing it in heat stress units (HSU, °C) derived from the heat-sum of the daily Tmax values above 30 °C. The daily PET values were determined according to the FAO-56 Penman-Monteith equation [48] and summed for the whole vegetation period of maize.
All dependent and independent variables were filtered in order to exclude the linear trends. All the independent variables were involved in the zero model, the ‘best’ models were determined by using stepwise regression analysis. The Akaike information criterion was used as the ‘best’ criterion [49]. Later, the correlations of the independent variables were included in the models, but we did not obtain a sufficient explanation. Even the best models showed low R-squared values (R2 = 0.2–0.3).
Due to the weak correlations—adapting the idea of Teasdale and Cavigelli [50] to the Hungarian conditions—we determined the periods which were the most critical from the point of view of the growth and development of maize on the basis of the correlation coefficients. The early and late periods for precipitation and temperature were identified as the range of weeks during crop establishment (early) and reproductive growth (late) that gave the highest correlation between yield and precipitation or temperature. For this, the daily meteorological data were aggregated to weekly ones. Only the basic data were used for the further development of the model; the calculated values were excluded to avoid multicollinearity problems. The weeks were numbered from the beginning of the year.
In the investigated period, the 16th week (third week in April) was considered the average sowing time, which corresponds to the practice in Hungary. The new explanatory variables were: early temperature (Tearly), late temperature (Tlate), heat stress unit, early precipitation (Pearly), and late precipitation (Plate).
Multiple regression analysis was used to analyse the relationships between weather conditions and maize yield (Y) (Equation (2)).
where β0 is the intercept, and β1 – β5 are the regression coefficients for the explanatory variables.
Y = β0 + β1 × Tearly + β2 × Tlate + β3 × HSU + β4 × Pearly + β5 × Plate
The critical periods were determined specifically for the four investigated regions of Hungary. Heat stress days most frequently occurred between the 20th and 35th weeks.
In order to select the ‘best’ model, all subset regression analyses were used. Including the zero model, 25 = 32 models can be set up from the five explanatory variables. All models were set up, and the best five were examined on the base of the adjusted R-square value. This value is more informative when showing the explanatory power of the model if it is run with new data. The adjusted R-square value can even increase if the non-significant explanatory variables are excluded. The simple R-square value is not a suitable way of finding the best model as it increases with the number of variables, leading the researcher in the direction of more complicated models. According to the principle of simplicity of Ockham’s approach, the simpler model must be chosen if the explanatory powers are the same. We chose the model where all the explanatory variables were statistically significant. The multicollinearity in the regression analysis was detected by the variance inflation factor (VIF). The VIF never exceeded 4 in the case of any predictors, which means that there was no redundancy among the independent variables.
Statistical computing was carried out using the R software [51]. Data analyses were completed using version R 4.0.0 (2020-04-24). Figures were created using the ggplot2 package [52].
3. Results and Discussion
3.1. Long-Term Maize Production Data in Hungary between 1970 and 2019
During the last 50 years, the maize production area in Hungary has fallen below 1 million hectares only once, in 2018 (Figure 2). Nowadays, Hungary has the third largest maize production area among the EU27 countries, surpassed only by Romania and France. During the decade between 1970 and 1980, the production area for maize exceeded 1.2 million ha in Hungary, being the highest in 1973 and 1974 when it reached 1.45 million ha. From the 1980s, the figure stood at 1 to 1.25 million ha, with some annual fluctuations. Taking the entire investigation period (1970–2019) into account, a decreasing tendency can be observed. From the mid-1970s to the mid-1980s, a 20% decrease occurred, which was probably the result of the fifth and the sixth Five-Year plan of the socialistic central directives of the country [53].
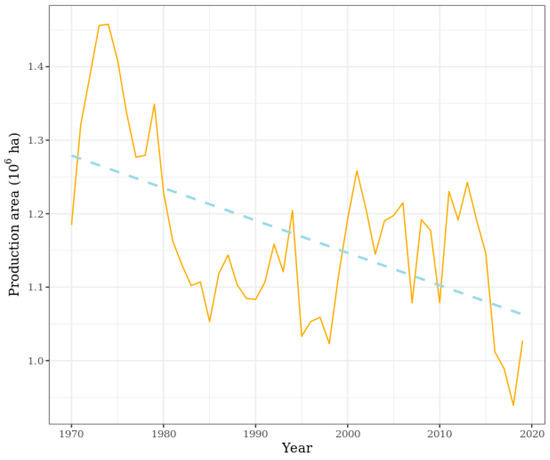
Figure 2.
Changes in the maize production area in Hungary (1970–2019).
The average yield of maize continuously and dynamically increased from the 1970s (Figure 3) until the mid-1980s when it reached 6 t ha−1. In the 1970s and 1980s, an intensive development started, not only in maize production but also in the entire Hungarian agricultural sector [54]. This development was apparent in the level of the technical background, human expertise, chemicals (fertilizers, pesticides, herbicides, etc.), and the new domestic as well as imported hybrids which were applied over the entire maize production area [55]. In that period, the average annual dose of NPK fertilizers applied was 278 kg ha−1 with a favorable composition of macronutrients, i.e., 40% N, 27% P2O5, and 33% K2O [56]. In the 1980s, Hungary ranked third behind the USA and France in terms of average maize yield per hectare. This period is known as the “golden age” of Hungarian agriculture. The maize yield was a dominant item in the national economy, and it increased continuously from the 1970s and reached its peak at 7 million metric tons in the 1980s.
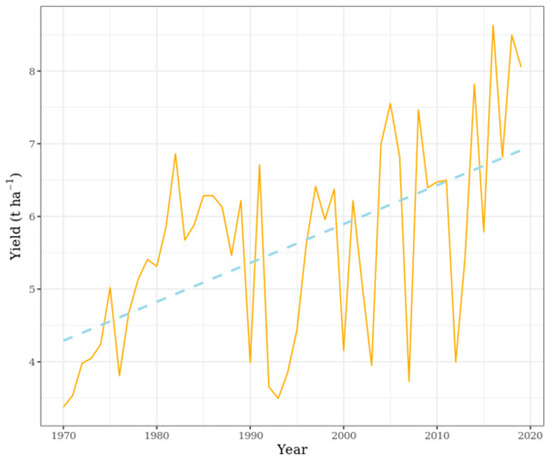
Figure 3.
Average yields of maize in Hungary (1970–2019).
The privatization of the land that started in 1989 had a negative effect on maize production, with the yields and stability of the production showing a significant decline [57,58,59]. It took 10 years to reach the level of the 1980s again. Minimal doses of fertilizers were applied for a decade, and a dose of 100 kg ha−1 NPK use was only reached in 2015; recently it has stood at around 120 kg ha−1. These unfavorable conditions were partly compensated by the modern hybrids that had a higher yield potential and disease resistance. In recent years the latest hybrids have been grown with high yield potential and good resistance against diseases. In terms of the fluctuation in average maize yields, two well-distinguished stages could be identified during the time period investigated. The fluctuation was only 10–20% prior to land privatization, but subsequently rose to 50–60%.
The total harvest area of maize covered 17–26% of the land in the West, 24–38% in the East, 29–41% in the Southwest, and 15–34% in the Southeast region in the period 1970–2019 (Figure 4). The area of maize production, despite some fluctuations, did not change considerably over time in the West and Southwest regions, while there was an increasing trend in the East region and some decrease in the Southeast over time.
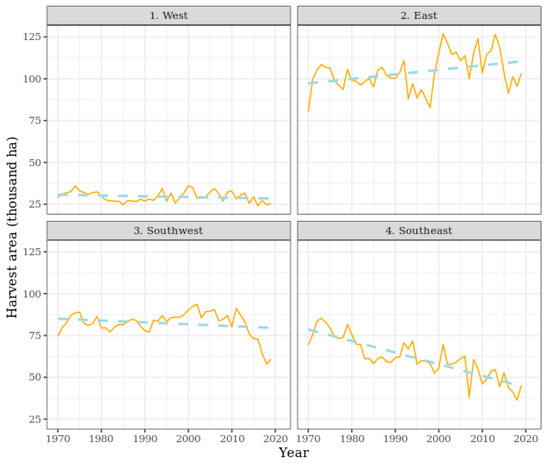
Figure 4.
Total harvest area of maize in the four investigated regions of Hungary (1970–2019).
We analyzed the normality of the yield data for the four investigated regions by means of the Shapiro–Wilk test. It was assumed that the yield data are normally distributed (null-hypothesis), since the normal distribution of the population is a significant condition of the application of parametric statistics. Decisions were made at the significance level of 5%, and the results are summarized in Table 1.

Table 1.
Results of the Shapiro–Wilk test.
In both investigation periods, yield data were normally distributed, as the p-values were higher than 0.05 for all the regions. Based on the results, it can be established that yield data were suitable for parametric statistical analysis.
The results of the linear trend analysis of the yields for the two investigated periods—1970–1989 and 1990–2019—are shown in Figure 5. The data were divided according to the social and economic changes characteristic of Hungary. The narrower the interval the more precise the estimation is, while the intervals are wider in the case of a larger fluctuation in the basic data. The two investigated periods differed from each other considerably. Between 1970 and 1989, the average yield increased gradually with small fluctuations, while after the large decline in the 1990s, the increase was characterized by extreme fluctuations. At the country scale, the least maize (4.8 million metric tons) was harvested in 2012. The peak occurred in 2014 with 9.3 million metric tons, almost double the total yield of 2012.
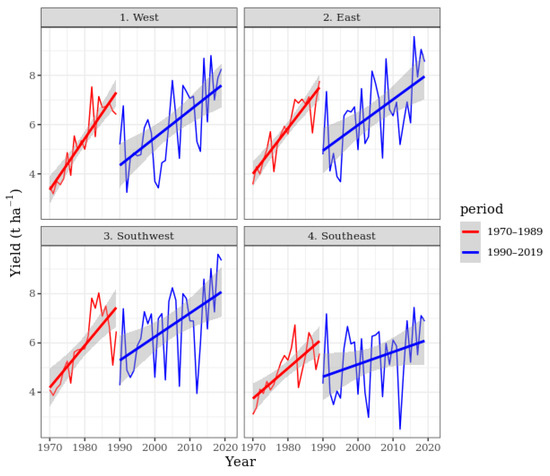
Figure 5.
Average yields of maize in the four investigated regions divided into two periods (1970–1990 and 1991–2019). The grey strips indicate the 95% confidence intervals representing the correctness of fit.
The results of the linear trend analysis of the yield changes are shown in Table 2. The estimates represent the steepness of the linear trends, i.e., the annual increase in the average yields. In the first period, the smallest increase was in the Southeast region, of 123 kg ha−1 annually. In the second period, the average annual increase was halved. At the same time, the error of trend fitting doubled due to the higher variance of the yield data. For the Southwest region, the steepness of the linear trend is not linear, therefore no value is shown. Although the trend increased for this region too, probably the extreme variance of the yield data resulted in the non-significant correlation (Figure 5).

Table 2.
Results of the annual linear trend analysis of yield changes.
The variance-mean plot of maize yields for the two investigated periods and four regions is shown in Figure 6.
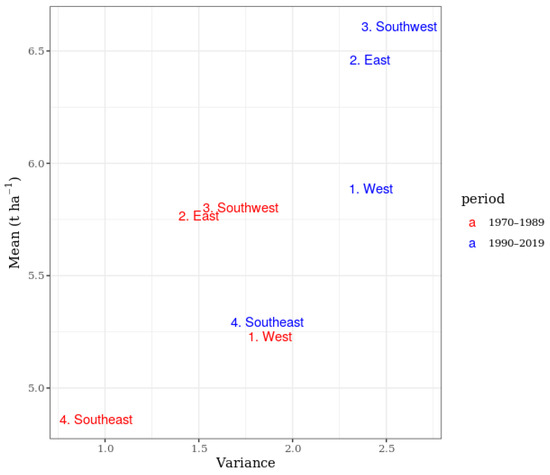
Figure 6.
Variance-mean plot of maize yields for the investigated regions and periods.
Yields and variances both increased in all four regions, and higher yields meant higher variances. The risk of maize production increased in the period 1990–2019.
During the period of communist large-scale agriculture (1970–1989), average yields of maize in Hungary ranked among the highest in the world. After the change in the political and economic system, the production level declined. In the period 1990–2019, the average annual maize yields showed extreme variations, suggesting a low yield safety during this period. As Collins et al. [24] emphasized, predicting socioeconomic development is more difficult than predicting the evolution of a physical system. It entails predicting human behavior, policy choices, technological advances, international competition and cooperation.
3.2. Long-Term Climatic Data in Hungary (1970–2019)
The mean annual temperature showed an increasing tendency in all four regions between 1970 and 2019 (Figure 7). The mean annual temperature in the West region of Hungary was approximately 9 °C in the 1970s, exceeding 10 °C only in the 1990s, and its trend line reached 11 °C by 2020. The minimum in the West region was 8.41 °C, the maximum was 11.79 °C, and the average was 10.05 °C. In the East region, the trend line started from 9.5 °C and reached 11.5 °C, crossing the 10 °C level in the 1980s. The minimum in the East region was 8.76 °C, the maximum was 12.46 °C, and the average was 10.52 °C. The trend lines of the two southern regions during the last 50 years were similar, starting from 10 °C and exceeding 12 °C. The similarity was also proven by the minimum, maximum and average temperature values. The average value was 10.06 °C in the Southwest region, while it was 10.03 °C in the Southeast. The minimum and maximum temperature values were also similar, at 9.32 °C (SW), 9.42 (SE) and 12.87 °C (SW), 12.92 °C (SE), respectively. In all four regions, the increase in the annual mean temperature was 2 °C.
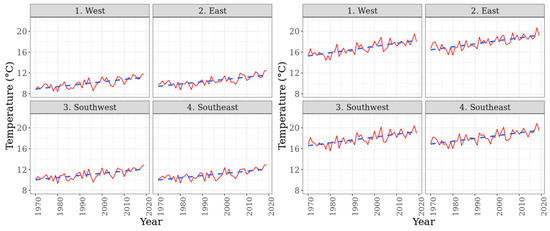
Figure 7.
Annual (left) and seasonal * (right) mean air temperature values in the four investigated regions (1970–2019). * Calculated for the vegetation period of maize (May–August).
Maize is suitable to be cultivated in warmer environment, its optimum growth occurs in climates with mid-summer temperatures between 21 and 27 °C [60]. The increase in the mean annual temperature itself can be considered beneficial for maize production. In fact, the production rate of new hybrids with high potential yield and heat demand further increased the total maize production of Hungary. In the last century, Hungary was considered the northern border of maize production, which should be revised based on the data and trends described above. A mean annual temperature of 11–13 °C is rather Mediterranean-like, thus the extension of the northern border of grain maize production farther to the north (Poland, Germany, etc.) is realistic, if frost does not become a limiting factor.
The amount of seasonal rainfall calculated for the vegetation period of maize (May–August) in the four investigated regions is shown in Figure 8. During the 50 years investigated, no statistically significant change in the amount of rainfall could be identified.
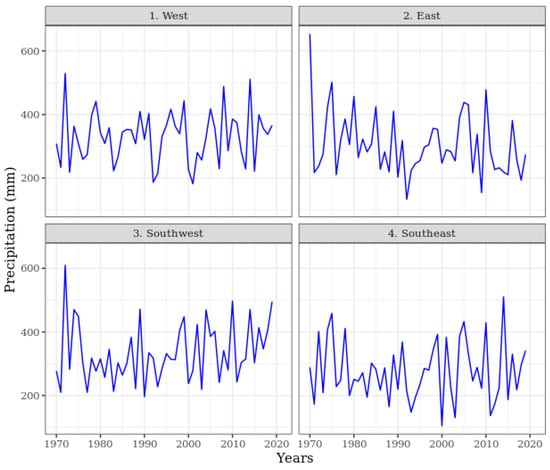
Figure 8.
Amount of seasonal * rainfall in the four investigated regions (1970–2019). * Calculated for the vegetation period of maize (May–August).
Figure 9 shows the biplots visualizing the relation between the long-term mean air temperature and the average amount of precipitation for the four regions during the vegetation period. The intersection of the lines represents the theoretical averages in terms of temperature and rainfall. It is obvious that the four regions are markedly different in this respect. Taking the annual data into account, the West region was slightly wetter and cooler than the average, while the East region was slightly arid and warm, the Southwest region was warm and rainy, and the Southeast region was warm and arid. These descriptions are not in harmony with the classification of the IPCC described above, especially because three of the investigated regions fall into two categories. Therefore, we believe climate classification based on region-specific meteorological data with higher resolution is more suitable for our assessments. Nevertheless, if we analyze the biplot that depicts the relationship between the long-term mean air temperature and the average amount of precipitation during the vegetation period of maize, a number of differences can be identified compared to the annual data. We have not considered the vegetation period of maize from sowing till harvest, but from sowing until the end of the transpiration period, i.e., the water uptake from the soil. In a weighing lysimetric experiment, Zsembeli et al. [61] established that maize does not transpirate a considerable amount of water in September under Hungarian climatic conditions, and if we also take its water and nutrient regime into account the vegetation period is over by the end of August. Based on the data of these five months, only the biplot position of the Southeast region is the same compared to the results generated from the annual data. The East region’s vegetation period is wetter with the same cooler climate. The Southwest region still has the best water supply due to natural precipitation both annually and seasonally, but its vegetation period is cooler compared to the entire year. We found the difference to be most considerable for the East region: although its water supply is still somewhat lower than the average, temperatures during its springs and summers are much warmer than those measured annually.
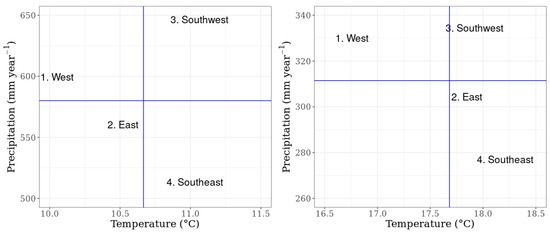
Figure 9.
Biplots of the annual (left) and seasonal * (right) mean air temperature and average amount of precipitation in the four investigated regions (1970–2019). * Calculated for the vegetation period of maize (May–August).
The biplots also show whether the climatic conditions (i.e., mean temperature and average rainfall) are close to or far from the optimal conditions for maize production in a certain period of time. The upper right quadrant of each biplot graph represents the desirable circumstances during the vegetation period. In this regard, the Southwest region can be considered the most suitable area for maize production in Hungary. In the Southeast region, the favorable temperature is accompanied by a low amount of precipitation, in the West region temperature is the limiting factor, while the East region is the closest to the average under Hungarian circumstances. It must be noted however, that in hot regions, the potential maize yields are most sensitive to the daily minimum and maximum temperatures. Kim et al. [62] concluded that in warm climates, lower maximum and higher minimum temperatures were generally beneficial for increasing the maize yield.
The climatic parameters analyzed above which are valid for the vegetation period are the most important ones regarding maize production. Nevertheless, the annual amount of precipitation (P) cannot be ignored due to the water storage capacity of the soil as it can supply water stored before the vegetation period in the crops. These two parameters do not provide full information on the climatic water balance (CWB), the most determinative ecological factor in Hungary. The CWB gives information about the sufficiency of the water supply for the undisturbed growth of a crop. It is calculated from the amount of potential evapotranspiration (PET) natural precipitation, determined for a given area and period of time according to Equation (3). Together with temperature, changes in PET values describe the dynamics of climatic changes in a region very well [63].
CWB = P − PET
PET values showed an increasing tendency in each region; approximately 200–250 mm more water could be evaporated in the recent years than 50 years ago (Figure 10). This increase was valid annually and for the vegetation period as well, since the annual PET is mostly determined by the meteorological conditions of the period May to August. If the increase in the amount of precipitation does not follow the increase in PET, the CWB becomes negative. This has practical importance for the application of irrigation and the determination of dosages.
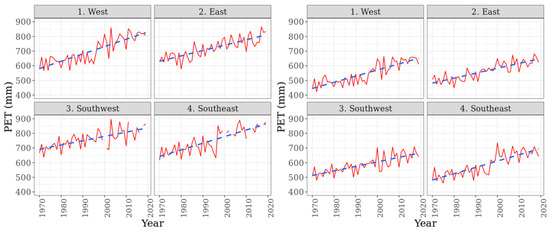
Figure 10.
Annual (left) and seasonal * (right) values of PET in the four investigated regions (1970–2019). * Calculated for the vegetation period of maize (May–August).
We found a decreasing tendency for the annual and seasonal CWB values (Figure 11), and hence an increasing water deficit for all the regions, though the steepness of the trend lines were different. The smallest change was found for the Southwest region, while even extremes were characteristic for the other three regions. The highest water shortage was calculated for the two eastern regions. It is reasonable to assume that the increase in the CWB has a negative effect on maize production.
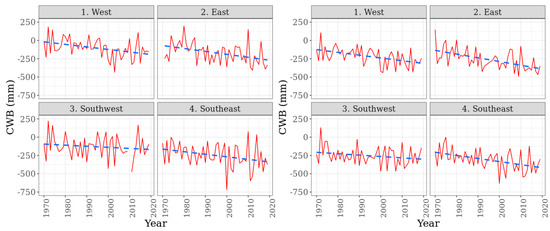
Figure 11.
Annual (left) and seasonal * (right) values of the climatic water balance (CWB) in the four investigated regions. * Calculated for the vegetation period of maize (May–August).
In conclusion, long-term meteorological data showed that negative effects were dominant, hence a drop in annual yields should have taken place if climate had been the only influencing factor.
3.3. Correlation of Climatic and Maize Yield Data in Hungary (1970–2019)
Considering the correlation between the average yield of maize and the meteorological data (early temperature, late temperature, heat stress unit, early precipitation, late precipitation) of the critical periods during the 1970–1989 period, the explanatory power of the models determined by all subset regression analysis was low (R-squared 0.1–0.3). This can be explained by the technological development that has overwritten the effect of the weather. The linear trend itself correlated to the change of the yield at 60–80%. The fluctuation around the trend was low (Figure 5); therefore, the correlation and regression parameters were low with low values of covariance. These results were not used for further predictions as the trend was broken at the end of the period.
The tendencies during the period after the change in the political and economic system in Hungary (1990–2019) completely changed. The explanatory power of the models determined for that period is much stronger. The critical weekly periods and the relevant correlation coefficients are shown in Table 3. The correlation between maize yield and heat stress unit is surprisingly strong, but the yield showed strong correlation with late precipitation and late temperature, too.

Table 3.
The critical weekly periods and the linear correlation coefficients for the period 1990–2019.
The correlation matrices of the model variables for each investigated region were similar. The data of the West region are shown in Figure 12. The variables of the final (‘best’) models determined by all subset regression analysis are shown in Table 4.
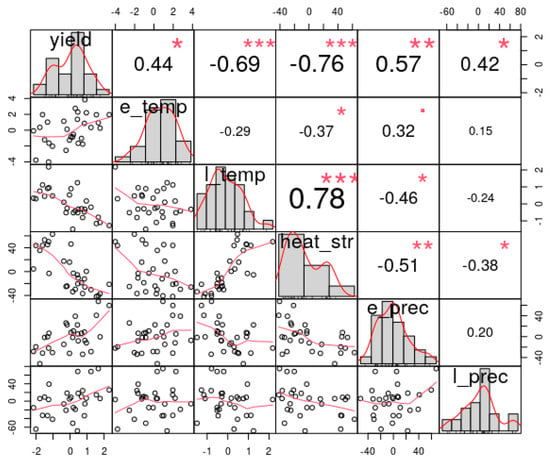
Figure 12.
Correlation matrix for the West region for the period 1990–2019. The distribution of the variables is in the diagonal, the correlation diagrams are shown in the lower triangle, and the linear correlation coefficients in the upper triangle of the graph. The font size of the numbers expresses the strength of the correlation. The significance levels are <0.05 (*), <0.01 (**), and <0.001 (***).

Table 4.
The best models for the period 1990–2019 (t means t-value).
Explanatory power above 60–70% can be considered good for a 30-year-long period. In the Southwest region, the explanatory power is almost 80%. The values of the adjusted R2 are lower by 0.01–0.03 than those of the linear one. All this means that our models are robust and can be utilized for predictions of the near future. For a period of 23 years in California, Lobell et al. [64] found that for most crops they investigated, fairly simple equations using only 2 to 3 variables explained more than two-thirds of the observed yield variance. They assumed that the unexplained variance arose from the different management aspects.
Different variables were considered in the ‘best’ models relevant to the different geographical regions, although heat stress is involved in all the four models. The change in the trends of the heat stress unit is shown in Figure 13. As the linear correlation coefficients showed, this variable has the strongest negative impact on maize yield. According to our estimations, a 1-degree day heat stress unit increase results in 14–37 kg ha−1 yield depression. The average amount of annual precipitation has not changed during the last 50 years, and we assumed that it will not change in the coming 31 years. Late temperature as a variable is in strong correlation with the heat stress units; this also confirms the possibility of not considering the temperature data. Finally, two variables were taken into account for the prediction of the maize yield to obtain the simplest universal prediction model: (1) the annual schedule of technological development, and (2) the heat stress unit. We considered continuous technological development in the next three decades, assuming the same trend as in the previous 30 years, since, for Nielsen [1] the ability to recognize “quantum leaps” in genetic potential or technology improvement is difficult in the short term, and the long-term effects of such improvements are not recognized for quite some time. The predicted changes for the following 31 years are summarized in Table 5.
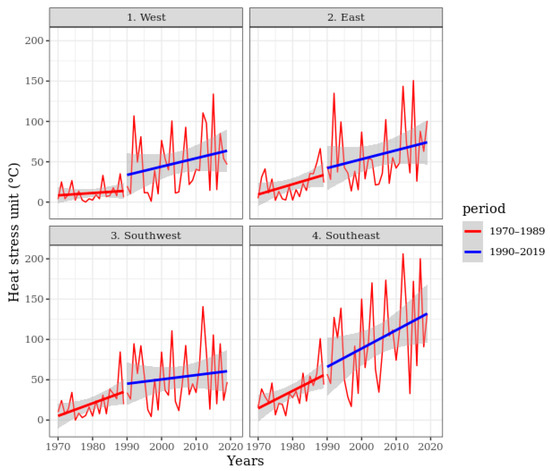
Figure 13.
Heat stress units in the four investigated regions divided into two periods (1970–1990 and 1991–2019).

Table 5.
Effect of technological development and heat stress on the average yield of maize in Hungary 2020–2050.
In three regions of Hungary, a yield increase in maize is predicted, but in the Southeast region a yield decrease can be expected as the effect of heat stress is the greatest in that region. The predicted average yield change weighted with the maize sowing area of the four investigated regions (0.12, 0.47, 0.29, 0.12) is 2.169 t ha−1 for Hungary. Therefore, according to our calculations, an 8.2 t ha−1 domestic average maize yield is predicted by 2050. Not taking into consideration the socio-economic change, Marton el al. [65] projected a yield of approximately 7.8 t ha−1 by 2050. Excluding the technological impact, 5.5 t ha−1 was calculated.
Since the explanatory power of the linear model was found high, it can be considered robust, its forecasts can be expected consistently relatively accurate even if the input variables would change due to unforeseen circumstances. Our predictions for the next 30 years are valid in the case of same trends in the climatic and technological trends as of the last 30 years. If e.g., the climate change is accelerating in the future, our predictions obviously will be less accurate.
In the EU, a simulation using historical weather data and average soil characteristics prognosticated an increase in maize yield for the northern countries, and a similar or slightly lower yield for the central countries, including Hungary with higher temperatures and less solar radiation in the future, at the country scale [11]. As the most extreme scenario, deterministic models based on plant, soil, and atmospheric parameters predict a 10% to 20% decrease in maize yield in Hungary by 2050 [12]. However, Angulo et al. [66] conducted an analysis for 533 climate zones in the European Union, considering 24 years of observed yield data, and proved that region-specific calibration of crop models is needed for Europe-wide assessments.
Granger [67] highlighted that climatic variables are not the only determinants of yield; soils, pests, fertilizers and farm management are also deterministic and can be interacting factors. Among the technological measures, the change of perspective in soil cultivation has to be taken into consideration. Given that soil, besides the climate and weather, is one of the main factors of production which basically determine the quality and economic conditions of production, the knowledge of the effects of plant production on soil is important. Among land use practices, soil cultivation has the most considerable effects on soil properties, and hence on crop production. The need for water and energy saving soil tillage systems is increasing as the consequences of improper soil cultivation practices which have characterized the last few decades are manifested in unfavorable soil properties [68]. In accordance with the combat against water shortages and soil degradation due to improper soil use, conventional soil cultivation methods should be replaced by conservation tillage, including different versions of reduced till, mulch-till, crop residue management, etc. These new soil tillage methods aim to reduce the depth of the regularly cultivated soil layer and to create a topsoil rich in moisture and organic matter [69].
4. Conclusions
Our study revealed that without considering the contribution of social factors, prediction models may overestimate the adverse effects of climate change on crop production. In the last 50 years in Hungary, both mean annual and seasonal temperatures have increased by 2 °C with no significant differences between regions representing Cold Temperate Dry and Warm Temperate Dry zones or a mix of the two, as classified by the Intergovernmental Panel on Climate Change. However, the absolute temperature ranges were found to be significantly different, suggesting that zone categories should be carefully predefined for climate projections. Annual precipitation has not changed, even in the long term; however, the increasing potential evapotranspiration has resulted in a gradually increasing deficit in the climatic water balance. In the period 1970–1989 of the communist era, large-scale farming ensured a continuous increase in maize yield (120–200 kg ha−1 year−1) with small fluctuations, while the increase became slower (100 kg ha−1 year−1) due to the complex socio-economic effects of the land reform implemented after 1989. In parallel with this, the degree of fluctuation showed an increasing frequency of extremes. The average increase of heat stress is 0.5–2 °C year−1 with some variations among the investigated regions. Up to 60–80% of the fluctuations in the yield can be explained by determining the meteorological data of the critical periods. Due to climate change, taking only heat stress into account gives sufficient accuracy to determine a robust prediction model. Although the increasing mean temperature would have an adverse effect on maize yields, technological development is expected to result in a slight yield increase in the regions of Hungary above 47 degrees north latitude by 2050. Below that latitude, however, technological development should be more intensified compared to that seen between 1990 and 2019, in order to maintain the yield.
Author Contributions
Conceptualization, L.H. and C.J.; methodology, L.H.; software, L.H.; validation, J.Z. and C.J.; formal analysis, J.Z. and E.K.; investigation, L.H., E.K., J.Z. and C.J.; resources, E.K.; data curation, L.H.; writing—original draft preparation, E.K.; writing—review and editing, J.Z.; visualization, L.H.; supervision, C.J.; project administration, E.K.; funding acquisition, C.J. All authors have read and agreed to the published version of the manuscript.
Funding
The research was financed by the Higher Education Institutional Excellence Programme (NKFIH-1150-6/2019) of the Ministry of Innovation and Technology in Hungary, and the National Research, Development and Innovation Fund of Hungary (TKP2020-IKA-04) under the 2020-4.1.1-TKP2020 funding scheme, within the framework of the 4th thematic programme of the University of Debrecen.
Acknowledgments
The authors thank Zoltán Macháty (Purdue University, West Lafayette, IN, USA) for the critical reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nielsen, R.L. Corn Grain Yield Trends: Eyes of the Beholder; Corny News Network; Purdue University Department of Agronomy: West Lafayette, IN, USA, 2006; Available online: http://www.kingcorn.org/news/articles.06/YieldTrends-0615.html (accessed on 30 September 2020).
- Olesen, J.E.; Trnka, M.; Kersebaum, K.C.; Skjelvag, A.O.; Seguin, B.; Peltonen-Saionio, P.; Rossi, F.; Kozyra, J.; Micale, F. Impacts and adaptation of European crop production systems to climate change. Eur. J. Agron. 2011, 34, 96–112. [Google Scholar] [CrossRef]
- Marton, L.C. Hybrid maize in Hungary is 60 years old. In 60 Years of Hungarian Hybrid Maize (1953–2013), Proceedings of the 2013 Hungarian Science Festival, Hybrid Maize Conference, Martonvásár, Hungary, 14 November 2013; Marton, L.C., Spitkó, T., Eds.; Pannonian Plant Biotechnology Association: Martonvásár, Hungary, 2013; pp. 10–16. ISBN 978-963-89129-4-7. [Google Scholar]
- Lipper, L.; McCarthy, N.; Zilberman, D.; Asfaw, S.; Branca, G. Climate Smart Agriculture. Building Resilience to Climate Change; Food and Agriculture Organization of the United Nations: Rome, Italy; Springer International Publishing AG: New York, NY, USA, 2018; pp. 1–630. ISBN 978-3-319-61193-8. [Google Scholar] [CrossRef]
- Nielsen, R.L. Historical Corn Grain Yields in the U.S; Purdue University Department of Agronomy: West Lafayette, IN, USA, 2020; Available online: http://www.kingcorn.org/news/timeless/YieldTrends.html (accessed on 30 September 2020).
- Csáki, C.; Lerman, Z. Land reform and farm restructuring in East Central Europe and CIS in the 1990’s: Expectations and achievements after the first five years. Eur. Rev. Agric. Econ. 1997, 24, 428–452. [Google Scholar] [CrossRef]
- Burger, A. Agricultural development and land concentration in a central European country: A case study of Hungary. Land Use Policy 2001, 18, 259–268. [Google Scholar] [CrossRef]
- Amanullah, K.; Fahad, S. Corn—Production and Human Health in Changing Climate; IntechOpen: London, UK, 2018; pp. 1–148. ISBN 978-1-78984-155-8. [Google Scholar] [CrossRef]
- Olesen, J.E.; Bindi, M. Consequences of climate change for European agricultural productivity, land use and policy. Eur. J. Agron. 2002, 16, 239–262. [Google Scholar] [CrossRef]
- Szerb, B.A. The opportunities of the Hungarian corn at the international agricultural markets in 2016. Reg. Bus. Stud. 2016, 8, 59–67. [Google Scholar]
- Wolf, J.; van Diepen, C.A. Effects of climate change on grain maize yields. Clim. Chang. 1995, 29, 299–331. [Google Scholar] [CrossRef]
- Fogarasi, J.; Kemény, G.; Molnár, A.; Kemény Horváth, Z.; Zubor-Nemes, A.; Kiss, A. Modelling climate effects on Hungarian winter wheat and maize yields. Stud. Agric. Econ. 2016, 118, 85–90. [Google Scholar] [CrossRef]
- Juhász, C.; Gálya, B.; Kovács, E.; Nagy, A.; Tamás, J.; Huzsvai, L. Seasonal predictability of weather and crop yield in regions of Central European continental climate. Comput. Electron. Agric. 2020, 173, 105400. [Google Scholar] [CrossRef]
- Roudier, P.; Sultan, B.; Quirion, P.; Berg, A. The impact of future climate change on West African crop yields: What does the recent literature say? Global Environ. Chang. 2011, 21, 1073–1083. [Google Scholar] [CrossRef]
- Carter, T.R.; Porter, J.H.; Parry, M.L. Climatic warming and crop potential in Europe: Prospects and uncertainties. Glob. Environ. Chang. 1991, 1, 291–312. [Google Scholar] [CrossRef]
- Alcamo, J.; Dronin, N.; Endejan, M.; Golubev, G.; Kirilenko, A. A new assessment of climate change impacts on food production shortfalls and water availability in Russia. Glob. Environ. Chang. 2007, 17, 429–444. [Google Scholar] [CrossRef]
- Waha, K.; Müller, C.; Bondeau, A.; Dietrich, J.P.; Kurukulasuriya, P.; Heinke, J.; Lotze-Campen, H. Adaptation to climate change through the choice of cropping system and sowing date in sub-Saharan Africa. Glob. Environ. Chang. 2013, 23, 130–143. [Google Scholar] [CrossRef]
- Dobor, L.; Barcza, Z.; Glásny, T.; Árendás, T.; Spitkó, T. Crop planting date matters: Estimation methods and effect on future yields. Agric. For. Meteorol. 2016, 223, 103–115. [Google Scholar] [CrossRef]
- Berzsenyi, Z.; Tokatlidis, I.S. Density dependence rather than maturity determines hybrid selection in dryland maize production. Agron. J. 2012, 104, 331–336. [Google Scholar] [CrossRef]
- Sárvári, M.; Pepó, P. Effect of production factors on maize yield and yield stability. Cereal Res. Commun. 2014, 42, 710–720. [Google Scholar] [CrossRef]
- Széles, A.; Nagy, J.; Rátonyi, T.; Harsányi, E. Effect of differential fertilization treatments on maize hybrid quality and performance under environmental stress conditions in Hungary. Maydica 2019, 62, 11–14. [Google Scholar]
- Parent, B.; Leclere, M.; Lacube, S.; Semenov, M.A.; Welcker, C.; Martre, P.; Fardieu, F. Maize yields over Europe may increase in spite of climate change, with appropriate use of genetic variability of flowering time. Proc. Natl. Acad. Sci. USA 2018, 115, 10642–10647. Available online: www.pnas.org/cgi/doi/10.1073/pnas.1720716115 (accessed on 30 September 2020). [CrossRef] [PubMed]
- Mercel, K.L.; Rerales, H.R.; Wainwright, J.D. Climate change and the transgenic adaptation strategy: Smallholder livelihoods, climate justice, and maize landraces in Mexico. Glob. Environ. Chang. 2012, 22, 495–504. [Google Scholar] [CrossRef]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.-L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term climate change: Projections, commitments and irreversibility. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Chapter 12; pp. 1029–1136. [Google Scholar] [CrossRef]
- Döös, B.R.; Shaw, R. Can we predict the future food production? A sensitivity analysis. Glob. Environ. Chang. 1999, 9, 261–283. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.-L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Biol. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Liu, B.; Piao, S.; Wang, X.; Lobell, D.B.; Huang, Y.; Huang, M.; Yao, Y.; Bassu, S.; Ciais, P.; et al. Temperature increase reduces global yields of major crops in four independent estimates. Proc. Natl. Acad. Sci. USA 2017, 114, 9326–9331. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.G.; Thornton, P.K. The potential impacts of climate change on maize production in Africa and Latin America in 2055. Glob. Environ. Chang. 2003, 13, 51–59. [Google Scholar] [CrossRef]
- Thornton, P.K.; Jones, P.G.; Alagarswamy, G.; Andersen, J. Spatial variation of crop yield response to climate change in East Africa. Glob. Environ. Chang. 2009, 19, 54–65. [Google Scholar] [CrossRef]
- Ma, J.; Maystadt, J.-F. The impact of weather variations on maize yields and household income: Income diversification as adaptation in rural China. Glob. Environ. Chang. 2017, 42, 93–106. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Metzger, M.J.; Bunce, R.G.H.; Jongman, R.H.G.; Mücher, C.A.; Watkins, J.W. A climatic stratification of the environment of Europe. Glob. Ecol. Biogeogr. 2005, 14, 549–563. [Google Scholar] [CrossRef]
- Durdu, Ö.F. Evaluation of climate change effects on future corn (Zea mays L.) yield in western Turkey. Int. J. Climatol. 2013, 33, 444–456. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Willems, P. Regional and global climate projections increase mid-century yield variability and crop productivity in Belgium. Reg. Environ. Chang. 2015, 16, 659–672. [Google Scholar] [CrossRef]
- Supit, I.; van Diepen, C.A.; de Wit, A.J.W.; Kabat, P.; Baruth, B.; Ludwig, F. Recent changes in the climatic yield potential of various crops in Europe. Agric. Syst. 2010, 103, 683–694. [Google Scholar] [CrossRef]
- Wu, F.; Guclu, H. Global maize trade and food security: Implications from a social network model. Risk Anal. 2013, 33, 2168–2178. [Google Scholar] [CrossRef]
- Fertő, I.; Szerb, A.B. The role of food crisis and trade costs in the Hungarian maize exports. Probl. Agric. Econ. 2017, 353, 110–124. [Google Scholar] [CrossRef]
- Juhász, A.; Wagner, H. An analysis of Hungarian agri-food export competitiveness. Stud. Agric. Econ. 2013, 115, 150–156. [Google Scholar] [CrossRef]
- United Nations Commodity Trade Statistics Database (UNComtrade). Available online: http://comtrade.un.org (accessed on 24 May 2020).
- Harvest Results of Main Crops. 2019. Available online: http://www.ksh.hu/docs/hun/xftp/stattukor/fobbnoveny/2019/index.html (accessed on 24 May 2020).
- Hungarian Meteorological Service, 2019. National Inventory Report for 1985–2017, Hungary. Available online: https://www.met.hu/eghajlat/magyarorszag_eghajlata/eghajlati_adatsorok (accessed on 24 May 2020).
- Statistical Book of the Agro-Economic Research Institute of Hungary. Available online: http://repo.aki.gov.hu/2581/1/Zsebkonyv_2016_magyar_web_pass.pdf (accessed on 24 May 2020).
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G. A European daily high-resolution gridded dataset of surface temperature and precipitation. J. Geophys. Res. Atmos. 2008, 113, D20119. [Google Scholar] [CrossRef]
- Royston, P. Algorithm AS 181: The W test for Normality. Appl. Stat. 1982, 31, 176–180. [Google Scholar] [CrossRef]
- Royston, P. An extension of Shapiro and Wilk’s W test for normality to large samples. Appl. Stat. 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Royston, P. Remark AS R94: A remark on Algorithm AS 181: The W test for normality. Appl. Stat. 1995, 44, 547–551. [Google Scholar] [CrossRef]
- Chambers, J.M. Linear models. In Statistical Models in S; Chambers, J.M., Hastie, T.J., Eds.; Wadsworth & Brooks/Cole: Pacific Grove, CA, USA, 1992; Chapter 4. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Chapter 4; Available online: www.fao.org (accessed on 30 September 2020).
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csáki, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Teasdale, J.R.; Cavigelli, M.A. Meteorological fluctuations define long-term crop yield patterns in conventional and organic production systems. Sci. Rep. 2017, 7, 688. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 30 September 2020).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; pp. 1–216. [Google Scholar]
- Swain, N. Hungary—The Rise and Fall of Feasible Socialism; Verso: Guildford, UK, 1992; pp. 1–272. ISBN 0860915697. [Google Scholar]
- Mathijs, E.; Mészáros, S. Privatisation and restructuring of Hungarian agriculture. In Agricultural Privatization, Land Reform and Farm Restructuring in Central and Eastern Europe; Swinnen, J.F.M., Buckwell, A., Mathijs, E., Eds.; CRC Press Series; Routledge Revivals: London, UK, 1997; pp. 161–188. ISBN 978-1859726488. [Google Scholar]
- Oros, I. The Hungarian agriculture and its output in the 20th century. Stat. Szle. 2000, 78, 3–23. [Google Scholar]
- Loch, J. Nutrient management in Hungary—A review. Agrochem. Soil Sci. 2015, 64, 273–382. [Google Scholar] [CrossRef][Green Version]
- Lerman, Z.; Csáki, C.; Feder, G. Land Policies and Evolving Farm Structures in Transition Countries; The World Bank: Washington, DC, USA, 2002; pp. 1–172. [Google Scholar] [CrossRef]
- Hartvigsen, M.B. Land Reform in Central and Eastern Europe after 1989 and Its Outcome in Form of Farm Structures and Land Fragmentation; FAO Land Tenure Working Paper 24; Food and Agriculture Organization of the United Nations: Rome, Italy, 2013; Available online: http://www.fao.org/docrep/017/aq097e/aq097e.pdf (accessed on 30 September 2020).
- Potori, N.; Chmielinski, P.; Fieldsend, A.F. Structural Changes in Polish and Hungarian Agriculture since EU Accession: Lessons Learned and Implications for the Design of Future Agricultural Policies; Research Institute of Agricultural Economics: Budapest, Hungary, 2014; pp. 1–292. ISBN 978-963-491-588-1. [Google Scholar]
- Shaw, R.H. Climate requirement. In Corn and Corn Improvement, 2nd ed.; Sprague, G.F., Ed.; American Society of Agronomy, Inc.: Madison, WI, USA, 1977; pp. 591–623. [Google Scholar]
- Zsembeli, J.; Kovács, G.; Mándoki, A. Water use efficiency of maize and different sorghum hybrids under lysimeter conditions. In Lysimeter in der Klimafolgenforschung und Wasserwirtschaft, Proceedings of the 14. Gumpensteiner Lysimetertagung, Raumberg-Gumpenstein, Austria, 3–4 May 2011; Lehr- und Forschungszentrum für Landwirtschaft Raumberg-Gumpenstein: Irdning, Austria, 2011; pp. 227–229. ISBN 978-3-902559-61-6. [Google Scholar]
- Kim, S.H.; Myoung, B.; Stack, D.; Kim, J.; Kafatos, M. Sensitivity of maize yield potential to regional climate in the Southern U.S. Trans. ASABE 2016, 59, 1745–1757. [Google Scholar] [CrossRef]
- Huzsvai, L.; Rajkai, K. Modeling of plant adaptation to climatic drought induced water deficit. Biologia 2009, 64, 536–540. [Google Scholar] [CrossRef][Green Version]
- Lobell, D.B.; Cahill, K.N.; Field, C.B. Historical effects of temperature and precipitation on California crop yields. Clim. Chang. 2007, 81, 187–203. [Google Scholar] [CrossRef]
- Marton, T.A.; Kis, A.; Zubor-Nemes, A.; Kern, A.; Fodor, N. Human impact promotes sustainable corn production in Hungary. Sustainability 2020, 12, 6784. [Google Scholar] [CrossRef]
- Angulo, C.; Rötter, R.; Lock, R.; Enders, A.; Frozek, S.; Ewert, F. Implication of crop model calibration strategies for assessing regional impacts of climate change in Europe. Agric. Forest Meteorol. 2013, 170, 32–46. [Google Scholar] [CrossRef]
- Granger, O.E. The impact of climatic variation on the yield of selected crops in three California counties. Agric. Meteorol. 1980, 22, 367–386. [Google Scholar] [CrossRef]
- Birkás, M.; Kalmár, T.; Fenyvesi, L.; Földesi, P. Realities and beliefs in sustainable soil tillage. Cereal Res. Comm. 2007, 35, 257–260. [Google Scholar] [CrossRef]
- Zsembeli, J.; Kovács, G. Dynamics of CO2-emission of the soil in conventional and reduced tillage systems. Cereal Res. Comm. 2007, 35, 1337–1340. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).