Abstract
Understanding the trends of reference evapotranspiration (ETo) and its influential meteorological variables due to climate change is required for studying the hydrological cycle, vegetation restoration, and regional agricultural production. Although several studies have evaluated these trends, they suffer from a number of drawbacks: (1) they used data series of less than 50 years; (2) they evaluated the individual impact of a few climatic variables on ETo, and thus could not represent the interactive effects of all forces driving trends of ETo; (3) they mostly studied trends of ETo and meteorological variables in similar climate regions; (4) they often did not eliminate the impact of serial correlations on the trends of ETo and meteorological variables; and finally (5) they did not study the extremum values of meteorological variables and ETo. This study overcame the abovementioned shortcomings by (1) analyzing the 50-year (1961–2010) annual trends of ETo and 12 meteorological variables from 18 study sites in contrasting climate types in Iran, (2) removing the effect of serial correlations on the trends analysis via the trend-free pre-whitening approach, (3) determining the most important meteorological variables that control the variations of ETo, and (4) evaluating the coincidence of annual extremum values of meteorological variables and ETo. The results showed that ETo and several meteorological variables (namely wind speed, vapor pressure deficit, cloudy days, minimum relative humidity, and mean, maximum and minimum air temperature) had significant trends at the confidence level of 95% in more than 50% of the study sites. These significant trends were indicative of climate change in many regions of Iran. It was also found that the wind speed (WS) had the most significant influence on the trend of ETo in most of the study sites, especially in the years with extremum values of ETo. In 83.3% of the study sites (i.e., all arid, Mediterranean and humid regions and 66.7% of semiarid regions), both ETo and WS reached their extremum values in the same year. The significant changes in ETo due to WS and other meteorological variables have made it necessary to optimize cropping patterns in Iran.
1. Introduction
Assessment of changes in reference evapotranspiration (ETo) is required in climate change studies, agricultural and forest meteorology, irrigation scheduling, surface water balance, drought analysis, long-term decision-making in food and water security policies, and optimum allocation of water resources [1,2,3,4,5,6,7]. Evaluating the trends of meteorological variables may help determine the effects of major factors on ETo and climate change [8,9].
Dadaser-Celik et al. [10] evaluated the 32-year trend of ETo in Turkey. Analysis of climatic data showed an upward trend in air temperature, and downward trends in wind speed and relative humidity in Turkey. Changes in these three variables explained the majority of variations in ETo. Song et al. [11] assessed the 46-year trend of ETo in the North China Plain. Their results indicated that the downward trends of net radiation and wind speed had a bigger impact on ETo compared to the upward trends of maximum and minimum air temperature. Wang et al. [12] characterized the 31-year trend of ETo in the western Heihe River Basin in China. They found that wind speed and sunshine duration were the two key meteorological variables that decreased ETo.
Darshana et al. [13] investigated the 30-year trend of ETo in the Tons River Basin in central India. Their outcomes showed that maximum air temperature and net radiation had a stronger impact on ETo compared to minimum air temperature and relative humidity. Zongxing et al. [14] studied the 49-year trend of ETo in the south-west of China. The decrease in wind speed was the main driving force for the reduction of ETo. This happened because the lower wind speed raised the vapor pressure, which ultimately reduced the evaporative demand of atmosphere. Li et al. [15] examined the 46-year trend of ETo in the Upper Mekong River Basin. They showed that sunshine duration had a more significant (at the confidence level 95%) effect on ETo compared to air temperature, relative humidity, and wind speed. Gao et al. [16] evaluated the 45-year trend of ETo in China, and found that sunshine duration, wind speed, and relative humidity had a more important influence on ETo than air temperature. Zhang et al. [17] assessed the changes in ETo and its controlling factors in China. They indicated that maximum air temperature, relative humidity, and wind speed affected ETo. A number of studies (e.g., [8,9,18,19,20]) showed that the increasing and decreasing trends of ETo were mainly due to the increase in air temperature and decrease in wind speed, respectively.
Tabari et al. [21,22] evaluated the 40-year (1966–2005) trend of ETo in the west and southwest of Iran with arid and semiarid climates. They studied the effect of air temperature, relative humidity, vapor pressure, wind speed, and rainfall on ETo, and found that wind speed had the most influence on ETo. Unfortunately, they did not consider the impact of serial correlations (autocorrelation) on the trends of ETo and meteorological variables. Kousari and Ahani [23] assessed trends of ETo and six meteorological variables (mean, minimum and maximum air temperature, relative humidity, wind speed and sunshine hours) in three climate regions (arid, semiarid and humid) of Iran during 1975–2005. They did not take into account the influence of serial correlations on the trends. Shadmani et al. [24] evaluated the 41-year (1965–2005) trend of ETo from 11 weather stations in arid regions of Iran but did not specify which meteorological variables controlled trend of ETo.
The existing studies (1) evaluated the impact of various climatic variables on ETo and (2) showed the signals of climate change in Iran based on upward/downward trends of ETo and meteorological variables [8,9,20,21,22,23]. However, they suffer from the following shortcomings: (1) they used data series of less than 50 years which are suitable only for evaluating climate variability and not climatic change. At least a 50-year period is necessary to study climate change [25,26,27,28,29,30,31,32]. Borman [26] used a 50-year period to analyze the sensitivity of ETo to climate change in Germany. Kingston et al. [27] found a considerable uncertainty in evaluating the changes of ETo due to climate change using 30-year data. Several studies assessed the response of ETo to climate change in China using 50-year data [28,29,30,31]. Hence, there is a consensus in the literature to use at least a 50-year period to evaluate the trend of ETo due to climate change. (2) They evaluated the individual impact of a few climatic variables on ETo, and thus could not represent the interactive effects of all forces driving trends of ETo. (3) They mostly studied trends of ETo and meteorological variables in similar climate regions. (4) They often did not eliminate the impact of serial correlations (autocorrelation) on the trends of ETo and meteorological variables. Finally (5) they did not assess if the extremum values of meteorological variables and ETo occur simultaneously. This study overcame the abovementioned drawbacks by analyzing the 50-year (1961–2010) trends of ETo estimates and 12 meteorological variables in Iran using the trend-free pre-whitening Mann–Kendall (TFPW-MK) and Spearman’s Rho tests. These sites were chosen to cover four different climates, namely arid, semiarid, Mediterranean and humid. Moreover, variations of 12 meteorological variables (mean, maximum, and minimum air temperature, difference between the maximum and minimum air temperature, rainfall, wind speed and direction, mean and minimum relative humidity, vapor pressure deficit, number of cloudy days, and sunshine hours) were investigated to characterize forces that drive trends of ETo. Furthermore, the effect of serial correlations on the trends was eliminated by the TFPW approach [24]. Finally, during the period 1961–2010, the coincidence of annual extremum values of ETo and meteorological variables was studied to identify the main meteorological variables that affect variations of ETo.
2. Data
Daily meteorological data in the 18 study sites were downloaded from the Iran Meteorological Organization (IMO) archive. These data cover a period of 50 years (1961–2010), and include mean, minimum, and maximum daily air temperature (°C), vapor pressure deficit (kPa), mean and minimum relative humidity (%), wind speed (m/s) at the screen-height of 2 m, rainfall (mm/day), number of cloudy days, and number of sunshine hours per day (hr/day).
Characteristics of the study sites are indicated in Table 1. Figure 1 shows the location of these sites in Iran. They are chosen to cover various climate regions (arid, semiarid, humid, and Mediterranean) across Iran.

Table 1.
Location, altitude, and climate of the 18 study sites.
Figure 1.
Location of the 18 study sites in Iran.
3. Models and Methods
3.1. FPM Equation
ETo is the rate of evapotranspiration from a uniform height, actively growing, well-watered, and completely shaded hypothetical crop [33]. The hypothetical crop has a height 0.12 (m), a fixed surface resistance of 70 (s/m), and an albedo of 0.23, closely resembling the evapotranspiration from an extensive surface of green grass [26]. In this study, daily meteorological variables from the 18 study sites were used in the Agricultural Organization of the United Nation (FAO)-Penman–Monteith (FPM) equation to estimate ETo on a daily basis. ETo estimates from the FPM equation were validated against the lysimeter measurements in the 18 study sites [34,35,36,37].
The FPM equation is given by [33]:
where ETo is the daily reference evapotranspiration (mm/day), γ is the psychrometric constant (kPa/°C), Δ is the slope of the saturation vapor pressure–temperature curve (kPa/°C), T is the mean daily air temperature (°C), and u is the mean daily wind speed at the screen-height of 2 m (m/s). G is the ground heat flux (MJ/m2/day) and is negligible on daily timescales [21,33].
es and ea are, respectively, the saturation and actual vapor pressures (kPa), which are given by [33]:
where and are the saturation vapor pressures (kPa) at daily maximum and minimum air temperatures, respectively. RHmax and RHmin are the daily maximum and minimum relative humidity (%), respectively.
Rn is the net radiation (MJ/m2/day), and is estimated by [21,33]:
where n is the number of sunshine hours per day (hr/day), nmax is the maximum possible duration of sunshine per day (hr/day), and Ra is the extraterrestrial radiation (MJ/m2/day). Ra and nmax depend on the latitude and julian day [33]. as and bs are empirical coefficients, which are obtained from [21] for each study site.
In this study, the annual averages of daily FPM ETo estimates and meteorological variables were used to analyze the annual trends.
3.2. Mann–Kendall (MK) Test
One of the most well-known methods for detecting trends in a time series is the non-parametric Mann–Kendall (MK) test [38,39,40]. Unlike the parametric statistical approaches, the non-parametric statistical tests are more suitable for non-Gaussian distributed data, which are frequently observed in hydrologic time series [34]. The MK test is defined as follows [38,39,40]:
where N is the number of data, S is the summation of signs, VAR is the variance, and xj and xi are the data values in years j and i, respectively (with j > i). tp and g indicate ties and the number of ties, respectively. The MK test determines whether to reject the null hypothesis (H0) or accept the alternative hypothesis (Ha), where H0: no monotonic trend is present and Ha: a monotonic trend is present. If 1.65 < Z ≤ 1.96, 1.96 < Z ≤ 2.58, Z > 2.58, the trend is significant at the confidence levels of 90%, 95%, and 99%, respectively [38,39,40].
If S > 0 then Z = (S − 1)/VAR (S) 0.5
If S = 0 then Z = 0
If S < 0 then Z = (S + 1)/VAR(S) 0.5
Local (at-site) significance levels for each trend test can be obtained from
where | | denotes the absolute value, and is defined as,
where θ is the random variable, and t is the variable for which the cumulative distribution function should be calculated. If p ≤ α, the existing trend is statistically significant at the significance level of α [41,42].
Sometimes the MK test detects trends because of the serial correlations of time series data, which leads to an increased rejection rate of the null hypothesis [41,43].
Hydrologic time series often have significant serial correlations that can undermine the ability of the MK test to correctly assess the significance of trend [41,43].
In this study, trend-free pre-whitening (TFPW) was used to effectively eliminate the impact of serial correlations on the MK test [41,43,44,45].
This method is defined by the following steps:
1. Calculate the slope of trend using the Sen’s slope estimator [43,44]:
where Q stands for the slope of trend. Qi is the Sen’s slope estimator for each value of i, xj and xk are the numerical values at times j and k (j > k), respectively.
2. There is no trend if Q is equal to zero. Otherwise, it is assumed that the existing trend is monotonic, and the time series data are de-trended as follows:
where Xt′ is the lag-1 autocorrelation of the de-trended time series and Xt is the autocorrelation of time series.
Xt′=Xt − Qt
3. Using the rank correlation coefficient estimator, the lag-1 autocorrelation of the de-trended time series is estimated by replacing the sample data by their ranks as follows [45]:
where rj is the lag-j autocorrelation coefficient, and is the average of the data. Then, the estimated lag-1 autocorrelation is removed from the time series as follows:
4. Adding the removed trend in step 2:
3.3. Spearman’s Rho Test
The Spearman’s Rho test was applied to investigate correlation among all the meteorological variables and ETo estimates from the FPM equation.
The Spearman’s Rho test is defined as [18]:
where ρ is the correlation coefficient of linear regression between series i (the order of the data in the original series) and x (data values) [18]. If |Z| > Zα at a significance level of α, then the null hypothesis of no trend is rejected [18].
Following the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], the confidence levels of 90%, 95%, and 99% were used in this study to evaluate the trends of ETo and meteorological variables.
If there is no mention of confidence level, it meant a confidence level of 95% was adopted. Otherwise, we explicitly mention the confidence levels of 90% and 99% wherever they were used.
4. Results and Discussions
4.1. Comparison of p-Values from the MK and TFPW-MK Tests
Table 2 compares p-values from the MK and TFPW-MK tests for ETo and the 12 meteorological variables in the 18 study sites.

Table 2.
Estimated p-values from the Mann–Kendall (MK) and trend-free pre-whitening Mann–Kendall (TFPW-MK) tests in the 18 study sites.
The p-value is a random variable derived from the distribution of the test statistic to analyze a data set and to test a null hypothesis [41,42]. If p-values from the abovementioned tests are different, but they result in an identical trend for a particular time series (i.e., an insignificant trend or a significant trend at the same confidence level), the cells in Table 2 are highlighted in yellow color. If the two tests yield different trends for a specific time series (i.e., one leads to a significant trend, while the other one results in an insignificant trend, or they both lead to a significant trend but with different confidence levels), the cells are highlighted in red color.
As shown, in each study site, p-values from the MK and TFPW-MK tests are different at least for three meteorological variables (yellow and red cells). Overall, 38% of the obtained p-values from the two tests are different due to the serial correlations of time series data. In each study site, the two tests also lead to different trends for at least one variable (red cells). As shown in Table 2, 15% of the trends from two tests are different. These results indicate that the serial correlation undermine the ability of the MK test to correctly determine the trends and their confidence level [41,43]. Hence, the TFPW method should be applied to eliminate the impact of the serial correlations on the MK test.
As can be seen in Table 2, some meteorological variables are subject to different p-values from the MK and TFPW-MK test more often than others. For example, wind direction (WD), wind speed (WS), and rainfall (P) were flagged for more study sites compared to mean air temperature (Tmean) and minimum air temperature (Tmin). This happens because WD, WS, and P time series have more serial correlations compared to Tmean and Tmin time series. Similar findings were reported in other studies [46,47,48,49].
4.2. Trends of ETo and Meteorological Variables in the Study Sites
Variations of the meteorological variables were assessed in all of the study sites to identify the ones that control the trend of annual mean of ETo. However, herein, the trends are presented only in two sites, Kerman and Qazvin (Figure 2 and Figure 3).
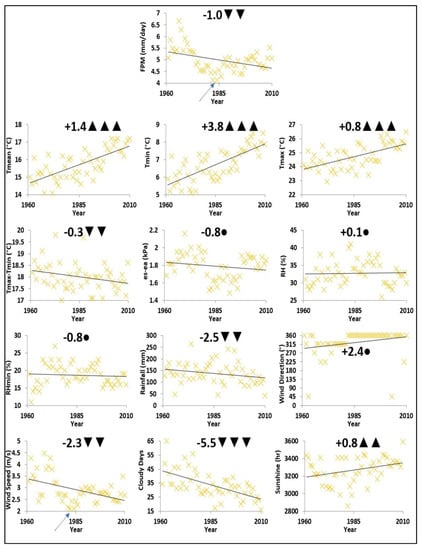
Figure 2.
The 50-year (1960–2010) trends of annually averaged reference evapotranspiration and meteorological variables in Kerman. Circles indicate an insignificant trend. One, two, and three triangles indicate a significant trend at a confidence level of 90%, 95%, and 99%, respectively. The value on the left of triangular symbols shows the increasing/decreasing rate over the 50-year period.
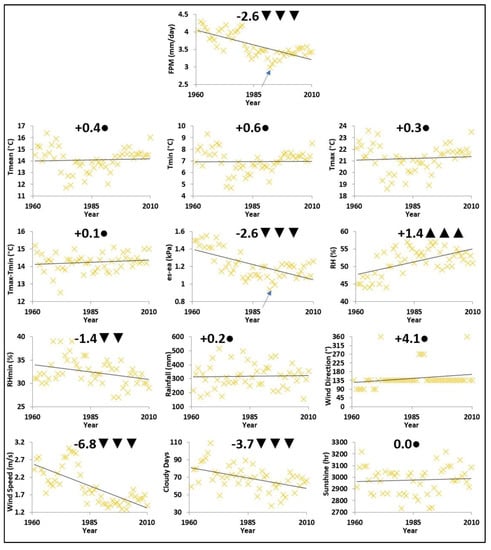
Figure 3.
The 50-year (1960–2010) trends of annually averaged reference evapotranspiration and meteorological variables in Qazvin. Circles indicate an insignificant trend. One, two, and three triangles indicate a significant trend at a confidence level of 90%, 95%, and 99%, respectively. The value on the left of triangular symbols shows the increasing/decreasing rate over the 50-year period.
4.2.1. Kerman
Figure 2 shows the 50-year trends in the annual averages of daily FPM ETo estimates, and meteorological variables including mean (Tmean), minimum (Tmin), and maximum (Tmax) air temperature, the difference between maximum and minimum air temperature (Tmax-Tmin), vapor pressure deficit (es-ea), relative humidity (RH), minimum relative humidity (RHmin), rainfall (P), wind speed and direction (WS and WD), number of cloudy days (CD), and sunshine hours (n) in Kerman.
As can be seen, the significant upward trends in Tmean, Tmin, Tmax, and n (at confidence level 95%) as well as the substantial downward trends in CD, Tmax-Tmin, P, and WS (at confidence level 95%) led to a negative trend (at confidence level 95%) in the FPM ETo estimates.
Although the upward trends in Tmax, Tmin, Tmean, and n could potentially increase ETo, a downward trend in WS and (es-ea) led to a significant decreasing trend in the FPM ETo values. It is worth mentioning that the minimum of both WS and ETo occurred in the same years (i.e., 1982 and 1984) (see the arrows in Figure 2). Similarly, the course of (es-ea) shows lower values in 1982–1986. Thus, WS and to a lesser extent (es-ea) may be the driving force for the variations of ETo in Kerman.
Although CD showed the strongest downward trend among all the meteorological variables in Kerman, it could not capture the variations of ETo as good as WS. Both WS and ETo showed significant trends at a confidence level of 95%, while CD showed a significant trend at a confidence level of 99%.
During 1960–1980s, the north-western wind was prevailing, which blows from the Zangi Abad region with an arid climate into Kerman [50,51]. However, from 1980 until 2010, the northern wind was dominant, which comes from Chatroud region with dry temperate climate [50,51]. Hence, the change in wind direction (WD) reduced the impact of the arid climate in Kerman, and consequently decreased ETo.
The decreasing rate of Tmax-Tmin (−0.3%/decade) was due to a more rapid increase in Tmin (+3.8%/decade) compared to Tmax (+0.8%/decade). Tmin, P, WS, and CD had the highest changes (larger than ±2% per decade), implying climate change in Kerman [50,51]. The lowest P and CD, and the highest Tmax and n values (during the 50-year period) were observed in 2010, which may an indication of drought in this region [50,52,53,54,55,56,57]. These results show the complexity of forces driving the trend of ETo and may highlight importance of considering different ETo models and variables in various climates for local and global studies.
4.2.2. Qazvin
Figure 3 shows the 50-year trends of annually averaged ETo and meteorological variables in Qazvin. As can be seen in Figure 3, the significant upward trend in RH as well as substantial downward trends in es-ea, WS, CD, and RHmin (at the confidence level 95%) led to a negative trend in the FPM ETo estimates. It is worth mentioning that these significant trends reduced ETo and may cause alarming climate change in Qazvin [57,58,59]. During the 50-year study period (1961–2010), Tmax reached its highest value in 2010. It should be noted that the minimum es-ea and ETo occurred in 1991 (see the arrows in Figure 3). The highest decreasing rate was for WS (−6.8%/decade). RH showed an upward trend as a result of decreasing WS and es-ea (Figure 3). The warm dry south-eastern winds (called Raz or Shareh) originated from the arid areas of central Iran (Yazd). They were prevailing from 1961 to 2010 and decreased RHmin in Qazvin [60,61,62,63].
4.3. Trends of ETo and Meteorological Variables in Iran
Table 3 and Figure 4 summarize trends of FPM ETo estimates and meteorological variables in the 18 study sites. The FPM ETo estimates showed significant upward and downward trends, respectively, in 33.3% (28.6% of arid regions vs. 44.4% of semiarid regions) and 22.2% (28.6% of arid regions vs. 22.2% of semiarid regions) of the study sites (Table 3 and Figure 4). Hence, the FPM ETo retrievals had significant variations in most parts of Iran (57.2% of arid regions vs. 66.6% of semiarid regions), which may indicate climatic change signals.

Table 3.
Trends of Agricultural Organization of the United Nation (FAO)-Penman–Monteith (FPM) evapotranspiration (ETo) estimates and 12 meteorological variables in the 18 study sites. U and D represent the significant upward and downward trends, respectively. NS denotes no significant trend.
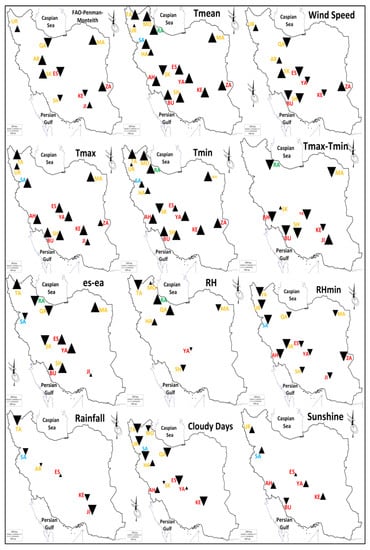
Figure 4.
The average of variations in reference evapotranspiration and meteorological variables in Iran from 1961 to 2010. Big, medium, and small triangles imply significant values at a confidence level of 99%, 95%, and 90%, respectively. Blue, red, yellow, and green colors indicate Mediterranean, arid, semiarid and humid climates, respectively.
Results showed that ETo had a significant positive (negative) trend in the west and east (center) of Iran. WS was the only meteorological variable with the same rising/falling trend.
As shown in Table 3, in eight of the study sites (i.e., 44.4% of sites), there were significant trends in both ETo and Tmean/RHmin/WS. Moreover, both ETo and Tmin/Tmax/es-ea showed significant trends in 33.3% of the study sites. Hence, these meteorological variables could be considered as driving forces to control variations of ETo in Iran.
WS had significant upward and downward trends in 22.2% (14.3% of arid regions vs. 33.3% of semiarid regions) and 33.3% (57.1% of arid regions vs. 22.2% of semiarid regions) of the study sites, respectively. Therefore, significant variations in WS were observed in 55.5% (71.4% of arid regions vs. 55.5% of semiarid regions) of the sites. Table 3 and Figure 2, Figure 3 and Figure 4 indicate that WS is the driving force for the trends of ETo in 55.5% of the study sites. Thus, WS may be the most important variable that controls the variations of ETo, particularly in the arid regions. These findings are further validated by our outcomes in Table 5 (Section 4.6) that lists the three meteorological variables with the highest correlation with ETo. As shown, WS has the highest significant correlation with ETo in all the study sites expect Rasht (RA). Studying the trends of ETo and meteorological variables over longer time periods and more sites across Iran leads to more reliable results.
Table 3 and Figure 4 also showed that there were significant upward trends for Tmean and Tmax in 77.8% (85.7% of arid regions vs. 55.6% of semiarid regions) and 66.7% (100.0% of arid regions vs. 33.3% of semiarid regions) of the study sites, respectively. In Jiroft, Mashhad, and Urmia (3 out of 18 study sites, i.e., 16.7% study sites), there were upward significant trends between ETo and Tmean/Tmax (Table 3). There was a significant downward trend for RHmin in 66.7% (71.4% of arid regions vs. 66.7% of semiarid regions) of the study sites (Figure 4).
Tmax, Tmean, Tmin, es-ea, and n had significant increasing trends, respectively, in 100.0%, 85.7%, 85.7%, 57.1%, and 57.1% of the arid sites. On the other hand, RHmin, Tmax-Tmin, and WS had significant decreasing trends in 71.4%, 57.1%, and 57.1% of the arid sites, respectively. These results indicated that the arid sites were affected more than the semiarid ones by climate change. In most of the semiarid sites, Tmin and Tmean showed increasing, and RHmin and CD indicated decreasing trends.
According to the results, P, WS, and CD showed significant trends in 42.9%, 28.6%, and 28.6% of the arid sites, respectively. WS, Tmin, RHmin, P, and CD had substantial trends in 44.4%, 22.2%, 11.1%, 11.1%, and 11.1% of the semiarid sites, respectively. Furthermore, WS, Tmin, and CD had a rate of more than ±2%/decade in 66.7% (85.7% of arid regions vs. 66.7% of semiarid regions), 66.7% (42.9% of arid regions vs. 77.8% of semiarid regions), and 55.6% (57.1% of arid regions vs. 55.6% of semiarid regions) of the study sites, respectively.
As mentioned above, variations of ETo in each study site are controlled by meteorological variables such as air temperature and wind speed. The Arak and Esfahan sites show contrasting trends in ETo although they are relatively close to each other. This happens because wind speed (which is the dominant controlling variable in both sites) has an increasing (decreasing) trend in Arak (Esfahan). Furthermore, Arak and Esfahan have different climate types. Arak is located in a cold mountainous area, while Esfahan is placed in a hot flat desert.
The focus of this study was to evaluate the annual trends of ETo and meteorological variables over a 50-year period (1961–2010). However, according to Table 3 and Figure 4, we can conclude that their seasonality is important. For example, the annual minimum air temperature, Tmin (that occurs in cold seasons, i.e., fall–winter) had significant increasing trends in 83.4% of sites. While, the annual maximum air temperature, Tmax (which happens in warm seasons, i.e., spring–summer) showed significant rising trends in 66.7% of sites. In addition, the significant downward trends of Tmax-Tmin were observed in 41.5% of sites, whereas its upward trends were seen only in 9.3% of sites. Its significant downward trends were due to the higher increasing rate of Tmin in cold seasons than that of Tmax in warm seasons. These results imply that the cold seasons have more influence on the significant trends than warm seasons. It should be noted that these findings are primitive, and future studies should be directed towards evaluating the seasonal variations of ETo and other climatic variables over long periods.
4.4. Range of Variations of ETo and Meteorological Variables
Figure 5 shows the box plots for the 50-year variations of ETo and meteorological variables in each study site.
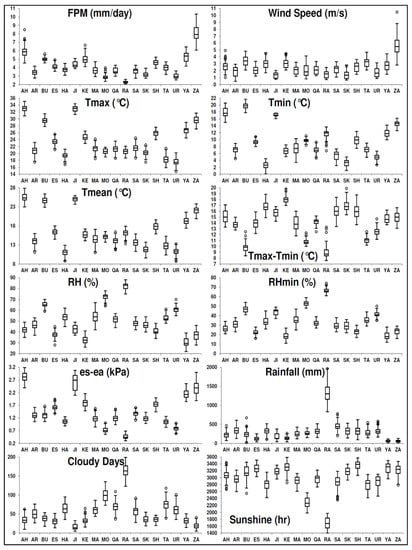
Figure 5.
Statistical boxplots of meteorological variables and reference evapotranspiration in each study site. For each distribution, the horizontal line within the box indicates the median (50% percentile). The upper and lower edges of the box represent the 75% and 25% percentile, respectively. The upper and lower ends of the whiskers represent the maximum and minimum values. Outliers are observations beyond the end of whiskers.
As can be seen, the largest 50-year variations in both ETo and WS happened in Zabol (ZA), which highlighted the significant influence of WS on ETo.
The second highest variations of ETo was seen in Ahvaz (AH). AH had also the highest variations of Tmean compared to the other study sites. Hence, the variations of ETo in Ahvaz can be related to that of Tmean.
The lowest variations in Tmax-Tmin, es-ea, and n values were observed in Rasht (RA), which led to the smallest 50-year change in ETo [9,10]. Most of the outliers occurred in 2010, which signaled a drought condition in different regions of Iran. The FPM ETo values ranged from 2 to 11 mm day−1 in various climates of Iran.
As shown in Equation (1), ETo is affected by the atmospheric vapor pressure deficit (es-ea). As expected, a high positive correlation exists between ETo and es-ea in Figure 5. For example, high values of ETo and es-ea are seen in Zabol (ZA). Moreover, the lowest ETo and es-ea values are observed in Rasht (RA). This happens because the atmospheric demand to water vapor increases as the vapor pressure deficit (es-ea) rises [33]. Positive correlations are also observed between ETo and Tmax, and ETo and n. A larger Tmax leads to more potential for converting soil moisture to water vapor and causes plants to open up their stomata and release more water vapor [33]. Furthermore, larger values of n yield higher Rn (Equation (4)) and ETo (Equation (1)). On the other hand, a negative correlation is found between ETo and RH. The highest ETo and lowest RH values are seen in RA. This is due to the fact that the atmospheric demand for water vapor decreases as RH increases.
4.5. Annual Extremum Values of ETo and Meteorological Variables during the Study Period (1961–2010)
Table 4 shows the years of occurrence of maximum and minimum values of ETo and meteorological variables in each study site during the 50-year study period (i.e., 1961–2010).

Table 4.
The years of occurrence of maximum and minimum values of ETo and meteorological variables in each study site during the 50-year study period. If the annual extremum values of ETo and a particular meteorological variable coincide, they are highlighted in green color.
If the annual extremum values of ETo and a particular meteorological variable coincide, they are highlighted by green color (Table 4).
As can be seen, the maximum of both ETo and WS in Ahvaz, Bushehr, Hamedan, Jiroft, Moghan, Rasht, Sanandaj, Shahrekord, Shiraz, Tabriz, Yazd, and Zabol happened in 1964, 1967, 1967, 2007, 1989, 1975, 1971, 2008, 1981, 1961, 1971, and 1984, respectively.
Similarly, the minimum of ETo and WS in Arak, Esfahan, Jiroft, Kerman, Moghan, Sanandaj, Shahrekord, Yazd, and Zabol occurred in 1966, 1996, 1996, 1984, 1994, 1986, 1968, 1995, and 1968, respectively.
Overall, in 83.3% (all arid, Mediterranean and humid regions and 66.7% of the semiarid regions) of the study sites, annual extremum values of ETo and WS occurred in the same year. These results imply that WS is the primary driver of the variations in ETo in Iran. In addition, the annual extremum values of ETo and RH coincided in 33.3% of the study sites, namely Ahvaz, Arak, Hamedan, Mashhad, Moghan, and Qazvin. Hence, RH is one of the main driving forces for variations of ETo in these study sites.
Figure 6 illustrates the frequency of maximum and minimum values of ETo and meteorological variables (namely Tmean, Tmax, Tmin, Tmax-Tmin, es-ea, P, RH, RHmin, CD, WS, WD, and n) in all the study sites for each year. Higher frequencies are observed in 1972, 1982, and 1992, indicating a large number of study sites reached their maximum and minimum values of ETo and meteorological variables in these years. This happened because 1972, 1982, and 1992 are El Niño-Southern Oscillation (ENSO) years [64,65,66]. The highest frequency during the 50-year period is observed in 2010. This year was considered as a dry year in Iran and most regions of Iran experienced drought alarms [50,52,53,54,55,56,57].
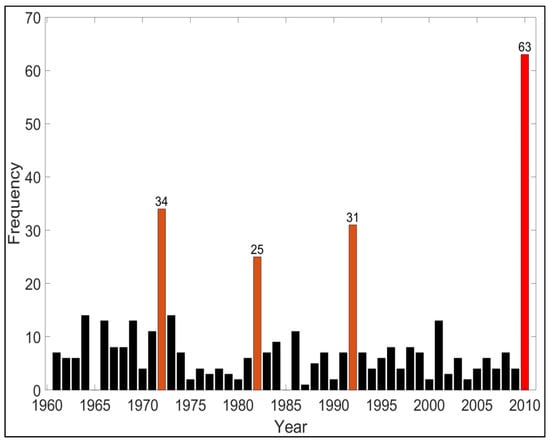
Figure 6.
Frequency of maximum and minimum values of ETo and 12 meteorological variables in 18 study sites for each year.
4.6. Correlation between ETo and Meteorological Variables
Figure 7 shows the correlation coefficient maps among the meteorological variables and reference evapotranspiration for the study sites in arid, Mediterranean, and humid regions. Similarly, Figure 8 indicates the correlation coefficient maps for the sites in semiarid region.
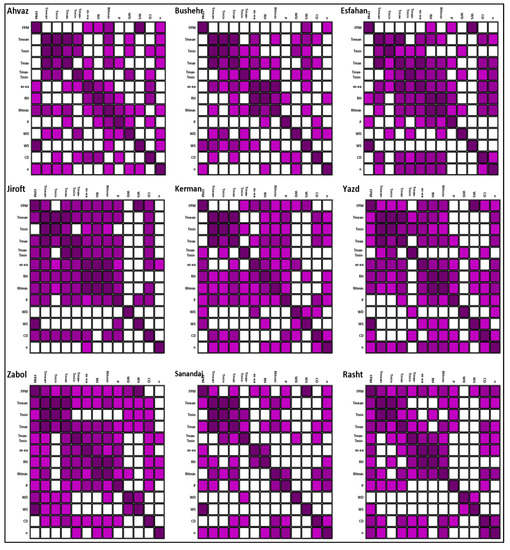
Figure 7.
Spearman’s Rho correlation coefficient (ρ) maps for weather stations located in arid, Mediterranean, and humid regions. Colored boxes show a significant correlation at the confidence level of 95%. Dark, medium, and light purples denote 0.8 ≤ ρ ≤1, 0.5 ≤ ρ < 0.8, and ρ < 0.5, respectively.
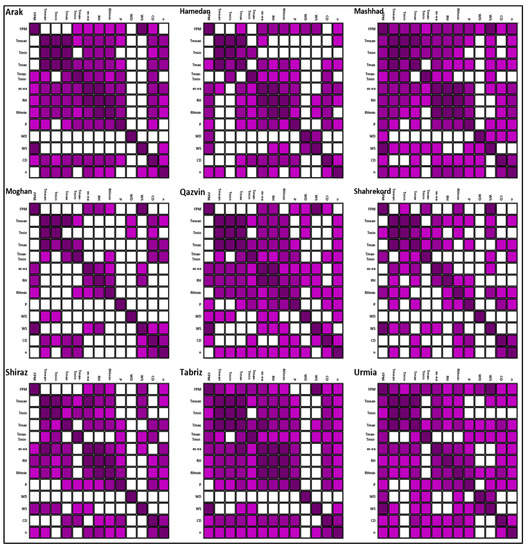
Figure 8.
Spearman’s Rho correlation coefficient (ρ) maps for weather stations located in semiarid region. Colored boxes show a significant correlation at the confidence level of 95%. Dark, medium, and light purples denote 0.8 ≤ ρ ≤ 1, 0.5 ≤ ρ < 0.8, and ρ < 0.5, respectively.
As indicated, WS was the only meteorological variable that had high correlation (ρ ≥ 0.8) with ETo in Ahvaz, Esfahan, Jiroft, Yazd, Zabol, Sanandaj, Arak, Mashhad, Moghan, Qazvin, Shahrekord, Tabriz, and Urmia. These results imply that WS was the driving force for the variations of ETo in most (72.2%) of the study sites in Iran, including 87.5% of arid regions and 77.8% of semiarid regions. This is in agreement with the results obtained by the TFPW-MK test (Table 3 and Figure 4).
WS and WD had the lowest correlation with the other meteorological variables. Hence, these variables may be controlled mainly by human activities such as desertification, land use change, and urban development [67,68,69,70,71,72,73,74,75,76,77,78,79]. The highest correlations were observed among the air temperature-related variables (i.e., Tmean, Tmax, Tmin, Tmax-Tmin) and humidity. In Mashhad and Urmia, the FPM ETo estimates had a good correlation with all of the meteorological variables. The upward trends of Tmin in all the study sites in Iran (except Shahrekord due to its high elevation) indicated a signal of climate change and signaled the need for the optimization of cropping pattern [80,81].
Table 5 shows the total number of meteorological variables in each study site with significant correlations with ETo. It also lists the three meteorological variables that have the highest significant correlation with ETo. As can be seen, ETo had the highest significant correlation with WS in all the sites except Rasht. ETo indicated the largest (the second largest) correlation with Tmax in Rasht (Mahshad, Tabriz, Urmia, and Zabol). According to Table 5, in 66.7% of the study sites, more than five meteorological variables had significant correlations with ETo. This highlights the complexity of the forces driving variations of ETo.

Table 5.
The total number of meteorological variables in each site with significant correlations with ETo, and the three meteorological variables with the highest significant correlation with ETo.
In this study, the TFPW-MK and Spearman’s Rho tests were used to identify significant (at the confidence levels 90%, 95% and 99%) trends of ETo and meteorological variables across Iran. These significant trends are indicative of climate change signals [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. For instance, in the Mashhad site, significant upward (downward) trends were seen for ETo, Tmean, Tmin, Tmax, and es-ea (Tmax – Tmin, WD, RH and RHmin), suggesting climate change alarms. These findings are consistent with those of other studies [82,83,84,85,86,87]. In the Shahrekord site, Tmax – Tmin (Tmean, Tmin, RHmin, and CD) showed significant increasing (decreasing) trends, which can be considered as climate change signals. These findings are also in agreement with those of [8,9,20,21,22,23]. In the Shiraz site, significant upward (downward) trends of ETo, Tmean, Tmin, Tmax, and es-ea (Tmax – Tmin, WS, RH and RHmin) represented signals of climate change [88]. In the Urmia site, growing (reducing) trends of ETo, Tmax, WS, n, Tmean and Tmax (RHmin and CD) signified climate change [89,90,91,92]. Finally, in the Zabol site, upward (downward) trends of ETo, Tmean, Tmin, and WS, and Tmax (RHmin) may be considered as alarms of climate change [84,93].
The FPM ETo retrievals mainly depend on climate variables such as air temperature and humidity, wind speed, and solar radiation. This equation assumes a stomatal resistance of 70 s/m and an albedo of 0.23 for a standard 12 cm grass, and thus it ignores changes in stomatal resistance response to the elevated CO2 and the surface albedo, ultimately causing uncertainty in the ETo estimates. Surface albedo varies with changes in vegetation and soil moisture [94].
Elevated CO2 emission influences plant physiology by diminishing stomatal conductance [95,96,97]. Ignoring changes in the surface albedo and vegetation response to the elevated CO2 emission lead to uncertainty in the FPM ETo estimates and results of this study. A similar uncertainty in the FPM ETo estimates was reported by other studies. For example, Milly and Dunne [98] showed that ignoring the stomatal resistance response to the increased CO2 emission in the FPM equation led to discrepancy between the ETo estimates from climate models and the FPM equation. In a similar effort, Li et al. [99] indicated that the variations in the FPM ETo estimates are only less than 10% for 40% changes in stomatal resistance. However, there are still high uncertainties in the amount of stomatal response to the raised CO2 emission. For example, Domec et al. [100] reported that vegetation responses of pine to long term elevated CO2 were manifested only when soil moisture was at a high level. Future studies should be directed toward evaluating the uncertainties in the FPM ETo estimates with respect to climate change and drought condition [101,102].
5. Conclusions
This study assessed the trends of meteorological variables (namely, mean, minimum, and maximum air temperature, difference between the maximum and minimum air temperature, mean and minimum relative humidity, wind speed and direction, vapor pressure deficit, rainfall, and sunshine hours) and reference evapotranspiration (ETo) in the 18 study sites in different climate regions of Iran.
The effect of meteorological variables on ETo was also evaluated. Using the trend-free pre-whitening Mann–Kendall (TFPW-MK) and Spearman’s Rho tests, wind speed (WS) was found to be the most important variable that controls the trend of ETo in most regions of Iran. Moreover, the increasing/decreasing trends of other meteorological variables (air temperature and humidity, rainfall, wind speed and direction, and sunshine hours) were indicative of climate change in many regions of Iran. The upward trend of minimum air temperature (Tmin) in all of the study sites in Iran (except Shahrekord due to its high elevation) indicated a signal of climate change and signaled the need for the optimization of cropping system. The significant increasing rate of Tmin may lead to a reduction in the growing degree day (GDD), ultimately decreasing the production of strategic and vital crops in future.
WS had significant upward and downward trends in 22.2% and 33.3% of the study sites, respectively. Therefore, significant variations in WS were observed in 55.5% of the investigated regions. The results also indicated that there were significant upward trends for mean air temperature (Tmean) and maximum air temperature (Tmax) in 77.8% and 66.7% of the study regions, respectively. In most of semiarid climates, Tmin and Tmean showed increasing, and minimum relative humidity (RHmin) and cloudy days (CD) indicated decreasing trends. This indicates that arid regions were affected more than semiarid areas by climate change. Precipitation (P), WS, and CD showed significant trends in 42.9%, 28.6%, and 28.6% of arid regions, respectively. However, WS, Tmin, RHmin, P, and CD had significant trends in 44.4%, 22.2%, 11.1%, 11.1%, and 11.1% of semiarid regions, respectively.
In 83.3% (all arid, Mediterranean and humid regions and 66.7% of semiarid regions) of the study sites, ETo and WS reached their maximum and/or minimum in the same year(s). Furthermore, ETo had the highest significant correlation with WS in all the sites except Rasht. This indicates that WS is the primary driver of the variations in ETo in most weather stations of Iran, especially in the years with extremum values of ETo. However, in a number of weather stations, the significant correlation between ETo and other meteorological variables such as Tmax, Tmax-Tmin, es-ea, P, RH, RHmin, and n made it difficult to characterize driving forces for the trend of ETo and signals of climate change. The results of this study highlighted the complexity of forces that drive variations of ETo.
Author Contributions
M.V. conceived and designed the study, performed the calculations, and prepared the original draft. S.M.B. supervised the study and revised the manuscript. M.A.G.S. and M.R.-S. supervised the study. V.P.S. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Xu, Y.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Efficient irrigation water allocation and its impact on agricultural sustainability and water scarcity under uncertainty. J. Hydrol. 2020, 586, 124888. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef] [PubMed]
- McEvoy, D.J.; Huntington, J.L.; Mejia, J.F.; Hobbins, M.T. Improved seasonal drought forecasts using reference evapotranspiration anomalies. Geophys. Res. Lett. 2016, 43, 377–385. [Google Scholar] [CrossRef]
- Yazdi, A.B.; Araghinejad, S.; Nejadhashemi, A.P.; Tabrizi, M.S. Optimal water allocation in irrigation networks based on real time climatic data. Agric. Water Manag. 2013, 117, 1–8. [Google Scholar]
- Meza, F.J. Variability of reference evapotranspiration and water demands Association to ENSO in the Maipo River Basin. Chile. Glob. Planet. Chang. 2005, 47, 212–220. [Google Scholar] [CrossRef]
- Hou, L.G.; Xiao, H.L.; Si, J.H.; Xiao, S.C.; Zhou, M.X.; Yang, Y.G. Evapotranspiration and crop coefficient of Populus euphratica Oliv forest during the growing season in the extreme arid region northwest China. Agric. Water Manag. 2010, 97, 351–356. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M.; Bannayan, M. Spatiotemporal reference evapotranspiration changes in humid and semi-arid regions of Iran: Past trends and future projections. Theor. Appl. Climatol. 2018, 133, 361–375. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M.; Bannayan, M. Quantitative trend, sensitivity and contribution analyses of reference evapotranspiration in some arid environments under climate change. Water Resour. Manag. 2017, 31, 2207–2224. [Google Scholar] [CrossRef]
- Dadaser-Celik, F.; Cengiz, E.; Guzel, O. Trends in reference evapotranspiration in Turkey: 1975–2006. Int. J. Climatol. 2016, 36, 1733–1743. [Google Scholar] [CrossRef]
- Song, Z.W.; Zhang, H.L.; Snyder, R.L.; Anderson, F.E.; Chen, F. Distribution and trends in reference evapotranspiration in the North China Plain. J. Irrig. Drain. Eng. 2010, 136, 240–247. [Google Scholar] [CrossRef]
- Wang, W.; Peng, S.; Yang, T.; Shao, Q.; Xu, J.; Xing, W. Spatial and temporal characteristics of reference evapotranspiration trends in the Haihe River basin, China. J. Hydrol. Eng. 2010, 16, 239–252. [Google Scholar] [CrossRef]
- Darshana; Pandey, A.; Pandey, R.P. Analysing trends in reference evapotranspiration and weather variables in the Tons River Basin in Central India. Stoch. Environ. Res. Risk Assess. 2013, 27, 1407–1421. [Google Scholar] [CrossRef]
- Li, Z.X.; Qi, F.; Liu, W.; Wang, T.T.; Gao, Y.; Wang, Y.M.; Cheng, A.F.; Li, J.G.; Liu, L. Spatial and temporal trend of potential evapotranspiration and related driving forces in Southwestern China, during 1961–2009. Quater. Int. 2014, 336, 127–144. [Google Scholar]
- Li, B.; Chen, F.; Guo, H. Regional complexity in trends of potential evapotranspiration and its driving factors in the Upper Mekong River Basin. Quater. Int. 2015, 380-381, 83–94. [Google Scholar] [CrossRef]
- Gao, G.; Chen, D.; Ren, G.; Chen, Y.; Liao, Y. Spatial and temporal variations and controlling factors of potential evapotranspiration in China: 1956–2000. J. Geograph. Sci. 2006, 16, 3–12. [Google Scholar] [CrossRef]
- Zhang, L.; Traore, S.; Cui, Y.; Luo, Y.; Zhu, G.; Liu, B.; Fipps, G.; Karthikeyan, R.; Singh, V. Assessment of spatiotemporal variability of reference evapotranspiration and controlling climate factors over decades in China using geospatial techniques. Agric. Water Manag. 2019, 213, 499–511. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. Trend analysis of reference evapotranspiration in Northwest China: The roles of changing wind speed and surface air temperature. Hydrol. Process. 2013, 27, 3941–3948. [Google Scholar] [CrossRef]
- Liuzzo, L.; Viola, F.; Noto, L.V. Wind speed and temperature trends impacts on reference evapotranspiration in Southern Italy. Theor. Appl. Climatol. 2016, 123, 43–62. [Google Scholar] [CrossRef]
- Khanmohammadi, N.; Rezaie, H.; Montaseri, M.; Behmanesh, J. The application of multiple linear regression method in reference evapotranspiration trend calculation. Stoch. Environ. Res. Risk Assess. 2018, 32, 661–673. [Google Scholar] [CrossRef]
- Tabari, H.; Aeini, A.; Talaee, P.H.; Some’e, B.S. Spatial distribution and temporal variation of reference evapotranspiration in arid and semi-arid regions of Iran. Hydrol. Process. 2012, 26, 500–512. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Hosseinzadeh Talaee, P. Temporal trends and spatial characteristics of drought and rainfall in arid and semiarid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Kousari, M.R.; Ahani, H. An investigation on reference crop evapotranspiration trend from 1975 to 2005 in Iran. Int. J. Climatol. 2012, 32, 2387–2402. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend analysis in reference evapotranspiration using Mann-Kendall and Spearman’s Rho tests in arid regions of Iran. Water Res. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef]
- Bonell, M.; Bruijnzeel, L.A. Forests, Water and People in the Humid Tropics: Past, Present and Future Hydrological Research for Integrated Land and Water Management; Cambridge University Press: London, UK, 2005. [Google Scholar]
- Bormann, H. Sensitivity analysis of 18 different potential evapotranspiration models to observed climatic change at German climate stations. Clim. Chang. 2011, 104, 729–753. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36, L20403. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of China during 1956–2015. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Hong, H. Assessing the effect of climate change on reference evapotranspiration in China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1871–1881. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, W.; Shao, Q.; Xing, W.; Ding, Y.; Fu, J. The response of reference evapotranspiration to climate change in Xinjiang, China: Historical changes, driving forces, and future projections. Int. J. Climatol. 2020, 40, 235–254. [Google Scholar] [CrossRef]
- Lin, P.; He, Z.; Du, J.; Chen, L.; Zhu, X.; Li, J. Impacts of climate change on reference evapotranspiration in the Qilian Mountains of China: Historical trends and projected changes. Int. J. Climatol. 2018, 38, 2980–2993. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Bakhtiari, B.; Ghahraman, N.; Liaghat, A.M.; Hoogenboom, G. Evaluation of reference evapotranspiration models for a semiarid environment using lysimeter measurements. J. Agric. Sci. Technol. 2011, 13, 223–237. [Google Scholar]
- Razzaghi, F.; Sepaskhah, A.R. Assessment of nine different equations for ETo estimation using lysimeter data in a semi-arid environment. Arch. Agron. Soil Sci. 2010, 56, 1–12. [Google Scholar] [CrossRef]
- Razzaghi, F.; Sepaskhah, A.R. Calibration and validation of four common ET0 estimation equations by lysimeter data in a semi-arid environment. Arch. Agron. Soil Sci. 2012, 58, 303–319. [Google Scholar] [CrossRef]
- Yarami, N.; Kamgar-Haghighi, A.A.; Sepaskhah, A.R.; Zand-Parsa, S. Determination of the potential evapotranspiration and crop coefficient for saffron using a water-balance lysimeter. Arch. Agron. Soil Sci. 2011, 57, 727–740. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 163–171. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: Oxford, UK, 1975. [Google Scholar]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Sarr, M.A.; Gachon, P.; Seidou, O.; Bryant, C.R.; Ndione, J.A.; Comby, J. Inconsistent linear trends in Senegalese rainfall indices from 1950 to 2007. Hydrol. Sci. J. 2015, 60, 1538–1549. [Google Scholar] [CrossRef]
- Park, K.I. Fundamentals of Probability and Stochastic Processes with Applications to Communications; Springer: Berlin, Germany, 2018. [Google Scholar]
- Thiel, H. A rank-invariant method of linear and polynomial regression analysis (Part 3). In Proceedings of the Koninalijke Nederlandse Akademie van Weinenschatpen A, Amsterdam, The Netherlands, 25 February 1950; pp. 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Salas, J.D.; Delleur, J.W.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series; Water Resources Publication: Littleton, CO, USA, 1980. [Google Scholar]
- Coumou, D.; Robinson, A.; Rahmstorf, S. Global increase in record-breaking monthly-mean temperatures. Clim. Chang. 2013, 118, 771–782. [Google Scholar] [CrossRef]
- Blain, G.C. Removing the influence of the serial correlation on the Mann-Kendall test. Rev. Bras. Meteorol. 2014, 29, 161–170. [Google Scholar] [CrossRef]
- Henry, R.C.; Chang, Y.S.; Spiegelman, C.H. Locating nearby sources of air pollution by nonparametric regression of atmospheric concentrations on wind direction. Atmos. Environ. 2002, 36, 2237–2244. [Google Scholar] [CrossRef]
- Sarmiento, C.; Valencia, C.; Akhavan-Tabatabaei, R. Copula autoregressive methodology for the simulation of wind speed and direction time series. J. Wind Eng. Ind. Aerod. 2018, 174, 188–199. [Google Scholar] [CrossRef]
- Fitchett, J.M.; Grab, S.W.; Thompson, D.I.; Roshan, G. Spatio-temporal variation in phenological response of citrus to climate change in Iran: 1960–2010. Agric. For. Meteorol. 2014, 198, 285–293. [Google Scholar] [CrossRef]
- Shirvani, A. Change point analysis of mean annual air temperature in Iran. Atmos. Res. 2015, 160, 91–98. [Google Scholar] [CrossRef]
- Ashraf, B.; Yazdani, R.; Mousavi-Baygi, M.; Bannayan, M. Investigation of temporal and spatial climate variability and aridity of Iran. Theor. Appl. Climatol. 2014, 118, 35–46. [Google Scholar] [CrossRef]
- Bazrafshan, J.; Nadi, M.; Ghorbani, K. Comparison of Empirical Copula-Based Joint Deficit Index (JDI) and Multivariate Standardized Precipitation Index (MSPI) for Drought Monitoring in Iran. Water Resour. Manag. 2015, 29, 2027–2044. [Google Scholar] [CrossRef]
- Kehl, M. Quaternary climate change in Iran—the state of knowledge. Erdkunde 2009, 63, 1–17. [Google Scholar] [CrossRef]
- Kousari, M.R.; Dastorani, M.T.; Niazi, Y.; Soheili, E.; Hayatzadeh, M.; Chezgi, J. Trend detection of drought in arid and semi-arid regions of Iran based on implementation of reconnaissance drought index (RDI) and application of non-parametrical statistical method. Water Resour. Manag. 2014, 28, 1857–1872. [Google Scholar] [CrossRef]
- Tabari, H.; Nikbakht, J.; Talaee, P.H. Identification of trend in reference evapotranspiration series with serial dependence in Iran. Water Res. Manag. 2012, 26, 2219–2232. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Nassaji Zavareh, M. Effects of adjustment for non-climatic discontinuities on determination of temperature trends and variability over Iran. Int. J. Climatol. 2014, 34, 2079–2096. [Google Scholar] [CrossRef]
- Soltani, S.; Saboohi, R.; Yaghmaei, L. Rainfall and rainy days trend in Iran. Climat. Chang. 2012, 110, 187–213. [Google Scholar] [CrossRef]
- Soltani, M.; Laux, P.; Kunstmann, H.; Stan, K.; Sohrabi, M.M.; Molanejad, M.; Sabziparvar, A.A.; SaadatAbadi, A.R.; Ranjbar, F.; Rousta, I.; et al. Assessment of climate variations in temperature and precipitation extreme events over Iran. Theor. Appl. Climatol. 2016, 126, 775–795. [Google Scholar] [CrossRef]
- Hamzeh Nezhad, M.; Rabbani, M.; Torabi, T. The role of wind in human health in Islamic medicine and its effect in layout and structure of Iranian classic towns. Naghsh Jahan 2015, 5, 43–57. [Google Scholar]
- Pirnia, M.K. Stylistics of Iranian Architecture; Sorush Danesh: Tehran, Iran, 2008. [Google Scholar]
- Amiraslani, F.; Dragovich, D. Cross-sectoral and participatory approaches to combating desertification: The Iranian experience. Natur. Resour. Forum 2010, 34, 140–154. [Google Scholar] [CrossRef]
- Amiraslani, F.; Dragovich, D. Combating desertification in Iran over the last 50 years: An overview of changing approaches. J. Environ. Manag. 2011, 92, 1–13. [Google Scholar] [CrossRef]
- Roghani, R.; Soltani, S.; Bashari, H. Influence of southern oscillation on autumn rainfall in Iran (1951–2011). Theor. Appl. Climatol. 2016, 124, 411–423. [Google Scholar] [CrossRef]
- Pourasghar, F.; Oliver, E.C.; Holbrook, N.J. Modulation of wet-season rainfall over Iran by the Madden–Julian Oscillation, Indian Ocean Dipole and El Niño–Southern Oscillation. Int. J. Climatol. 2019, 39, 4029–4040. [Google Scholar] [CrossRef]
- Grove, R.; Adamson, G. El Niño in World History; Palgrave Macmillan: London, UK, 2018. [Google Scholar]
- Azami, M.; Mirzaee, E.; Mohammadi, A. Recognition of urban unsustainability in Iran (case study: Sanandaj City). Cities 2015, 49, 159–168. [Google Scholar] [CrossRef]
- Barzani, M.M.; Khairulmaini, O.S. Desertification risk mapping of the Zayandeh Rood Basin in Iran. J. Earth Sys. Sci. 2013, 122, 1269–1282. [Google Scholar] [CrossRef]
- Emadodin, I.; Bork, H.R. Degradation of soils as a result of long-term human-induced transformation of the environment in Iran: An overview. J. Land Use Sci. 2012, 7, 203–219. [Google Scholar] [CrossRef]
- Hashemimanesh, M.; Matinfar, H. Evaluation of desert management and rehabilitation by petroleum mulch base on temporal spectral analysis and field study (case study: Ahvaz, Iran). Ecol. Eng. 2012, 46, 68–74. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Sadrafshari, S.; Fayzolahpour, M. Desertification hazard zoning in Sistan Region, Iran. J. Geograph. Sci. 2012, 22, 885–894. [Google Scholar] [CrossRef]
- Jafari, R.; Bakhshandehmehr, L. Quantitative mapping and assessment of environmentally sensitive areas to desertification in central Iran. Land Degrad. Dev. 2016, 27, 108–119. [Google Scholar] [CrossRef]
- Khaledian, Y.; Kiani, F.; Ebrahimi, S. The effect of land use change on soil and water quality in northern Iran. J. Mount. Sci. 2012, 9, 798–816. [Google Scholar] [CrossRef]
- Malmir, M.; Zarkesh, M.M.K.; Monavari, S.M.; Jozi, S.A.; Sharifi, E. Urban development change detection based on Multi-Temporal Satellite Images as a fast tracking approach—A case study of Ahwaz County, southwestern Iran. Environ. Monit. Assess. 2015, 187, 1–10. [Google Scholar] [CrossRef]
- Sadeghiravesh, M.H.; Ahmadi, H.; Zehtabian, G. Application of sensitivity analysis for assessment of de-desertification alternatives in the central Iran by using Triantaphyllou method. Environ. Monit. Assess. 2011, 179, 31–46. [Google Scholar] [CrossRef]
- Sepehr, A.; Hassanli, A.M.; Ekhtesasi, M.R.; Jamali, J.B. Quantitative assessment of desertification in south of Iran using MEDALUS method. Environ. Monit. Assess. 2007, 134, 243–254. [Google Scholar] [CrossRef] [PubMed]
- Tabari, H.; Somee, B.S.; Zadeh, M.R. Testing for long-term trends in climatic variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspiration in the western half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Nadoushani, S.M.; Willems, P.; Marchetto, A. A survey of temperature and precipitation based aridity indices in Iran. Quater. Int. 2014, 345, 158–166. [Google Scholar] [CrossRef]
- Eyshi Rezaie, E.; Bannayan, M. Rainfed wheat yields under climate change in northeastern Iran. Meteorol. Appl. 2012, 19, 346–354. [Google Scholar] [CrossRef]
- Eyshi Rezaei, E.; Webber, H.; Gaiser, T.; Naab, J.; Ewert, F. Heat stress in cereals: Mechanisms and modelling. Europ. J. Agron. 2015, 64, 98–113. [Google Scholar] [CrossRef]
- Banimahd, S.A.; Khalili, D.; Kamgar-Haghighi, A.A.; Zand-Parsa, S. In-depth investigation of precipitation-based climate change and cyclic variation in different climatic zones. Theor. Appl. Climatol. 2014, 116, 565–583. [Google Scholar] [CrossRef]
- Farhangfar, S.; Bannayan, M.; Khazaei, H.R.; Baygi, M.M. Vulnerability assessment of wheat and maize production affected by drought and climate change. Int. J. Disaster Risk Reduct. 2015, 13, 37–51. [Google Scholar] [CrossRef]
- Koocheki, A.; Nasiri, M.; Kamali, G.A.; Shahandeh, H. Potential impacts of climate change on agroclimatic indicators in Iran. Arid Land Res. Manag. 2006, 20, 245–259. [Google Scholar] [CrossRef]
- Lashkari, A.; Alizadeh, A.; Rezaei, E.E.; Bannayan, M. Mitigation of climate change impacts on maize productivity in northeast of Iran: A simulation study. Mitigat. Adapt. Strateg. Glob. Chang. 2012, 17, 1–16. [Google Scholar] [CrossRef]
- Moradi, R.; Koocheki, A.; Mahallati, M.N. Adaptation of maize to climate change impacts in Iran. Mitigat. Adapt. Strateg. Glob. Chang. 2014, 19, 1223–1238. [Google Scholar] [CrossRef]
- Soltani, E.; Soltani, A. Climatic change of Khorasan, North-East of Iran, during 1950–2004. Res. J. Environ. Sci. 2008, 2, 316–322. [Google Scholar]
- Abolverdi, J.; Ferdosifar, G.; Khalili, D.; Kamgar-Haghighi, A.A.; Haghighi, M.A. Recent trends in regional air temperature and precipitation and links to global climate change in the Maharlo watershed, Southwestern Iran. Meteorol. Atmos. Physic. 2014, 126, 177–192. [Google Scholar] [CrossRef]
- Delju, A.H.; Ceylan, A.; Piguet, E.; Rebetez, M. Observed climate variability and change in Urmia Lake Basin, Iran. Theor. Appl. Climatol. 2013, 111, 285–296. [Google Scholar] [CrossRef]
- Fathian, F.; Dehghan, Z.; Bazrkar, M.H.; Eslamian, S. Trends in hydrological and climatic variables affected by four variations of the Mann-Kendall approach in Urmia Lake basin, Iran. Hydrol. Sci. J. 2016, 61, 892–904. [Google Scholar] [CrossRef]
- Fathian, F.; Morid, S.; Kahya, E. Identification of trends in hydrological and climatic variables in Urmia Lake basin, Iran. Theore. Appl. Climatol. 2014, 119, 443–464. [Google Scholar] [CrossRef]
- Malekian, A.; Kazemzadeh, M. Spatio-temporal analysis of regional trends and shift changes of autocorrelated temperature series in Urmia Lake Basin. Water Resour. Manag. 2016, 30, 785–803. [Google Scholar] [CrossRef]
- Valizadeh, J.; Ziaei, S.M.; Mazloumzadeh, S.M. Assessing climate change impacts on wheat production (a case study). J. Saudi Soci. Agric. Sci. 2014, 13, 107–115. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, W.C.; Fang, X.; Ye, Y.; Zheng, J. Agriculture development induced surface albedo changes and climatic implications across northeastern China. Chin. Geogr. Sci. 2012, 22, 264–277. [Google Scholar] [CrossRef]
- Sun, S.; Chen, H.; Sun, G.; Ju, W.; Wang, G.; Li, X.; Yan, G.; Gao, C.; Huang, J.; Zhang, F.; et al. Attributing the changes in reference evapotranspiration in Southwestern China using a new separation method. J. Hydrometeorol. 2017, 18, 777–798. [Google Scholar] [CrossRef]
- Field, C.B.; Jackson, R.B.; Mooney, H.A. Stomatal responses to increased CO2: Implications from the plant to the global scale. Plant Cell Environ. 1995, 18, 1214–1225. [Google Scholar] [CrossRef]
- Betts, R.A.; Boucher, O.; Collins, M.; Cox, P.M.; Falloon, P.D.; Gedney, N.; Hemming, D.L.; Huntingford, C.; Jones, C.D.; Sexton, D.M.; et al. Projected increase in continental runoff due to plant responses to increasing carbon dioxide. Nature 2007, 448, 1037–1041. [Google Scholar] [CrossRef]
- Milly, P.C.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Chang. 2016, 6, 946–949. [Google Scholar] [CrossRef]
- Li, X.; Kang, S.; Niu, J.; Huo, Z.; Liu, J. Improving the representation of stomatal responses to CO2 within the Penman-Monteith model to better estimate evapotranspiration responses to climate change. J. Hydrol. 2019, 572, 692–705. [Google Scholar] [CrossRef]
- Domec, J.C.; Palmroth, S.; Ward, E.; Maier, C.A.; Thérézien, M.; Oren, R. Acclimation of leaf hydraulic conductance and stomatal conductance of Pinus taeda (loblolly pine) to long-term growth in elevated CO2 (free-air CO2 enrichment) and N-fertilization. Plant Cell Environ. 2009, 32, 1500–1512. [Google Scholar] [CrossRef] [PubMed]
- Almazroui, M.; Saeed, F.; Saeed, S.; Islam, M.N.; Ismail, M.; Klutse, N.A.B.; Siddiqui, M.H. Projected Change in Temperature and Precipitation Over Africa from CMIP6. Earth Syst. Environ. 2020, 4, 455–475. [Google Scholar] [CrossRef]
- Almazroui, M.; Saeed, S.; Saeed, F.; Islam, M.N.; Ismail, M. Projections of Precipitation and Temperature over the South Asian Countries in CMIP6. Earth Syst. Environ. 2020, 4, 297–320. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).