Mass Transport of Gases across the Air–Water Interface: Implications for Aldehyde Emissions in the Uinta Basin, Utah, USA

Abstract

When they dissolve in water, aldehydes become hydrated to gem-diols: $\mathrm{R}-\mathrm{COH}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow \mathrm{RCH}{\left(\mathrm{OH}\right)}_2$. Such reactions can complicate air–water transport models. Because of a persistent belief that the gem-diols do not exist in the vapor phase, typical models do not allow them to pass through the air–water interface, but in fact, they do. Therefore, transport models that allow both molecular forms to exist in both phases and to pass through the interface are needed. Such a model is presented here as a generalization of Whitman’s two-film model. Since Whitman’s model has fallen into disuse, justification of its use is also given. There are hypothetical instances for which the flux predicted by the current model is significantly larger than the flux predicted when models forbid the diol form from passing through the interface. However, for formaldehyde and acetaldehyde, the difference is about 6% and 2%, respectively.

1. Introduction

Exceptionally high ozone concentrations occur during many winters in the Uinta basin of eastern Utah [1,2,3,4,5]. The physics and chemistry of winter ozone formation given the prevailing emissions and meteorology are not completely understood. For example, models routinely underestimate ozone concentrations. Some models suggest that there is a missing source of formaldehyde and other carbonyls [6,7,8]. This has led us to consider other possible carbonyl sources [9], including produced water evaporation ponds [10,11,12] and the snowpack [13,14,15], and to an examination of models of the transport of aldehydes across the air–water interface. Ice crystals in the environment have a surface liquid-like layer. To an initial approximation, transport between snow and the atmosphere resembles transport across the air–liquid water interface [16,17,18]. This paper is a result of that study.

The theory of mass transport of volatile gases between a liquid and a vapor phase is well developed but becomes more complex when the gas undergoes a reaction in the aqueous phase. Examples include the following reactions:

$$\begin{array}{cc}formaldehyde\leftrightarrow methanediol& \mathrm{HCHO}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow {\mathrm{H}}_2\mathrm{C}{\left(\mathrm{OH}\right)}_2\end{array}$$

$$\begin{array}{cc}acetaldehyde\leftrightarrow 1,1 ethanediol& {\mathrm{CH}}_3\mathrm{COH}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow {\mathrm{CH}}_3\mathrm{CH}{\left(\mathrm{OH}\right)}_2\end{array}$$

$$carbon dioxide \leftrightarrow carbonic acid \leftrightarrow bicarbonate\leftrightarrow carbonate$$

$${\mathrm{CO}}_2+{\mathrm{H}}_2\mathrm{O}\leftrightarrow \mathrm{HO}\left(\mathrm{CO}\right)\mathrm{OH}\leftrightarrow \mathrm{HC}{O}_3^{-}+H^{+}\leftrightarrow \mathrm{C}{O}_3^{2-}+2H^{+}$$

$$dissociation of \mathrm{HCl} \left(and other acids\right)\hspace{1em}\mathrm{HCl}\leftrightarrow {\mathrm{H}}^{+}+{\mathrm{Cl}}^{-}$$

I will represent all these reactions as 1 ↔ 2, where 1 represents the compound on the left that dominates in the vapor phase. Based on the assumption that the diols, carbonic acid, bicarbonate, carbonate, and chloride do not exist in the vapor phase, it has always been assumed that when form 1 reacts in the aqueous phase to give form 2, then 2 must convert back to 1 while still in the aqueous phase before it can cross into the vapor phase. The primary purpose of this paper is to examine models that challenge this assumption. Of course, the ions do not exist in the vapor phase, but the diols do. Many measurements have detected methanediol vapor in equilibrium with aqueous formaldehyde solutions [19,20]. Methanediol hydrolysis is catalyzed by water and other small molecules, and methanediol has extreme stability in isolation [21,22,23,24]. 1,1-Ethanediol in the gas phase has not been studied experimentally, but its reactions are probably similar to methanediol. Once we accept the gas-phase existence of these molecules, we also have to assume that they cross the air–water interface in the diol form. In this paper, I generalize existing models to the case in which both compounds are assumed to exist in both phases and are also assumed to cross the interface. I apply these models to formaldehyde and acetaldehyde transport across the air–water interface.

Interestingly, the existence of carbonic acid molecules in the gas phase has also been established, and they are also predicted to be highly stable in isolation [25,26,27,28,29,30,31,32]; thus, it is also safe to assume that they cross the air–water interface. However, at the acidities expected in the environment, only a small fraction of dissolved carbon dioxide is found in the carbonic acid form; much more is present as free carbon dioxide, bicarbonate, or carbonate. Therefore, when we write 1 ↔ 2 for the carbon dioxide system, we can assume that form 1 is free carbon dioxide, while form 2 is bicarbonate plus carbonate, and we can ignore carbonic acid altogether. Whenever form 2 is ionic, it is appropriate to assume that it does not cross the interface and that existing models suffice. New models are needed for the aldehydes, but not for carbon dioxide or hydrogen chloride.

Mass-transfer theory of transport across the air–water interface has been under development for nearly a century, beginning with Whitman [33] and his “two-film” model. Later decades saw the development of “surface renewal” and “penetration” models [34,35,36,37,38,39] and arguments based on the Schmidt number [40,41,42]. The Whitman model is relatively simple and today is used mainly only for pedagogy [43]. However, it was the first model to postulate that to cross the interface, solute molecules must traverse two separate, stagnant films, one on each side of the interface, under conditions in which transport only occurs by molecular diffusivity. It predicts mass-transfer coefficients that scale with molecular diffusivity D to the first power. Later models are more in line with experiments with D^1/2 or D^2/3 scaling laws [44,45,46,47,48,49,50,51,52]. There have also been generalizations that allow both for irreversible [37,53] and reversible [54,55] aqueous phase reactions. However, to the best of my knowledge, no one has ever studied models that allow for reactions in both phases and for both forms to cross the interface.

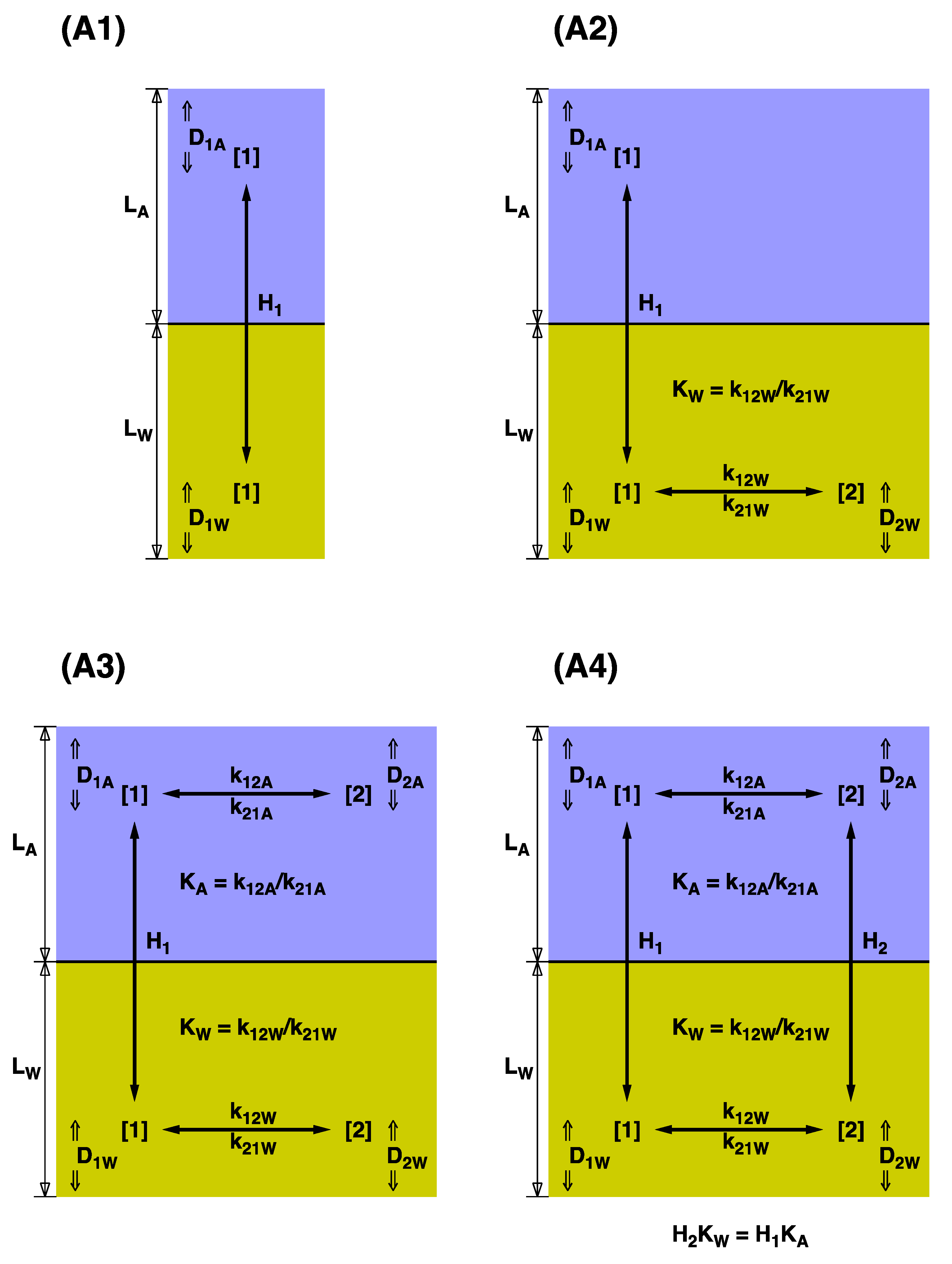
2. Description of the Models

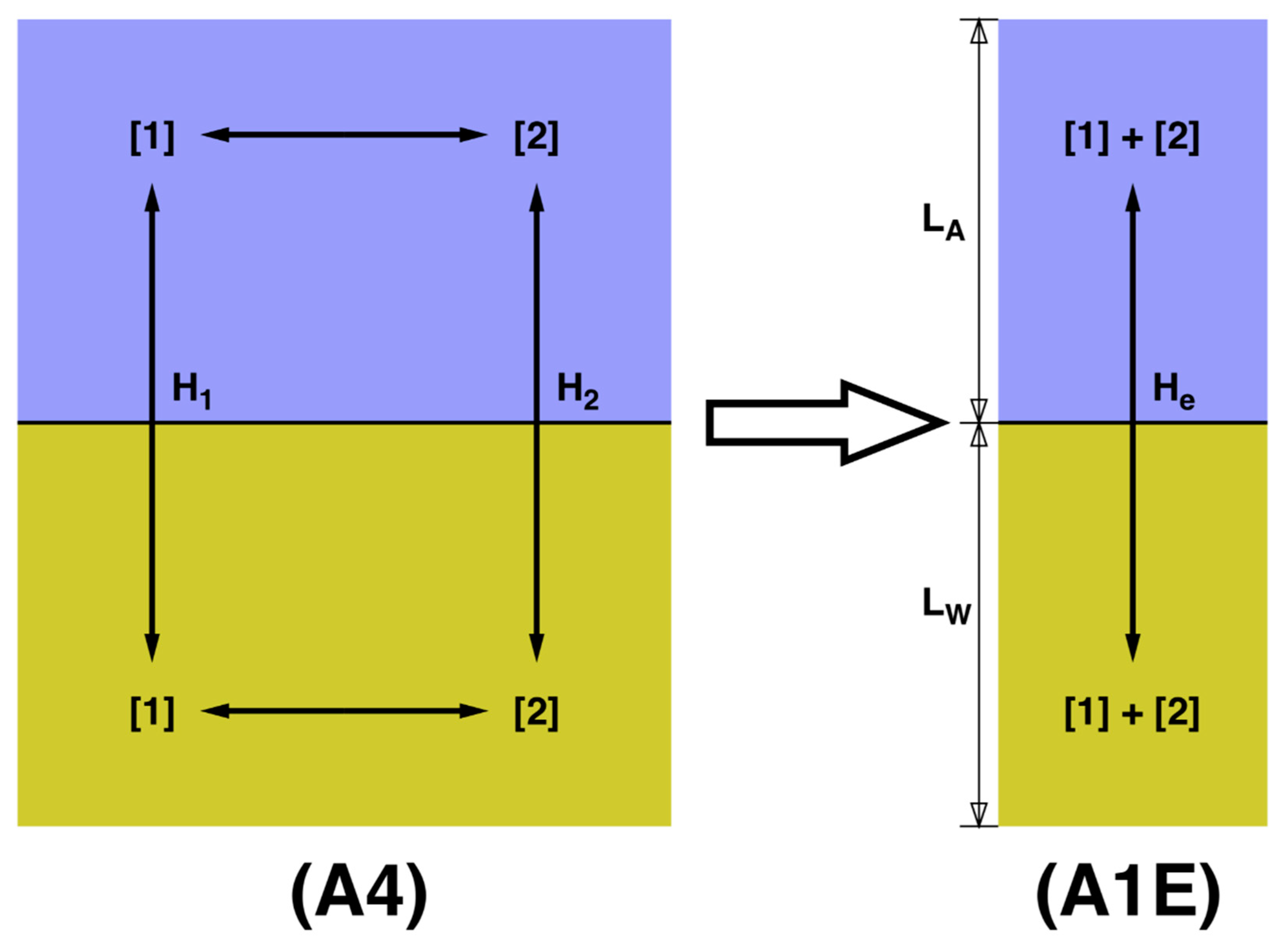
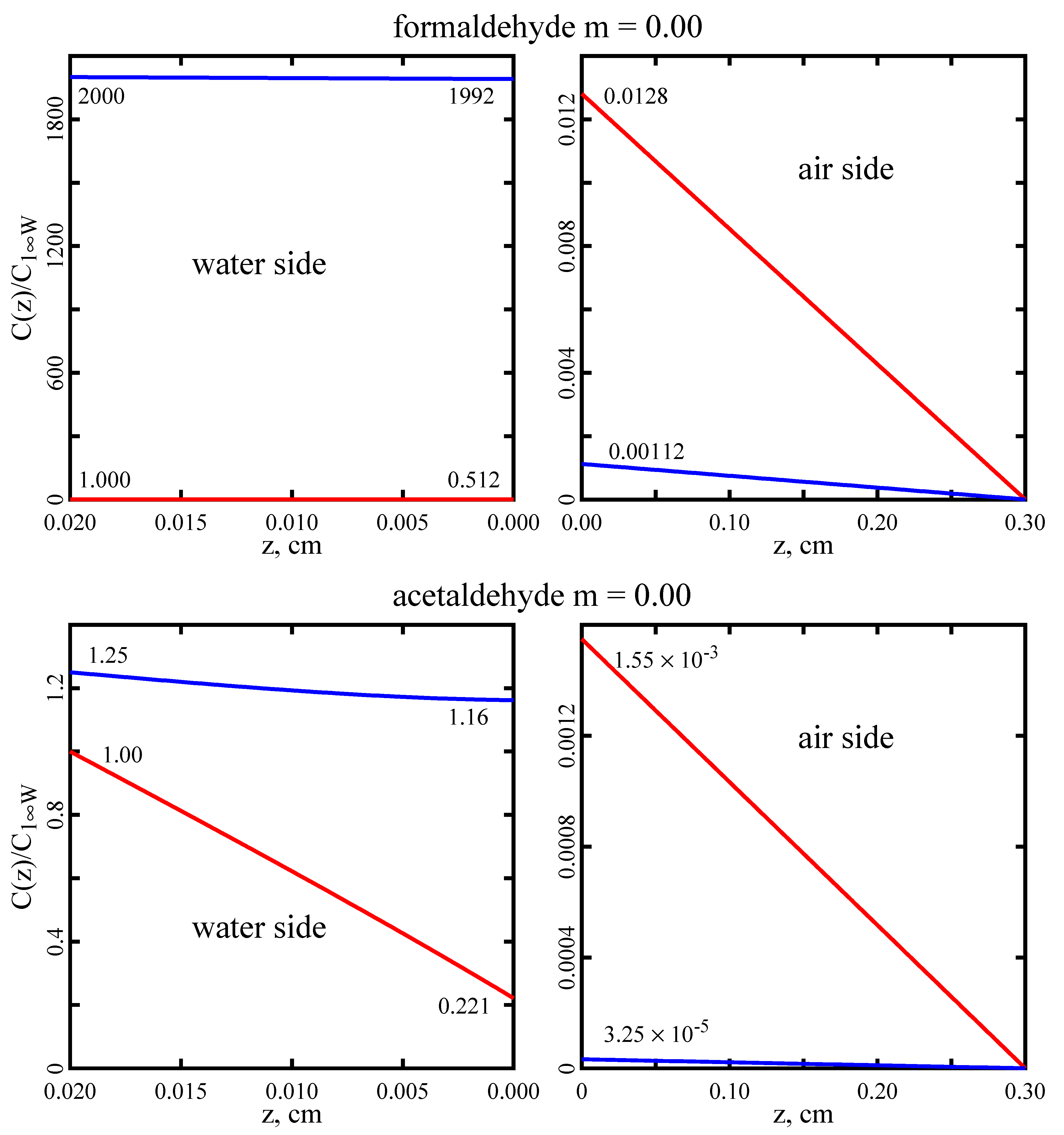
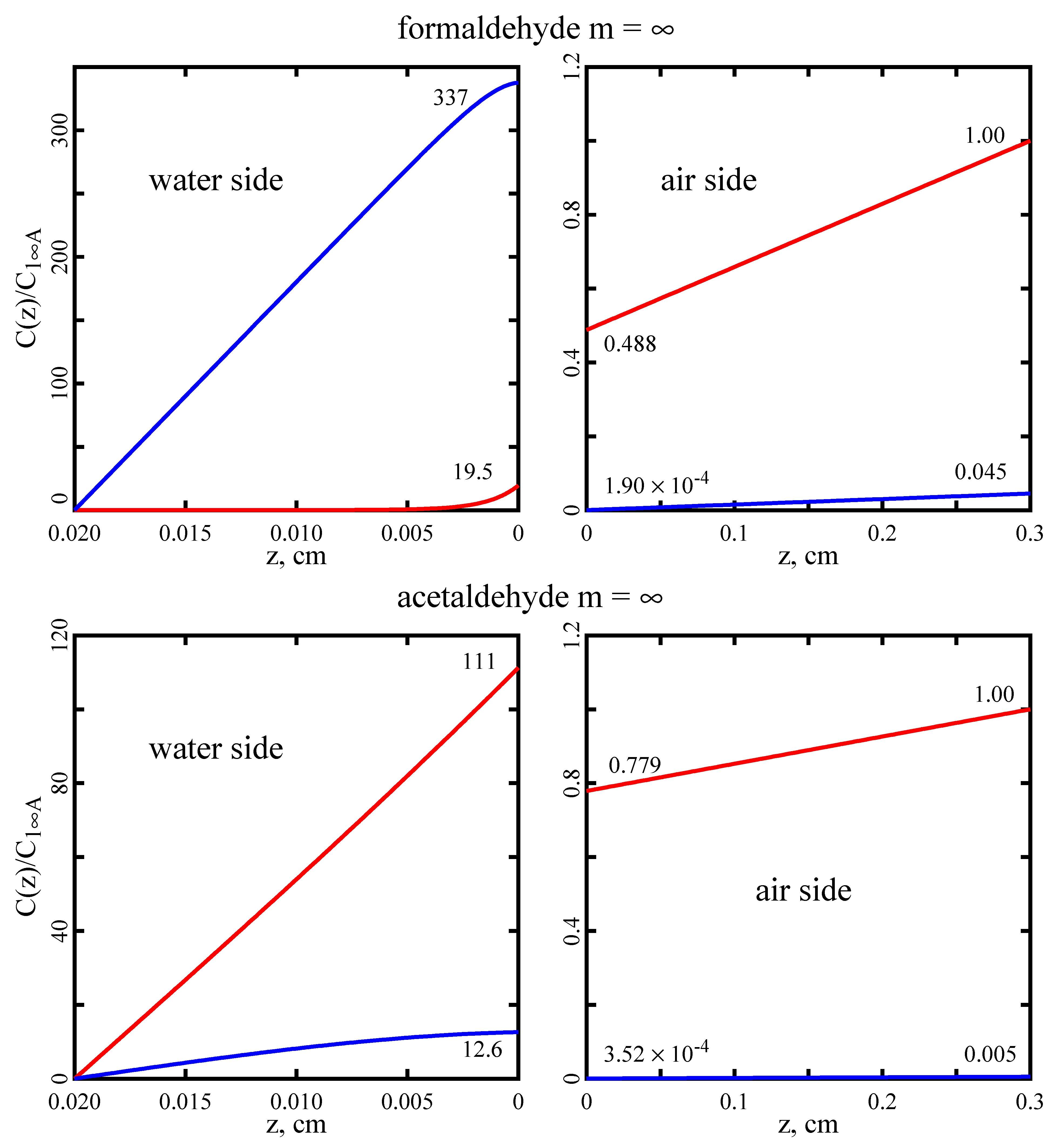
In this paper, I generalize the Whitman model [33] to the case of two reacting species. Five separate models, represented in Figure 1 and Figure 2, will be discussed in this paper. Whitman’s model [33] is denoted A1. It models a single compound able to move between the water and air phases. Model A2 was first introduced by Hoover and Berkshire [54]. It permits the reversible reaction 1 ↔ 2 only in the water phase, and only form 1 is able to move across the barrier and exist in the vapor phase. Model A3 assumes that 1 and 2 react reversibly in both phases, but still, only form 1 is able to cross the barrier. Model A4 allows for the reaction in both phases, and it allows for both compounds to cross the barrier. To the best of my knowledge, models A3 and A4 have never been presented in the literature. A fifth model is considered when, without ignoring the existence of both forms of the compound, our analytical techniques do not permit us to distinguish them, and we treat 1 + 2 as a blended compound. Let A1E refer to the model designed to be a single-compound effective representation of A4. Below, I give best techniques for designing an appropriate A1E model.

The steady-state reaction–diffusion equations can be solved exactly for all models A1 through A4 if we restrict ourselves to generalizations of the Whitman model [33]. Numerical treatments of model A2 in the context of surface renewal and other more modern models have been considered by Glasscock and Rochelle [55]. Despite yielding exact solutions, each succeeding model is algebraically and numerically more complex than the previous. Therefore, the exact solutions will only be summarized here; details and derivations are given in the Supplementary Material.

3. Definition of Variables

Table 1. List of system and concentration variables.

Notation	Description	Units
SYSTEM VARIABLES
$D_{1A}, D_{2A}, D_{1W}, D_{2W}{}_{}^{}$	Molecular diffusivities	${\mathrm{cm}}^2{\mathrm{s}}^{-1}$
$k_{12A}, k_{21A}, k_{12W}, k_{21W}{}_{}^{}$	Reaction rate constants	${\mathrm{s}}^{-1}$
$K_A, K_W{}_{}^{}$	Equilibrium constants	dimensionless
$H_1, H_2{}_{}^{}$	Intrinsic Henry’s constants	dimensionless
$H_e$	Effective Henry’s constant	dimensionless
$L_A, L_W{}_{}^{}$	Film thicknesses	cm
$F_1, F_2, F_t{}_{}^{}$	Fluxes through the interface	${\mathrm{mol}\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$
$f_1, f_2, f_t{}_{}^{}$	Mass transfer coefficients	${\mathrm{cm}\mathrm{s}}^{-1}$
CONCENTRATION VARIABLES
$C_{1\infty W}, C_{1\infty A}, C_{2\infty W}, C_{2\infty A}{}_{}$	Concentrations at specific depths	${\mathrm{mol}\mathrm{cm}}^{-3}$
$C_{10W}, C_{10A}, C_{20W}, C_{20A}{}_{}$
DERIVED VARIABLES
$Q=\frac{D_1}{D_2}$	Diffusivity ratios	dimensionless
$m={\frac{C_{1\infty A}}{H_1{C}_{1\infty W}}}_{}^{}$	Equilibrium indicator	dimensionless
$d_1={\left(\frac{D_1}{k_{12}}\right)}^{1/2}{}_{}$	Reaction–diffusion distances	cm
$d_2={\left(\frac{D_2}{k_{21}}\right)}^{1/2}{}_{}^{}$
$d={\left(d_1^{-2}+d_2^{-2}\right)}^{-1/2}{}_{}^{}$
$\mathsf{\Lambda }={\frac{L}{d}}_{}^{}$	Reduced film thickness	dimensionless
$\begin{array}{c}{\zeta }_A=\frac{D_{2A}}{L_A}, {\zeta }_W=\frac{D_{2W}}{L_W}\\ Q_A{\zeta }_A=\frac{D_{1A}}{L_A}, Q_W{\zeta }_W=\frac{D_{1W}}{L_W}\end{array}$	Zeta-notation	${\mathrm{cm}\mathrm{s}}^{-1}$
$E=\frac{\mathsf{\Lambda }\left(Q+K\right)}{\mathsf{\Lambda }Q+K\tanh \mathsf{\Lambda }}$	Enhancement factors	dimensionless

defines the variables employed. We distinguish between “system” variables that define the physical and chemical properties of the system, “concentration” variables that represent concentrations of the two compounds at specific depths, and “derived” variables, used for notational convenience. The subscripts “1” and “2” identify variables that are specific to compounds 1 and 2, respectively. The subscripts “A” and “W” identify variables specific to the air and water phases, respectively. The subscript “t” for total represents a sum of properties over both compounds, e.g., F_t = F₁ + F₂ is the total flux. The subscripts “0” and “∞” attached to concentration variables indicate interfacial and far-field concentrations, respectively. A generic expression valid for either phase or for either compound can appear in this paper without the relevant subscripts.

The reaction rate constants k₁₂ and k₂₁ are pseudo-first order, since variations in water concentration are negligible. k₁₂ refers to the rate of 1 → 2 and vice versa. Enhancement factors appear in models A2 and A3 as multipliers of certain transfer coefficients. As defined, enhancement factors are always greater than 1, so these models predict that reactions can accelerate transfer. Because diffusivities of small molecules agree better than an order of magnitude, we can usually expect that $Q\approx 1$. Because compounds 1 and 2 usually do not have the same mass, molar concentrations are used throughout. The equilibrium constants are defined as K = [diol]/[aldehyde]. I use the dimensionless air-over-water form of Henry’s constant.

$$H_1=\frac{C_{1A,eq}}{C_{1W,eq}} , H_2=\frac{C_{2A,eq}}{C_{2W,eq}}$$

(1)

with the subscript “eq” denoting equilibrium concentrations. It is important to distinguish between “intrinsic” and “effective” Henry’s constants. H₁ and H₂ as they are used here are intrinsic. H₁ is the ratio of aldehyde concentrations only, excluding the gem-diol form. H₂ is the ratio of only the gem-diol concentrations. Effective Henry’s constants blur the distinction between the aldehyde and the gem-diol forms:

$$H_e=\frac{C_{1\infty A}+C_{2\infty A}}{C_{1\infty W}+C_{2\infty W}}=\frac{H_1+H_2{K}_W}{1+K_W}=\frac{H_1\left(1+K_A\right)}{\left(1+K_W\right)}$$

(2)

Effective Henry’s constants appear commonly in the literature, especially when measurement techniques are unable to distinguish the two forms of the molecule. Not all the variables given in Table 1 are independent. Interrelations between variables are listed in

Table 2. Relationships between variables reduce the number of degrees of freedom in any model.

RELATIONSHIP	JUSTIFICATION
$K_A={\frac{k_{12A}}{k_{21A}}}_{}^{}$	Equilibrium constants are ratios of forward and reverse rate constants.
$K_W={\frac{k_{12W}}{k_{21W}}}_{}^{}$
$H_2{K}_W=H_1{K}_A{}_{}^{}$	Required by detailed balance.
$C_{2\infty W}=K_W C_{1\infty W}{}_{}^{}$	Assumption of far-field chemical equilibrium.
$C_{2\infty A}=K_A C_{1\infty A}{}_{}^{}$
$C_{10A}=H_1 C_{10W}{}_{}^{}$	Assumption of rapid exchange through the interface and local equilibrium across the interface.
$C_{20A}=H_2 C_{20W}{}_{}^{}$

. These interrelations are results of physical laws or of fundamental assumptions in the models.

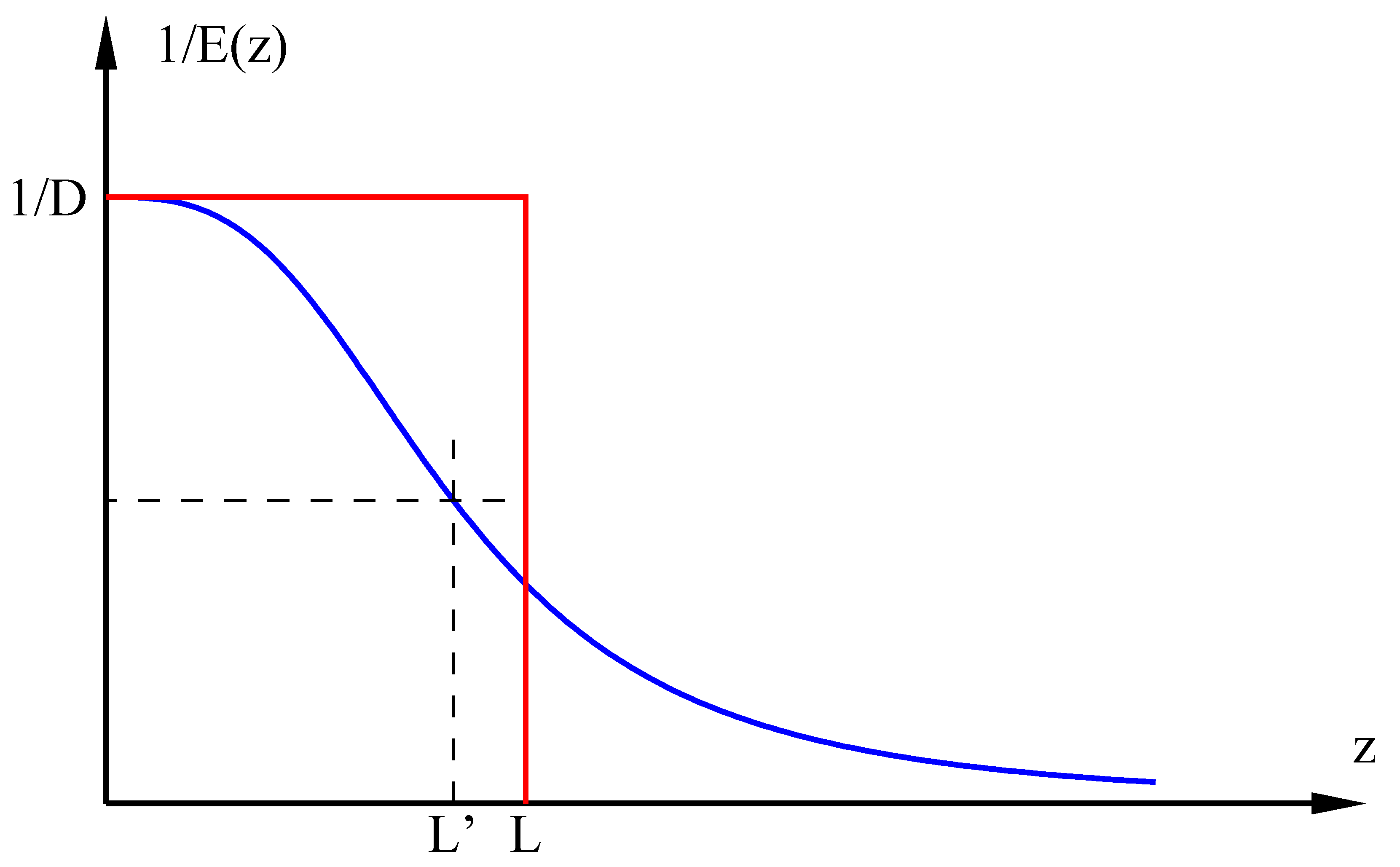
4. Justification of the Whitman Model

Because the Whitman model [33] has fallen into disuse, I now justify using generalizations of it in this study. The essential argument is that when Whitman’s film thickness is chosen to duplicate the flux of any of the more recent models, we can expect that it gives the same qualitative dynamics, the difference in D-scaling notwithstanding. Fundamentally, the difference between the Whitman model and, for example, the Schmidt number models is the assumed mathematical form of the eddy diffusivity. For Whitman, we have

$$E\left(z\right)=\{\begin{array}{c}D, if 0<z<L\\ \infty , if z>L\end{array}$$

(3)

The eddy diffusivity for the Schmidt number models can be written as

$$E\left(z\right)=D\left[1+{\left(\frac{z}{L\prime }\right)}^p\right]$$

(4)

L′ is a lumped quantity with units of length. Physical arguments require p = 2 or 3 [40,41,42]. Interestingly, Equation (3) is the large-p version of Equation (4). Calculation of the transfer coefficient involves the integral

$$k^{-1}={{\displaystyle \int }}_0^{\infty }\frac{dz}{E\left(z\right)}$$

(5)

The integrands 1/E(z) of Equations (3) and (4) are both plotted in Figure 3. L′ and 1/D are measures, respectively, of the breadth and height of the area under the blue curve, meaning that Equation (4) gives this scaling law: $k ~ D/L\prime$. Equation (3) implies $k=D/L$. Therefore, when properly chosen, there is a value of $L\cong L\prime$ for which both models give the same k. Because the Whitman model has the same effective film thickness as the Schmidt number model, and because its diffusivity is approximately equal to the eddy diffusivity in the film, we expect that the two models give the same qualitative dynamics.

However, the scaling law $k ~ D/L\prime$ does not seem to be appropriate for the Schmidt number models, which give $k ~ D^{1/2}$ or $D^{2/3}$. The explanation of the discrepancy is that L′ is indeed a measure of film thickness, but as a lumped variable, it has its own D dependence. The scaling law for the Schmidt number models emerges from the assumptions (1) that E(0) = D, and (2) that the term in z^p is determined only by fluid-dynamic properties of the solvent; no property of the solute, including D, is assumed to enter. Rather, the coefficient of the term in z^p is assumed to depend only on three parameters, solvent viscosity η, solvent density ρ, and friction velocity at the interface, u* [42]. For any given p, there is only one combination of these three parameters that yields the correct units. The resultant scaling laws for L′ and k are:

$$L^{\prime }~{\left(\frac{\eta }{\rho }\right)}^{\left(p-1\right)/p}{\left(u^{*}\right)}^{-1}{D}^{1/p}$$

(6)

$$k ~ {\left(Sc\right)}^{-n}{u}^{*} with n=\left(p-1\right)/p$$

(7)

Here, $Sc=\eta /\rho D$ is the Schmidt number of the solvent; u* is the friction velocity; and n is 1/2 and 2/3 respectively, when p = 2 or 3. Dependence on wind speed enters L′ through the parameter u*.

5. Properties of the Models

See the Supplementary Material for derivations of all the models and a detailed discussion of their properties. In this section, I summarize some of the more important properties of the models.

5.1. Independent Concentration Variables and Equilibrium Conditions

Because of the interrelations between concentration variables listed in Table 2, only two concentration variables are independent in any of the models. For model A1, $C_{\infty W}$ and $C_{\infty A}$ are the logical choices for independent concentration variables, while for the other models, $C_{1\infty W}$ and $C_{1\infty A}$ make the most sense. This is because the most natural boundary conditions on the problem are the specification of the far-field concentrations. Then $C_{2\infty W}$ and $C_{2\infty A}$ are fixed by the far-field equilibrium assumption, Table 2, Row 3. The ratios $C_{10A}/C_{10W}$ and $C_{20A}/C_{20W}$ are fixed by the assumption of rapid equilibration across the interface, Table 2, Row 4. The values of $C_{10W}$ and $C_{20W}$ are fixed by the steady-state requirement that all fluxes through the interface be balanced.

Furthermore, I define the following dimensionless ratio

$$m={\frac{C_{1\infty A}}{H_1{C}_{1\infty W}}}_{}^{}$$

(8)

or, for model A1,

$$m=\frac{C_{\infty A}}{H{C}_{\infty W}}$$

(9)

I use m to replace dependence on $C_{1\infty A}$. m is useful because it indicates whether air or water concentrations are in excess and it indicates the direction of flow between the two phases. For this reason, I call it the “equilibrium indicator.” In any of the models, the total flux through the interface can be factored into three terms:

$$F=\left(1-m\right)C_{1\infty W} f$$

(10)

I observe the convention that positive flux flows from the water to the air. Then m < 1 corresponds to net positive flux, m > 1 to net negative flux, and m = 1 corresponds to equilibrium with zero flux. f plays the role of a mass-transfer coefficient and has units of velocity. It will be written with subscripts “A1,” “A2,” etc., to distinguish between the different models. However, other definitions of the mass-transfer coefficients are found in the literature; for examples, see Section 7.3.

5.2. Converting Model A1 to A1E

Here I give the complete description of model A1E. The total flux for the original Whitman model, model A1 (see the Supplementary Material), is

$$F=\frac{k_W{k}_A}{\left(H{k}_A+k_W\right)}\left(H{C}_{\infty W}-C_{\infty A}\right)$$

with

$$k_W=\frac{D_W}{L_W}, k_A=\frac{D_A}{L_A}, H=\frac{C_{A0}}{C_{W0}}$$

To obtain model A1E, use the effective Henry’s constant, Equation (2), and weighted averages of the diffusivities:

$$D_{eA}=\frac{D_{1A}+K_A{D}_{2A}}{1+K_A}$$

$$D_{eW}=\frac{D_{1W}+K_W{D}_{2W}}{1+K_W}$$

$${\zeta }_{eA}=\frac{D_{eA}}{L_A}={\zeta }_A\left(\frac{Q_A+K_A}{1+K_A}\right)$$

$${\zeta }_{eW}=\frac{D_{eW}}{L_W}={\zeta }_W\left(\frac{Q_W+K_W}{1+K_W}\right)$$

and write this for the flux:

$$F_{A1E}=\frac{{\zeta }_{eW}{\zeta }_{eA}}{(H_e{\zeta }_{eA}+{\zeta }_{eW})}\left[H_e\left(C_{1\infty W}+C_{2\infty W}\right)-\left(C_{1\infty A}+C_{2\infty A}\right)\right]$$

With these substitutions: $C_{1\infty A}=m{H}_1{C}_{1\infty W}$, $C_{2\infty W}=K_W{C}_{1\infty W}$, $C_{2\infty A}=K_A{C}_{1\infty A}$, we can write

$$F_{A1E}=f_{A1E}\left(1-m\right)C_{1\infty W}$$

where

$$f_{A1E}=\frac{{\zeta }_{eW}{\zeta }_{eA}}{\left(H_e{\zeta }_{eA}+{\zeta }_{eW}\right)}{H}_1\left(1+K_A\right)$$

or

$$\frac{1}{f_{A1E}}=\frac{1}{\left(Q_A+K_A\right)H_1{\zeta }_A}+\frac{1}{\left(Q_W+K_W\right){\zeta }_W}$$

(11)

5.3. Properties of the Models

All the following properties are established fully in the supplementary information.

(1) Whitman showed us [33] that one or the other of the two films is often rate-determining. In such cases, the mass-transfer coefficients depend only on system parameters of the rate-limiting film, and we speak of “air-layer” or “water-layer control”. ${\zeta }_A\ll {\zeta }_W$ produces air control and vice versa. The two variables R_A and R_W satisfy $R_A+R_W=1$ (see the supplementary information) and indicate the extent of control by one side or the other. When $R_A\cong 1$, the system is under air-barrier control; when $R_W\cong 1$, it is under water barrier control.

(2) In all cases, $f_{A1}<f_{A2}<f_{A3}<f_{A4}<f_{A1E}$, but there are limiting cases in which any two may become arbitrarily close. The first two inequalities are not surprising; we expect any kinetic process to speed up when new pathways open up. $f_{A1E}\cong f_{A4}$ often occurs when the system is under either air- or water-barrier control. It also occurs when the reactions are so fast that the two molecular forms have no individual identity.

(3) f_A3 < f_A4 always, but they often agree well. Good agreement occurs, for example, whenever flux of 2 through the interface is negligible. However, poor agreement is also observed, indicating that there are conditions in which models A2 or A3 are inadequate. The passage of both forms through the interface should not generally be ignored.

(4) Instances of $f_{A1E}\cong f_{A4}$ or $f_{A3}\cong f_{A4}$ are beneficial because of the numerical complexity of model A4. Unfortunately, it is generally not possible to know when the approximations are valid without actually performing the calculations.

(5) The reaction–diffusion distances d₁, d₂, and d defined in Table 1 measure the typical distance over which molecules diffuse before they react. The dimensionless ratio Λ distinguishes between systems with fast or slow reactions: if Λ << 1, then molecules do not interconvert as they diffuse through the film, while if Λ >> 1, they interconvert many times.

(6) Results of all models simplify in certain limits summarized in

Table 3. Results of all models simplify in certain limits.

Limiting Value	Air-Side Control ${\zeta }_W\gg {\zeta }_A$		Water-Side Control ${\zeta }_W\ll {\zeta }_A$
$f_{A1E}\cong$	${\zeta }_A{H}_1\left(Q_A+K_A\right)$		${\zeta }_W\left(Q_W+K_W\right)$
$f_{A2}\cong$	${\zeta }_A{H}_1{Q}_A$		${\zeta }_W{Q}_W{E}_W$
			$\begin{array}{c}\left({\mathsf{\Lambda }}_W\ll 1\right)\\ {\zeta }_W{Q}_W\end{array}$	$\begin{array}{c}\left({\mathsf{\Lambda }}_W\gg 1\right)\\ {\zeta }_W\left(Q_W+K_W\right)\end{array}$
$f_{A3}\cong$	${\zeta }_A{H}_1{Q}_A{E}_A$		${\zeta }_W{Q}_W{E}_W$
	$\begin{array}{c}\left({\mathsf{\Lambda }}_A\ll 1\right)\\ {\zeta }_A{H}_1{Q}_A\end{array}$	$\begin{array}{c}\left({\mathsf{\Lambda }}_A\gg 1\right)\\ {\zeta }_A{H}_1\left(Q_A+K_A\right)\end{array}$	$\begin{array}{c}\left({\mathsf{\Lambda }}_W\ll 1\right)\\ {\zeta }_W{Q}_W\end{array}$	$\begin{array}{c}\left({\mathsf{\Lambda }}_W\gg 1\right)\\ {\zeta }_W\left(Q_W+K_W\right)\end{array}$
$f_{A4}\cong$	${\zeta }_A{H}_1\left(Q_A+K_A\right)$		${\zeta }_W\left(Q_W+K_W\right)$

. Models A2 and A3 both involve enhancement factors that change from $E\cong 1$ (no enhancement) when $\mathsf{\Lambda }\ll 1,$ to $E\cong \left(Q+K\right)/Q$ when $\mathsf{\Lambda }\gg 1$. The enhancement factors can be very large when K >> 1. In model A4, the enhancement terms do not directly factor out of the formulas, but enhancement is occurring as can be seen in Table 3. However, in model A4, the magnitude of the enhancement does not evolve with changing Λ, but remains near (Q + K)/Q for all Λ.

(7) Table 3 lets us identify several regimes for which model A3 and A4 differ significantly; for example, under air-side control when ${\mathsf{\Lambda }}_A\ll 1$ and $K_A\gg 1,$ and under water-side control when ${\mathsf{\Lambda }}_W\ll 1$ and $K_W\gg 1$.

6. Aldehyde ↔ Gem-Diol Reactions

We consider the hydration reaction of formaldehyde to form methanediol:

$$\mathrm{HCHO}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow {\mathrm{CH}}_2{\left(\mathrm{OH}\right)}_2$$

and of acetaldehyde to form 1,1-ethanediol:

$${\mathrm{CH}}_3-\mathrm{COH}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow {\mathrm{CH}}_3-\mathrm{CH}{\left(\mathrm{OH}\right)}_2$$

In aqueous solution, the diols can continue to add aldehyde units to form higher oligomers [56], but at the aldehyde and diol concentrations expected in the environment, those compounds can be neglected [57].

According to theoretical estimates [21,23] the unimolecular decay rate of methanediol is very low, giving a half-life at 300 K in an extreme vacuum longer than the age of the universe. However, in the atmosphere and in the aqueous phase, the reaction is catalyzed by H₂O, by organic and inorganic acids, by bases, and by the hydroperoxyl radical. The reaction is probably also autocatalytic [22,58,59,60]. Calculations also indicate that the acid and radical catalysts may be more efficient than water, although the relative abundance of water still means that it is the most important catalyst.

A half-century ago, Eigen [61] suggested that water catalysis proceeds via a concerted exchange of protons involving two water molecules. That view has been confirmed theoretically, along with the suggestion that three-water catalysis is even faster [21,23,62,63]. These findings imply that the absolute rate constants are probably second or third order in water. The gas-phase pseudo-first-order reaction rates k_12A and k_21A are then expected to be strong functions of the concentrations of any catalysts and to be slower than the equivalent reactions in the aqueous phase where the catalyst concentration is larger. The air film at the interface is expected to be water saturated, which translates into a strong temperature dependence for k_12A and k_21A arising from the dependence of absolute humidity on temperature. The aqueous reactions are also catalyzed by H₃O⁺ and OH⁻ so that k_12W and k_21W are pH dependent, and their values are lowest at about pH 7.

The rigorously defined gas-phase equilibrium constant for the reaction aldehyde + H₂O ↔ diol is written in terms of the partial pressures of each gas as

$${\kappa }_A=\frac{P_{diol} P_0}{P_{aldehyde} P_{H_{2}O}}$$

where P₀ is a reference pressure of 1 atm. The expression we use for K_A is

$$K_A=\frac{\left[diol\right]}{\left[aldehyde\right]}=\frac{P_{diol}}{P_{aldehyde}}=\left(\frac{P_{H_{2}O}}{P_0}\right) {\kappa }_A$$

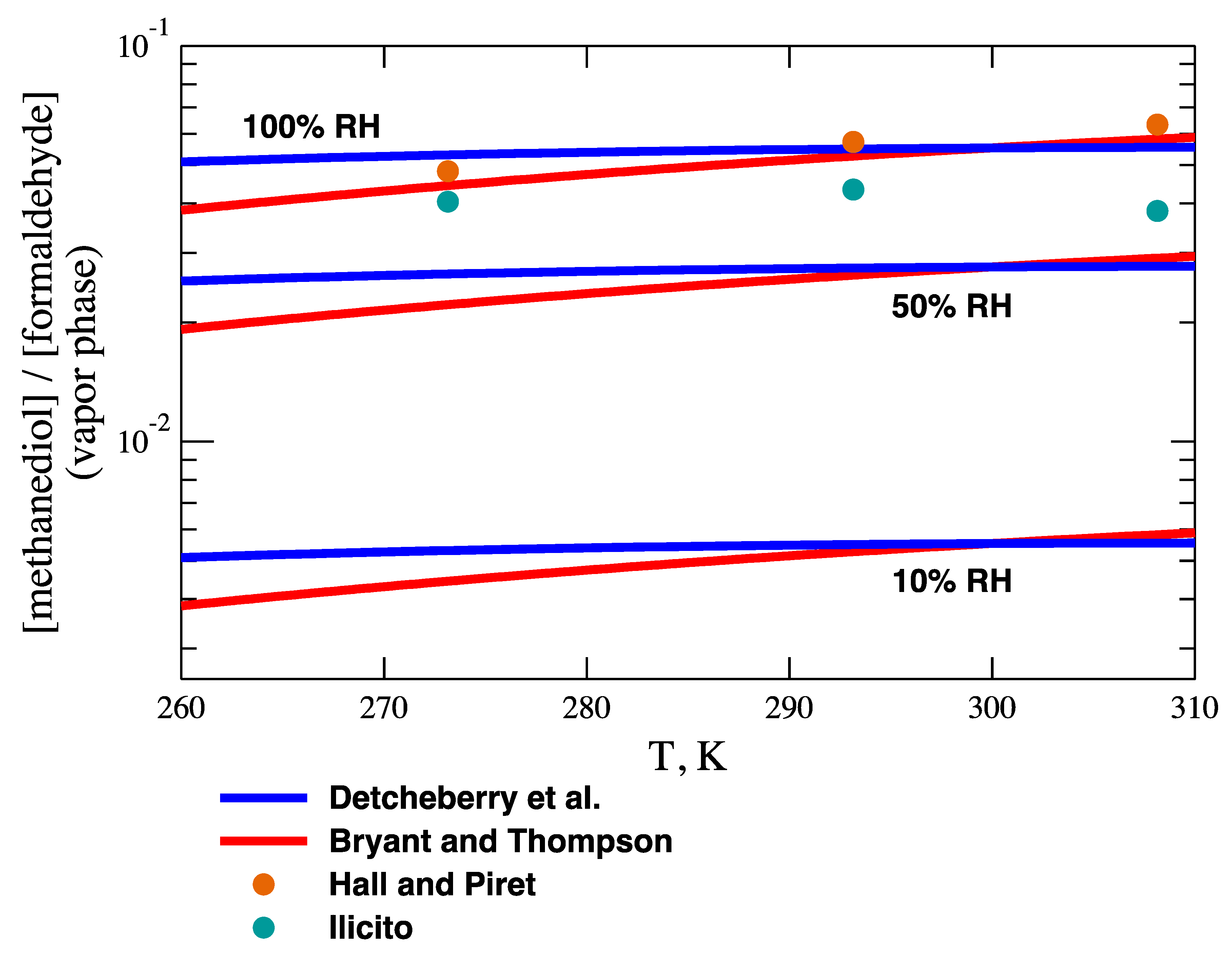
meaning that literature values of ${\kappa }_A$ must be corrected using the partial pressure of water vapor (0.039 atm at 298.15 K). The rigorous equilibrium constant has strong temperature dependence [64,65], but so does the partial pressure of water vapor [66]. Interestingly, the two effects largely compensate, and K_A for the formaldehyde reaction is essentially independent of temperature, as shown in Figure 4. The effect of relative humidity on K_A is also displayed in Figure 4. Of course, in the air film at the air–water interface, 100% relative humidity can be assumed.

Table 4. Data relevant to the $\mathrm{HCHO}\leftrightarrow {\mathrm{CH}}_2{\left(\mathrm{OH}\right)}_2$ reaction at ≈ 300K and pH 7.

Variable	Value or Range	Source
$H_1$	0.025	Median from [67], corrected to intrinsic.
$H_2$	$\approx {10}^{-7}$	Never measured, but constrained by H1, KA, KW.
$D_{1W}$	$1.87\times {10}^{-5} {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[68,70,71]
$D_{2W}$	$1.57\times {10}^{-5} {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[68,70,71]
$D_{1A}$	$0.155 {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[69,71]
$D_{2A}$	$0.124 {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[69,71]
$K_A$	0.045	Figure 4.
$K_W$	1800 to 2270	Middle seven of thirteen independent datapoints (experimental and theoretical) [63,64,72,73,74,75,76]
$L_A$	0.3 cm	[43]
$L_W$	0.02 cm	[43]
$k_{12W}$	$9.8 {\mathrm{s}}^{-1}\mathrm{to}10.6{\mathrm{s}}^{-1}$	Middle four of six independent datapoints (experimental and theoretical) [74,75,77]
$k_{21W}$	$\left(4.5\mathrm{to}5.3\right)\times {10}^{-3}{\mathrm{s}}^{-1}$	Middle four of six independent datapoints (experimental and theoretical) [59,75,78]
$k_{12A}$	Unknown	Never measured, but ratio $k_{12A}/k_{21A}$ is constrained.
$k_{21A}$	Unknown	Never measured, but ratio $k_{12A}/k_{21A}$ is constrained.

and

Table 5. Data relevant to the ${\mathrm{CH}}_3-\mathrm{COH}\leftrightarrow {\mathrm{CH}}_3-\mathrm{CH}{\left(\mathrm{OH}\right)}_2$ reaction at ≈ 300K and pH 7.

Variable	Value or Range	Source
H1	$7.0\times {10}^{-3}$	Median from [67] corrected to intrinsic.
H2	$\approx {10}^{-5}$	Never measured, but constrained by H1, KA, KW.
$D_{1A}$	$0.119{\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[69,71]
$D_{2A}$	$0.103{\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[69,71]
$D_{1W}$	$1.46\times {10}^{-5} {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[68,70,71]
$D_{2W}$	$1.29\times {10}^{-5} {\mathrm{cm}}^2 {\mathrm{s}}^{-1}$	[68,70,71]
KA	$\approx 0.005$	Poorly constrained. See text.
KW	1.19 to 1.35	The middle thirteen of 27 independent datapoints (experimental and theoretical) [73,76,79,80,81,82]
LA	0.3 cm	[43]
LW	0.02 cm	[43]
k12A	Unknown	Never measured, but ratio $k_{12A}/k_{21A}$ is constrained.
k21A	Unknown	Never measured, but ratio $k_{12A}/k_{21A}$ is constrained.
k12W	$\left(0.005 \mathrm{to} 0.015\right) {\mathrm{s}}^{-1}$	Middle four of eight independent datapoints (experimental and theoretical) [75,77].
k21W	$\left(0.0041 \mathrm{to} 0.012\right) {\mathrm{s}}^{-1}$	Middle four of eight independent datapoints (experimental and theoretical) [75,80].

contain literature data on each aldehyde reaction. Henry’s constants H₁ for the aldehydes have been retrieved from Sander’s compilation [67]. H₂ for the gem-diols does not appear in his compilation, but it is constrained by the values of H₁, K_A, and K_W. Henry’s constants are often difficult to measure, and there is usually considerable scatter in Sander’s compilation for any one compound, often by more than an order of magnitude. Here, I take the median Henry’s constants from the compilation, which appear to be good consensus values. Sander tabulates effective Henry’s constants, H_e, for formaldehyde and acetaldehyde. Therefore, his entries must also be converted to intrinsic constants.

Molecular diffusivities were calculated using several different empirical correlations [68,69,70,71]. The quantities K_W, k_12W and k_21W have been extensively measured and calculated theoretically. For these quantities, Table 4 and Table 5 report ranges of values equal to the middle half of datasets of independently measured or computed values. The value of the formaldehyde K_A is taken from Figure 4 at 100% relative humidity.

Apparently, the only publication considering the equilibrium constant of the vapor-phase hydration of acetaldehyde is a theoretical calculation by Rayne and Forest [83] obtaining ${\kappa }_A\approx 0.005$ (geometric mean of three separate estimates) at 298.15 K. For formaldehyde at 298.15 K, Rayne and Forest obtain ${\kappa }_A\approx 0.07$ (geometric mean of three separate estimates), whereas experimental values are around 1.75 [64], i.e., the Rayne–Forest formaldehyde estimate is a factor of about 25 too low. Applying the same ratio to acetaldehyde yields ${\kappa }_A\approx 0.12$ and $K_A\approx 0.005$. Therefore, in the following, we will estimate $K_A\approx 0.005$ for acetaldehyde, all the while considering this to be a poorly constrained value.

The rates k_12A and k_21A have never been measured for either system, but their ratio is constrained by K_A. Therefore, the only available constraints on k_12A and k_21A are $k_{21A}\lesssim k_{21W}$ and $k_{12A}\lesssim k_{12W}$, as explained above. In calculations reported below, I have allowed k_12A and k_21A to vary by about four orders of magnitude while enforcing these constraints.

7. Results

7.1. Numerical Results for Formaldehyde and Acetaldehyde

Table 6. Sample calculations. k_21A was allowed to assume eight different values as indicated. Each of these generated eight different values for k_12A, d_A, and Λ_A, but all remaining variables were insensitive to these variations, at least to the number of significant figures given.

Variable	Formaldehyde	Acetaldehyde
H1	0.025	$7.0\times {10}^{-3}$
$D_{1W}/\left({\mathrm{cm}}^2{\mathrm{s}}^{-1}\right)$	$1.87\times {10}^{-5}$	$1.46\times {10}^{-5}$
$D_{2W}/\left({\mathrm{cm}}^2{\mathrm{s}}^{-1}\right)$	$1.57\times {10}^{-5}$	$1.29\times {10}^{-5}$
$D_{1A}/\left({\mathrm{cm}}^2{\mathrm{s}}^{-1}\right)$	0.155	0.119
$D_{2A}/\left({\mathrm{cm}}^2{\mathrm{s}}^{-1}\right)$	0.124	0.103
$k_{12W}/{\mathrm{s}}^{-1}$	10.0	0.01
$k_{21W}/{\mathrm{s}}^{-1}$	$5.0\times {10}^{-3}$	0.008
KA	0.045	0.005
LW/cm	0.02	0.02
LA/cm	0.3	0.3
$k_{21A}/{\mathrm{s}}^{-1}$	$\left\{{10}^{-X}\right\}$a	$\left\{{10}^{-X}\right\}$a
KW	2000	1.25
$k_{12A}/{\mathrm{s}}^{-1}$	$0.045\times \left\{{10}^{-X}\right\}$a	$0.005\times \left\{{10}^{-X}\right\}$a
H2	$5.625\times {10}^{-7}$	$2.8\times {10}^{-5}$
dA/cm	{6.15, 10.9, 19.5, 34.6, 61.5, 109, 195, 346}	{5.69, 10.1, 18.0, 32.0, 56.9, 101, 180, 320}
dW/cm	$1.37\times {10}^{-3}$	$2.77\times {10}^{-2}$
QA	1.25	1.16
QW	1.19	1.13
ΛA	$\text{{}488,274,154,86.7,48.8,27.4,15.4,8.67\text{}}\times {10}^{-4}$	$\text{{}527,296,167,93.7,52.7,29.6,16.7,9.37\text{}}\times {10}^{-4}$
ΛW	14.6	0.723
$H_e$	$1.3\times {10}^{-5}$	$3.1\times {10}^{-3}$
${\zeta }_A/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	0.413	0.343
${\zeta }_W/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$7.85\times {10}^{-4}$	$6.45\times {10}^{-4}$
RA	0.544	0.234
$f_{A1E}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	0.0133	$9.91\times {10}^{-4}$
$f_{A4}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$7.08\times {10}^{-3}$	$6.25\times {10}^{-4}$
$f_{A3}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$6.62\times {10}^{-3}$	$6.15\times {10}^{-4}$
$f_{A2}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$6.62\times {10}^{-3}$	$6.15\times {10}^{-4}$

^a$X\in \left\{2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5,6.0\right\}$.

summarizes numerical calculations for formaldehyde and acetaldehyde assuming the values given in Table 4 and Table 5. Because it is poorly constrained, k_21A was allowed to vary from ${10}^{-6}{\mathrm{s}}^{-1}$ to ${10}^{-2.5}{\mathrm{s}}^{-1}$, but the final results for f are insensitive to this variation. Neither the air- nor the water-side dominates in either system (R_A = 0.544 or 0.234). f_A1E is 87% and 58% larger than f_A4 for formaldehyde and acetaldehyde, respectively, so model A1E is not accurate in these cases. The ratios $f_{A2}/f_{A4}$ and $f_{A3}/f_{A4}$ are, respectively, 0.935 and 0.984, so model A3 is adequate for formaldehyde and acetaldehyde.

Figure 5 displays concentration profiles in the two films when $m=0$ (corresponding to zero far-field concentration in the air side). The [diol]/[aldehyde] ratios are in excess of K_A and K_W throughout the air and water films. Similarly, Figure 6 displays concentration profiles in the $m\to \infty$ limit (corresponding to zero far-field concentration in the water side). Then, the [diol]/[aldehyde] ratios fall below K_A and K_W.

7.2. Sensitivity to Parameter Variations

Most of the variables in Table 4 and Table 5 are sensitive to temperature, humidity, pH, salinity, etc., and are also subject to experimental uncertainty. To judge the impact of such variations on the results, I performed Monte Carlo calculations in which values of the input variables H₁, D_1W, D_2W, D_1A, D_2A, k_12W, k_21W, K_A, L_W, and L_A were sampled independently from log-normal distributions

$$P\left(X\right)={\left(2\pi {\sigma }^2\right)}^{-1/2}\exp \left[\frac{-{\left(x-\mu \right)}^2}{2{\sigma }^2}\right], x={\log }_{10}X$$

Consistent with the range of entries in Table 4 and Table 5 and defined in

Table 7. Distribution of variables used with the formaldehyde and acetaldehyde models.

Variable	Formaldehyde		Acetaldehyde
	μ	σ	μ	σ
H1	−1.6	0.15	−2.2	0.15
$D_{1W}/\left({\mathrm{cm}}^2 {\mathrm{s}}^{-1}\right)$	−4.7	0.15	−4.8	0.15
$D_{2W}/\left({\mathrm{cm}}^2 {\mathrm{s}}^{-1}\right)$	−4.8	0.15	−4.9	0.15
$D_{1A}/\left({\mathrm{cm}}^2 {\mathrm{s}}^{-1}\right)$	−0.8	0.15	−0.9	0.15
$D_{2A}/\left({\mathrm{cm}}^2 {\mathrm{s}}^{-1}\right)$	−0.9	0.15	−1.0	0.15
$k_{12W}/\left({\mathrm{s}}^{-1}\right)$	1.0	0.2	−2.0	0.3
$k_{21W}/\left({\mathrm{s}}^{-1}\right)$	−2.3	0.2	−2.1	0.3
KA	−1.3	0.15	−2.3	0.5
LW/cm	−1.7	0.15	−1.7	0.15
LA/cm	−0.5	0.15	−0.5	0.15
k21A	Unconstrained, except to enforce $k_{21A}<k_{21W}$ and $k_{12A}<k_{12W}$
KW	$=k_{12W}/k_{21W}$
k12A	$=K_A k_{21A}$
H2	$=H_1{K}_A/K_W$

. The mode of a log-normal distribution is at $X={10}^{\mu }$, while σ controls the breadth. k_21A was allowed to vary subject to the constraints k_21A < k_21W and k_12A < k_12W. The variables K_W, k_12A, and H₂ were then calculated to enforce constraints given in Table 2. When σ = 0.15, 95% of the log-normal distribution lies within the range $0.5\times {10}^{\mu }$ and $2\times {10}^{\mu }$. Because K_A for formaldehyde is not well known, its σ has been set at 0.5, which places 95% of the distribution between one order of magnitude below and one order of magnitude above ${10}^{\mu }$. Other less well-constrained variables have been assigned σ’s of 0.2 or 0.3.

Figure 7 shows the distributions of f_A1E, f_A2, f_A3, and f_A4 for both the formaldehyde and acetaldehyde models. The results obviously satisfy the inequalities f_A2 < f_A3 < f_A4 < f_A1E, although the f_A2, f_A3 and f_A4 curves are almost completely superimposable. Figure 8 shows the distributions of R_A for both models. These rather broad distributions, with R_A occurring over much of the available range 0 < R_A < 1, indicate that neither model has exclusively air- or water-barrier control. Both models are near a tipping point: modulations of less than an order of magnitude in the model parameters significantly shift the balance between air- and water-control. Figure 9 shows the distributions of the ratios f_A1E/f_A4, which confirms the inequality f_A4 < f_A1E. f_A1E is on the order of 20% and 50% higher than f_A4 for the two respective models. Figure 10 displays the distribution of f_A3/f_A4 and f_A2/f_A4 for the formaldehyde and acetaldehyde models. The f_A3 and f_A2 curves are indistinguishable because f_A2 is very near f_A3 for these models. For acetaldehyde, f_A2 and f_A3 are typically 94.5% of f_A4, but distributed broadly, while for formaldehyde, the ratio is about 99.7%.

7.3. Comparison with Experiment

Two separate measurement sets are considered here. (1) Seyfioglu and Odabasi [84] measured transport of formaldehyde from air to water, which corresponds to the $m\to \infty$ limit. In their notation, $F=-K_g{C}_g$ (with the sign flipped to be consistent with my sign convention). C_g is the gas-phase concentration, equivalent to $C_{1\infty A}+C_{2\infty A}$. In the limit $m\to \infty$ of model A4, $F=-C_{1\infty A}{f}_{A4}/H_1$. Therefore, the connection between the two notations is $f_{A4}=H_1\left(1+K_A\right)K_g.$ (2) Liu et al. [85] measured H_e for formaldehyde at 23 °C to be in the range ($0.896\mathrm{to}1.23)\times {10}^{-5}$, near the consensus value, $1.3\times {10}^{-5}$, reported by Sander [67]. They also measured water-to-air fluxes of formaldehyde. In their notation, $F=K_{0L}{C}_L$, with $C_L=C_{1\infty W}+C_{2\infty W}$. Compare this with the notation $F=C_{1\infty W}{f}_{A4}$ in the $m\to 0$ limit of model A4. The connection between the two notations is $f_{A4}=\left(1+K_W\right)K_{0L}$.

Table 8. Comparison with experiment.

Seyfioglu and Odabasi [84]; Formaldehyde; Air → Water Experiments; Model A4.
Experimental conditions	$U_{10}/\left({\mathrm{m}\mathrm{s}}^{-1}\right)$	$K_g{H}_1\left(1+K_A\right)/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$f_{A4}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$
Laboratory	8	$\left(15.1\pm 5.5\right)\times {10}^{-3}$	$\left(5 \mathrm{to} 10\right)\times {10}^{-3}$
Field	4	$\left(6.3\pm 3.1\right)\times {10}^{-3}$
Liu et al. [85]; Formaldehyde; Water → Air Experiments; Model A4.
Experimental conditions	$U_{10}/\left({\mathrm{m}\mathrm{s}}^{-1}\right)$	$K_{0L}\left(1+K_W\right)/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$	$f_{A4}/\left({\mathrm{cm}\mathrm{s}}^{-1}\right)$
Without stirring	0.4	$4.66\times {10}^{-3}$	$\left(5 \mathrm{to} 10\right)\times {10}^{-3}$
		$4.51\times {10}^{-3}$
With stirring	0.4	$5.61\times {10}^{-3}$
		$6.06\times {10}^{-3}$
		$6.06\times {10}^{-3}$

compares predictions from data in Table 6 against the two sets of measurements. Wind speeds as cited in each paper have been adjusted to U₁₀, the wind speed at 10 m above the water surface, using the 1/7-th power law [86]. As expected, the data display variations due to variable wind speed or agitation of the water phase. However, the model predictions are all consistent with the experiment, especially at lower wind speeds. In Section 4, we saw that L_A or L_W are effective film thicknesses, free to be chosen to give agreement with experiment. Therefore, the agreement displayed in Table 8 is mainly a testament to the ability of Schwarzenbach et al. [43] to estimate good L_A and L_W values.

8. Summary

Volatile gases such as formaldehyde and acetaldehyde undergo hydration reactions in aqueous solution, forming methanediol and 1,1 ethanediol, respectively. Conventional wisdom has dictated that the hydrated forms do not exist in the vapor phase. Therefore, models designed to treat the transport of these compounds between an aqueous phase (oceans, lakes, wastewater lagoons, aqueous aerosols, etc.) and the atmosphere have always assumed that molecules traverse the interface only in the anhydrous form [37,43,53,54,55]. We now know that the conventional wisdom is wrong—the diols exit in the vapor phase [19,20,21,22,23,24]. The hydrated molecules are inherently very stable, but catalysts are readily available in the atmosphere leading to chemical equilibrium between both forms. These equilibria strongly favor the anhydrous form [21,22,23,61,62].

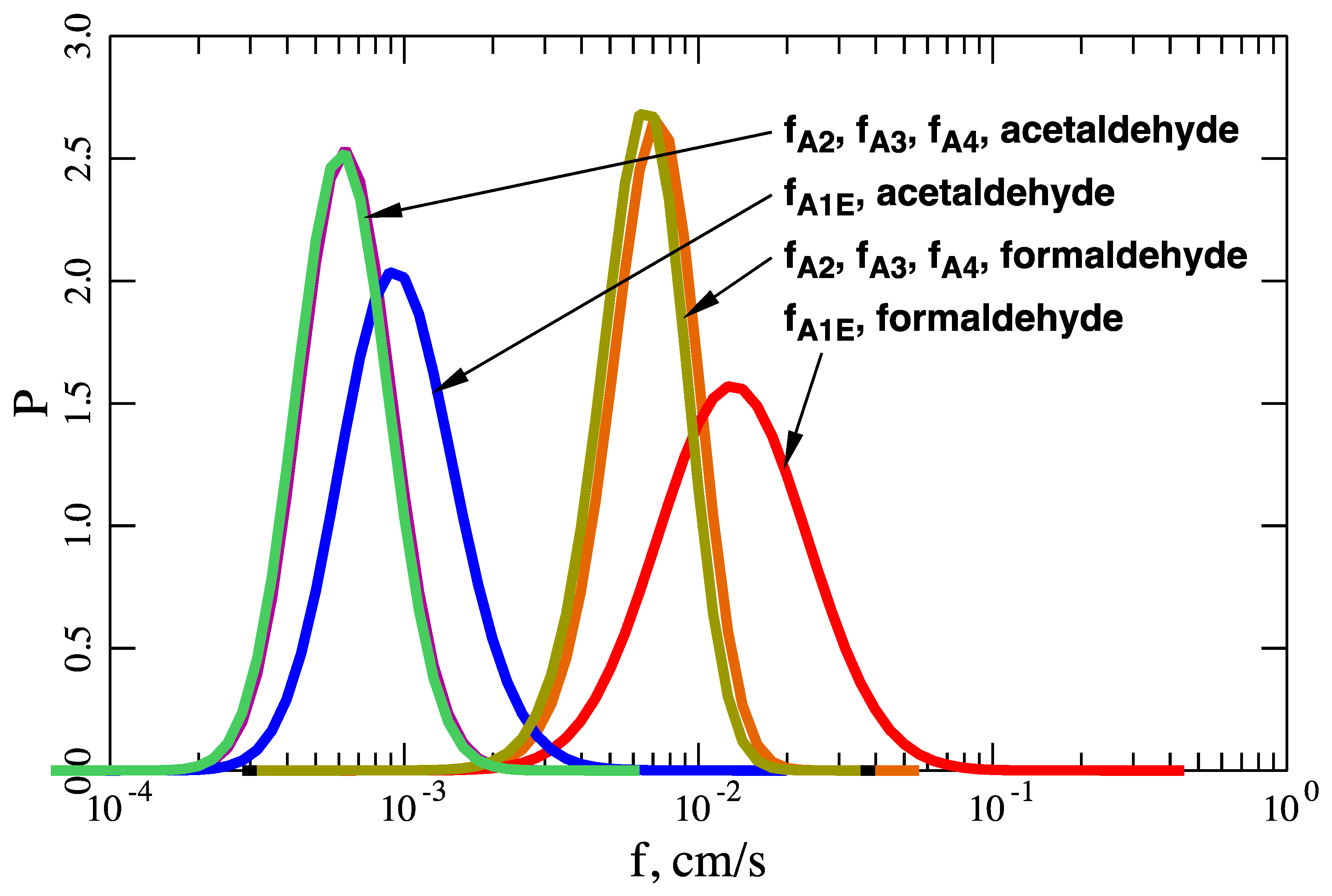
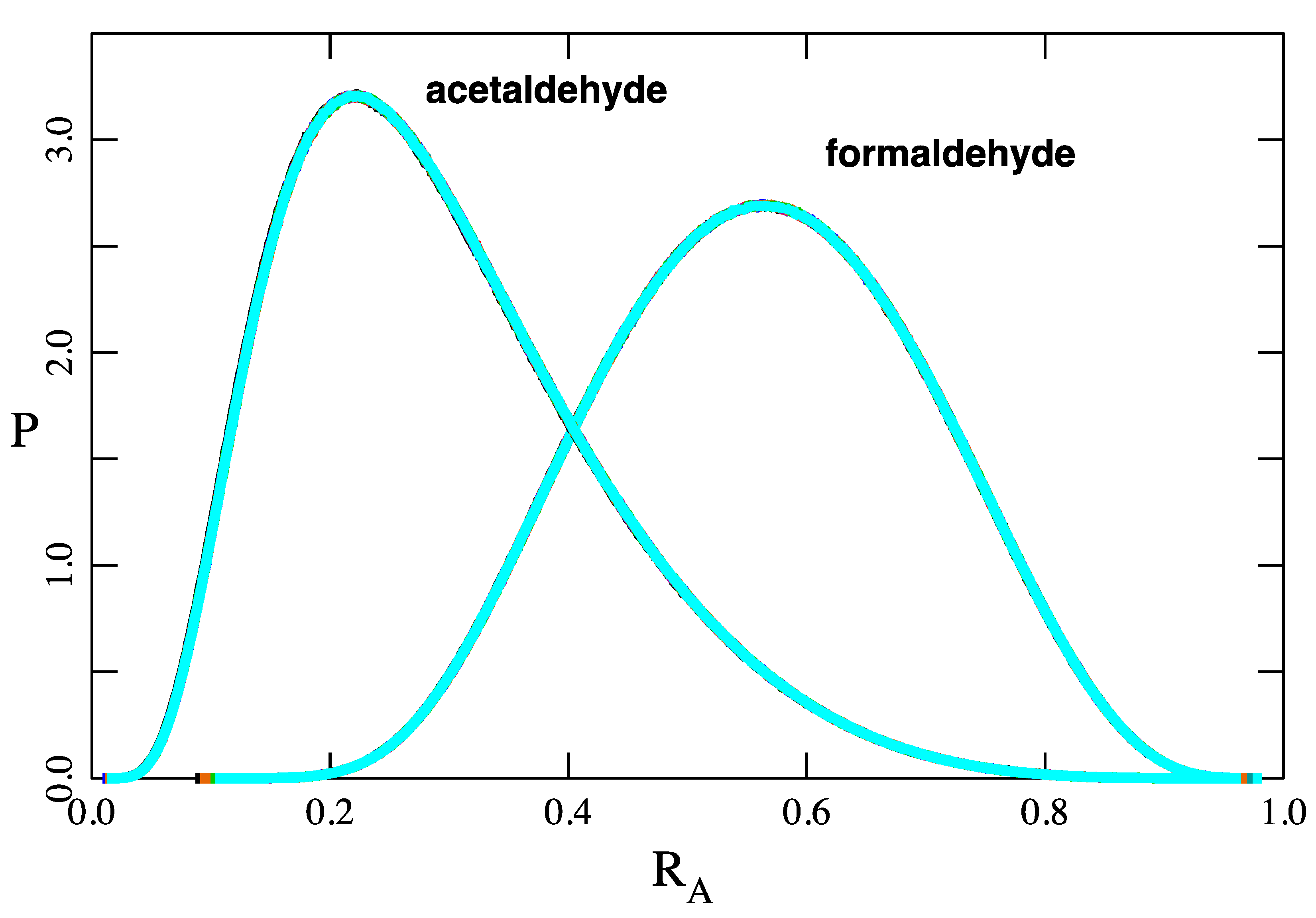
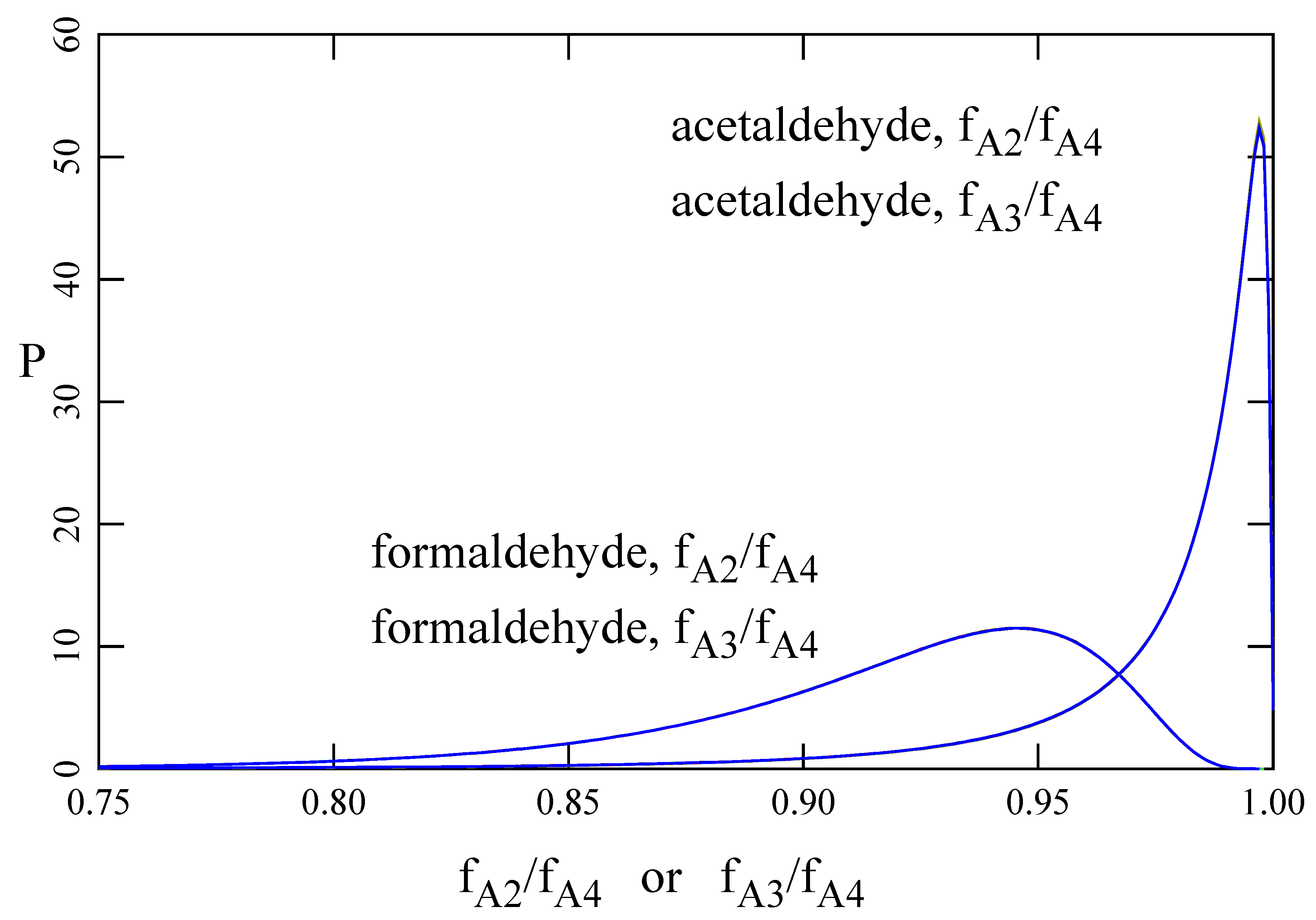
This paper introduces a model of the transport of molecules across the air–water interface that exist in two interconvertible forms, 1 ↔ 2, in both phases and in which both forms are assumed to cross the interface. For formaldehyde and acetaldehyde, the former model (A3) predicts fluxes a few percent less that the new one (A4). However, there are conditions for which the differences between the two models may be much greater.

It is also important to emphasize the difference between intrinsic and effective Henry’s constants. For formaldehyde and acetaldehyde, the model employing an effective Henry’s constant (A1E) overpredicts fluxes by about 90% and 60%, respectively. This is significant because most literature citations report the effective Henry’s constant [67].