Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy
Abstract
1. Introduction
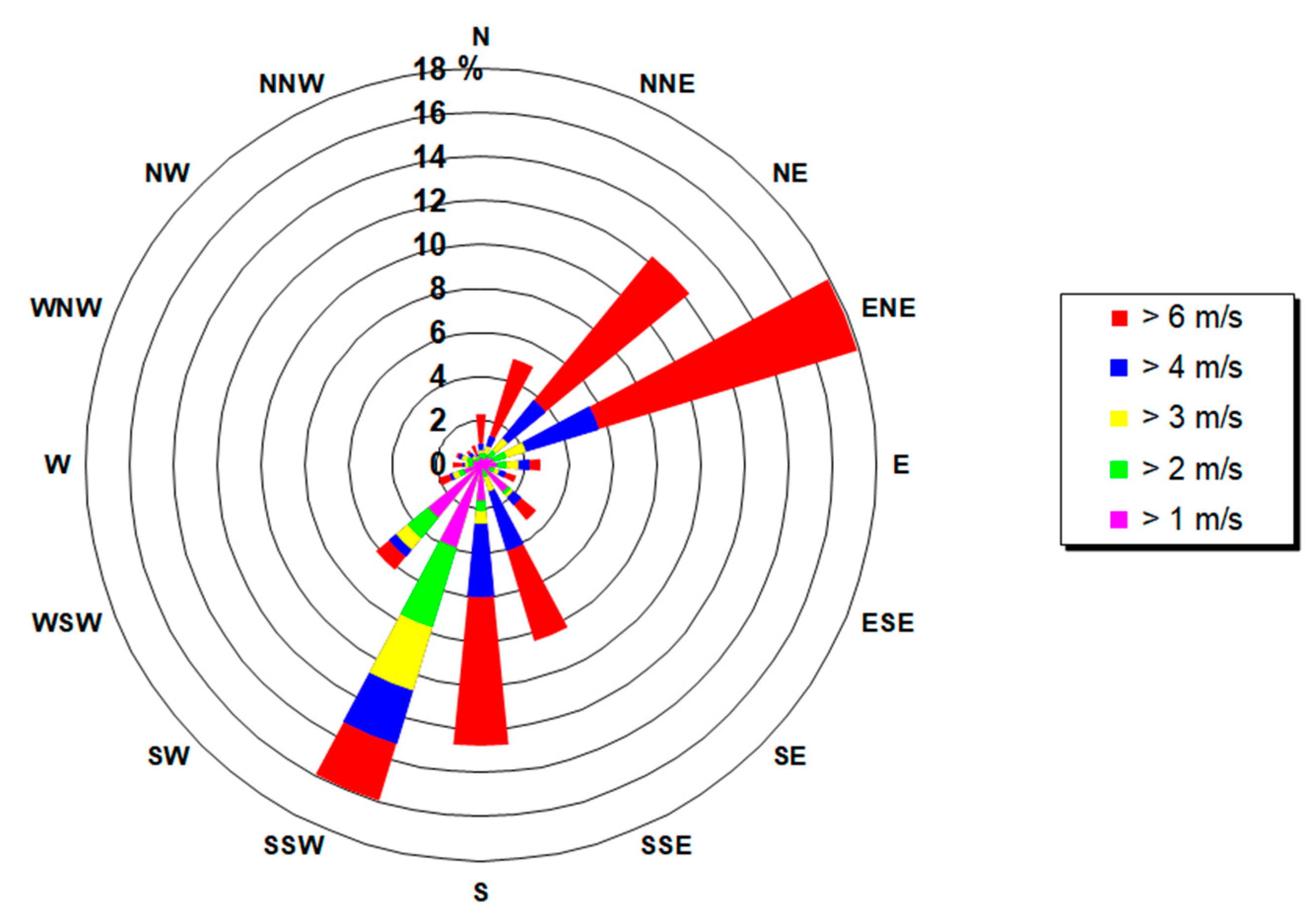
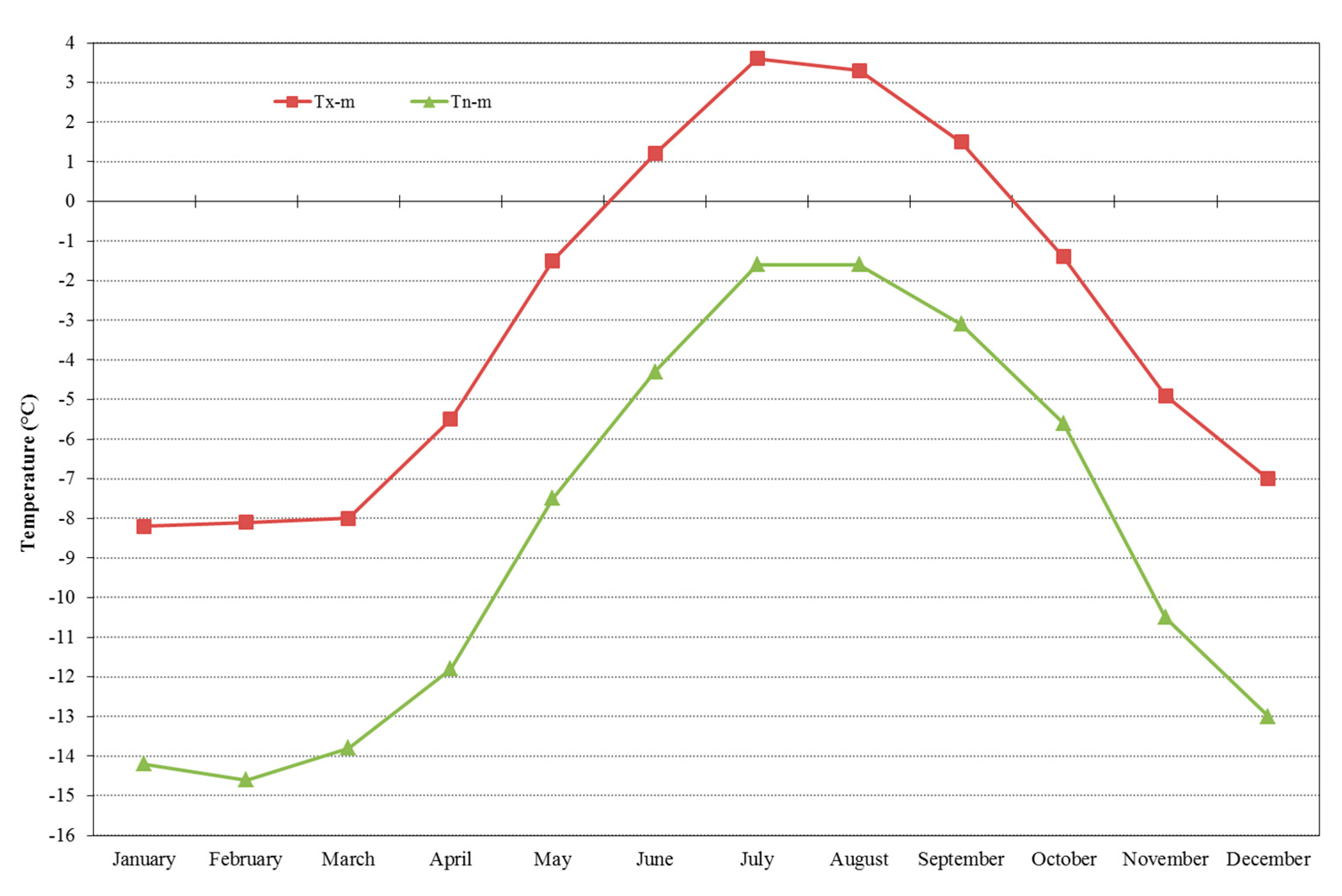
2. Plateau Rosa Monitoring Station
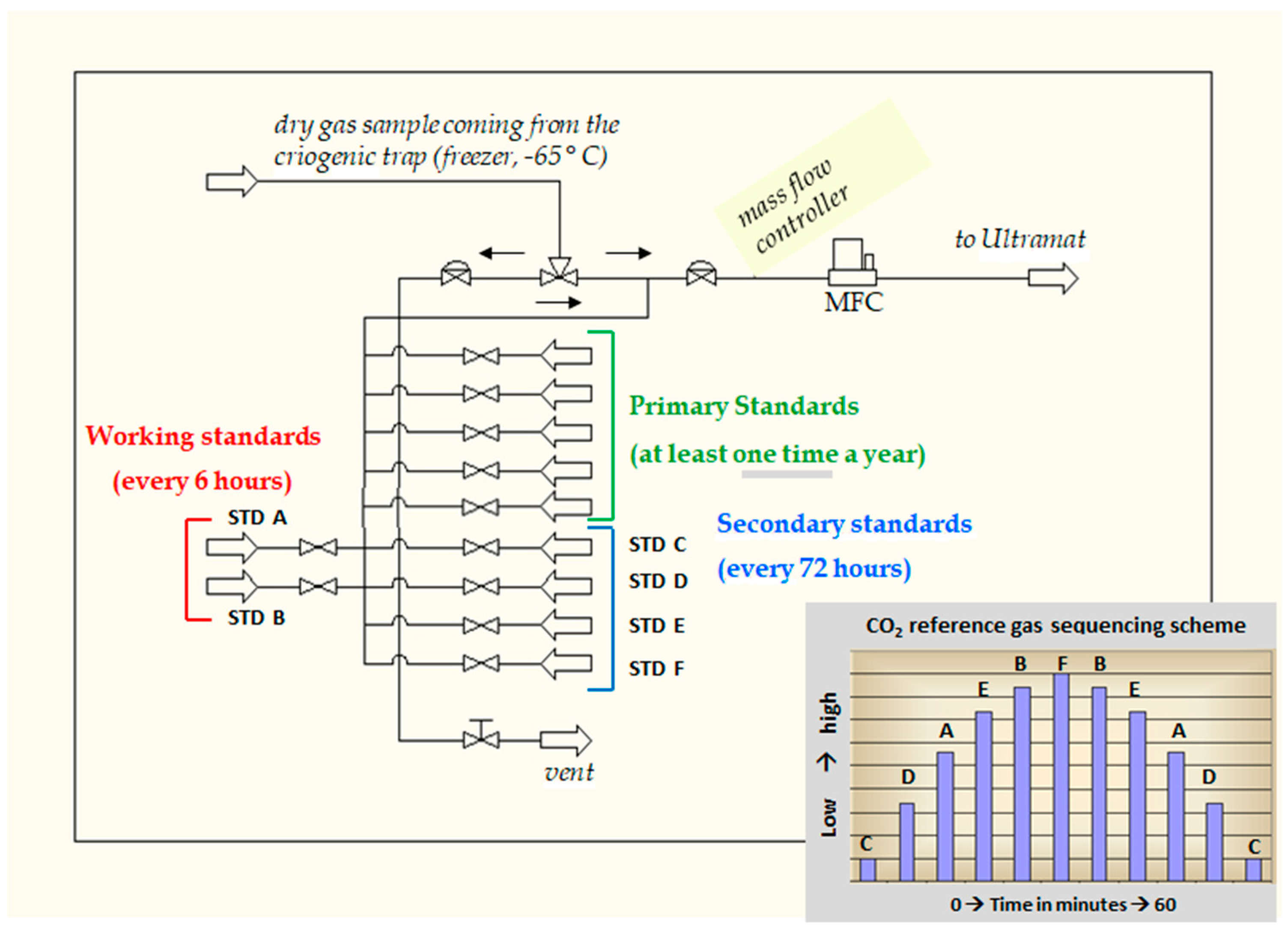
3. CO2 Measurement Instrumentation
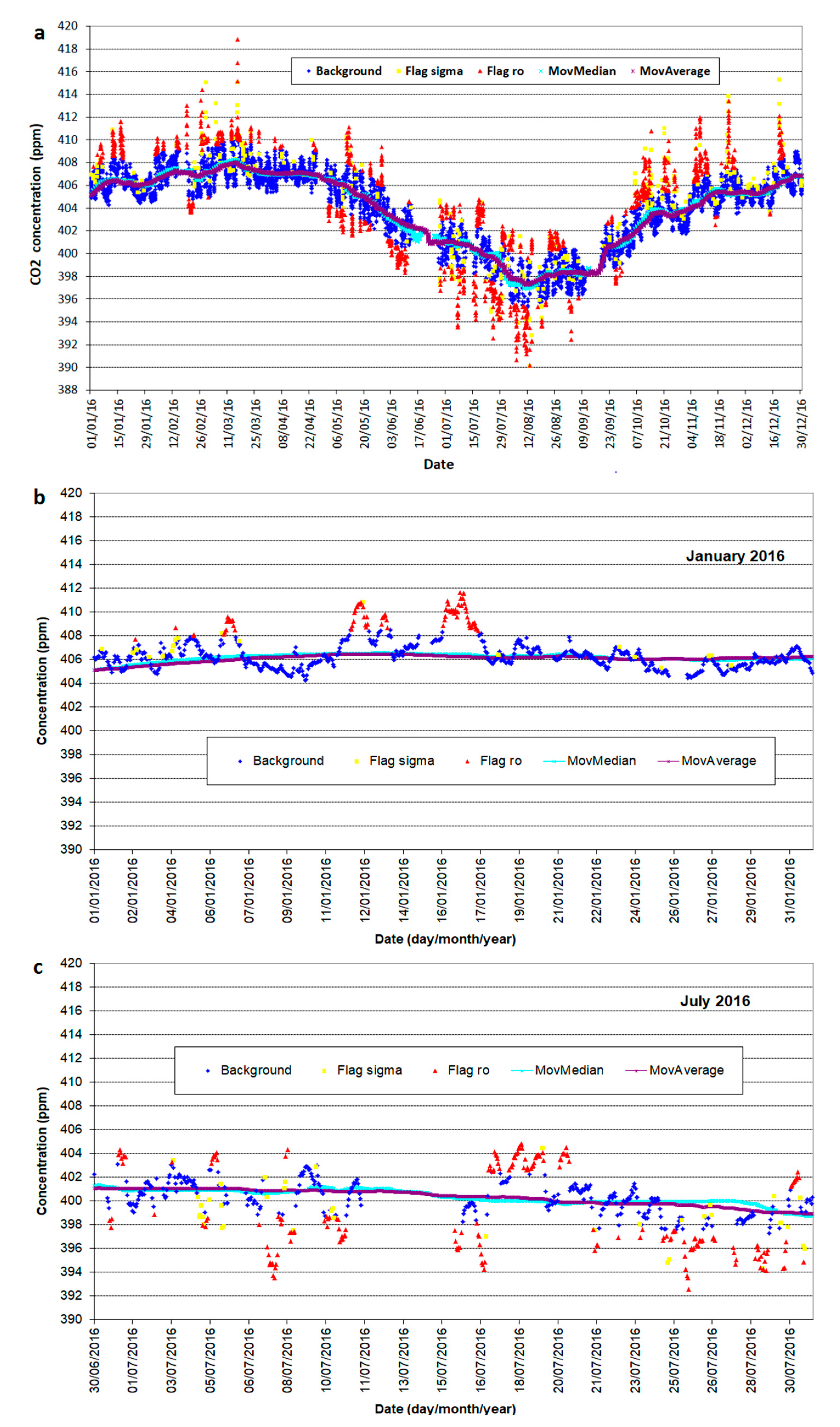
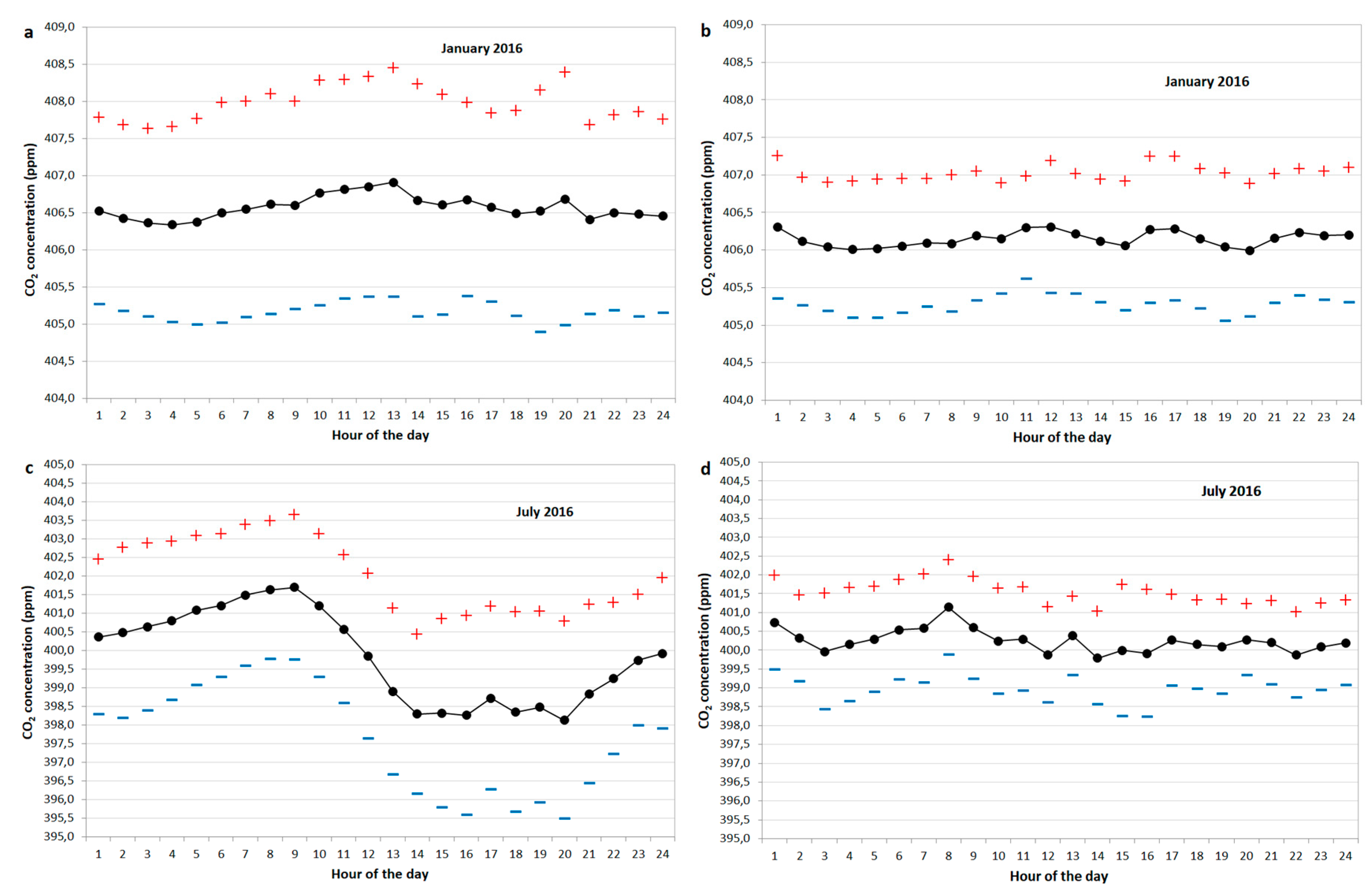
4. Background Data Selection
- The procedure first examines the standard deviation assigned to each hourly average; the datum is flagged if the value exceeds a given threshold (PRS cut-off value σ = 0.7 ppm);
- subsequently, each datum (hourly mean value) is compared with the previous one, and the datum is flagged if the difference exceeds a given threshold (PRS cut-off value δ = 0.3 ppm);
- a moving median (computed only if there is at least 25% of valid data in the list of the 504 theoretically available hourly data, corresponding to 21 days of hourly measurements) is applied to the data that have passed the previous steps, and each hourly measurement is compared with the corresponding moving median value: if the difference exceeds a given threshold (PRS cut-off value ), the datum is flagged and considered as a no-background datum;
- a moving average (computed only if there is at least 10% of valid data in the list of the 504 above mentioned hourly data) is applied to the data that have passed the previous steps, and each hourly measurement is compared with its corresponding moving mean value; the same procedure described in the previous point is applied to identify the background data using the same threshold ;
- finally, all the hourly averages flagged in the above descripted steps are readmitted and are considered background data if their residuals from the moving average are less than or equal to .
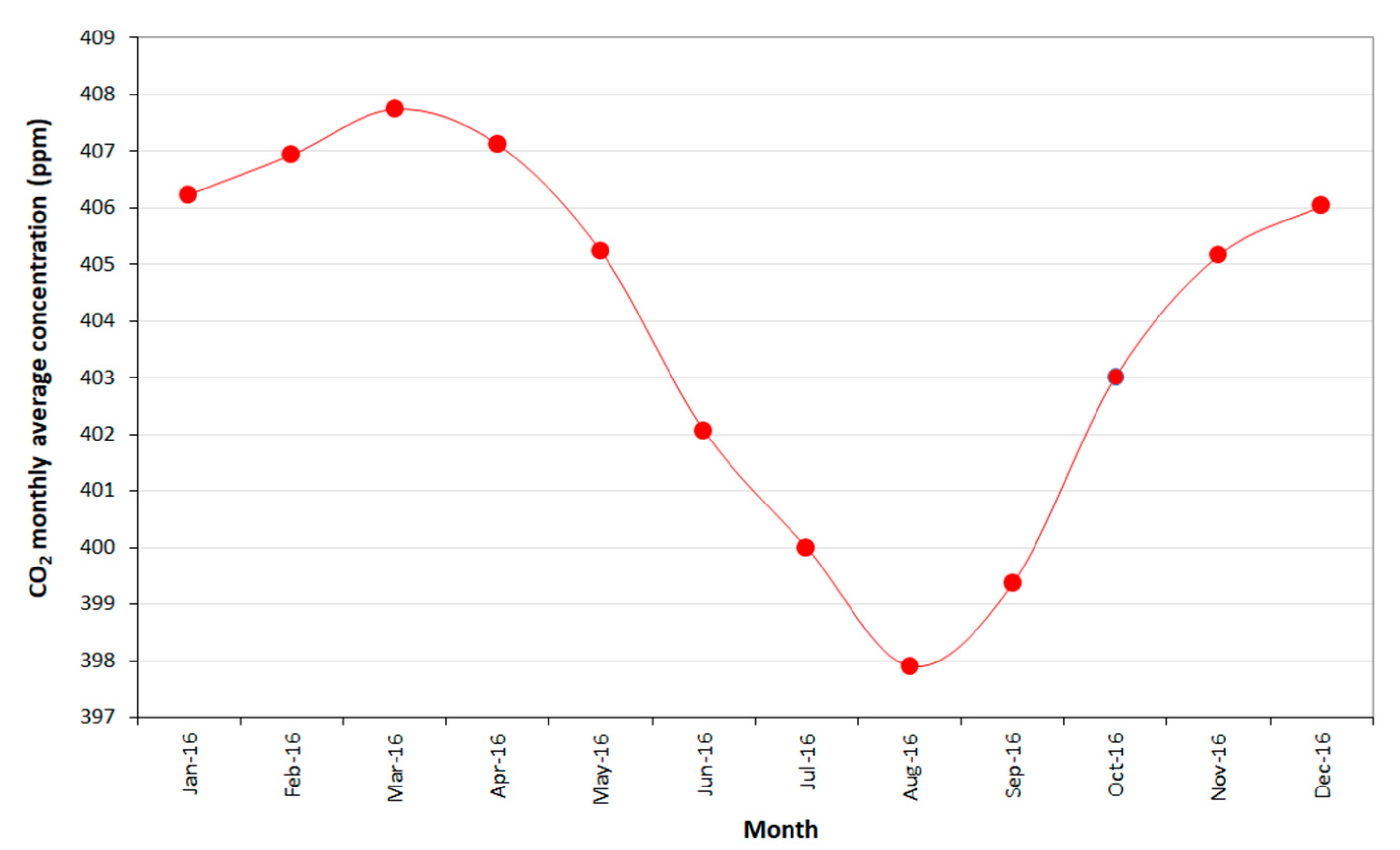
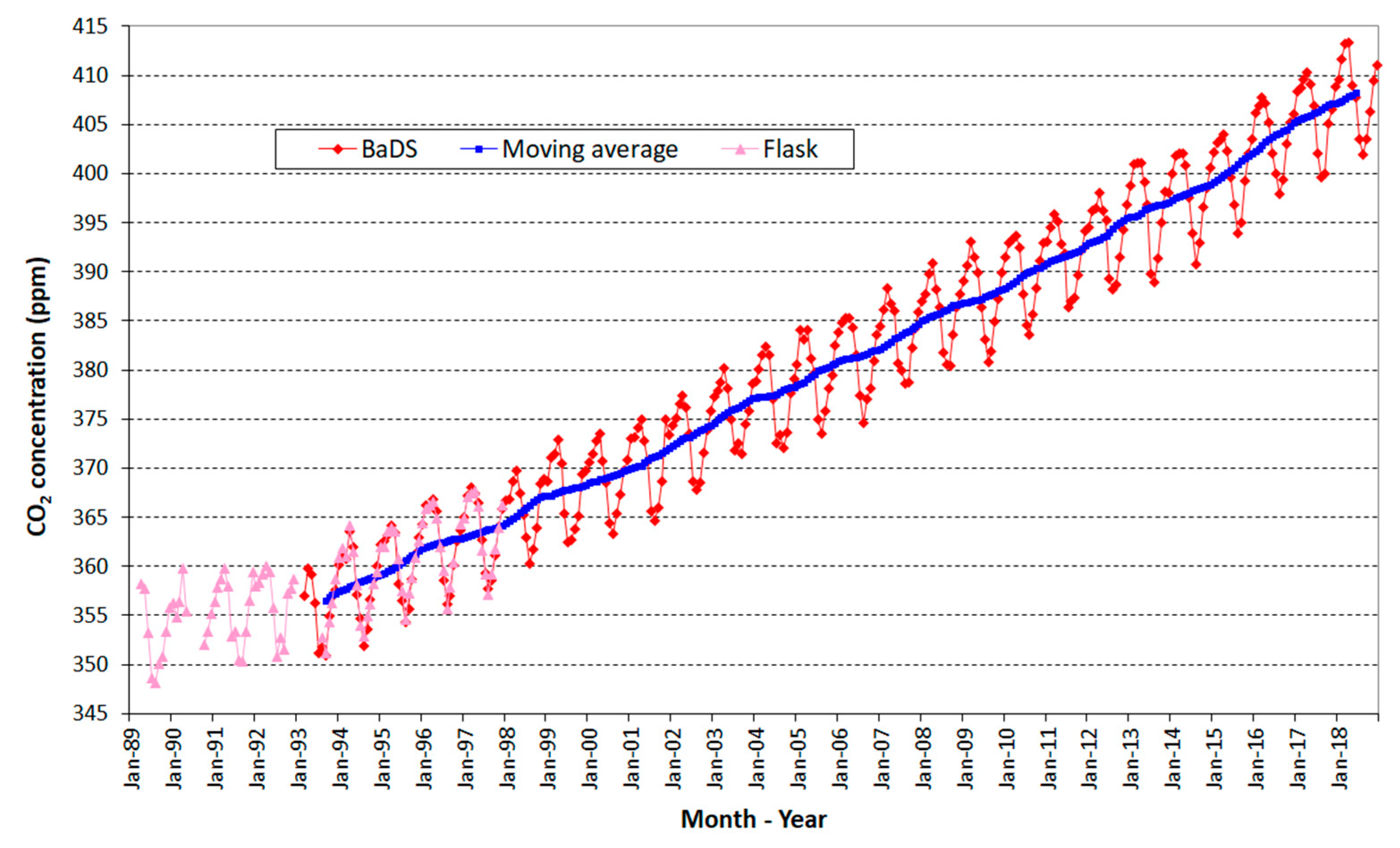
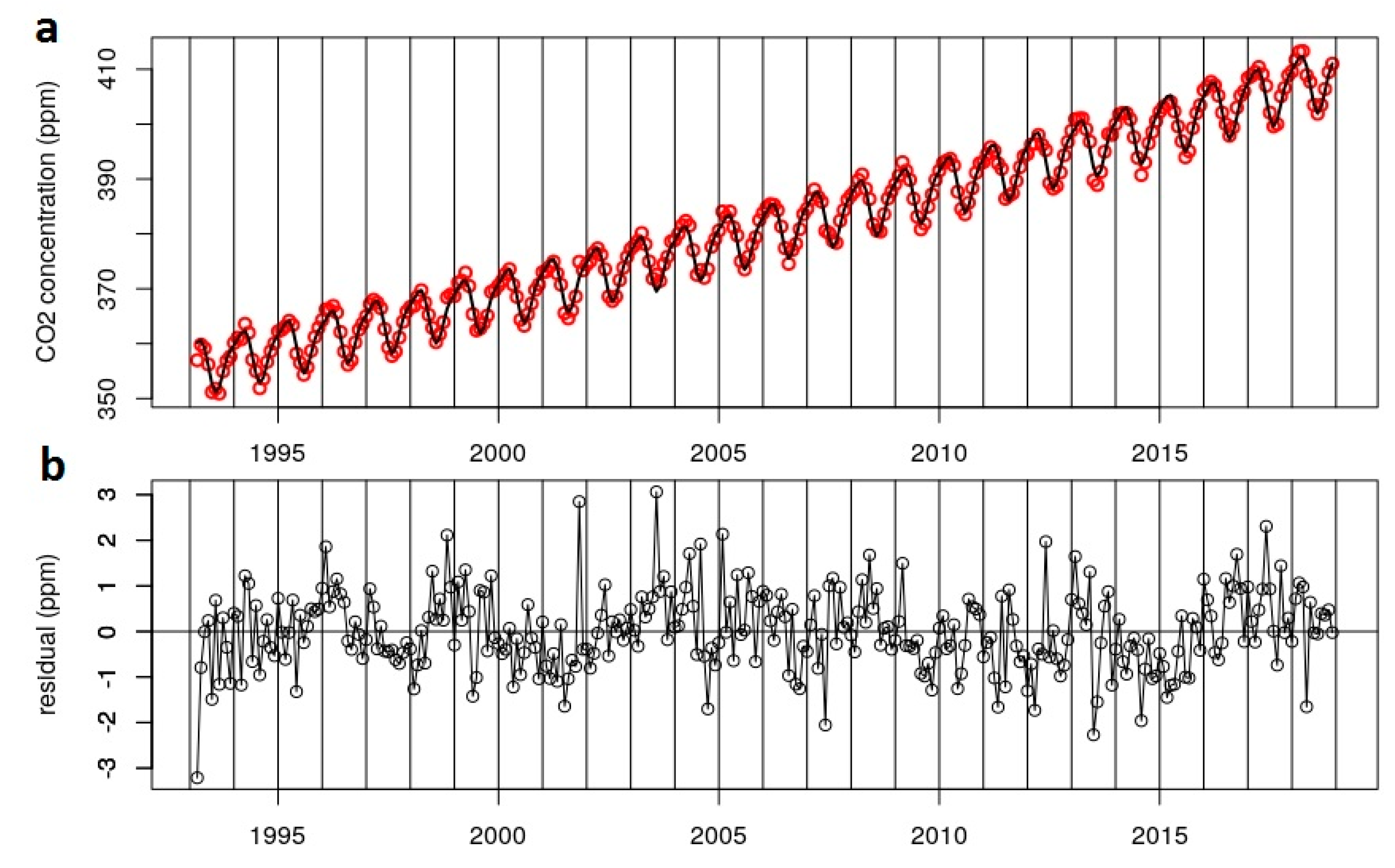
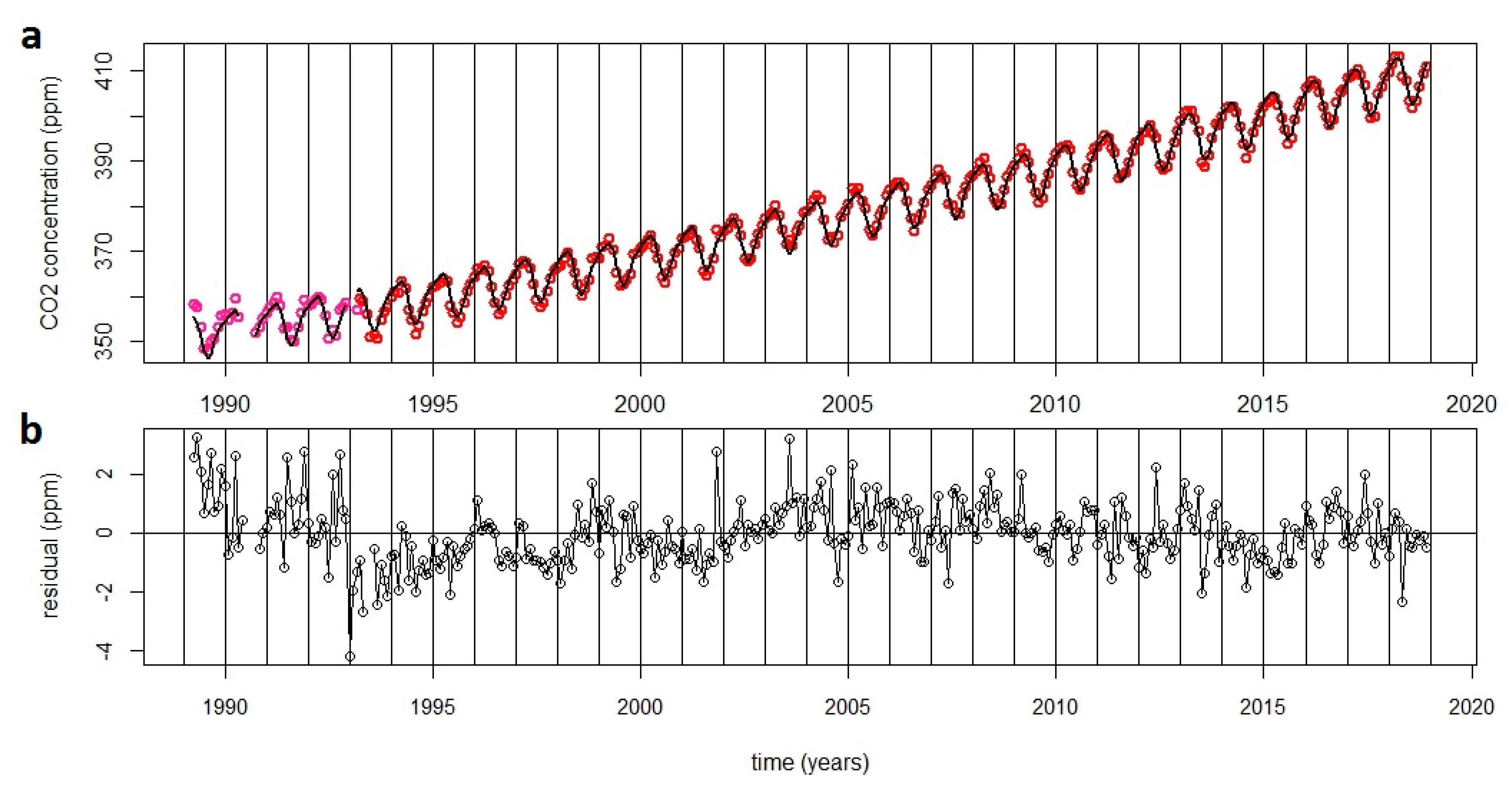
5. The Time Series of the Monthly Averaged CO2 Background Concentrations
5.1. An Overview
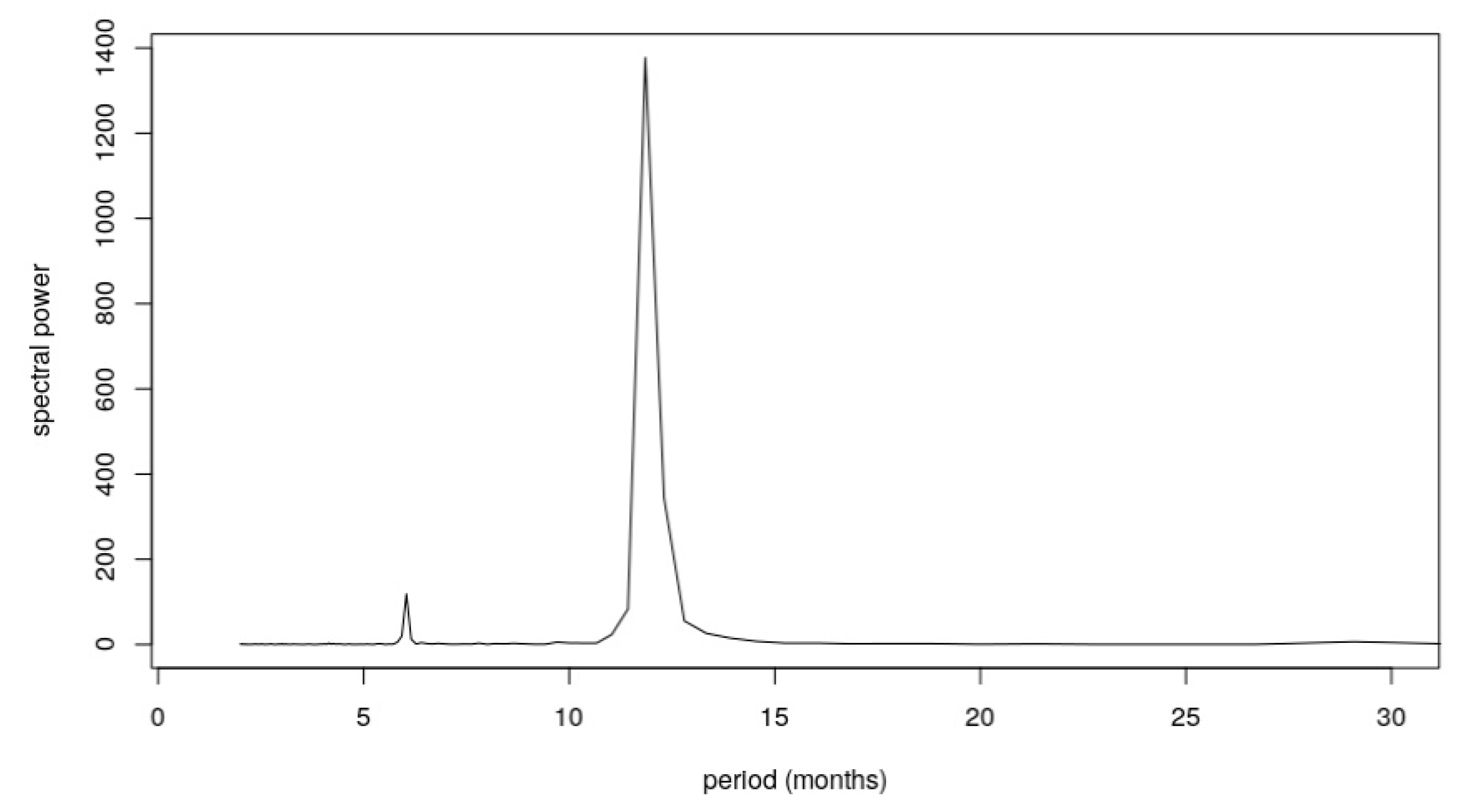
5.2. Curve Fitting: The Long-Term Trend and The Seasonal Cycle
PRS CO2 Curve Fits
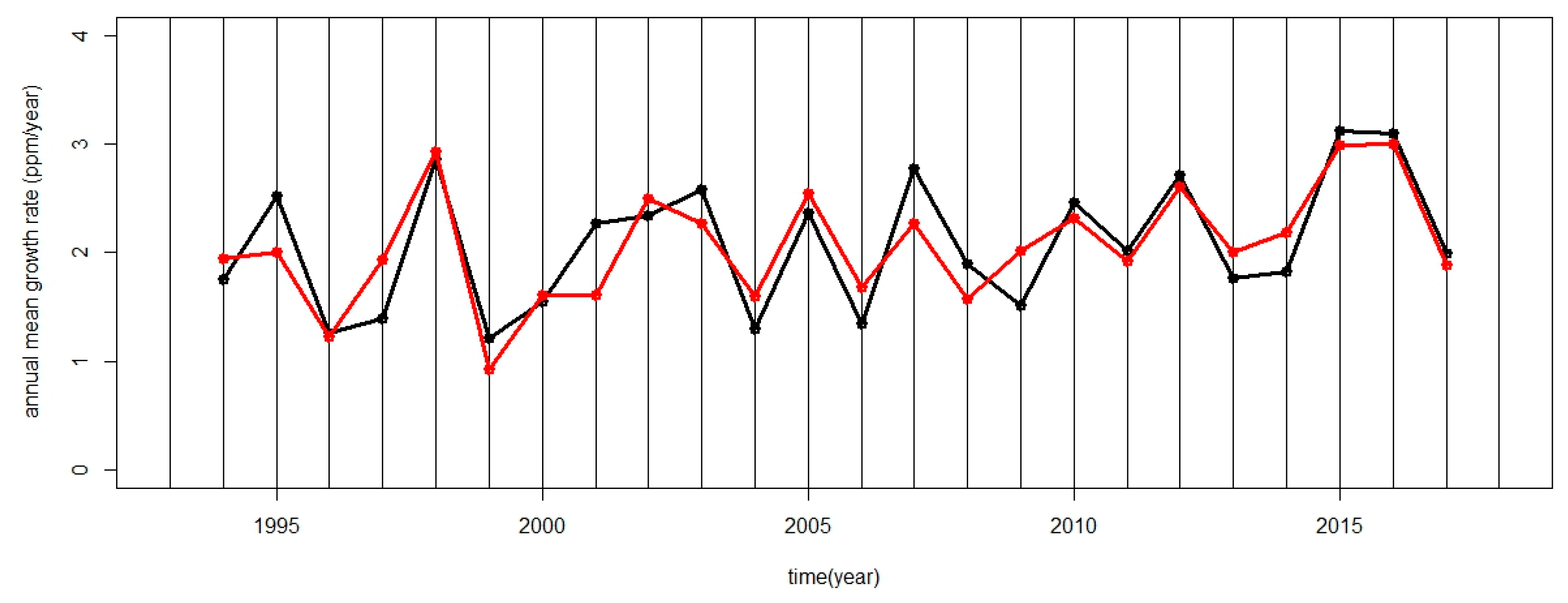
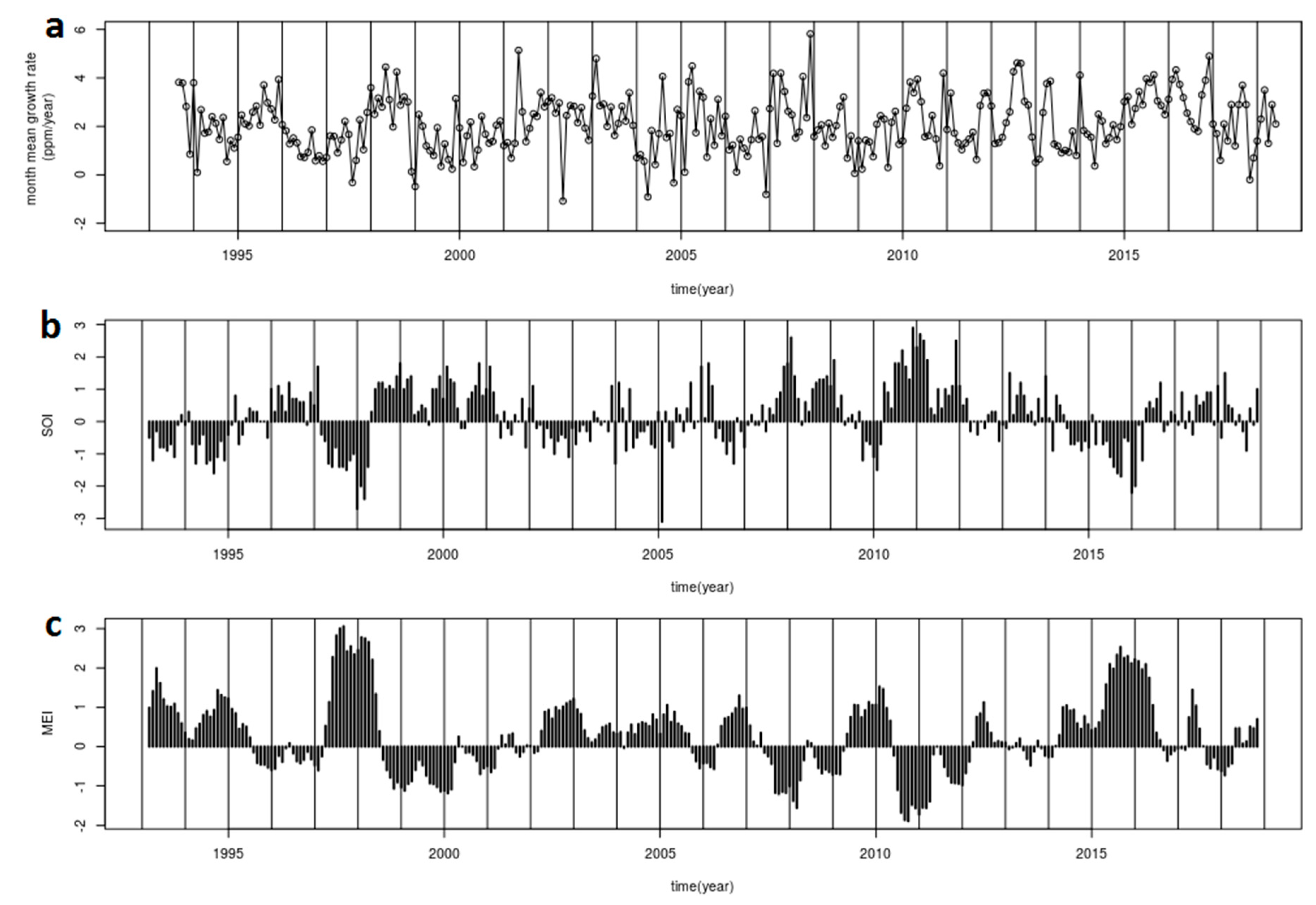
6. Correlation between the Growth Rate and the Natural Indexes
6.1. Annual Mean Growth Rate
6.2. Monthly Mean Growth Rate
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- WMO Greenhouse Gas Bulletin. The State of Greenhouse Gases in the Atmosphere Based on Global Observations through 2017. WMO No. 14. 22 November 2018. Available online: https://library.wmo.int/doc_num.php?explnum_id=5455 (accessed on 18 June 2019).
- Advanced Global Atmospheric Experiment. Available online: https://agage.mit.edu (accessed on 18 June 2019).
- Global Greenhouse Gas Reference Network. Available online: https://www.esrl.noaa.gov/gmd/ccgg (accessed on 18 June 2019).
- Word Data Centre for Greenhouse Gases. Available online: https://gaw.kishou.go.jp (accessed on 18 June 2019).
- Integrated Carbon Observation System. Available online: https://www.icos-ri.eu/icos-national-networks (accessed on 18 June 2019).
- WMO Greenhouse Gas Bulletin. The State of Greenhouse Gases in the Atmosphere Based on Global Observations through 2012. WMO No. 9. 6 November 2013. Available online: https://library.wmo.int/doc_num.php?explnum_id=7288 (accessed on 18 June 2019).
- Longhetto, A.; Apadula, F.; Bacci, P.; Bonelli, P.; Cassardo, C.; Ferrarese, S.; Giraud, C.; Vannini, C. A study of greenhouse gases and air trajectories at Plateau Rosa. Il Nuovo Cim. C 1995, 18, 583–601. [Google Scholar] [CrossRef]
- Longhetto, A.; Ferrarese, S.; Cassardo, C.; Giraud, C.; Apadula, F.; Bacci, P.; Bonelli, P.; Marzorati, A. Relationships between atmospheric circulation patterns and CO2 greenhouse–gas concentration levels in the Alpine troposphere. Adv. Atmos. Sci. 1997, 14, 309–322. [Google Scholar] [CrossRef]
- Ferrarese, S.; Longhetto, A.; Cassardo, C.; Apadula, F.; Bertoni, D.; Giraud, C.; Gotti, A. A study of seasonal and yearly modulation of carbon dioxide sources and sinks, with a particular attention to the Boreal Atlantic Ocean. Atmos. Environ. 2002, 36, 5517–5526. [Google Scholar] [CrossRef]
- Ferrarese, S. Sensitivity test of a source-receptor model. Il Nuovo Cim. 2002, 25, 501–511. [Google Scholar]
- Apadula, F.; Gotti, A.; Pigini, A.; Longhetto, A.; Rocchetti, F.; Cassardo, C.; Ferrarese, S.; Forza, R. Localization of source and sink regions of carbon dioxide through the method of the synoptic air trajectory statistics. Atmos. Environ. 2003, 37, 3757–3770. [Google Scholar] [CrossRef]
- Ferrarese, S.; Apadula, F.; Bertiglia, F.; Cassardo, C.; Ferrero, A.; Fialdini, L.; Francone, C.; Heltai, D.; Lanza, A.; Longhetto, A.; et al. Inspection of high–concentration CO2 events at the Plateau Rosa Alpine station. Atmos. Pollut. Res. 2015, 6, 415–427. [Google Scholar] [CrossRef]
- Peylin, P.; Rayner, P.J.; Bousquet, P.; Carouge, C.; Hourdin, F.; Heinrich, P.; Ciais, P. AEROCARB contributors: Daily CO2 flux estimates over Europe from continuous atmospheric measurements: 1, inverse methodology. Atmos. Chem. Phys. 2005, 5, 3173–3186. [Google Scholar] [CrossRef]
- Peters, W.; Krol, M.C.; van Der Werf, G.R.; Houweling, S.; Jones, C.D.; Hughes, J.; Schaefer, K.; Masarie, K.A.; Jacobson, A.R.; Miller, J.B.; et al. Seven years of recent European net terrestrial carbon dioxide exchange constrained by atmospheric observations. Glob. Chang. Biol. 2010, 16, 1317–1337. [Google Scholar] [CrossRef]
- Broquet, G.; Chevallier, F.; Bréon, F.-M.; Kadygrov, N.; Alemanno, M.; Apadula, F.; Hammer, S.; Haszpra, L.; Meinhardt, F.; Morguí, J.A.; et al. Regional inversion of CO2 ecosystem fluxes from atmospheric measurements: Reliability of the uncertainty estimates. Atmos. Chem. Phys. 2103, 13, 9039–9056. [Google Scholar] [CrossRef]
- Climatological Temperature at PRS. Available online: http://clima.meteoam.it/web_clima_sysman/Clino6190/CLINO052.txt (accessed on 18 June 2019).
- WMO X2007 Reference Scale. Available online: http://www.esrl.noaa.gov/gmd/ccl/co2_scale.html (accessed on 19 July 2019).
- Komhyr, W.D.; Harris, T.B.; Waterman, L.S.; Chin, J.F.S.; Thoning, K.W. Atmospheric carbon dioxide at Mauna Loa Observatory, 1, NOAA Global Climatic Measurement with a Nondispersive Infrared Analyser, 1974–1985. J. Geophys. Res. 1989, 94, 8533–8547. [Google Scholar] [CrossRef]
- Cundari, V.; Colombo, T.; Ciattaglia, L. Thirteen years of atmospheric carbon dioxide measurements at Mt. Cimone station, Italy. Il Nuovo Cim. C 1995, 18, 33–47. [Google Scholar] [CrossRef]
- Laurent, O. ICOS Atmospheric Station Specifications, Version 1.2; August 2016. Available online: https://icos-atc.lsce.ipsl.fr/filebrowser/download/27251 (accessed on 20 May 2019).
- Observation Package. Available online: https://www.esrl.noaa.gov/gmd/ccgg/obspack/labinfo.html (accessed on 18 June 2019).
- Ruckstuhl, A.F.; Henne, S.; Reimann, S.; Steinbacher, M.; Vollmer, M.K.; O’Doherty, S.; Buchmann, B.; Hueglin, C. Robust extraction of baseline signal of atmospheric trace species using local regression. Atmos. Meas. Technol. 2012, 5, 2613–2624. [Google Scholar] [CrossRef]
- Thoning, K.; Tans, P.; Komhyr, W. Atmospheric Carbon Dioxide at Mauna Loa Observatory. 2. Analysis of the NOAA GMCC Data, 1974–1985. J. Geophys. Res. 1989, 94, 8549–8565. [Google Scholar] [CrossRef]
- Novelli, P.; Masarie, K.; Lang, P. Distributions and recent changes of carbon monoxide in the lower troposphere. J. Geophys. Res. 1998, 103, 19015–19033. [Google Scholar] [CrossRef]
- Schuepbach, E.; Friedli, T.; Zanis, P.; Monks, P.; Penkett, S. State space analysis of changing seasonal ozone cycles (1988–1997) at Jungfraujoch (3580 m above sea level) in Switzerland. J. Geophys. Res. 2001, 106, 20413–20427. [Google Scholar] [CrossRef]
- Novelli, P.; Masarie, K.; Lang, P.; Hall, B.; Myers, R.; Elkins, J. Reanalysis of tropospheric CO trends: Effect of the 1997–1998 wildfires. J. Geophys. Res. 2003, 108, 4464. [Google Scholar] [CrossRef]
- Zellweger, C.; Hüglin, C.; Klausen, J.; Steinbacher, M.; Vollmer, M.; Buchmann, B. Inter-comparison of four different carbon monoxide measurement techniques and evaluation of the long-term carbon monoxide time series of Jungfraujoch. Atmos. Chem. Phys. 2009, 9, 3491–3503. [Google Scholar] [CrossRef]
- Moody, J.L.; Samson, P.J. The influence of atmospheric transport on precipitation chemistry at two sites in the midwestern United States. Atmos. Environ. 1989, 23, 2117–2132. [Google Scholar] [CrossRef]
- Harris, J.M.; Kahl, J.D. A descriptive atmospheric transport climatology for the Mauna Loa Observatory, using clustered trajectories. J. Geophys. Res. 1990, 95, 13651–13667. [Google Scholar] [CrossRef]
- Prinn, R.G.; Huang, J.; Weiss, R.F.; Cunnold, D.M.; Fraser, P.J.; Simmonds, P.G.; McCulloch, A.; Harth, C.; Salameh, P.; O’Doherty, S.; et al. Evidence for substantial variations of atmospheric hydroxyl radicals in the past two decades. Science 2001, 292, 1882–1888. [Google Scholar] [CrossRef]
- Cox, M.L.; Sturrock, G.A.; Fraser, P.J.; Siems, S.T.; Krummel, P.B. Identification of Regional Sources of Methyl Iodide from AGAGE Observations at Cape Grim, Tasmania. J. Atmos. Chem. 2005, 50, 59–77. [Google Scholar] [CrossRef]
- Reimann, S.; Manning, A.J.; Simmonds, P.G.; Cunnold, D.M.; Wang, R.H.J.; Li, J.; McCulloch, A.; Prinn, R.G.; Huang, J.; Weiss, R.F.; et al. Low European methyl chloroform emissions inferred from long-term atmospheric measurements. Nature 2005, 433, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Greally, B.R.; Manning, A.J.; Reimann, S.; McCulloch, A.; Huang, J.; Dunse, B.L.; Simmonds, P.G.; Prinn, R.G.; Fraser, P.J.; Cunnold, D.M.; et al. Observations of 1,1-difluoroethane (HFC-152a) at AGAGE and SOGE monitoring stations in 1994–2004 and derived global and regional emission estimates. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Graziosi, F.; Arduini, J.; Furlani, F.; Giostra, U.; Cristofanelli, P.; Fang, X.; Hermanssene, O.; Lunder, C.; Maenhout, G.; O’Doherty, S.; et al. European emissions of the powerful greenhouse gases hydrofluorocarbons inferred from atmospheric measurements and their comparison with annual national reports to UNFCCC. Atmos. Environ. 2017, 158, 85–97. [Google Scholar] [CrossRef]
- Ryall, D.B.; Maryon, R.H.; Derwent, R.G.; Simmonds, P.G. Modelling long-range transport of CFCs to Hace Head, Ireland. Q. J. Roy Meteorol. Soc. 1998, 124, 417–446. [Google Scholar] [CrossRef]
- Balzani Lööv, J.M.; Henne, S.; Legreid, G.; Staehelin, J.; Reimann, S.; Prevot, A.S.H.; Steinbacher, M.; Vollmer, M.K. Estimation of background concentrations of trace gases at the Swiss Alpine site Jungfraujoch (3580 m asl). J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Carpenter, L.; Green, T.; Mills, G.; Bauguitte, S.; Penkett, S.; Zanis, P.; Schuepbach, E.; Schmidbauer, N.; Monks, P.; Zellweger, C. Oxidized nitrogen and ozone production efficiencies in the springtime free troposphere over the Alps. J. Geophys. Res. 2000, 105, 14547–14559. [Google Scholar] [CrossRef]
- Zanis, P.; Ganser, A.; Zellweger, C.; Henne, S.; Steinbacher, M.; Staehelin, J. Seasonal variability of measured ozone production efficiencies in the lower free troposphere of Central Europe. Atmos. Chem. Phys. 2007, 7, 223–236. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, L.; Conway, T.J.; Tans, P.P.; Wang, Y. Short-term variations of atmospheric CO2 and dominant causes in summer and winter: Analysis of 14-year continuous observational data at Waliguan, China. Atmos. Environ. 2013, 77, 140–148. [Google Scholar] [CrossRef]
- Artuso, F.; Chamard, P.; Piacentino, S.; Sferlazzo, D.M.; De Silvestri, L.; di Sarra, A.; Meloni, D.; Monteleone, F. Influence of transport and trends in atmospheric CO2 at Lampedusa. Atmos. Environ. 2009, 43, 3044–3051. [Google Scholar] [CrossRef]
- Derwent, R.; Simmonds, P.; O’Doherty, S.; Ciais, P.; Ryall, D. European source strengths and northern hemisphere baseline concentrations of radiatively active trace gases at Mace Head, Ireland. Atmos. Environ. 1998, 32, 3703–3715. [Google Scholar] [CrossRef]
- Forrer, J.; Rüttimann, R.; Schneiter, D.; Fischer, A.; Buchmann, B.; Hofer, P. Variability of trace gases at the high-Alpine site Jungfraujoch caused by meteorological transport processes. J. Geophys. Res. 2000, 105, 12241–12251. [Google Scholar] [CrossRef]
- Zellweger, C.; Forrer, J.; Hofer, P.; Nyeki, S.; Schwarzenbach, B.; Weingartner, E.; Ammann, M.; Baltensperger, U. Partitioning of reactive nitrogen (NOy) and dependence on meteorological conditions in the lower free troposphere. Atmos. Chem. Phys. 2003, 3, 779–796. [Google Scholar] [CrossRef]
- Henne, S.; Furger, M.; Prevot, A. Climatology of mountain venting-induced elevated moisture layers in the lee of the Alps. J. Appl. Meteorol. 2005, 44, 620–633. [Google Scholar] [CrossRef]
- Ryall, D.B.; Derwent, R.; Manning, A.; Simmonds, P.; O’Doherty, S. Estimating source regions of European emissions of trace gases from observations at Mace Head. Atmos. Environ. 2001, 35, 2507–2523. [Google Scholar] [CrossRef]
- Hirdman, D.; Sodemann, H.; Eckhardt, S.; Burkhart, J.F.; Jefferson, A.; Mefford, T.; Quinn, P.K.; Sharma, S.; Ström, J.; Stohl, A. Source identification of short-lived air pollutants in the Arctic using statistical analysis of measurement data and particle dispersion model output. Atmos. Chem. Phys. 2010, 10, 669–693. [Google Scholar] [CrossRef]
- Yuan, Y.; Ries, L.; Petermeier, H.; Steinbacher, M.; Gómez-Peláez, A.J.; Leuenberger, M.C.; Schumacher, M.; Trickl, T.; Couret, C.; Meinhardt, F.; Menzel, A. Adaptive selection of diurnal minimum variation: A statistical strategy to obtain representative atmospheric CO2 data and its application to European elevated mountain stations. Atmos. Meas. Technol. 2018, 11, 1501–1514. [Google Scholar] [CrossRef]
- Uglietti, C.; Leuenberger, M.; Brunner, D. European source and sink areas of CO2 retrieved from Lagrangian transport model interpretation of combined O2 and CO2 measurements at the high alpine research station Jungfraujoch. Atmos. Chem. Phys. 2011, 11, 8017–8036. [Google Scholar] [CrossRef]
- Sun, Y.; Bian, L.; Tang, J.; Gao, Z.; Lu, C.; Schnell, R.C. CO2 monitoring and background mole fraction at Zhongshan station, Antarctica. Atmosphere 2014, 5, 686–698. [Google Scholar] [CrossRef]
- Schmidt, M.; Graul, R.; Sartorius, H.; Levin, I. The Schauinsland CO2 record: 30 years of continental observations and their implications for the variability of the European CO2 budget. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Valentino, F.L.; Leuenberger, M.; Uglietti, C.; Sturm, P. Measurements and trend analysis of O2, CO2 and δ13C of CO2 from high altitude research station Junfgraujoch, Switzerland—A comparison with the observations from the remote site Puy de Dome, France. Sci. Total Environ. 2008, 391, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.S.; Zhou, L.X.; Tans, P.P.; Cias, P.; Steinbacher, M.; Xu, L.; Luan, T. In situ measurements of atmospheric CO2 at the four WMO/GAW stations in China. Atmos. Chem. Phys. 2014, 14, 2541–2554. [Google Scholar] [CrossRef]
- Necki, J.; Schmidt, M.; Rozanski, K.; Zimnoch, M.; Korus, A.; Lasa, J.; Graul, R.; Levin, I. Six-years record of atmospheric carbon dioxide and methane at a high-altitude mountain site in Poland. Tellus B 2003, 55, 94–104. [Google Scholar] [CrossRef]
- Sanchez, M.L.; Perez, I.A.; Garcia, M.A. Study of CO2 variability at different temporal scales recorded in a rural Spanish site. Agric. For. Meteorol. 2010, 150, 1168–1173. [Google Scholar] [CrossRef]
- Wu, J.; Guan, D.; Yuan, F.; Yang, H.; Wang, A.; Jin, C. Evolution of atmoaspheric carbon dioxide concentration at different temporal scales recorded in a tall forest. Atmos. Environ. 2012, 61, 9–14. [Google Scholar] [CrossRef]
- Timokhina, A.V.; Prokushkin, A.S.; Onuchin, A.A.; Panov, A.V.; Kofman, G.B.; Heimann, M. Variability of ground CO2 concentration in the middle taiga subzone of the Yenisei region of Siberia. Russ. J. Ecol. 2015, 46, 143–151. [Google Scholar] [CrossRef]
- Erickson, D.J., III; Mills, R.T.; Gregg, J.; Blasing, T.J.; Hoffman, F.M.; Andres, R.H.; Devries, M.; Zhu, Z.; Kawa, S.R. An estimate of monthly global emissions of anthropogenic CO2: Impact on the seasonal cycle of atmospheric CO2. J. Geophys. Res. 2008, 113, G01023. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Rödenbeck, C.; Keeling, R.; Heimann, M.; Thonicke, K.; Zaehle, S.; Reichstein, M. Enhanced Seasonal CO2 Exchange Caused by Amplified Plant Productivity in Northern Ecosystems. Science 2016, 351, 696–699. [Google Scholar] [CrossRef]
- Curve Fitting. Available online: https://www.esrl.noaa.gov/gmd/ccgg/mbl/crvfit/crvfit.html (accessed on 18 June 2019).
- Bacastow, R.B. Modulation of atmospheric carbon dioxide by the Southern Oscillation. Nature 1976, 261, 116–118. [Google Scholar] [CrossRef]
- Jones, C.D.; Cox, P.M. Modeling the volcanic signal in the atmospheric CO2 record. Glob. Biogeochem. Cycles 2001, 15, 453–465. [Google Scholar] [CrossRef]
- Annual Growths Rate at Mauna Loa Station. Available online: www.esrl.noaa.gov/gmd/ccgg/trends/gr.html (accessed on 27 May 2019).
- Betts, R.A.; Jones, C.D.; Knight, J.R.; Keeling, R.F.; Kennedy, J.J. El Niño and a record CO2 rise. Nat. Clim. Chang. 2016, 6, 806–810. [Google Scholar] [CrossRef]
- SOI Index. Available online: www.cpc.ncep.noaa.gov/data/indices/soi (accessed on 27 May 2019).
- Patra, P.K.; Maksyutov, S.; Nakazawa, T. Analysis of atmospheric CO2 growth rates at Mauna Loa using CO2 fluxes derived from an inverse model. Tellus B 2005, 57, 357–365. [Google Scholar] [CrossRef]
- Chamard, P.; Thiery, F.; Di Sarra, A.; Ciattaglia, L.; De Silvestri, L.; Grigioni, F.; Monteleone, F.; Piacentino, S. Interannual variability of atmospheric CO2 in the Mediterranean: Measurements at the island of Lampedusa. Tellus B 2003, 55, 83–93. [Google Scholar] [CrossRef]
- MEI Index. Available online: https://www.esrl.noaa.gov/psd/enso/mei.old/table.html (accessed on 27 May 2019).
- Rödenbeck, C.; Bakker, D.C.E.; Metzl, N.; Olsen, A.; Sabine, C.; Cassar, N.; Reum, F.; Keeling, R.F.; Heimann, M. Interannual sea–air CO2 flux variability from an observation-driven ocean mixed-layer scheme. Biogeosciences 2014, 11, 4599–4613. [Google Scholar] [CrossRef]

| Coefficients | Values |
|---|---|
| b | 0.171 ± 0.001 ppm month−1 |
| c1 | 4.94 ± 0.09 ppm |
| c2 | 1.41 ± 0.09 ppm |
| Coefficients | Values |
|---|---|
| b2 | 0.0010 ± 0.0001 month−1 |
| c1 | 4.59 ± 0.14 ppm |
| c2 | 1.39 ± 0.07 ppm |
| d | 0.0025 ± 0.0008 ppm month−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apadula, F.; Cassardo, C.; Ferrarese, S.; Heltai, D.; Lanza, A. Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy. Atmosphere 2019, 10, 418. https://doi.org/10.3390/atmos10070418
Apadula F, Cassardo C, Ferrarese S, Heltai D, Lanza A. Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy. Atmosphere. 2019; 10(7):418. https://doi.org/10.3390/atmos10070418
Chicago/Turabian StyleApadula, Francesco, Claudio Cassardo, Silvia Ferrarese, Daniela Heltai, and Andrea Lanza. 2019. "Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy" Atmosphere 10, no. 7: 418. https://doi.org/10.3390/atmos10070418
APA StyleApadula, F., Cassardo, C., Ferrarese, S., Heltai, D., & Lanza, A. (2019). Thirty Years of Atmospheric CO2 Observations at the Plateau Rosa Station, Italy. Atmosphere, 10(7), 418. https://doi.org/10.3390/atmos10070418







