1. Introduction
The complex chain of processes in the atmosphere, ionosphere, and magnetosphere before earthquakes result in precipitating particles producing ionization of the lower ionosphere. Earthquake preparation is accompanied by a set of precursory phenomena connected with the transformations within the Earth’s crust. The ionization leads to an increase in the electron concentration in the D-region of the ionosphere, which is equivalent to lowering the ionosphere [
1]. This lowering changes the condition of radio wave propagation in different frequency bands from VLF up to VHF.
Several ionospheric precursors of earthquakes are currently under investigation (for details see [
2] or [
3]). The electromagnetic precursors of earthquakes (not limited to the VLF part of the electromagnetic spectrum) are discussed with case studies in a recent paper [
4].
In the case when the resultant electromagnetic field at the receiver site can be considered as the sum of a large number of plane, cylindrical, or spherical waves with a uniformly distributed random phase, such a field can be regarded as a Gaussian random field. As a result of the central limit theorem at any point, the sum of these individual plane-wave contributions exhibits a Gaussian distribution. This is the case of the VLF signal propagation when different waves arrive at the place of the receiver via different propagation paths (with different time delays) and combine in the resultant oscillating signal. The stochastic properties of this oscillating signal carry information about random chaotic processes taking place in the ionosphere, which are, herein, studied for the first time using the methods of random matrix theory.
2. Theoretical Framework
In a previous work [
5], we described the link between the stochastic properties of the lower ionosphere (the D-layer) and seismic activity. The stochastic properties were investigated by means of reflected VLF signals. The D-layer acts as a Gaussian random plane for VLF wave reflection. Reflected waves have the properties of random waves, this being manifested in the fact that their auto-correlation function in time is a Bessel function of the second kind and it is zero-order. We showed that the properties of the Bessel function are connected with the seismic activity in the area near the great circle path of VLF waves.
The integral representation of the Bessel function of the first kind and zeroth order is according to [
6]
If we assume the signal strength at the antenna to be a result of the superposition of (for simplicity) two plane waves of the same frequency, the other reflected from the ionosphere so that the two incoming waves have angular separation . Then, their correlation would vary like , because the projection of the wavelength of the other wave along the direction of propagation of the other is multiplied by . Now, we can treat as a random variable uniformly distributed over the circle and compute the average. Thus, the Bessel function emerges as a consequence of the underlying geometry.
Measurable changes in the auto-correlation function were found in the cases when the great circle path of the VLF signal crossed an earthquake preparation zone with radius
calculated by the equation proposed by Scholz et al. [
7]
where
M is the magnitude of the earthquake. Statistically significant (an uncertainty level better than
) changes were found for shallow earthquakes with magnitudes
. For the further study of the stochastic properties of the ionosphere, random matrix theory was chosen.
Random Matrix Theory
Random matrix theory is a powerful tool for studying chaotic phenomena and is also used in the statistical analysis of large samples. It can reveal underlying order in chaotic data, which cannot be seen from the raw datasets. Random matrices were introduced in nuclear physics when Eugene Wigner modeled the nuclei of heavy atoms. He postulated that for the spacings between the lines in the spectrum of a heavy atom nucleus, the same equations hold as for the spacings between the eigenvalues of a random matrix. Since then, random matrices have been successfully applied in the field of stock market analysis [
8], human EEG data processing [
9], and HLA -peptide binding predictions in biology [
10].
Random matrix theory states that for a set of entirely random matrices, the eigenvalues of the correlation matrix of these matrices are governed by the Wigner distribution with probability density function
This Wigner distribution is present in the eigenvalues before stock market crashes or in EEG data during epileptic seizures. Under normal circumstances, data appear not to be interdependent. However, when the level spacing of such chaotic systems starts to exhibit behavior similar to predictions of random matrix theory, abrupt changes follow, as is described below.
3. Materials and Methods
A very simple experimental setup was used to obtain the field strengths. A loop antenna made of 20 turns of enameled wire was connected to the JFET amplifier and NE5534 precision instrumental amplifier. The signal was fed to the sound card of an ordinary personal computer with a sampling frequency of 196 kHz. The sampling frequency of the sound card was sufficient for VLF signals according to Shanon–Kotelnikovov theorem. 2-bin fast Fourier transformation was performed with custom software using the Cooley–Tukey algorithm to obtain the frequencies of interest.
Five transmitters were used (see
Table 1). The described effects were found only for the Denizköy VLF transmitter located in Turkey (
N
E), because the great circle path of the signal to the Czech Republic crosses the Mediterranean region, which is seismically active because of the northward convergence (4–10 mm/year) of the African plate with respect to the Eurasian plate along a complex plate boundary. There were some earthquakes in Norway during the survey period, but with smaller magnitudes (
) and with preparation zones not directly under the great circle path of the signal from the DHO38 transmitter, so no measurable changes were found in the data.
The analysis of the amplitude time series data was performed as follows: Firstly, diurnal patterns were removed with digital filtering and data were divided into individual quartiles of the day (times from 00:00 to 06:00, from 06:00 to 12:00, from 12:00 to 18:00, and from 18:00 to 24:00 UTC). Then, we divided the signal into 90 sampling points and put these splintered sections into the matrix. This calculation gave us a matrix of 90 rows and 24 columns. Then, the correlation matrix of this matrix and its eigenvalues were calculated. These numbers were sorted by size. Then, unfolding of these eigenvalues was performed and histograms of the unfolded eigenvalues were created. These histograms essentially corresponded to the probability density of this variable.
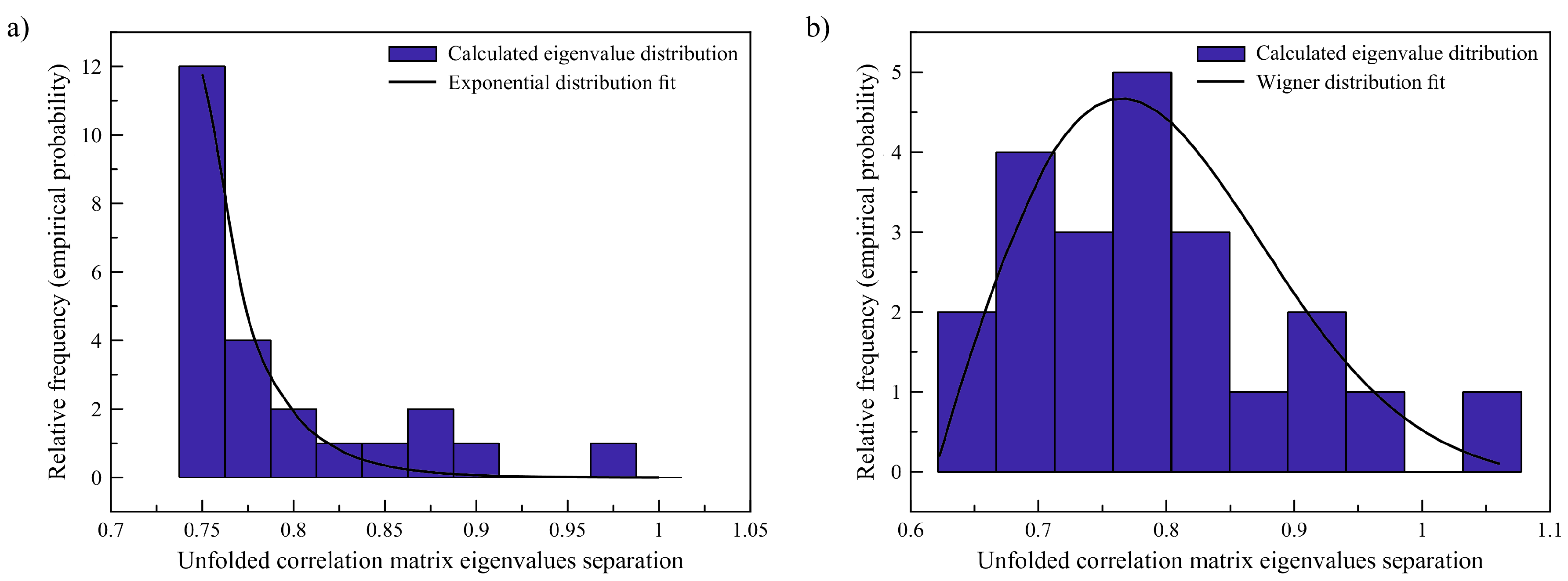
Under normal circumstances, the histogram shows a typical exponential distribution (see
Figure 1a) with probability density function
This is the sign that the physical processes in the ionosphere can be regarded as a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. Before the earthquake, the histogram shows a different behavior, resembling the Wigner distribution (see
Figure 1b).
4. Results and Discussion
This behavior was found before several earthquakes studied in the past with the auto-correlation minimum method described in [
5]. Over forty earthquakes with magnitude
were studied over the year; the best results were obtained for M5.0+ earthquakes.
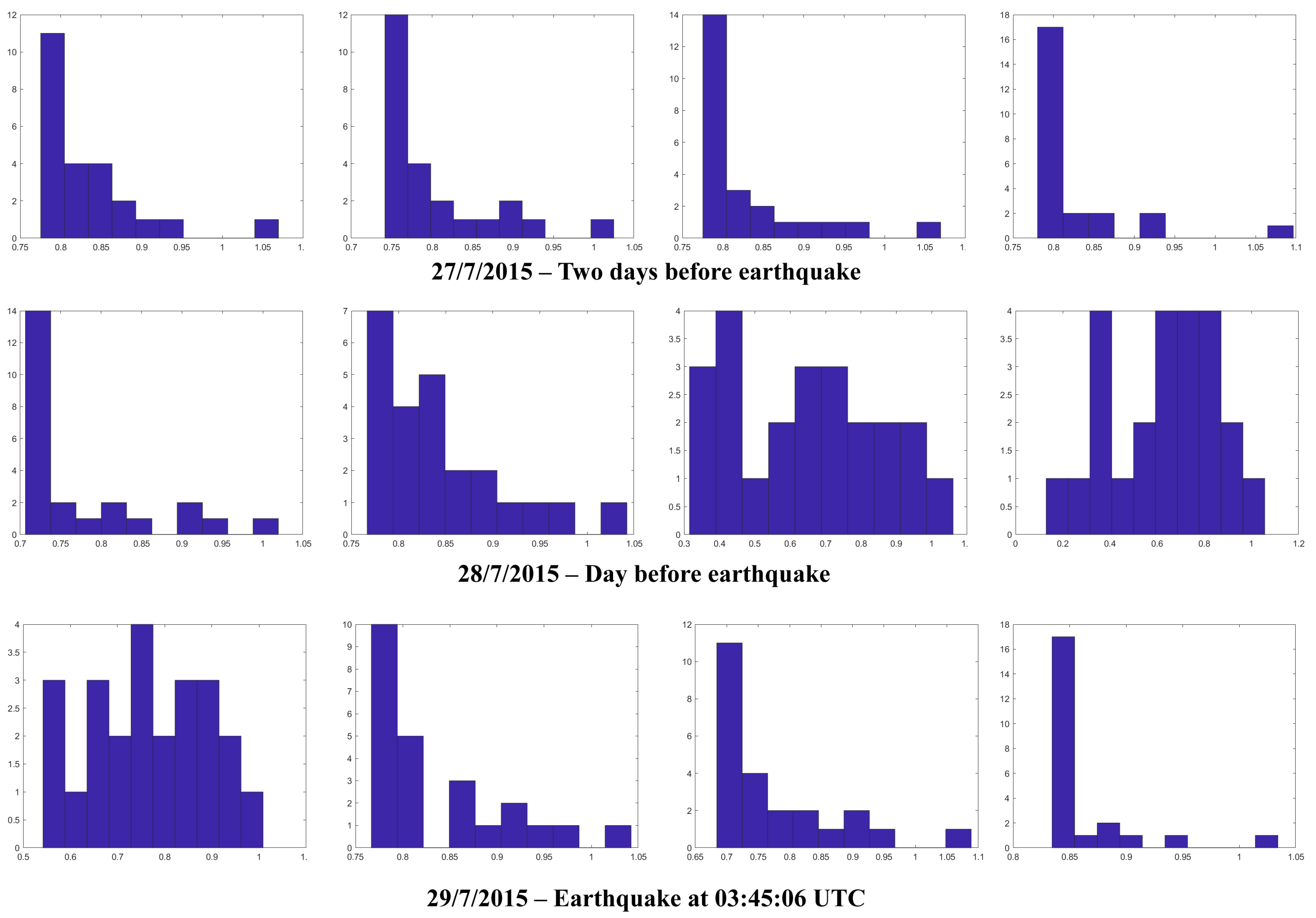
Figure 2 shows histograms for three days centered on the M5.8 Adamas earthquake. On the day of the earthquake, abrupt changes in the cross-correlation matrix eigenvalues separation can be clearly seen. The transient region between exponential and Wigner distribution can be seen in the third image in the second row because part of the process has become completely uncorrelated and part of the process in that time window has already begun to show collective behavior. In the fourth image of the second row and the first image in the third row, a Wigner-like distribution can be seen. After the earthquake, the ionosphere returns to its previous uncorrelated state.
These effects can be caused by the penetration of the electric field of the seismic source into the plasmasphere. Cyclotron-resonance interaction between waves and particles leads to precipitation of energetic electrons into the lower atmosphere, leading to an increase in electron density in the ionospheric D-region. Furthermore, the dynamics of the plasma motion can change, leading to a measurable alteration in the stochastic parameters of the ionosphere.
Data were statistically investigated by calculating the Pearson product-moment correlation coefficient. For all the earthquakes studied in the selected region, no direct correlation was found, but for earthquakes with preparation zones under the VLF propagation path, the Pearson correlation coefficient was calculated as 0.84 (which is some ten percent worse than with the method described in [
5]). Using a table of critical values for the two-tailed test from [
11], the significance level is better than
= 0.05.
Changes were found only for shallow earthquakes. Theoretical calculations (see for example [
1]) show that the vertical ground electric field starts to penetrate effectively into the ionosphere and creates irregularities in the electron concentration when the size of the area on the ground surface occupied by the anomalous field exceeds 200 km in diameter.
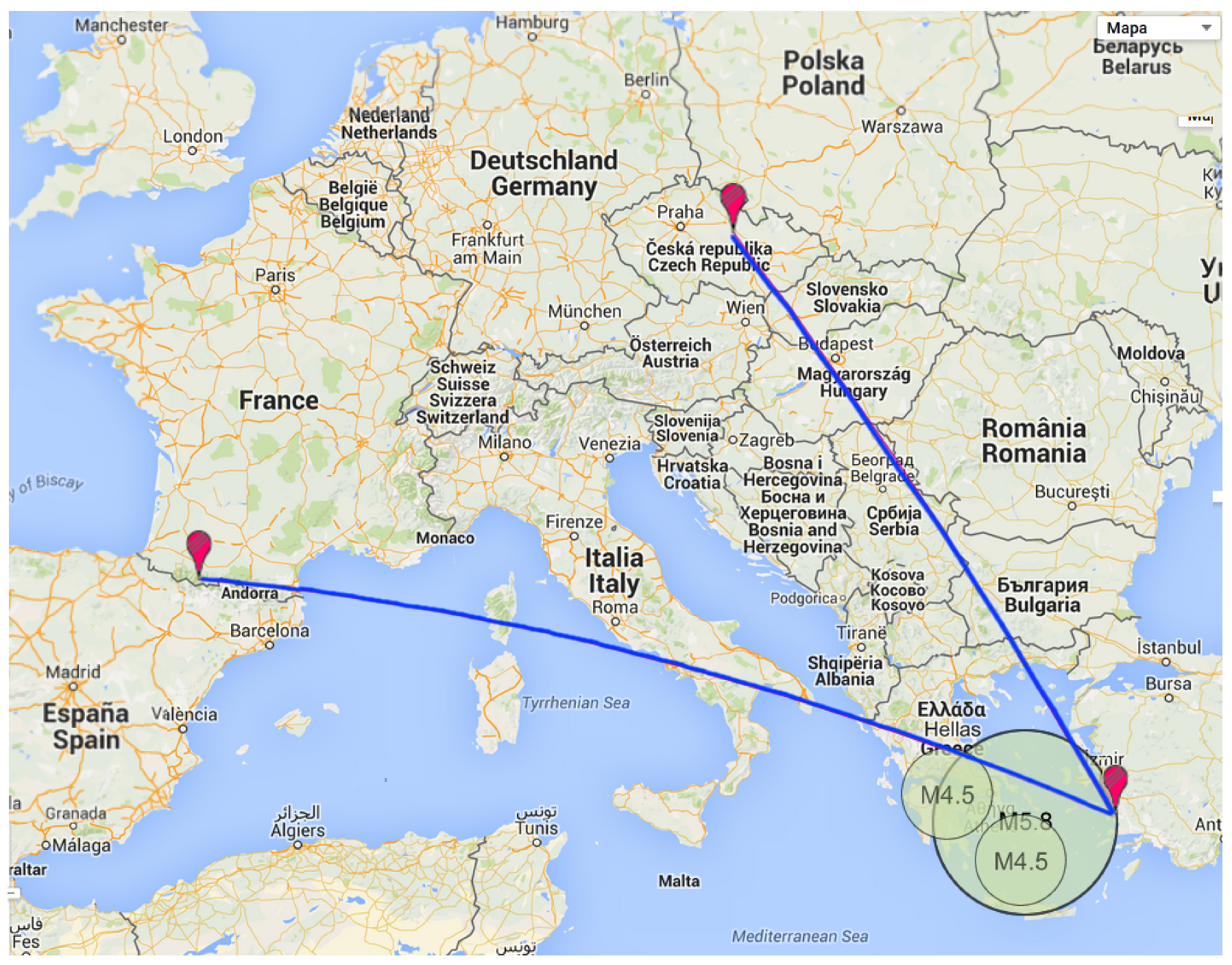
Figure 3 shows the geometry of the signal propagation from the TBB transmitter to the receiver in the Czech Republic and the control receiver in France. Two receivers were used to detect possible changes in emission power. Earthquake preparation zones according to Equation (
2) are also depicted. Only the M5.8 Adamas earthquake produced detectable changes in the eigenvalue distribution of the correlation matrix for both receivers; the M4.5 earthquake near Sami, Greece, was apparent in data received in France but not in data from the Czech Republic. If the earthquake preparation zone was not under the great circle path, no measurable changes were detected.
The data were also examined to study the terminator effect, associated with phase changes of received components of diffracted waves during sunrise and sunset, manifested by minima in both the amplitude and phase of the received VLF signal diurnal variation. Data were tested in 10 min samples during the day and by checking the behavior for days before and after the earthquake. It was found that no significant changes were seen for days before the earthquake.
Because the ionosphere is a highly dynamic medium, many other phenomena not related to earthquakes can change the properties of the scattered VLF waves. For reliable earthquake forecasting, the impact of these processes has to be ruled out.
It is known that ionization of the lower ionosphere can increase during solar flares as the X-ray and UV part of the solar spectrum penetrates the D-layer and the VLF signal amplitude can increase or decrease due to changes in the geometry of propagation during such a flare. Details can be found in [
12] or [
13], for example. A conducted statistical study of solar flares up to the X1.6 level showed that such flares had statistically negligible (
= 0.05) influence on the auto-correlation function computed over 24 h or the random matrix spacing calculated over the six hour time slot, leading to the conclusion that the measured phenomena can be separated from changes in the signal amplitudes that occur during such solar storms. However, this will have to be carefully verified in future studies of the cross-correlation matrix eigenvalues separation behavior during solar X-ray flares.
During the considered time period, Geostationary Operational Environmental Satellite (GOES) recorded three solar X-ray flares [
14]. However, all of them were of a low intensity (B class) and it is not expected that they affect the low ionosphere enough to have influenced the present analysis. In addition, only one of them occurred during the daytime when the solar influence is important for VLF signal propagation.
The influence of moderate magnetic storms is negligible at higher latitudes ([
15]), only extreme geomagnetic storms can impact electron density at high latitudes, resulting in measurable changes in VLF data. Data from the local magneto-metric station Budkov (BDV, [
16]) in the Czech Republic were used to exclude the influence of magnetic storms.
The European Severe Weather Database [
17] was used to ascertain whether at the time of measurement there were meteorological conditions on the signal path or at the receiver site that could affect the signal, but no severe lightning strikes or other meteorological phenomena were found.
Additionally, the transmitter and receiver influence was checked to show if the changes of the particular signal were detected by both receivers to exclude effects outside the ionosphere.
5. Conclusions
In this paper, we describe a novel method for the study of the chaotic properties of the ionosphere, using random matrix theory for the first time in this field. Future research should be aimed at searching for methods that can discriminate between low-level and more severe earthquakes. In the study of random matrix theory precursors of earthquakes with , the dependence of the seismo-ionospheric effects on the epicenter depth have to be considered.
The concept of an earthquake preparation zone, which joins geophysical and geochemical precursors with ionospheric precursors of earthquakes, seems to show that ionospheric precursors belong to the same family of precursors as the other two.
The validity of this forecasting approach needs to be tested in other areas before it can be considered a method for the detection of possible earthquake precursors. For instance, Japan might be a very good location for study due to large-scale earthquakes occurring as a result of the subduction of the Philippine Sea Plate beneath the continental Amurian Plate and Okinawa Plate, and the subduction of the Pacific Plate under the Okhotsk Plate, as well as frequent low intensity earthquakes caused by the fact that Japan is situated in a volcanic zone of the Pacific Ring of Fire.
The described precursor effects have one advantage—the technical realization of the VLF receiver is very simple and inexpensive due to the frequency range being in the tens of kilohertz. Such receivers and detectors can, therefore, be manufactured inexpensively and in large quantities and placed in appropriate areas.
Author Contributions
Conceptualization, J.Š.; methodology, F.S.; software, F.S.; validation, J.K.; formal analysis, L.B.; data curation, F.S.; writing—original draft preparation, J.Š.; writing—review and editing, L.B.; supervision, J.K.
Funding
This research was funded by University of Hradec Kralové Specific Research grant number 2108/2019.
Acknowledgments
Data from European Severe Weather Database (ESWB), GOES satellite and Budkov (BDV) geomagnetic observatory were used to evaluate the independence of the results to solar storms, changes in the geomagnetic field and to eliminate the effects of severe meteorological phenomena.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, V.P.; Pulinets, S.A.; Hegai, V.V. Theoretical model of possible disturbances in the nighttime mid-latitude ionospheric D-region over an area of strong earthquake preparation. Radiophys. Quantum Electron. 2002, 45, 262–268. [Google Scholar] [CrossRef]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-540-20839-6. [Google Scholar]
- Perrone, L.; Korsunova, L.P.; Mikhailov, A.V. Ionospheric precursors for crustal earthquakes in Italy. Ann. Geophys. 2010, 28, 941–950. [Google Scholar] [CrossRef]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2015. [Google Scholar] [CrossRef]
- Šlégr, J.; Váňová, K. Stochastic properties of lower ionosphere as earthquake precursor. J. Seismol. 2017, 21, 243–248. [Google Scholar] [CrossRef]
- Stuber, G.L. Principles of Mobile Communication; Kluwer Academic: Boston, MA, USA, 1996; ISBN 0792397320. [Google Scholar]
- Scholz, C.H.; Sykes, L.R.; Aggarwal, Y.P. Earthquake prediction: A physical basis. Science 1973, 181, 803–809. [Google Scholar] [CrossRef] [PubMed]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.N.; Stanley, H.E. A random matrix theory approach to financial cross-correlations. Phys. A Stat. Mech. Its Appl. 2000, 278, 374–382. [Google Scholar] [CrossRef]
- Šeba, P. Random matrix analysis of human EEG data. Phys. Rev. Lett. 2003, 9, 198104. [Google Scholar] [CrossRef] [PubMed]
- Košmrlj, A.; Read, E.L.; Qi, Y.; Allen, T.M.; Altfeld, M.; Deeks, S.G.; Pereyra, F.; Carrington, M.; Walker, B.D.; Chakraborty, A.K. Effects of thymic selection of the T-cell repertoire on HLA class I-associated control of HIV infection. Nature 2010, 465, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Freund, J. Modern Elementary Statistics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Mitra, A.P. Ionospheric Effects of Solar Flares; Springer: Dordrecht, The Netherlands, 1974; p. 249. ISBN 978-94-010-2231-6. [Google Scholar]
- Davies, K. Ionospheric Radio; Peter Peregrinus: London, UK, 1990; p. 580. [Google Scholar]
- Tolbert, K. GOES X-ray Events for 2015. Last modified 21 January 2016. Available online: https://hesperia.gsfc.nasa.gov/goes/goes_event_listings/goes_xray_event_list_2015.txt (accessed on 2 July 2019).
- Atulkar, R.; Bhardwaj, S.; Khatarkar, P.; Purohit, P.K. Geomagnetic disturbances and its impact on ionospheric critical frequency (foF2) at high, mid and low latitude region. Am. J. Astron. Astrophys. 2014, 6, 61–65. [Google Scholar] [CrossRef]
- Budkov (BDV). INTERMAGNET—The Global Network of Magnetic Observatories Monitoring the Earth’s Magnetic Field. Available online: http://www.intermagnet.org/imos/imos-list/imos-details-eng.php?iaga_code=BDV (accessed on 2 July 2019).
- Groenemeijer, P.; Dotzek, N.; Stel, F.; Brooks, H.; Doswell, C.; Elsom, D.; Giaiotti, D.; Gilbert, A.; Holzer, A.; Meaden, T.; et al. 2004: ESWD—A standardized, flexible data format for severe weather reports. In Proceedings of the Third European Conference on Severe Storms, León, Spain, 9–12 November 2004; University of León: León, Spain, 2004. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).