Inferring Fine-Mode and Coarse-Mode Aerosol Complex Refractive Indices from AERONET Inversion Products over China
Abstract
1. Introduction
2. Data and Method
2.1. AERONET Inversion Products
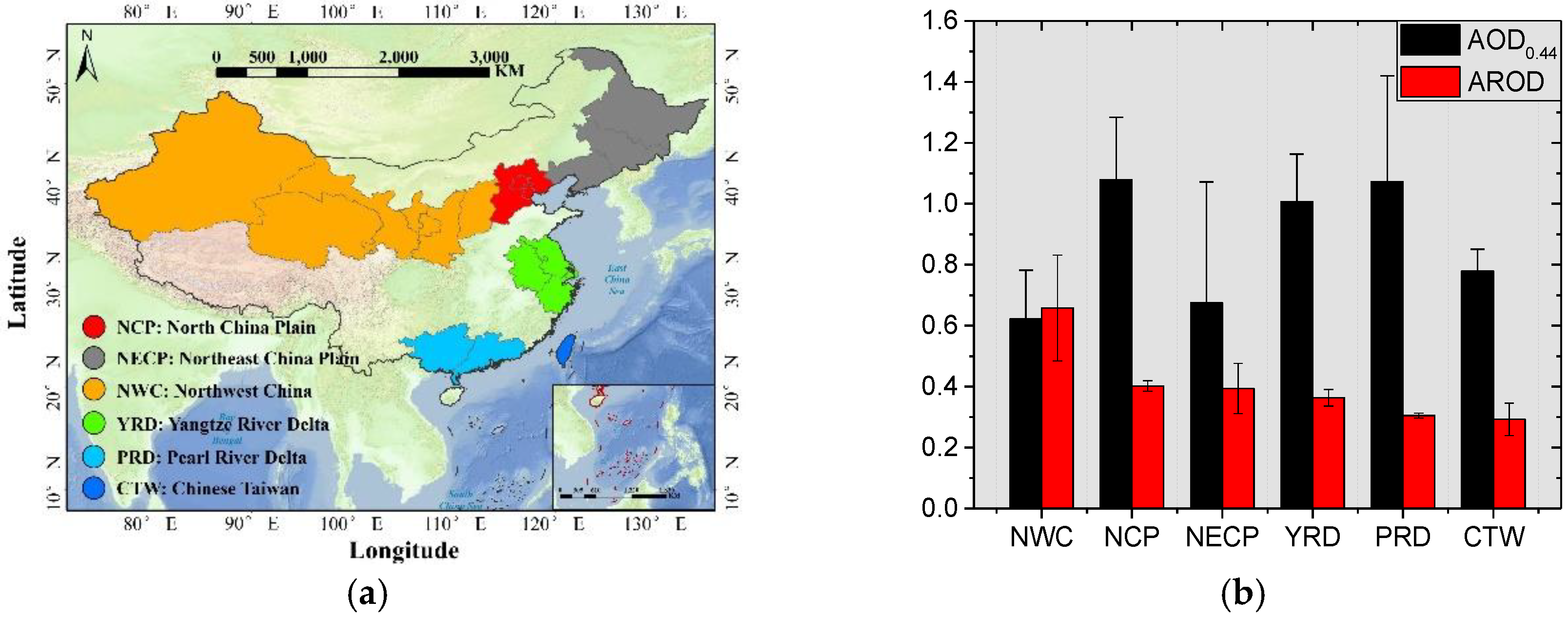
2.2. Aerosol Mode Classification
2.3. Mie Theory
2.4. Determination of the Objective Function
2.5. Minimization of the Objective Function
- , where epsmch denotes the machine precision and is automatically generated by the code; factor is a user defined parameter and is selected to terminate the run when the change in F(x) is sufficiently small. We chose for moderate accuracy.
- , where pgtol was set to a default value of 10−4.
- No further progress can be made during the line search. When the line search program fails to find a point with an acceptably low objective value after twenty iterations of calculating F(x) or along the steepest descent direction, the calculation terminates. Further details regarding the algorithm and code can be found in the work of Zhu et al. [40].
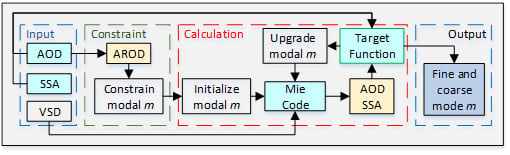
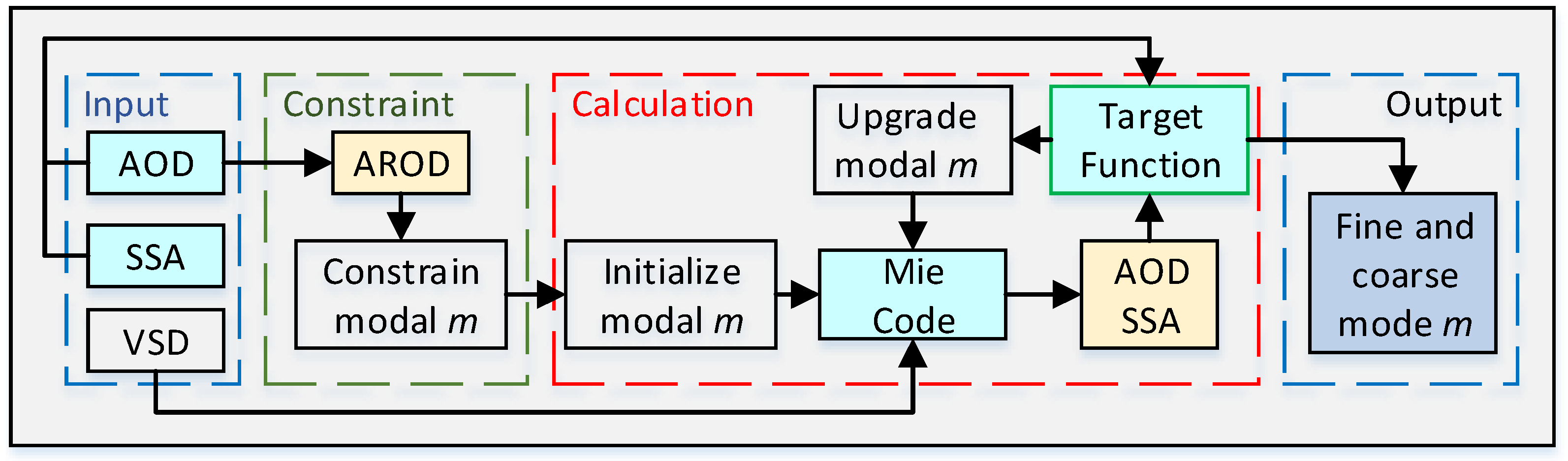
2.6. Process for Inferring Modal m Values
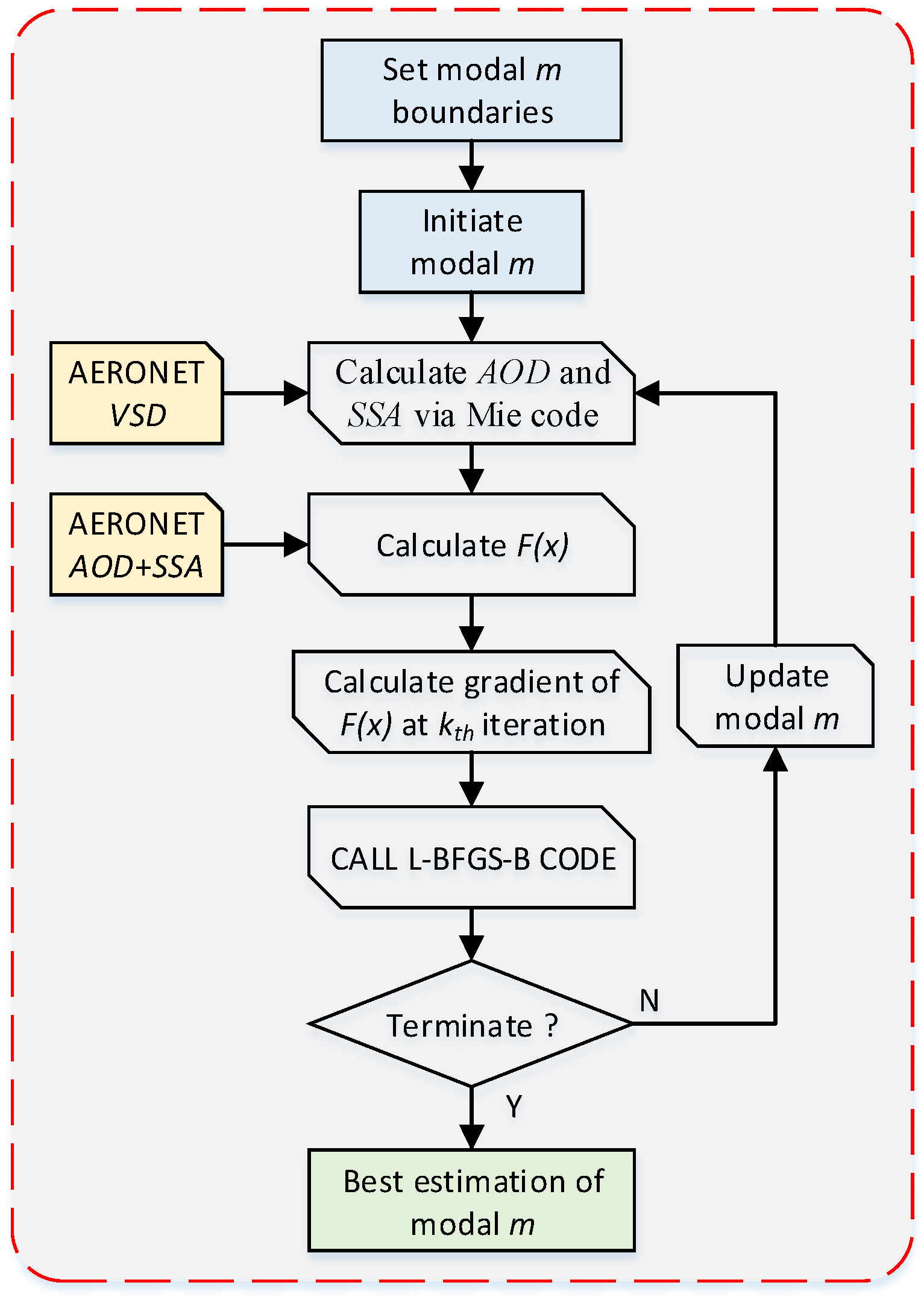
- Initiating modal m values: , , , and .
- Calculating spectral AOD and SSA using Mie theory and AERONET VSD information. Consistent with AERONET, AOD and SSA are calculated in 22 logarithmically spaced particle-size bins over the range of 0.05–15 µm, where Equations (4)–(6) can be expressed in the following form:where AODλ and SAODλ are the estimated AOD and SAOD resulting from scattering effects at wavelength λ; ri denotes the radius of the ith particle size bin; V(ri) is the volume within the ith particle size bin; Qext,i(x) and Qsca,i(x) are the attenuation and scattering factors, respectively, from Mie theory at ri; and represents the modal refractive index vector to be retrieved, where the subscripts f and c represent the fine- and coarse-mode aerosols, respectively.
- Calculating the value of F(x) based on Equation (10).
- Calculating the gradient of F(x) under the current iteration k with .
- Calling the L-BGRS-B code to search for probable solutions.
- Checking whether the output from step 6 meets the termination requirements. If so, the best estimations of the modal m values are exported; if not, the modal m values are updated and the loop is repeated.
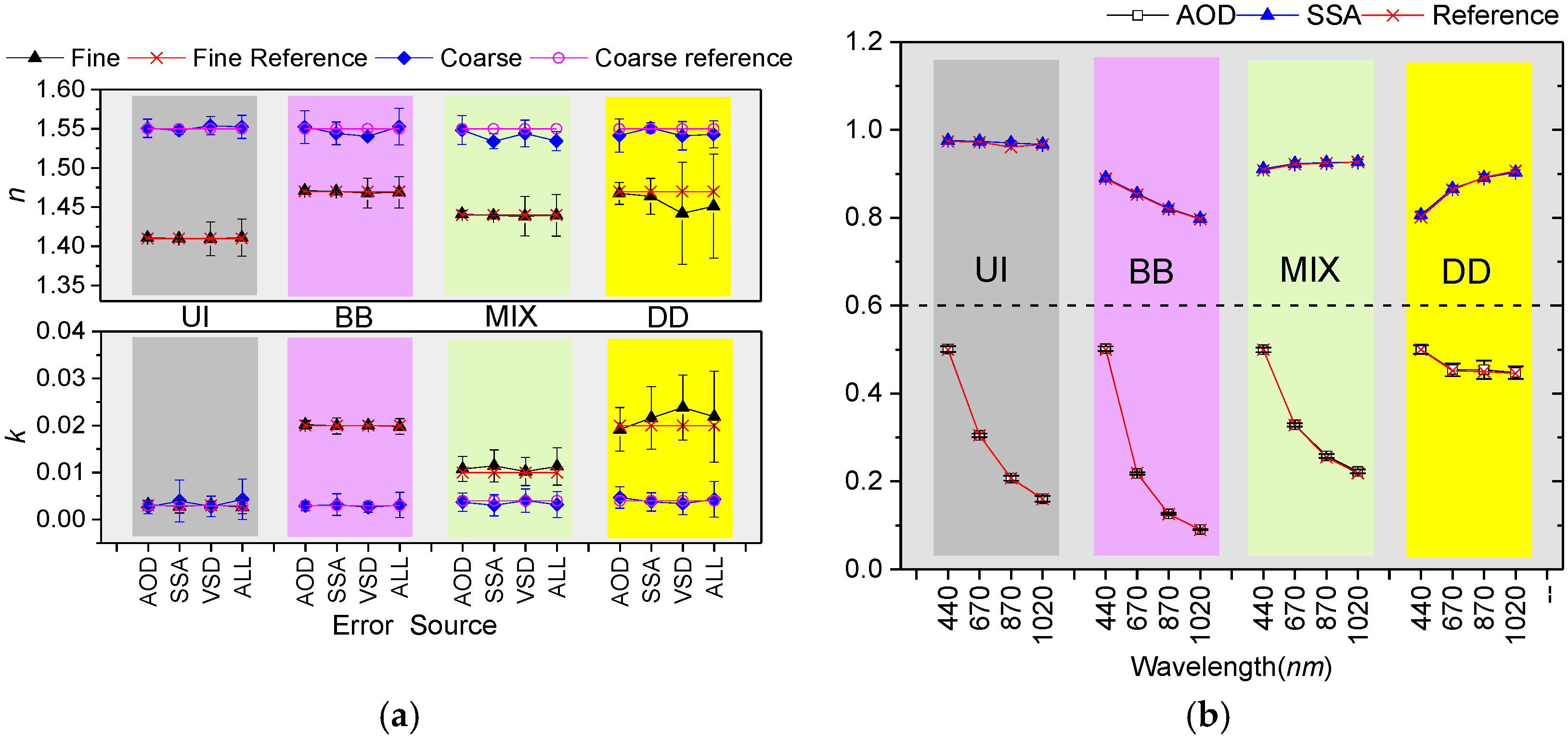
3. Numerical Tests
3.1. Aerosol Models
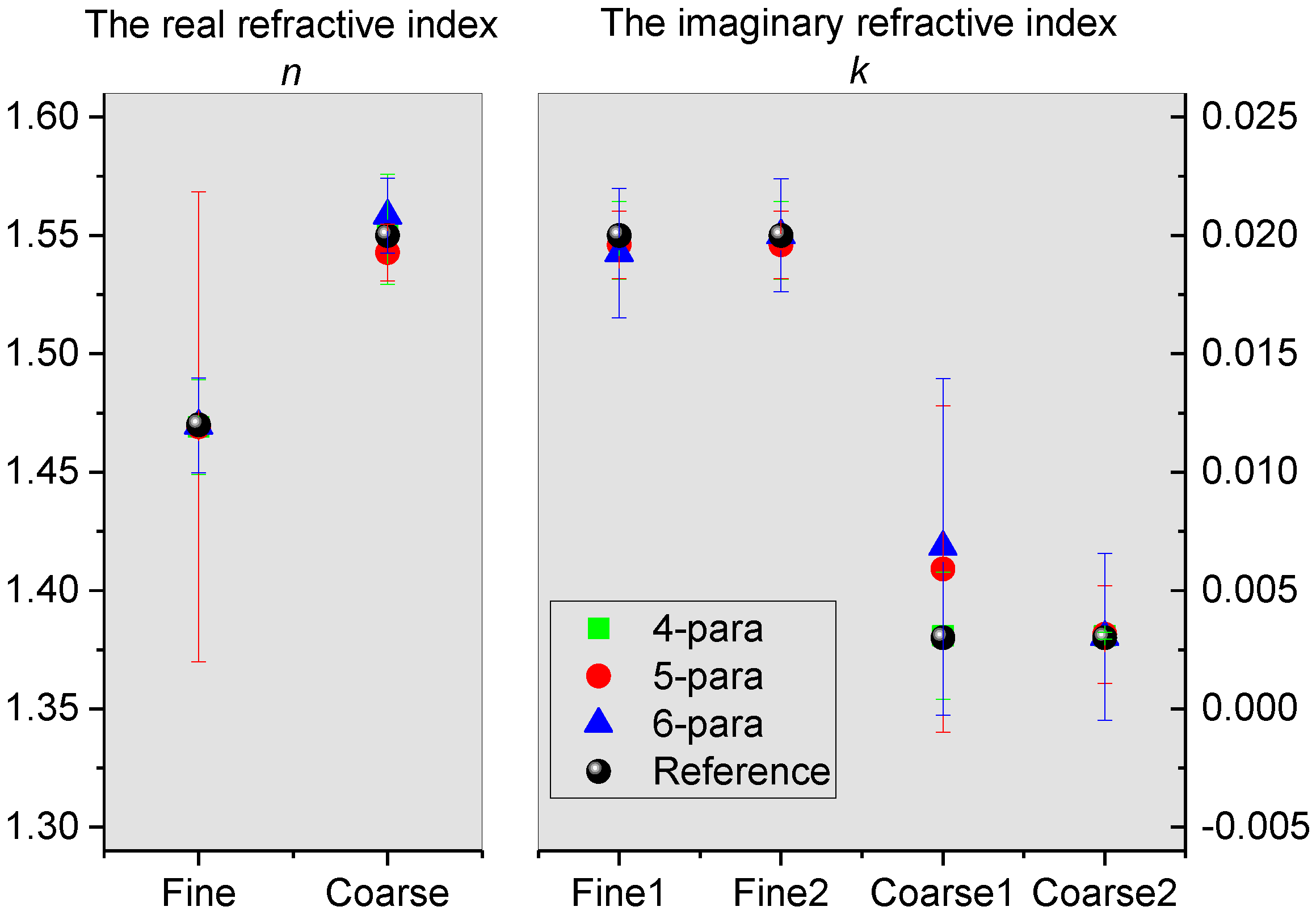
3.2. Self-Consistency Analysis
3.3. Simulation of Input Errors
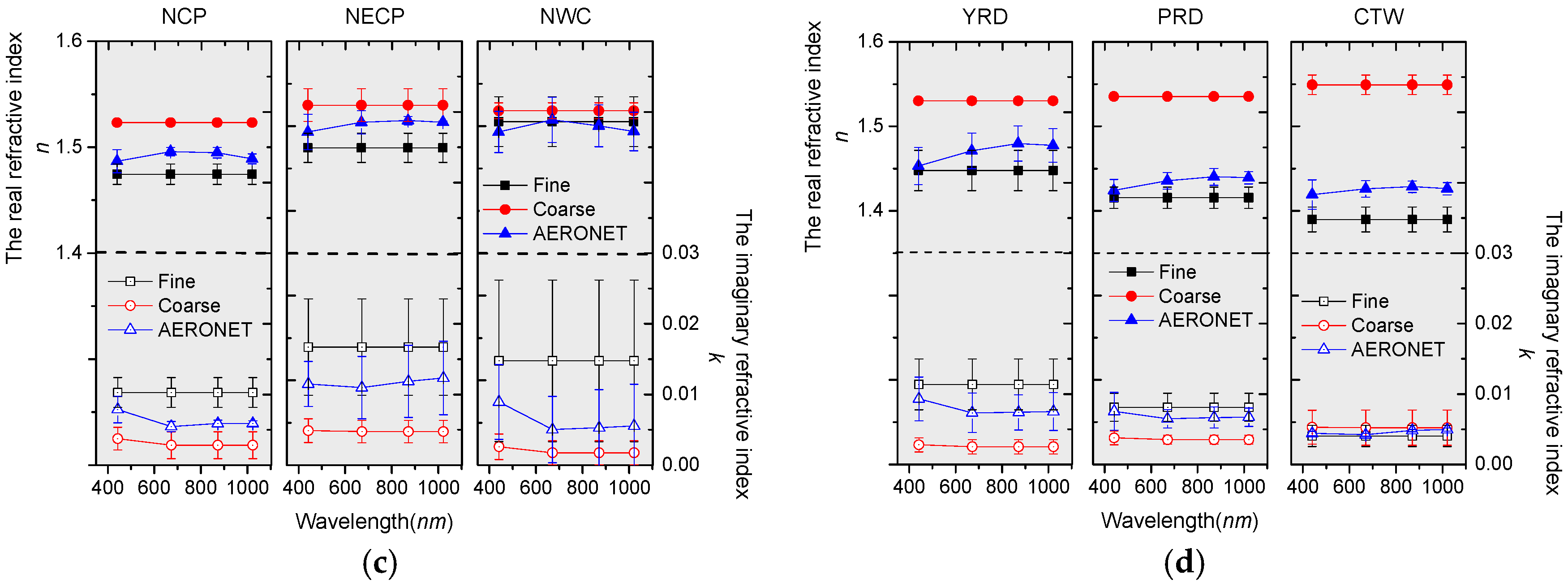
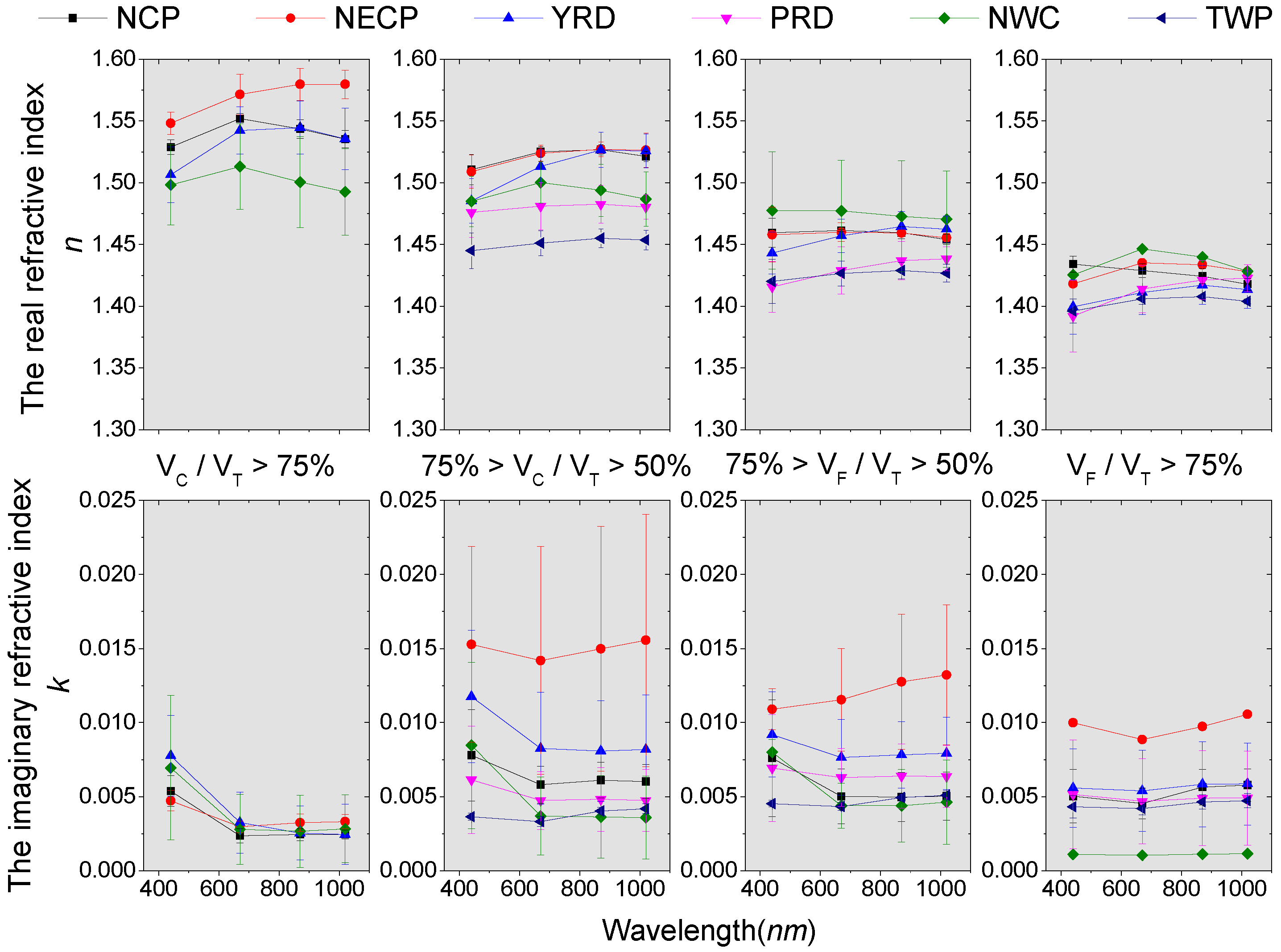
4. Modal Refractive Indices in Typical Regions of China
5. Discussion
5.1. Constraint of Aerosol Complex Refractive Indices
5.2. Rationality of the Use of VSD
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ealo, M.; Alastuey, A.; Perez, N.; Ripoll, A.; Querol, X.; Pandolfi, M. Impact of aerosol particle sources on optical properties in urban, regional and remote areas in the north-western mediterranean. Atmos. Chem. Phys. 2018, 18, 1149–1169. [Google Scholar] [CrossRef]
- Chen, Q.-X.; Shen, W.-X.; Yuan, Y.; Tan, H.-P. Verification of aerosol classification methods through satellite and ground-based measurements over harbin, northeast china. Atmos. Res. 2019, 216, 167–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.Q.; Zhang, Y.H.; Li, D.H.; Qie, L.L.; Che, H.Z.; Xu, H. Estimation of aerosol complex refractive indices for both fine and coarse modes simultaneously based on aeronet remote sensing products. Atmos. Meas. Tech. 2017, 10, 3203–3213. [Google Scholar] [CrossRef]
- Bran, S.H.; Jose, S.; Srivastava, R. Investigation of optical and radiative properties of aerosols during an intense dust storm: A regional climate modeling approach. J. Atmos. Sol.-Terr. Phy. 2018, 168, 21–31. [Google Scholar] [CrossRef]
- Mallet, M.; Solmon, F.; Roblou, L.; Peers, F.; Turquety, S.; Waquet, F.; Jethva, H.; Torres, O. Simulation of optical properties and direct and indirect radiative effects of smoke aerosols over marine stratocumulus clouds during summer 2008 in california with the regional climate model regcm. J. Geophys. Res.-Atmos. 2017, 122, 10288–10313. [Google Scholar] [CrossRef]
- Chen, Q.; Yuan, Y.; Huang, X.; He, Z.; Tan, H. Assessment of column aerosol optical properties using ground-based sun-photometer at urban Harbin, Northeast China. J. Environ. Sci. China 2018, 74, 50–57. [Google Scholar] [CrossRef]
- Nakayama, T.; Sato, K.; Imamura, T.; Matsumi, Y. Effect of oxidation process on complex refractive index of secondary organic aerosol generated from isoprene. Environ. Sci. Technol. 2018, 52, 2566–2574. [Google Scholar] [CrossRef] [PubMed]
- Rafferty, A.; Preston, T.C. Measuring the size and complex refractive index of an aqueous aerosol particle using electromagnetic heating and cavity-enhanced raman scattering. Phys. Chem. Chem. Phys. 2018, 20, 17038–17047. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.F.; Zhang, Y.; Martin, S.T. Complex refractive indices of thin films of secondary organic materials by spectroscopic ellipsometry from 220 to 1200 nm. Environ. Sci. Technol. 2013, 47, 13594–13601. [Google Scholar] [CrossRef] [PubMed]
- Marley, N.A.; Gaffney, J.S.; Baird, C.; Blazer, C.A.; Drayton, P.J.; Frederick, J.E. An empirical method for the determination of the complex refractive index of size-fractionated atmospheric aerosols for radiative transfer calculations. Aerosol. Sci. Technol. 2001, 34, 535–549. [Google Scholar] [CrossRef]
- Shepherd, R.H.; King, M.D.; Marks, A.A.; Brough, N.; Ward, A.D. Determination of the refractive index of insoluble organic extracts from atmospheric aerosol over the visible wavelength range using optical tweezers. Atmos. Chem. Phys. 2018, 18, 5235–5252. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanre, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Gong, C.S.; Xin, J.Y.; Wang, S.G.; Wang, Y.S.; Zhang, T.J. Anthropogenic aerosol optical and radiative properties in the typical urban/suburban regions in china. Atmos. Res. 2017, 197, 177–187. [Google Scholar] [CrossRef]
- Tuet, W.Y.; Chen, Y.L.; Xu, L.; Fok, S.; Gao, D.; Weber, R.J.; Ng, N.L. Chemical oxidative potential of secondary organic aerosol (soa) generated from the photooxidation of biogenic and anthropogenic volatile organic compounds. Atmos. Chem. Phys. 2017, 17, 839–853. [Google Scholar] [CrossRef]
- Mao, Q.J. Recent developments in geometrical configurations of thermal energy storage for concentrating solar power plant. Renew. Sustain. Energy Rev. 2016, 59, 320–327. [Google Scholar] [CrossRef]
- Mao, Q.J.; Chen, H.Z.; Zhao, Y.Z.; Wu, H.J. A novel heat transfer model of a phase change material using in solar power plant. Appl. Therm. Eng. 2018, 129, 557–563. [Google Scholar] [CrossRef]
- Hu, W.; Niu, H.Y.; Zhang, D.Z.; Wu, Z.J.; Chen, C.; Wu, Y.S.; Shang, D.J.; Hu, M. Insights into a dust event transported through Beijing in spring 2012: Morphology, chemical composition and impact on surface aerosols. Sci. Total Environ. 2016, 565, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.H.; Cheng, C.L.; Huang, Y.; Tao, J.; Ren, Y.Q.; Wu, F.; Meng, J.J.; Li, J.J.; Cheng, Y.T.; Cao, J.J.; et al. Evolution of aerosol chemistry in Xi’an, Inland China, during the dust storm period of 2013—Part 1: Sources, chemical forms and formation mechanisms of nitrate and sulfate. Atmos. Chem. Phys. 2014, 14, 11571–11585. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Cairns, B.; Kopp, G.; Schueler, C.F.; Fafaul, B.A.; Hansen, J.E.; Hooker, R.J.; Itchkawich, T.; Maring, H.B.; Travis, L.D. Accurate monitoring of terrestrial aerosols and total solar irradiance—Introducing the glory mission. B Am. Meteorol. Soc. 2007, 88, 677. [Google Scholar] [CrossRef]
- Hasekamp, O.P.; Litvinov, P.; Butz, A. Aerosol properties over the ocean from parasol multiangle photopolarimetric measurements. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Woo, C.G.; You, S.; Lee, J. Determination of refractive index for absorbing spheres. Optik 2013, 124, 5254–5258. [Google Scholar] [CrossRef]
- Patterson, E.M.; Gillette, D.A.; Stockton, B.H. Complex index of refraction between 300 and 700 nm for saharan aerosols. J. Geophys. Res.-Atmos. 1977, 82, 3153–3160. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from sun and sky radiance measurements. J. Geophys. Res.-Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Nakajima, T.; Tonna, G.; Rao, R.Z.; Boi, P.; Kaufman, Y.; Holben, B. Use of sky brightness measurements from ground for remote sensing of particulate polydispersions. Appl. Opt. 1996, 35, 2672–2686. [Google Scholar] [CrossRef] [PubMed]
- Fedarenka, A.; Dubovik, O.; Goloub, P.; Li, Z.Q.; Lapyonok, T.; Litvinov, P.; Barel, L.; Gonzalez, L.; Podvin, T.; Crozel, D. Utilization of aeronet polarimetric measurements for improving retrieval of aerosol microphysics: Gsfc, beijing and dakar data analysis. J. Quant. Spectrosc. Radiat. Transf. 2016, 179, 72–97. [Google Scholar] [CrossRef]
- He, Z.Z.; Mao, J.K.; Han, X.S. Non-parametric estimation of particle size distribution from spectral extinction data with pca approach. Powder Technol. 2018, 325, 510–518. [Google Scholar] [CrossRef]
- He, Z.Z.; Qi, H.; Yao, Y.C.; Ruan, L.M. Inverse estimation of the particle size distribution using the fruit fly optimization algorithm. Appl. Therm. Eng. 2015, 88, 306–314. [Google Scholar] [CrossRef]
- Danylevsky, V.; Ivchenko, V.; Milinevsky, G.; Sosonkin, M.; Goloub, P.; Li, Z.Q.; Dubovik, O. Atmosphere aerosol properties measured with aeronet/photons sun-photometer over kyiv during 2008–2009. Nato Sci. Peace Secur. 2011, 285–294. [Google Scholar]
- Dubovik, O.; Smirnov, A.; Holben, B.N.; King, M.D.; Kaufman, Y.J.; Eck, T.F.; Slutsker, I. Accuracy assessments of aerosol optical properties retrieved from aerosol robotic network (aeronet) sun and sky radiance measurements. J. Geophys Res.-Atmos. 2000, 105, 9791–9806. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Gitelson, A.; Karnieli, A.; Ganor, E.; Fraser, R.S.; Nakajima, T.; Mattoo, S.; Holben, B.N. Size distribution and scattering phase function of aerosol-particles retrieved from sky brightness measurements. J. Geophys. Res.-Atmos. 1994, 99, 10341–10356. [Google Scholar] [CrossRef]
- Xu, X.G.; Wang, J.; Zeng, J.; Spurr, R.; Liu, X.; Dubovik, O.; Li, L.; Li, Z.Q.; Mishchenko, M.I.; Siniuk, A.; et al. Retrieval of aerosol microphysical properties from aeronet photopolarimetric measurements: 2. A new research algorithm and case demonstration. J. Geophys. Res.-Atmos. 2015, 120, 7079–7098. [Google Scholar] [CrossRef]
- Torres, B.; Dubovik, O.; Fuertes, D.; Schuster, G.; Cachorro, V.E.; Lapyonok, T.; Goloub, P.; Blarel, L.; Barreto, A.; Mallet, M.; et al. Advanced characterisation of aerosol size properties from measurements of spectral optical depth using the grasp algorithm. Atmos. Meas. Tech. 2017, 10, 3743–3781. [Google Scholar] [CrossRef]
- Chen, Q.X.; Yuan, Y.; Huang, X.; Jiang, Y.Q.; Tan, H.P. Estimation of surface-level pm2.5 concentration using aerosol optical thickness through aerosol type analysis method. Atmos. Environ. 2017, 159, 26–33. [Google Scholar] [CrossRef]
- Yuan, Y.; Shuai, Y.; Li, X.W.; Liu, B.; Tan, H.P. Using a new aerosol relative optical thickness concept to identify aerosol particle species. Atmos. Res. 2014, 150, 1–11. [Google Scholar] [CrossRef]
- Chen, Q.X.; Yuan, Y.; Shuai, Y.; Tan, H.P. Graphical aerosol classification method using aerosol relative optical depth. Atmos. Environ. 2016, 135, 84–91. [Google Scholar] [CrossRef]
- Lee, S.; Hong, J.; Cho, Y.; Choi, M.; Kim, J.; Park, S.S.; Ahn, J.Y.; Kim, S.K.; Moon, K.J.; Eck, T.F.; et al. Characteristics of classified aerosol types in south korea during the maps-seoul campaign. Aerosol. Air Qual. Res. 2018, 18, 2195–2206. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Yang, P. Far-field lorenz-mie scattering in an absorbing host medium: Theoretical formalism and fortran program. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 241–252. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, J.M.; Lock, J.A.; Yurkin, M.A. Far-field far-field lorenz-mie scattering in an absorbing host medium. Ii: Improved stability of the numerical algorithm. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 274–277. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanre, D.; Deuze, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Byrd, R.H.; Lu, P.H.; Nocedal, J. Algorithm 778: L-bfgs-b: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.Q.; Liu, L.; Zhou, L.J.; Cribb, M.; Zhang, F. Distinct weekly cycles of thunderstorms and a potential connection with aerosol type in china. Geophys. Res. Lett. 2016, 43, 8760–8768. [Google Scholar] [CrossRef]
- Che, H.Z.; Zhao, H.J.; Wu, Y.F.; Xia, X.G.; Zhu, J.; Dubovik, O.; Estelles, V.; Ma, Y.J.; Wang, Y.F.; Wang, H.; et al. Application of aerosol optical properties to estimate aerosol type from ground-based remote sensing observation at urban area of northeastern china. J. Atmos. Sol.-Terr. Phy. 2015, 132, 37–47. [Google Scholar] [CrossRef]
- Kumar, K.R.; Kang, N.; Yin, Y. Classification of key aerosol types and their frequency distributions based on satellite remote sensing data at an industrially polluted city in the yangtze river delta, china. Int. J. Climatol. 2018, 38, 320–336. [Google Scholar] [CrossRef]
- Mao, Q.J.; Huang, C.L.; Zhang, H.X.; Chen, Q.X.; Yuan, Y. Aerosol optical properties and radiative effect under different weather conditions in Harbin, China. Infrared Phys. Technol. 2018, 89, 304–314. [Google Scholar] [CrossRef]
- Sun, T.Z.; Che, H.Z.; Qi, B.; Wang, Y.Q.; Dong, Y.S.; Xia, X.G.; Wang, H.; Gui, K.; Zheng, Y.; Zhao, H.J.; et al. Aerosol optical characteristics and their vertical distributions under enhanced haze pollution events: Effect of the regional transport of different aerosol types over eastern china. Atmos. Chem. Phys. 2018, 18, 2949–2971. [Google Scholar] [CrossRef]
- Arola, A.; Schuster, G.; Myhre, G.; Kazadzis, S.; Dey, S.; Tripathi, S.N. Inferring absorbing organic carbon content from aeronet data. Atmos. Chem. Phys. 2011, 11, 215–225. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.Q.; Tian, Q.J.; Ma, Y.; Zhang, F.X.; Zhang, Y.; Li, D.H.; Li, K.T.; Li, L. Estimate of aerosol absorbing components of black carbon, brown carbon, and dust from ground-based remote sensing data of sun-sky radiometers. J. Geophys. Res.-Atmos. 2013, 118, 6534–6543. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.Q.; Sun, Y.L.; Lv, Y.; Xie, Y.S. Estimation of atmospheric columnar organic matter (om) mass concentration from remote sensing measurements of aerosol spectral refractive. Atmos. Environ. 2018, 179, 107–117. [Google Scholar] [CrossRef]
- Holben, B.N.; Kim, J.; Sano, I.; Mukai, S.; Eck, T.F.; Giles, D.M.; Schafer, J.S.; Sinyuk, A.; Slutsker, I.; Smirnov, A.; et al. An overview of mesoscale aerosol processes, comparisons, and validation studies from dragon networks. Atmos. Chem. Phys. 2018, 18, 655–671. [Google Scholar] [CrossRef]
- Reid, J.S.; Jonsson, H.H.; Maring, H.B.; Smirnov, A.; Savoie, D.L.; Cliff, S.S.; Reid, E.A.; Livingston, J.M.; Meier, M.M.; Dubovik, O.; et al. Comparison of size and morphological measurements of coarse mode dust particles from Africa. J. Geophys. Res.-Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Reid, J.S.; Reid, E.A.; Walker, A.; Piketh, S.; Cliff, S.; Al Mandoos, A.; Tsay, S.C.; Eck, T.F. Dynamics of southwest asian dust particle size characteristics with implications for global dust research. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Schafer, J.E.; Eck, T.F.; Thornhill, K.L.; Holben, B.N.; Anderson, B.E.; Sinyuk, A.; Ziemba, L.D.; Giles, D.M.; Winstead, E.; Beyersdorf, A.J.; et al. Intercomparison of aerosol optical and micro-physical properties derived from aeronet surface radiometers and large in-situ aircraft profiles during the 2011 dragon-md and discover-aq experiments. In Proceedings of the American Geophysical Union, Fall Meeting, San Francisco, CA, USA, 9–13 December 2014. A31K-06. [Google Scholar]
| Site | Longitude | Latitude | Observation Period | Daily Observations | Site Description |
|---|---|---|---|---|---|
| North China Plain (NCP) | |||||
| Beijing | 116.4° E | 40.0° N | 2001.03–2018.06 | 1044 | Urban |
| Xianghe | 117.0° E | 39.8° N | 2001.03–2017.05 | 1341 | Mixed |
| Xinglong | 117.6° E | 40.4° N | 2006.02–2014.10 | 179 | Background |
| Northeast China Plain (NECP) | |||||
| Harbin | 126.5° E | 46.5° N | 2016.05–2016.06 | 26 | Urban |
| Liangning | 121.7° E | 41.5° N | 2005.04–2005.06 | 20 | Agricultural |
| Yangtze River Delta (YRD) | |||||
| Hefei | 117.2° E | 31.9° N | 2005.11–2008.11 | 28 | Urban |
| Nanjing | 118.7° E | 32.2° N | 2008.03–2008.08 | 41 | Industrial |
| Hangzhou | 120.2° E | 30.3° N | 2008.04–2009.02 | 59 | Urban |
| Shouxian | 116.8° E | 32.6° N | 2008.05–2008.12 | 65 | Mixed |
| Taihu | 120.2° E | 31.4° N | 2005.09–2016.07 | 495 | Lake |
| Pearl River Delta (PRD) | |||||
| Guangzhou | 113.4° E | 21.5° N | 2009.11–2009.12 | 10 | Urban |
| Kaiping | 112.5° E | 21.3° N | 2008.10–2008.11 | 13 | Suburban |
| Hong Kong | 114.2° E | 21.3° N | 2005.11–2017.03 | 289 | Urban |
| Northwest China (NWC) | |||||
| Lanzhou | 104.1° E | 35.9° N | 2006.08–2013.04 | 380 | Mixed |
| Baotou | 109.6° E | 40.9° N | 2013.10–2013.10 | 5 | Dust |
| Jingtai | 104.1° E | 37.3° N | 2008.03–2008.05 | 18 | Dust |
| Minqin | 103.0° E | 38.6° N | 2010.05–2010.06 | 3 | Desert |
| Zhangye | 100.3° E | 39.1° N | 2008.05–2008.06 | 13 | Dust |
| Dunhuang | 94.8° E | 40.0° N | 2012.04–2012.04 | 12 | Desert |
| Chinese Taiwan (CTW) | |||||
| Tainan | 120.2° E | 23.0° N | 2002.03–2016.05 | 503 | Urban |
| Chiayi | 120.5° E | 23.5° N | 2013.09–2018.04 | 361 | Mixed |
| VSD | C1/C2 | R1/μm | R2/μm | D1 | D2 |
| UI | 2/1 | 0.25 | 2.8 | 0.6 | 0.6 |
| BB | 10/7 | 0.14 | 3.8 | 0.4 | 0.6 |
| MIX | 1/3 | 0.2 | 2.8 | 0.6 | 0.6 |
| DD | 1/20 | 0.12 | 2.3 | 0.4 | 0.7 |
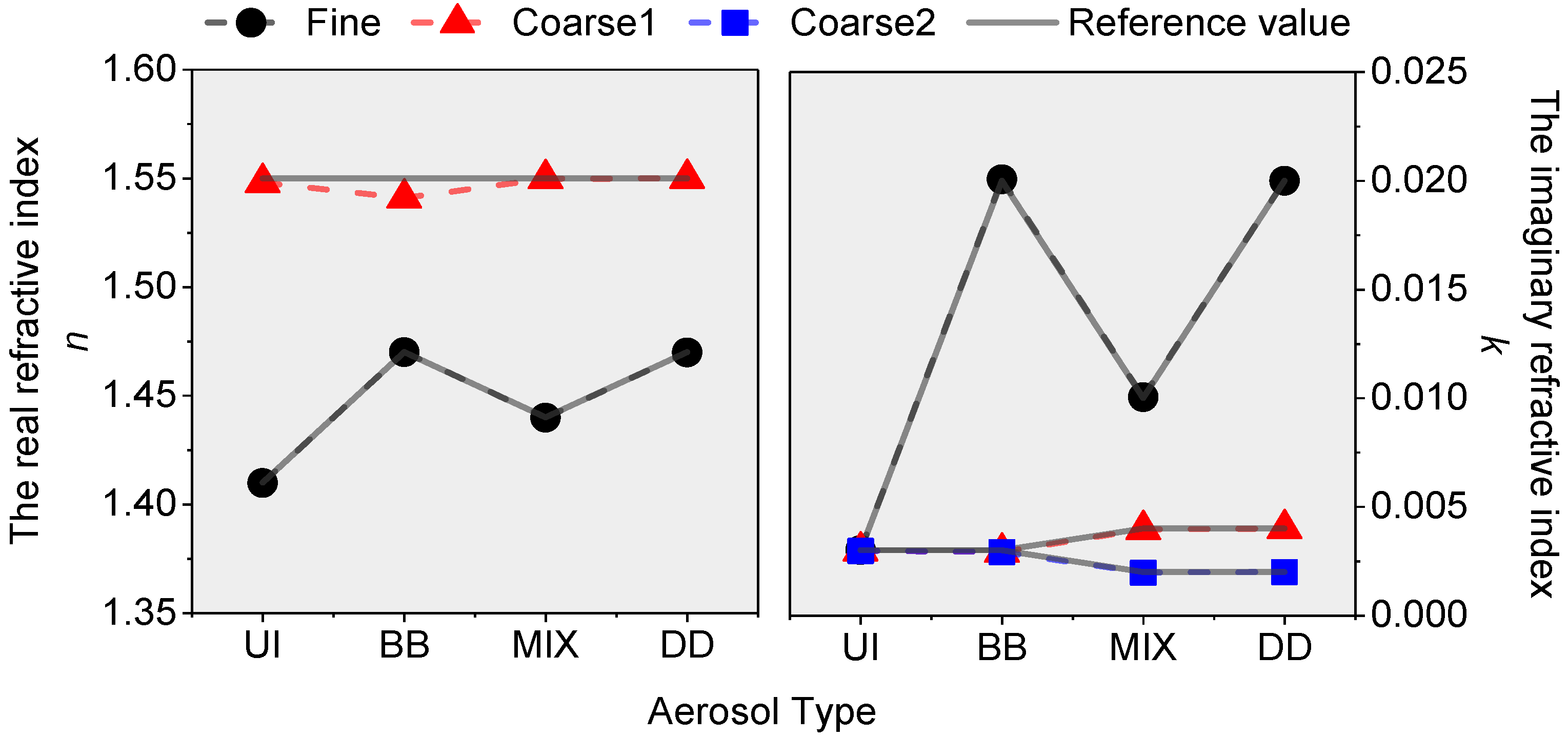
| m | nf | kf | nc | kc,0.44 | kc,0.67–1.02 |
| UI | 1.41 | 0.003 | 1.55 | 0.003 | 0.003 |
| BB | 1.47 | 0.02 | 1.55 | 0.003 | 0.003 |
| MIX | 1.44 | 0.01 | 1.55 | 0.004 | 0.002 |
| DD | 1.47 | 0.02 | 1.55 | 0.004 | 0.002 |
| AOD | 0.44 μm | 0.67 μm | 0.87 μm | 1.02 μm | AROD |
| UI | 0.500 | 0.305 | 0.207 | 0.160 | 0.319 |
| BB | 0.500 | 0.219 | 0.126 | 0.090 | 0.180 |
| MIX | 0.500 | 0.328 | 0.255 | 0.219 | 0.439 |
| DD | 0.500 | 0.452 | 0.450 | 0.446 | 0.892 |
| SSA | 0.44 μm | 0.67 μm | 0.87 μm | 1.02 μm | |
| UI | 0.974 | 0.972 | 0.961 | 0.967 | |
| BB | 0.889 | 0.853 | 0.820 | 0.797 | |
| MIX | 0.908 | 0.922 | 0.924 | 0.927 | |
| DD | 0.801 | 0.864 | 0.892 | 0.907 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.-X.; Shen, W.-X.; Yuan, Y.; Xie, M.; Tan, H.-P. Inferring Fine-Mode and Coarse-Mode Aerosol Complex Refractive Indices from AERONET Inversion Products over China. Atmosphere 2019, 10, 158. https://doi.org/10.3390/atmos10030158
Chen Q-X, Shen W-X, Yuan Y, Xie M, Tan H-P. Inferring Fine-Mode and Coarse-Mode Aerosol Complex Refractive Indices from AERONET Inversion Products over China. Atmosphere. 2019; 10(3):158. https://doi.org/10.3390/atmos10030158
Chicago/Turabian StyleChen, Qi-Xiang, Wen-Xiang Shen, Yuan Yuan, Ming Xie, and He-Ping Tan. 2019. "Inferring Fine-Mode and Coarse-Mode Aerosol Complex Refractive Indices from AERONET Inversion Products over China" Atmosphere 10, no. 3: 158. https://doi.org/10.3390/atmos10030158
APA StyleChen, Q.-X., Shen, W.-X., Yuan, Y., Xie, M., & Tan, H.-P. (2019). Inferring Fine-Mode and Coarse-Mode Aerosol Complex Refractive Indices from AERONET Inversion Products over China. Atmosphere, 10(3), 158. https://doi.org/10.3390/atmos10030158