The Effect of Genome Parametrization and SNP Marker Subsetting on Genomic Selection in Autotetraploid Alfalfa
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material and Phenotyping
2.2. Experimental Design Solution, BLUPs Computation, and Heritability
2.3. DNA Extraction, Library Preparation, and Sequencing
2.4. SNP Calling, Filtering, and Genome Parametrization
2.5. Genomic Regression
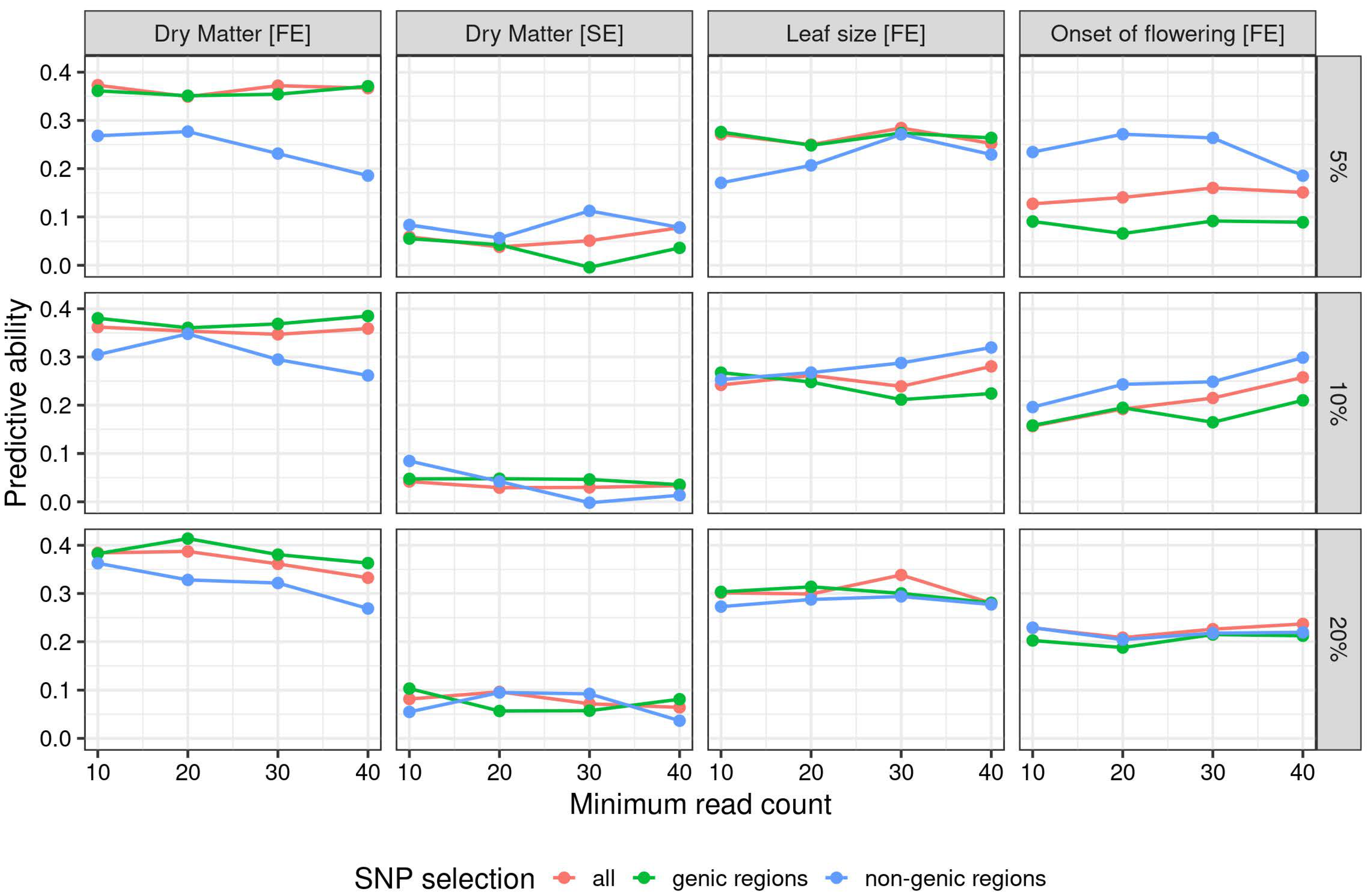
3. Results
3.1. Phenotypic Analysis
3.2. Sequencing, SNP Calling, and Filtering
3.3. Genomic Regressions
3.4. Released Software: Legpipe2
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Annicchiarico, P.; Barrett, B.; Brummer, E.C.; Julier, B.; Marshall, A.H. Achievements and challenges in improving temperate perennial forage legumes. Crit. Rev. Plant Sci. 2015, 34, 327–380. [Google Scholar] [CrossRef]
- Sanford, G.R.; Jackson, R.D.; Booth, E.G.; Hedtcke, J.L.; Picasso, V. Perenniality and diversity drive output stability and resilience in a 26-year cropping systems experiment. Field Crops Res. 2021, 263, 108071. [Google Scholar] [CrossRef]
- Wu, S.; Wu, P.; Feng, H.; Merkley, G.P. Effects of alfalfa coverage on runoff, erosion and hydraulic characteristics of overland flow on loess slope plots. Front. Environ. Sci. Eng. China 2011, 5, 76–83. [Google Scholar] [CrossRef]
- Bingham, E.T.; Groose, R.W.; Woodfield, D.R.; Kidwell, K.K. Complementary gene interactions in alfalfa are greater in autotetraploids than diploids. Crop Sci. 1994, 34, 823–829. [Google Scholar] [CrossRef]
- Li, X.; Brummer, E.C. Inbreeding depression for fertility and biomass in advanced generations of inter-and intrasubspecific hybrids of tetraploid alfalfa. Crop Sci. 2009, 49, 13–19. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Pecetti, L. Comparison among nine alfalfa breeding schemes based on actual biomass yield gains. Crop Sci. 2021, 61, 2355–2371. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Nazzicari, N.; Li, X.; Wei, Y.; Pecetti, L.; Brummer, E.C. Accuracy of genomic selection for alfalfa biomass yield in different reference populations. BMC Genom. 2015, 16, 1020. [Google Scholar] [CrossRef] [PubMed]
- Torkamaneh, D.; Laroche, J.; Belzile, F. Fast-GBS v2. 0: An analysis toolkit for genotyping-by-sequencing data. Genome 2020, 63, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Qi, P.; Gimode, D.; Saha, D.; Schröder, S.; Chakraborty, D.; Wang, X.; Dida, M.M.; Malmberg, R.L.; Devos, K.M. UGbS-Flex, a novel bioinformatics pipeline for imputation-free SNP discovery in polyploids without a reference genome: Finger millet as a case study. BMC Plant Biol. 2018, 18, 117. [Google Scholar] [CrossRef]
- Clark, L.V.; Lipka, A.E.; Sacks, E.J. polyRAD: Genotype calling with uncertainty from sequencing data in polyploids and diploids. G3 Genes Genomes Genet. 2019, 9, 663–673. [Google Scholar] [CrossRef]
- Thakral, V.; Yadav, H.; Padalkar, G.; Kumawat, S.; Raturi, G.; Kumar, V.; Mandlik, R.; Rajora, N.; Singh, M. Recent Advances and Applicability of GBS, GWAS, and GS in Polyploid Crops. Genotyping Seq. Crop Improv. 2022, 328–354. [Google Scholar] [CrossRef]
- Batista, L.G.; Mello, V.H.; Souza, A.P.; Margarido, G.R. Genomic prediction with allele dosage information in highly polyploid species. Theor. Appl. Genet. 2022, 135, 723–739. [Google Scholar] [CrossRef] [PubMed]
- Ferrão, L.F.V.; Amadeu, R.R.; Benevenuto, J.; de Bem Oliveira, I.; Munoz, P.R. Genomic selection in an outcrossing autotetraploid fruit crop: Lessons from blueberry breeding. Front. Plant Sci. 2021, 12, 676326. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, A.J.; Chao, S.; Asoro, F.G.; Heffner, E.L.; Hayashi, T.; Iwata, H.; Smith, K.P.; Sorrells, M.E.; Jannink, J.L. Genomic selection in plant breeding: Knowledge and prospects. Adv. Agron. 2011, 110, 77–123. [Google Scholar]
- Schmidt, P.; Hartung, J.; Bennewitz, J.; Piepho, H.P. Heritability in plant breeding on a genotype-difference basis. Genetics 2019, 212, 991–1008. [Google Scholar] [CrossRef] [PubMed]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2008, 161, 209–228. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Preprocessing Tools for Data Preparation. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Berlin/Heidelberg, Germany, 2022; pp. 35–70. [Google Scholar]
- Lozano-Isla, F. Inti: Tools and Statistical Procedures in Plant Science. R Package Version 0.6.3. Available online: https://CRAN.R-project.org/package=inti (accessed on 26 March 2024).
- Itoh, Y.; Yamada, Y. Relationships between genotype x environment interaction and genetic correlation of the same trait measured in different environments. Theor. Appl. Genet. 1990, 80, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Elshire, R.J.; Glaubitz, J.C.; Sun, Q.; Poland, J.A.; Kawamoto, K.; Buckler, E.S.; Mitchell, S.E. A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 2011, 6, e19379. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Zhang, F.; Zhang, Z.; Li, M.; Chen, L.; Wang, X.; Liu, W.; Zhang, T.; Yu, L.X.; He, F.; et al. Genome assembly of alfalfa cultivar zhongmu-4 and identification of SNPs associated with agronomic traits. Genom. Proteom. Bioinform. 2022, 20, 14–28. [Google Scholar] [CrossRef]
- Gerard, D.; Ferrão, L.F.V.; Garcia, A.A.F.; Stephens, M. Genotyping polyploids from messy sequencing data. Genetics 2018, 210, 789–807. [Google Scholar] [CrossRef]
- Endelman, J.B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef]
- Nazzicari, N.; Biscarini, F. Stacked kinship CNN vs. GBLUP for genomic predictions of additive and complex continuous phenotypes. Sci. Rep. 2022, 12, 19889. [Google Scholar] [CrossRef] [PubMed]
- Puritz, J.B.; Hollenbeck, C.M.; Gold, J.R. dDocent: A RADseq, variant-calling pipeline designed for population genomics of non-model organisms. PeerJ 2014, 2, e431. [Google Scholar] [CrossRef] [PubMed]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The variant call format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef] [PubMed]
- Gerard, D.; Ferrão, L.F.V. Priors for genotyping polyploids. Bioinformatics 2020, 36, 1795–1800. [Google Scholar] [CrossRef] [PubMed]
- Van der Auwera, G.A.; O’Connor, B.D. Genomics in the Cloud: Using Docker, GATK, and WDL in Terra; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Langmead, B.; Wilks, C.; Antonescu, V.; Charles, R. Scaling read aligners to hundreds of threads on general-purpose processors. Bioinformatics 2019, 35, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Danecek, P.; Bonfield, J.K.; Liddle, J.; Marshall, J.; Ohan, V.; Pollard, M.O.; Whitwham, A.; Keane, T.; McCarthy, S.A.; Davies, R.M.; et al. Twelve years of SAMtools and BCFtools. Gigascience 2021, 10, giab008. [Google Scholar] [CrossRef] [PubMed]
- Gordon, A.; Hannon, G. Fastx-Toolkit, FASTQ/A Short-Reads Preprocessing Tools. Available online: http://hannonlab.cshl.edu/fastx_toolkit (accessed on 29 February 2024).
- Annicchiarico, P.; Nazzicari, N.; Bouizgaren, A.; Hayek, T.; Laouar, M.; Cornacchione, M.; Basigalup, D.; Monterrubio Martin, C.; Brummer, E.C.; Pecetti, L. Alfalfa genomic selection for different stress-prone growing regions. Plant Genome 2022, 15, e20264. [Google Scholar] [CrossRef]
- de CLara, L.A.; Santos, M.F.; Jank, L.; Chiari, L.; Vilela, M.d.M.; Amadeu, R.R.; Dos Santos, J.P.; Pereira, G.D.; Zeng, Z.B.; Garcia, A.A. Genomic selection with allele dosage in Panicum maximum jacq. G3 Genes Genomes Genet. 2019, 9, 2463–2475. [Google Scholar] [CrossRef]
- Matias, F.I.; Alves, F.C.; Meireles, K.G.X.; Barrios, S.C.L.; do Valle, C.B.; Endelman, J.B.; Fritsche-Neto, R. On the accuracy of genomic prediction models considering multi-trait and allele dosage in Urochloa spp. interspecific tetraploid hybrids. Mol. Breed. 2019, 39, 100. [Google Scholar] [CrossRef]
- de Bem Oliveira, I.; Resende, M.F., Jr.; Ferrão, L.F.V.; Amadeu, R.R.; Endelman, J.B.; Kirst, M.; Coelho, A.S.; Munoz, P.R. Genomic prediction of autotetraploids; influence of relationship matrices, allele dosage, and continuous genotyping calls in phenotype prediction. G3 Genes Genomes Genet. 2019, 9, 1189–1198. [Google Scholar] [CrossRef] [PubMed]
| Trait | Broad-Sense Heritability | CVg (%) | CVe (%) | Mean | Range |
|---|---|---|---|---|---|
| Onset of flowering (FE) | 0.690 | 6.2 *** | 7.2 | 20.61 | 18.24–22.79 |
| Leaf size (FE) | 0.550 | 6.1 *** | 13.4 | 3.31 | 2.94–3.78 |
| Dry Matter (SE) | 0.302 | 5.5 * | 15.2 | 6.84 | 6.23–7.34 |
| Dry Matter (FE) | 0.529 | 9.2 *** | 15.4 | 16.50 | 14.06–19.56 |
| Minimum Reads Per Locus | Maximum Missing Rate per Locus | Dosage SNPs | Ratios SNPs | ||
|---|---|---|---|---|---|
| All | Genic (%) | All | Genic (%) | ||
| 10 | 5% | 5758 | 4342 (75.41%) | 11,965 | 8771 (73.31%) |
| 10 | 10% | 11,440 | 8453 (73.89%) | 15,422 | 11,197 (72.6%) |
| 10 | 20% | 17,933 | 13,088 (72.98%) | 19,668 | 14,058 (71.48%) |
| 20 | 5% | 4162 | 3147 (75.61%) | 7813 | 5758 (73.7%) |
| 20 | 10% | 8576 | 6338 (73.9%) | 10,660 | 7791 (73.09%) |
| 20 | 20% | 13,491 | 9916 (73.5%) | 14,243 | 10,321 (72.46%) |
| 30 | 5% | 3225 | 2439 (75.63%) | 5688 | 4205 (73.93%) |
| 30 | 10% | 6715 | 5006 (74.55%) | 8021 | 5919 (73.79%) |
| 30 | 20% | 10,876 | 8035 (73.88%) | 11,306 | 8251 (72.98%) |
| 40 | 5% | 2387 | 1814 (75.99%) | 4076 | 3024 (74.19%) |
| 40 | 10% | 5386 | 4034 (74.9%) | 6248 | 4630 (74.1%) |
| 40 | 20% | 9065 | 6733 (74.27%) | 9278 | 6822 (73.53%) |
| Trait | SNP Selection | Parametrization | Maximum Missing Rate per Locus | Minimum Reads per Locus | Predictive Ability |
|---|---|---|---|---|---|
| Dry Matter (FE) | coding regions | tetraploid | 20% | 20 | 0.414 |
| Dry Matter (SE) | non-coding regions | diploid | 5% | 30 | 0.168 |
| Leaf size (FE) | coding regions | diploid | 5% | 10 | 0.347 |
| Onset of flowering (FE) | non-coding regions | allele ratio | 5% | 40 | 0.301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazzicari, N.; Franguelli, N.; Ferrari, B.; Pecetti, L.; Annicchiarico, P. The Effect of Genome Parametrization and SNP Marker Subsetting on Genomic Selection in Autotetraploid Alfalfa. Genes 2024, 15, 449. https://doi.org/10.3390/genes15040449
Nazzicari N, Franguelli N, Ferrari B, Pecetti L, Annicchiarico P. The Effect of Genome Parametrization and SNP Marker Subsetting on Genomic Selection in Autotetraploid Alfalfa. Genes. 2024; 15(4):449. https://doi.org/10.3390/genes15040449
Chicago/Turabian StyleNazzicari, Nelson, Nicolò Franguelli, Barbara Ferrari, Luciano Pecetti, and Paolo Annicchiarico. 2024. "The Effect of Genome Parametrization and SNP Marker Subsetting on Genomic Selection in Autotetraploid Alfalfa" Genes 15, no. 4: 449. https://doi.org/10.3390/genes15040449
APA StyleNazzicari, N., Franguelli, N., Ferrari, B., Pecetti, L., & Annicchiarico, P. (2024). The Effect of Genome Parametrization and SNP Marker Subsetting on Genomic Selection in Autotetraploid Alfalfa. Genes, 15(4), 449. https://doi.org/10.3390/genes15040449






