Mechanical Adaptations of Epithelial Cells on Various Protruded Convex Geometries
Abstract
1. Introduction
2. Materials and Methods
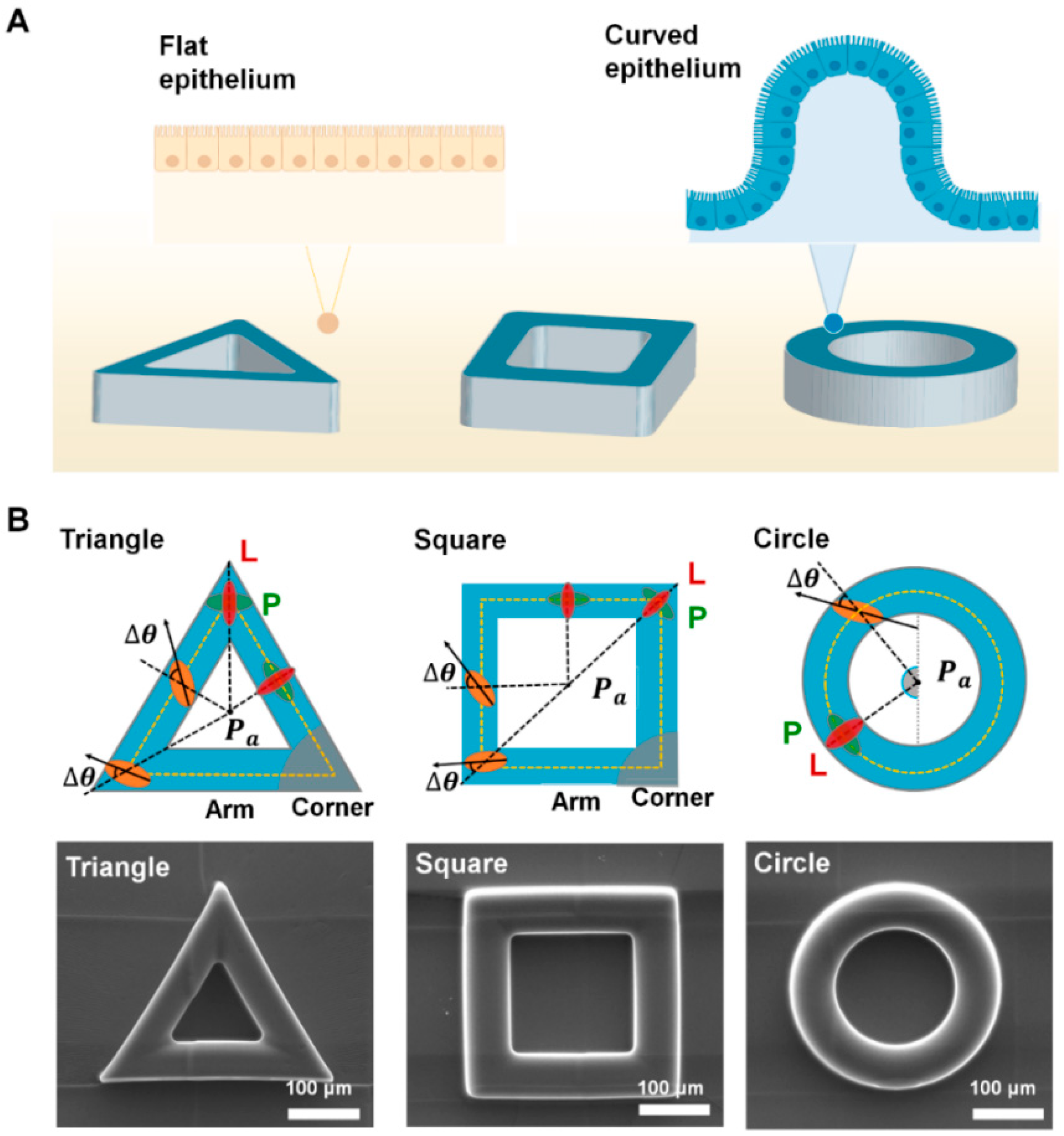
2.1. Fabrication of Protruded Convex Structure
2.2. Surface Characterization of 3D Structure
2.3. Cell Culture and Growth
2.4. Cell Immunofluorescence
2.5. Confocal Fluorescence Imaging
2.6. Imaging Analysis
2.7. Cell Morphological Index and Mathematical Correction
2.8. Pharmacological Interventions
2.9. 3-(4,5-Dimethylthiazol-2-yl)−2,5-Diphenyltetrazolium Bromide Assay
2.10. Data Analysis
3. Results
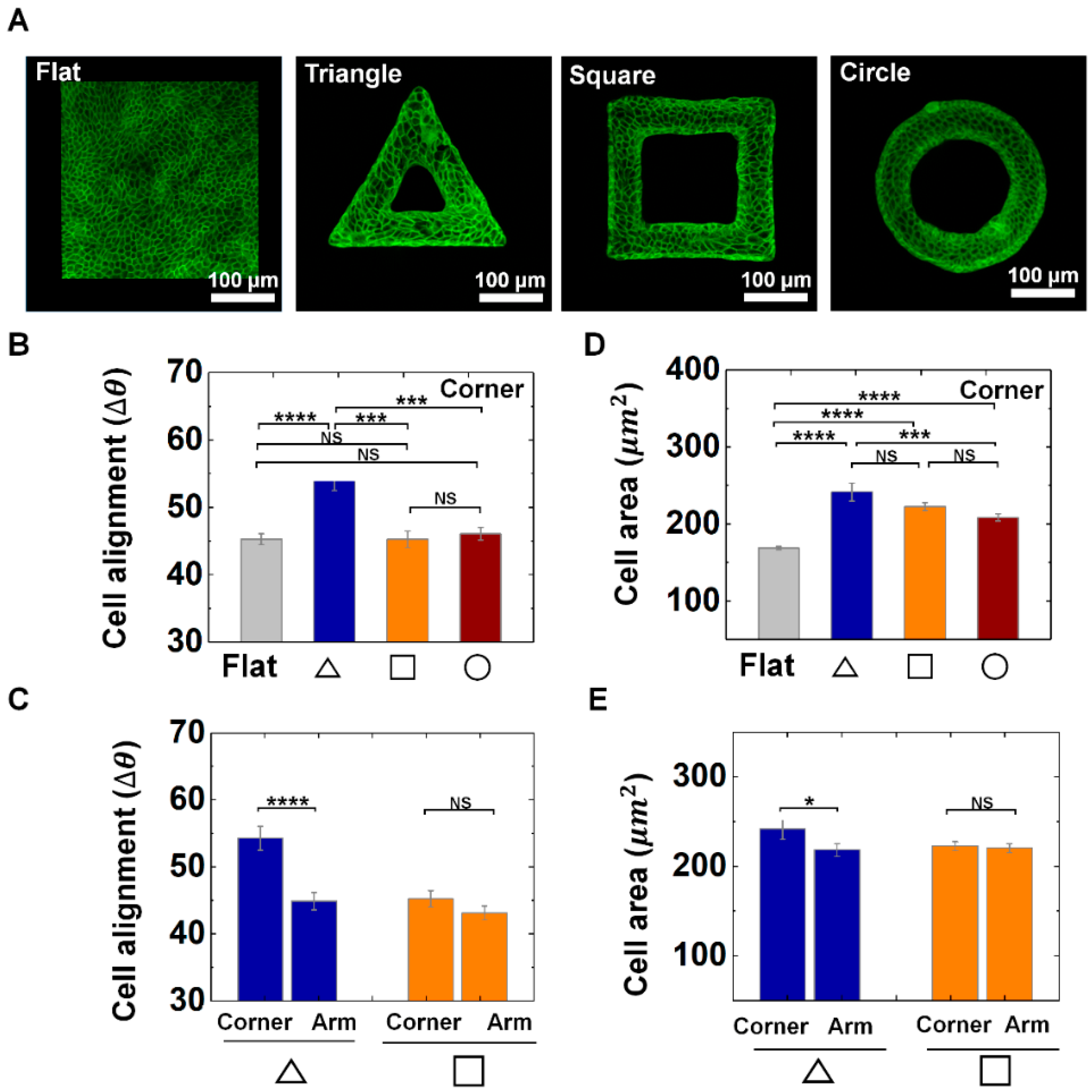
3.1. Epithelial Cells Exhibit the Adaptive Morphology on Convex Geometric Structure
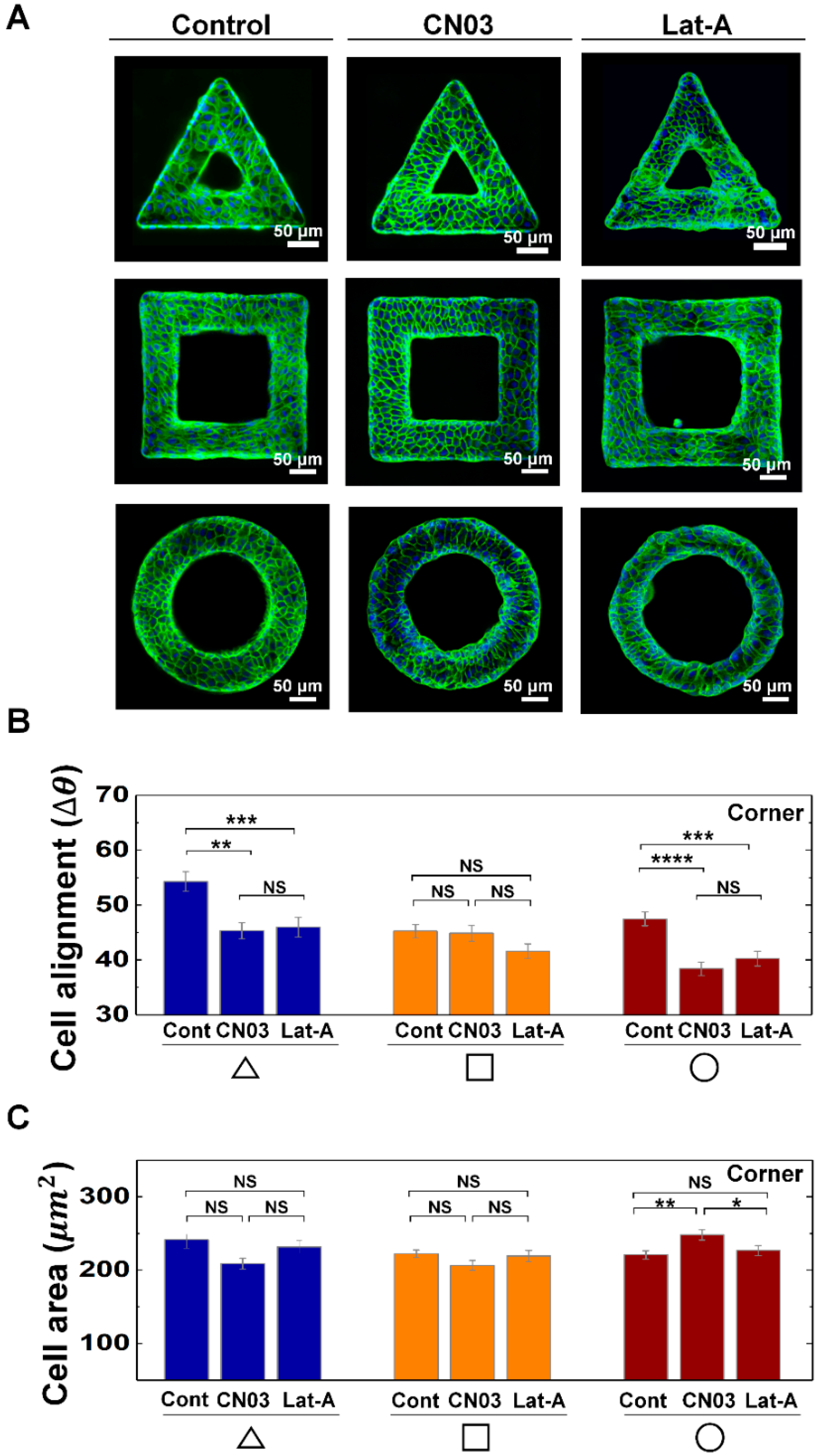
3.2. Actin Contractility Controls the Morphological Adaption of Epithelial Cells on Protruded Convex Structure
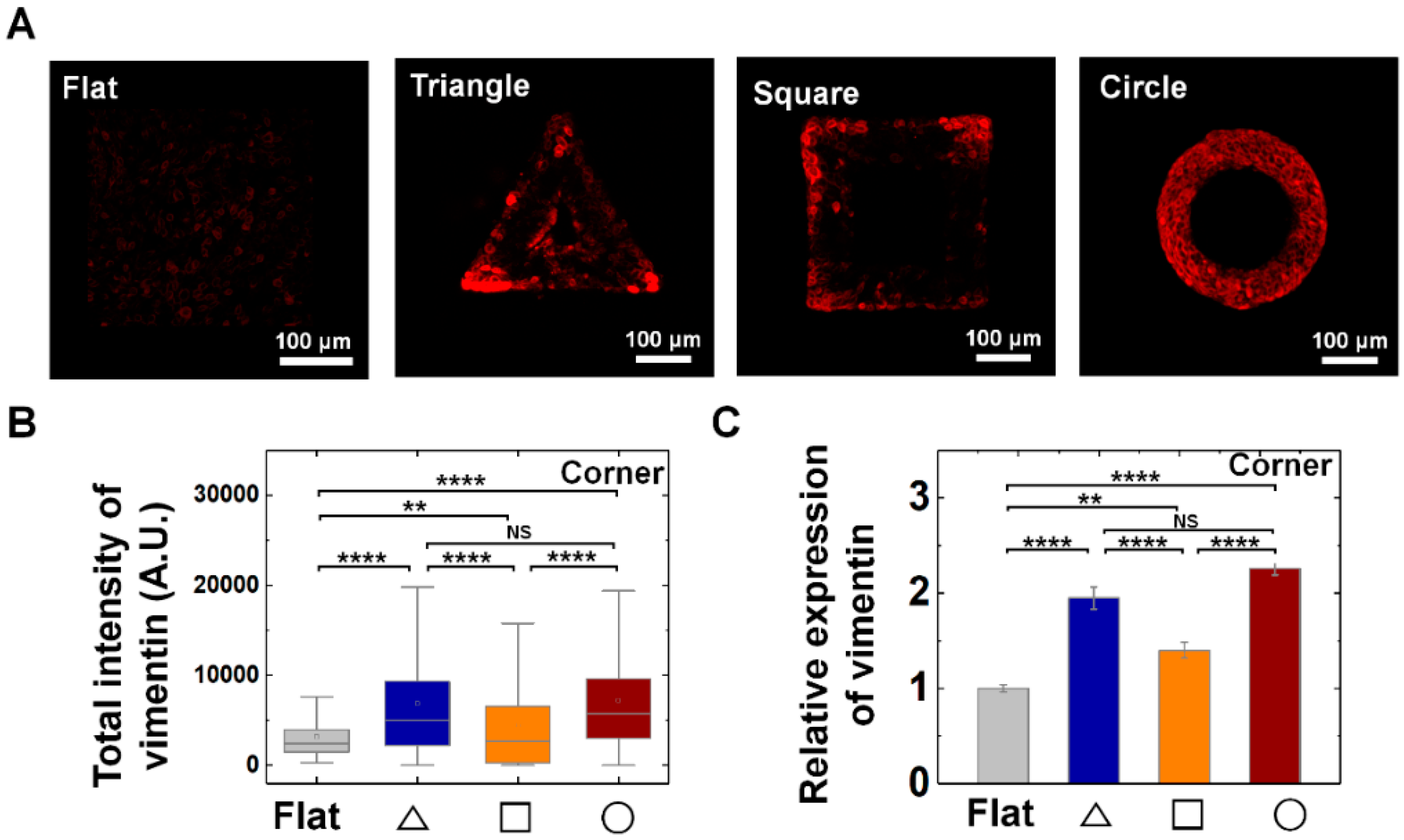
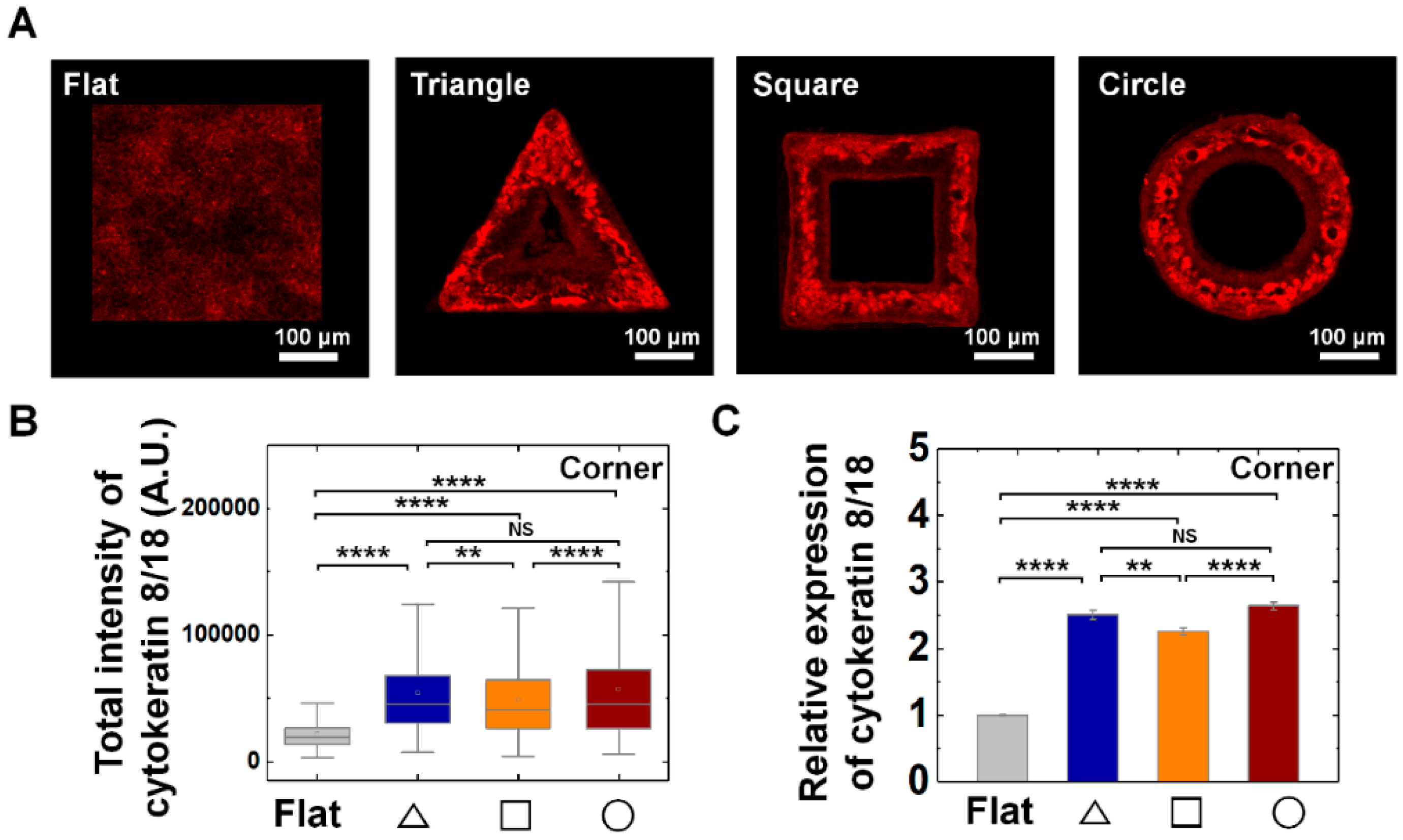
3.3. Vimentin and Keratin Intermediate Filaments are Essential for Growth and Adaptation of Epithelial Cells on Convex Geometric Structure
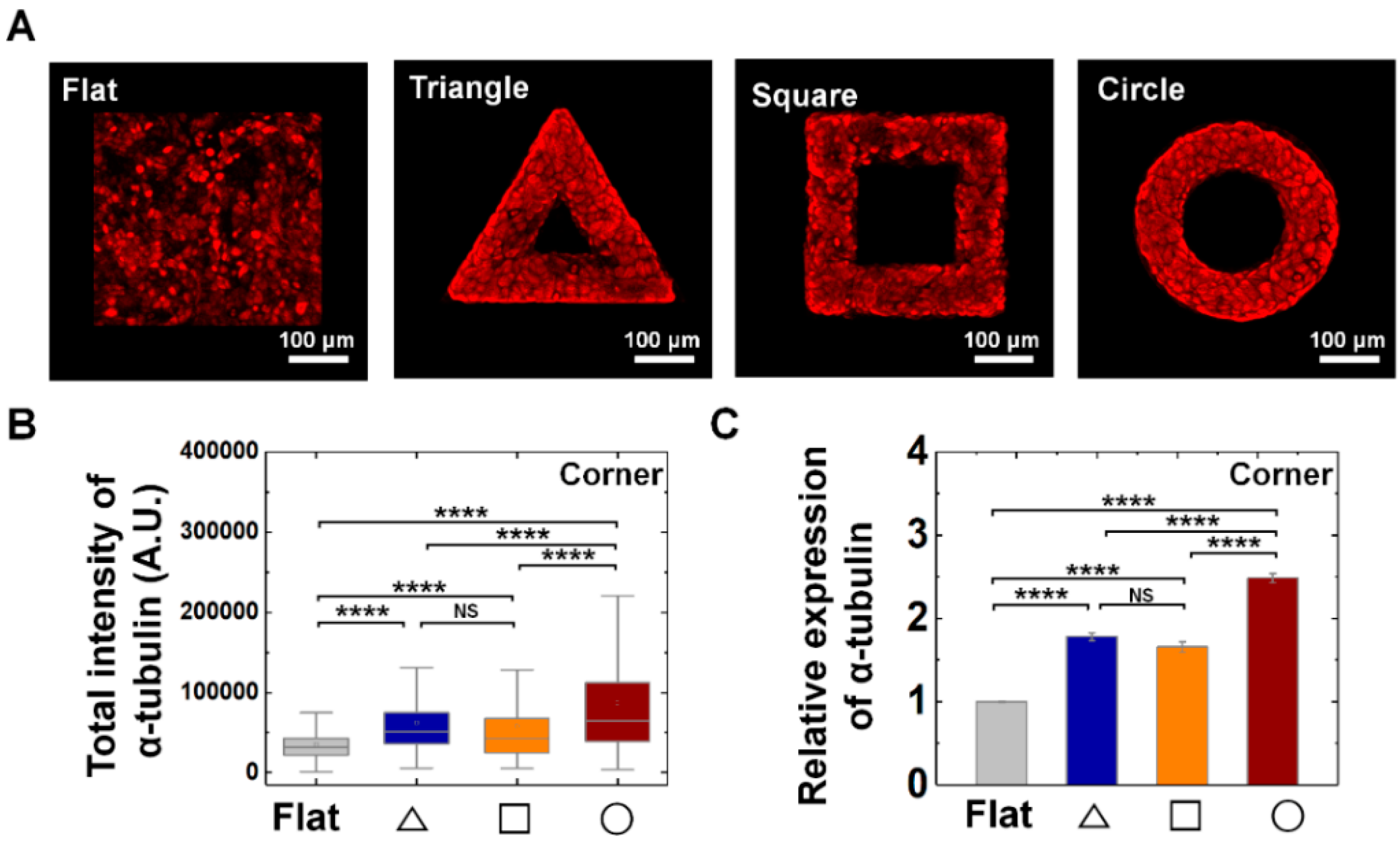
3.4. Tubulin, Microtubule Buildng Blocks, Involves in Mechanical Adaptation of Epithelial Cells on Convex Geometric Structure
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, P.D. Polycystic kidney disease. N. Engl. J. Med. 2004, 350, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Shyer, A.E.; Huycke, T.R.; Lee, C.H.; Mahadevan, L.; Tabin, C.J. Bending gradients: How the intestinal stem cell gets its home. Cell 2015, 161, 569–580. [Google Scholar] [CrossRef] [PubMed]
- Krndija, D.; El Marjou, F.; Guirao, B.; Richon, S.; Leroy, O.; Bellaiche, Y.; Hannezo, E.; Vignjevic, D.M. Active cell migration is critical for steady-state epithelial turnover in the gut. Science 2019, 365, 705–710. [Google Scholar] [CrossRef] [PubMed]
- Nowell, C.S.; Radtke, F. Corneal epithelial stem cells and their niche at a glance. J. Cell. Sci. 2017, 130, 1021–1025. [Google Scholar] [CrossRef] [PubMed]
- Messal, H.A.; Alt, S.; Ferreira, R.M.M.; Gribben, C.; Wang, V.M.Y.; Cotoi, C.G.; Salbreux, G.; Behrens, A. Tissue curvature and apicobasal mechanical tension imbalance instruct cancer morphogenesis. Nature 2019, 566, 126–130. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, J.; Loskill, P.; Huebsch, N.; Koo, S.; Svedlund, F.L.; Marks, N.C.; Hua, E.W.; Grigoropoulos, C.P.; Conklin, B.R.; et al. Self-organizing human cardiac microchambers mediated by geometric confinement. Nat. Commun. 2015, 6, 7413. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Abdeen, A.A.; Zhang, D.; Kilian, K.A. Directing stem cell fate on hydrogel substrates by controlling cell geometry, matrix mechanics and adhesion ligand composition. Biomaterials 2013, 34, 8140–8148. [Google Scholar] [CrossRef]
- Gomez, E.W.; Chen, Q.K.; Gjorevski, N.; Nelson, C.M. Tissue geometry patterns epithelial-mesenchymal transition via intercellular mechanotransduction. J. Cell Biochem. 2010, 110, 44–51. [Google Scholar] [CrossRef]
- von Erlach, T.C.; Bertazzo, S.; Wozniak, M.A.; Horejs, C.M.; Maynard, S.A.; Attwood, S.; Robinson, B.K.; Autefage, H.; Kallepitis, C.; Del Rio Hernandez, A.; et al. Cell-geometry-dependent changes in plasma membrane order direct stem cell signalling and fate. Nat. Mater. 2018, 17. [Google Scholar] [CrossRef]
- Kilian, K.A.; Bugarija, B.; Lahn, B.T.; Mrksich, M. Geometric cues for directing the differentiation of mesenchymal stem cells. Proc. Natl. Acad. Sci. USA 2010, 107, 4872–4877. [Google Scholar] [CrossRef]
- Xue, X.F.; Sun, Y.B.; Resto-Irizarry, A.M.; Yuan, Y.; Yong, K.M.A.; Zheng, Y.; Weng, S.N.; Shao, Y.; Chai, Y.M.; Studer, L.; et al. Mechanics-guided embryonic patterning of neuroectoderm tissue from human pluripotent stem cells. Nat. Mater. 2018, 17, 633–641. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Abdeen, A.A.; Wycislo, K.L.; Fan, T.M.; Kilian, K.A. Interfacial geometry dictates cancer cell tumorigenicity. Nat. Mater. 2016, 15, 856–862. [Google Scholar] [CrossRef] [PubMed]
- Bao, M.; Xie, J.; Huck, W.T.S. Recent advances in engineering the stem cell microniche in 3D. Adv. Sci. 2018, 5, 1800448. [Google Scholar] [CrossRef]
- Chaudhuri, P.K.; Low, B.C.; Lim, C.T. Mechanobiology of tumor growth. Chem. Rev. 2018, 118, 6499–6515. [Google Scholar] [CrossRef]
- Xi, W.; Sonam, S.; Saw, T.B.; Ladoux, B.; Lim, C.T. Emergent patterns of collective cell migration under tubular confinement. Nat. Commun. 2017, 8, 1517. [Google Scholar] [CrossRef]
- Biton, Y.Y.; Safran, S.A. The cellular response to curvature-induced stress. Phys. Biol. 2009, 6. [Google Scholar] [CrossRef]
- Wyatt, T.P.J.; Fouchard, J.; Lisica, A.; Khalilgharibi, N.; Baum, B.; Recho, P.; Kabla, A.J.; Charras, G.T. Actomyosin controls planarity and folding of epithelia in response to compression. Nat. Mater. 2020, 19, 109–117. [Google Scholar] [CrossRef]
- Baptista, D.; Teixeira, L.; van Blitterswijk, C.; Giselbrecht, S.; Truckenmuller, R. Overlooked? underestimated? effects of substrate curvature on cell behavior. Trends Biotechnol. 2019, 37, 838–854. [Google Scholar] [CrossRef]
- Yu, S.M.; Oh, J.M.; Lee, J.; Lee-Kwon, W.; Jung, W.; Amblard, F.; Granick, S.; Cho, Y.K. Substrate curvature affects the shape, orientation, and polarization of renal epithelial cells. Acta Biomater. 2018, 77, 311–321. [Google Scholar] [CrossRef]
- Ehrig, S.; Schamberger, B.; Bidan, C.M.; West, A.; Jacobi, C.; Lam, K.; Kollmannsberger, P.; Petersen, A.; Tomancak, P.; Kommareddy, K.; et al. Surface tension determines tissue shape and growth kinetics. Sci. Adv. 2019, 5, eaav9394. [Google Scholar] [CrossRef]
- Gomez-Galvez, P.; Vicente-Munuera, P.; Tagua, A.; Forja, C.; Castro, A.M.; Letran, M.; Valencia-Exposito, A.; Grima, C.; Bermudez-Gallardo, M.; Serrano-Perez-Higueras, O.; et al. Scutoids are a geometrical solution to three-dimensional packing of epithelia. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Bidan, C.M.; Kommareddy, K.P.; Rumpler, M.; Kollmannsberger, P.; Fratzl, P.; Dunlop, J.W.C. Geometry as a factor for tissue growth: Towards shape optimization of tissue engineering scaffolds. Adv. Healthc. Mater. 2013, 2, 186–194. [Google Scholar] [CrossRef]
- Bade, N.D.; Xu, T.N.; Kamien, R.D.; Assoian, R.K.; Stebe, K.J. Gaussian curvature directs stress fiber orientation and cell migration. Biophys. J. 2018, 114, 1467–1476. [Google Scholar] [CrossRef]
- Deforet, M.; Hakim, V.; Yevick, H.G.; Duclos, G.; Silberzan, P. Emergence of collective modes and tri-dimensional structures from epithelial confinement. Nat. Commun. 2014, 5, 3747. [Google Scholar] [CrossRef]
- Yevick, H.G.; Duclos, G.; Bonnet, I.; Silberzan, P. Architecture and migration of an epithelium on a cylindrical wire. Proc. Natl. Acad. Sci. USA 2015, 112, 5944–5949. [Google Scholar] [CrossRef]
- Martini, F.H.; Bartholomew, E.F. Kidneys are highly vascular structures containing functional units called nephrons, which perform filtration, reabsorption, and secretion. In Fundamentals of Anatomy & Physiology; Pearson Benjamin Cummings: San Francisco, CA, USA, 2009; pp. 967–975. [Google Scholar]
- Maechler, F.A.; Allier, C.; Roux, A.; Tomba, C. Curvature-dependent constraints drive remodeling of epithelia. J. Cell Sci. 2019, 132. [Google Scholar] [CrossRef]
- Latorre, E.; Kale, S.; Casares, L.; Gomez-Gonzalez, M.; Uroz, M.; Valonl, L.; Nair, R.V.; Garreta, E.; Montserrat, N.; del Campo, A.; et al. Active superelasticity in three-dimensional epithelia of controlled shape. Nature 2018, 563, 203–208. [Google Scholar] [CrossRef]
- Cerruti, B.; Puliafito, A.; Shewan, A.M.; Yu, W.; Combes, A.N.; Little, M.H.; Chianale, F.; Primo, L.; Serini, G.; Mostov, K.E.; et al. Polarity, cell division, and out-of-equilibrium dynamics control the growth of epithelial structures. J. Cell Biol. 2013, 203, 359–372. [Google Scholar] [CrossRef]
- Togawa, H.; Nakanishi, K.; Mukaiyama, H.; Hama, T.; Shima, Y.; Sako, M.; Miyajima, M.; Nozu, K.; Nishii, K.; Nagao, S.; et al. Epithelial-to-mesenchymal transition in cyst lining epithelial cells in an orthologous PCK rat model of autosomal-recessive polycystic kidney disease. Am. J. Physiol.-Renal Physiol. 2011, 300, F511–F520. [Google Scholar] [CrossRef]
- Nelson, C.M.; VanDuijn, M.M.; Inman, J.L.; Fletcher, D.A.; Bissell, M.J. Tissue geometry determines sites of mammary branching morphogenesis in organotypic cultures. Science 2006, 314, 298–300. [Google Scholar] [CrossRef]
- Salomon, J.; Gaston, C.; Magescas, J.; Duvauchelle, B.; Canioni, D.; Sengmanivong, L.; Mayeux, A.; Michaux, G.; Campeotto, F.; Lemale, J.; et al. Contractile forces at tricellular contacts modulate epithelial organization and monolayer integrity. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef]
- Flatau, G.; Lemichez, E.; Gauthier, M.; Chardin, P.; Paris, S.; Fiorentini, C.; Boquet, P. Toxin-induced activation of the G protein p21 Rho by deamidation of glutamine. Nature 1997, 387, 729–733. [Google Scholar] [CrossRef]
- Schmidt, G.; Sehr, P.; Wilm, M.; Selzer, J.; Mann, M.; Aktories, K. Gln 63 of Rho is deamidated by Escherichia coli cytotoxic necrotizing factor-1. Nature 1997, 387, 725–729. [Google Scholar] [CrossRef]
- Kaibuchi, K.; Kuroda, S.; Amano, M. Regulation of the cytoskeleton and cell adhesion by the Rho family GTPases in mammalian cells. Annu. Rev. Biochem. 1999, 68, 459–486. [Google Scholar] [CrossRef]
- Antonacci, G.; Braakman, S. Biomechanics of subcellular structures by non-invasive Brillouin microscopy. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Mendez, M.G.; Kojima, S.I.; Goldman, R.D. Vimentin induces changes in cell shape, motility, and adhesion during the epithelial to mesenchymal transition. Faseb J. 2010, 24, 1838–1851. [Google Scholar] [CrossRef]
- Hu, J.; Li, Y.; Hao, Y.; Zheng, T.; Gupta, S.K.; Parada, G.A.; Wu, H.; Lin, S.; Wang, S.; Zhao, X.; et al. High stretchability, strength, and toughness of living cells enabled by hyperelastic vimentin intermediate filaments. Proc. Natl. Acad. Sci. USA 2019, 116, 17175–17180. [Google Scholar] [CrossRef]
- Costigliola, N.; Ding, L.Y.; Burckhardt, C.J.; Han, S.J.; Gutierrez, E.; Mota, A.; Groisman, A.; Mitchison, T.J.; Danuser, G. Vimentin fibers orient traction stress. Proc. Natl. Acad. Sci. USA 2017, 114, 5195–5200. [Google Scholar] [CrossRef]
- Sanghvi-Shah, R.; Weber, G.F. Intermediate Filaments at the Junction of Mechanotransduction, Migration, and Development. Front. Cell Dev. Biol. 2017, 5. [Google Scholar] [CrossRef]
- Cheah, J.S.; Jacobs, K.A.; Heinrich, V.; Lo, S.H.; Yamada, S. Force-induced recruitment of cten along keratin network in epithelial cells. Proc. Natl. Acad. Sci. USA 2019, 116, 19799–19801. [Google Scholar] [CrossRef]
- Wang, Y.L.; Gunasekara, D.B.; Reed, M.I.; DiSalvo, M.; Bultman, S.J.; Sims, C.E.; Magness, S.T.; Allbritton, N.L. A microengineered collagen scaffold for generating a polarized crypt-villus architecture of human small intestinal epithelium. Biomaterials 2017, 128, 44–55. [Google Scholar] [CrossRef]
- Wakhloo, N.T.; Anders, S.; Badique, F.; Eichhorn, M.; Brigaud, I.; Petithory, T.; Vassaux, M.; Milan, J.L.; Freund, J.N.; Ruhe, J.; et al. Actomyosin, vimentin and LINC complex pull on osteosarcoma nuclei to deform on micropillar topography. Biomaterials 2020, 234. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.-M.; Li, B.; Granick, S.; Cho, Y.-K. Mechanical Adaptations of Epithelial Cells on Various Protruded Convex Geometries. Cells 2020, 9, 1434. https://doi.org/10.3390/cells9061434
Yu S-M, Li B, Granick S, Cho Y-K. Mechanical Adaptations of Epithelial Cells on Various Protruded Convex Geometries. Cells. 2020; 9(6):1434. https://doi.org/10.3390/cells9061434
Chicago/Turabian StyleYu, Sun-Min, Bo Li, Steve Granick, and Yoon-Kyoung Cho. 2020. "Mechanical Adaptations of Epithelial Cells on Various Protruded Convex Geometries" Cells 9, no. 6: 1434. https://doi.org/10.3390/cells9061434
APA StyleYu, S.-M., Li, B., Granick, S., & Cho, Y.-K. (2020). Mechanical Adaptations of Epithelial Cells on Various Protruded Convex Geometries. Cells, 9(6), 1434. https://doi.org/10.3390/cells9061434




