Affinity Selection in Germinal Centers: Cautionary Tales and New Opportunities
Abstract
1. Introduction
2. General Theoretical Framework and Derived Properties for Antibody– and BCR–ligand Interactions
2.1. Experimentally Estimated Effective on and off Constant Rates
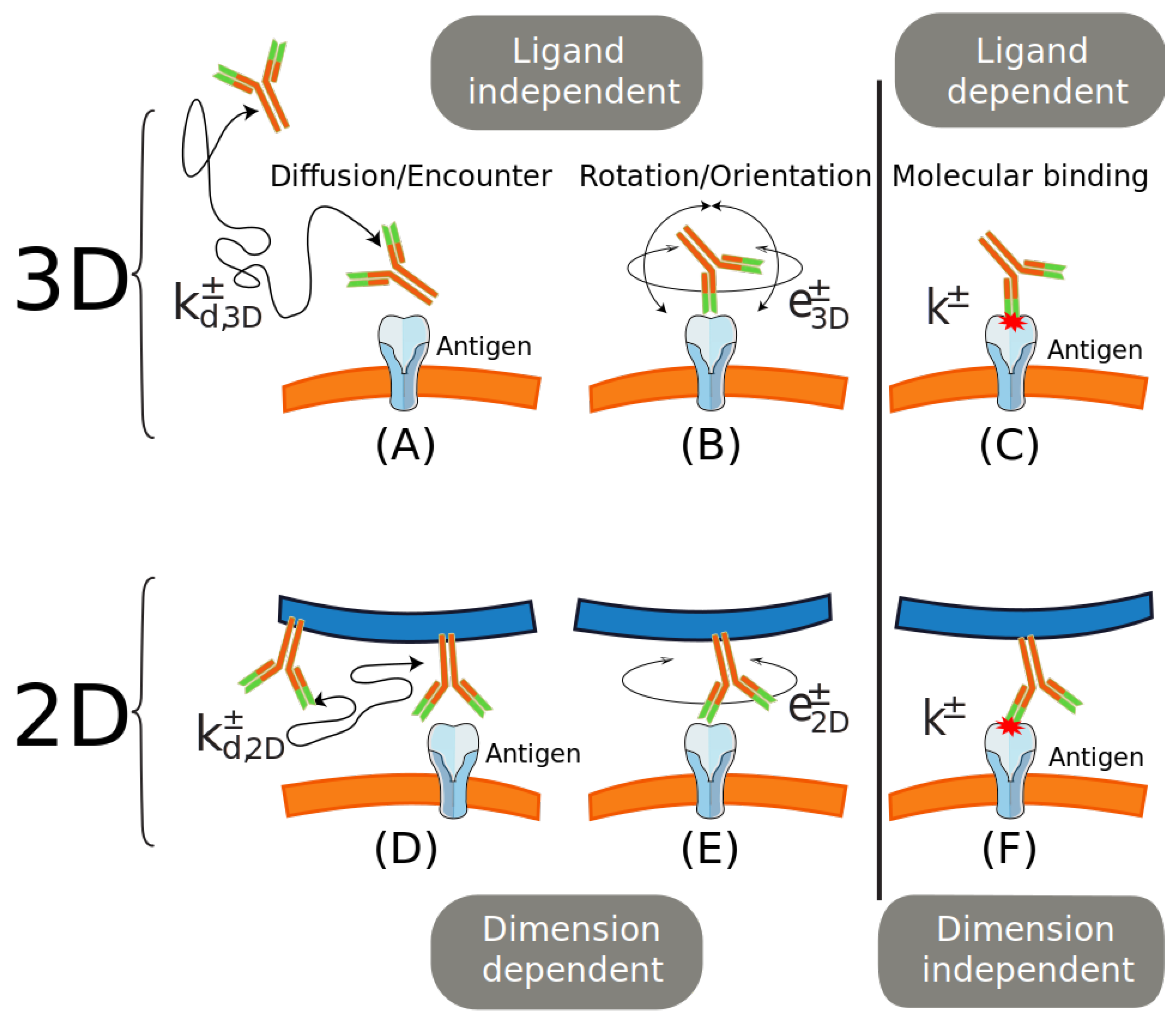
2.2. The Role of Translational Diffusion
2.3. The Role of Rotational Diffusion
2.4. The Role of Dimension
3. Is There a Role for Catch-Bonds in BCR–ligand Interactions?
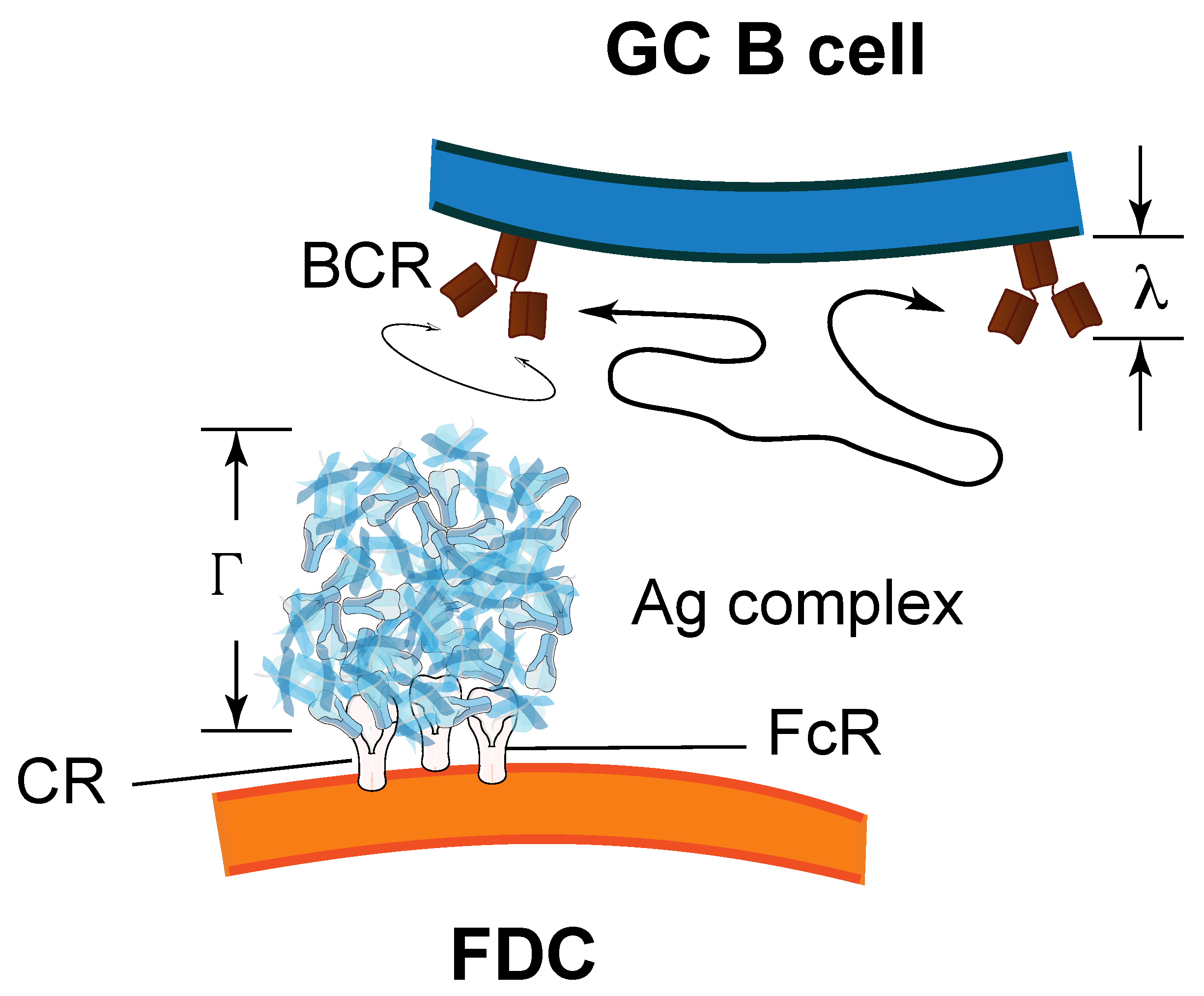
3.1. Evidence for Mechanical Forces in B-Cell Synapses and Their Relationship to Kinetic Rate Constants
3.2. An Extension of the Theoretical Framework
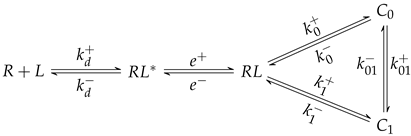
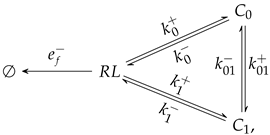
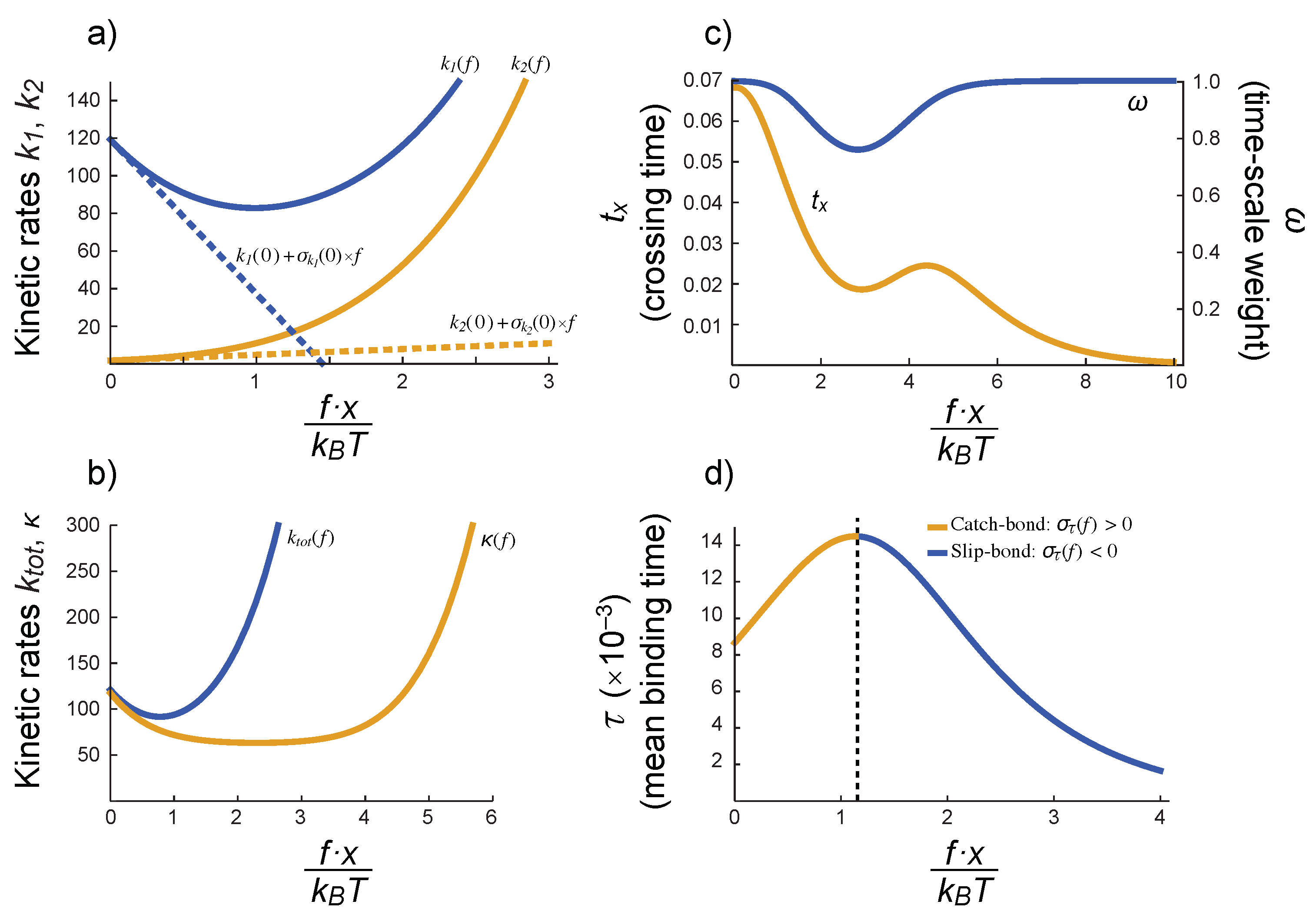
3.3. Conditions for the Existence of Catch-Slip Bonds in BCR–Ag Interactions
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AF | Adhesion Frequency |
| BCR | B-cell receptor |
| BFP | Biomembrane Force Probe |
| FDC | Follicular dendritic cell |
| GC | Germinal center |
| SPR | Surface Plasmon Resonance |
| TCR | T-cell receptor |
Appendix A. Some Mathematical Results
Appendix A.1. Full Model for the General Reaction Scheme
Appendix A.2. Master Equations
Appendix A.3. Effect of k+-Threshold Increase (or Decrease) on and
References
- Huang, J.; Zarnitsyna, V.; Liu, B.; Edwards, L.; Jiang, N.; Evavold, B.; Zhu, C. The kinetics of two dimensional TCR and pMHC interactions determine T cell responsiveness. Nature 2010, 464, 932. [Google Scholar] [CrossRef]
- Huppa, J.; Axmann, M.; Mörtelmaier, M.; Lillemeier, B.; Newell, E.; Brameshuber, M.; Klein, L.; Schütz, G.; Davis, M. TCR–peptide–MHC interactions in situ show accelerated kinetics and increased affinity. Nature 2010, 463, 963–967. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.T.; Shin, Y.; Brazin, K.; Mallis, R.J.; Sun, Z.Y.J.; Wagner, G.; Lang, M.J.; Reinherz, E.L. TCR Mechanobiology: Torques and Tunable Structures Linked to Early T Cell Signaling. Front. Immunol. 2012, 3, 76. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Chen, W.; Evavold, B.D.; Zhu, C. Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell 2014, 157, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Bell, G.I. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. [Google Scholar] [CrossRef]
- Dembo, M.; Torney, D.C.; Saxman, K.; Hammer, D.A. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. Ser. Biol. 1988, 234, 55–83. [Google Scholar] [CrossRef]
- Marshall, B.T.; Long, M.; Piper, J.W.; Yago, T.; McEver, R.P.; Zhu, C. Direct observation of catch bonds involving cell-adhesion molecules. Nature 2003, 423, 190–193. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Mallis, R.J.; Lang, M.J.; Reinherz, E.L. The αβTCR mechanosensor exploits dynamic ectodomain allostery to optimize its ligand recognition site. Proc. Natl. Acad. Sci. USA 2020, 117, 21336–21345. [Google Scholar] [CrossRef]
- Liu, Y.; Blanchfield, L.; Ma, V.P.Y.; Andargachew, R.; Galior, K.; Liu, Z.; Evavold, B.; Salaita, K. DNA-based nanoparticle tension sensors reveal that T-cell receptors transmit defined pN forces to their antigens for enhanced fidelity. Proc. Natl. Acad. Sci. USA 2016, 113, 5610–5615. [Google Scholar] [CrossRef]
- Faro, J.; Or-Guil, M. How oligoclonal are germinal centers? A new method for estimating clonal diversity from immunohistological sections. BMC Bioinform. 2013, 14. [Google Scholar] [CrossRef] [PubMed]
- Tas, J.M.J.; Mesin, L.; Pasqual, G.; Targ, S.; Jacobsen, J.T.; Mano, Y.M.; Chen, C.S.; Weill, J.C.; Reynaud, C.A.; Browne, E.P.; et al. Visualizing antibody affinity maturation in germinal centers. Science 2016, 351, 1048–1054. [Google Scholar] [CrossRef]
- Castro, M.; Lythe, G.; Molina-París, C.; Ribeiro, R.M. Mathematics in modern immunology. Interface Focus 2016, 6, 20150093. [Google Scholar] [CrossRef] [PubMed]
- Faro, J.; Castro, M.; Molina-París, C. A unifying mathematical framework for experimental TCR-pMHC kinetic constants. Sci. Rep. 2017, 7, 46741. [Google Scholar] [CrossRef] [PubMed]
- Mason, D.W.; Williams, A.F. The kinetics of antibody binding to membrane antigens in solution and at the cell surface. Biochem. J. 1980, 187, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.F. Out of equilibrium. Nature 1991, 352, 473–474. [Google Scholar] [CrossRef] [PubMed]
- Tolar, P.; Hanna, J.; Krueger, P.D.; Pierce, S.K. The Constant Region of the Membrane Immunoglobulin Mediates B cell–receptor Clustering and Signaling in Response to Membrane Antigens. Immunity 2009, 30, 44–55. [Google Scholar] [CrossRef]
- Treanor, B.; Depoil, D.; Gonzalez-Granja, A.; Barral, P.; Weber, M.; Dushek, O.; Bruckbauer, A.; Batista, F.D. The membrane skeleton controls diffusion dynamics and signaling through the B cell receptor. Immunity 2010, 32, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Xu, C.; Chen, X.; Xie, H.; Li, Z.; Wang, J.; Ji, X.; Chen, H.; Ji, Q.; Shaheen, S.; et al. PI(4,5)P2 determines the threshold of mechanical force-induced B cell activation. J Cell Biol. 2018, 217, 2565–2582. [Google Scholar] [CrossRef]
- Cantor, C.R.; Schimmel, P.R. Biophysical Chemistry Part 2; Freeman: San Francisco, CA, USA, 1980; p. 584. [Google Scholar]
- Saltzman, W.M.; Radomsky, M.L.; Whaley, K.J.; Cone, R.A. Antibody diffusion in human cervical mucus. Biophys. J. 1994, 66, 508–515. [Google Scholar] [CrossRef]
- Stingaciu, L.R.; Ivanova, O.; Ohl, M.; Biehl, R.; Richter, D. Fast antibody fragment motion: Flexible linkers act as entropic spring. Sci. Rep. 2016, 6, 22148. [Google Scholar] [CrossRef]
- Lauffenburger, D.; Linderman, J. Receptors: Models for Binding, Trafficking, and Signaling; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Reth, M. Matching cellular dimensions with molecular sizes. Nat. Immunol. 2013, 14, 765. [Google Scholar] [CrossRef]
- Wrigley, N.; Brown, E.; Skehel, J. Electron microscopic evidence for the axial rotation and inter-domain flexibility of the fab regions of immunoglobulin G. J. Mol. Biol. 1983, 169, 771–774. [Google Scholar] [CrossRef]
- Wade, R.; Taveau, J.; Lamy, J. Concerning the axial rotational flexibility of the Fab regions of immunoglobulin G. J. Mol. Biol. 1989, 206, 349–356. [Google Scholar] [CrossRef]
- Roux, K.H.; Strelets, L.; Michaelsen, T.E. Flexibility of human IgG subclasses. J. Immunol. 1997, 159, 3372–3382. Available online: https://www.jimmunol.org/content/159/7/3372.full.pdf (accessed on 13 July 2019). [PubMed]
- Saphire, E.O.; Stanfield, R.L.; Crispin, M.M.; Parren, P.W.; Rudd, P.M.; Dwek, R.A.; Burton, D.R.; Wilson, I.A. Contrasting IgG Structures Reveal Extreme Asymmetry and Flexibility. J. Mol. Biol. 2002, 319, 9–18. [Google Scholar] [CrossRef]
- Løset, G.Å.; Roux, K.H.; Zhu, P.; Michaelsen, T.E.; Sandlie, I. Differential Segmental Flexibility and Reach Dictate the Antigen Binding Mode of Chimeric IgD and IgM: Implications for the Function of the B Cell Receptor. J. Immunol. 2004, 172, 2925–2934. [Google Scholar] [CrossRef]
- Arnold, J.N.; Wormald, M.R.; Sim, R.B.; Rudd, P.M.; Dwek, R.A. The Impact of Glycosylation on the Biological Function and Structure of Human Immunoglobulins. Annu. Rev. Immunol. 2007, 25, 21–50. [Google Scholar] [CrossRef] [PubMed]
- Ramaraj, T.; Angel, T.; Dratz, E.A.; Jesaitis, A.J.; Mumey, B. Antigen–antibody interface properties: Composition, residue interactions, and features of 53 non-redundant structures. Biochim. Biophys. Acta (BBA)-Proteins Proteom. 2012, 1824, 520–532. [Google Scholar] [CrossRef]
- Saini, S.S.; Farrugia, W.; Muthusamy, N.; Ramsland, P.A.; Kaushik, A.K. Structural Evidence for a New IgG1 Antibody Sequence Allele of Cattle. Scand. J. Immunol. 2007, 65, 32–38. [Google Scholar] [CrossRef]
- Torres, M.; Fernández-Fuentes, N.; Fiser, A.; Casadevall, A. The Immunoglobulin Heavy Chain Constant Region Affects Kinetic and Thermodynamic Parameters of Antibody Variable Region Interactions with Antigen. J. Biol. Chem. 2007, 282, 13917–13927. [Google Scholar] [CrossRef]
- Oi, V.T.; Vuong, T.M.; Hardy, R.; Reidler, J.; Dangl, J.; Herzenberg, L.A.; Stryer, L. Correlation between segmental flexibility and effector function of antibodies. Nature 1984, 307, 136–140. [Google Scholar] [CrossRef]
- Hussain, R.; Dawood, G.; Abrar, N.; Toossi, Z.; Minai, A.; Dojki, M.; Ellner, J.J. Selective increases in antibody isotypes and immunoglobulin G subclass responses to secreted antigens in tuberculosis patients and healthy household contacts of the patients. Clin. Diagn. Lab. Immunol. 1995, 2, 726–732. Available online: https://cvi.asm.org/content/2/6/726.full.pdf (accessed on 22 July 2019). [CrossRef]
- Golding, B. Cytokine Regulation of Humoral Immune Responses; Topics in Vaccine Adjuvant Research; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Hanson, D.C.; Yguerabide, J.; Schumaker, V.N. Segmental flexibility of immunoglobulin G antibody molecules in solution: A new interpretation. Biochemistry 1981, 20, 6842–6852. [Google Scholar] [CrossRef]
- Saffman, P.; Delbrück, M. Brownian motion in biological membranes. Proc. Natl. Acad. Sci. USA 1975, 72, 3111–3113. [Google Scholar] [CrossRef]
- Schlessinger, J. Lateral and rotational diffusion of EGF-receptor complex: Relationship to receptor-mediated endocytosis. Biopolymers 1983, 22, 347–353. [Google Scholar] [CrossRef] [PubMed]
- Hanson, D.C.; Yguerabide, J.; Schumaker, V.N. Rotational dynamics of immunoglobulin G antibodies anchored in protein a soluble complexes. Mol. Immunol. 1985, 22, 237–244. [Google Scholar] [CrossRef]
- Schumaker, V.N.; Phillips, M.L.; Hanson, D.C. Dynamic aspects of antibody structure. Mol. Immunol. 1991, 28, 1347–1360. [Google Scholar] [CrossRef]
- Torres, M.; May, R.; Scharff, M.D.; Casadevall, A. Variable-Region-Identical Antibodies Differing in Isotype Demonstrate Differences in Fine Specificity and Idiotype. J. Immunol. 2005, 174, 2132–2142. [Google Scholar] [CrossRef]
- Szakal, A.; Kosco, M.; Tew, J. A novel in vivo follicular dendritic cell-dependent iccosome-mediated mechanism for delivery of antigen to antigen-processing cells. J. Immunol. 1988, 140, 341–353. [Google Scholar] [PubMed]
- Natkanski, E.; Lee, W.Y.; Mistry, B.; Casal, A.; Molloy, J.E.; Tolar, P. B cells use mechanical energy to discriminate antigen affinities. Science 2013, 340, 1587–1590. [Google Scholar] [CrossRef]
- Nowosad, C.R.; Spillane, K.M.; Tolar, P. Germinal center B cells recognize antigen through a specialized immune synapse architecture. Nat. Immunol. 2016, 17, 870–877. [Google Scholar] [CrossRef]
- Spillane, K.M.; Tolar, P. B cell antigen extraction is regulated by physical properties of antigen-presenting cells. J. Cell Biol. 2017, 216, 217–230. [Google Scholar] [CrossRef]
- Wang, J.; Lin, F.; Wan, Z.; Sun, X.; Lu, Y.; Huang, J.; Wang, F.; Zeng, Y.; Chen, Y.H.; Shi, Y.; et al. Profiling the origin, dynamics, and function of traction force in B cell activation. Sci. Signal. 2018, 11. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Grigorova, I.; Phan, T.G.; Kelly, L.M.; Cyster, J.G. Visualizing B cell capture of cognate antigen from follicular dendritic cells. J. Exp. Med. 2009, 206, 1485–1493. [Google Scholar] [CrossRef] [PubMed]
- Pereverzev, Y.V.; Prezhdo, E.; Sokurenko, E.V. The two-pathway model of the biological catch-bond as a limit of the allosteric model. Biophys. J. 2011, 101, 2026–2036. [Google Scholar] [CrossRef] [PubMed]
- Das, D.K.; Feng, Y.; Mallis, R.J.; Li, X.; Keskin, D.B.; Hussey, R.E.; Brady, S.K.; Wang, J.H.; Wagner, G.; Reinherz, E.L.; et al. Force-dependent transition in the T-cell receptor β-subunit allosterically regulates peptide discrimination and pMHC bond lifetime. Proc. Natl. Acad. Sci. USA 2015, 112, 1517–1522. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Liu, S.; Li, X.; Wan, Z.; Mao, Y.; Chen, C.; Liu, W. Conformational change within the extracellular domain of B cell receptor in B cell activation upon antigen binding. eLife 2019, 8. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Estevez, A.; Schlothauer, T.; Wecksler, A.T. Antigen physiochemical properties allosterically effect the IgG Fc-region and Fc neonatal receptor affinity. mAbs 2020, 12, 1802135. [Google Scholar] [CrossRef]
- Qaraghuli, M.M.A.; Kubiak-Ossowska, K.; Ferro, V.A.; Mulheran, P.A. Antibody-protein binding and conformational changes: Identifying allosteric signalling pathways to engineer a better effector response. Sci. Rep. 2020, 10, 13696. [Google Scholar] [CrossRef]
- Foote, J.; Milstein, C. Conformational isomerism and the diversity of antibodies. Proc. Natl. Acad. Sci. USA 1994, 91, 10370–10374. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Pomarici, N.D.; Math, B.A.; Kroell, K.B.; Waibl, F.; Bujotzek, A.; Georges, G.; Liedl, K.R. Antibodies exhibit multiple paratope states influencing VH–VL domain orientations. Commun. Biol. 2020, 3. [Google Scholar] [CrossRef] [PubMed]
- Ju, L.; Dong, J.F.; Cruz, M.A.; Zhu, C. The N-terminal Flanking Region of the A1 Domain Regulates the Force-dependent Binding of von Willebrand Factor to Platelet Glycoprotein. J. Biol. Chem. 2013, 288, 32289–32301. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Turányi, T. Sensitivity analysis of complex kinetic systems. Tools and applications. J. Math. Chem. 1990, 5, 203–248. [Google Scholar] [CrossRef]
- Faro, J.; von Haeften, B.; Gardner, R.; Faro, E. A Sensitivity Analysis Comparison of Three Models for the Dynamics of Germinal Centers. Front. Immunol. 2019, 10. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, S.; Fan, Y.; Liu, K.; Du, F.; Davey, A.M.; Zhang, H.; Han, W.; Xiong, C.; Liu, W. B cell activation is regulated by the stiffness properties of the substrate presenting the antigens. J. Immunol. 2013, 190, 4661–4675. [Google Scholar] [CrossRef]
- Kwak, K.; Quizon, N.; Sohn, H.; Saniee, A.; Manzella-Lapeira, J.; Holla, P.; Brzostowski, J.; Lu, J.; Xie, H.; Xu, C.; et al. Intrinsic properties of human germinal center B cells set antigen affinity thresholds. Sci. Immunol. 2018, 3. [Google Scholar] [CrossRef]
- Huse, M. Mechanical forces in the immune system. Nat. Rev. Immunol. 2017, 17, 679–690. [Google Scholar] [CrossRef]
- González, C.; Chames, P.; Kerfelec, B.; Baty, D.; Robert, P.; Limozin, L. Nanobody-CD16 Catch Bond Reveals NK Cell Mechanosensitivity. Biophys. J. 2019, 116, 1516–1526. [Google Scholar] [CrossRef]
- Huang, J. TCR-Mediated Internalization of Peptide-MHC Complexes Acquired by T Cells. Science 1999, 286, 952–954. [Google Scholar] [CrossRef]
- Wyman, J. The turning wheel: A study in steady states. Proc. Natl. Acad. Sci. USA 1975, 72, 3983–3987. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faro, J.; Castro, M. Affinity Selection in Germinal Centers: Cautionary Tales and New Opportunities. Cells 2021, 10, 1040. https://doi.org/10.3390/cells10051040
Faro J, Castro M. Affinity Selection in Germinal Centers: Cautionary Tales and New Opportunities. Cells. 2021; 10(5):1040. https://doi.org/10.3390/cells10051040
Chicago/Turabian StyleFaro, Jose, and Mario Castro. 2021. "Affinity Selection in Germinal Centers: Cautionary Tales and New Opportunities" Cells 10, no. 5: 1040. https://doi.org/10.3390/cells10051040
APA StyleFaro, J., & Castro, M. (2021). Affinity Selection in Germinal Centers: Cautionary Tales and New Opportunities. Cells, 10(5), 1040. https://doi.org/10.3390/cells10051040





