Data-Driven Mathematical Model of Apoptosis Regulation in Memory Plasma Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cell Culture and Flow-Cytometric Measurements of Apoptosis Proteins
2.2. Data Analysis and Statistics
2.3. Mathematical Models and Numerical Simulations
3. Results
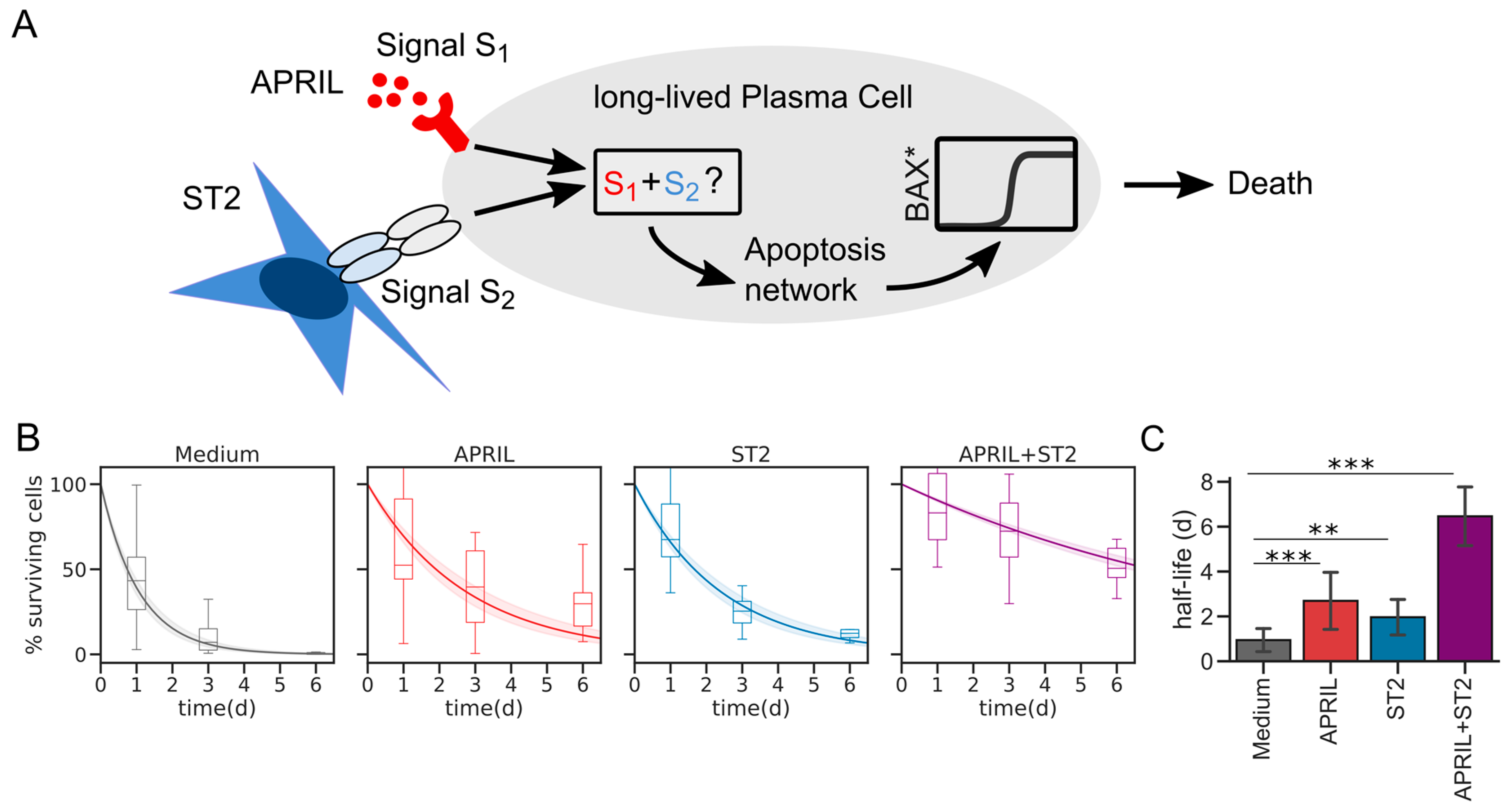
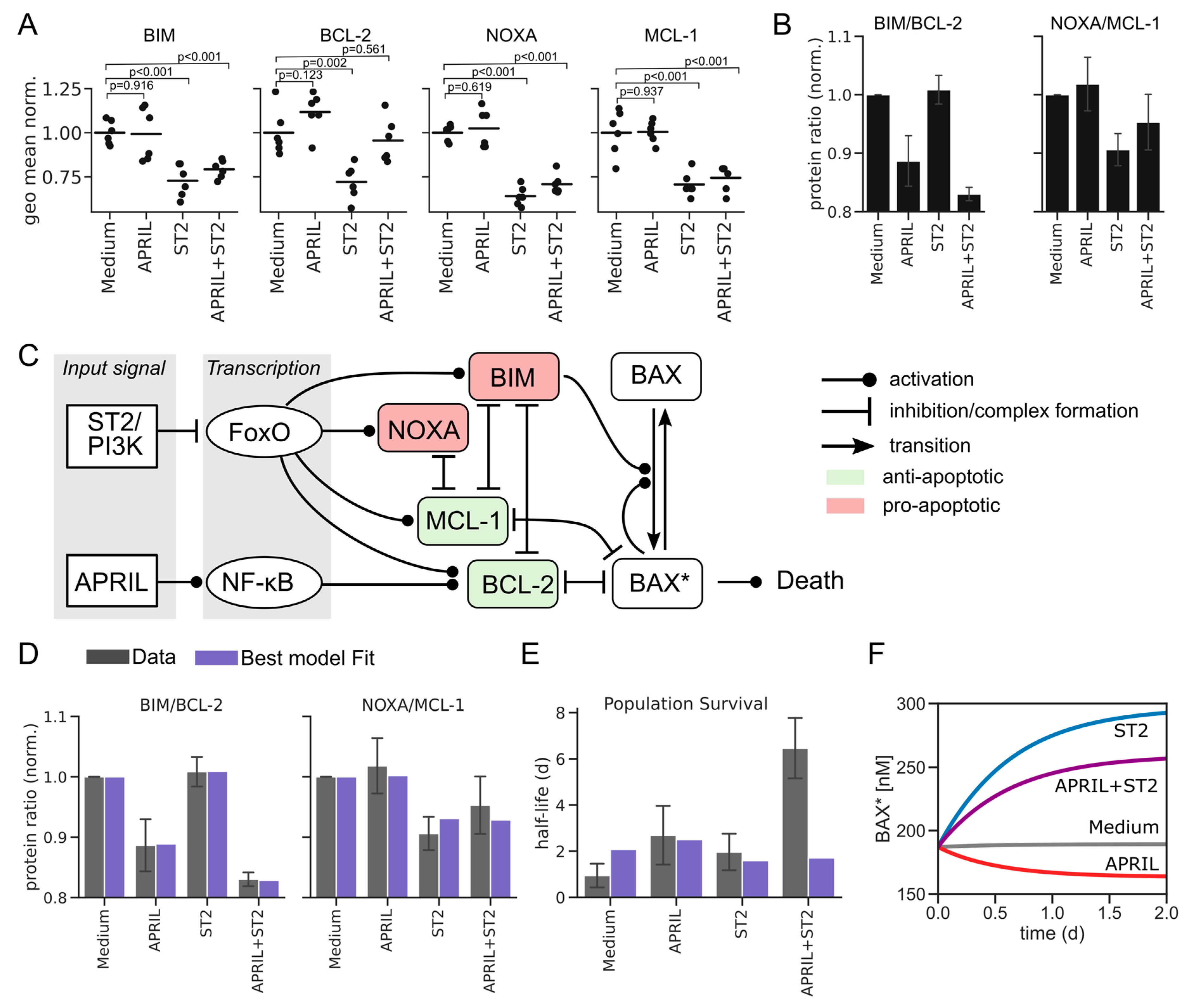
3.1. A Quantitative Model of BAX-Dependent Apoptosis in Plasma Cells
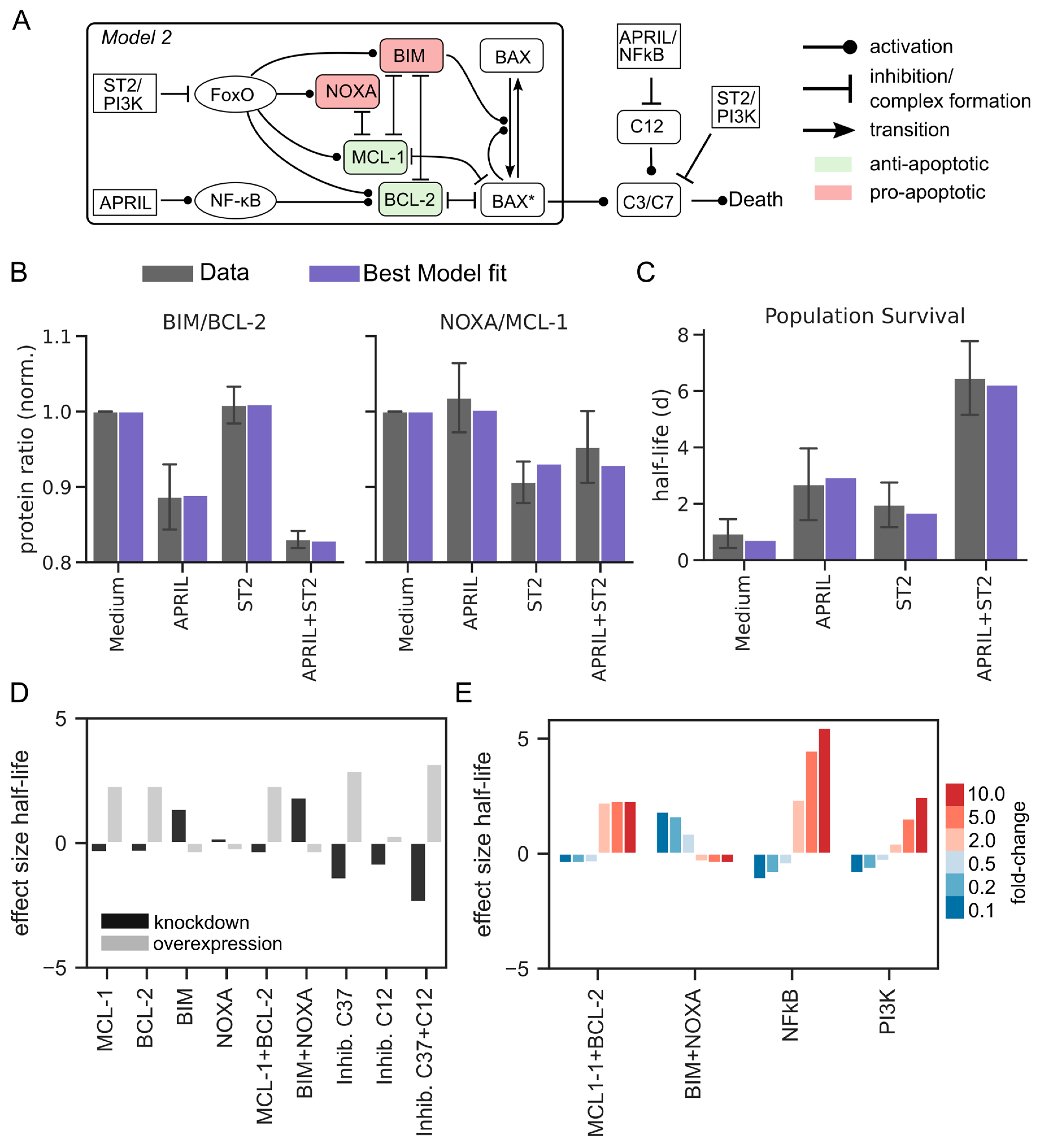
3.2. Direct Regulation of Caspase Proteins Is Required for Effective Control
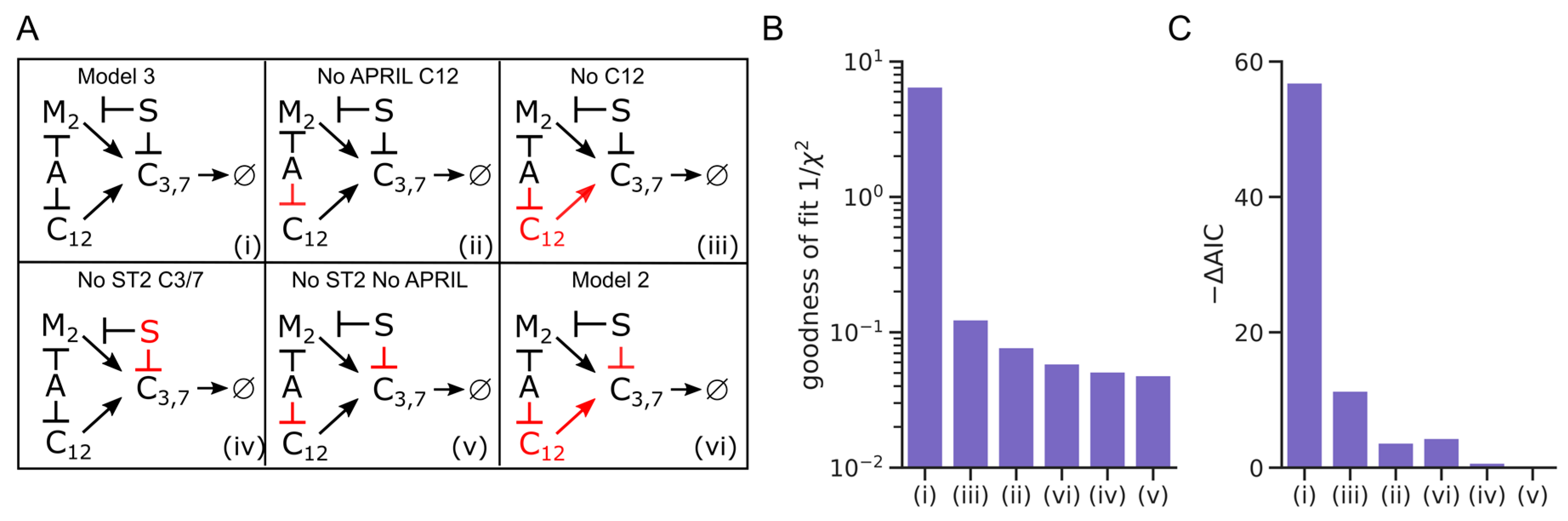
3.3. Full Model Topology Is Essential to Describe Plasma Cell Survival
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khodadadi, L.; Cheng, Q.; Radbruch, A.; Hiepe, F. The Maintenance of Memory Plasma Cells. Front. Immunol. 2019, 10, 721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hiepe, F.; Radbruch, A. Plasma cells as an innovative target in autoimmune disease with renal manifestations. Nat. Rev. Nephrol. 2016, 12, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Maschmeyer, P.; Chang, H.-D.; Cheng, Q.; Mashreghi, M.-F.; Hiepe, F.; Alexander, T.; Radbruch, A. Immunological memory in rheumatic inflammation—A roadblock to tolerance induction. Nat. Rev. Rheumatol. 2021, 17, 291–305. [Google Scholar] [CrossRef] [PubMed]
- Nutt, S.L.; Hodgkin, P.D.; Tarlinton, D.M.; Corcoran, L.M. The generation of antibody-secreting plasma cells. Nat. Rev. Immunol. 2015, 15, 160–171. [Google Scholar] [CrossRef] [PubMed]
- Chu, V.T.; Berek, C. The establishment of the plasma cell survival niche in the bone marrow. Immunol. Rev. 2013, 251, 177–188. [Google Scholar] [CrossRef]
- Manz, R.A.; Thiel, A.; Radbruch, A. Lifetime of plasma cells in the bone marrow. Nature 1997, 388, 133–134. [Google Scholar] [CrossRef]
- DiLillo, D.J.; Hamaguchi, Y.; Ueda, Y.; Yang, K.; Uchida, J.; Haas, K.M.; Kelsoe, G.; Tedder, T.F. Maintenance of Long-Lived Plasma Cells and Serological Memory Despite Mature and Memory B Cell Depletion during CD20 Immunotherapy in Mice. J. Immunol. 2008, 180, 361–371. [Google Scholar] [CrossRef]
- Benson, M.J.; Dillon, S.R.; Castigli, E.; Geha, R.S.; Xu, S.; Lam, K.-P.; Noelle, R.J. Cutting Edge: The Dependence of Plasma Cells and Independence of Memory B Cells on BAFF and APRIL. J. Immunol. 2008, 180, 3655–3659. [Google Scholar] [CrossRef] [Green Version]
- Landsverk, O.J.B.; Snir, O.; Casado, R.B.; Richter, L.; Mold, J.E.; Réu, P.; Horneland, R.; Paulsen, V.; Yaqub, S.; Aandahl, E.M.; et al. Antibody-secreting plasma cells persist for decades in human intestine. J. Exp. Med. 2017, 214, 309–317. [Google Scholar] [CrossRef] [Green Version]
- Zehentmeier, S.; Roth, K.; Cseresnyes, Z.; Sercan, Ö.; Horn, K.; Niesner, R.A.; Chang, H.-D.; Radbruch, A.; Hauser, A.E. Static and dynamic components synergize to form a stable survival niche for bone marrow plasma cells. Eur. J. Immunol. 2014, 44, 2306–2317. [Google Scholar] [CrossRef] [Green Version]
- Hoyer, B.F.; Moser, K.; Hauser, A.E.; Peddinghaus, A.; Voigt, C.; Eilat, D.; Radbruch, A.; Hiepe, F.; Manz, R.A. Short-lived plasmablasts and long-lived plasma cells contribute to chronic humoral autoimmunity in NZB/W mice. J. Exp. Med. 2004, 199, 1577–1584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cornelis, R.; Hahne, S.; Taddeo, A.; Petkau, G.; Malko, D.; Durek, P.; Thiem, M.; Heiberger, L.; Peter, L.; Mohr, E.; et al. Stromal Cell-Contact Dependent PI3K and APRIL Induced NF-κB Signaling Prevent Mitochondrial- and ER Stress Induced Death of Memory Plasma Cells. Cell Rep. 2020, 32, 107982. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, N.; Casamayor-Pallejà, M.; De Luca, K.; Mondière, P.; Saltel, F.; Jurdic, P.; Bella, C.; Genestier, L.; Defrance, T. The Endoplasmic Reticulum Is a Key Component of the Plasma Cell Death Pathway. J. Immunol. 2006, 176, 1340–1347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fussenegger, M.; Bailey, J.E.; Varner, J. A mathematical model of caspase function in apoptosis. Nat. Biotechnol. 2000, 18, 768–774. [Google Scholar] [CrossRef] [PubMed]
- Spencer, S.L.; Sorger, P.K. Measuring and modeling apoptosis in single cells. Cell 2011, 144, 926–939. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, J.C.; Waterhouse, N.J.; Juin, P.; Evan, G.I.; Green, D.R. The coordinate release of cytochrome c during apoptosis is rapid, complete and kinetically invariant. Nat. Cell Biol. 2000, 2, 156–162. [Google Scholar] [CrossRef]
- Rehm, M.; Düßmann, H.; Jänicke, R.U.; Tavaré, J.M.; Kögel, D.; Prehn, J.H.M. Single-cell fluorescence resonance energy transfer analysis demonstrates that caspase activation during apoptosis is a rapid process: Role of caspase-3. J. Biol. Chem. 2002, 277, 24506–24514. [Google Scholar] [CrossRef] [Green Version]
- Eissing, T.; Conzelmann, H.; Gilles, E.D.; Allgöwer, F.; Bullinger, E.; Scheurich, P. Bistability analyses of a caspase activation model for receptor-induced apoptosis. J. Biol. Chem. 2004, 279, 36892–36897. [Google Scholar] [CrossRef] [Green Version]
- Legewie, S.; Blüthgen, N.; Herzel, H. Mathematical modeling identifies inhibitors of apoptosis as mediators of positive feedback and bistability. PLoS Comput. Biol. 2006, 2, 1061–1073. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Cui, J.; Lu, H.; Wang, R.; Zhang, S.; Shen, P. Modeling of the role of a Bax-activation switch in the mitochondrial apoptosis decision. Biophys. J. 2007, 92, 4304–4315. [Google Scholar] [CrossRef] [Green Version]
- McKenna, S.; García-Gutiérrez, L.; Matallanas, D.; Fey, D. BAX and SMAC regulate bistable properties of the apoptotic caspase system. Sci. Rep. 2021, 11, 3272. [Google Scholar] [CrossRef] [PubMed]
- Hantusch, A.; Brunner, T.; Frickey, T.; Rehm, M. Bcl-2-Ome-a database and interactive web service for dissecting the Bcl-2 interactome. Cell Death Differ. 2017, 24, 192. [Google Scholar] [CrossRef] [Green Version]
- Hatzoglou, A.; Roussel, J.; Bourgeade, M.-F.; Rogier, E.; Madry, C.; Inoue, J.; Devergne, O.; Tsapis, A. TNF Receptor Family Member BCMA (B Cell Maturation) Associates with TNF Receptor-Associated Factor (TRAF) 1, TRAF2, and TRAF3 and Activates NF-κB, Elk-1, c-Jun N-Terminal Kinase, and p38 Mitogen-Activated Protein Kinase. J. Immunol. 2000, 165, 1322–1330. [Google Scholar] [CrossRef] [Green Version]
- Chu, V.T.; Fröhlich, A.; Steinhauser, G.; Scheel, T.; Roch, T.; Fillatreau, S.; Lee, J.J.; Löhning, M.; Berek, C. Eosinophils are required for the maintenance of plasma cells in the bone marrow. Nat. Immunol. 2011, 12, 151–159. [Google Scholar] [CrossRef]
- O’Connor, B.P.; Raman, V.S.; Erickson, L.D.; Cook, W.J.; Weaver, L.K.; Ahonen, C.; Lin, L.-L.; Mantchev, G.T.; Bram, R.J.; Noelle, R.J. BCMA Is Essential for the Survival of Long-lived Bone Marrow Plasma Cells. J. Exp. Med. 2004, 199, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Van Spriel, A.B.; De Keijzer, S.; Van Der Schaaf, A.; Gartlan, K.H.; Sofi, M.; Light, A.; Linssen, P.C.; Boezeman, J.B.; Zuidscherwoude, M.; Reinieren-Beeren, I.; et al. The tetraspanin CD37 orchestrates the α4β1 integrin-Akt signaling axis and supports long-lived plasma cell survival. Sci. Signal. 2012, 5, ra82. [Google Scholar] [CrossRef]
- Cosentino, K.; García-Sáez, A.J. Bax and Bak Pores: Are We Closing the Circle? Trends Cell Biol. 2017, 27, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Peperzak, V.; Vikström, I.; Walker, J.; Glaser, S.P.; Lepage, M.; Coquery, C.M.; Erickson, L.D.; Fairfax, K.; Mackay, F.; Strasser, A.; et al. Mcl-1 is essential for the survival of plasma cells. Nat. Immunol. 2013, 14, 290–297. [Google Scholar] [CrossRef]
- Gomez-Bougie, P.; Bataille, R.; Amiot, M. The imbalance between Bim and Mcl-1 expression controls the survival of human myeloma cells. Eur. J. Immunol. 2004, 34, 3156–3164. [Google Scholar] [CrossRef]
- Nakajima, W.; Hicks, M.A.; Tanaka, N.; Krystal, G.W.; Harada, H. Noxa determines localization and stability of MCL-1 and consequently ABT-737 sensitivity in small cell lung cancer. Cell Death Dis. 2014, 5, e1052. [Google Scholar] [CrossRef] [Green Version]
- Rooswinkel, R.W.; Van De Kooij, B.; De Vries, E.; Paauwe, M.; Braster, R.; Verheij, M.; Borst, J. Antiapoptotic potency of Bcl-2 proteins primarily relies on their stability, not binding selectivity. Blood 2014, 123, 2806–2815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, X.; Deng, X.; May, W.S. Cleavage of Bax to p18 Bax accelerates stress-induced apoptosis, and a cathepsin-like protease may rapidly degrade p18 Bax. Blood 2003, 102, 2605–2614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meller, R.; Cameron, J.A.; Torrey, D.J.; Clayton, C.E.; Ordonez, A.N.; Henshall, D.C.; Minami, M.; Schindler, C.K.; Saugstad, J.A.; Simon, R.P. Rapid degradation of bim by the ubiquitin-proteasome pathway mediates short-term ischemic tolerance in cultured neurons. J. Biol. Chem. 2006, 281, 7429–7436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dengler, M.A.; Weilbacher, A.; Gutekunst, M.; Staiger, A.M.; Vöhringer, M.C.; Horn, H.; Ott, G.; Aulitzky, W.E.; Van Der Kuip, H. Discrepant NOXA (PMAIP1) transcript and NOXA protein levels: A potential Achilles’ heel in mantle cell lymphoma. Cell Death Dis. 2014, 5, e1013. [Google Scholar] [CrossRef] [Green Version]
- Lakhani, S.A.; Masud, A.; Kuida, K.; Porter, G.A.; Booth, C.J.; Mehal, W.Z.; Inayat, I.; Flavell, R.A. Caspases 3 and 7: Key mediators of mitochondrial events of apoptosis. Science 2006, 311, 847–851. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, T.; Zhu, H.; Morishima, N.; Li, E.; Xu, J.; Yankner, B.A.; Yuan, J. Caspase-12 mediates endoplasmic-reticulum-specific apoptosis and cytotoxicity by amyloid-β. Nature 2000, 403, 98–103. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdiscip. Rev. Comput. Stat. 2019, 11, 1460. [Google Scholar] [CrossRef]
- Gass, J.N.; Gunn, K.E.; Sriburi, R.; Brewer, J.W. Stressed-out B cells? Plasma-cell differentiation and the unfolded protein response. Trends Immunol. 2004, 25, 17–24. [Google Scholar] [CrossRef]
- Turner, J.S.; Kim, W.; Kalaidina, E.; Goss, C.W.; Rauseo, A.M.; Schmitz, A.J.; Hansen, L.; Haile, A.; Klebert, M.K.; Pusic, I.; et al. SARS-CoV-2 infection induces long-lived bone marrow plasma cells in humans. Nature 2021, 595, 421–425. [Google Scholar] [CrossRef]
- Gett, A.V.; Hodgkin, P.D. A cellular calculus for signal integration by T cells. Nat. Immunol. 2000, 1, 239–244. [Google Scholar] [CrossRef]
- Heinzel, S.; Binh Giang, T.; Kan, A.; Marchingo, J.M.; Lye, B.K.; Corcoran, L.M.; Hodgkin, P. A Myc-dependent division timer complements a cell-death timer to regulate T cell and B cell responses. Nat. Immunol. 2017, 18, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Hammer, Q.; Rückert, T.; Borst, E.M.; Dunst, J.; Haubner, A.; Durek, P.; Heinrich, F.; Gasparoni, G.; Babic, M.; Tomic, A.; et al. Peptide-specific recognition of human cytomegalovirus strains controls adaptive natural killer cells. Nat. Immunol. 2018, 19, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Mohr, M.; Hose, D.; Seckinger, A.; Marciniak-Czochra, A. Quantification of plasma cell dynamics using mathematical modeling. R. Soc. Open Sci. 2018, 5, 170759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Höfer, T.; Muehlinghaus, G.; Moser, K.; Yoshida, T.; Mei, H.E.; Hebel, K.; Hauser, A.E.; Hoyer, B.; Luger, E.O.; Dörner, T.; et al. Adaptation of humoral memory. Immunol. Rev. 2006, 211, 295–302. [Google Scholar] [CrossRef]
- Westphal, D.; Dewson, G.; Czabotar, P.E.; Kluck, R.M. Molecular biology of BAX and BAK activation and action. BBA Mol. Cell Res. 2011, 1813, 521–531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Westphal, D.; Kluck, R.M.; Dewson, G. Building blocks of the apoptotic pore: How BAX and BAK are activated and oligomerize during apoptosis. Cell Death Differ. 2014, 21, 196–205. [Google Scholar] [CrossRef] [Green Version]
- Du, H.; Wolf, J.; Schafer, B.; Moldoveanu, T.; Chipuk, J.E.; Kuwana, T. BH3 domains other than BIM and BID can directly activate BAX/BAK. J. Biol. Chem. 2011, 286, 491–501. [Google Scholar] [CrossRef] [Green Version]
- Czabotar, P.E.; Lessene, G.; Strasser, A.; Adams, J.M. Control of apoptosis by the BCL-2 protein family: Implications for physiology and therapy. Nat. Rev. Mol. Cell Biol. 2014, 15, 49–63. [Google Scholar] [CrossRef]
| Antibody Clone | Manufacturer | Catalog nr. |
|---|---|---|
| Anti-mouse BCL-2, REA356 | Miltenyi Biotec | Catalog # 130-105-474 |
| Anti-mouse BIM, 14A8 | Milipore | Catalog # MAB17001 |
| Anti-mouse CD138, REA104 | Miltenyi Biotec | Catalog # 130-102-318 |
| Anti-mouse MCL-1, Y37 | Abcam | Catalog # ab32087 |
| Anti-mouse NOXA, 114C307 | Abcam | Catalog # ab13654 |
| Parameter | Value | Unit | Role | Source |
|---|---|---|---|---|
| aBCL-2 | 0.11 | - | Effect APRIL on gBCL-2 | Fit |
| sMCL-1 | 0.37 | - | Effect ST2 on gMCL-1 | Fit |
| sBCL-2 | 0.53 | - | Effect ST2 on gBCL-2 | Fit |
| sBIM | 0.49 | - | Effect ST2 on gBIM | Fit |
| sNOXA | 0.40 | - | Effect ST2 on gNOXA | Fit |
| γ | 0.43 | d−1 | Max. effect size BAX* | Fit |
| κ | 1.78 | - | Max. effect Caspase 12 | Fit |
| β | 2.65 | - | Inhibition strength ST2 on Caspase 3,7 | Fit |
| dMCL-1 | 16.4 | d−1 | Decay rate MCL-1 | [31] |
| dBCL-2 | 0.86 | d−1 | Decay rate BCL-2 | [31] |
| dBIM | 5.94 | d−1 | Decay rate BIM | [33] |
| dNOXA | 32.8 | d−1 | Decay rate NOXA | [34] |
| dBAX | 1.38 | d−1 | Decay rate BAX | [32] |
| Kd,3 | 2.0 | nM | Dissociation constant | [22] |
| Kd,4 | 22.0 | nM | Dissociation constant | [22] |
| Kd,5 | 40.0 | nM | Dissociation constant | [22] |
| Kd,6 | 2.50 | nM | Dissociation constant | [22] |
| Kd,7 | 68.0 | nM | Dissociation constant | [22] |
| k+ | 0.17 | µM d−1 | Complex association rate | - |
| k1 | 43.2 | µM d−1 | BAX activation rate | - |
| k2 | 8.64 | µM d−1 | BAX* deactivation rate | - |
| gp,0 | 0.86 | µM d−1 | Basal protein growth | - |
| α | 10.0 | - | Inhibition strength APRIL on Caspase 12 | - |
| KBAX | 200 | nM | Half-saturation constant BAX-half-life | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burt, P.; Cornelis, R.; Geißler, G.; Hahne, S.; Radbruch, A.; Chang, H.-D.; Thurley, K. Data-Driven Mathematical Model of Apoptosis Regulation in Memory Plasma Cells. Cells 2022, 11, 1547. https://doi.org/10.3390/cells11091547
Burt P, Cornelis R, Geißler G, Hahne S, Radbruch A, Chang H-D, Thurley K. Data-Driven Mathematical Model of Apoptosis Regulation in Memory Plasma Cells. Cells. 2022; 11(9):1547. https://doi.org/10.3390/cells11091547
Chicago/Turabian StyleBurt, Philipp, Rebecca Cornelis, Gustav Geißler, Stefanie Hahne, Andreas Radbruch, Hyun-Dong Chang, and Kevin Thurley. 2022. "Data-Driven Mathematical Model of Apoptosis Regulation in Memory Plasma Cells" Cells 11, no. 9: 1547. https://doi.org/10.3390/cells11091547
APA StyleBurt, P., Cornelis, R., Geißler, G., Hahne, S., Radbruch, A., Chang, H.-D., & Thurley, K. (2022). Data-Driven Mathematical Model of Apoptosis Regulation in Memory Plasma Cells. Cells, 11(9), 1547. https://doi.org/10.3390/cells11091547






