Developing a Universal Framework for Estimating Soybean Leaf Area Index Growth
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and Data Collection
2.2. Statistics
2.2.1. Leaf Area and LAI
2.2.2. Effective Accumulated Temperature
2.2.3. Characteristics of Leaf Area Index Growth
2.2.4. Modified Logistic Model Estimating Leaf Area Index
3. Results
3.1. Development Stages of Soybean Under Different Planting Dates
3.2. LAI of Soybean
3.3. Universal Model of Soybean Leaf Area Index
3.4. Validation of the Universal Model for Soybean Leaf Area Index
3.4.1. Back-Substitution Test
3.4.2. Independent Sample Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Ling, X.; Ma, C.; Liu, C.; Zhang, W.; Huang, J.; Peng, S.; Deng, N. Can China get out of soy dilemma? A yield gap analysis of soybean in China. Agron. Sustain. Dev. 2023, 43, 47. [Google Scholar] [CrossRef]
- Gale, F.; Valdes, C.; Ash, M. Interdependence of China, United States, and Brazil in Soybean Trade. USDA, Economic Research Service. 2019. Available online: https://www.ers.usda.gov/webdocs/outlooks/93390/ocs-19f-01.pdf (accessed on 3 September 2025).
- Watson, D.J. Comparative physiological studies on the growth of field crops: I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- Tesemma, Z.K.; Wei, Y.; Western, A.W.; Peel, M.C. Leaf area index variation for crop, pasture, and tree in response to climatic variation in the Goulburn–Broken Catchment, Australia. J. Hydrometeorol. 2014, 15, 1592–1606. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.M.; Jin, G.; Qi, Y. Estimating seasonal variations of leaf area index using litterfall collection and optical methods in four mixed evergreen-deciduous forests. Agric. Forest Meteorol. 2015, 209–210, 36–48. [Google Scholar] [CrossRef]
- Soudani, K.; François, C.; Maire, G.L.; Dantec, V.L.; Dufrêne, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ. 2006, 102, 161–175. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Garcia-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, M.Y.; Xue, Y.F. Spatial variability and relationships of rice leaf area index and yield. Trans. CSAE 2006, 22, 10–14. [Google Scholar]
- Lavorel, S.; Garnier, E. Predicting changes in community composition and ecosystem functioning from plant traits: Revisiting the Holy Grail. Funct. Ecol. 2010, 16, 545–556. [Google Scholar] [CrossRef]
- Chai, Y.F.; Yue, M.; Wang, M.; Xu, J.S.; Liu, X.; Zhang, R.C.; Wan, P.C. Plant functional traits suggest a change in novel ecological strategies for dominant species in the stages of forest succession. Oecologia 2016, 180, 771–783. [Google Scholar] [CrossRef]
- Inman-Bamber, N.G. Temperature and seasonal effects on canopy development and light interception of sugarcane. Field Crops Res. 1994, 36, 41–51. [Google Scholar] [CrossRef]
- Sinclaira, T.R.; Gilbertb, R.A.; Perdomoc, R.E.; Shine, J.M., Jr.; Powellc, G.; Montes, G. Sugarcane leaf area development under field conditions in Florida, USA. Field Crops Res. 2004, 88, 171–178. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol 2004, 21, 19–35. [Google Scholar] [CrossRef]
- Breda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Colaizzi, P.; Evett, S.R.; Brauer, D.K.; Howell, T.R.; Tolk, J.R.; Copeland, K.S. Allometric method to estimate leaf area index for row crops. Agron. J. 2017, 109, 883–894. [Google Scholar] [CrossRef]
- Chason, J.W.; Baldocchi, D.D.; Huston, M.A. A comparison of direct and indirect methods for estimating forest canopy leaf-area. Agric. For. Meteor. 1991, 57, 107–128. [Google Scholar] [CrossRef]
- Olivas, P.C.; Oberbauer, S.F.; Clark, D.B.; Clark, D.A.; Ryan, M.G.; Brien, J.J.; Ordonez, H. Comparison of direct and indirect methods for assessing leaf area index across a tropical rain forest landscape. Agric. For. Meteor. 2013, 177, 110–116. [Google Scholar] [CrossRef]
- Hu, R.; Yan, G.; Mu, X.; Luo, J. Indirect measurement of leaf area index on the basis of path length distribution. Remote Sens. Environ. 2014, 155, 239–247. [Google Scholar] [CrossRef]
- Bonnett, G.D. Rate of leaf appearance in sugarcane, including a comparison of a range of varieties. Aust. J. Plant Physiol. 1998, 25, 829–834. [Google Scholar] [CrossRef]
- Campbell, J.A.; Robertson, M.J.; Grof, C.P.L. Temperature effects on node appearance in sugarcane. Aust. J. Plant Physiol. 1998, 25, 815–818. [Google Scholar] [CrossRef]
- Robertson, M.J.; Bonnett, G.D.; Hughes, R.M.; Muchow, R.C.; Campbell, J.A. Temperature and leaf area expansion of sugarcane: Integration of controlled-environment, field and model studies. Aust. J. Plant Physiol. 1998, 25, 819–828. [Google Scholar] [CrossRef]
- Mcmaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef]
- Xiao, Z.; Lei, H.; Jin, C.; Pan, H.; Lian, Y. Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses. Agronomy 2023, 13, 116. [Google Scholar] [CrossRef]
- Miguez, F.E.; Zhu, X.; Humphries, S.; Bollero, G.A.; Long, S.P. A semimechanistic model predicting the growth and production of the bioenergy crop Miscanthus giganteus: Description, parameterization and validation. GCB Bioenergy 2009, 1, 282–296. [Google Scholar] [CrossRef]
- Archontoulis, S.A.; Miguez, F.E. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 107, 786–798. [Google Scholar] [CrossRef]
- Ding, D.Y.; Feng, H.; Zhao, Y.; Robert, L.H.; Yan, H.M.; Chen, H.X.; Hou, H.J.; Chu, X.S.; Liu, J.C.; Wang, N.J.; et al. Effects of continuous plastic mulching on crop growth in a winter wheat-summer maize rotation system on the Loess Plateau of China. Agric. For. Meteorol. 2019, 271, 385–397. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, S.; Fan, J.; Zhang, F.; Xiang, Y.; Zheng, J.; Guo, J. Responses of growth, fruit yield, quality and water productivity of greenhouse tomato to deficit drip irrigation. Sci. Hortic. 2021, 275, 109710. [Google Scholar] [CrossRef]
- Diel, M.I.; Lúcio, A.D.C.; Valera, O.V.S.; Sari, B.G.; Olivoto, T.; Pinheiro, M.V.M.; Melo, P.J.d.; Tartaglia, F.d.L.; Schmidt, D. Production of biquinho pepper in different growing seasons characterized by the logistic model and its critical points. Cienc. Rural 2020, 50, e20190477. [Google Scholar] [CrossRef]
- Lucio, A.D.; Nunes, L.F.; Rego, F. Nonlinear models to describe production of fruit in Cucurbita pepo and Capiscum annuum. Sci. Hortic. 2015, 193, 286–293. [Google Scholar] [CrossRef]
- Tong, P.Y.; Ling, B.Y.; Guan, Y.X. Dynamic simulation of dry matter accumulation in summer maize. Beijing Agric. Sci. 1996, 5, 22–25. (In Chinese) [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Schrader, J.; Shi, P.; Royer, D.L.; Peppe, D.J.; Gallagher, R.V.; Li, Y.; Wang, R.; Wright, I.J. Leaf size estimation based on leaf length, width and shape. Ann Bot. 2021, 128, 395–406. [Google Scholar] [CrossRef]
- Yin, X.; Goudriaan, J.; Lantinga, E.A.; Vos, J.; Spiertz, H.J. A flexible sigmoidfunction of determinate growth. Ann. Bot. 2003, 91, 361–371. [Google Scholar] [CrossRef]
- Hasegawa, T.; Wakatsuki, H.; Ju, H.; Vyas, S.; Nelson, G.C.; Farrell, A.; Deryng, D.; Meza, F.; Makowski, D. A global dataset for the projected impacts of climate change on four major crops. Sci. Data 2022, 9, 58. [Google Scholar] [CrossRef]
- Ma, S.X.; Churkina, G.; Trusilova, K. Investigating the impact of climate change on crop phenological events in Europe with a phenology model. Int. J. Biometeorol. 2012, 56, 749–763. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.L.; Zhang, S.A.; Zhang, Z. Spatiotemporal changes of wheat phenology in China under the effects of temperature, day length and cultivar thermal characteristics. Eur. J. Agron. 2012, 43, 201–212. [Google Scholar] [CrossRef]
- Xiao, D.P.; Tao, F.L.; Liu, Y.J.; Shi, W.J.; Wang, M.; Liu, F.S.; Zhang, S.; Zhu, Z. Observed changes in winter wheat phenology in the North China Plain for 1981–2009. Int. J. Biometeorol. 2013, 57, 275–285. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Chen, Z.; Tang, B.; Zeng, Q.; Guo, H.; Huang, W.; Luo, Y.; Shen, S.; Zhou, S. The effects of sowing date on maize: Phenology, morphology, and yield formation in a hot subtropical monsoon region. Field Crops Res. 2024, 309, 109309. [Google Scholar] [CrossRef]
- Cicchino, M.; Edreira, J.I.R.; Uribelarrea, M.; Otegui, M.E. Heat stress in field-grown maize: Response of physiological determinants of grain yield. Crop Sci. 2010, 50, 1438–1448. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Y.; Bai, N.; Xiao, D.; Bai, H.; Tao, F.; Ge, Q. Divergent climate feedbacks on winter wheat growing and dormancy periods as affected by sowing date in the North China Plain. Biogeosciences 2021, 18, 2275–2287. [Google Scholar] [CrossRef]
- Fang, S.L.; Kuo, Y.H.; Kang, L.; Chen, C.C.; Hsieh, C.Y.; Yao, M.H.; Kuo, B.J. Using sigmoid growth models to simulate greenhouse tomato growth and development. Horticulturae 2022, 8, 1021. [Google Scholar] [CrossRef]
- Li, G.Q.; Tang, L.; Zhang, W.Y.; Cao, W.X.; Zhu, Y. Dynamic analysis on response of dry matter accumulation and partitioning to nitrogen fertilizer in wheat cultivars with different plant types. Acta Agron. Sin. 2009, 35, 2258–2265. (In Chinese) [Google Scholar] [CrossRef]
- Shabani, A.; Sepaskhah, A.; Kamgar-Haghighi, A.A. Estimation of yield and dry matter of rapeseed using Logistic model under water, salinity and deficit irrigation. Arch. Agron. Soil Sci. 2014, 60, 951–969. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H.; Merzouki, A.; Pacheco, A. Estimation of Leaf Area Index (LAI) in corn and soybeans using multi-polarization C- and L-band radar data. Remote Sens. Environ. 2015, 170, 77–89. [Google Scholar] [CrossRef]
- Luo, S.; Liu, W.; Ren, Q.; Wei, H.; Wang, C.; Xi, X.; Nie, S.; Li, D.; Ma, D.; Zhou, G. Leaf area index estimation in maize and soybean using UAV LiDAR data. Precis. Agric. 2024, 25, 1915–1932. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, D.L. Observed variations of leaf area index and its relationship with surface temperature during warm seasons. Meteorol. Atmos. Phys. 2002, 80, 117–129. [Google Scholar] [CrossRef]
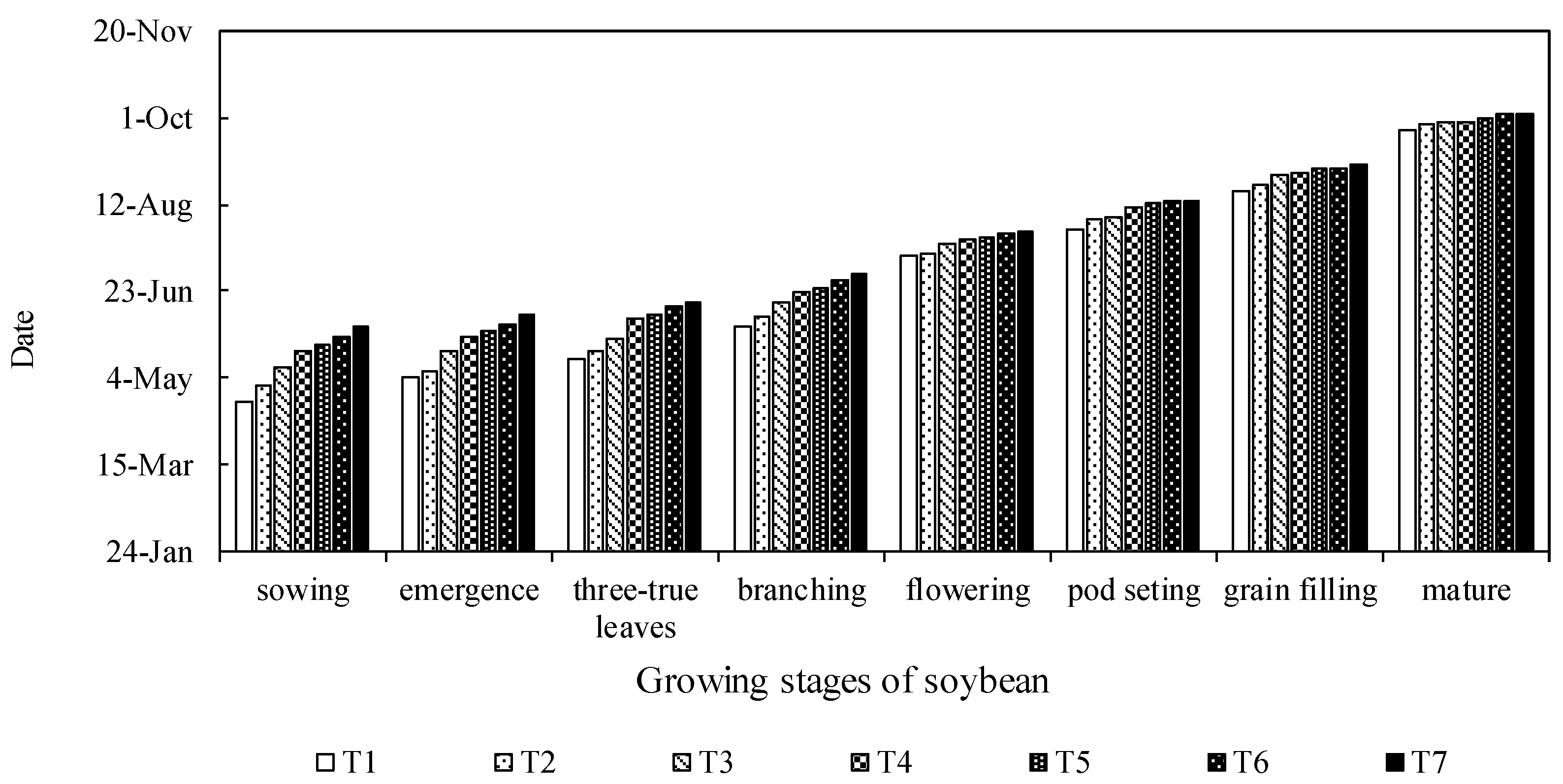
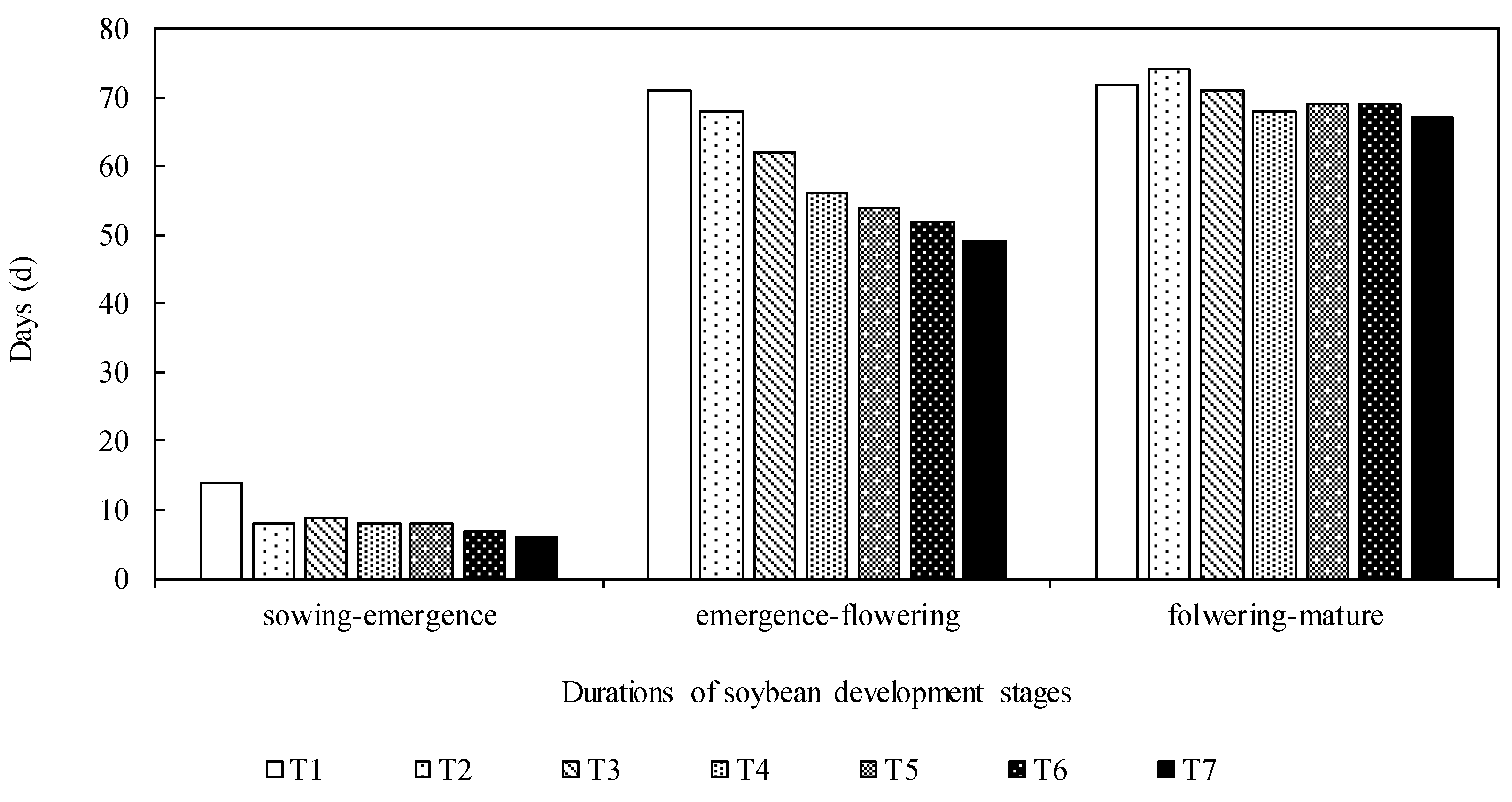
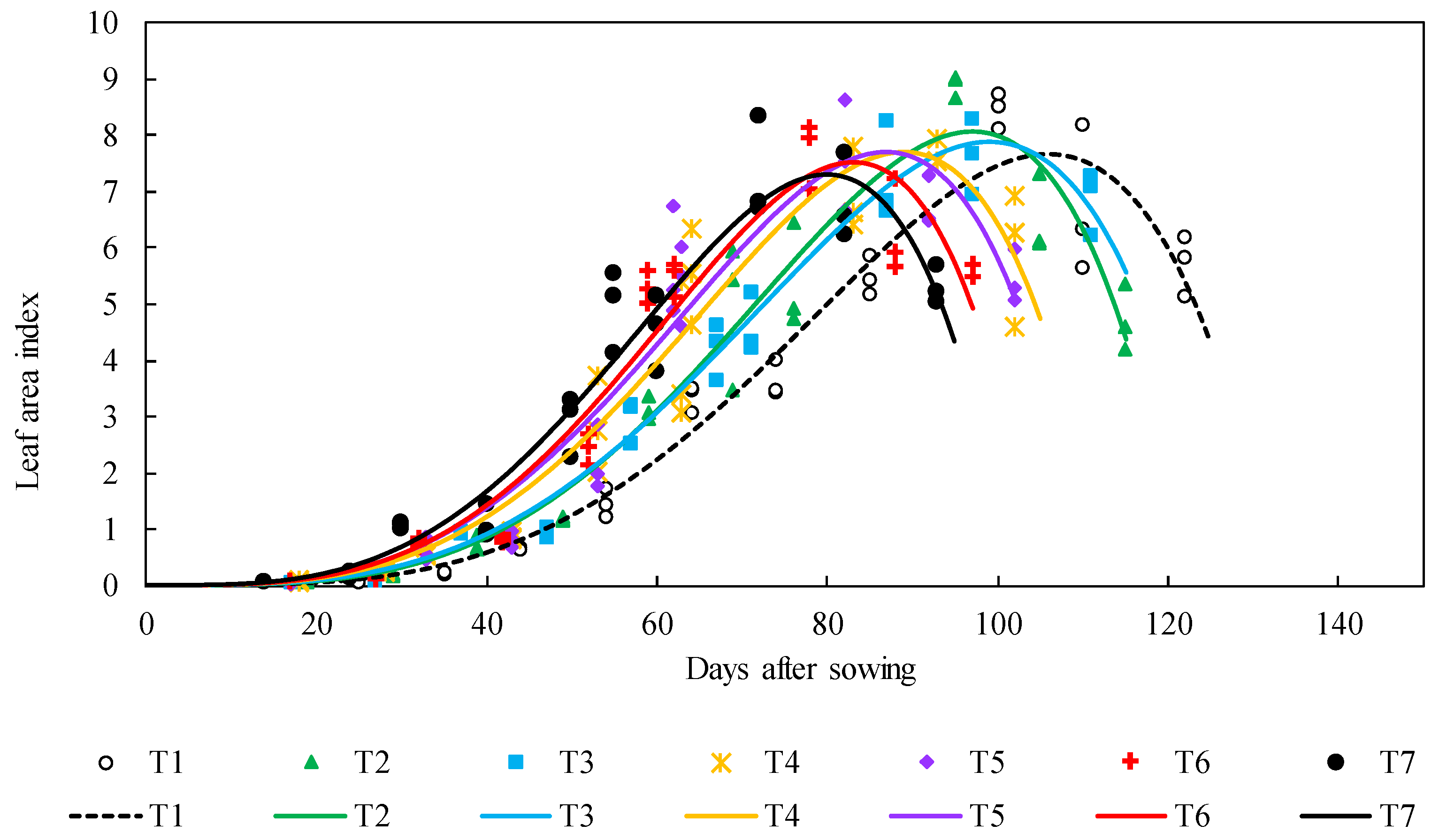
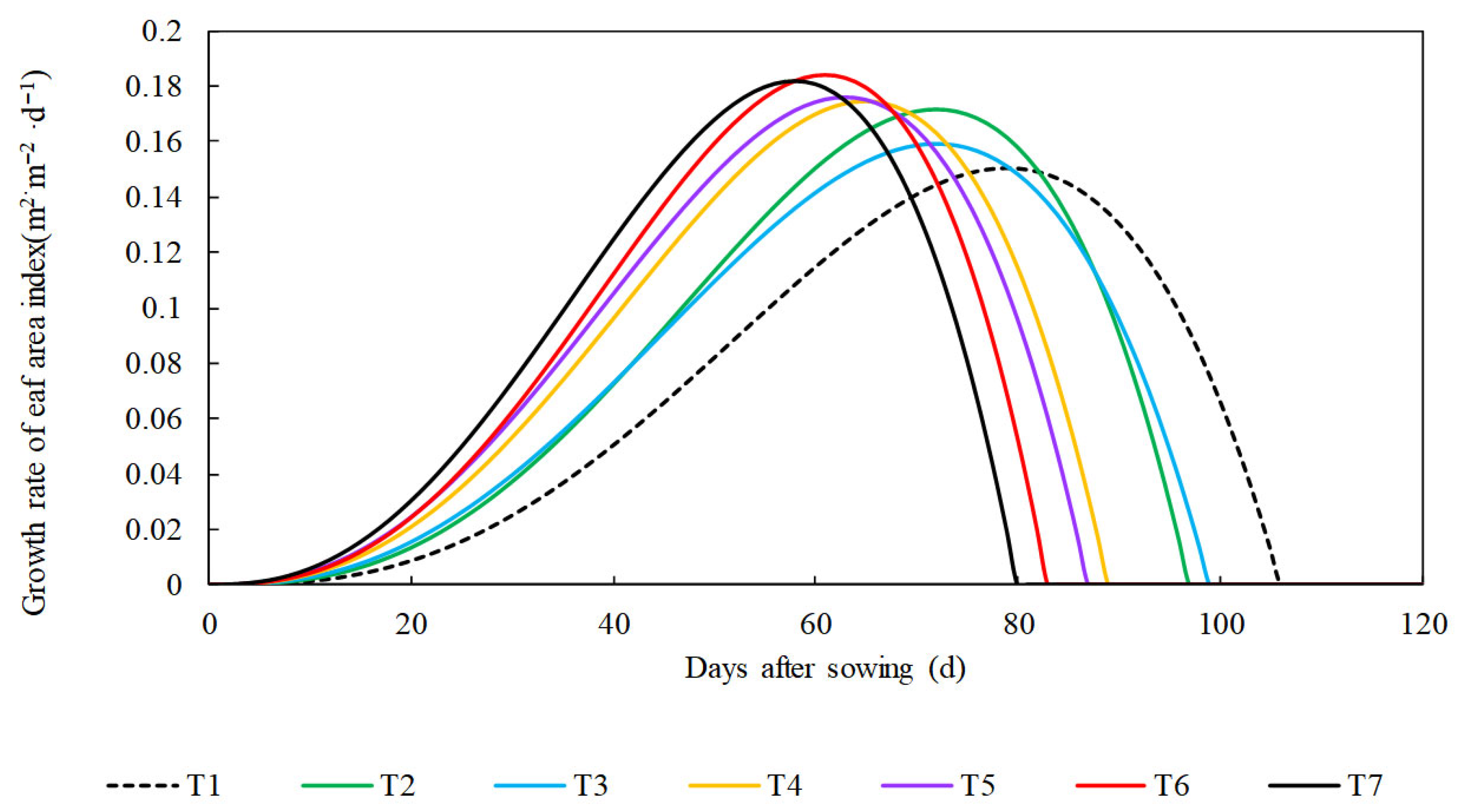
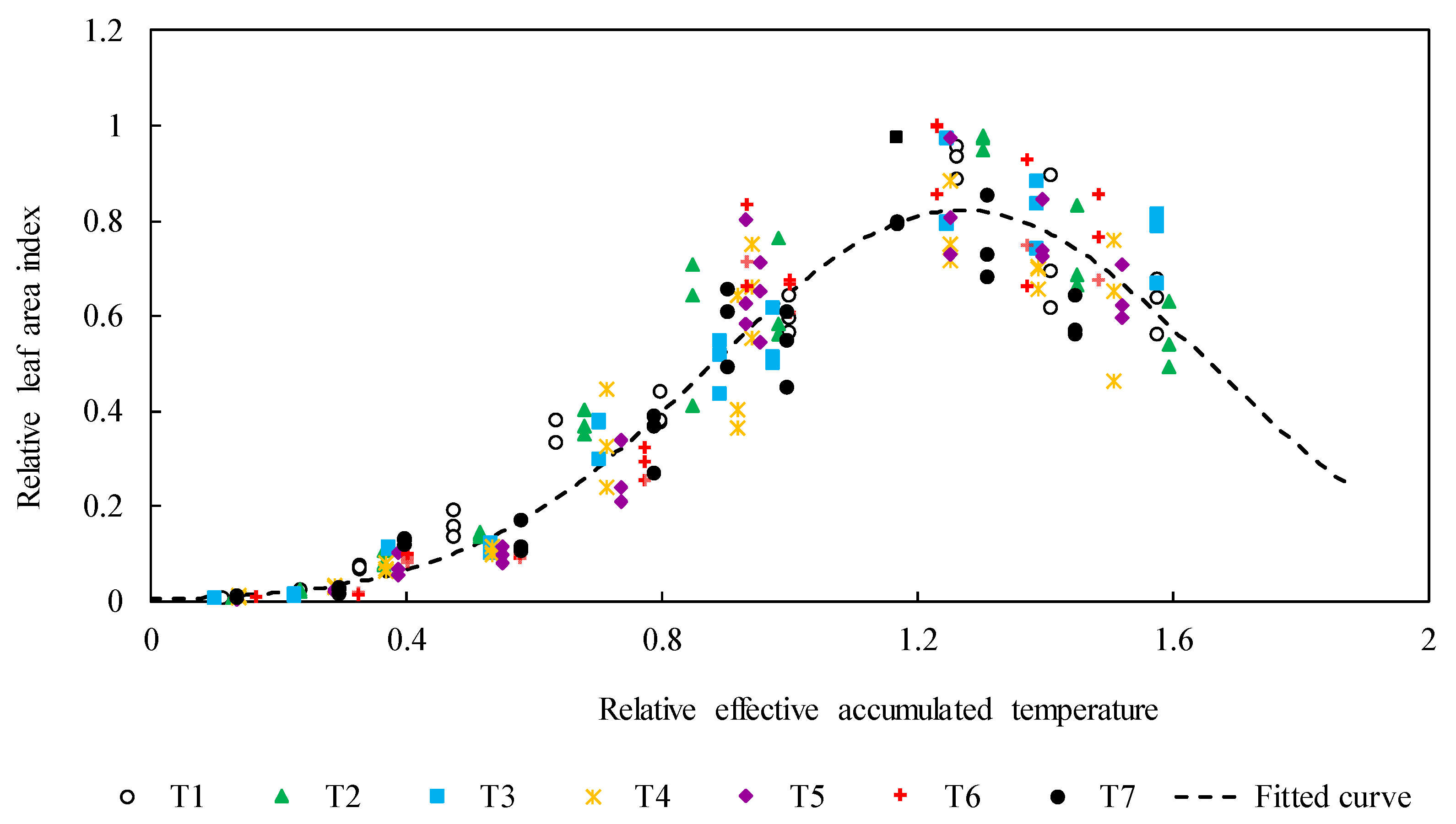
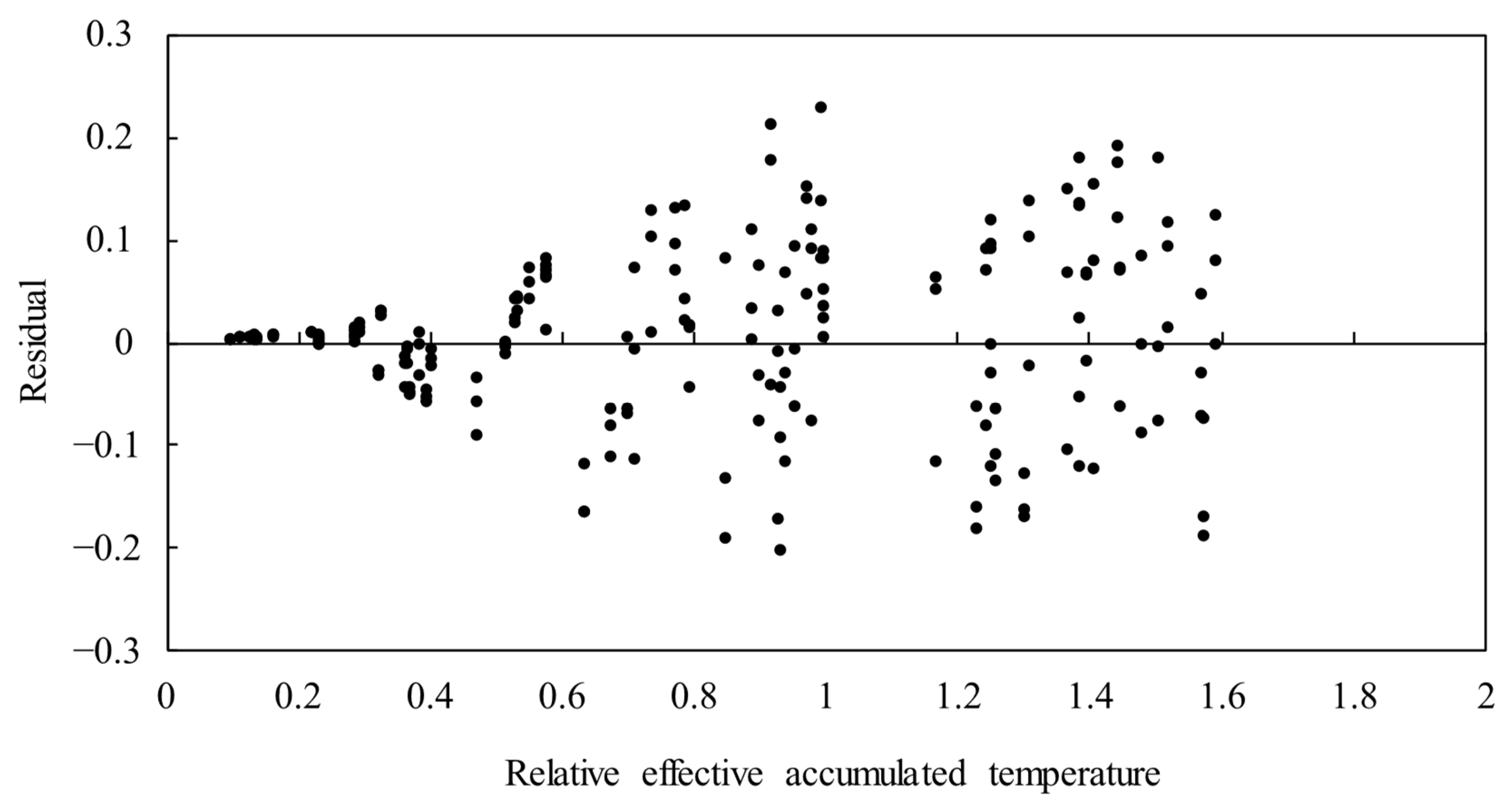
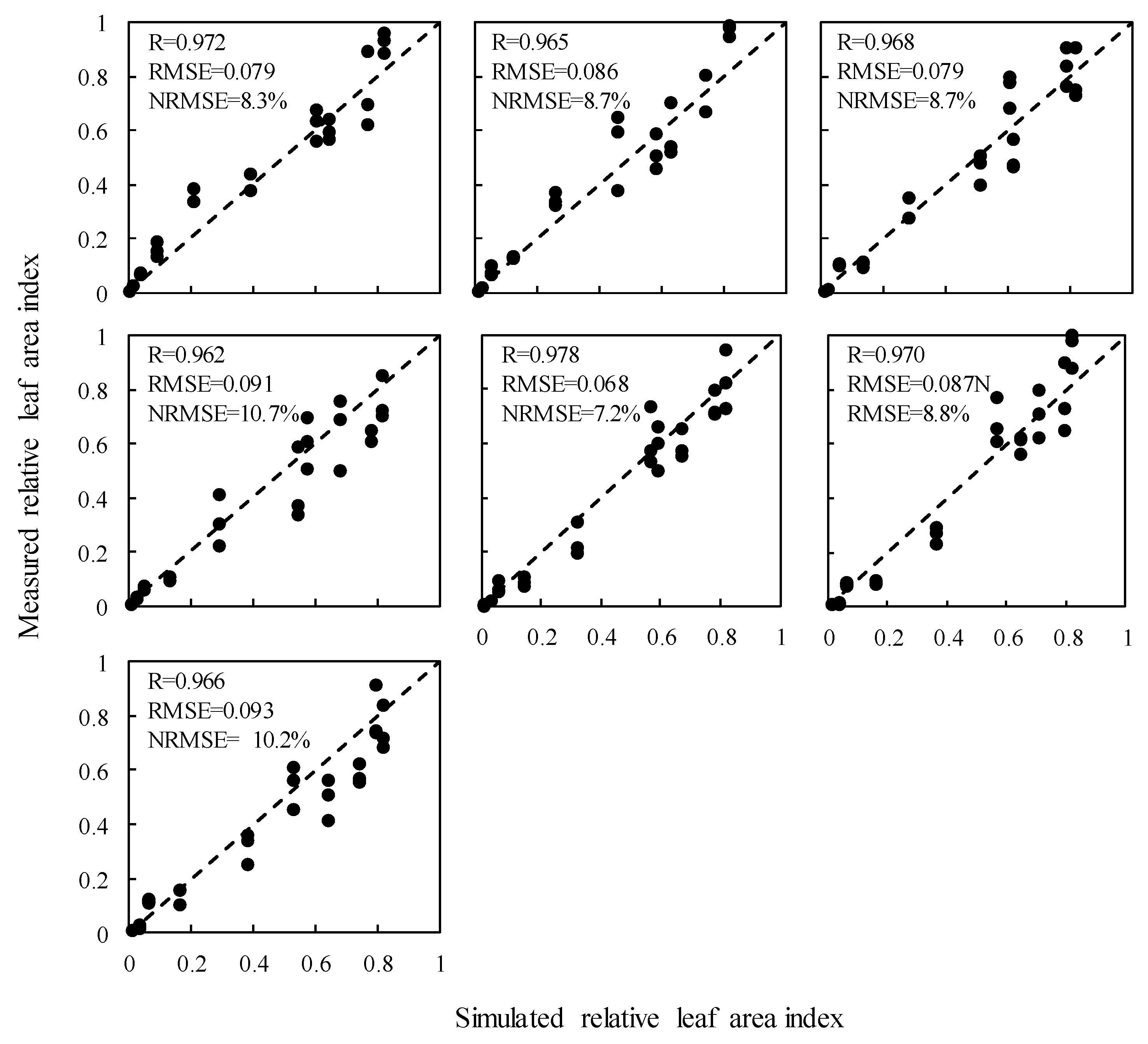
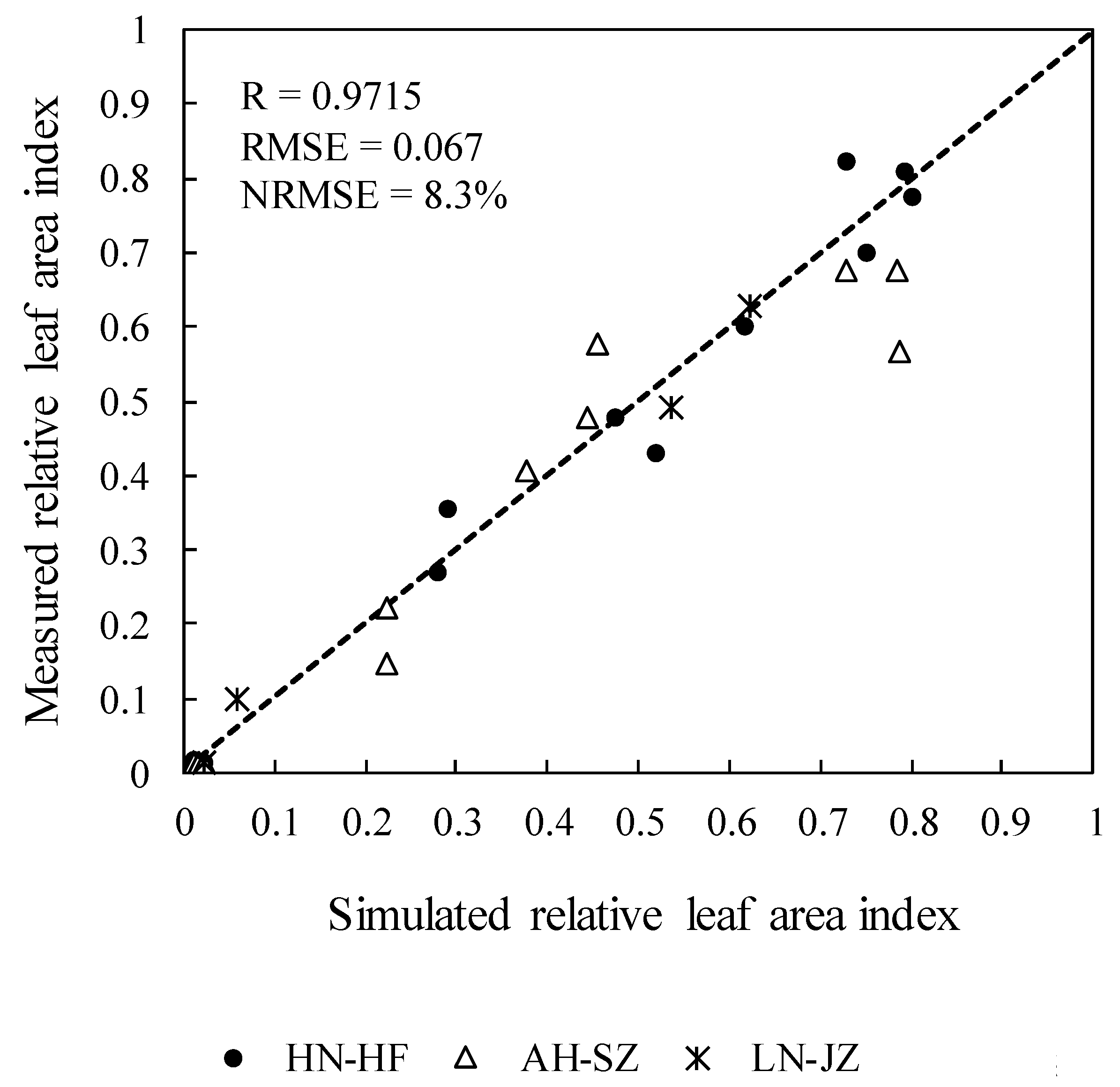
| Treat | T1 | T2 | T3 | T4 | T5 | T6 | T7 |
|---|---|---|---|---|---|---|---|
| Sowing dates | 20 April | 30 April | 10 May | 20 May | 23 May | 28 May | 3 June |
| Model | Parameters | Determination Coefficient | |||
|---|---|---|---|---|---|
| k | a | b | c | ||
| 19.74 | 8.636 | −8.664 | 3.412 | 0.929 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Guo, J. Developing a Universal Framework for Estimating Soybean Leaf Area Index Growth. Agronomy 2025, 15, 2231. https://doi.org/10.3390/agronomy15092231
Wang Q, Guo J. Developing a Universal Framework for Estimating Soybean Leaf Area Index Growth. Agronomy. 2025; 15(9):2231. https://doi.org/10.3390/agronomy15092231
Chicago/Turabian StyleWang, Qi, and Jianping Guo. 2025. "Developing a Universal Framework for Estimating Soybean Leaf Area Index Growth" Agronomy 15, no. 9: 2231. https://doi.org/10.3390/agronomy15092231
APA StyleWang, Q., & Guo, J. (2025). Developing a Universal Framework for Estimating Soybean Leaf Area Index Growth. Agronomy, 15(9), 2231. https://doi.org/10.3390/agronomy15092231





