Optimization of Irrigation Leaching Regime During the Cotton Growth Period Based on Multi-Model Integration and Fuzzy Borda Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Data and Experiment Site Description
2.2. Experiment Design
2.3. Measurements and Data Collection
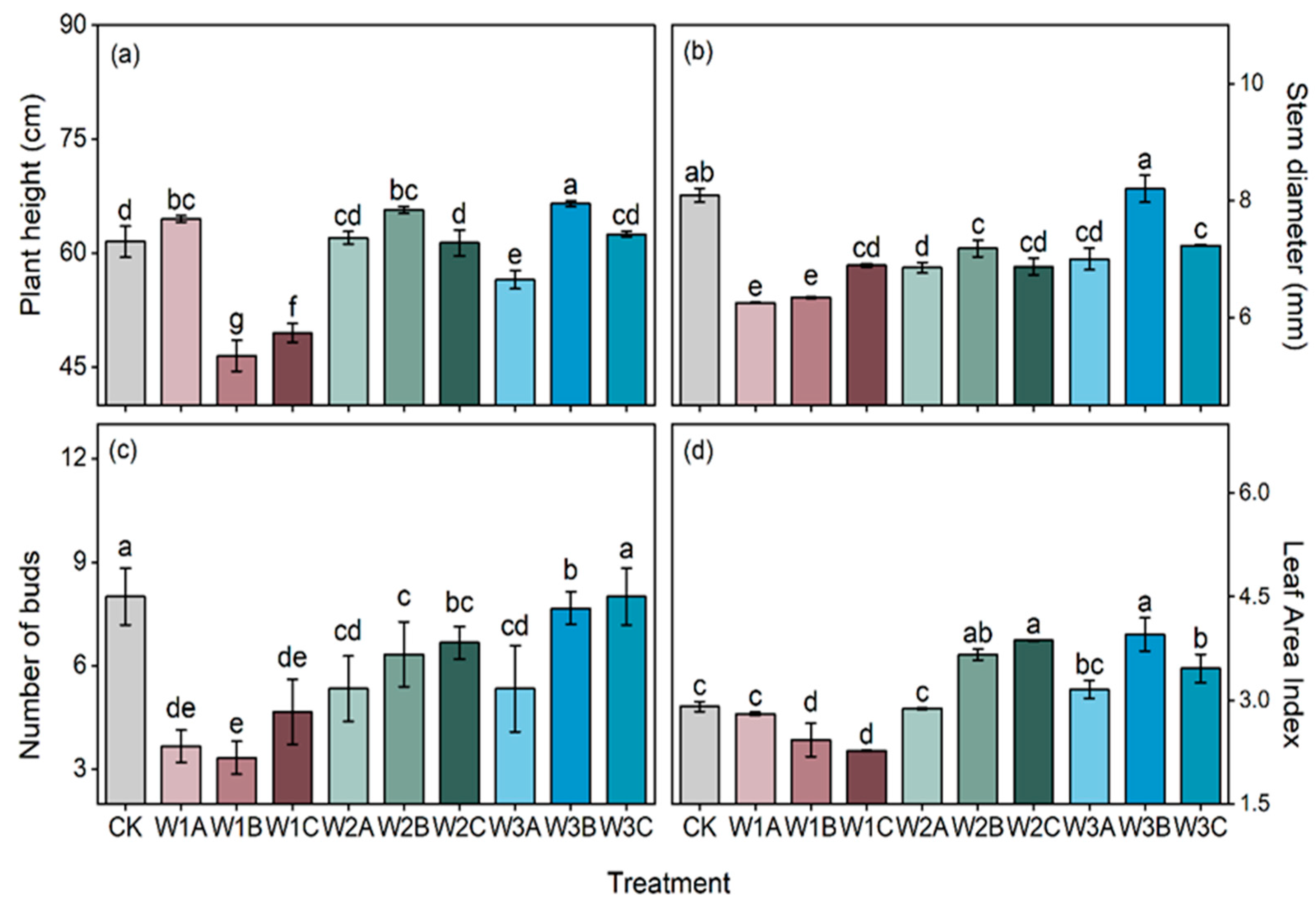
2.3.1. Growth Parameter Measurement
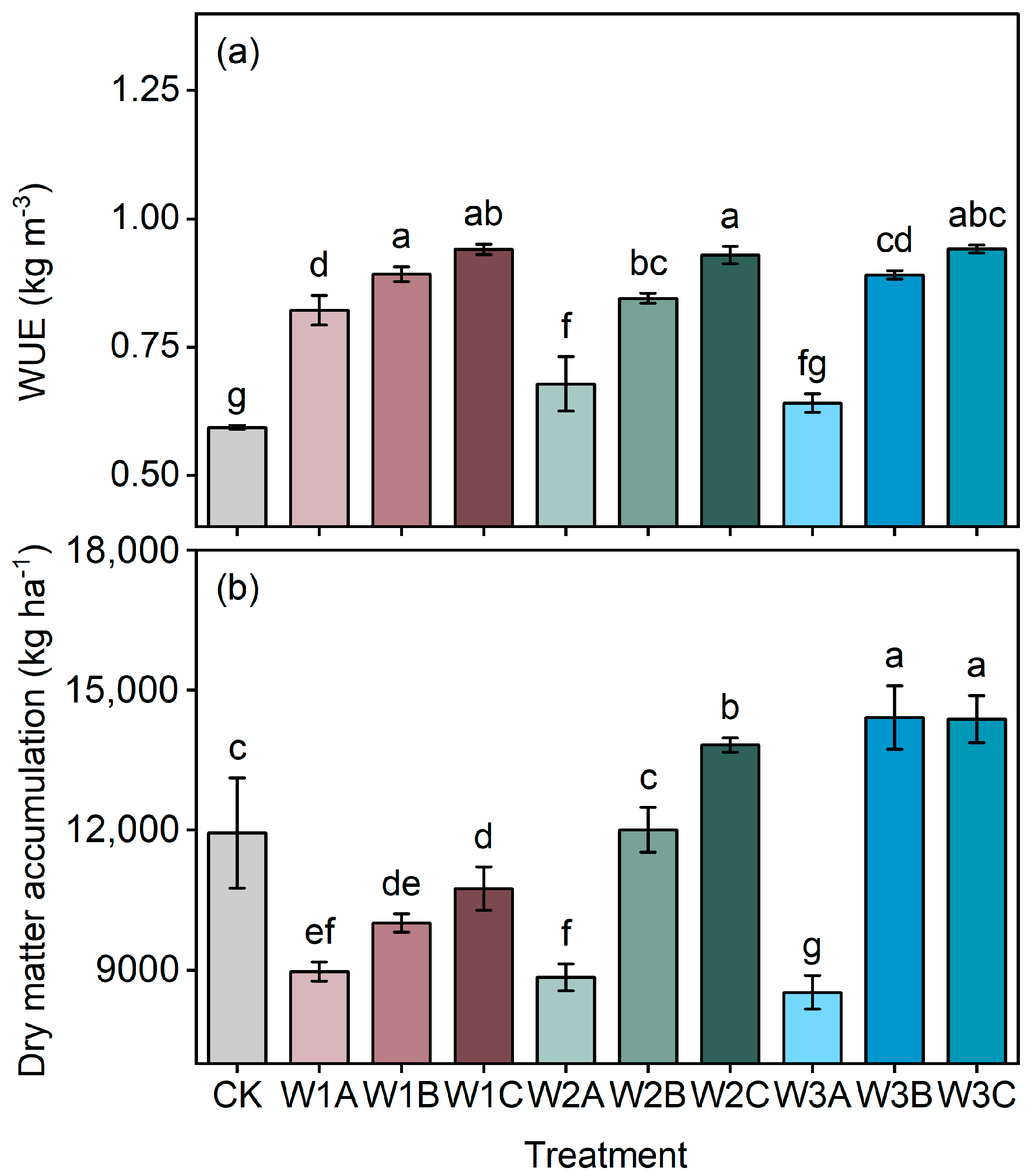
2.3.2. Calculation of WUE
2.3.3. Cotton Quality
2.4. Model Building Method
2.5. Statistical Analysis
3. Results
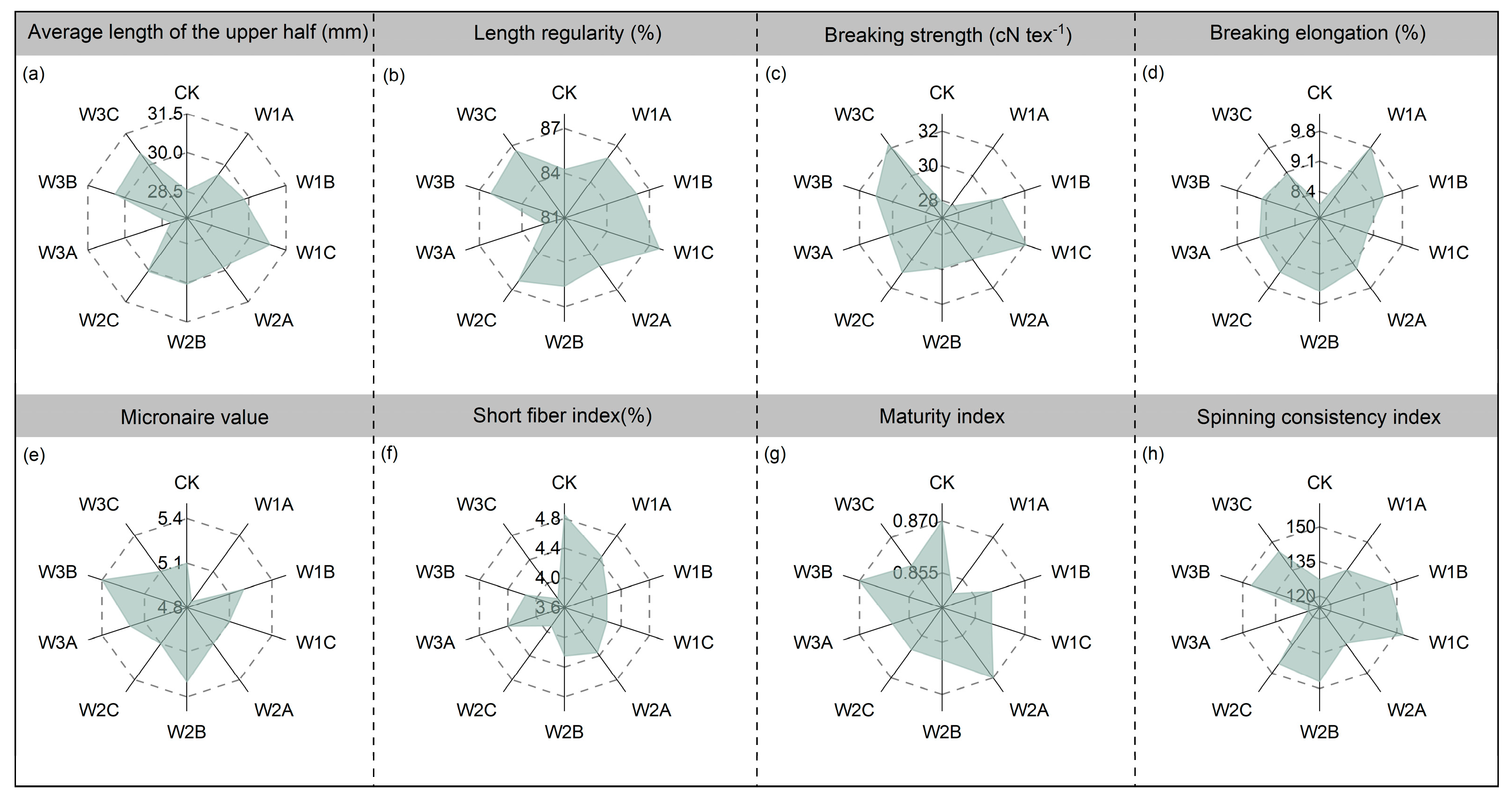
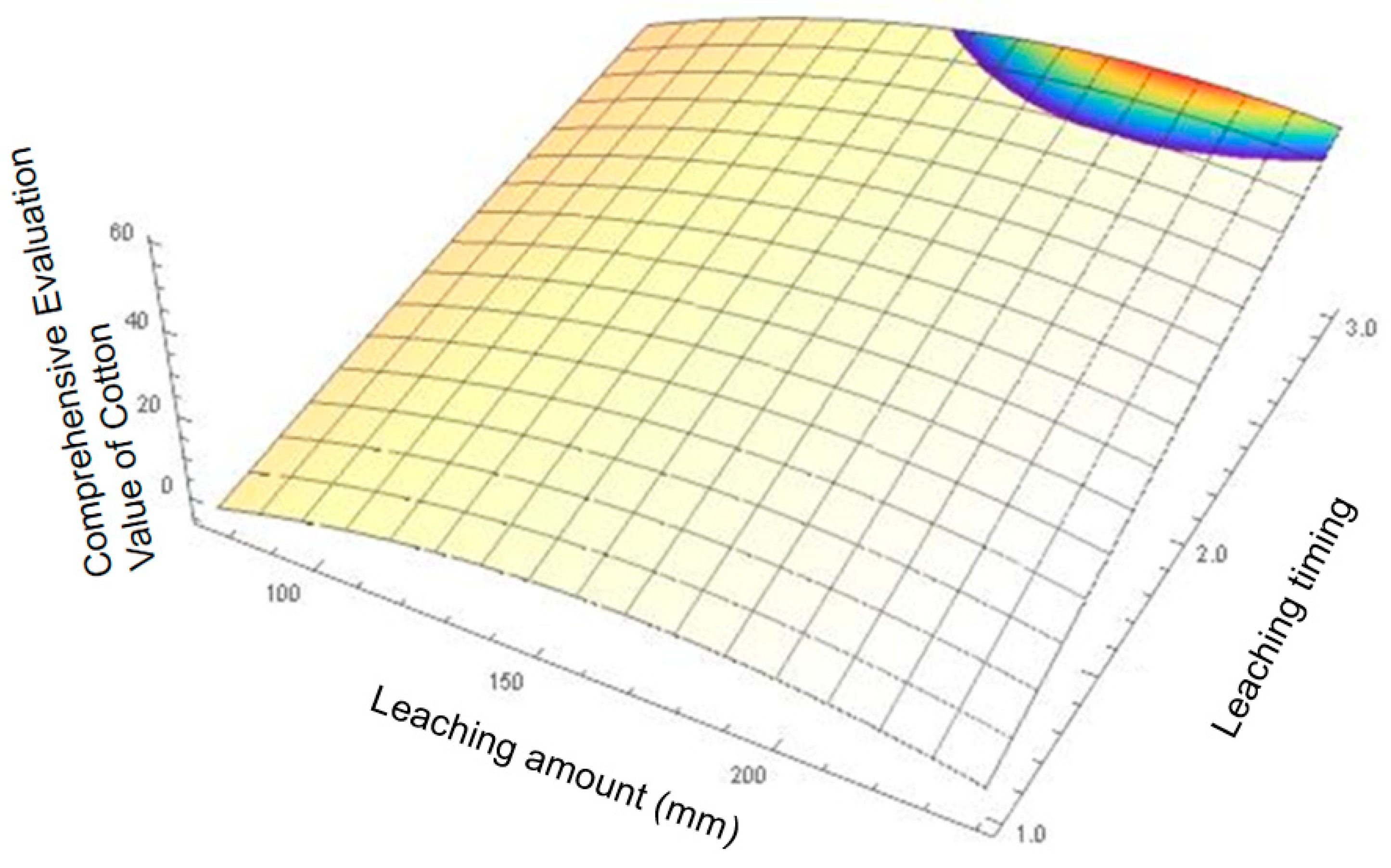
3.1. Seed Cotton Yield and Fiber Quality Responses to Leaching Amount and Timing Interactions
3.2. Evaluation of Comprehensive Cotton Indices Based on a Single Method and Pre-Testing of the Single Evaluation Method
3.3. Construction and Validation of a Comprehensive Cotton Index Evaluation Model
3.4. Constructing a Comprehensive Index Evaluation Model for Cotton and Post-Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, S.; Jia, X.; Zhao, C.; Shao, M. A review of saline-alkali soil improvements in China: Efforts and their impacts on soil properties. Agric. Water Manag. 2025, 317, 109617. [Google Scholar] [CrossRef]
- Song, Y.; Sun, J.; Li, Z. Intercropping increases land use efficiency and reduces soil salinity in salt-affected soils, but has minimal effect on pH. Field Crops Res. 2025, 332, 110028. [Google Scholar] [CrossRef]
- Zhao, X.; Grossart, H.-P. Enhancing crop yield and microbial diversity in saline-affected paddy soil through biochar amendment under aquaculture wastewater irrigation. Eur. J. Soil Biol. 2024, 123, 103681. [Google Scholar] [CrossRef]
- Egamberdieva, D.; Wirth, S.; Bellingrath-Kimura, S.D.; Mishra, J.; Arora, N.K. Salt-tolerant plant growth promoting rhizobacteria for enhancing crop productivity of saline soils. Front. Microbiol. 2019, 10, 2791. [Google Scholar] [CrossRef] [PubMed]
- Yuan, R.; Wang, K.; Ren, D.; Chen, Z.; Guo, B.; Zhang, H.; Li, D.; Zhao, C.; Han, S.; Li, H. An Analysis of Uncertainties in Evaluating Future Climate Change Impacts on Cotton Production and Water Use in China. Agronomy 2025, 15, 1209. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Zhang, J.; Zong, R. Soil salinity variations and cotton growth under long-term mulched drip irrigation in saline-alkali land of arid oasis. Irrig. Sci. 2022, 40, 103–113. [Google Scholar] [CrossRef]
- Ning, S.; Zhou, B.; Shi, J.; Wang, Q. Soil water/salt balance and water productivity of typical irrigation schedules for cotton under film mulched drip irrigation in northern Xinjiang. Agric. Water Manag. 2021, 245, 106651. [Google Scholar] [CrossRef]
- Chen, W.; Jin, M.; Ferré, T.P.A.; Liu, Y.; Xian, Y.; Shan, T.; Ping, X. Spatial distribution of soil moisture, soil salinity, and root density beneath a cotton field under mulched drip irrigation with brackish and fresh water. Field Crops Res. 2018, 215, 207–221. [Google Scholar] [CrossRef]
- Wang, H.; Cao, H.; Jiang, F.; Wang, X.; Gao, Y. Analysis of soil moisture, temperature, and salinity in cotton field under non-mulched drip irrigation in South Xinjiang. Agriculture 2022, 12, 1589. [Google Scholar] [CrossRef]
- Li, L.; Liu, H.; He, X.; Lin, E.; Yang, G. Winter irrigation effects on soil moisture, temperature and salinity, and on cotton growth in salinized fields in northern Xinjiang, China. Sustainability 2020, 12, 7573. [Google Scholar] [CrossRef]
- Feng, D.; Cui, Y.; Tang, G.; Cao, G.; Chen, J.; Ding, Y.; Wang, J.; Ge, C.; Xu, W. Effects of salt water irrigation at the ripening stage on yield and quality of grown-in-substrate mini-watermelon (Citrullus lanatus) within an arched shed. Agric. Water Manag. 2025, 317, 109631. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Zou, M.; Lai, H.; Javed, T.; Wang, Z. Optimizing irrigation salinity for cotton production through cotton yield and fiber quality and water use efficiency in arid regions. Ind. Crops Prod. 2025, 233, 121375. [Google Scholar] [CrossRef]
- Lou, B.; Hu, Y.; Li, T.; Liu, Q.; Wang, J.; Dong, X.; Tian, L.; Zhang, X.; Bian, W.; Liu, T.; et al. Assessment of saline water irrigation on biomass and quality of alfalfa: A sustainable agriculture perspective. Agric. Water Manag. 2025, 314, 109504. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Hartman, S.; Chiarelli, D.D.; Rulli, M.C.; D’Odorico, P. The tradeoff between water savings and salinization prevention in dryland irrigation. Adv. Water Resour. 2024, 183, 104604. [Google Scholar] [CrossRef]
- Hu, Q.; Cao, H.; He, Z.; Shi, H.; Ren, Z.; Qi, C. Effects of leaching amounts and drip irrigation types on water-salt distribution and seed cotton yield in northern Xinjiang, China. Field Crops Res. 2025, 328, 109947. [Google Scholar] [CrossRef]
- He, Z.; Cao, H.; Hu, Q.; Qi, C.; Li, Z. Salt leaching with alternate surface and subsurface drip irrigation enhance cotton yield, water use efficiency, desalination rate, desalination efficiency and economic benefit. Field Crops Res. 2025, 325, 109804. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.; Buttar, N.A. Analysis of mechanical properties for tea stem using grey relational analysis coupled with multiple linear regression. Sci. Hortic. 2020, 260, 108886. [Google Scholar] [CrossRef]
- Fang, Y.; Zheng, X.; Peng, H.; Wang, H.; Xin, J. A new method of the relative membership degree calculation in variable fuzzy sets for water quality assessment. Ecol. Indic. 2019, 98, 515–522. [Google Scholar] [CrossRef]
- Ramamurthy, V.; Reddy, G.P.O.; Kumar, N. Assessment of land suitability for maize (Zea mays L) in semi-arid ecosystem of southern India using integrated AHP and GIS approach. Comput. Electron. Agric. 2020, 179, 105806. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, Z.; Li, H. Symbiotic technology assessment in iron and steel industry based on entropy TOPSIS method. J. Clean. Prod. 2020, 260, 120900. [Google Scholar] [CrossRef]
- He, Z.; Li, M.; Cai, Z.; Zhao, R.; Hong, T.; Yang, Z.; Zhang, Z. Optimal irrigation and fertilizer amounts based on multi-level fuzzy comprehensive evaluation of yield, growth and fruit quality on cherry tomato. Agric. Water Manag. 2021, 243, 106360. [Google Scholar] [CrossRef]
- Wang, F.; Kang, S.; Du, T.; Li, F.; Qiu, R. Determination of comprehensive quality index for tomato and its response to different irrigation treatments. Agric. Water Manag. 2011, 98, 1228–1238. [Google Scholar] [CrossRef]
- Zhong, F.; Hou, M.; He, B.; Chen, I. Assessment on the coupling effects of drip irrigation and organic fertilization based on entropy weight coefficient model. PeerJ 2017, 5, e3855. [Google Scholar] [CrossRef]
- Jung, K.-C.; Chang, S.-H. Advanced deep learning model-based impact characterization method for composite laminates. Compos. Sci. Technol. 2021, 207, 108713. [Google Scholar] [CrossRef]
- Firouzi, S.; Allahyari, M.S.; Isazadeh, M.; Nikkhah, A.; Van Haute, S. Hybrid multi-criteria decision-making approach to select appropriate biomass resources for biofuel production. Sci. Total Environ. 2021, 770, 144449. [Google Scholar] [CrossRef] [PubMed]
- Mohebali, S.; Maghsoudy, S.; Doulati Ardejani, F.; Shafaei, F. Developing a coupled environmental impact assessment (C-EIA) method with sustainable development approach for environmental analysis in coal industries. Environ. Dev. Sustain. 2020, 22, 6799–6830. [Google Scholar] [CrossRef]
- Kilgour, D.M.; Grégoire, J.-C.; Foley, A.M. Weighted scoring elections: Is Borda best? Soc. Choice Welf. 2022, 58, 365–391. [Google Scholar] [CrossRef]
- Terzopoulou, Z.; Endriss, U. The Borda class: An axiomatic study of the Borda rule on top-truncated preferences. J. Math. Econ. 2021, 92, 31–40. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Zheng, L.; Chen, J.; Sun, X.; Guo, X. Optimization of the regulated deficit irrigation strategy for greenhouse tomato based on the fuzzy borda model. Agriculture 2022, 12, 324. [Google Scholar] [CrossRef]
- Yao, X.; Deng, H.; Zhang, T.; Qin, Y. Multistage fuzzy comprehensive evaluation of landslide hazards based on a cloud model. PLoS ONE 2019, 14, e0224312. [Google Scholar] [CrossRef]
- Zhou, G.-Y.; Wu, E.; Tu, S.-T. Optimum selection of compact heat exchangers using non-structural fuzzy decision method. Appl. Energy 2014, 113, 1801–1809. [Google Scholar] [CrossRef]
- Kang, S.; Gu, B.; Du, T.; Zhang, J. Crop coefficient and ratio of transpiration to evapotranspiration of winter wheat and maize in a semi-humid region. Agric. Water Manag. 2003, 59, 239–254. [Google Scholar] [CrossRef]
- Luo, Q.; Bange, M.; Johnston, D. Environment and cotton fibre quality. Clim. Change 2016, 138, 207–221. [Google Scholar] [CrossRef]
- Weng, S.; Fan, Z.; Gou, J. A fast DBSCAN algorithm using a bi-directional HNSW index structure for big data. Int. J. Mach. Learn. Cybern. 2024, 15, 3471–3494. [Google Scholar] [CrossRef]
- Bai, Z.; Bai, W.; Xie, C.; Yu, J.; Dai, Y.; Pei, S.; Zhang, F.; Li, Y.; Fan, J.; Yin, F. Irrigation depth and nitrogen rate effects on seed cotton yield, fiber quality and water-nitrogen utilization efficiency in southern Xinjiang, China. Agric. Water Manag. 2023, 290, 108583. [Google Scholar] [CrossRef]
- Liu, X.; Li, M.; Xue, D.; He, S.; Fan, J.; Zhang, F.; Yin, F. Optimal drip irrigation leaching amount and timing enhanced cotton fiber yield, quality and nitrogen uptake by regulating soil salinity and nitrate nitrogen in saline-alkaline fields. J. Integr. Agric. 2025, 24, 2389–2409. [Google Scholar] [CrossRef]
- Ul-Allah, S.; Rehman, A.; Hussain, M.; Farooq, M. Fiber yield and quality in cotton under drought: Effects and management. Agric. Water Manag. 2021, 255, 106994. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Wang, Z.; Zou, J.; He, J.; Wang, Y.; Wang, S.; Zhou, Z.; Zhao, W.; Hu, W. Waterlogging restricted cotton fiber elongation by reducing osmolyte accumulation and cell wall biosynthesis. Environ. Exp. Bot. 2023, 216, 105547. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Q.; Ning, S.; Hu, X.; Song, Z. Enhancing cotton (Gossypium hirsutum L.) productivity and quality with magnetized ionized water and Bacillus subtilis intervention under film-mulched drip irrigation in saline soil in Xinjiang. Field Crops Res. 2024, 311, 109377. [Google Scholar] [CrossRef]
- Shi, X.; Hao, X.; Yang, Y.; Li, N.; Shi, F.; Tian, Y.; Zhang, H.; Li, H.; Liu, P.; Wang, J. Enhancing cotton yield and fiber quality via the optimization of within-boll yield components with potassium application under limited drip irrigation in arid regions. Ind. Crops Prod. 2024, 222, 119957. [Google Scholar] [CrossRef]
- Liu, H.; Li, H.; Ning, H.; Zhang, X.; Li, S.; Pang, J.; Wang, G.; Sun, J. Optimizing irrigation frequency and amount to balance yield, fruit quality and water use efficiency of greenhouse tomato. Agric. Water Manag. 2019, 226, 105787. [Google Scholar] [CrossRef]
- Wang, F.-X.; Kang, Y.; Liu, S.-P. Effects of drip irrigation frequency on soil wetting pattern and potato growth in North China Plain. Agric. Water Manag. 2006, 79, 248–264. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Bi, L.; Wang, Y.; Fan, J.; Zhang, F.; Hou, X.; Cheng, M.; Hu, W.; Wu, L. Multi-objective optimization of water and fertilizer management for potato production in sandy areas of northern China based on TOPSIS. Field Crops Res. 2019, 240, 55–68. [Google Scholar] [CrossRef]
- Xue, R.; Zhang, C.; Yan, H.; Lakhiar, I.A.; Disasa, K.N.; Zhou, Y.; Li, J.; Wang, X.; Zhou, R.; Wang, B. Evaluating effect of micro-spray on tomatoes for resisting summer heat stress using a Fuzzy Borda combination evaluation model. Environ. Exp. Bot. 2024, 218, 105605. [Google Scholar] [CrossRef]
- Herva, M.; Roca, E. Review of combined approaches and multi-criteria analysis for corporate environmental evaluation. J. Clean. Prod. 2013, 39, 355–371. [Google Scholar] [CrossRef]
- Lokhande, S.; Reddy, K.R. Reproductive and fiber quality responses of upland cotton to moisture deficiency. Agron. J. 2014, 106, 1060–1069. [Google Scholar] [CrossRef]
- Wang, R.; Gao, M.; Ji, S.; Wang, S.; Meng, Y.; Zhou, Z. Carbon allocation, osmotic adjustment, antioxidant capacity and growth in cotton under long-term soil drought during flowering and boll-forming period. Plant Physiol. Biochem. 2016, 107, 137–146. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, B.; Zhang, G.; Li, J.; Wang, Y.; Meng, Y.; Zhou, Z. Effect of soil salinity, soil drought, and their combined action on the biochemical characteristics of cotton roots. Acta Physiol. Plant. 2013, 35, 3167–3179. [Google Scholar] [CrossRef]
- Sharif, I.; Aleem, S.; Farooq, J.; Rizwan, M.; Younas, A.; Sarwar, G.; Chohan, S.M. Salinity stress in cotton: Effects, mechanism of tolerance and its management strategies. Physiol. Mol. Biol. Plants 2019, 25, 807–820. [Google Scholar] [CrossRef]
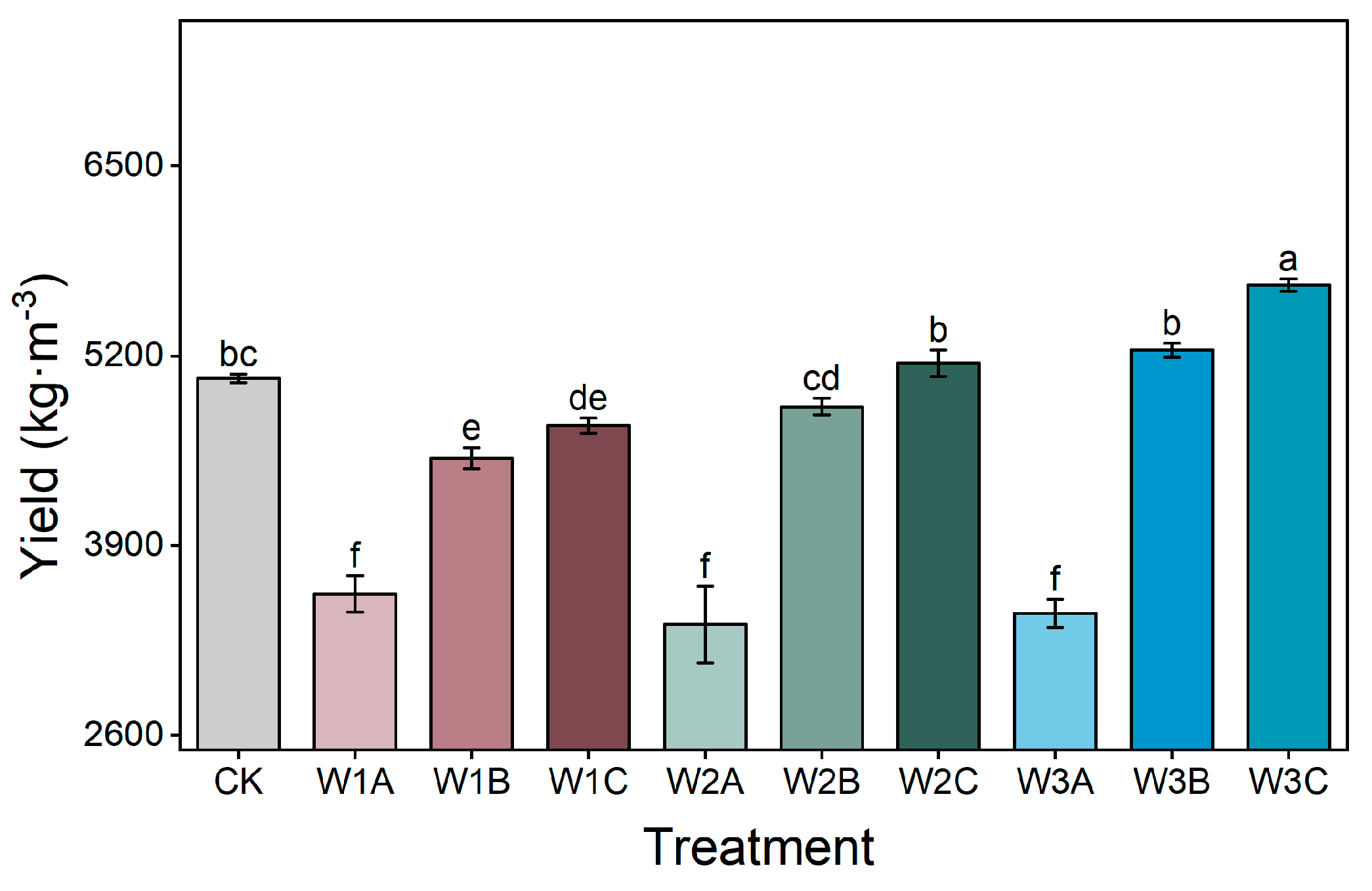
| Irrigation Treatment | Non-Reproductive Period Flushing Amount (mm) | Irrigation Amount During the Reproductive Period | Total Irrigation Amount (mm) | |||
|---|---|---|---|---|---|---|
| Seedling Stage | Budding Stage | Flower Bell Stage | Spinning Stage | |||
| CK | 450 | 80%ETc | 80%ETc | 80%ETc | - | 776.3 |
| W1A | 75 mm + 80%ETc | 80%ETc | 80%ETc | - | 401.3 | |
| W1B | 37.5 mm + 80%ETc | 37.5 mm + 80%ETc | 80%ETc | - | 401.3 | |
| W1C | 25 mm + 80%ETc | 25 mm + 80%ETc | 25 mm + 80%ETc | - | 401.3 | |
| W2A | 150 mm + 80%ETc | 80%ETc | 80%ETc | - | 476.3 | |
| W2B | 75 mm + 80%ETc | 75 mm + 80%ETc | 80%ETc | - | 476.3 | |
| W2C | 50 mm + 80%ETc | 50 mm + 80%ETc | 50 mm + 80%ETc | - | 476.3 | |
| W3A | 240 mm + 80%ETc | 80%ETc | 80%ETc | - | 566.3 | |
| W3B | 120 mm + 80%ETc | 120 mm + 80%ETc | 80%ETc | - | 566.3 | |
| Treatment | PCA | TOPSIS | GRDA | MFA | Ranking Standard Deviation | ||||
|---|---|---|---|---|---|---|---|---|---|
| Evaluation Value | Ranking | Evaluation Value | Ranking | Evaluation Value | Ranking | Evaluation Value | Ranking | ||
| CK | −0.88 | 6 | 0.46 | 6 | 0.99 | 5 | 44.38 | 6 | 0.50 |
| W1A | −3.48 | 9 | 0.38 | 9 | 0.86 | 10 | 33.74 | 9 | 0.50 |
| W1B | −1.81 | 7 | 0.45 | 7 | 0.92 | 8 | 42.09 | 7 | 0.50 |
| W1C | −0.09 | 5 | 0.55 | 5 | 1.02 | 4 | 55.43 | 5 | 0.50 |
| W2A | −2.43 | 8 | 0.43 | 8 | 0.94 | 7 | 40.12 | 8 | 0.50 |
| W2B | 2.33 | 4 | 0.60 | 4 | 0.98 | 6 | 63.39 | 4 | 1.00 |
| W2C | 4.43 | 1 | 0.69 | 2 | 1.11 | 2 | 76.98 | 1 | 0.58 |
| W3A | −4.37 | 10 | 0.31 | 10 | 0.89 | 9 | 27.53 | 10 | 0.50 |
| W3B | 3.10 | 3 | 0.63 | 3 | 1.05 | 3 | 70.46 | 3 | 0.00 |
| W3C | 3.21 | 2 | 0.70 | 1 | 1.23 | 1 | 76.00 | 2 | 0.58 |
| PCA | TOPSIS | GRDA | MFA | Mean | |
|---|---|---|---|---|---|
| PCA | 1.00 | 0.96 | 0.78 | 1.00 | 0.93 |
| TOPSIS | 0.96 | 1.00 | 0.82 | 0.96 | 0.93 |
| GRDA | 0.78 | 0.82 | 1.00 | 0.78 | 0.84 |
| MFA | 1.00 | 0.96 | 0.78 | 1.00 | 0.93 |
| Treatment | Borda | Copeland | FBorda | ODCA | Ranking Standard Deviation | ||||
|---|---|---|---|---|---|---|---|---|---|
| Evaluation Value | Ranking | Evaluation Value | Ranking | Evaluation Value | Ranking | Evaluation Value | Ranking | ||
| CK | 4.00 | 6 | −1.00 | 6 | 11.21 | 6 | −0.11 | 6 | 0.00 |
| W1A | 1.00 | 9 | −7.00 | 9 | 0.87 | 9 | −1.46 | 9 | 0.00 |
| W1B | 3.00 | 7 | −3.00 | 7 | 5.47 | 7 | −0.59 | 7 | 0.00 |
| W1C | 5.00 | 5 | 1.00 | 5 | 16.29 | 5 | 0.32 | 5 | 0.00 |
| W2A | 2.00 | 8 | −5.00 | 8 | 3.68 | 8 | −0.90 | 8 | 0.00 |
| W2B | 6.00 | 4 | 3.00 | 4 | 19.40 | 4 | 1.55 | 4 | 0.00 |
| W2C | 8.00 | 1 | 7.00 | 1 | 40.88 | 1 | 2.66 | 1 | 0.00 |
| W3A | 0.00 | 10 | −9.00 | 10 | 0.37 | 10 | −1.92 | 10 | 0.00 |
| W3B | 7.00 | 3 | 5.00 | 3 | 28.00 | 3 | 1.96 | 3 | 0.00 |
| W3C | 8.00 | 1 | 7.00 | 1 | 40.67 | 2 | 2.07 | 2 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Jiang, Y.; Liu, X.; Nie, W.; Hu, Y.; Yang, Y.; Chu, S.; Xu, X.; Xiao, C. Optimization of Irrigation Leaching Regime During the Cotton Growth Period Based on Multi-Model Integration and Fuzzy Borda Validation. Agronomy 2025, 15, 2113. https://doi.org/10.3390/agronomy15092113
Huang H, Jiang Y, Liu X, Nie W, Hu Y, Yang Y, Chu S, Xu X, Xiao C. Optimization of Irrigation Leaching Regime During the Cotton Growth Period Based on Multi-Model Integration and Fuzzy Borda Validation. Agronomy. 2025; 15(9):2113. https://doi.org/10.3390/agronomy15092113
Chicago/Turabian StyleHuang, Hongyuan, Yunling Jiang, Xi Liu, Wanqing Nie, Yuli Hu, Yang Yang, Shuangshuang Chu, Xintong Xu, and Chao Xiao. 2025. "Optimization of Irrigation Leaching Regime During the Cotton Growth Period Based on Multi-Model Integration and Fuzzy Borda Validation" Agronomy 15, no. 9: 2113. https://doi.org/10.3390/agronomy15092113
APA StyleHuang, H., Jiang, Y., Liu, X., Nie, W., Hu, Y., Yang, Y., Chu, S., Xu, X., & Xiao, C. (2025). Optimization of Irrigation Leaching Regime During the Cotton Growth Period Based on Multi-Model Integration and Fuzzy Borda Validation. Agronomy, 15(9), 2113. https://doi.org/10.3390/agronomy15092113






