Soil Hydraulic Properties Estimated from Evaporation Experiment Monitored by Low-Cost Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensor Selection and Assembly of the SOILHP Device
2.2. Algorithms
2.3. Sensor Calibration
2.4. Soil Sampling for the Evaporation Experiment
2.5. Inverse Modeling with Hydrus-1D
2.6. Application Example: Forward Simulation for Estimating the Field Capacity
3. Results and Discussion
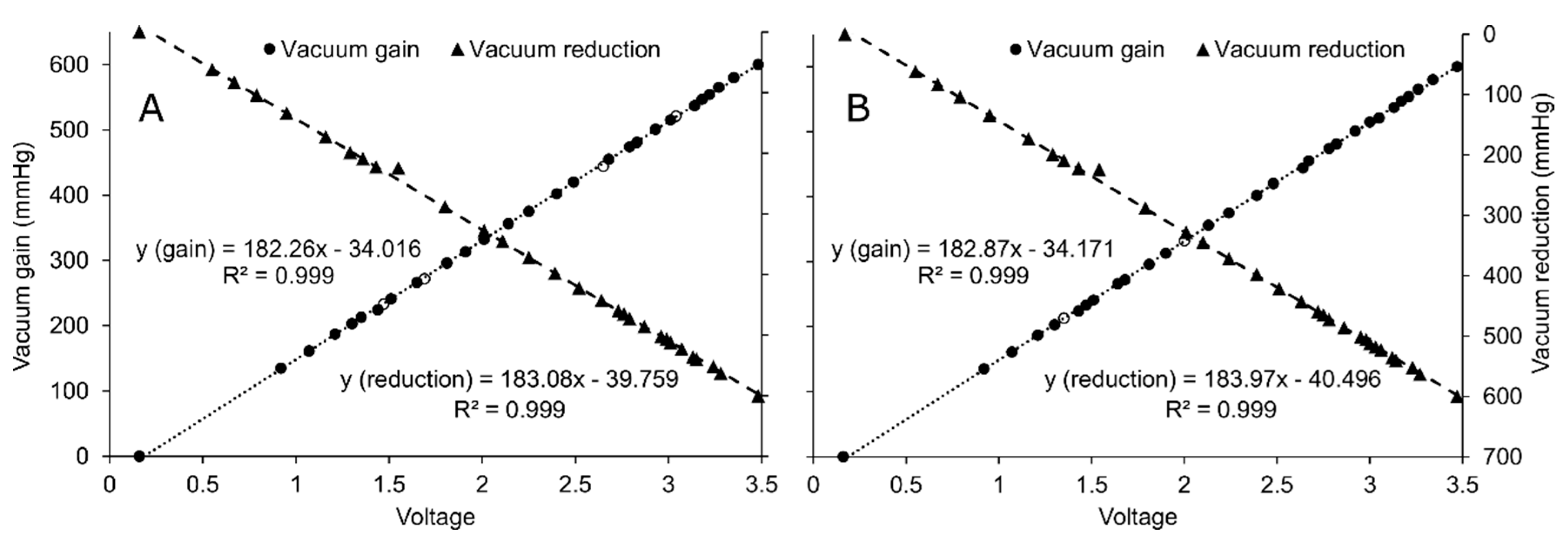
3.1. Calibration and Sensor Test
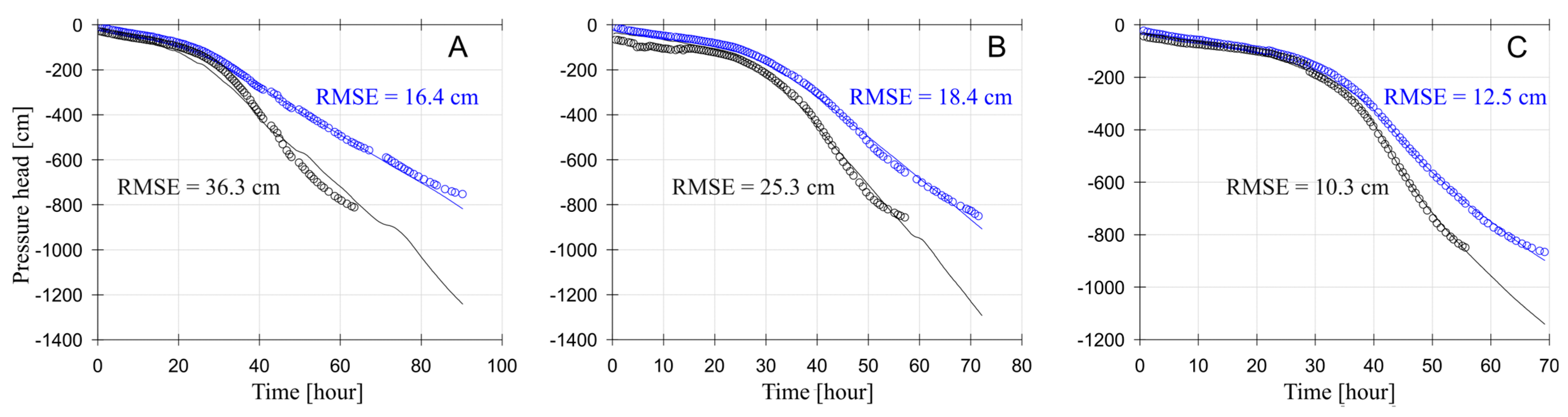
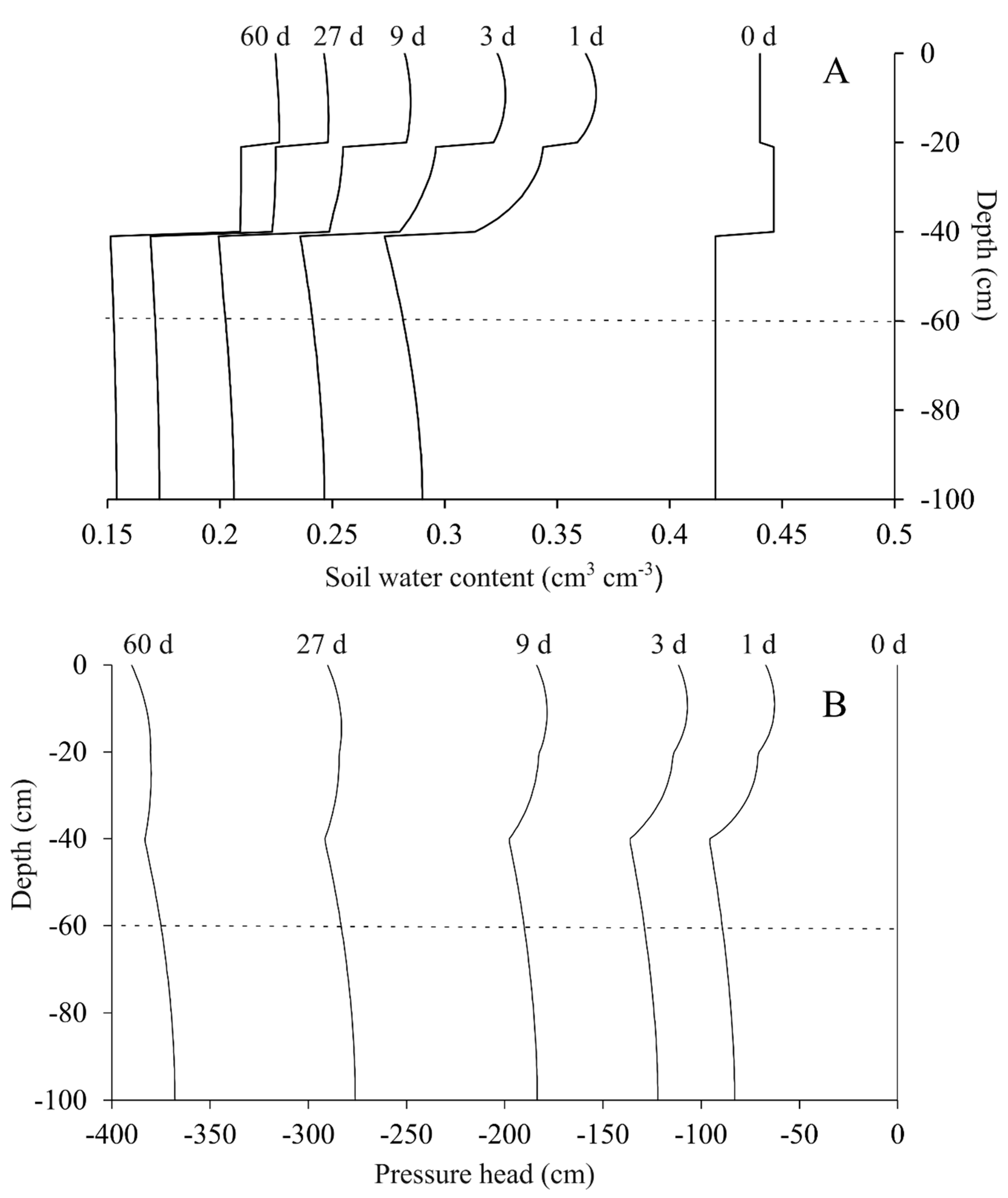
3.2. Optimization of the Hydraulic Parameters for a Soil Profile
3.3. Field Capacity Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vogel, M.M.; Orth, R.; Cheruy, F.; Hagemann, S.; Lorenz, R.; Hurk, B.J.J.M.; Seneviratne, S.I. Regional amplification of projected changes in extreme temperatures strongly controlled by soil moisture-temperature feedbacks. Geophys. Res. Lett. 2017, 44, 1511–1519. [Google Scholar] [CrossRef]
- Barbosa Júnior, M.R.; de Almeida Moreira, B.R.; dos Santos Carreira, V.; de Brito Filho, A.L.; Trentin, C.; de Souza, F.L.P.; Tedesco, D.; Setiyono, T.; Flores, J.R.; Ampatzidis, Y.; et al. Precision agriculture in the United States: A comprehensive meta-review inspiring further research, innovation, and adoption. Comput. Electron. Agric. 2024, 221, 108993. [Google Scholar]
- Bonfante, A.; Sellami, M.H.; Abi Saab, M.T.; Albrizio, R.; Basile, A.; Fahed, S.; Giorio, P.; Langella, G.; Monaco, E.; Bouma, J. The role of soils in the analysis of potential agricultural production: A case study in Lebanon. Agric. Syst. 2017, 156, 67–75. [Google Scholar] [CrossRef]
- de Jong van Lier, Q.; Wendroth, O. Reexamination of the Field Capacity Concept in a Brazilian Oxisol. Soil Sci. Soc. Am. J. 2016, 80, 264–274. [Google Scholar] [CrossRef]
- Romano, N.; Palladino, M.; Chirico, G.B. Parameterization of a bucket model for soil-vegetation-atmosphere modeling under seasonal climatic regimes. Hydrol. Earth Syst. Sci. 2011, 15, 3877–3893. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Sakai, M.; Šimůnek, J. An objective analysis of the dynamic nature of field capacity. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.G.; van Genuchten, M.T. Using Pedotransfer Functions to Estimate the van Genuchten–Mualem Soil Hydraulic Properties: A Review. Vadose Zone J. 2010, 9, 795–820. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.H.; Wendroth, O. Parameter Estimation Analysis of the Evaporation Method for Determining Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 1998, 62, 894–905. [Google Scholar] [CrossRef]
- Wendroth, O.; Ehlers, W.; Hopmans, J.W.; Kage, H.; Halbertsma, J.; Wösten, J.H.M. Reevaluation of the Evaporation Method for Determining Hydraulic Functions in Unsaturated Soils. Soil Sci. Soc. Am. J. 1993, 57, 1436–1443. [Google Scholar] [CrossRef]
- Dane, J.H.; Hopmans, J.W. 3.3.2 Laboratory. In Methods of Soil Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; pp. 675–720. Available online: https://acsess.onlinelibrary.wiley.com/doi/abs/10.2136/sssabookser5.4.c25 (accessed on 15 June 2024).
- Bittelli, M.; Flury, M. Errors in Water Retention Curves Determined with Pressure Plates. Soil Sci. Soc. Am. J. 2009, 73, 1453–1460. [Google Scholar] [CrossRef]
- Gardner, W.R.; Miklich, F.J. Unsaturated Conductivity and Diffusivity Measurements by a Constant Flux Method. Soil Sci. 1962, 93, 271–274. [Google Scholar] [CrossRef]
- Durner, W.; Iden, S.C. Extended multistep outflow method for the accurate determination of soil hydraulic properties near water saturation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Comegna, A.; Hassan, S.B.M.; Coppola, A. Development and Application of an IoT-Based System for Soil Water Status Monitoring in a Soil Profile. Sensors 2024, 24, 2725. [Google Scholar] [CrossRef] [PubMed]
- Gomes Alves, R.; Filev Maia, R.; Lima, F. Discrete-event simulation of an irrigation system using Internet of Things. IEEE Lat. Am. Trans. 2022, 20, 941–947. [Google Scholar] [CrossRef]
- Dos Santos, H.G.; Jacomine, P.K.T.; dos Anjos, L.H.C.; Lumbreras, J.F.; de Oliveira, J.B.; de Oliveira, V.A.; Coelho, M.R.; de Almeida, J.A.; Cunha, T.J.F. Proposta de Atualização Da Segunda Edição Do Sistema Brasileiro de Classificação de Solos. 2009. Available online: http://www.infoteca.cnptia.embrapa.br/handle/doc/664470 (accessed on 30 March 2025).
- United States Department of Agriculture. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys, 2nd ed.; U.S. Department of Agriculture Handbook 436; Natural Resources Conservation Service: Washington, DC, USA, 1999. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.H.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, vzj2016.04. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- De van Jong Lier, Q. Field capacity, a valid upper limit of crop available water? Agric. Water Manag. 2017, 193, 214–220. [Google Scholar] [CrossRef]
- Reynolds, W.D. An analytic description of field capacity and its application in crop production. Geoderma 2018, 326, 56–67. [Google Scholar] [CrossRef]
- Turek, M.E.; de Jong van Lier, Q.; Armindo, R.A. Estimation and mapping of field capacity in Brazilian soils. Geoderma 2020, 376, 114557. [Google Scholar] [CrossRef]
- Sanches, A.C.; de Alves, C.O.; de Jesus, F.L.F.; Theodoro, F.L.; da Cruz, T.A.C.; Gomes, E.P. Low-cost and high-efficiency automated tensiometer for real-time irrigation monitoring. Rev. Bras. Eng. Agríc. Ambient. 2022, 26, 390–395. [Google Scholar] [CrossRef]
- Amaral, A.M.; Cabral Filho, F.R.; Vellame, L.M.; Teixeira, M.B.; Soares, F.A.L.; dos Santos, L.N.S. Uncertainty of weight measuring systems applied to weighing lysimeters. Comput. Electron. Agric. 2018, 145, 208–216. [Google Scholar] [CrossRef]
- Schindler, U.; Müller, L. Simplifying the evaporation method for quantifying soil hydraulic properties. J. Plant Nutr. Soil Sci. 2006, 169, 623–629. [Google Scholar] [CrossRef]
- Wesseling, J.; Kroes, J.; Oliveira, T.C.; Damiano, F. The impact of sensitivity and uncertainty of soil physical parameters on the terms of the water balance: Some case studies with default R packages. Part II: Theory, methods and case descriptions. Comput. Electron. Agric. 2020, 170, 105072. [Google Scholar] [CrossRef]
- Dos Brito, A.S.; Libardi, P.L.; Mota, J.C.A.; Moraes, S.O. Estimativa da capacidade de campo pela curva de retenção e pela densidade de fluxo da água. Rev. Bras. Ciênc. Solo. 2011, 35, 1939–1948. [Google Scholar] [CrossRef]





| Depth | Sand | Silt | Clay | Textural Class | Bulk Density |
|---|---|---|---|---|---|
| cm | -----------------%----------------- | g cm−3 | |||
| 0–20 | 31.73 | 17.39 | 50.88 | Clay | 1.17 |
| 20–40 | 28.07 | 17.39 | 54.55 | Clay | 1.22 |
| 40–60 | 25.29 | 20.55 | 54.16 | Clay | 1.11 |
| Date/Time | Weight (g) | Upper Tensiometer (cm) | Lower Tensiometer (cm) |
|---|---|---|---|
| 4/13/2024 5:47:37 PM | 1538.80 | −20.09 | −29.47 |
| 4/13/2024 5:57:38 PM | 1546.24 | −20.09 | −29.47 |
| 4/13/2024 6:07:40 PM | 1544.21 | 13.05 | −2.35 |
| 4/13/2024 6:17:41 PM | 1543.35 | 19.78 | 3.57 |
| 4/13/2024 6:27:43 PM | 1542.44 | 21.92 | 5.51 |
| 4/13/2024 6:37:45 PM | 1541.91 | 22.64 | 6.12 |
| 4/13/2024 6:47:46 PM | 1540.93 | 23.45 | 6.83 |
| Observation | Loading | Unloading | Difference (%) | RMSE |
|---|---|---|---|---|
| -----g----- | % | g | ||
| 1 | 0.00 | 0.00 | 0.00 | 1.94 |
| 2 | 147.31 | 147.63 | 0.22 | |
| 3 | 294.96 | 295.67 | 0.24 | |
| 4 | 444.94 | 445.57 | 0.14 | |
| 5 | 592.73 | 593.87 | 0.19 | |
| 6 | 746.42 | 747.73 | 0.18 | |
| 7 | 898.89 | 900.70 | 0.20 | |
| 8 | 1047.87 | 1049.62 | 0.17 | |
| 9 | 1202.55 | 1205.01 | 0.20 | |
| 10 | 1351.05 | 1351.4 | 0.03 | |
| 11 | 1498.94 | 1502.62 | 0.25 | |
| 12 | 1643.13 | 1645.68 | 0.16 | |
| 13 | 1791.13 | 1793.79 | 0.15 | |
| 14 | 1938.25 | 1941.84 | 0.19 | |
| 15 | 2000.00 | 2000.00 | 0.00 | |
| VGM | Average Value | Standard Error | 95% Confidence Limits |
|---|---|---|---|
| 0–20 cm | |||
| θr [cm3 cm−3] | 0.0581 | 0.0049 | 0.0485–0.0678 |
| θs [cm3 cm−3] | 0.4401 | 0.0133 | 0.4140–0.4663 |
| α [cm−1] | 0.0159 | 0.0008 | 0.0143–0.0175 |
| n [–] | 1.4436 | 0.0304 | 1.3840–1.5032 |
| Ks [cm h−1] | 0.2890 | 0.0538 | 0.1835–0.3946 |
| l [–] | −1.0732 | 0.0998 | −1.2693–−0.8772 |
| 20–40 cm | |||
| θr [cm3 cm−3] | 0.1556 | 0.0067 | 0.1425–0.1688 |
| θs [cm3 cm−3] | 0.4462 | 0.0042 | 0.4380–0.4545 |
| α [cm−1] | 0.0177 | 0.0005 | 0.0168–0.0185 |
| n [–] | 1.8793 | 0.0357 | 1.8091–1.9494 |
| Ks [cm h−1] | 0.3953 | 0.0357 | 0.3253–0.4654 |
| l [–] | −1.0987 | 0.0269 | −1.1516–−1.0459 |
| 40–60 cm | |||
| θr [cm3 cm−3] | 0.0775 | 0.0037 | 0.0703–0.0847 |
| θs [cm3 cm−3] | 0.4203 | 0.0038 | 0.4128–0.4278 |
| α [cm−1] | 0.0175 | 0.0003 | 0.0168–0.0181 |
| n [–] | 1.7998 | 0.0146 | 1.7711–1.8284 |
| Ks [cm h−1] | 5.8997 | 0.2073 | 5.4926–6.3069 |
| l [–] | 0.0002 | 0.0001 | 0.0001–0.0004 |
| qfc | ψfc | θfc | Time |
|---|---|---|---|
| mm d−1 | cm | cm3 cm−3 | d |
| 1 | −239 | 0.230 | 17 |
| 2 | −191 | 0.250 | 9 |
| 4 | −154 | 0.264 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonfim-Silva, T.H.; Alves Rodrigues Pinheiro, E.; Araújo da Silva, T.J.; Franco Duarte, T.; Menegaz Meneghetti, L.A.; Bonfim-Silva, E.M. Soil Hydraulic Properties Estimated from Evaporation Experiment Monitored by Low-Cost Sensors. Agronomy 2025, 15, 2009. https://doi.org/10.3390/agronomy15082009
Bonfim-Silva TH, Alves Rodrigues Pinheiro E, Araújo da Silva TJ, Franco Duarte T, Menegaz Meneghetti LA, Bonfim-Silva EM. Soil Hydraulic Properties Estimated from Evaporation Experiment Monitored by Low-Cost Sensors. Agronomy. 2025; 15(8):2009. https://doi.org/10.3390/agronomy15082009
Chicago/Turabian StyleBonfim-Silva, Tallys Henrique, Everton Alves Rodrigues Pinheiro, Tonny José Araújo da Silva, Thiago Franco Duarte, Luana Aparecida Menegaz Meneghetti, and Edna Maria Bonfim-Silva. 2025. "Soil Hydraulic Properties Estimated from Evaporation Experiment Monitored by Low-Cost Sensors" Agronomy 15, no. 8: 2009. https://doi.org/10.3390/agronomy15082009
APA StyleBonfim-Silva, T. H., Alves Rodrigues Pinheiro, E., Araújo da Silva, T. J., Franco Duarte, T., Menegaz Meneghetti, L. A., & Bonfim-Silva, E. M. (2025). Soil Hydraulic Properties Estimated from Evaporation Experiment Monitored by Low-Cost Sensors. Agronomy, 15(8), 2009. https://doi.org/10.3390/agronomy15082009






