Numerical Simulation and Orthogonal Test of Droplet Impact on Soybean Leaves Based on VOF Method and High-Speed Camera Technology
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
2.2. Numerical Simulation of Motion Characteristics of Droplet Impact on Soybean Leaves
2.2.1. Three-Dimensional Soybean Leaf Reconstruction Cloud Technology
2.2.2. Control Equation Setting
2.2.3. Grid Partitioning and Parameter Setting
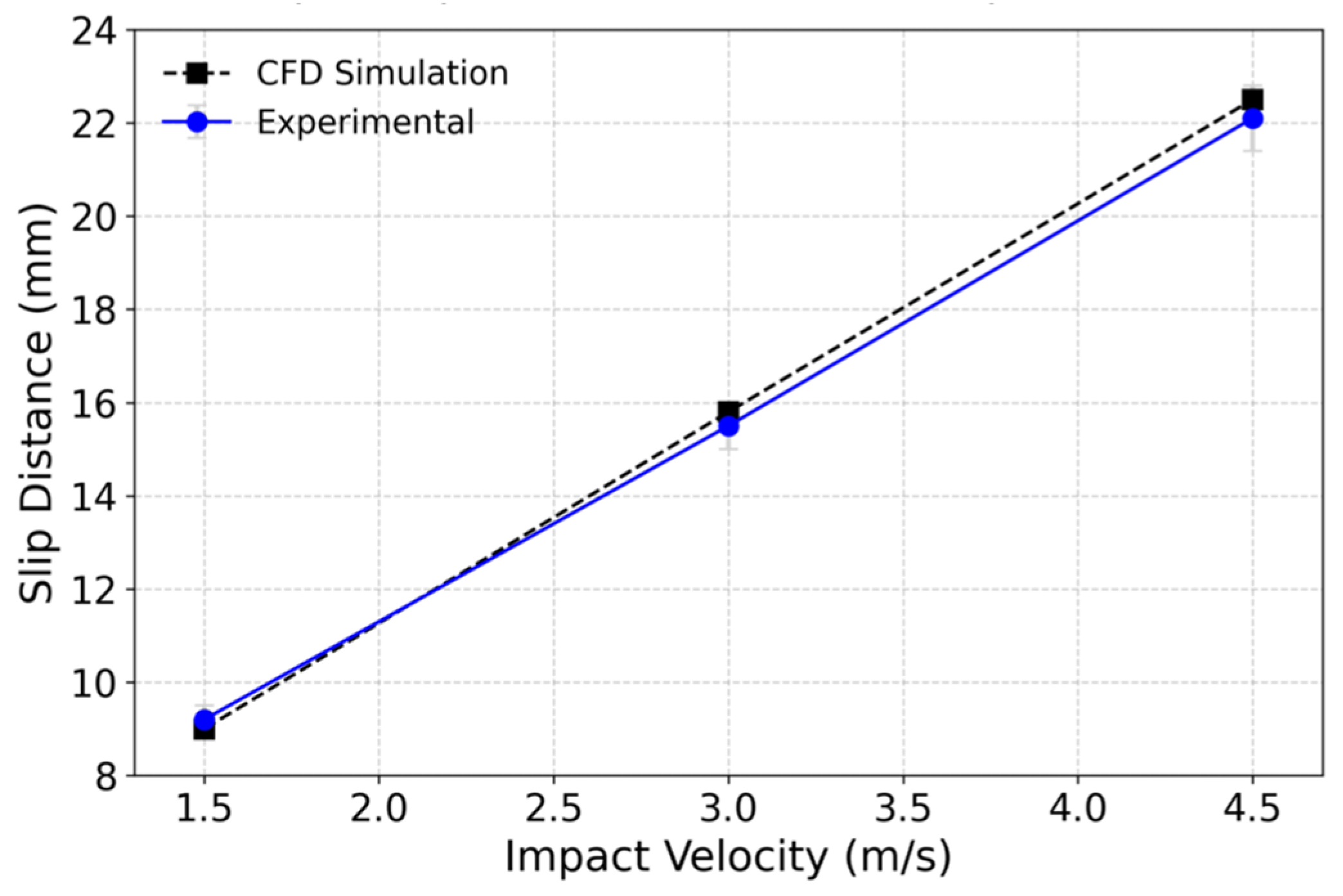
2.2.4. Model Validation and Dimensionless Analysis
3. Results and Discussion
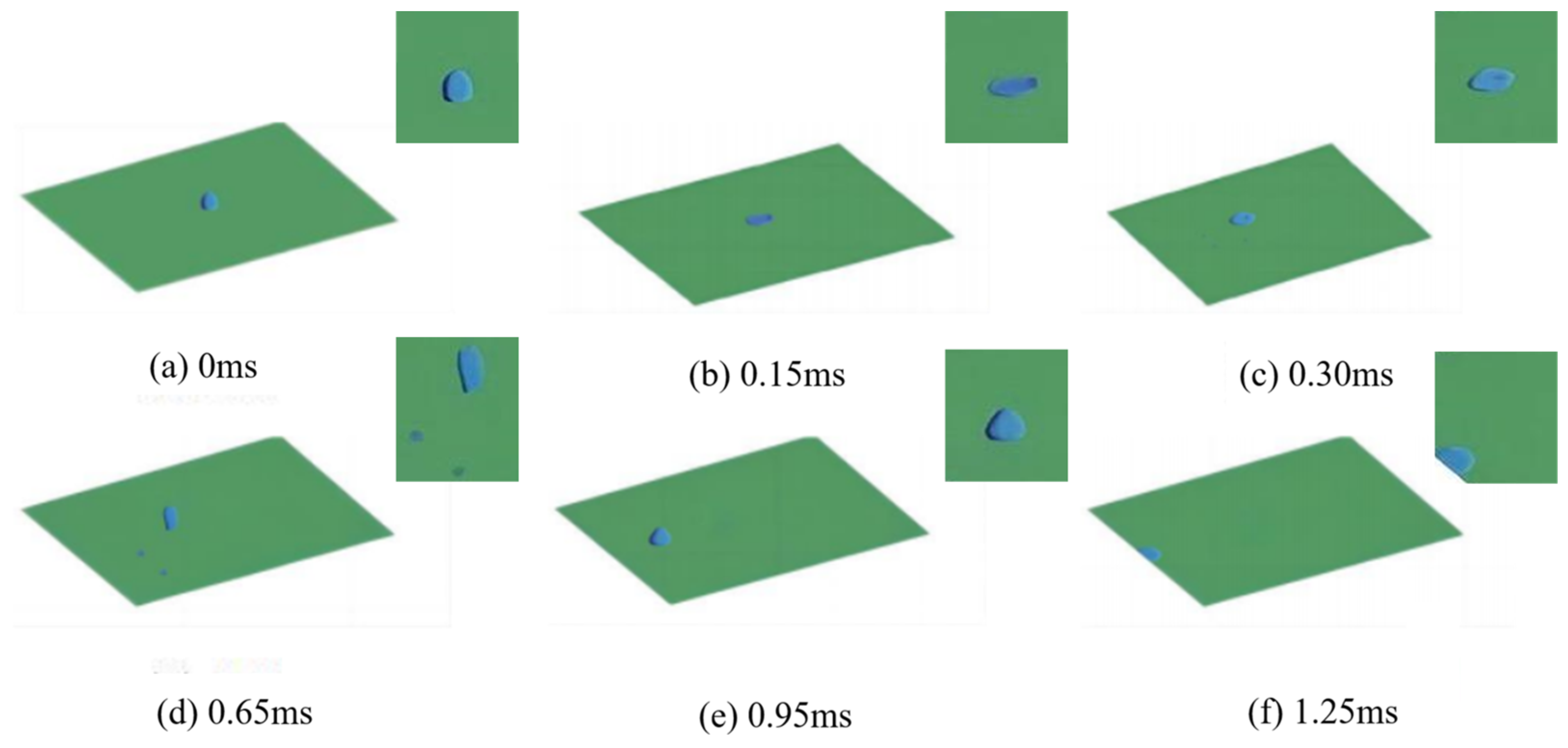
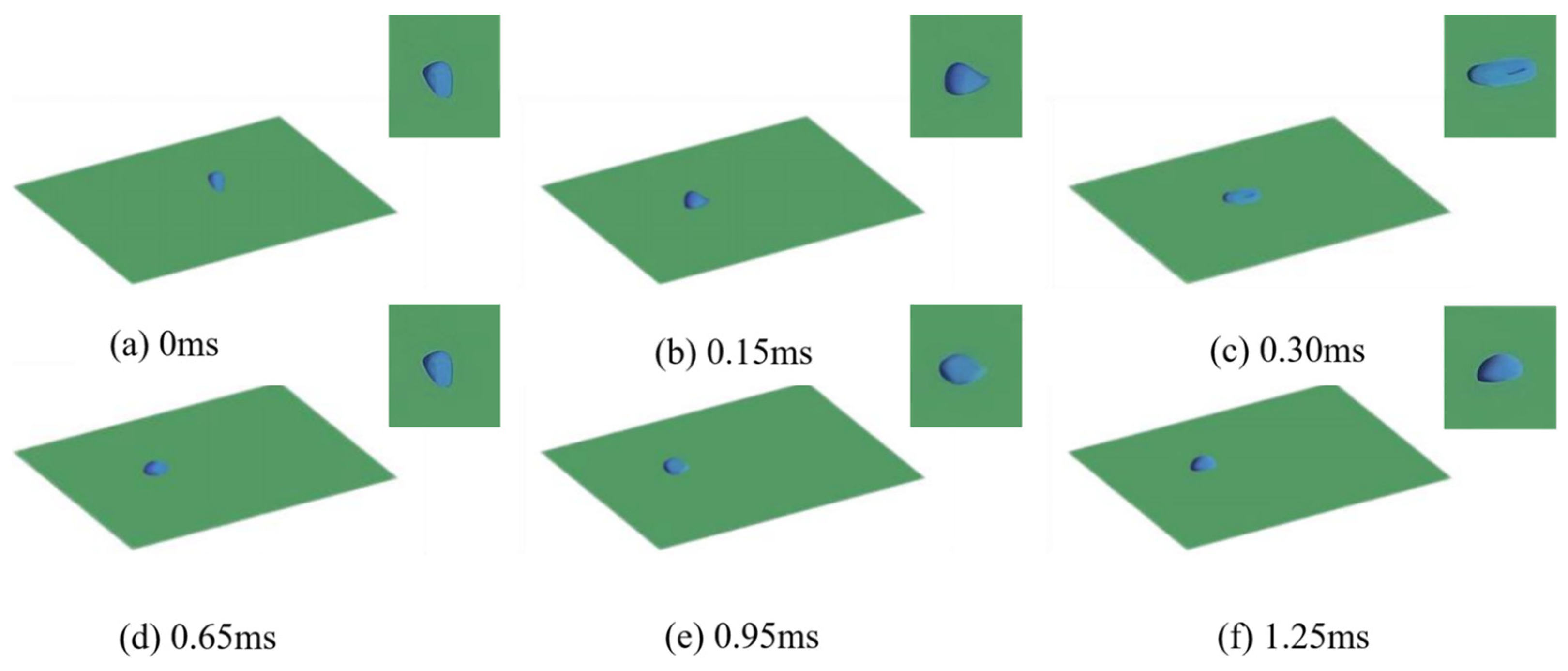
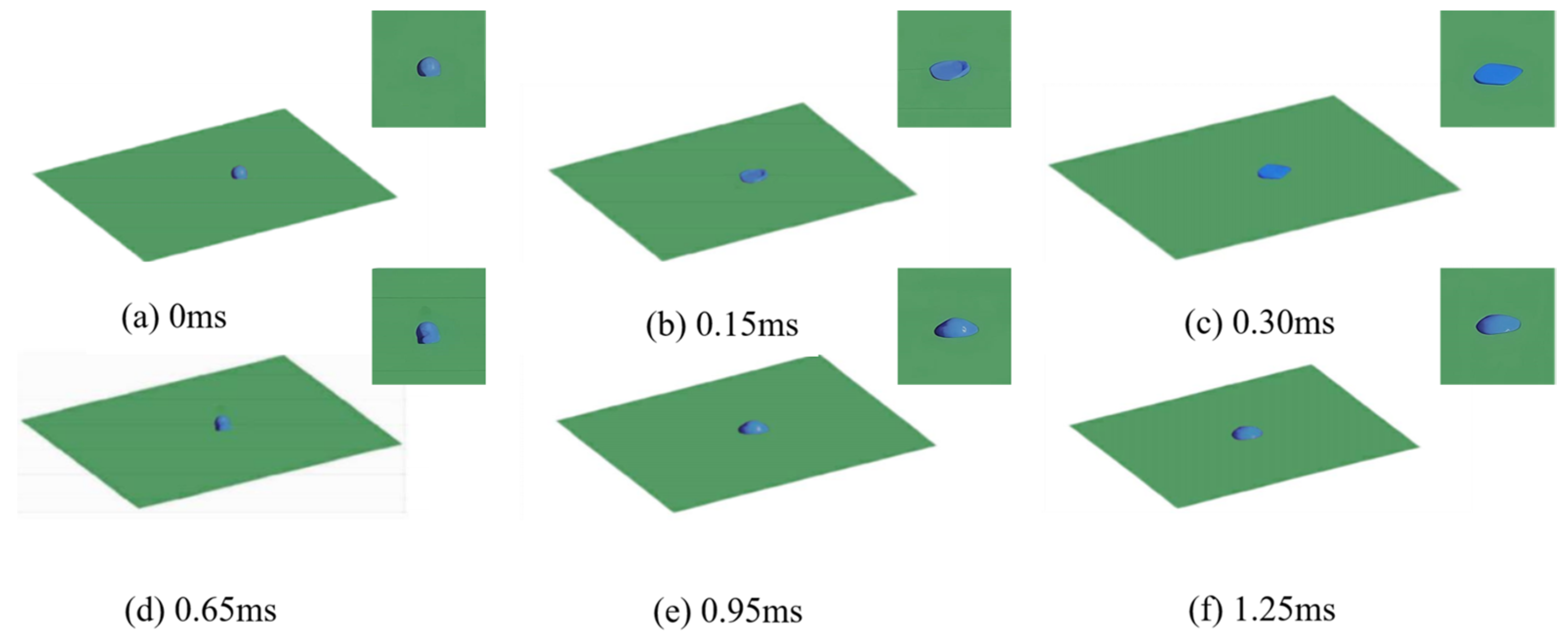
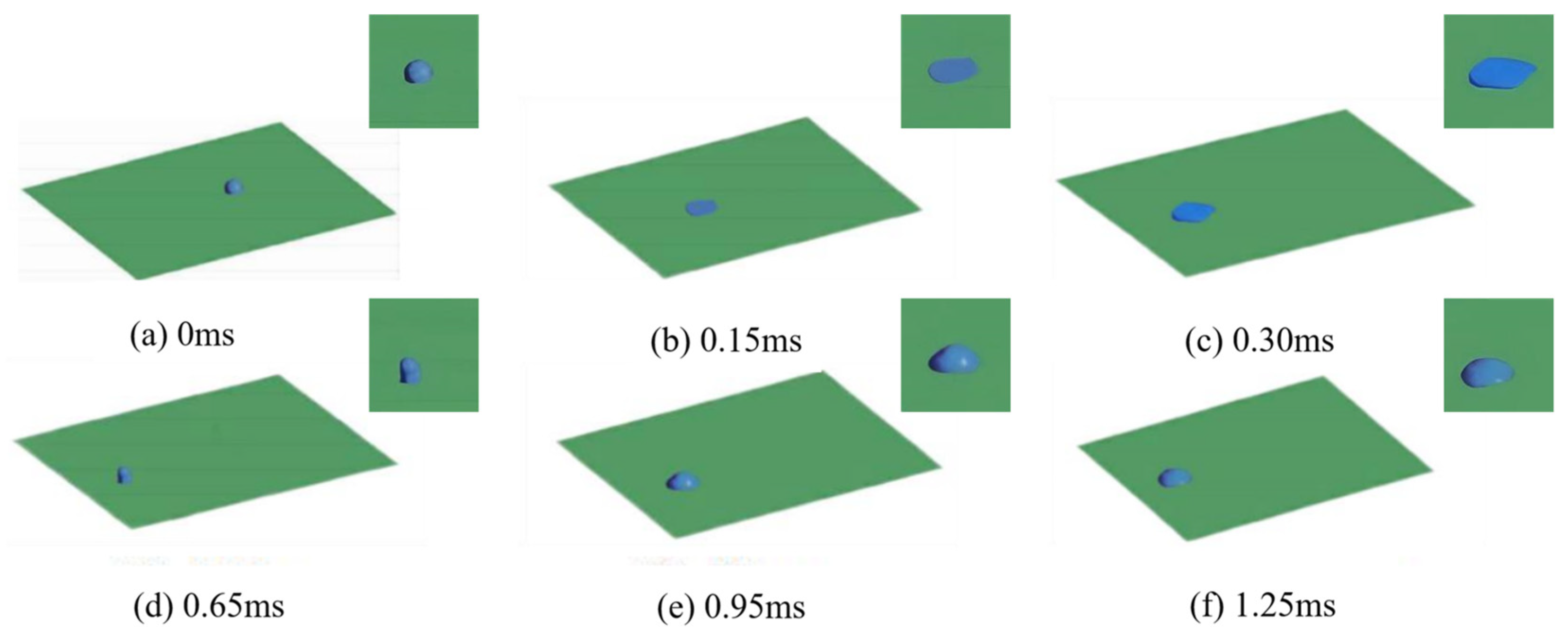
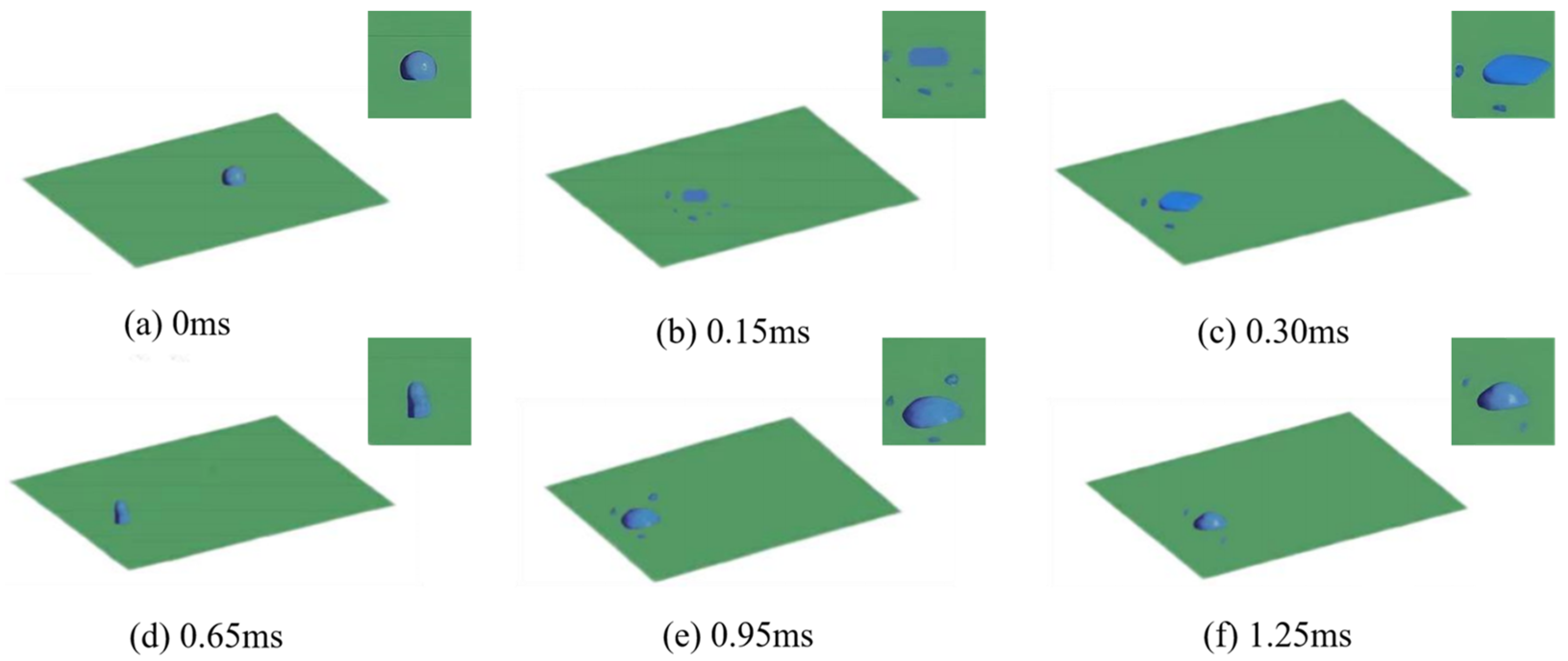
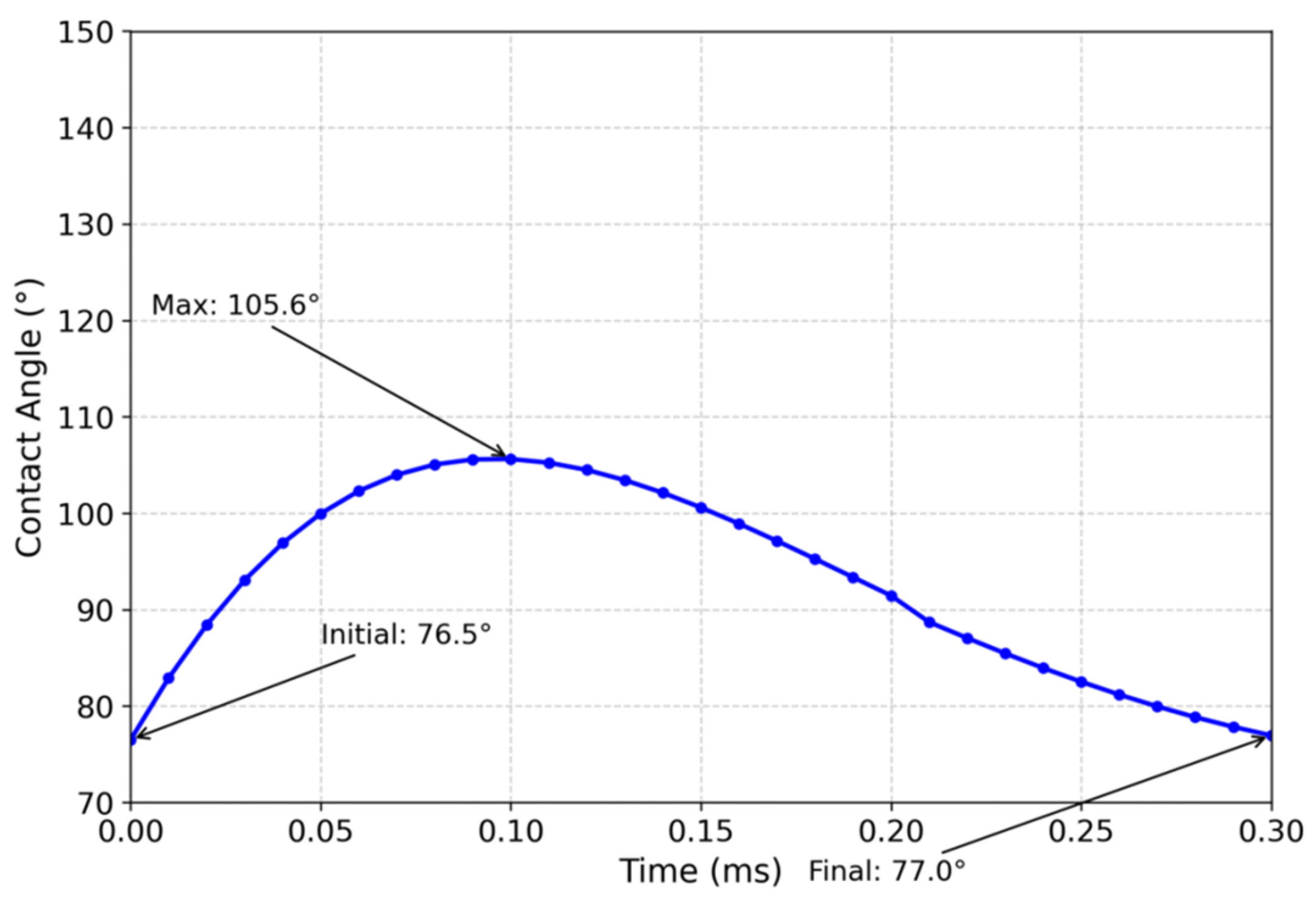
3.1. Numerical Simulation Analysis
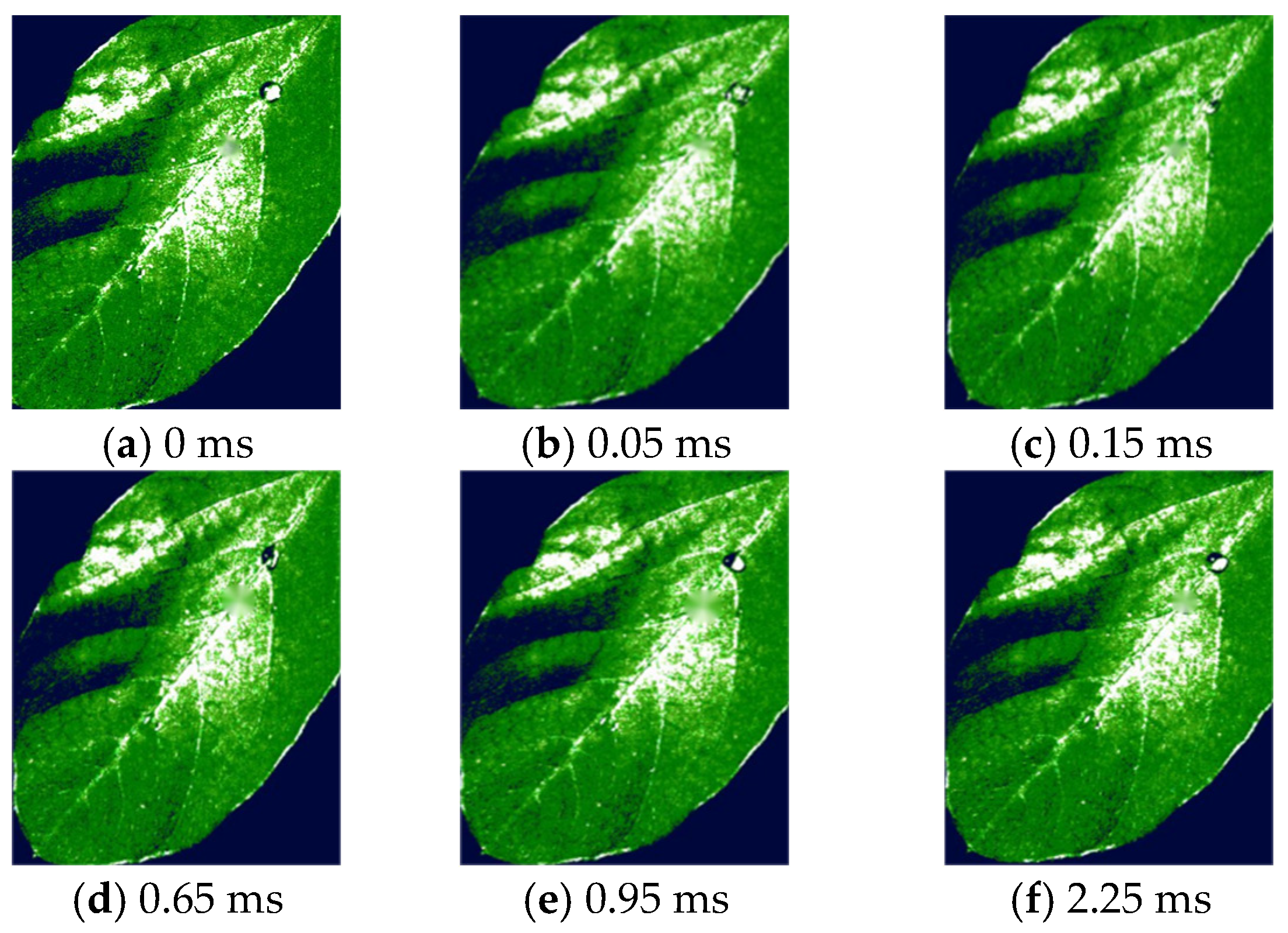
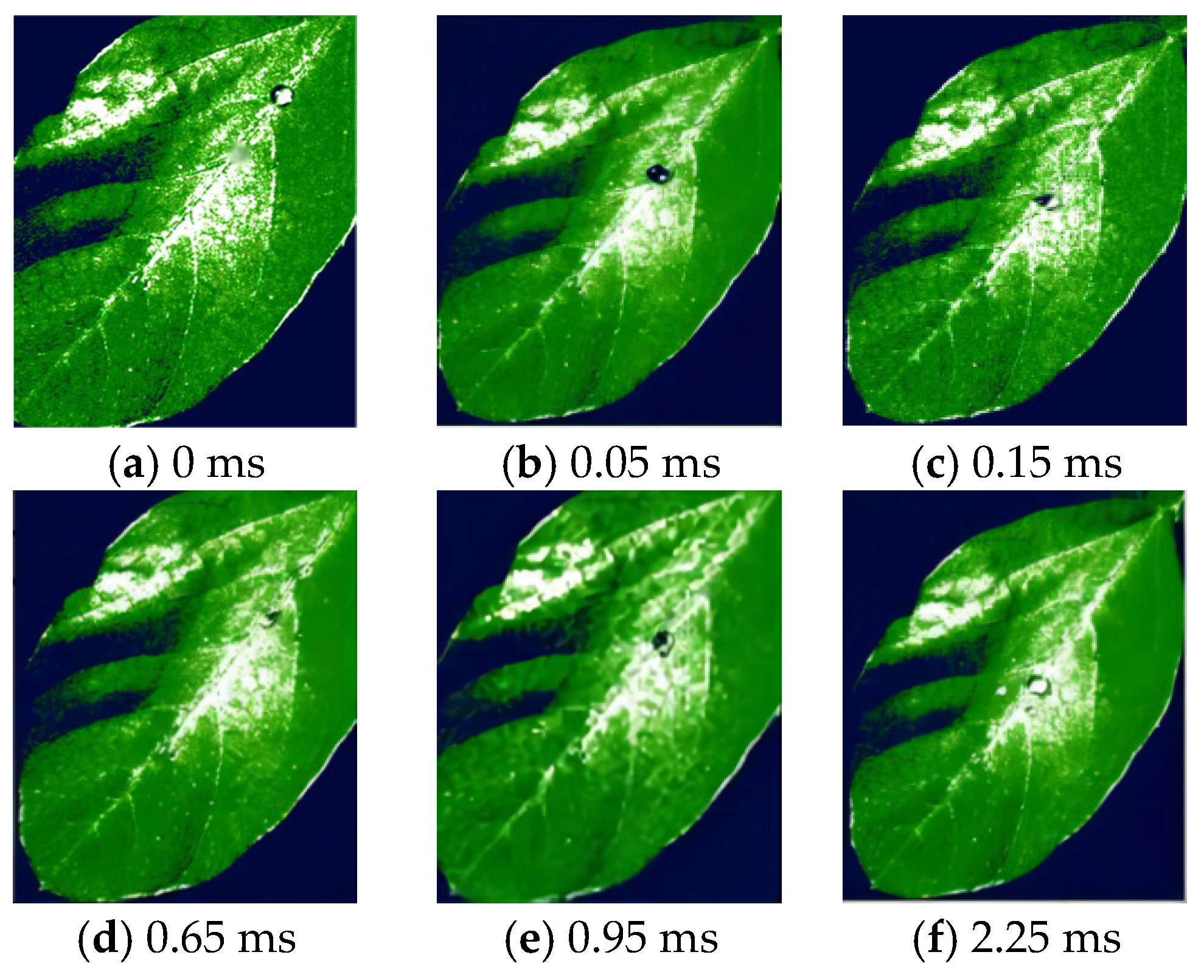
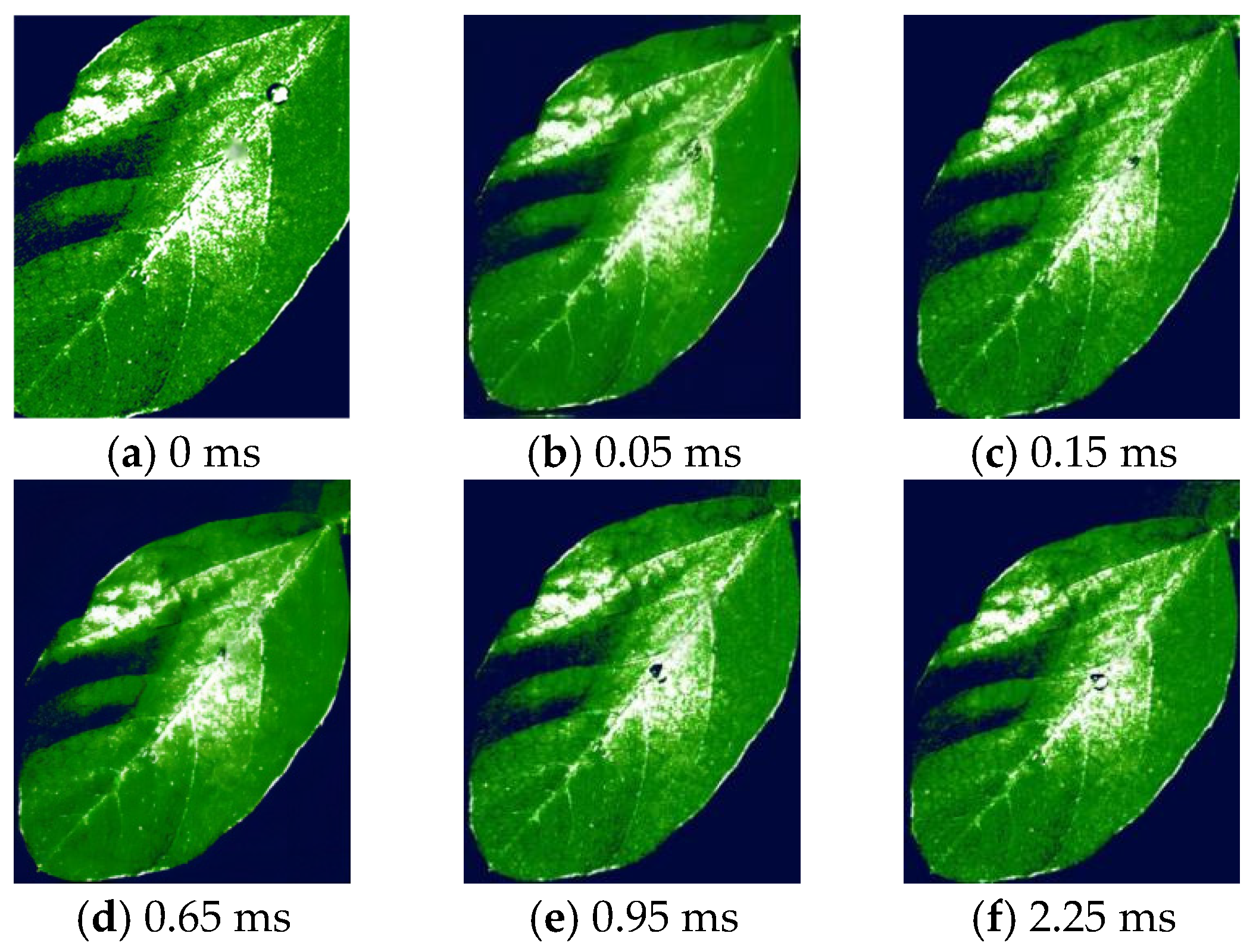
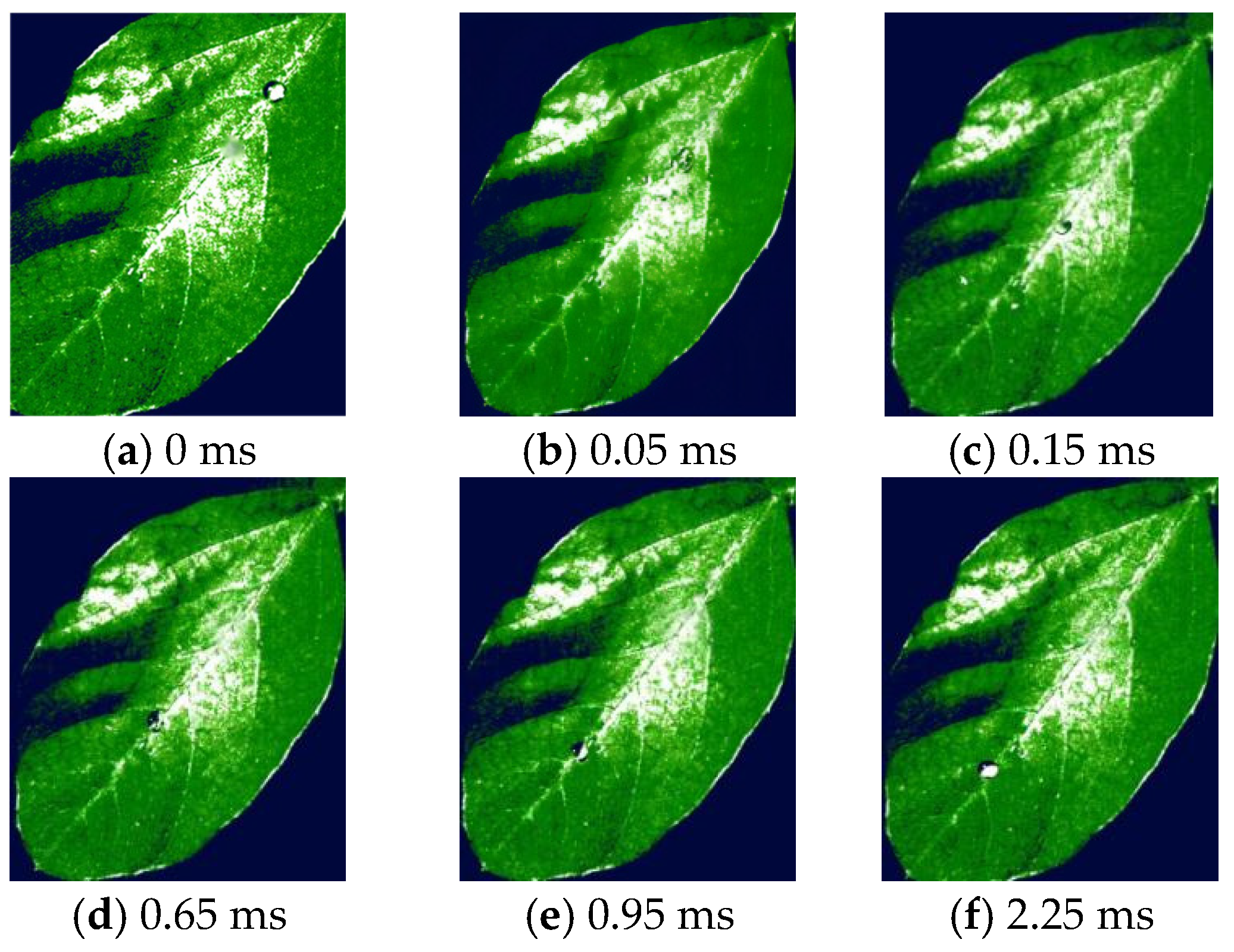
3.2. Droplet Deposition Characteristics Determined by High-Speed Camera Technology Analysis
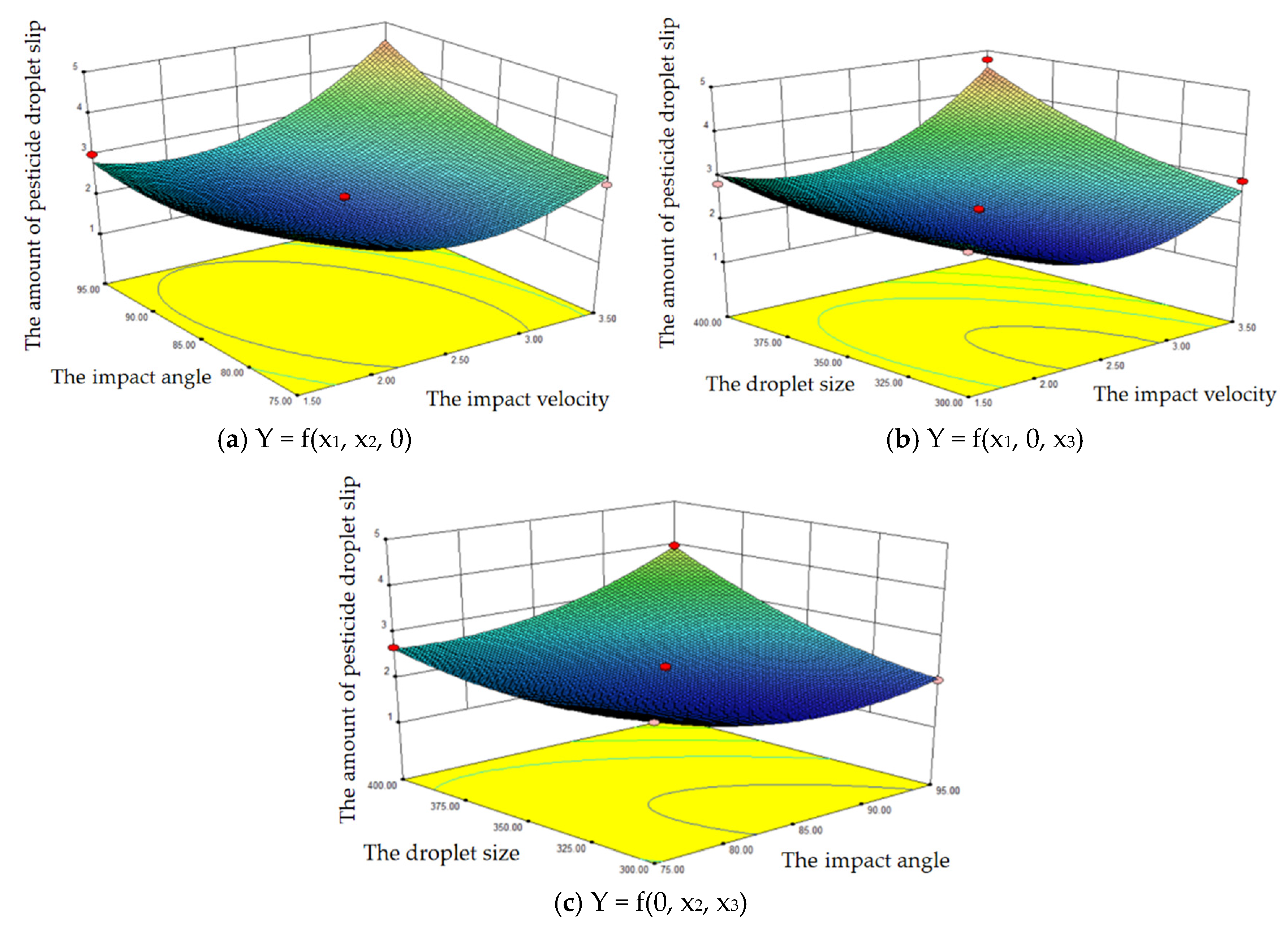
3.3. Pesticide Droplet Slip Based on Response Surface Method Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Liu, X.; Cui, H.; Yuan, J. Research Progress and Trend Analysis of Crop Canopy Droplet Deposition. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. (In Chinese) [Google Scholar]
- He, X. Research progress of plant protection machinery and pesticide application technology in China. Chin. J. Pestic. 2019, 21, 921–930. (In Chinese) [Google Scholar]
- Liu, C.; Hu, J.; Li, Y.; Zhao, S.; Zhang, W.; Li, Q. Optimization of the inner flow channel of conical wind field anti-drift spray device and anti-drift characteristics. Trans. CSAE 2021, 37, 11–20. (In Chinese) [Google Scholar]
- Wang, G.; Ou, M.; Jia, W.; Zhou, H.; Dai, S.; Dong, X.; Wang, X.; Jiang, L.; Lu, W.; Wang, M. The dynamic evaporation characteristics of thiophanate-methyl droplets and their enhancement under different wind conditions. Horticulturae 2022, 8, 721. [Google Scholar] [CrossRef]
- Li, J.; Cui, H.; Ma, Y.; Xun, L.; Li, Z.; Yang, Z.; Lu, H. Orchard Spray Study: A Prediction Model of Droplet Deposition States on Leaf Surfaces. Agronomy 2020, 10, 747. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Wang, J.; Hao, D.; Wang, R. The Motion of Strawberry Leaves in an Air-Assisted Spray Field and its Influence on Droplet Deposition. Trans. ASABE 2021, 64, 83–93. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Ma, Y.; Cui, H.; Yang, Z.; Lu, H. Effects of leaf response velocity on spray deposition with an air-assisted orchard sprayer. Int. J. Agric. Biol. Eng. 2021, 14, 123–132. [Google Scholar] [CrossRef]
- Lee, I.-B.; Bitog, J.P.P.; Hong, S.-W.; Seo, I.-H.; Kwon, K.-S.; Bartzanas, T.; Kacira, M. The past, present and future of CFD for agro-environmental applications. Comput. Electron. Agric. 2013, 93, 168–183. [Google Scholar] [CrossRef]
- Liu, C.; Hu, J.; Li, Y.; Zhao, S.; Li, Q.; Zhang, W.; Zhao, M. Numerical Simulation of the Trajectory of UAVs Electrostatic Droplets Based on VOF-UDF Electro-Hydraulic Coupling and High-Speed Camera Technology. Agronomy 2023, 13, 512. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Guo, J.; Qiu, B. Numerical Simulation and Validation of Droplet Deposition on Tomato Leaf Surface under Air-Assisted Spraying. Agronomy 2024, 14, 1661. [Google Scholar] [CrossRef]
- Mark, N.; Malay, M.; Robert, C. Predicting particle trajectories on an electrodynamic screen-theory and experiment. J. Electrost. 2013, 71, 185–188. [Google Scholar]
- Wang, Z.; Zhang, Y.; Guo, T. Experimental study on size and velocity of charged droplets. Procedia Eng. 2015, 126, 522–526. [Google Scholar] [CrossRef]
- Cui, H.; Wang, C.; Liu, X.; Yuan, J.; Liu, Y.; Song, L. Cotton canopy airflow simulation and velocity attenuation model based upon 3D phenotype and stratified sub-regional porous medium. Comput. Electron. Agric. 2022, 201, 107282. [Google Scholar] [CrossRef]
- Liu, D.; Chen, Z.; Zhou, H.; Chen, Q.; Yang, H. Numerical simulation and verification of flow field characteristics of spray droplets on tea leaves. J. Agric. Chem. China 2022, 43, 58–66. (In Chinese) [Google Scholar]
- Zheng, J.; Zhang, H.; Xu, Y.; Zhou, H. Research review on modeling and simulation technology of pesticide spraying system. J. Agric. Sci. Technol. 2024, 26, 76–90. (In Chinese) [Google Scholar]
- Appah, S.; Jia, W.; Ou, M.; Wang, P.; Asante, E.A. Analysis of potential impaction and phytotoxicity of surfactant-plant surface interaction in pesticide application. Crop. Prot. 2020, 127, 104961. [Google Scholar] [CrossRef]
- Ma, J.; Liu, K.; Dong, X.; Chen, C.; Qiu, B.; Zhang, S. Effects of Leaf Surface Roughness and Contact Angle on In Vivo Measurement of Droplet Retention. Agronomy 2022, 12, 2228. [Google Scholar] [CrossRef]
- Shi, Q.; Mao, H.; Guan, X. Numerical Simulation and Experimental Verification of the Deposition Concentration of an Unmanned Aerial Vehicle. Appl. Eng. Agric. 2019, 35, 367–376. [Google Scholar] [CrossRef]
- Qiu, W.; Guo, H.; Zheng, H.; Cao, Y.; Lv, X.; Fang, J.; Zhai, C.; Yu, H. CFD modelling to analyze the droplets deposition behavior on vibrating rice leaves. Comput. Electron. Agric. 2022, 201, 107330. [Google Scholar] [CrossRef]
- Cao, Y.; Xi, T.; Xu, L.; Qiu, W.; Guo, H.; Lv, X.; Li, C. Computational fluid dynamics simulation experimental verification and analysis of droplets deposition behaviour on vibrating pear leaves. Plant Methods 2022, 18, 80. [Google Scholar] [CrossRef]
- Zaboon, J.K.; Jassim, S.F. Numerical and analytical analysis for deflection and stress in a simply supported beam. Mater. Today Proc. 2022, 49, 2912–2915. [Google Scholar] [CrossRef]
- Delele, M.A.; Jaeken, P.; Debaer, C.; Baetens, K.; Endalew, A.M.; Ramon, H.; Nicolai, B.M.; Verboven, P. CFD prototyping of an air-assisted orchard sprayer aimed at drift reduction. Comput. Electron. Agric. 2007, 55, 16–27. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolaï, B.M.; Verboven, P. Modelling pesticide flow and deposition from air-assisted orchard spraying in orchards: A new integrated CFD approach. Agric. For. Meteorol. 2010, 150, 1383–1392. [Google Scholar] [CrossRef]
- Sun, C. Design and experimental assessment of a field-spraying system with nozzles employing reciprocating up-and-down movements. Pest Manag. Sci. 2023, 79, 5387–5392. [Google Scholar] [CrossRef]
- Miao, Y.; Chen, X.; Gong, Y.; Liu, D.; Chen, J.; Wang, G.; Zhang, X. Design and test of powerful air-assisted sprayer for high stalk crops. Front. Plant Sci. 2023, 14, 1266791. [Google Scholar] [CrossRef]
- Rocamora, M.; Val, L.; Pérez, M. PM—Power and Machinery: Modelling the Performance of Air-assisted Spraying on Artichoke. Biosyst. Eng. 2002, 81, 385–393. [Google Scholar] [CrossRef]
- Range, K.; Feuillebois, F. Influence of Surface Roughness on Liquid Drop Impact. J. Colloid Interface Sci. 1998, 203, 16–30. [Google Scholar] [CrossRef]









| Solution Type | Surface Tension (mN/m) | Density (g/cm3) | Contact Angle (°) | Remarks |
|---|---|---|---|---|
| 20% permethrin emulsion | 38.5 ± 0.3 | 1.08 ± 0.02 | 70.2 ± 1.5 | 20% emulsion, pH = 6.5 |
| 20% permethrin emulsion + 1/2000 Yunzhan | 25.1 ± 0.2 | 1.00 ± 0.01 | 50.5 ± 1.2 | silicone surfactants |
| 20% permethrin emulsion + 1/2000 Jijian | 32.4 ± 0.4 | 1.02 ± 0.01 | 60.8 ± 1.3 | alkyl polyoxyethylene ether |
| 20% permethrin emulsion + 1/2000 Sujie | 35.6 ± 0.3 | 1.03 ± 0.02 | 55.3 ± 1.4 | plant oil derivatives |
| Grid Type | Total Cells | Minimum Cell Size (μm) | Spread Diameter D/D0 (t = 5 ms) | Slip Distance Smax (mm) |
|---|---|---|---|---|
| Coarse | 285,600 | 50 | 1.82 | 1.96 |
| Medium | 583,200 | 30 | 1.78 | 1.89 |
| Fine | 921,800 | 15 | 1.77 | 1.88 |
| Physical Characteristics | Air Phase | Liquid Phase |
|---|---|---|
| Temperature (K) | 298 | 298 |
| Density (kg/m3) | 1.225 | 998.2 |
| Dynamic viscosity (N·s/m2) | 1.7894 × 10−2 | 1.003 × 10−3 |
| Turbulent intensity (%) | 10 | 10 |
| Impact Velocity (m/s) | Weber Number We = ρlU2d0/σlg | Reynolds Number Re = ρlUd0/σlg | Capillary Number Ca = μlU/σlg |
|---|---|---|---|
| 1.0 | 42 | 300 | 0.013 |
| 2.0 | 168 | 600 | 0.027 |
| 3.0 | 378 | 900 | 0.040 |
| Coded Value | Impact Velocity (m/s) | Impact Angle (°) | Droplet Size (μm) |
|---|---|---|---|
| −1 | 1.5 | 75 | 300 |
| 0 | 2.5 | 85 | 350 |
| 1 | 3.5 | 95 | 400 |
| No. | Impact Velocity X1 (m/s) | Impact Angle X2 (°) | Droplet Size X3 (μm) | Amount of Pesticide Droplet Slip Y (cm) |
|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 3.62 |
| 2 | 1 | −1 | 0 | 2.91 |
| 3 | −1 | 1 | 0 | 3.02 |
| 4 | 1 | 1 | 0 | 4.38 |
| 5 | −1 | 0 | −1 | 2.74 |
| 6 | 1 | 0 | −1 | 2.98 |
| 7 | −1 | 0 | 1 | 2.82 |
| 8 | 1 | 0 | 1 | 4.78 |
| 9 | 0 | −1 | −1 | 2.54 |
| 10 | 0 | 1 | −1 | 2.05 |
| 11 | 0 | −1 | 1 | 2.68 |
| 12 | 0 | 1 | 1 | 3.96 |
| 13 | 0 | 0 | 0 | 2.27 |
| 14 | 0 | 0 | 0 | 1.99 |
| 15 | 0 | 0 | 0 | 2.31 |
| 16 | 0 | 0 | 0 | 1.87 |
| 17 | 0 | 0 | 0 | 1.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Liu, C.; Sun, H.; Hu, J.; Li, Y.; Guo, W. Numerical Simulation and Orthogonal Test of Droplet Impact on Soybean Leaves Based on VOF Method and High-Speed Camera Technology. Agronomy 2025, 15, 2578. https://doi.org/10.3390/agronomy15112578
Wu S, Liu C, Sun H, Hu J, Li Y, Guo W. Numerical Simulation and Orthogonal Test of Droplet Impact on Soybean Leaves Based on VOF Method and High-Speed Camera Technology. Agronomy. 2025; 15(11):2578. https://doi.org/10.3390/agronomy15112578
Chicago/Turabian StyleWu, Shuangshuang, Changxi Liu, Hao Sun, Jun Hu, Yufei Li, and Wei Guo. 2025. "Numerical Simulation and Orthogonal Test of Droplet Impact on Soybean Leaves Based on VOF Method and High-Speed Camera Technology" Agronomy 15, no. 11: 2578. https://doi.org/10.3390/agronomy15112578
APA StyleWu, S., Liu, C., Sun, H., Hu, J., Li, Y., & Guo, W. (2025). Numerical Simulation and Orthogonal Test of Droplet Impact on Soybean Leaves Based on VOF Method and High-Speed Camera Technology. Agronomy, 15(11), 2578. https://doi.org/10.3390/agronomy15112578







