Abstract
The absence of accurate measurement or calculation techniques for crop water requirements in greenhouses frequently results in over- or under-irrigation. In order to find a better method, this study analyzed the accuracy, data consistency and practicability of the Penman–Monteith (PM), Hargreaves–Samani (HS), Pan Evaporation (PAN), and Artificial Neural Network (ANN) models. Model-calculated crop evapotranspiration (ETC) was compared with lysimeter-measured crop evapotranspiration (ETC) in the National Precision Agriculture Demonstration Station in Beijing, China. The results showed that the actual ETC over the entire experimental period was 176.67 mm. The ETC calculated with the PM, HS, PAN, and ANN model were 146.07 mm, 189.45 mm, 197.03 mm, and 174.7 mm, respectively, which were different from the actual value by −17.32%, 7.23%, 11.52%, and −1.12%, respectively. The order of the calculation accuracy for the four models is as follows: ANN model > PAN model > PM model > HS model. By comprehensively evaluating the statistical indicators of each model, the ANN model was found to have a significantly higher calculation accuracy compared to the other three models. Therefore, the ANN model is recommended for estimating ETC under greenhouse conditions. The PM and PAN models can also be used after improvement.
1. Introduction
The water demand of agricultural crops is one of the key factors in agricultural production. Accurately calculating crop evapotranspiration can provide a theoretical basis for irrigation strategies [,]. Calculating greenhouse evapotranspiration is an important issue in greenhouse agriculture and has significant implications for greenhouse environment management and crop growth regulation []. At present, different methods are used for measuring evapotranspiration in greenhouses.
In the Weighing Lysimeter method, scientists utilize the weight sensors of the lysimeter to automatically record the daily changes in crop and growth substrate weight and calculate daily evapotranspiration (ETC) [,,].
With the Pan Evaporation method, researchers can obtain daily evapotranspiration in a greenhouse by measuring water surface evaporation and using the evaporation coefficient. This method is simple, feasible, and suitable for small-scale greenhouses [,,,,]. By installing evapotranspiration-monitoring sensors in greenhouses, it is easy and efficient to obtain and calculate daily evapotranspiration [,].
Scientists use various meteorological models, such as Priestley–Taylor, Hargreaves, and Penman–Monteith, to calculate evapotranspiration inside and outside the greenhouse; this is based on meteorological parameters near the experimental site and is currently a commonly used indirect calculation method to obtain evapotranspiration [,,]. These mathematical models are primarily based on the principles of energy balance and mass transfer, taking into account meteorological factors, greenhouse structure, and crop characteristics, in addition to employing complex mathematical calculations to estimate crop evapotranspiration. The Hargreaves–Samani equation was recommended for the practical estimation of ETO in plastic greenhouses in Mediterranean climatic conditions, as, in the conditions of Mediterranean plastic greenhouses, the original Penman–Monteith equation clearly underestimated measured ETO [].
The use of an AI model is another option. For the calculation of evapotranspiration, most scholars use the Penman–Monteith equation to calculate reference evapotranspiration based on environmental parameters [,]. However, in a greenhouse environment, the accuracy of this equation is reduced due to the wind speed usually being 0, which limits its application in greenhouses. To solve this problem, some scholars have proposed using artificial intelligence algorithms such as machine learning combined with measured greenhouse environmental data to calculate evapotranspiration []. At present, some scholars use various environmental sensors installed in greenhouses, combined with crop growth patterns, to calculate evapotranspiration in greenhouses, using methods such as Random Forest (RFR), the BP neural network, and the GA-BP neural network. The results of the research show that the Random Forest (RFR) algorithm has higher computational accuracy []. In addition, through comparative analysis of climate data from 1998 to 2012, Tao et al. found that the adaptive fuzzy neural network model has good computational performance []. These studies demonstrate that utilizing machine learning and artificial intelligence algorithms can improve the accuracy of calculating evapotranspiration in greenhouses, providing more accurate data support for greenhouse management and agricultural production.
By studying current ETC calculation models, four models were selected in this article to calculate ETC in a greenhouse, and these were then compared with actual ETC values. A detailed description of the methods used in this study is provided in Section 2 of this paper. Firstly, a small-scale lysimeter was installed in the greenhouse for data collection and obtaining ETC. Additionally, a small meteorological station and an evaporimeter were installed in the experimental area to gather meteorological and water evaporation data within the experimental range. The Penman–Monteith, Hargreaves–Samani, Pan Evaporation, and Artificial Neural Network models were employed in this study to calculate the ETO. The crop coefficient was determined using empirical coefficients, which were then used to calculate daily crop evapotranspiration. As described in Section 3 and Section 4, the measured data obtained from the field measurement method were compared with the calculated data from the meteorological models, evaporimeter method, and AI model. This comparison allowed for the analysis of the advantages and disadvantages of each calculation method for determining ETC in a greenhouse. Finally, based on the advantages and disadvantages of each model and the actual equipment conditions of the users, this paper provides recommendations for selecting models when measuring ETC in a greenhouse.
2. Materials and Methods
2.1. Test Overview
The experimental site is located at the National Precision Agriculture Demonstration Station in Beijing (China), with a geographical location of 40.18° N and 116.45° E and a warm temperate, in addition to a semi-humid and semi-arid monsoon climate. The annual average temperature ranges from 11 to 13 °C, and the annual precipitation ranges from 500 to 700 mm. The long-term average temperature is 11.1 °C, indicating a temperate continental monsoon climate. The experimental solar greenhouse is 60 m long and 7 m wide. The greenhouse is designed to face south. The surface was covered with a plastic film with a thickness of 0.1 mm to increase the transparency effect inside the greenhouse. The inclination angle of the surface is about 45°. The experimental crop for this study was tomato, grown using the rockwool cultivation method. A set of irrigation and fertilization systems were installed to provide a nutrient solution for the tomato cultivation experiment. The experiment started on 2 March 2023 and was concluded on 5 June 2023.
2.2. Measurement Items
2.2.1. Crop Evapotranspiration Measurement
Because rockwool was used for the cultivation of the experimental tomatoes, rockwool cultivation strips were directly placed in a lysimeter cultivation tank. When installing the lysimeter cultivation tank, a certain installation angle was set to facilitate the discharge of excess irrigation liquid by relying on the self-weight of the solution. A matching flow meter was installed below the cultivation tank of the lysimeter to measure the leaked liquid. A total of 4 tomatoes were planted in each rockwool strip, and each rockwool strip was connected with 2 dripping arrows, with a flow rate of 2 L/h. The irrigation pipeline was directly connected to a digital water meter, which could accurately regulate the irrigation amount. A bracket composed of steel wire ropes was installed above the cultivation tank of the lysimeter, and a supporting hanging scale was directly installed above the steel wire rope bracket. As the tomatoes gradually grew, the tomato vine remained directly connected to the hanging scale through a traction rope, which could measure the tomatoes’ daily weight increase in real-time through the hanging scale (Figure 1).
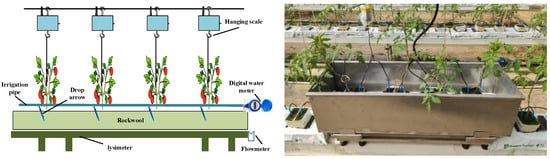
Figure 1.
Measurement structure and actual site layout of the tomatoes cultivated with rockwool.
2.2.2. Meteorological Environment Measurement
Two WS-1802 remote meteorological stations (Nongxin Technology (Beijing) Co., Ltd., Beijing, China) were installed, one inside and one outside the experimental greenhouse, and these stations are used as comprehensive remote automatic monitoring equipment, with the automatic collection, storage, and remote transmission of field meteorological information. WS-1802 can collect meteorological information, such as temperature, humidity, atmospheric pressure, net radiation, wind speed and direction, and rainfall in an experimental area. In our study, meteorological data were automatically collected every 10 min.
The evaporation pan installed in the experimental greenhouse had a diameter of 220 mm and a height of 200 mm. Sensors were used to measure the weight change of the liquid in the evaporation pan, and a 485 bus was used for signal output. Weight data were collected every 10 min, and the height of the changes in the level of the liquid could be calculated based on weight change data in order to obtain the daily evaporation amount (Figure 2).

Figure 2.
Meteorological stations inside the greenhouse and meteorological stations outside the greenhouse, as well as the evaporation pan.
2.3. Model and Evaluation Indicators
2.3.1. Penman–Monteith Model
The Penman–Monteith (PM) model utilizes an ETO calculation model proposed in Technical Report No. 56 by the Food and Agriculture Organization of the United Nations []. The PM model takes multiple meteorological factors into account, such as air temperature, humidity, wind speed, and net radiation to estimate ETO. Compared to the simplified models, the PM model is more accurate in calculating ETO and is suitable for a wider range of climate conditions and regions []. When calculating ETO, the PM model requires a large amount of meteorological data, including net radiation, soil heat flux, daily average temperature, wind speed, saturated water vapor pressure, and actual water vapor pressure. These data can be obtained through meteorological observation stations or other meteorological data. The calculation formula of the PM model is as follows:
where ETO is reference crop evapotranspiration (mm/d), Rn is net radiation (MJ/m2/d), G is soil heat flux (MJ/m2/d), T is air temperature (°C), U is wind speed (m/s), es is saturation vapor pressure (kPa), ea is actual vapor pressure (kPa), Δ is slope of the saturation vapor pressure–temperature relationship (kPa/°C), and γ is psychometric constant (kPa/°C).
2.3.2. Hargreaves–Samani Model
The Hargreaves–Samani (HS) model is a commonly used simplified model for calculating ETO, and it collects the lowest, highest, and average temperature data of the day; calculates the local net radiation through longitude and latitude; and then estimates the ETO of the day [,]. The HS model assumes a linear relationship between ETO and surface temperature, and it estimates ETO based on the daily average temperature. The calculation formula is as follows:
where ETO is reference crop evapotranspiration (mm/d), Ra is daily radiation, T is daily average air temperature (°C), Tmax is daily maximum air temperature (°C), and Tmin is daily minimum air temperature (°C).
2.3.3. Pan Evaporation Model
The Pan Evaporation method is a simplified method for estimating ETO, suitable for use in areas lacking meteorological observation data. When using the Pan Evaporation method, it is important to first select a suitable evaporation pan, typically a shallow flat-bottomed container, and ensure that it can hold an adequate amount of water. The evaporation pan should be placed in the vicinity of the vegetation in the experimental area, such as next to a lawn, soil, or potted plants. Obstruction and interference must be avoided so that the pan evaporation can remain consistently exposed to the natural environment. At the same time, water level reduction in the evaporation pan must be observed daily at regular intervals and the measurement data obtained should be recorded. The formula for calculating ETO using the Pan Evaporation method is as follows:
where ETO represents reference crop evapotranspiration (mm/d); kp represents the pan coefficient, with kp at 0.85 []. E represents the amount of water surface reduction in the evaporation pan (mm).
2.3.4. Neural Network Model
The BP neural network is a common Artificial Neural Network model, and its typical architecture mainly consists of an input layer, hidden layer, and output layer. The input layer is mainly responsible for receiving external input signals and transmitting them to the hidden layer of the network. The hidden layer is mainly composed of multiple neurons, which perform nonlinear transformation and feature extraction on the input signal. There can be one or more hidden layers, and the number of neurons in each hidden layer can vary. The output layer mainly receives information from the hidden layer and generates the final output result. Each layer of neurons is connected to neighboring neurons through weights and bias coefficients, while neurons in the same layer are independent of each other. The neurons in the hidden layer and output layer usually use activation functions to perform nonlinear transformations on the input. The model calculates the error between the predicted output and the actual output, and it propagates the error back from the output layer to the hidden layer to update the weights and biases so that the network’s output approximates the actual output.
The following Figure 3 shows the basic architecture of the BP neural network. It can adjust and expand the network based on specific problems to improve its performance and generalization ability. This article took the temperature, humidity, net radiation, and wind speed in the greenhouse as input data and the ETO as output data. In the case of using a lysimeter to obtain crop evapotranspiration data, 80% of the data was used for training the model, while the remaining 20% was used for model validation.
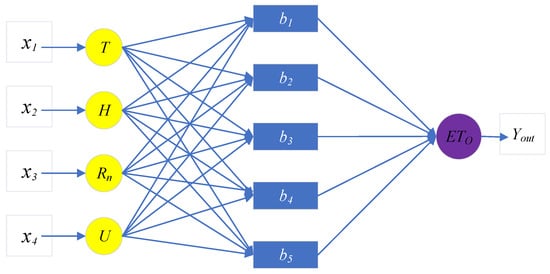
Figure 3.
Schematic diagram of the BP neural network structure.
2.3.5. ETC Calculation Model
According to the recommendations of the Food and Agriculture Organization (FAO) of the United Nations, the calculation formula for crop evapotranspiration under full irrigation conditions is as follows:
where ETC represents the current crop water requirement; KC is the crop coefficient, which reflects the ratio of the crop’s water requirement to the reference crop’s water requirement based on standard evapotranspiration (ETO); and ETO represents the reference evapotranspiration (mm/d).
The recommended crop coefficients (KC) for different growth stages of tomatoes by the Food and Agriculture Organization (FAO) are as follows: seedling stage KC was 0.6; anthesis stage KC was 1.15; mature stage KC was 0.8.
These crop coefficients represent the proportion of the water requirement of tomatoes at different growth stages relative to the reference crop’s water requirement based on standard evapotranspiration (ETO). By multiplying these crop coefficients with region-specific reference evapotranspiration data (ETO), the current crop water requirement (ETC) for tomatoes can be calculated at each growth stage.
2.3.6. Evaluation Indicators
According to the information provided in the paper, a sample statistical analysis can be conducted on the ETC sample data obtained using the PM, HS, PAN, and ANN models. This analysis can utilize statistical indicators such as Mean Absolute Error (MAE), Mean Bias Error (MBE), Root Mean Square Error (RMSE), and Index of Agreement (d). By calculating these statistical indicators, we can assess the differences and consistency between the ETC sample data obtained from different models. These statistical indicators provide an evaluation of model performance and accuracy, helping to optimize and improve the predictive capabilities of the models. The formula for calculating the sample statistical indicators is as follows:
where Pi and Qi represent the simulated values (mm/day) and measured values (mm/day) of each model method, respectively; O represents the average of the measured values (mm/day); n represents the number of samples.
3. Results
3.1. Analysis of the Test Environment
It is possible to see from the daily average temperature variation curve shown in Figure 4 that, during the experimental period, the daily average temperature of the tomatoes did not change much during the seedling stage, anthesis stage, and mature stage. The average temperature during the seedling stage, anthesis stage, and mature stage was 21.74 °C, 20.56 °C, and 23.16 °C, respectively. From the daily average humidity change curve, it is possible to see that the humidity changes during the experimental period were relatively gentle, with a humidity of 65.35% during the seedling stage, 73.16% during the flowering and fruiting stage, and 73.18% during the mature stage. From the net radiation changes, it is possible to see that the daily average net radiation changes were not significant during the seedling stage and anthesis stage, which were 9.04 MJ/m2/d and 9.16 MJ/m2/d, respectively. During the mature stage, the daily average net radiation was 10.04 MJ/m2/d. Due to the fact that this experiment was conducted in a solar greenhouse, indoor wind speed can be ignored.
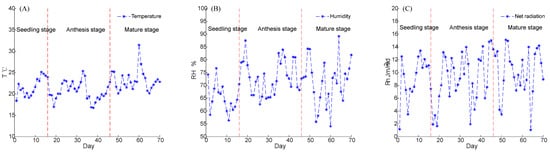
Figure 4.
The daily variation chart of the greenhouse climate in the experimental area: (A) describes the temperature change curve inside the greenhouse during the experiment; (B) describes the humidity change curve inside the greenhouse during the experiment; (C) describes the change curve of net radiation inside the greenhouse during the experiment.
3.2. Analysis of Evapotranspiration Variation
Figure 5 shows a comparison of the daily ETC values obtained through actual measurements using the lysimeter, as well as those predicted by the PM model, HS model, PAN model, and ANN model, with the field data. The cumulative ETC values of the tomatoes measured using the lysimeter system was 17.84 mm during the seedling stage, 73.74 mm during the anthesis stage, and 85.09 mm during the mature stage. The total ETC value of tomatoes measured using the lysimeter system was 176.67 mm. The total ETC value of tomatoes calculated using the PM model was 13.33 mm during the seedling stage, 60.2 mm during the anthesis stage, and 72.54 mm during the mature stage. The total ETC of tomatoes measured using the PM model was 146.07 mm, and the difference between the total ETC calculated and the measured value using the lysimeter system was about −17.32%. The cumulative ETC values of the tomatoes calculated using the HS model were 16.73 mm during the seedling stage, 73.24 mm during the anthesis stage, and 99.48 mm during the mature stage. The total ETC value of the tomatoes calculated using the HS model was 189.45 mm, with a difference of approximately 7.23% between the total ETC calculated and the measured value using the lysimeter system. The cumulative ETC values of the tomatoes calculated using the PAN model were 21.61 mm during the seedling stage, 76.91 mm during the anthesis stage, and 98.51 mm during the mature stage. The total ETC value of the tomatoes calculated using the PAN model was 197.03 mm, and the difference between the total ETC calculated and the measured value using the lysimeter system was about 11.52%. The cumulative ETC values of the tomatoes calculated using the ANN model were 17.72 mm during the seedling stage, 72.93 mm during the anthesis stage, and 84.05 mm during the mature stage. The total ETC value of the tomatoes calculated using the ANN model was 174.7 mm, and the difference between the total ETC calculated and the measured value using the lysimeter system was about −1.12%. The cumulative ETC value of outdoor fields during the seedling stage was 19.87 mm; during the anthesis stage, it was 104.51 mm; during the mature stage, it was 117.42 mm; and the total ETC value of the tomatoes in open fields was 241.8 mm. The difference between the total ETC calculated value and the measured value using the lysimeter system was about 36.87%.
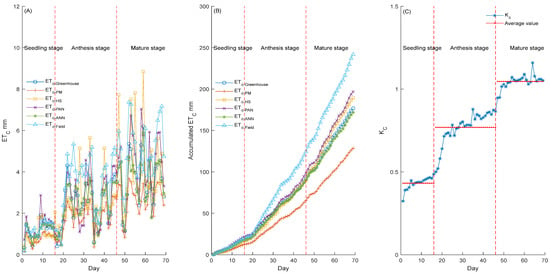
Figure 5.
Comparison of ETC calculated with different models in the greenhouse and in the fields, with measured values. (A) Describes the comparison of daily ETC calculated using different models. (B) Describes the comparison of cumulative ETC calculated using different models. (C) Describes changes in KC during the experiment.
During the seedling stage, the KC gradually increased from 0.32 to 0.49, with an average KC of 0.43. During the anthesis stage, the Kc increased from 0.49 to 0.87, with an average KC of 0.77. During the mature stage, the KC gradually stabilized, increasing from 0.87 to 1.05, with an average KC of 1.05. Throughout the entire experimental period, the KC gradually increased during the seedling and anthesis stages; when the tomatoes reached maturity, it tended to stabilize.
From the analysis above, it is possible to see that, during the seedling stage, the overall ETC values in the greenhouse and outside the greenhouse are not significantly different. From the anthesis stages to the mature stage, the ETC values in the open field gradually surpassed those in the greenhouse. The maximum difference between the total ETC calculated using the PM model in the greenhouse and the values calculated using the lysimeter system was −30.6 mm, with an error of −17.32% of the total amount. The difference between the total ETC calculated using the ANN model and the values calculated using the lysimeter system was the smallest, with a difference of −1.97 mm and an error of −1.12% of the total. The difference between the calculated values of the HS model and PAN model and the calculated values of the lysimeter system was relatively small—12.78 mm and 20.36 mm, respectively—with errors reaching 7.23% and 11.52% of the total amount.
3.3. Irrigation Effect Analysis
This paper first compares and analyzes the cumulative ETC calculated using four models—namely, the PM model, HS model, PAN model, and ANN model—using a lysimeter system. Based on preliminary findings, it was noted that the ANN model had the smallest error in calculating the ETC, while the PM model had the highest error in calculating the ETC. In Figure 6, a scatter plot was created by using actual ETC data as the x-axis and the ETC values calculated using the PM model, HS model, PAN model, and ANN model as the y-axis. Regression analysis was then conducted to analyze the relationship between the model-calculated values and the actual ETC values.
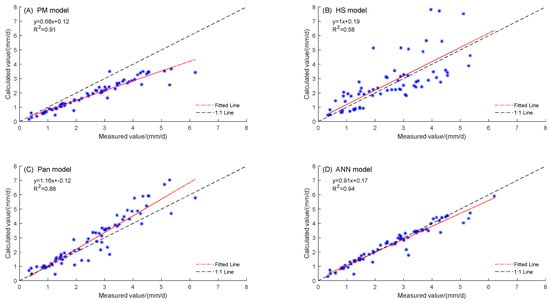
Figure 6.
Comparison chart of the correlation between four ETC calculation models and measured values. (A) Describes the comparison between the calculated values obtained using the PM model and the actual values; (B) describes the comparison between the calculated values obtained using the HS model and the actual values; (C) describes the comparison between the calculated values obtained using the PAN model and the actual values; (D) describes the comparison between the calculated values obtained using the ANN model and the actual values.
The correlation coefficient of the PM model data was 0.91, indicating good consistency (Figure 6A). While the cumulative ETC values calculated using the PM model were lower than the actual cumulative ETC values, this deviation could be calibrated using coefficients based on the data model, which provided better simulation results.
(Figure 6B) is a comparison chart of the correlation between the HS model and the actual values. From the chart, it is possible to observe the fact that the correlation coefficient of the HS model data was 0.58, indicating poor consistency among the data. It is evident from the chart that the calculated cumulative ETC data using the HS model exhibited significant fluctuations compared to the actual cumulative ETC values. Although the cumulative ETC values calculated using the HS model were slightly close to the actual values, correlation analysis indicated that the HS model had high variability and relatively low accuracy when used in greenhouse environments. In summary, the HS model showed a relatively low correlation with the actual values, and the calculated cumulative ETC values exhibited significant fluctuations compared to the real values in greenhouse settings. Although the HS model provided relatively small differences from the actual cumulative ETC values, its relatively low precision was not suitable for practical usage.
(Figure 6C) shows a correlation comparison chart between the PAN model and the actual values. From the chart, it is possible to observe the fact that the correlation coefficient of the PAN model data was 0.88, indicating good consistency between the calculated results and the actual observed values. Furthermore, from the chart, it is evident that the cumulative ETC data calculated using the PAN model tended to be slightly higher than the actual cumulative ETC values. Overall, the data consistency between the PAN model and the actual values was relatively good, with only small differences in the total cumulative ETC values. In summary, the PAN model exhibited a high correlation with the actual values, and the calculated cumulative ETC values were generally consistent with the real values in greenhouse environments. Therefore, the PAN model can be considered as having good accuracy and reliability in predicting evapotranspiration in greenhouse settings.
The correlation coefficient of the ANN model data was 0.94, indicating a very high linear correlation between the calculated results and the actual observed values (Figure 6D). Its data consistency was the best among the models compared.
The statistical analysis in this study examined the correlation between the ETC values calculated using the PM model, HS model, PAN model, ANN model, and the ETC values measured using several statistical indicators. These indicators include the coefficient of determination (R2), mean absolute error (MAE), mean bias error (MBE), root mean square error (RMSE), and index of agreement (d). The statistical results are shown in Table 1 below.

Table 1.
Statistical results of ETC calculations and data measured using different models.
From the perspective of the coefficient of determination (R2), the obtained R2 for the HS model was 0.58, while the R2 values calculated for the PM, PAN, and ANN models were 0.91, 0.88, and 0.94, respectively. It is possible to observe that the ETC data obtained from the HS model calculation were more scattered, indicating the lower reliability of its regression model. From the MAE analysis, it is possible to see that the ANN model obtained the highest accuracy for ETC, with an MAE of 0.3 mm/d. The PM and PAN models had slightly lower accuracy for ETC, with MAE values of 0.6 mm/d and 0.54 mm/d, respectively. The HS model had the lowest accuracy for ETC, with an MAE value of 0.88 mm/d. As for the MBE, it is possible to observe the fact that the ANN model had the highest accuracy for ETC, with a computed MBE of −0.15 mm/d. The HS model had a uniform distribution around the 1:1 line, resulting in an MBE of 0.19 mm/d. The PAN model had a better MBE than the PM model, with values of 0.3 mm/d and −0.57 mm/d, respectively. From the perspective of RMSE, the ANN model had the smallest calculated RMSE value for ETC, which was 0.42 mm/d. The HS model, with a uniform distribution around the 1:1 line, had an RMSE of 1.19 mm/d. The PAN model had a better RMSE than the PM model, with values of 0.7 mm/d and 0.8 mm/d, respectively.
From the perspective of the consistency index (d), it is possible to observe the fact that the ANN model had the highest consistency between the calculated ETC values and the measured ETC values, with a consistency index (d) of 0.95. The HS model had the lowest consistency between the calculated ETC values and the measured ETC values, with a consistency index (d) of 0.73. The PAN model had better consistency than the PM model, with consistency index (d) values of 0.9 and 0.81, respectively, for the two models.
Based on the analysis above, it is possible to conclude that the higher the values of the coefficient of determination (R2) and the consistency index (d), the higher the correlation between the model’s calculated values and the actual values. On the other hand, the smaller the values of the mean absolute error (MAE), mean bias error (MBE), and root mean square error (RMSE), the smaller the difference between the model’s calculated values and the actual values. The accuracy of calculating ETC is as follows: ANN model > PAN model > PM model > HS model (Figure 7).
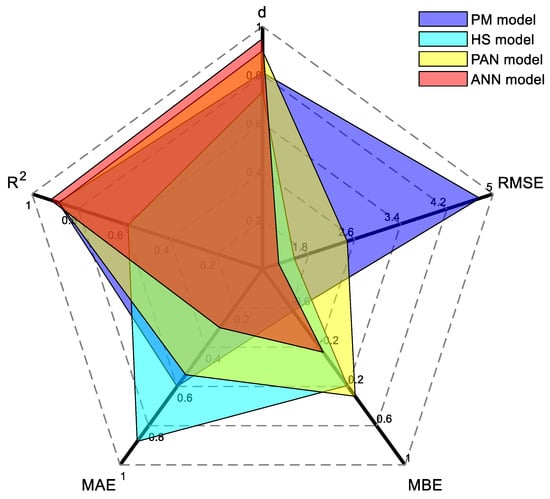
Figure 7.
Distribution of statistical indicators for ETC calculations and data measured using different models.
In this article, rockwool was used for tomato cultivation in a solar greenhouse. The cultivation bracket was 6 m long, and a set of brackets was installed every 2 m. Each row of brackets was equipped with six rockwool strips, and four beads of tomatoes were planted on each rockwool strip. Each of the four sets of cultivation brackets formed an experimental group, and their irrigation strategy was tested according to the ETC calculated with the corresponding model. The daily irrigation volume of each group during the experiment is shown in Figure 8. During the experiment, the PM model, HS model, PAN model, and ANN model were used to irrigate 7.01 m3, 9.09 m3, 9.46 m3, and 8.39 m3, respectively. At the same time, 258.62 kg, 298.62 kg, 331.68 kg, and 339.38 kg of tomatoes were produced in each experimental area. The water use efficiency of the PM model, HS model, PAN model, and ANN model during the experiment was 36.89 kg/m3, 32.85 kg/m3, 35.06 kg/m3, and 40.45 kg/m3, respectively. The statistical results of the experiment are shown in Table 2.
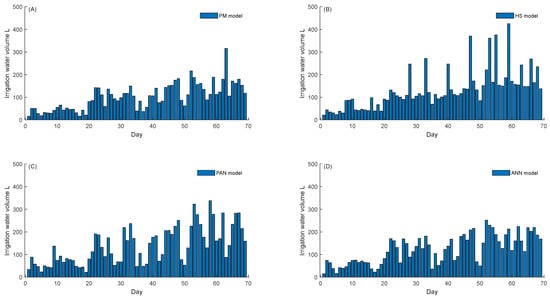
Figure 8.
Daily irrigation volume of ETC calculated based on different models. (A) Describes the daily irrigation amount based on the PM model; (B) Describes the daily irrigation amount based on the HS model; (C) Describes the daily irrigation amount based on the PAN model; (D) Describes the daily irrigation amount based on the ANN model.

Table 2.
Statistical results of crop yield and water consumption based on different models.
Through the analysis of the irrigation experiment results above, it is possible to see that the PM model had the lowest tomato yield among the various experimental groups, with a total irrigation volume of 7.01 m3, which was less than the water required for the crops. The yield was only 258.62 kg. The use of the HS model resulted in significant fluctuations in daily irrigation volume due to its low accuracy in calculating ETC, resulting in the lowest water use efficiency of 32.85 kg/m3 among the experimental groups. The maximum irrigation amount using the PAN model in each experimental group was 9.46 m3, which was 12.75% higher than the ANN model. However, the crop yield and water use efficiency were lower than the ANN model. By using the ANN model, the irrigation amount was closest to the actual water demand of the crops, and its yield and water use efficiency were the highest among the various experimental groups. In summary, the irrigation experiment results of each model are as follows: ANN model > PAN model > PM model > HS model.
4. Discussion
The PM model, based on the energy balance and water vapor diffusion theory, is currently widely applied in fields around the world. ETC was calculated assuming no wind speed because this experiment was carried out in a greenhouse, only using temperature, humidity, and net radiation in a comprehensive manner, resulting in a significant difference between the calculated ETC and the measured values. By conducting statistical analysis on the sample data of the PM model, the MAE and MBE were 0.6 mm/d and −0.57 mm/d, respectively. The RMSE of 0.8 mm/d indicates a significant fluctuation in the data. The d value of 0.81 suggests poor consistency with the measured ETC values. This indicates that the ETC values calculated using the PM model are underestimated in comparison to the actual values.
The HS model is the most simplified mathematical model currently used in calculating ETC values and only requires temperature values. Previous research has shown that it performs well in calculating ETC values in arid and semi-arid regions []. This paper applied the HS model to calculate ETC in a greenhouse. In our experiment, the statistical results showed that the data had a relatively scattered distribution, and the reliability of the regression model was low (R2 = 0.58). The MAE was 0.88 mm/d, and the MBE was 0.19 mm/d, suggesting that the HS model overestimated the ETC values compared to the actual measurements. It had the highest RMSE value among the four calculation models used, indicating a large dispersion in the HS model’s results and poor predictive correlation overall. The consistency index (d) was 0.73, indicating poor consistency with the actual measured ETC values. The HS model is better applied in arid areas based on temperature and empirical coefficients, and the ETC calculated using the HS Method are higher in humid environments such as greenhouses.
The PAN model is primarily used in greenhouses, where it utilizes evaporation pans to calculate ETC values based on the water evaporation recorded. In theory, the larger the size of the evaporation pan, the more accurate the calculated values are. In reality, the limited size of the evaporation pan definitely results in an overestimation of ETC. Although the cumulative ETC values calculated were higher than the actual measurements and the RMSE was 0.7 mm/d, indicating some level of data fluctuation, the statistical analysis of the sample data demonstrated good consistency in the sample data (Table 1). The PAN model demonstrated high data consistency in terms of data correlation, which could improve the accuracy of ETC estimation. The RMSE was 0.7 mm/d, indicating some level of data fluctuation. The d value of 0.9 implies high consistency with the actual measured ETC values.
The ANN model primarily gathers environmental variables such as temperature, humidity, and net radiation inside a greenhouse. It utilizes the measured ETC data as training data for the model. By inputting environmental variables like temperature, humidity, and net radiation from different locations within the greenhouse into the ANN model, ETC values can be directly calculated. The results also indicated that the R2 value was 0.92, demonstrating a high level of consistency in the regression of the calculated results. Also, the calculated data were more accurate compared to other models, with small data fluctuation. The d value of 0.95 indicates the highest level of consistency with the actual measured values.
5. Conclusions
In this paper, the ETC of greenhouse crops was measured using lysimeter as a reference. Then, based on greenhouse meteorological conditions, four models (the PM model, HS model, PAN model, and ANN model) were used to calculate the ETC. Finally, by comprehensively evaluating statistical indicators such as R2, MAE, MBE, RMSE, and d, the accuracy of the ETC models for greenhouse crop calculations was discovered to be as follows: ANN model > PAN model > PM model > HS model. Although the HS model outperformed the PM model in terms of calculating the ETC, it had significantly lower accuracy in calculating daily ETC. Therefore, from a production standpoint, the HS model is not suitable for effectively guiding greenhouse irrigation practices. Additionally, based on statistical data from the PM and PAN models, it is possible to observe that, when applying these models directly to different locations, it is necessary to calibrate the coefficients of the PM and PAN models using standard data. This calibration process can further enhance the accuracy of the model calculations and predictions.
If a user’s production facilities have a high level of automation, this article recommends using an ANN model to calculate ETC in a greenhouse. If the user is in a remote rural area with a low automation level in greenhouse production equipment, this article recommends using the PAN model to calculate ETC. The main advantage of using the PAN model for measurement is that it requires fewer instruments and is relatively convenient to install and maintain compared to other measurement methods.
Based on the research mentioned in this article, irrigation management based on ETC is beneficial for maintaining crop growth while effectively avoiding environmental pollution caused by excessive water and fertilizer usage. This current study only compares the differences in ETC calculation among four models in a greenhouse. In the future, we will further investigate the impact of different irrigation models on crop quality and yield in greenhouses, in order to provide more effective irrigation management advice to users.
Author Contributions
Conceptualization, X.X.; methodology, X.Z.; software, W.S.; validation, W.S.; formal analysis, W.Z.; investigation, L.C.; resources, X.Z.; data curation, W.S.; writing—original draft preparation, W.S.; writing—review and editing, W.S.; visualization, F.F.; supervision, X.X.; project administration, L.C.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research and development of intelligent irrigation regulation equipment with deep integration of water and fertilizer information diagnosis, decision-making, and control (2022YFD1900404-02), Innovation Ability Construction Project of the Beijing Academy of Agriculture and Forestry Sciences (KJCX20210402), Natural Science foundation of Henan Province (232300420105) and Construction Project of Beijing Engineering Laboratory of Agricultural Internet of Things Technology (PT2023-29).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ge, J.; Zhao, L.; Yu, Z.; Liu, H.; Zhang, L.; Gong, X.; Sun, H. Prediction of Greenhouse Tomato Crop Evapotranspiration Using XGBoost Machine Learning Model. Plants 2022, 11, 1923. [Google Scholar] [CrossRef]
- Xu, G.; Xue, X.; Wang, P.; Yang, Z.; Yuan, W.; Liu, X.; Lou, C. A lysimeter study for the effects of different canopy sizes on evapotranspiration and crop coefficient of summer maize. Agric. Water Manag. 2018, 208, 1–6. [Google Scholar] [CrossRef]
- Incrocci, L.; Thompson, R.B.; Fernandez-Fernandez, M.D.; De Pascale, S.; Pardossi, A.; Stanghellini, C.; Rouphael, Y.; Gallardo, M. Irrigation management of European greenhouse vegetable crops. Agric. Water Manag. 2020, 242, 106393. [Google Scholar] [CrossRef]
- Evett, S.R.; Marek, G.W.; Colaizzi, P.D.; Ruthardt, B.B.; Copeland, K.S. A Subsurface Drip Irrigation System for Weighing Lysimetry. Appl. Eng. Agric. 2018, 34, 213–221. [Google Scholar] [CrossRef]
- Helmer, T.; Ehret, D.L.; Bittman, S. CropAssist, an automated system for direct measurement of greenhouse tomato growth and water use. Comput. Electron. Agric. 2005, 48, 198–215. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Local Calibration of the Hargreaves and Priestley-Taylor Equations for Estimating Reference Evapotranspiration in Arid and Cold Climates of Iran Based on the Penman-Monteith Model. J. Hydrol. Eng. 2011, 16, 837–845. [Google Scholar] [CrossRef]
- Singh, P.; Patel, S.K.; Jayswal, P.S.; Chinchorkar, S. Usefulness of class A Pan coefficient models for computation of reference evapotranspiration for a semi-arid region. Mausam 2014, 65, 521–528. [Google Scholar] [CrossRef]
- Liu, H.-J.; Kang, Y. Sprinkler irrigation scheduling of winter wheat in the North China Plain using a 20 cm standard pan. Irrig. Sci. 2006, 25, 149–159. [Google Scholar] [CrossRef]
- Snyder, R.L.; Orang, M.; Matyac, S.; Grismer, M.E. Simplified estimation of reference evapotranspiration from pan evaporation data in California. J. Irrig. Drain. Eng. 2005, 131, 249–253. [Google Scholar] [CrossRef]
- Gundekar, H.G.; Khodke, U.M.; Sarkar, S.; Rai, R.K. Evaluation of pan coefficient for reference crop evapotranspiration for semi-arid region. Irrig. Sci. 2008, 26, 169–175. [Google Scholar] [CrossRef]
- Sabziparvar, A.A.; Tabari, H.; Aeini, A.; Ghafouri, M. Evaluation of Class A Pan Coefficient Models for Estimation of Reference Crop Evapotranspiration in Cold Semi-Arid and Warm Arid Climates. Water Resour. Manag. 2010, 24, 909–920. [Google Scholar] [CrossRef]
- Wang, H.; Sánchez-Molina, J.A.; Li, M.; Berenguel, M.; Yang, X.T.; Bienvenido, J.F. Leaf area index estimation for a greenhouse transpiration model using external climate conditions based on genetics algorithms, back-propagation neural networks and nonlinear autoregressive exogenous models. Agric. Water Manag. 2017, 183, 107–115. [Google Scholar] [CrossRef]
- Heydari, M.M.; Heydari, M. Evaluation of pan coefficient equations for estimating reference crop evapotranspiration in the arid region. Arch. Agron. Soil Sci. 2013, 60, 715–731. [Google Scholar] [CrossRef]
- Rahimikhoob, A.; Behbahani, M.R.; Fakheri, J. An Evaluation of Four Reference Evapotranspiration Models in a Subtropical Climate. Water Resour. Manag. 2012, 26, 2867–2881. [Google Scholar] [CrossRef]
- Tabari, H. Evaluation of Reference Crop Evapotranspiration Equations in Various Climates. Water Resour. Manag. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
- Trajkovic, S.; Kolakovic, S. Evaluation of Reference Evapotranspiration Equations under Humid Conditions. Water Resour. Manag. 2009, 23, 3057–3067. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Gong, X.; Wang, S.; Xu, C.; Zhang, H.; Ge, J. Evaluation of Several Reference Evapotranspiration Models and Determination of Crop Water Requirement for Tomato in a Solar Greenhouse. Hortscience 2020, 55, 244–250. [Google Scholar] [CrossRef]
- Li, L.; Chen, S.; Yang, C.; Meng, F.; Sigrimis, N. Prediction of plant transpiration from environmental parameters and relative leaf area index using the random forest regression algorithm. J. Clean. Prod. 2020, 261, 121136. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; Paper No. 56; Food and Agricultural Organization of the United Nations (FAO) Irrigation and Drain: Rome, Italy, 1998. [Google Scholar]
- Subedi, A.; Chávez, J.L.; Andales, A.A. ASCE-EWRI standardized Penman-Monteith evapotranspiration (ET) equation performance in southeastern Colorado. Agric. Water Manag. 2017, 179, 74–80. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Niranjan, S.; Nandagiri, L. Effect of local calibration on the performance of the Hargreaves reference crop evapotranspiration equation. J. Water Clim. Chang. 2021, 12, 2654–2673. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).