Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia
Abstract
1. Introduction
2. Materials and Methods
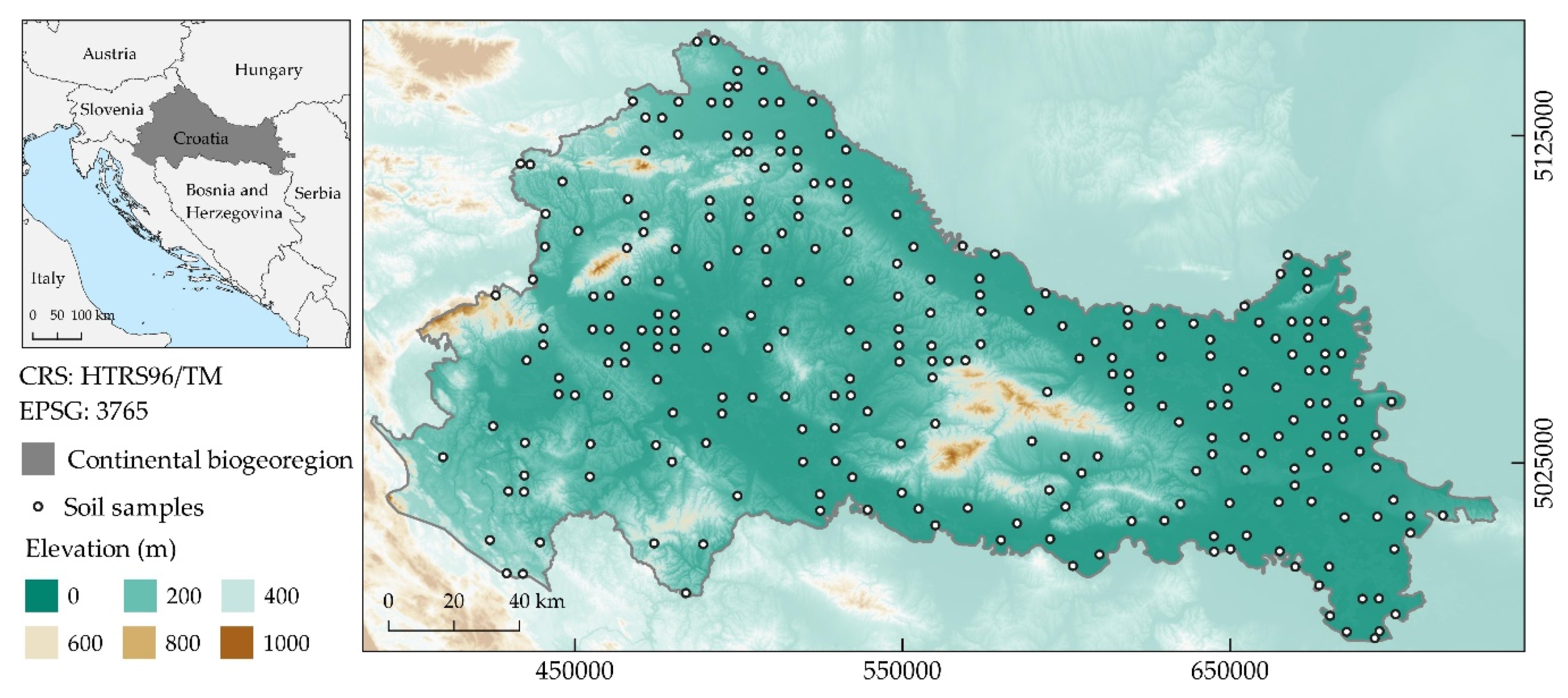
2.1. Study Area
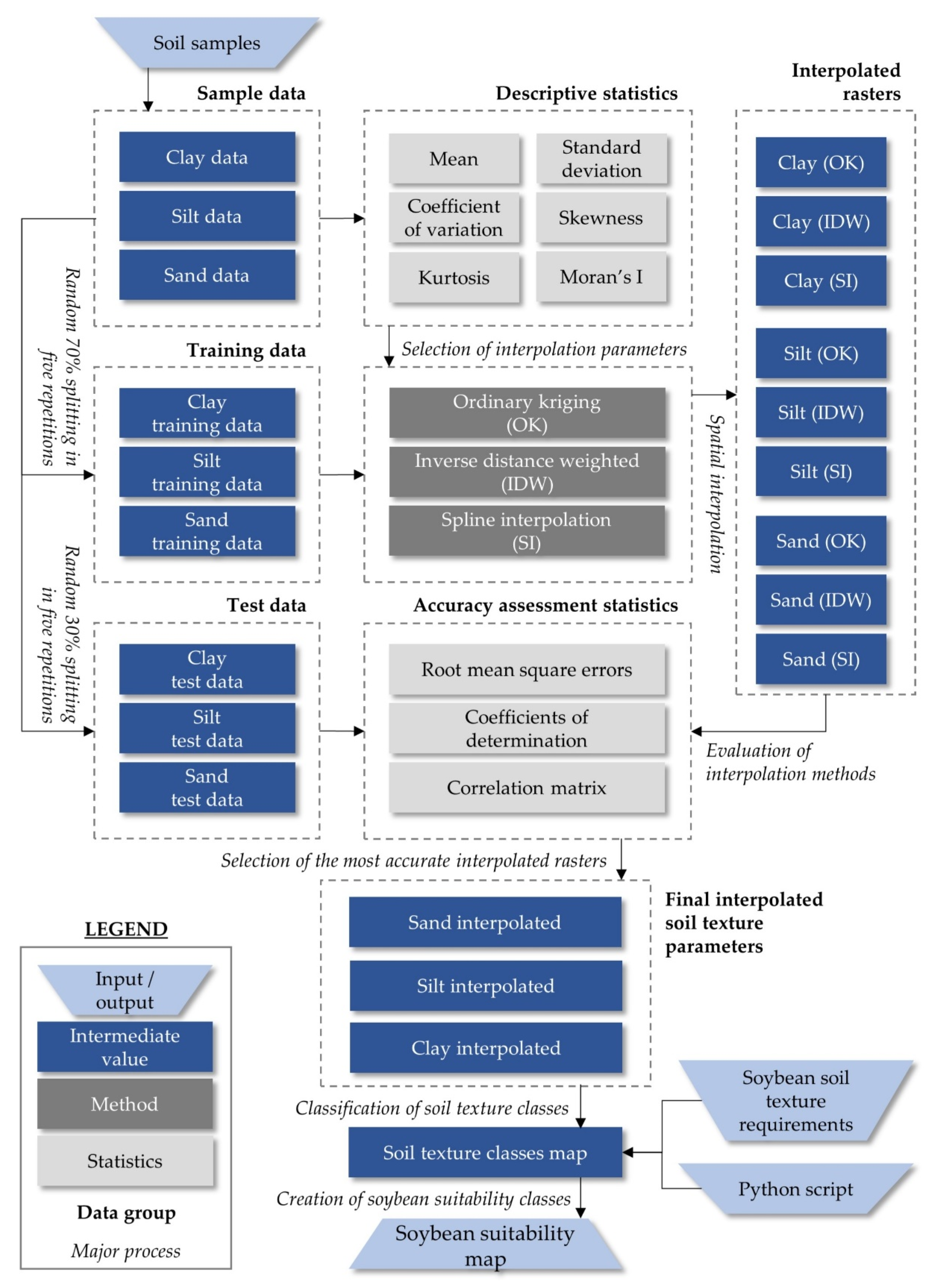
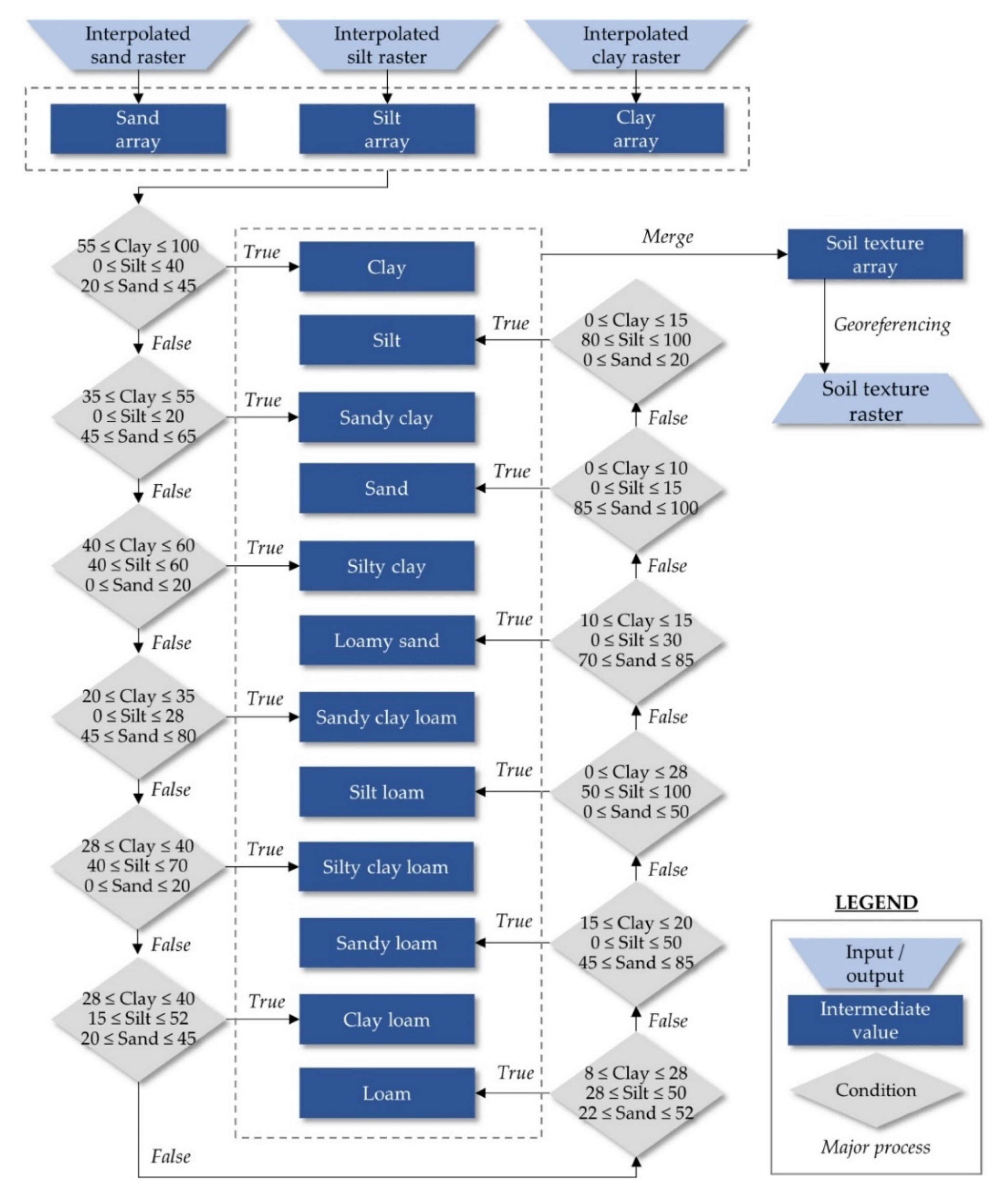
2.2. Automated Classification for Delineation of Soil Texture Suitability Zones for Soybean Cultivation in a GIS Environment
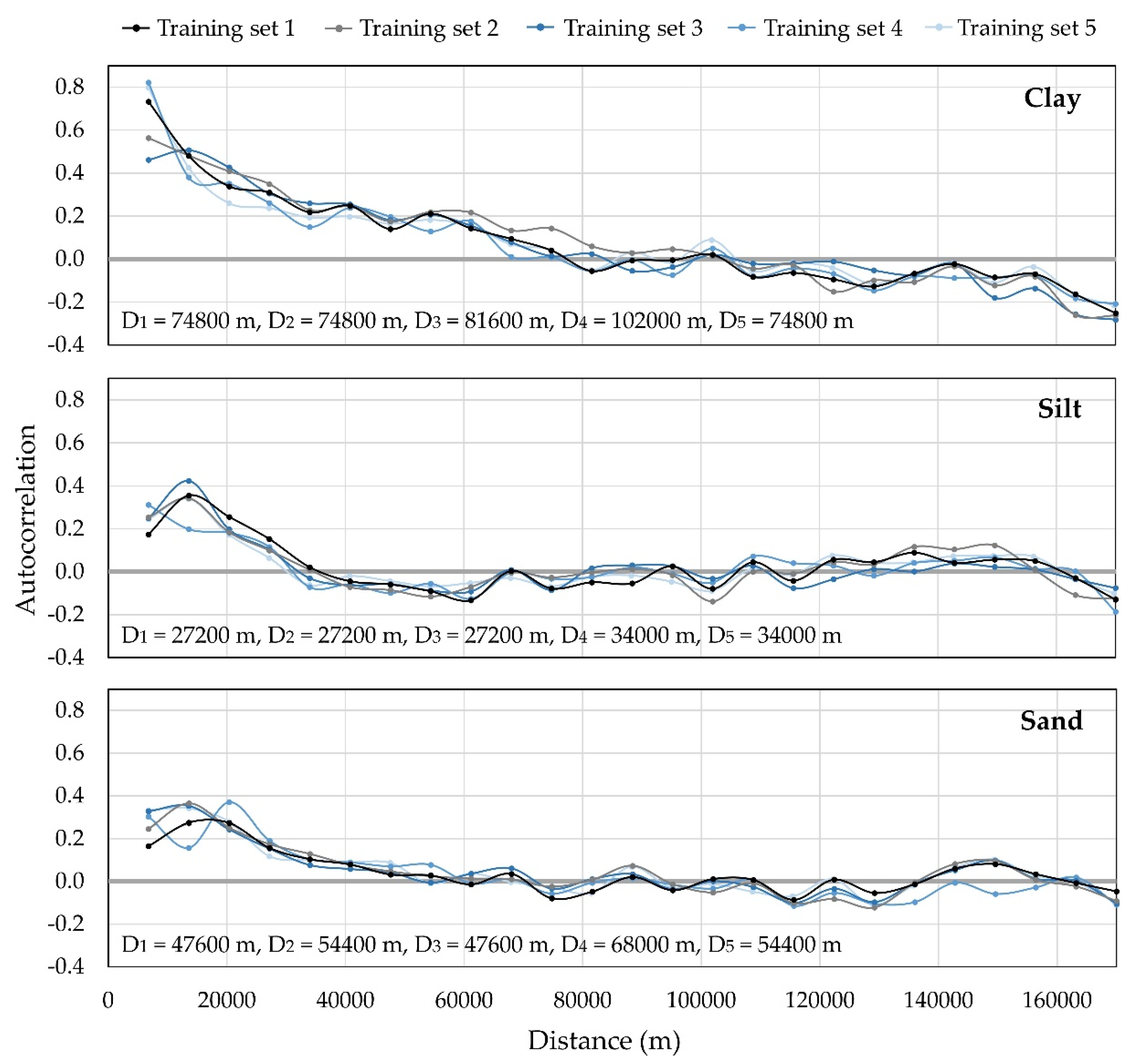
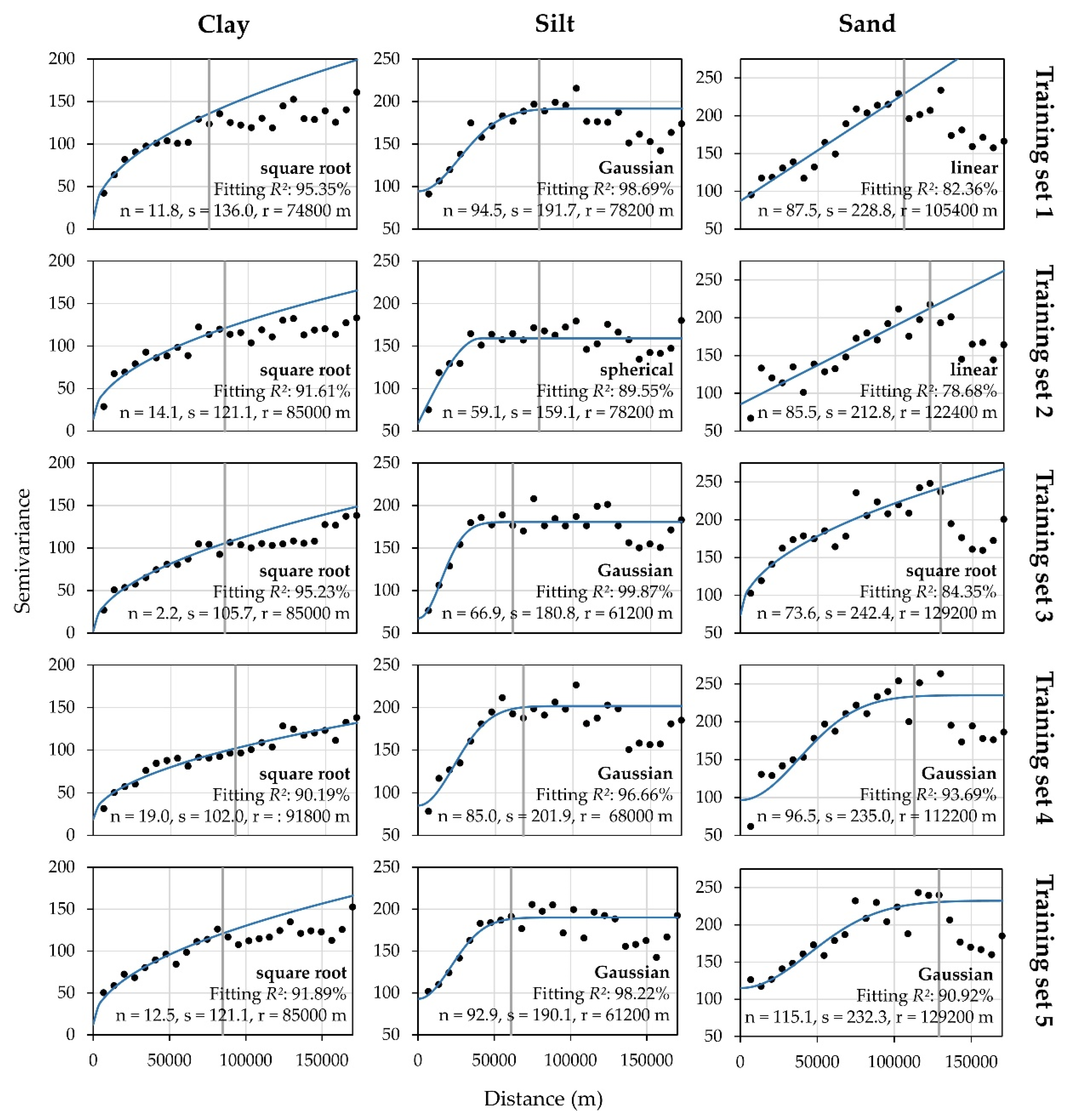
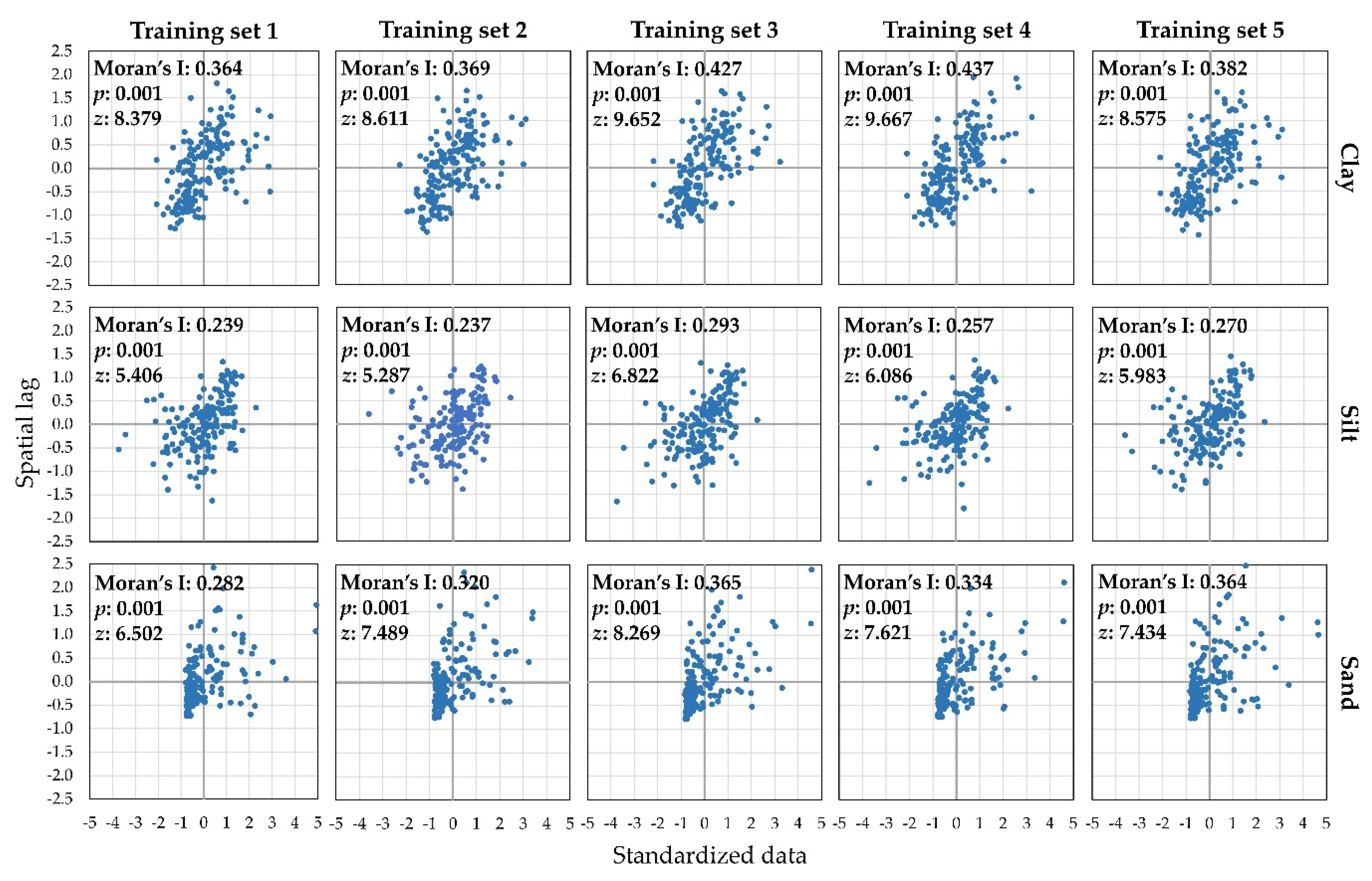
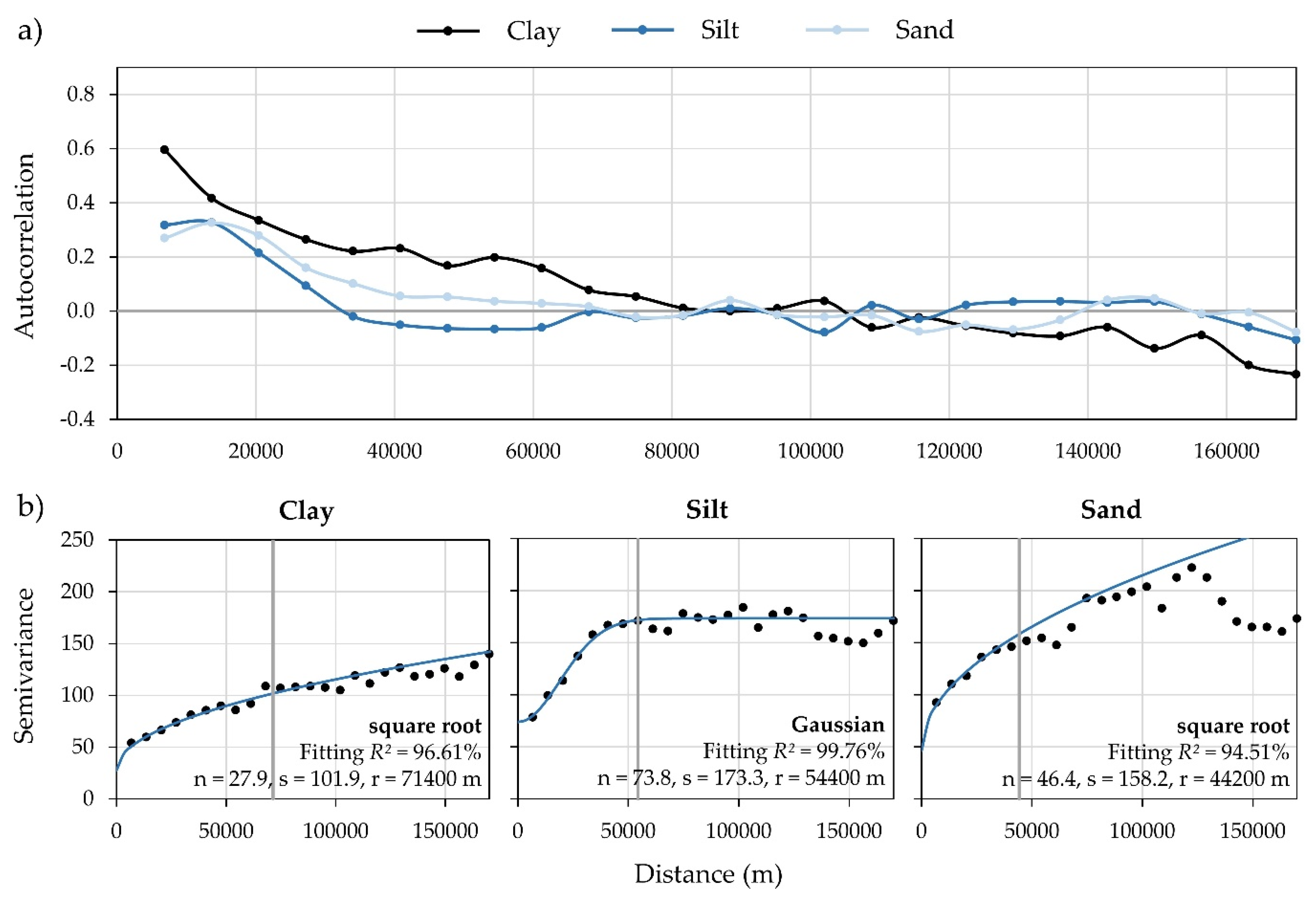
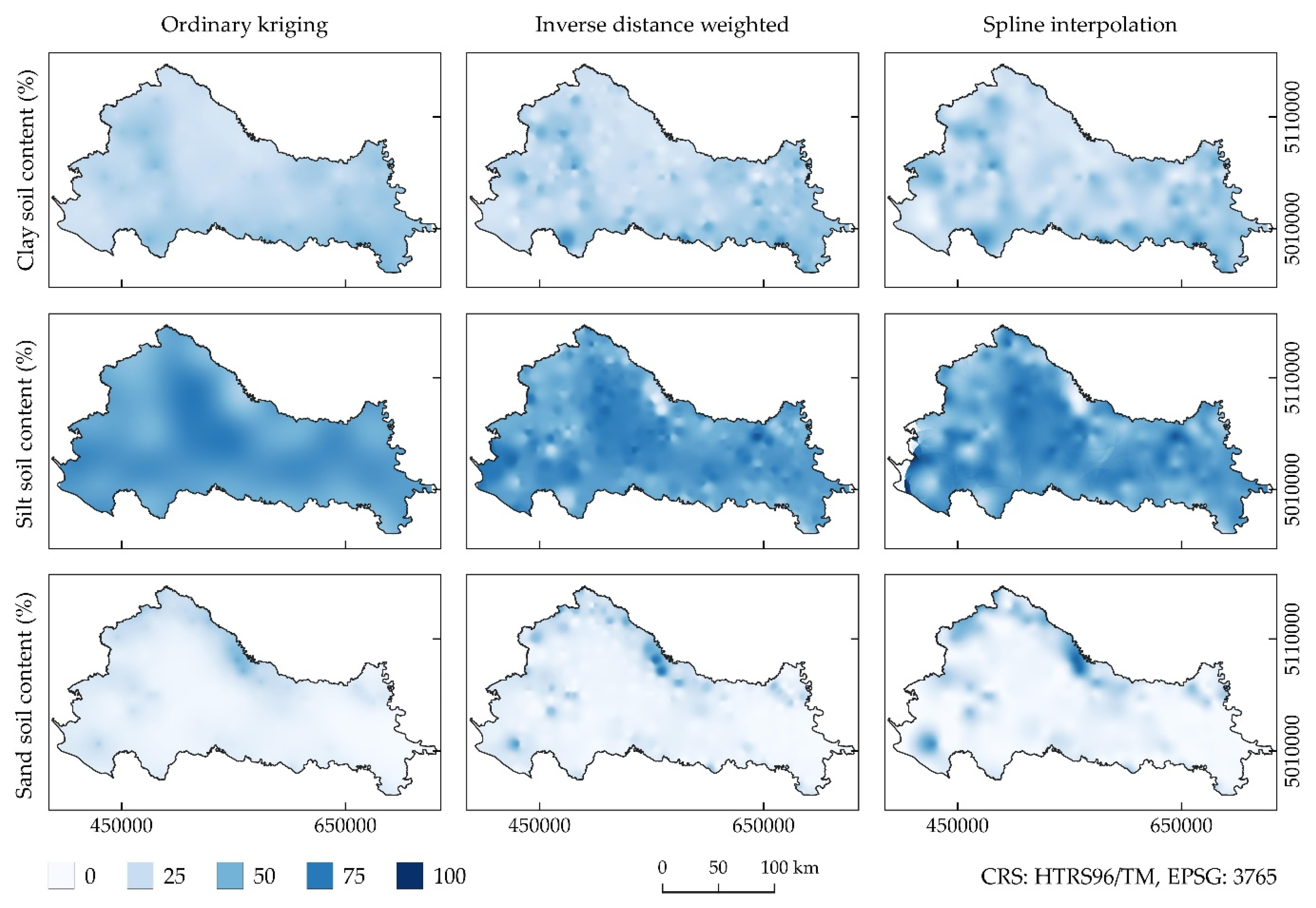
2.3. Accuracy Assessment of Interpolated Rasters
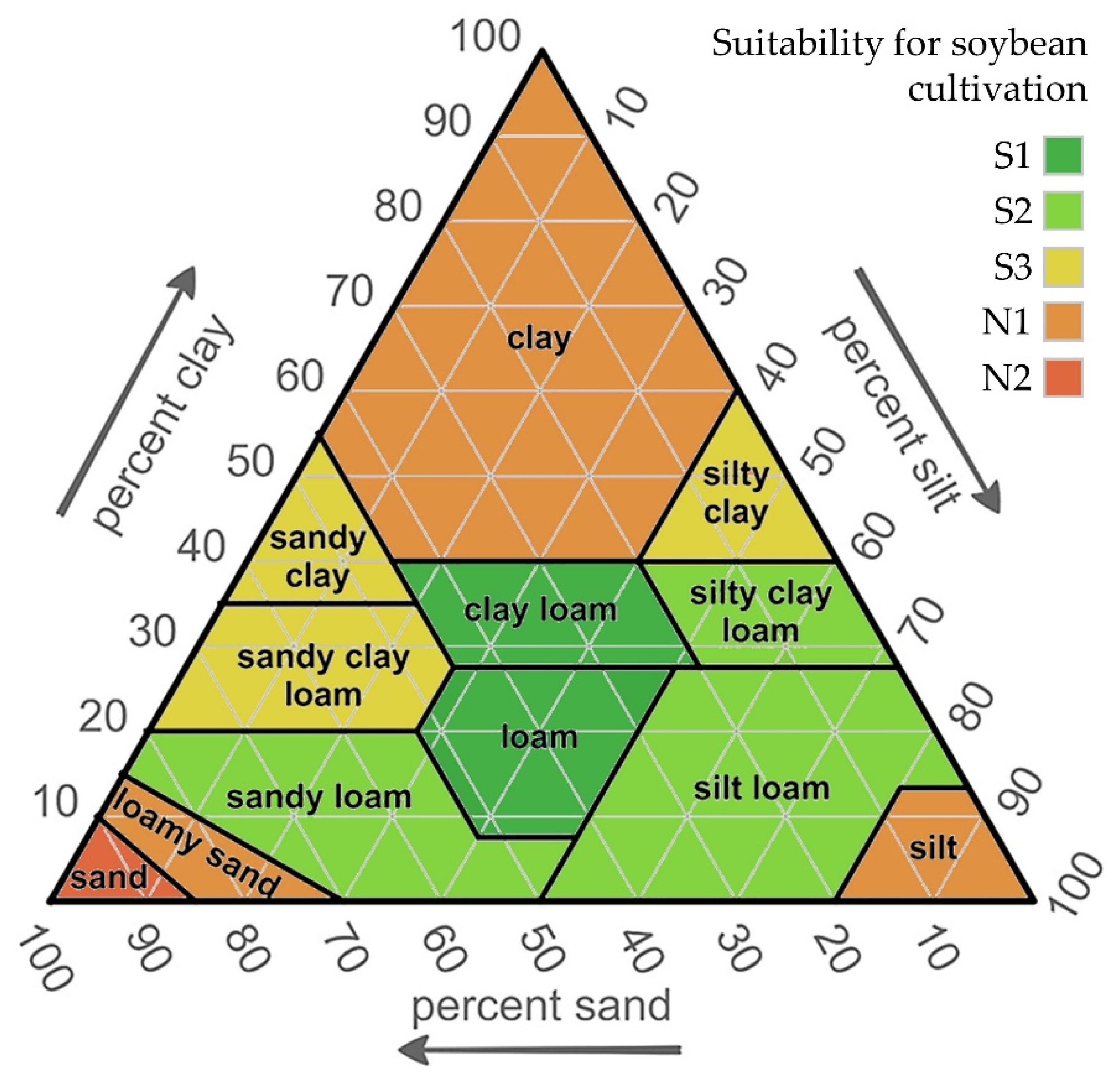
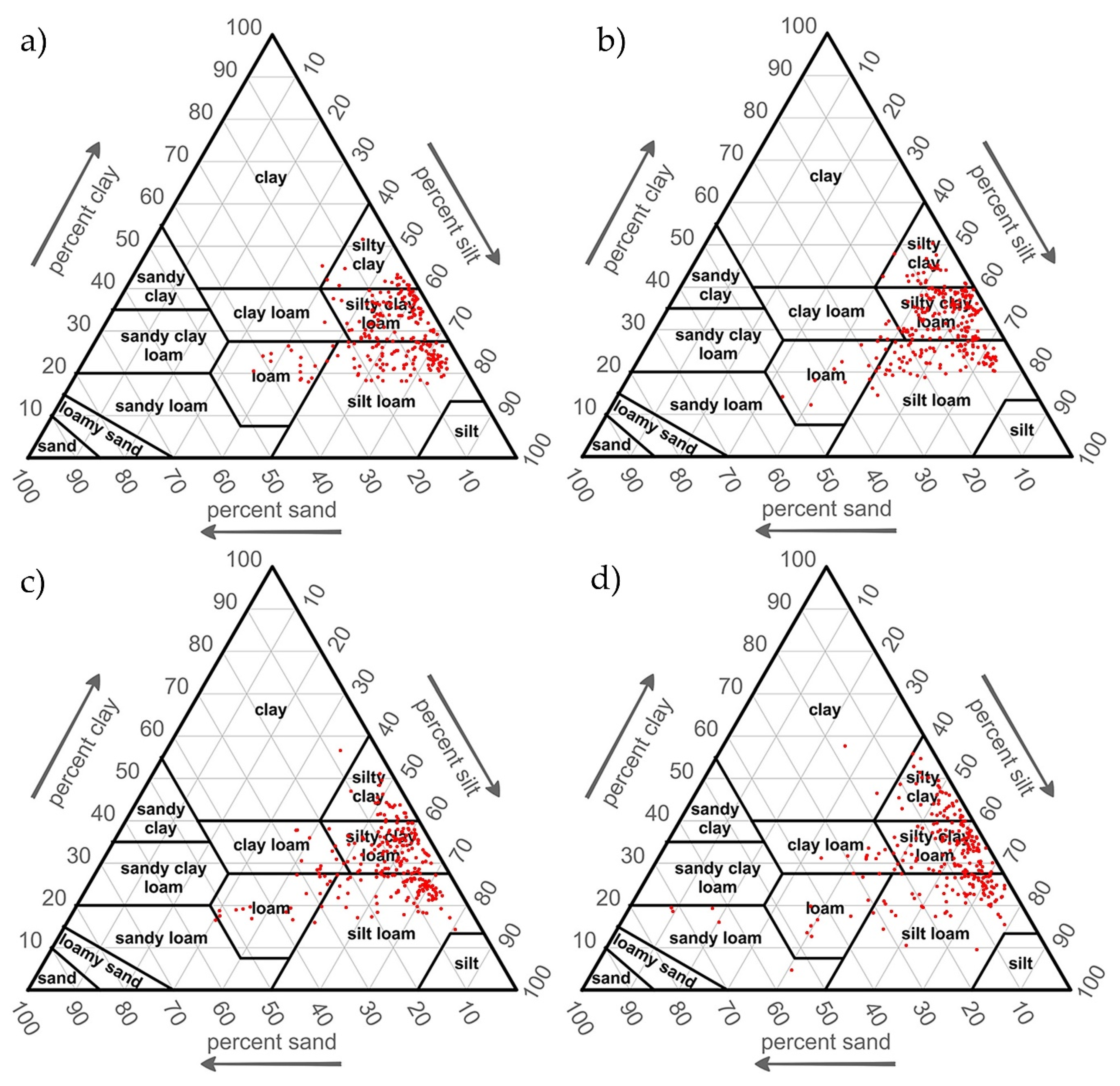
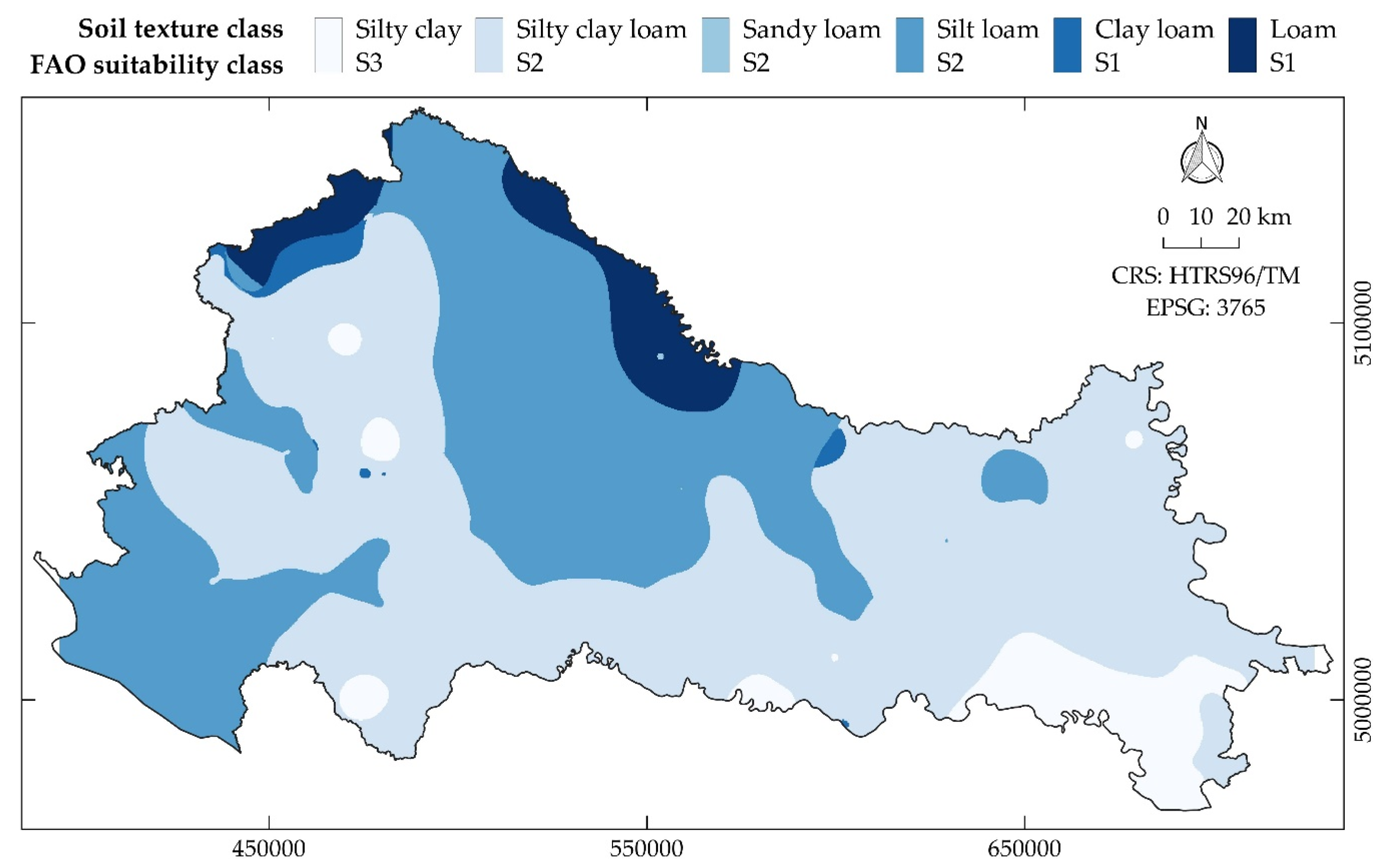
2.4. Determination of Soybean Suitability Zones According to Soil Texture Classes
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Automatic Soil Texture Classification Algorithm Scripted in Python
Appendix B. Interpolation Parameters of Training Sample Sets
References
- Plaščak, I.; Jurišić, M.; Radočaj, D.; Barač, Ž.; Glavaš, J. Hazel plantation planning using GIS and multicriteria decision analysis. Poljoprivreda 2019, 25, 79–85. [Google Scholar] [CrossRef]
- El Baroudy, A.A. Mapping and evaluating land suitability using a GIS-based model. Catena 2016, 140, 96–104. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M.; Plaščak, I. Optimal Soybean (Glycine max L.) Land Suitability Using GIS-Based Multicriteria Analysis and Sentinel-2 Multitemporal Images. Remote Sens. 2020, 12, 1463. [Google Scholar] [CrossRef]
- Kazemi, H.; Akinci, H. A land use suitability model for rainfed farming by Multi-criteria Decision-making Analysis (MCDA) and Geographic Information System (GIS). Ecol. Eng. 2018, 116, 1–6. [Google Scholar] [CrossRef]
- Greve, M.H.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K. Quantifying the ability of environmental parameters to predict soil texture fractions using regression-tree model with GIS and LIDAR data: The case study of Denmark. Ecol. Indic. 2012, 18, 1–10. [Google Scholar] [CrossRef]
- García-Tomillo, A.; Mirás-Avalos, J.M.; Dafonte-Dafonte, J.; Paz-González, A. Mapping Soil Texture Using Geostatistical Interpolation Combined with Electromagnetic Induction Measurements. Soil Sci. 2017, 182, 278–284. [Google Scholar] [CrossRef]
- Zebec, V.; Semialjac, Z.; Marković, M.; Tadić, V.; Radić, D.; Rastija, D. Influence of physical and chemical properties of different soil types on optimal soil moisture for tillage. Poljoprivreda 2017, 23, 10–18. [Google Scholar] [CrossRef]
- Zipper, S.C.; Soylu, M.E.; Booth, E.G.; Loheide, S.P. Untangling the effects of shallow groundwater and soil texture as drivers of subfield-scale yield variability. Water Resour. Res. 2015, 51, 6338–6358. [Google Scholar] [CrossRef]
- Bach, E.M.; Baer, S.G.; Meyer, C.K.; Six, J. Soil texture affects soil microbial and structural recovery during grassland restoration. Soil Biol. Biochem. 2010, 42, 2182–2191. [Google Scholar] [CrossRef]
- Chau, J.F.; Bagtzoglou, A.C.; Willig, M.R. The effect of soil texture on richness and diversity of bacterial communities. Environ. Forensics 2011, 12, 333–341. [Google Scholar] [CrossRef]
- Gašparović, M.; Zrinjski, M.; Gudelj, M. Automatic cost-effective method for land cover classification (ALCC). Comput. Environ. Urban Syst. 2019, 76, 1–10. [Google Scholar] [CrossRef]
- Gilliot, J.M.; Vaudour, E.; Michelin, J. Soil surface roughness measurement: A new fully automatic photogrammetric approach applied to agricultural bare fields. Comput. Electron. Agric. 2017, 134, 63–78. [Google Scholar] [CrossRef]
- Sirsat, M.S.; Cernadas, E.; Fernández-Delgado, M.; Barro, S. Automatic prediction of village-wise soil fertility for several nutrients in India using a wide range of regression methods. Comput. Electron. Agric. 2018, 154, 120–133. [Google Scholar] [CrossRef]
- Bonini Neto, A.; Bonini, C.S.B.; Reis, A.R.; Piazentin, J.C.; Coletta, L.F.S.; Putti, F.F.; Heinrichs, R.; Moreira, A. Automatic recovery estimation of degraded soils by artificial neural networks in function of chemical and physical attributes in Brazilian Savannah soil. Commun. Soil Sci. Plant Anal. 2019, 50, 1785–1798. [Google Scholar] [CrossRef]
- Adhikari, K.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K.; Malone, B.P.; Minasny, B.; McBratney, A.; Greve, M.H. High-resolution 3-D mapping of soil texture in Denmark. Soil Sci. Soc. Am. J. 2013, 77, 860–876. [Google Scholar] [CrossRef]
- Gomez, C.; Dharumarajan, S.; Féret, J.B.; Lagacherie, P.; Ruiz, L.; Sekhar, M. Use of sentinel-2 time-series images for classification and uncertainty analysis of inherent biophysical property: Case of soil texture mapping. Remote Sens. 2019, 11, 565. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; John Wiley & Sons: Chichester, UK, 2007; p. 330. [Google Scholar]
- Augusto Filho, O.; Soares, W.; Irigaray, C. Mapping of compactness by depth in a quaternary geological formation using deterministic and geostatistical interpolation models. Environ. Earth Sci. 2017, 76, 607. [Google Scholar] [CrossRef]
- Oliver, M.A. The variogram and kriging. In Handbook of Applied Spatial Analysis; Ficher, M., Getis, A., Eds.; Springer: Berlin, Germany, 2010; pp. 319–352. [Google Scholar] [CrossRef]
- Bhunia, G.S.; Shit, P.K.; Maiti, R. Comparison of GIS-based interpolation methods for spatial distribution of soil organic carbon (SOC). J. Saudi Soc. Agric. Sci. 2018, 17, 114–126. [Google Scholar] [CrossRef]
- Long, J.; Liu, Y.; Xing, S.; Qiu, L.; Huang, Q.; Zhou, B.; Shen, J.; Zhang, L. Effects of sampling density on interpolation accuracy for farmland soil organic matter concentration in a large region of complex topography. Ecol. Indic. 2018, 93, 562–571. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, Q.; Chen, L.; Yao, X.; Xie, F. Effect of Drought Stress at Reproductive Stages on Growth and Nitrogen Metabolism in Soybean. Agronomy 2020, 10, 302. [Google Scholar] [CrossRef]
- Kumagai, E.; Takahashi, T. Soybean (Glycine max (L.) Merr.) Yield Reduction due to Late Sowing as a Function of Radiation Interception and Use in a Cool Region of Northern Japan. Agronomy 2020, 10, 66. [Google Scholar] [CrossRef]
- Ray, D.K.; Mueller, N.D.; West, P.C.; Foley, J.A. Yield trends are insufficient to double global crop production by 2050. PLoS ONE 2013, 8, e66428. [Google Scholar] [CrossRef] [PubMed]
- Masuda, T.; Goldsmith, P.D. World soybean production: Area harvested, yield, and long-term projections. Int. Food Agribus. Manag. Rev. 2009, 12, 1–20. [Google Scholar] [CrossRef]
- Toleikienė, M.; Brophy, C.; Arlauskienė, A.; Rasmussen, J.; Gecaitė, V.; Kadžiulienė, Ž. The introduction of soybean in an organic crop rotation in the Nemoral zone: The impact on subsequent spring wheat productivity. Zemdirbyste 2019, 106, 321–328. [Google Scholar] [CrossRef]
- Melakeberhan, H.; Avendaño, F.; Pierce, F. Spatial analysis of soybean yield in relation to soil texture, soil fertility and soybean cyst nematode. Nematology 2004, 6, 527–545. [Google Scholar] [CrossRef]
- Arora, V.K.; Singh, C.B.; Sidhu, A.S.; Thind, S.S. Irrigation, tillage and mulching effects on soybean yield and water productivity in relation to soil texture. Agric. Water Manag. 2011, 98, 563–568. [Google Scholar] [CrossRef]
- Pagano, M.C.; Miransari, M. The importance of soybean production worldwide. In Abiotic and Biotic Stresses in Soybean Production; Miransari, M., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 1–26. [Google Scholar] [CrossRef]
- European Environment Agency—Biogeographical Regions. Available online: https://www.eea.europa.eu/data-and-maps/data/biogeographical-regions-europe-3 (accessed on 9 May 2020).
- Robinson, T.P.; Metternicht, G. Testing the performance of spatial interpolation techniques for mapping soil properties. Comput. Electron. Agric. 2006, 50, 97–108. [Google Scholar] [CrossRef]
- Croatian Geological Institute—Description and Explanation of Applied Methods. Available online: http://www.haop.hr/sites/default/files/uploads/news/2017-12/Opis_i_obrazlozenje_koristenih_metoda_istrazivanja_HGI.pdf (accessed on 9 May 2020).
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Jurišić, M.; Plaščak, I.; Antonić, O.; Radočaj, D. Suitability Calculation for Red Spicy Pepper Cultivation (Capsicum annum L.) Using Hybrid GIS–Based Multicriteria Analysis. Agronomy 2020, 10, 3. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Negreiros, J.; Painho, M.; Aguilar, F.; Aguilar, M. Geographical information systems principles of ordinary kriging interpolator. J. Appl. Sci. 2010, 10, 852–867. [Google Scholar] [CrossRef]
- Ciotoli, G.; Lombardi, S.; Annunziatellis, A. Geostatistical analysis of soil gas data in a high seismic intermontane basin: Fucino Plain, central Italy. J. Geophys. Res. Solid Earth 2007, 112, B05407. [Google Scholar] [CrossRef]
- Pesquer, L.; Cortés, A.; Pons, X. Parallel ordinary kriging interpolation incorporating automatic variogram fitting. Comput. Geosci. 2011, 37, 464–473. [Google Scholar] [CrossRef]
- De Mesnard, L. Pollution models and inverse distance weighting: Some critical remarks. Comput. Geosci. 2013, 52, 459–469. [Google Scholar] [CrossRef]
- Fortin, M.J.; Drapeau, P.; Legendre, P. Spatial autocorrelation and sampling design in plant ecology. In Progress in Theoretical Vegetation Science; Grabherr, G., Mucina, L., Dale, M.B., Ter Braak, C.J.F., Eds.; Springer: Dordecht, The Netherlands, 1990; pp. 209–222. [Google Scholar]
- Gribov, A.; Krivoruchko, K. New flexible non–parametric data transformation for trans–gaussian kriging. In Geostatistics Oslo 2012; Abrahamsen, P., Hauge, R., Kolbjørnsen, O., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 51–65. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A robust method of thin plate spline and its application to DEM construction. Comput. Geosci. 2012, 48, 9–16. [Google Scholar] [CrossRef]
- Ditzler, C.; Scheffe, K.; Monger, H.C. Soil Survey Manual; Government Printing Office: Washington, DC, USA, 2017; p. 639.
- An, D.; Zhao, G.; Chang, C.; Wang, Z.; Li, P.; Zhang, T.; Jia, J. Hyperspectral field estimation and remote-sensing inversion of salt content in coastal saline soils of the Yellow River Delta. Int. J. Remote Sens. 2016, 37, 455–470. [Google Scholar] [CrossRef]
- Merdun, H.; Çınar, Ö.; Meral, R.; Apan, M. Comparison of artificial neural network and regression pedotransfer functions for prediction of soil water retention and saturated hydraulic conductivity. Soil Tillage Res. 2006, 90, 108–116. [Google Scholar] [CrossRef]
- University of Florida—Soil Texture. Available online: https://ufdcimages.uflib.ufl.edu/IR/00/00/31/07/00001/SS16900.pdf (accessed on 9 May 2020).
- Food and Agriculture Organization—The Structure of the FAO Framework Classification. Available online: http://www.fao.org/3/x5648e/x5648e0j.htm (accessed on 9 May 2020).
- Gaillard, R.; Duval, B.D.; Osterholz, W.R.; Kucharik, C.J. Simulated effects of soil texture on nitrous oxide emission factors from corn and soybean agroecosystems in Wisconsin. J. Environ. Qual. 2016, 45, 1540–1548. [Google Scholar] [CrossRef] [PubMed]
- Avendaño, F.; Pierce, F.J.; Schabenberger, O.; Melakeberhan, H. The spatial distribution of soybean cyst nematode in relation to soil texture and soil map unit. Agron. J. 2004, 96, 181–194. [Google Scholar] [CrossRef]
- Butcher, K.; Wick, A.F.; DeSutter, T.; Chatterjee, A.; Harmon, J. Corn and soybean yield response to salinity influenced by soil texture. Agron. J. 2018, 110, 1243–1253. [Google Scholar] [CrossRef]
- Miransari, M.; Smith, D. Using signal molecule genistein to alleviate the stress of suboptimal root zone temperature on soybean-Bradyrhizobium symbiosis under different soil textures. J. Plant Interact. 2008, 3, 287–295. [Google Scholar] [CrossRef]
- Hassink, J. Effects of soil texture and structure on carbon and nitrogen mineralization in grassland soils. Biol. Fertil. Soils 1992, 14, 126–134. [Google Scholar] [CrossRef]
- Rosolem, C.A.; Sgariboldi, T.; Garcia, R.A.; Calonego, J.C. Potassium leaching as affected by soil texture and residual fertilization in tropical soils. Commun. Soil Sci. Plant Anal. 2010, 41, 1934–1943. [Google Scholar] [CrossRef]
- Workneh, F.; Yang, X.B.; Tylka, G.L. Soybean brown stem rot, Phytophthora sojae, and Heterodera glycines affected by soil texture and tillage relations. Phytopathology 1999, 89, 844–850. [Google Scholar] [CrossRef] [PubMed][Green Version]
- He, W.Y.; Luo, X.L.; Sun, G.J. The Trend of GIS-Based suitable planting areas for Chinese soybean under the future climate scenario. In Ecosystem Assessment and Fuzzy Systems Management; Cao, B.Y., Ma, S.Q., Cao, H.H., Eds.; Springer International Pubishing: Cham, Switzerland, 2014; pp. 325–338. [Google Scholar]
- Subiyanto, H.; Arief, U.M.; Nafi, A.Y. An accurate assessment tool based on intelligent technique for suitability of soybean cropland: Case study in Kebumen Regency, Indonesia. Heliyon 2018, 4, e00684. [Google Scholar] [CrossRef] [PubMed]
- Boix, L.R.; Zinck, J.A. Land–use planning in the Chaco plain (Burruyacú, Argentina). Part 1: Evaluating land–use options to support crop diversification in an agricultural frontier area using physical land evaluation. Environ. Manag. 2008, 42, 1043–1063. [Google Scholar] [CrossRef] [PubMed]
- Seyedmohammadi, J.; Sarmadian, F.; Jafarzadeh, A.A.; Ghorbani, M.A.; Shahbazi, F. Application of SAW, TOPSIS and fuzzy TOPSIS models in cultivation priority planning for maize, rapeseed and soybean crops. Geoderma 2018, 310, 178–190. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Jaiswal, R.K.; Hegde, V.S.; Jayaraman, V. Assessment of land suitability potentials for agriculture using a remote sensing and GIS based approach. Int. J. Remote Sens. 2009, 30, 879–895. [Google Scholar] [CrossRef]
- Song, Y.Q.; Zhao, X.; Su, H.Y.; Li, B.; Hu, Y.M.; Cui, X.S. Predicting Spatial Variations in Soil Nutrients with Hyperspectral Remote Sensing at Regional Scale. Sensors 2018, 18, 3086. [Google Scholar] [CrossRef] [PubMed]
- Metwally, M.S.; Shaddad, S.M.; Liu, M.; Yao, R.-J.; Abdo, A.I.; Li, P.; Jiao, J.; Chen, X. Soil Properties Spatial Variability and Delineation of Site–Specific Management Zones Based on Soil Fertility Using Fuzzy Clustering in a Hilly Field in Jianyang, Sichuan, China. Sustainability 2019, 11, 7084. [Google Scholar] [CrossRef]
- Delbari, M.; Afrasiab, P.; Loiskandl, W. Geostatistical analysis of soil texture fractions on the field scale. Soil Water Res. 2011, 6, 173–189. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Chen, Y.; Shi, T.; Luo, M.; Ju, Q.; Zhang, H.; Wang, S. Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sens. 2019, 11, 1683. [Google Scholar] [CrossRef]
- Zhang, C.; Fay, D.; McGrath, D.; Grennan, E.; Carton, O.T. Use of trans-Gaussian kriging for national soil geochemical mapping in Ireland. Geochem. Explor. Environ. A 2008, 8, 255–265. [Google Scholar] [CrossRef]
- Barłóg, P.; Hlisnikovský, L.; Kunzová, E. Effect of Digestate on Soil Organic Carbon and Plant-Available Nutrient Content Compared to Cattle Slurry and Mineral Fertilization. Agronomy 2020, 10, 379. [Google Scholar] [CrossRef]
- Bogunović, I.; Telak, J.L.; Pereira, P. Agriculture Management Impacts on Soil Properties and Hydrological Response in Istria (Croatia). Agronomy 2020, 10, 282. [Google Scholar] [CrossRef]
- Dong-Sheng, Y.; Zhang, Z.; Hao, Y.; Xue-Zheng, S.; Man-Zhi, T.; Wei-Xia, S.; Hong-Jie, W. Effect of soil sampling density on detected spatial variability of soil organic carbon in a red soil region of China. Pedosphere 2011, 21, 207–213. [Google Scholar] [CrossRef]
- Nanni, M.R.; Povh, F.P.; Demattê, J.A.M.; Oliveira, R.B.D.; Chicati, M.L.; Cezar, E. Optimum size in grid soil sampling for variable rate application in site-specific management. Sci. Agric. 2011, 68, 386–392. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Taylor, R.K.; Milliken, G.A. Evaluating the potential for site-specific phosphorus applications without high-density soil sampling. Soil Sci. Soc. Am. J. 2002, 66, 276–283. [Google Scholar] [CrossRef]
- Ballabio, C.; Panagos, P.; Monatanarella, L. Mapping topsoil physical properties at European scale using the LUCAS database. Geoderma 2016, 261, 110–123. [Google Scholar] [CrossRef]
- Cruz-Cárdenas, G.; López-Mata, L.; Ortiz-Solorio, C.A.; Villaseñor, J.L.; Ortiz, E.; Silva, J.T.; Estrada-Godoy, F. Interpolation of Mexican soil properties at a scale of 1:1,000,000. Geoderma 2014, 213, 29–35. [Google Scholar] [CrossRef]
- Zebec, V.; Rastija, D.; Lončarić, Z.; Bensa, A.; Popović, B.; Ivezić, V. Comparison of chemical extraction methods for determination of soil potassium in different soil types. Eurasian Soil Sci. 2017, 50, 1420–1427. [Google Scholar] [CrossRef]
- Pennock, D.; Yates, T.; Braidek, J. Soil sampling designs. In Soil Sampling and Methods of Analysis; Carter, M.R., Gregorich, E.G., Eds.; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–14. [Google Scholar]
- Lloyd, C.D.; Atkinson, P.M. Assessing uncertainty in estimates with ordinary and indicator kriging. Comput. Geosci. 2001, 27, 929–937. [Google Scholar] [CrossRef]
- AlShahrani, A.M.; Al–Abadi, M.A.; Al–Malki, A.S.; Ashour, A.S.; Dey, N. Automated system for crops recognition and classification. In Computer Vision: Concepts, Methodologies, Tools, and Applications; Khosrow-Pour, M., Ed.; IGI Global: Hershey, PA, USA, 2018; pp. 1208–1223. [Google Scholar]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Quintero, G.; Prieto-Amparán, J.A.; Pinedo-Alvarez, A.; Valles-Aragón, M.C.; Morales-Nieto, C.R.; Villarreal-Guerrero, F. GIS-Based Multicriteria Evaluation of Land Suitability for Grasslands Conservation in Chihuahua, Mexico. Sustainability 2020, 12, 185. [Google Scholar] [CrossRef]
- Rodríguez Sousa, A.A.; Barandica, J.M.; Rescia, A. Ecological and Economic Sustainability in Olive Groves with Different Irrigation Management and Levels of Erosion: A Case Study. Sustainability 2019, 11, 4681. [Google Scholar] [CrossRef]
- Hamdi, L.; Suleiman, A.; Hoogenboom, G.; Shelia, V. Response of the Durum Wheat Cultivar Um Qais (Triticum turgidum subsp. durum) to Salinity. Agriculture 2019, 9, 135. [Google Scholar] [CrossRef]
- Wijitkosum, S.; Sriburi, T. Fuzzy AHP Integrated with GIS Analyses for Drought Risk Assessment: A Case Study from Upper Phetchaburi River Basin, Thailand. Water 2019, 11, 939. [Google Scholar] [CrossRef]
- Hayashi, K.; Kawashima, H. Integrated evaluation of greenhouse vegetable production: Toward sustainable management. In ISHS Acta Horticulturae 655, Proceedings of the XV International Symposium on Horticultural Economics and Management, Berlin, Germany, 1 September 2004; Bokelmann, W., Ed.; ISHS: Leuven, Belgium, 2004; pp. 489–496. [Google Scholar] [CrossRef]

| Source | Soil Texture Classes in the Study | Application |
|---|---|---|
| [48] | loamy sand, sandy loam, silt loam | Nitrous oxide emission in agricultural fields |
| [49] | loamy sand, sandy clay loam | Cyst nematode population density |
| [50] | sandy loam, silty clay loam | Yield response to salinity |
| [51] | loamy textures, sandy textures, clay textures | Effect of root zone temperatures on interorganismal signal molecules |
| [52] | loamy textures, clay textures, sandy textures | Carbon and nitrogen mineralization |
| [53] | clay, sandy clay loam | Canopy dry matter production |
| [54] | sandy loam, silt loam, loam, sandy clay loam, clay loam, silty clay loam, clay | Incidence of brown stem rot in conservation-till fields |
| Source | Suitability Level for Soybean Cultivation | ||||
|---|---|---|---|---|---|
| S1 | S2 | S3 | N1 | N2 | |
| [55] | loam | sandy loam, clay loam, silt loam | sandy clay, silty clay | other classes | sand |
| [56] | loam, clay loam, silty clay loam, silt loam | sandy loam, clay, silty clay, silty clay loam | loamy sand, silt | sand | |
| [57] | silt loam, silty clay loam, loam | sandy clay loam | sandy loam | / | / |
| [58] | silty clay loam, sandy clay loam, clay loam | loam, silt, silty loam, sandy clay, silty clay | sandy loam, clay | loamy sand | sand |
| [59] | clay loam | sandy clay loam | loamy sand | sandy loam | / |
| Set No. | Soil Parameter | Mean (%) | CV | SK | KT |
|---|---|---|---|---|---|
| Clay | 30.997 | 0.368 | 0.678 | 0.228 | |
| Set 1 | Silt | 58.141 | 0.223 | −0.760 | 0.833 |
| Sand | 10.862 | 1.207 | 2.322 | 6.515 | |
| Clay | 31.355 | 0.332 | 0.584 | 0.336 | |
| Set 2 | Silt | 57.945 | 0.211 | −0.599 | 0.391 |
| Sand | 10.701 | 1.150 | 2.065 | 5.093 | |
| Clay | 29.889 | 0.343 | 0.581 | 0.159 | |
| Set 3 | Silt | 57.958 | 0.225 | −0.800 | 0.874 |
| Sand | 12.153 | 1.141 | 2.060 | 4.861 | |
| Clay | 29.899 | 0.354 | 0.633 | 0.334 | |
| Set 4 | Silt | 58.276 | 0.225 | −0.805 | 0.860 |
| Sand | 11.826 | 1.173 | 2.116 | 5.000 | |
| Clay | 30.795 | 0.353 | 0.594 | 0.241 | |
| Set 5 | Silt | 57.305 | 0.228 | −0.688 | 0.674 |
| Sand | 11.900 | 1.151 | 2.082 | 5.050 | |
| Clay | 30.587 | 0.350 | 0.614 | 0.260 | |
| Mean | Silt | 57.925 | 0.222 | −0.730 | 0.726 |
| Sand | 11.488 | 1.164 | 2.129 | 5.304 |
| Set No. | Stat. Value | OK | IDW | SI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clay | Silt | Sand | Clay | Silt | Sand | Clay | Silt | Sand | ||
| Set 1 | RMSE | 1.85 | 3.04 | 1.79 | 3.13 | 2.91 | 2.51 | 3.50 | 4.80 | 3.79 |
| R2 | 0.786 | 0.632 | 0.740 | 0.456 | 0.560 | 0.645 | 0.490 | 0.328 | 0.444 | |
| Set 2 | RMSE | 2.01 | 1.80 | 1.52 | 2.51 | 2.06 | 2.68 | 3.19 | 4.15 | 2.90 |
| R2 | 0.733 | 0.727 | 0.846 | 0.720 | 0.703 | 0.680 | 0.475 | 0.437 | 0.597 | |
| Set 3 | RMSE | 2.70 | 3.59 | 1.60 | 3.00 | 3.28 | 3.28 | 5.50 | 3.85 | 3.77 |
| R2 | 0.655 | 0.469 | 0.842 | 0.598 | 0.422 | 0.537 | 0.313 | 0.385 | 0.497 | |
| Set 4 | RMSE | 2.78 | 3.08 | 2.45 | 2.75 | 2.58 | 2.62 | 3.24 | 3.27 | 2.61 |
| R2 | 0.538 | 0.630 | 0.673 | 0.552 | 0.632 | 0.637 | 0.441 | 0.472 | 0.528 | |
| Set 5 | RMSE | 2.13 | 3.98 | 1.70 | 1.81 | 3.14 | 2.42 | 4.03 | 3.66 | 2.40 |
| R2 | 0.788 | 0.503 | 0.820 | 0.809 | 0.528 | 0.710 | 0.446 | 0.392 | 0.580 | |
| Mean | RMSE | 2.29 | 3.10 | 1.81 | 2.64 | 2.79 | 2.70 | 3.89 | 3.94 | 3.09 |
| R2 | 0.700 | 0.592 | 0.784 | 0.627 | 0.569 | 0.642 | 0.433 | 0.403 | 0.529 | |
| Clay | Silt | Sand | |||||||
|---|---|---|---|---|---|---|---|---|---|
| OK | IDW | SI | OK | IDW | SI | OK | IDW | SI | |
| OK | 1.000 | 1.000 | 1.000 | ||||||
| IDW | 0.869 | 1.000 | 0.826 | 1.000 | 0.818 | 1.000 | |||
| SI | 0.775 | 0.868 | 1.000 | 0.803 | 0.914 | 1.000 | 0.726 | 0.869 | 1.000 |
| Coverage | Silty Clay | Silty Clay Loam | Clay Loam | Loam | Sandy Loam | Silt Loam |
|---|---|---|---|---|---|---|
| Area (%) | 6.04 | 53.26 | 0.99 | 4.74 | 0.01 | 34.96 |
| Area (km2) | 1861 | 16,412 | 306 | 1460 | 2 | 10,773 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radočaj, D.; Jurišić, M.; Zebec, V.; Plaščak, I. Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia. Agronomy 2020, 10, 823. https://doi.org/10.3390/agronomy10060823
Radočaj D, Jurišić M, Zebec V, Plaščak I. Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia. Agronomy. 2020; 10(6):823. https://doi.org/10.3390/agronomy10060823
Chicago/Turabian StyleRadočaj, Dorijan, Mladen Jurišić, Vladimir Zebec, and Ivan Plaščak. 2020. "Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia" Agronomy 10, no. 6: 823. https://doi.org/10.3390/agronomy10060823
APA StyleRadočaj, D., Jurišić, M., Zebec, V., & Plaščak, I. (2020). Delineation of Soil Texture Suitability Zones for Soybean Cultivation: A Case Study in Continental Croatia. Agronomy, 10(6), 823. https://doi.org/10.3390/agronomy10060823









