Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials
Abstract
:1. Introduction
1.1. Natural Fibers and Bio-Based Resins
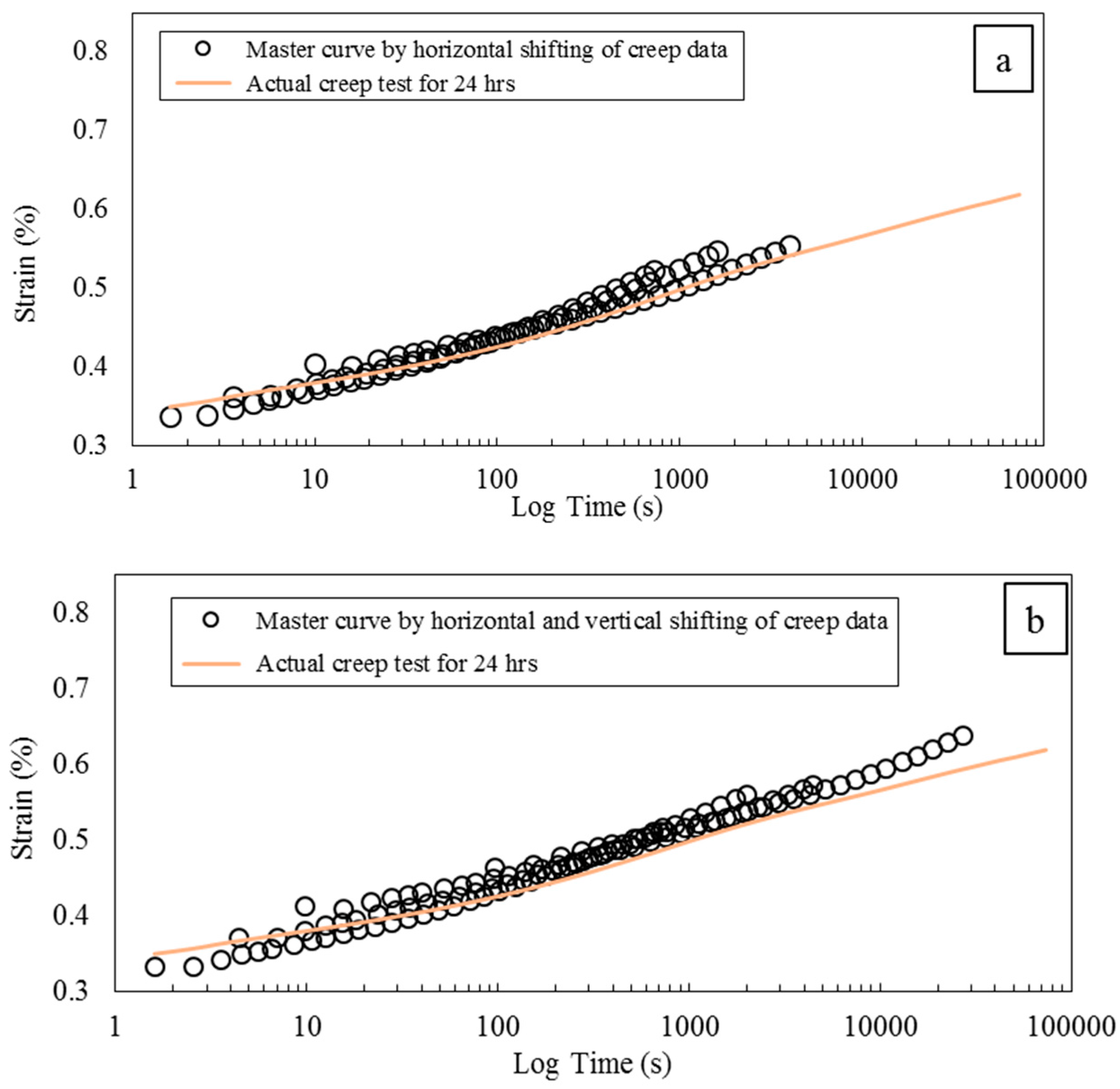
1.2. Long-Term and Thermal Behavior
1.3. Creep Modeling
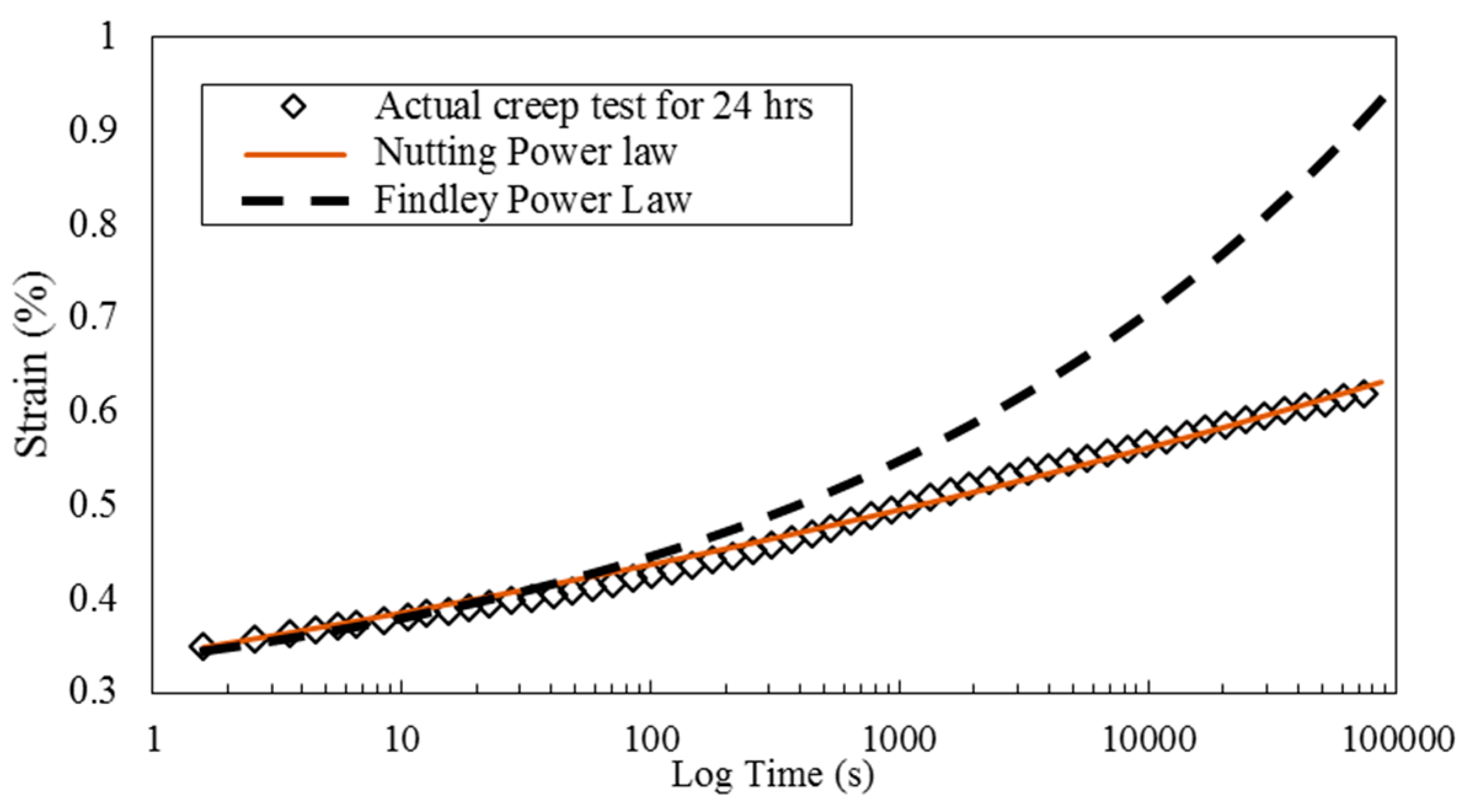
1.3.1. Nutting Power Law
1.3.2. Findley Power Law
2. Materials and Methods
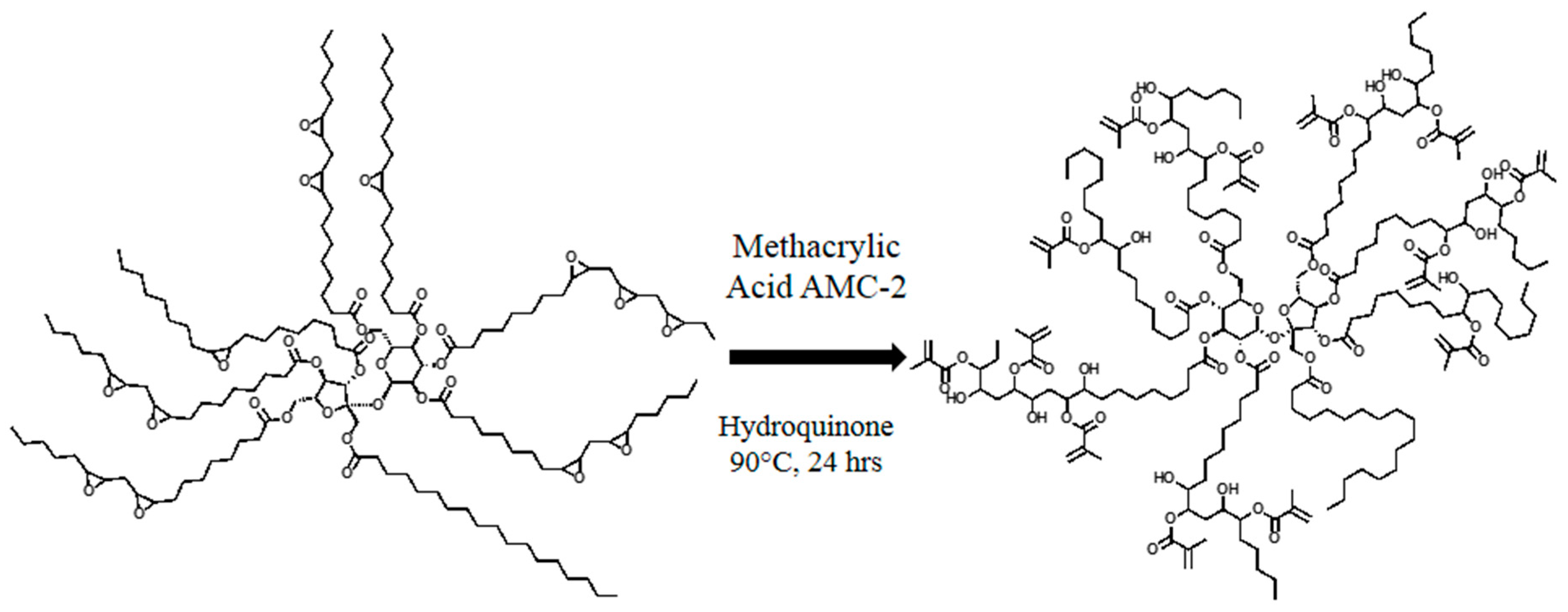
2.1. Characterization of MESS
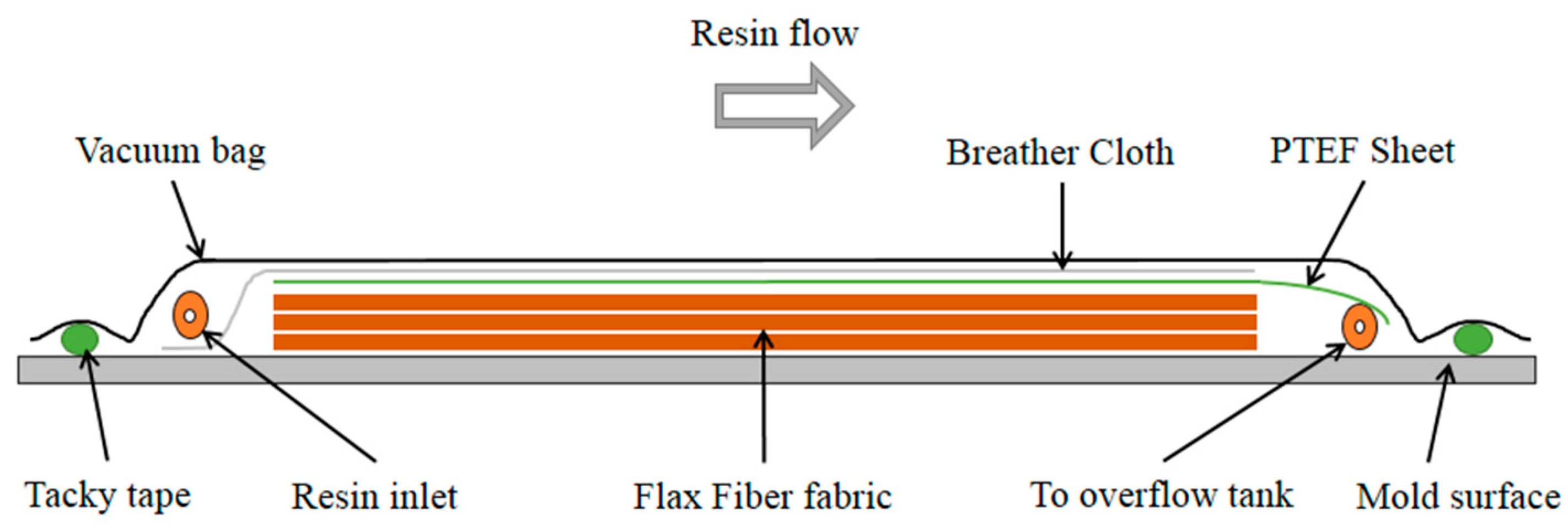
2.2. Composite Preparation
2.3. Composite Characterization
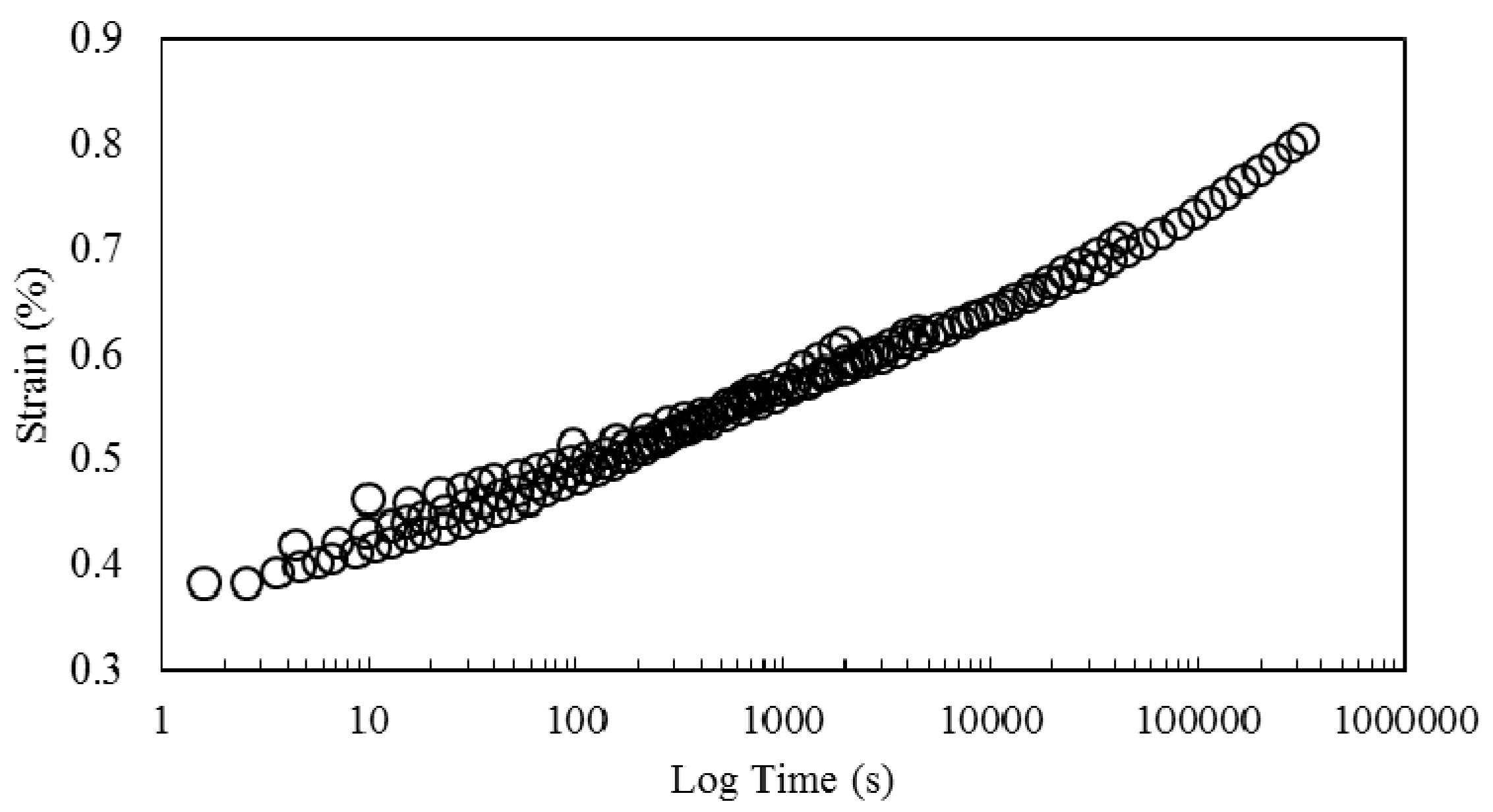
3. Results and Discussion
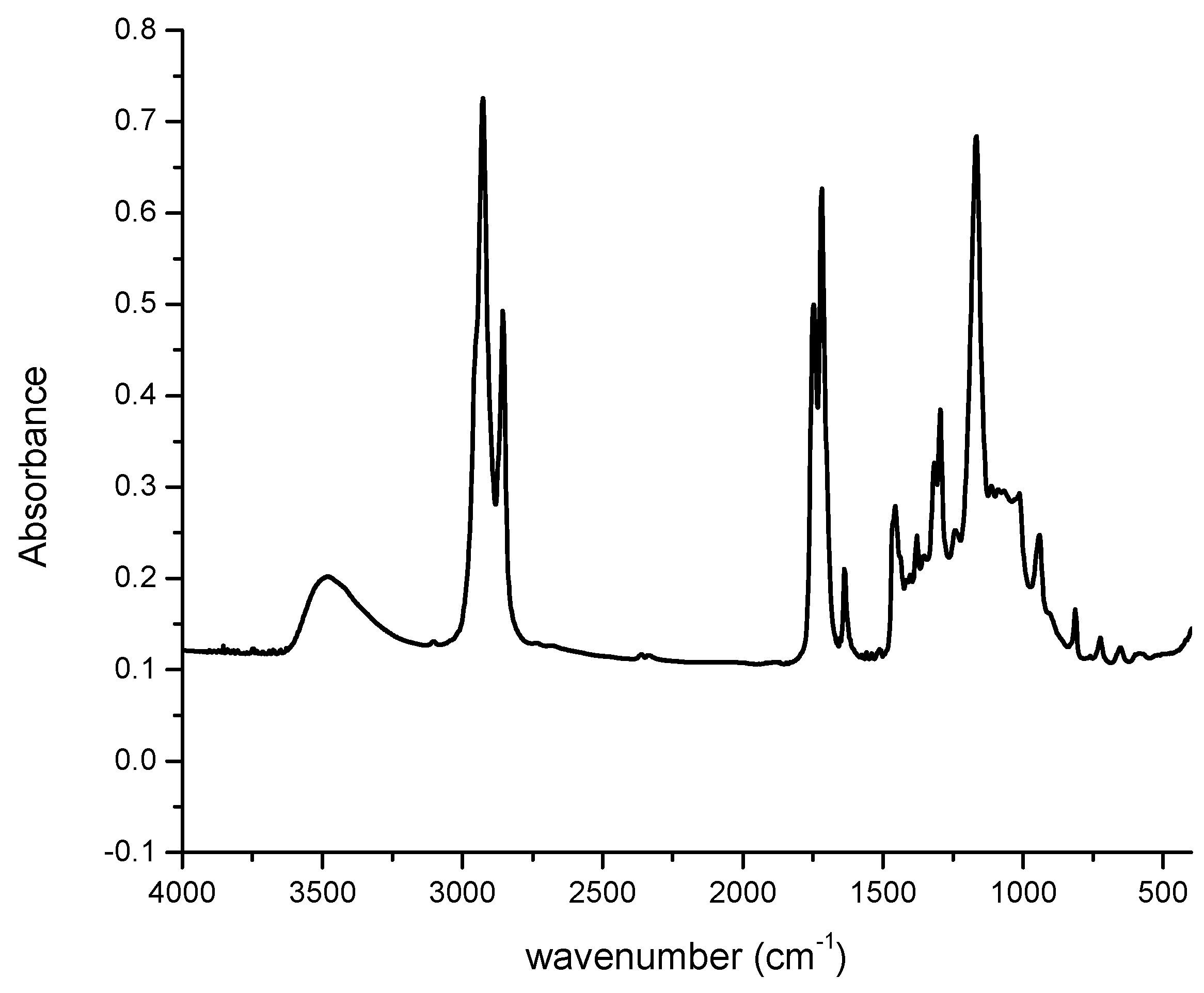
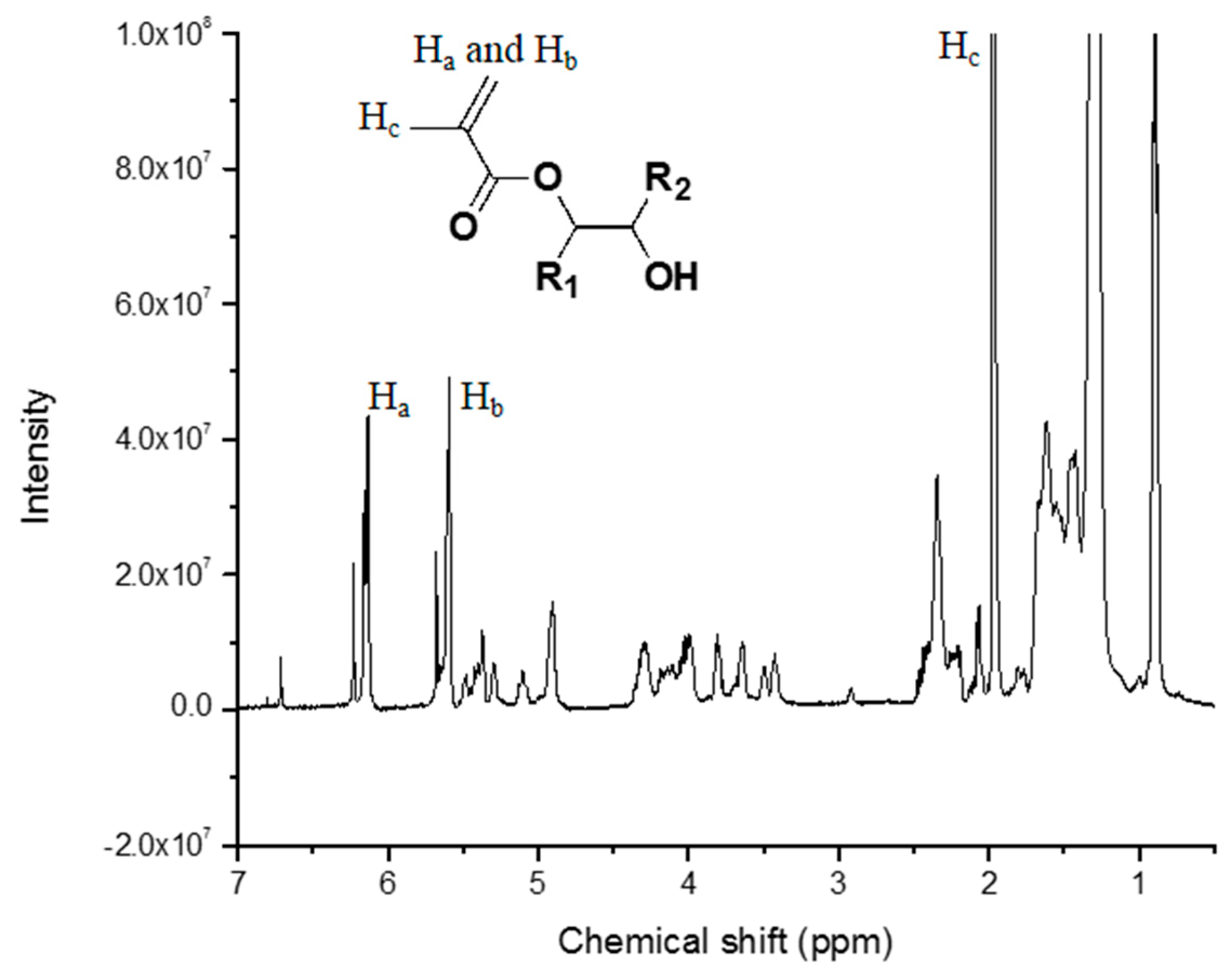
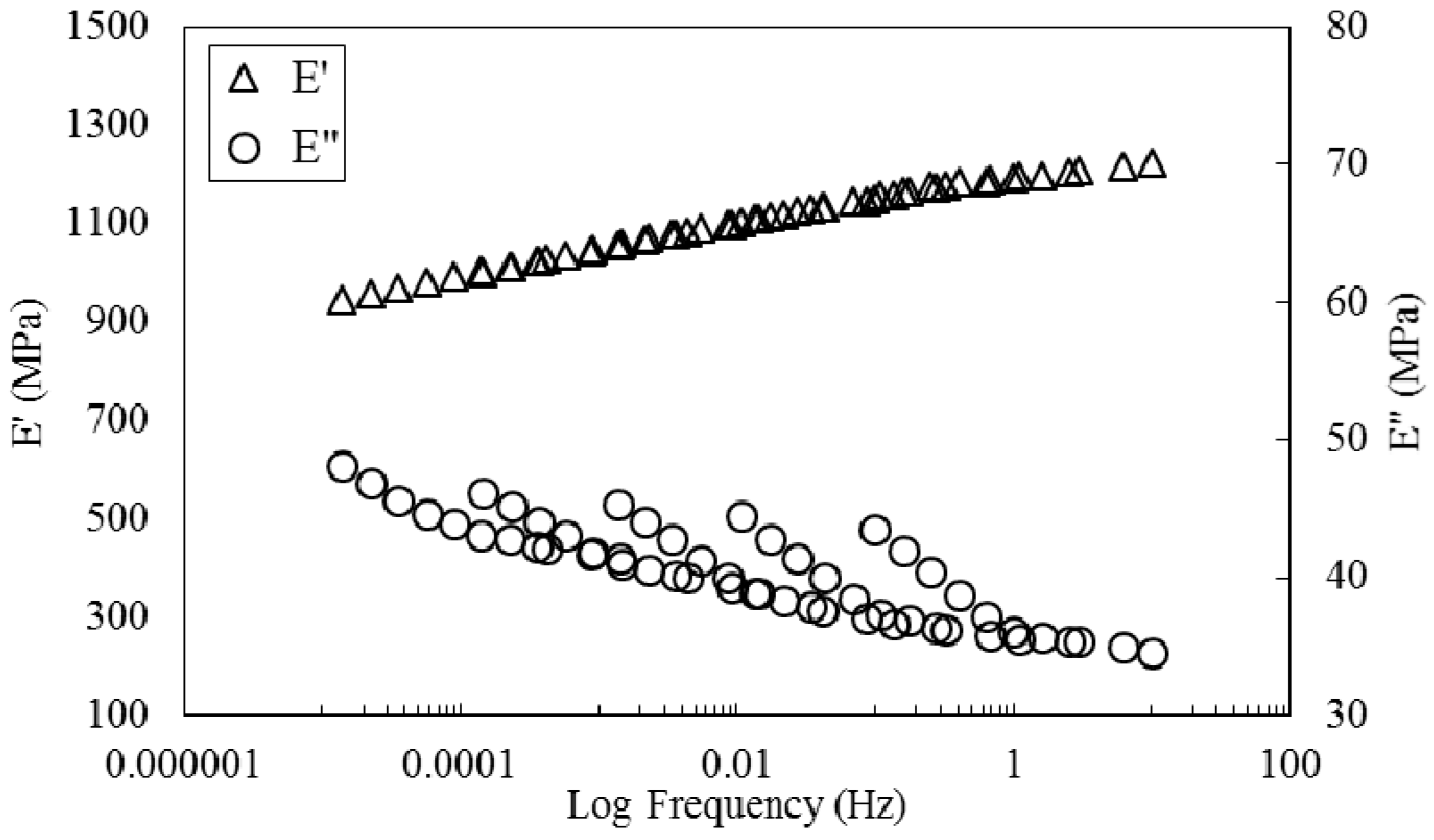
3.1. Resin Properties
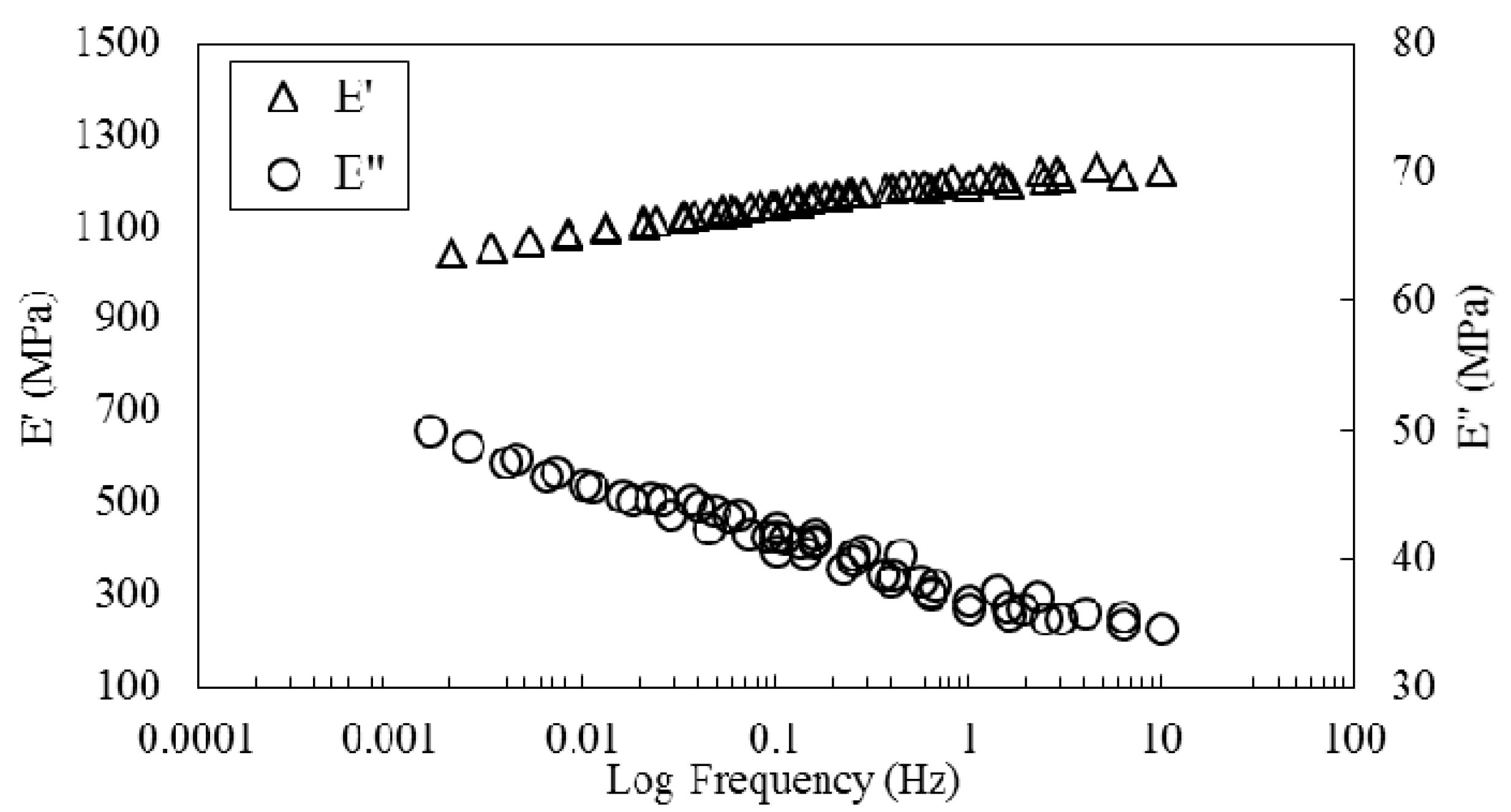
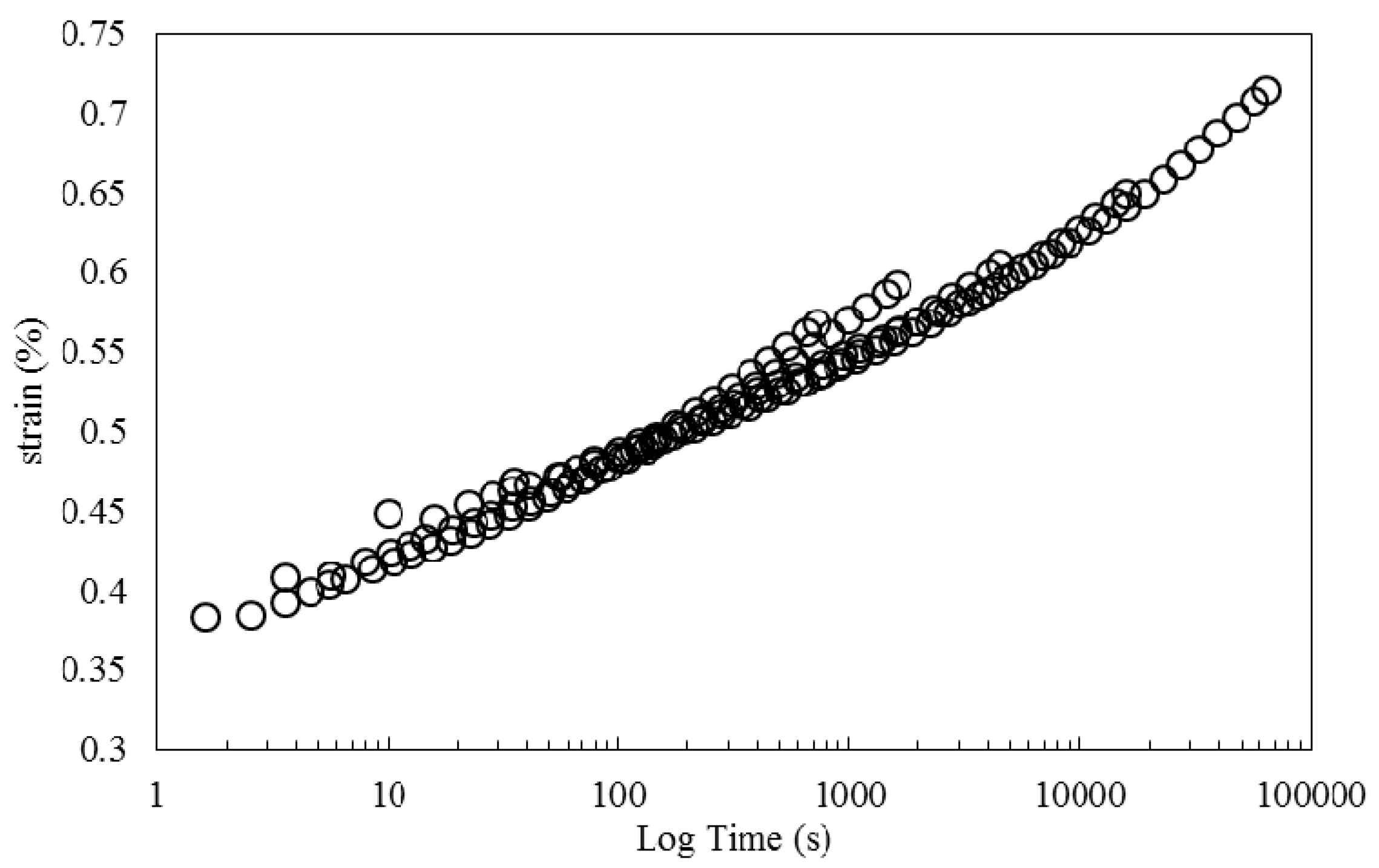
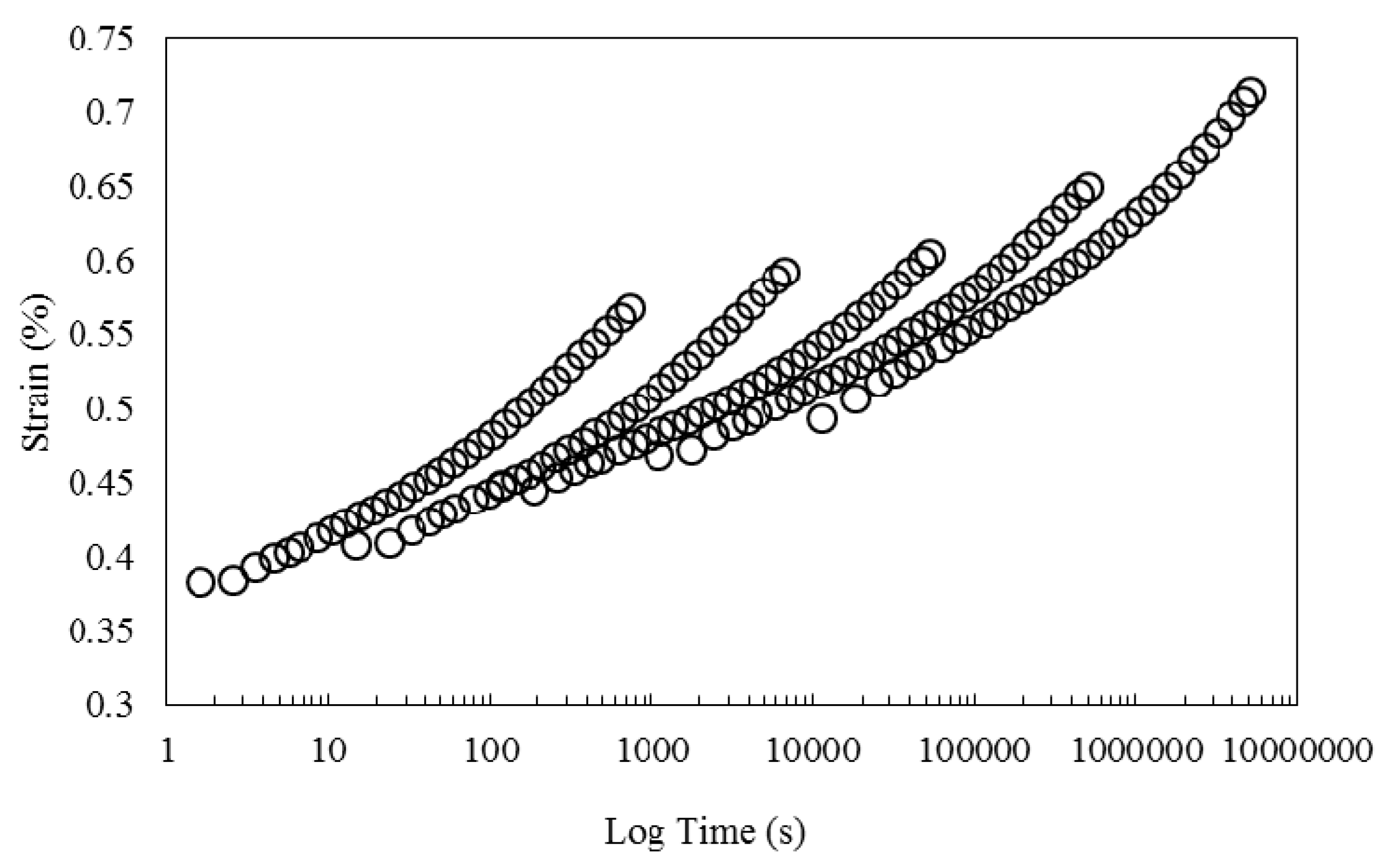
3.2. Mechanical Properties of the Composite
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Amiri, A.; Hosseini, N.; Ulven, C.A. Long-term creep behavior of flax/vinyl ester composites using time-temperature superposition principle. J. Renew. Mater. 2015, 3, 224–233. [Google Scholar] [CrossRef]
- Miller, S.A.; Srubar, W.V.; Billington, S.L.; Lepech, M.D. Integrating durability-based service-life predictions with environmental impact assessments of natural fiber–reinforced composite materials. Resour. Conserv. Recycl. 2015, 99, 72–83. [Google Scholar] [CrossRef]
- Amiri, A.; Ulven, C. Surface treatment of flax fiber. In Proceedings of the 65th Flax Institute of the United States, Fargo, ND, USA, 27–28 March 2014; pp. 117–125.
- Fuqua, M.A.; Huo, S.; Ulven, C.A. Natural fiber reinforced composites. Polym. Rev. 2012, 52, 259–320. [Google Scholar] [CrossRef]
- Amiri, A.; Hosseini, N.; Ulven, C.; Webster, D. Advanced bio-composites made from methacrylated epoxidized sucrose soyate resin reinforced with flax fibers. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015; p. 3503.
- Zhu, J.; Abhyankar, H.; Nassiopoulos, E.; Njuguna, J. Tannin-based flax fibre reinforced composites for structural applications in vehicles. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bedfordshire, UK, 2–4 July 2012.
- Avril, C.; Bailly, P.; Njuguna, J.; Nassiopoulos, E.; de Larminat, A. Development of flax-reinforced bio-composites for high-load bearing automotive parts. In Proceeding of the European Conference on Composite Materials (ECCM), Venice, Italy, 24–28 June 2012.
- Lincoln, J.D.; Shapiro, A.; Earthman, J.C.; Saphores, J.-M.; Ogunseitan, O. Design and evaluation of bioepoxy-flax composites for printed circuit boards. IEEE Trans. Electron. Packag. Manuf. 2008, 31, 211–220. [Google Scholar] [CrossRef]
- Le Duigou, A.; Davies, P.; Baley, C. Interfacial bonding of flax fibre/poly(l-lactide) bio-composites. Compos. Sci. Technol. 2010, 70, 231–239. [Google Scholar] [CrossRef]
- Newman, R.H. Auto-accelerative water damage in an epoxy composite reinforced with plain-weave flax fabric. Compos. Part A 2009, 40, 1615–1620. [Google Scholar] [CrossRef]
- Newman, R.H.; Battley, M.A.; Carpenter, J.E.; Le Guen, M.J. Energy loss in a unidirectional flax-polyester composite subjected to multiple tensile load–unload cycles. J. Mater. Sci. 2012, 47, 1164–1170. [Google Scholar] [CrossRef]
- Whitacre, R.; Amiri, A.; Ulven, C. The effects of corn zein protein coupling agent on mechanical properties of flax fiber reinforced composites. Ind. Crops Prod. 2015, 77, 232–238. [Google Scholar] [CrossRef]
- John, M.J.; Thomas, S. Biofibres and biocomposites. Carbohydr. Polym. 2008, 71, 343–364. [Google Scholar]
- Cheung, H.-Y.; Ho, M.-P.; Lau, K.-T.; Cardona, F.; Hui, D. Natural fibre-reinforced composites for bioengineering and environmental engineering applications. Compos. Part B 2009, 40, 655–663. [Google Scholar] [CrossRef]
- Yan, J.; Webster, D.C. Thermosets from highly functional methacrylated epoxidized sucrose soyate. Green Mater. 2014, 2, 132–143. [Google Scholar] [CrossRef]
- Michel, A.; Billington, S. Nonlinear constitutive model for anisotropic biobased composite materials. J. Eng. Mech. 2014, 140, 04014083. [Google Scholar] [CrossRef]
- Amiri, A.; Ulven, C.A.; Huo, S. Effect of chemical treatment of flax fiber and resin manipulation on service life of their composites using time-temperature superposition. Polymers 2015, 7, 1965–1978. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Guedes, R.M. Creep and Fatigue in Polymer Matrix Composites; Elsevier: Amsterdam, the Netherlands, 2010. [Google Scholar]
- Tajvidi, M.; Falk, R.H.; Hermanson, J.C. Time–temperature superposition principle applied to a kenaf-fiber/high-density polyethylene composite. J. Appl. Polym. Sci. 2005, 97, 1995–2004. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Van Gurp, M.; Palmen, J. Time-temperature superposition for polymeric blends. Rheol. Bull. 1998, 67, 5–8. [Google Scholar]
- Landel, R.F.; Nielsen, L.E. Mechanical Properties of Polymers and Composites; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Djoković, V.; Kostoski, D.; Dramićanin, M. Viscoelastic behavior of semicrystalline polymers at elevated temperatures on the basis of a two-process model for stress relaxation. J. Polym. Sci. Part B 2000, 38, 3239–3246. [Google Scholar] [CrossRef]
- Hughes, M.; Carpenter, J.; Hill, C. Deformation and fracture behaviour of flax fibre reinforced thermosetting polymer matrix composites. J. Mater. Sci. 2007, 42, 2499–2511. [Google Scholar] [CrossRef]
- Nutting, P. A study of elastic viscous deformation. Proc. Am. Soc. Test Mater. 1921, 21, 1162–1171. [Google Scholar]
- Blair, G.S.; Caffyn, J. An application of the theory of quasi-properties to the treatment of anomalous strain-stress relations. Philos. Mag. 1949, 40, 80–94. [Google Scholar] [CrossRef]
- Blair, G.S.; Veinoglou, B. A study of the firmness of soft materials based on Nutting’s equation. J. Sci. Instrum. 1944, 21, 149. [Google Scholar] [CrossRef]
- Betten, J. Creep Mechanics; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publications: Mineola, NY, USA, 1976. [Google Scholar]
- ASTM. ASTM D2990-09 Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics; ASTM International: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Pan, X.; Sengupta, P.; Webster, D.C. Novel biobased epoxy compounds: Epoxidized sucrose esters of fatty acids. Green Chem. 2011, 13, 965–975. [Google Scholar] [CrossRef]
- Monono, E.M.; Webster, D.C.; Wiesenborn, D.P. Pilot scale (10 kg) production and characterization of epoxidized sucrose soyate. Ind. Crops Prod. 2015, 74, 987–997. [Google Scholar] [CrossRef]
- Shaw, M.T.; MacKnight, W.J. Introduction to Polymer Viscoelasticity; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Harper, B.; Weitsman, Y. Characterization method for a class of thermorheologically complex materials. J. Rheol. 1985, 29, 49–66. [Google Scholar] [CrossRef]
- Feng, D.; Caulfield, D.; Sanadi, A. Effect of compatibilizer on the structure-property relationships of kenaf-fiber/polypropylene composites. Polym. Compos. 2001, 22, 506–517. [Google Scholar] [CrossRef]
- Behera, A.K.; Avancha, S.; Basak, R.K.; Sen, R.; Adhikari, B. Fabrication and characterizations of biodegradable jute reinforced soy based green composites. Carbohydr. Polym. 2012, 88, 329–335. [Google Scholar] [CrossRef]
- O’donnell, A.; Dweib, M.; Wool, R. Natural fiber composites with plant oil-based resin. Compos. Sci. Technol. 2004, 64, 1135–1145. [Google Scholar] [CrossRef]
- Zhu, J.; Chandrashekhara, K.; Flanigan, V.; Kapila, S. Curing and mechanical characterization of a soy-based epoxy resin system. J. Appl. Polym. Sci. 2004, 91, 3513–3518. [Google Scholar] [CrossRef]
- Guo, A.; Cho, Y.; Petrović, Z.S. Structure and properties of halogenated and nonhalogenated soy-based polyols. J. Polym. Sci. Part A 2000, 38, 3900–3910. [Google Scholar] [CrossRef]
- Williams, G.I.; Wool, R.P. Composites from natural fibers and soy oil resins. Appl. Compos. Mater. 2000, 7, 421–432. [Google Scholar] [CrossRef]
- Kim, J.T.; Netravali, A.N. Mechanical and thermal properties of sisal fiber-reinforced green composites with soy protein/gelatin resins. J. Biobased Mater. Bioenergy 2010, 4, 338–345. [Google Scholar] [CrossRef]
- Galià, M.; de Espinosa, L.M.; Ronda, J.C.; Lligadas, G.; Cádiz, V. Vegetable oil-based thermosetting polymers. Eur. J. Lipid Sci. Technol. 2010, 112, 87–96. [Google Scholar] [CrossRef]




| Acid number | % Solid | Viscosity (Pa·s) a | Mn (kg/mol) b | Đ c | |
|---|---|---|---|---|---|
| MESS | 19 | 98.51 | 438.73 | 3,610 | 1.009 |
| Wavenumber (cm−1) | Vibration type |
|---|---|
| 3,480 | OH stretching |
| 1,747 | Fatty acid ester C=O stretching |
| 1,718 | Methacrylate C=O stretching |
| 1,637 | Methacrylate C=C stretching |
| 941 | Methacrylate =C–H out of plane bending |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amiri, A.; Yu, A.; Webster, D.; Ulven, C. Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials. Polymers 2016, 8, 153. https://doi.org/10.3390/polym8040153
Amiri A, Yu A, Webster D, Ulven C. Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials. Polymers. 2016; 8(4):153. https://doi.org/10.3390/polym8040153
Chicago/Turabian StyleAmiri, Ali, Arvin Yu, Dean Webster, and Chad Ulven. 2016. "Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials" Polymers 8, no. 4: 153. https://doi.org/10.3390/polym8040153
APA StyleAmiri, A., Yu, A., Webster, D., & Ulven, C. (2016). Bio-Based Resin Reinforced with Flax Fiber as Thermorheologically Complex Materials. Polymers, 8(4), 153. https://doi.org/10.3390/polym8040153








