A Parametric Study of Epoxy-Bonded CF/QF-BMI Composite Joints Using a Method Combining RBF Neural Networks and NSGA-II Algorithm
Abstract
1. Introduction
2. Specimen Preparation and Experimental Tests
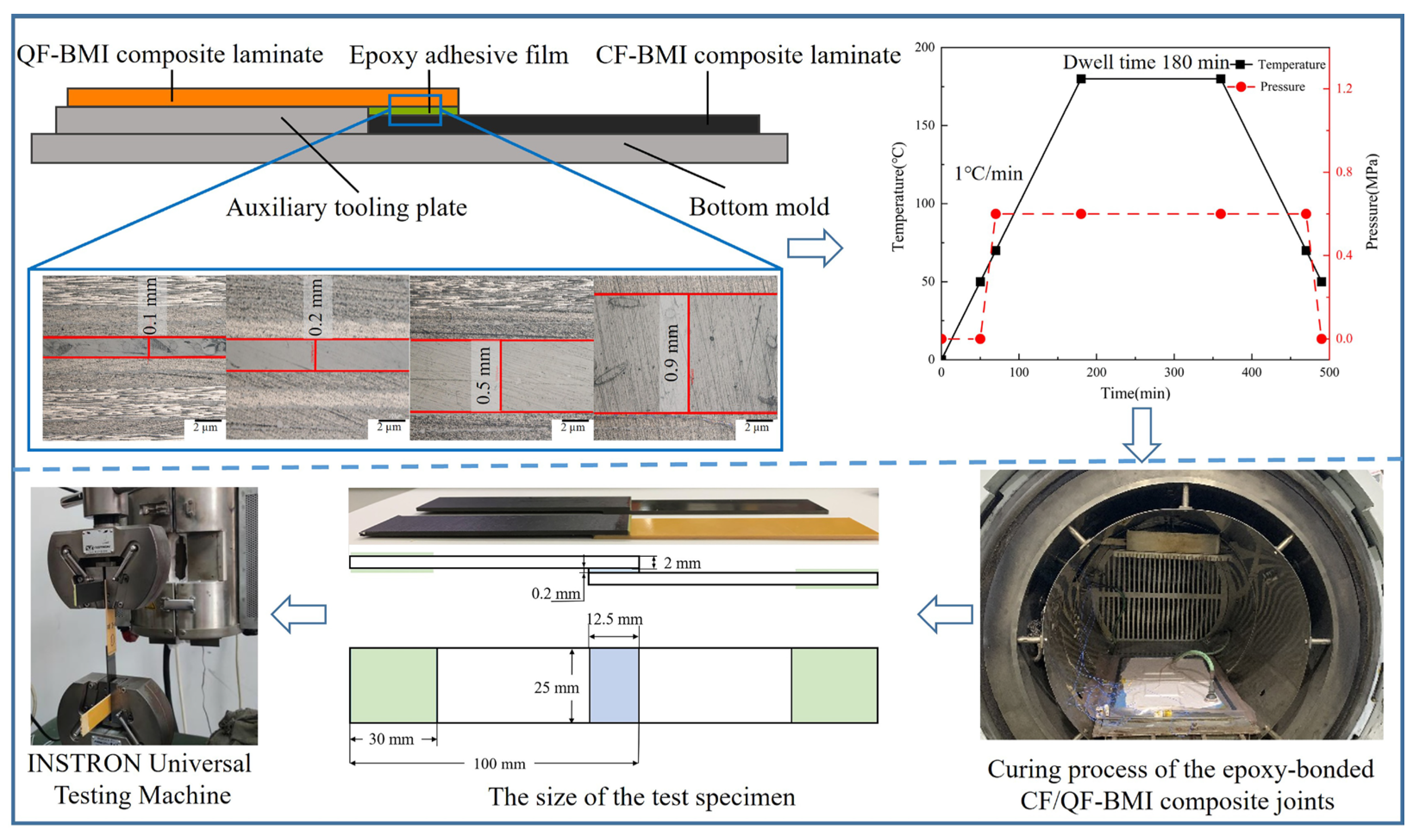
2.1. Material and Sample Preparation
2.2. Performance Test and Characterization
3. Theoretical Model
3.1. Intrinsic Model and Failure Criteria
- Fiber tensile failure:
- Fiber compression failure:
- Matrix tensile failure:
- Matrix compression failure:where and represent the longitudinal tensile strength and the transverse tensile strength, respectively. and represent the longitudinal compressive strength and the transverse compressive strength, respectively. Notably, the longitudinal direction is designated as the fiber direction, and the transverse direction is designated as perpendicular to the fiber direction. represents the stress components, represents the shear strength, and the indices and take the values of 1, 2, or 3. Index 1 corresponds to the fiber direction, while indices 2 and 3 represent directions perpendicular to the fiber.
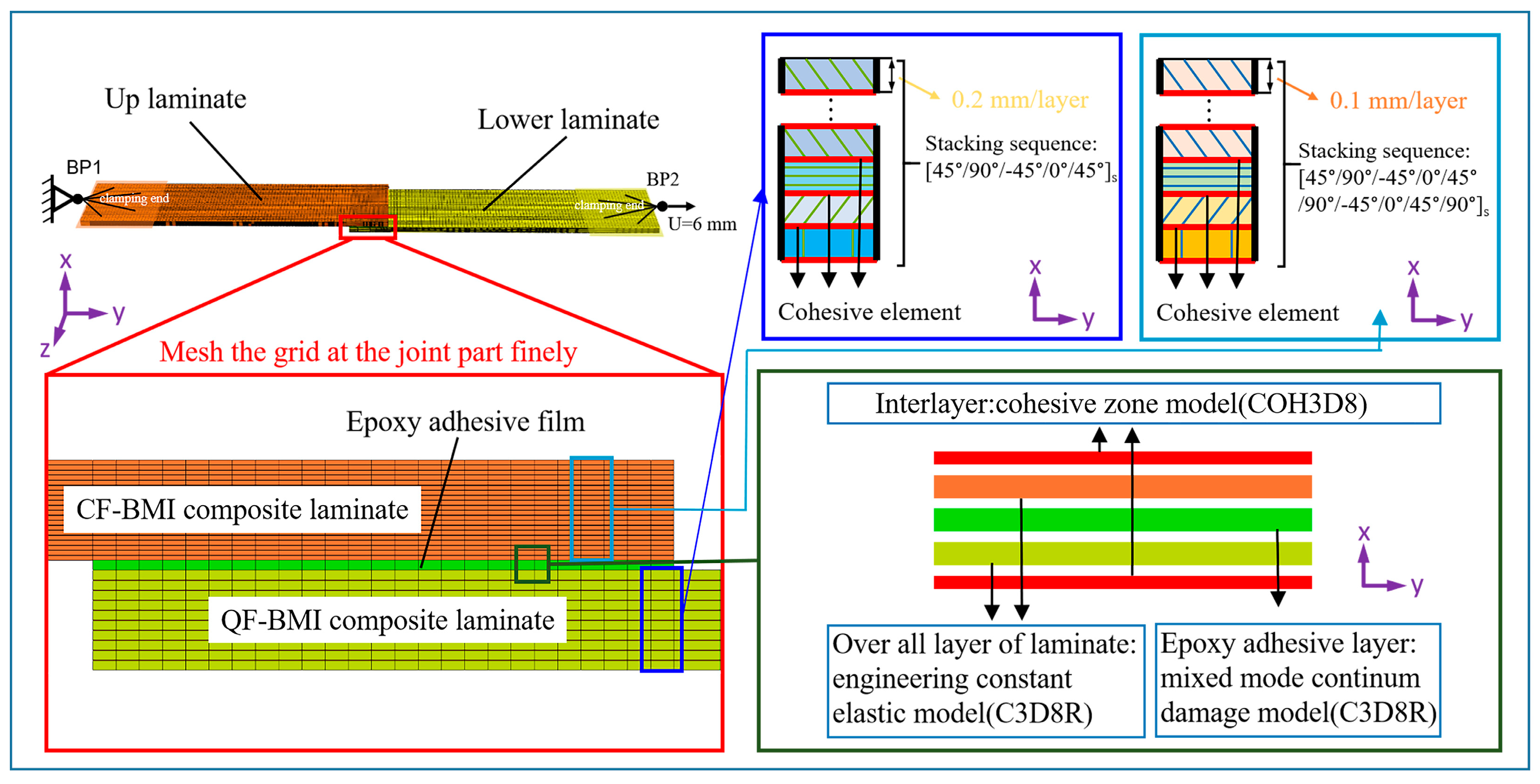
3.2. Finite Element Simulation Model
3.3. Machine-Learning Model
3.4. Multi-Objective Optimization Method
4. Results and Discussion
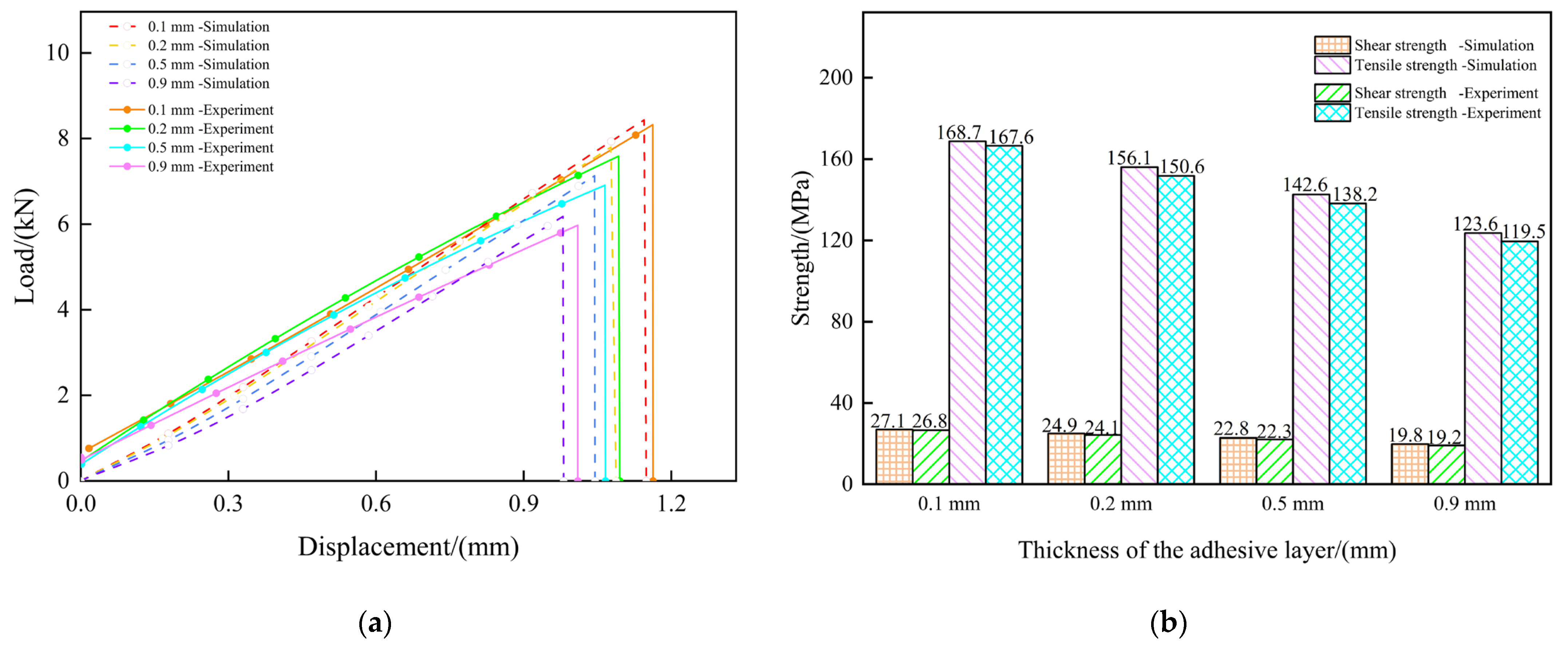
4.1. Finite Element Model Verification
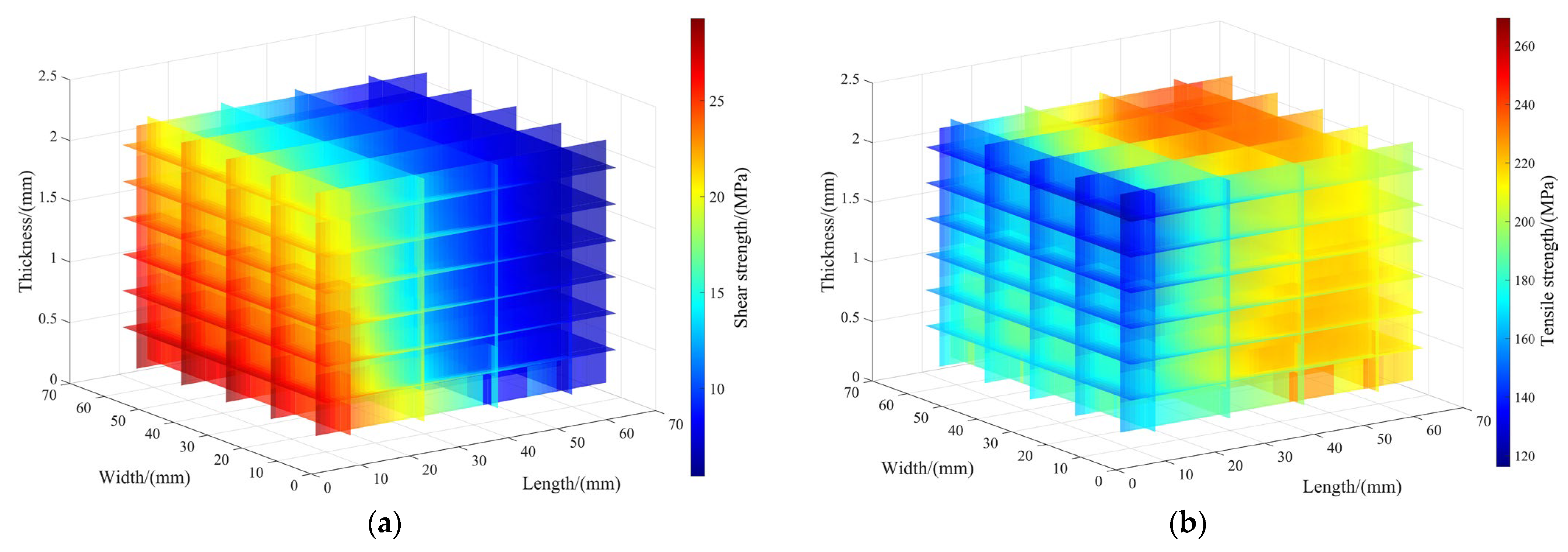
4.2. Machine-Learning Result Analysis
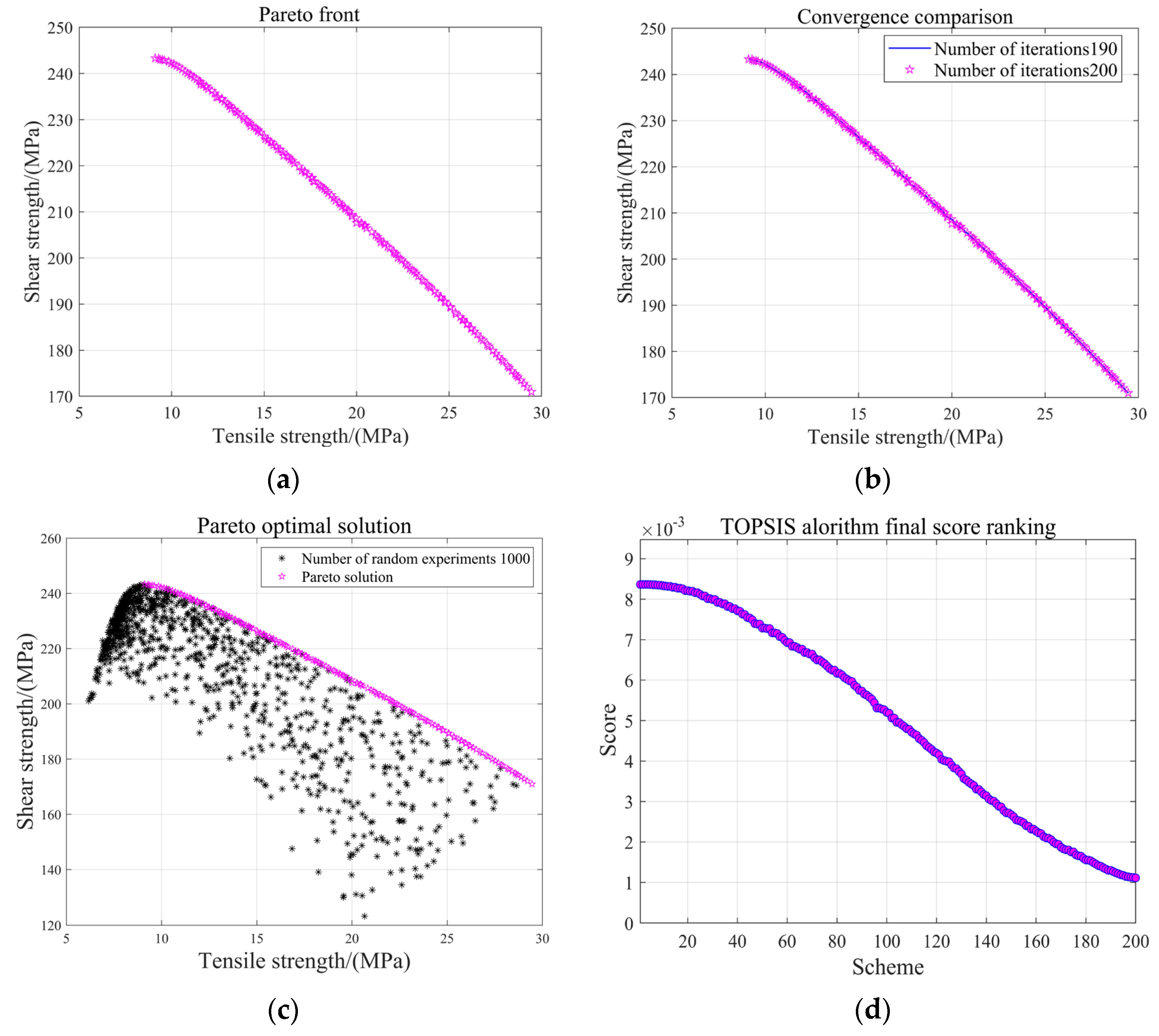
4.3. Multi-Objective Optimization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tiwary, A.; Kumar, R.; Chohan, J.S. A review on characteristics of composite and advanced materials used for aerospace applications. Mater. Today Proc. 2022, 51, 865–870. [Google Scholar]
- Ma, Y.; Wang, J.; Zhao, Y.; Wei, X.; Ju, L.; Chen, Y. A new vacuum pressure infiltration CFRP method and preparation experimental study of composite. Polymers 2020, 12, 419. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, Z.; Han, M.; Zhang, J.; Tang, Y.; Gu, J. Block copolymer functionalized quartz fibers/cyanate ester wave-transparent laminated composites. J. Mater. Sci. Technol. 2023, 139, 189–197. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, M.; Zhan, L.; Ma, B.; Wu, X.; Liu, C.; Xiang, H. Effects of Curing Defects in Adhesive Layers on Carbon Fiber–Quartz Fiber Bonded Joint Performance. Polymers 2024, 16, 1406. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.D.; Barros, S. An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes. 2017, 72, 30–42. [Google Scholar] [CrossRef]
- Wang, Z.; Xian, G. Cohesive zone model prediction of debonding failure in CFRP-to-steel bonded interface with a ductile adhesive. Compos. Sci. Technol. 2022, 230, 109315. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, Y.; Hughes, D.J. A parametric study of adhesive bonded joints with composite material using black-box and grey-box machine learning methods: Deep neuron networks and genetic programming. Compos. Part B Eng. 2021, 217, 108894. [Google Scholar] [CrossRef]
- Wahab, S.; Salami, B.A.; Danish, H. A hybrid machine learning approach for predicting fiber-reinforced polymer-concrete interface bond strength. Eng. Appl. Artif. Intell. 2025, 148, 110458. [Google Scholar] [CrossRef]
- Rośkowicz, M.; Godzimirski, J.; Komorek, A.; Jasztal, M. The Effect of Adhesive Layer Thickness on Joint Static Strength. Materials 2021, 14, 1499. [Google Scholar] [CrossRef] [PubMed]
- Neto, J.; Campilho, R.D.S.G.; da Silva, L.F.M. Parametric study of adhesive joints with composites. Int. J. Adhes. Adhes. 2012, 37, 96–101. [Google Scholar] [CrossRef]
- Pisharody, A.; Smith, D.E. An experimental and numerical investigation into the effects of bond line thickness variations on the strength of composite bonded joints. Compos. Struct. 2022, 279, 114789. [Google Scholar] [CrossRef]
- Chen, Q.; Du, B.; Zhang, X. Parametric investigation into the shear strength of adhesively bonded single-lap joints. Materials 2022, 15, 8013. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Tie, Y. Experimental and numerical investigations of adhesively bonded CFRP single-lap joints subjected to tensile loads. Int. J. Adhes. Adhes. 2019, 95, 102402. [Google Scholar] [CrossRef]
- Kim, M.H.; Ri, J.H.; Hong, H.S.A. 3-D numerical modeling for prediction of mixed failure characteristics in composite single lap joints with hybrid adhesive layer. Int. J. Adhes. Adhes. 2022, 118, 103223. [Google Scholar] [CrossRef]
- Yang, K.; Liu, Z.; Qi, X. Failure analysis and size optimization of CFRP composite single-lap bonded joints based on the influence of multiple parameters. Sci. Rep. 2024, 14, 32034. [Google Scholar] [CrossRef]
- Li, W.; Liang, Y.; Liu, Y. Failure load prediction and optimisation for adhesively bonded joints enabled by deep learning and fruit fly optimisation. Adv. Eng. Inform. 2022, 54, 101817. [Google Scholar] [CrossRef]
- Ribeiro, F.L.; Borges, L.; Almeida, J.R.M. Numerical stress analysis of carbon-fibre-reinforced epoxy composite single-lap joints. Int. J. Adhes. Adhes. 2011, 31, 331–337. [Google Scholar] [CrossRef]
- Tang, J.H.; Sridhar, I.; Srikanth, N. Static and fatigue failure analysis of adhesively bonded thick composite single lap joints. Compos. Sci. Technol. 2013, 86, 18–25. [Google Scholar] [CrossRef]
- Chen, R.; Li, S.; Zhou, Y. Damage formation and evolution mechanisms in drilling CFRP with prefabricated delamination defects: Simulation and experimentation. J. Mater. Res. Technol. 2023, 26, 6994–7011. [Google Scholar] [CrossRef]
- Agius, S.L.; Magniez, K.J.C.; Fox, B.L. Fracture behaviour of a rapidly cured polyethersulfone toughened carbon fibre/epoxy composite. Compos. Struct. 2010, 92, 2119–2127. [Google Scholar] [CrossRef]
- Nele, L.; Caggiano, A.; Teti, R. Autoclave cycle optimization for high performance composite parts manufacturing. Procedia CIRP 2016, 57, 241–246. [Google Scholar] [CrossRef]
- GB/T 7124-2008; Adhesives—Determination of Tensile Lap-Shear Strength of Rigid-to-Rigid Bonded Assemblies. Standardization Administration of the People’s Republic of China: Beijing, China, 2008.
- Li, S.; Zou, S.; Dai, L. Damage mechanism of carbon fiber reinforced plastic pipe based on reverse and forward curvature drilling. Compos. Struct. 2022, 292, 115700. [Google Scholar] [CrossRef]
- Echaabi, J.; Trochu, F.; Gauvin, R. Review of failure criteria of fibrous composite materials. Polym. Compos. 1996, 17, 786–798. [Google Scholar] [CrossRef]
- An, Z.; Cheng, X.; Zhao, D.; Ma, Y.; Guo, X.; Cheng, Y. Tensile and Compressive Properties of Woven Fabric Carbon Fiber-Reinforced Polymer Laminates Containing Three-Dimensional Microvascular Channels. Polymers 2024, 16, 665. [Google Scholar] [CrossRef]
- Wang, S.; Wang, C.; Shu, Y. Vickers indentation crack propagation analysis and finite element simulation verification based on the cohesive zone model in silicon carbide ceramics. Eng. Fract. Mech. 2025, 323, 111202. [Google Scholar] [CrossRef]
- Rong, C.; Shujian, L.; Pengnan, L. Effect of fiber orientation angles on the material removal behavior of CFRP during cutting process by multi-scale characterization. Int. J. Adv. Manuf. Technol. 2020, 106, 5017–5031. [Google Scholar] [CrossRef]
- Phadnis, V.A.; Makhdum, F.; Roy, A. Drilling in carbon/epoxy composites: Experimental investigations and finite element implementation. Compos. Part. A Appl. Sci. Manuf. 2013, 47, 41–51. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, J.; Sun, B. X-ray tomography and numerical study on low-velocity impact damages of three-dimensional angle-interlock woven composites. Compos. Struct. 2019, 230, 111525. [Google Scholar] [CrossRef]
- Gu, J.; Lu, H.; Guo, S. FEA on Process Induced Distortion of Hybrid Fiber Composite Based on ABAQUS. Aerosp. Mater. Technol. 2018, 48, 5. [Google Scholar]
- Chang, T.; Zhan, L.; Tan, W. Cohesive zone modeling of the autoclave pressure effect on the delamination behavior of composite laminates. J. Reinf. Plast. Compos. 2018, 37, 1468–1480. [Google Scholar] [CrossRef]
- Guo, X.; Guan, Z.; Nie, H. Damage tolerance analysis of adhesively bonded composite single lap joints containing a debond flaw. J. Adhes. 2017, 93, 216–234. [Google Scholar] [CrossRef]
- Hu, D.; Shao, W.; Lu, D. Design and material optimization of carbon fiber composite winding reinforcement layer for vehicle Type-IV hydrogen storage vessels. J. Energy Storage 2024, 100, 113459. [Google Scholar] [CrossRef]
- Mottaghian, F.; Taheri, F. Machine learning/finite element analysis-A collaborative approach for predicting the axial impact response of adhesively bonded joints with unique sandwich composite adherends. Compos. Sci. Technol. 2023, 242, 110162. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Liu, L. Prediction and fitting of weld morphology of Al alloy-CFRP welding-rivet hybrid bonding joint based on GA-BP neural network. J. Manuf. Process 2021, 63, 109–120. [Google Scholar] [CrossRef]
- Kiran, M.D.; BR, L.Y.; Babbar, A. Tribological properties of CNT-filled epoxy-carbon fabric composites: Optimization and modelling by machine learning. J. Mater. Res. Technol. 2024, 28, 2582–2601. [Google Scholar] [CrossRef]
- Hui, X.; Xu, Y.; Zhang, W. Cure process evaluation of CFRP composites via neural network: From cure kinetics to thermochemical coupling. Compos. Struct. 2022, 288, 115341. [Google Scholar] [CrossRef]
- Mukherjee, A.; Gupta, D.; Bhattacharyya, D. Mass-Constrained hybrid Gaussian radial basis neural networks: Development, training, and applications to modeling nonlinear dynamic noisy chemical processes. Comput. Chem. Eng. 2025, 197, 109080. [Google Scholar] [CrossRef]
- Batista, L.P.; da Silva Rodrigues, L.L.L.; de Freitas Souza, M.; das Chagas, P.S.F.; de Melo, S.B.; de Jesus Passos, A.B.R.; Hernández, M.C.R.; Araújo, M.A.S.; Silva, D.V. Artificial neural networks to estimate the sorption and desorption of the herbicide linuron in Brazilian soils. Environ. Pollut. 2025, 368, 125702. [Google Scholar] [CrossRef]
- Xu, Y.; Gai, Y.; Li, H. Multi-objective shape-section optimization of free-form latticed shells using the RBF-NSGA-II algorithm. Thin Wall. Struct. 2024, 200, 111918. [Google Scholar] [CrossRef]
- Zhang, T.; Wei, Z.; Wang, L. Multi-objective optimization of composite stiffened panels for mass and buckling load using PNN-NSGA-III algorithm and TOPSIS method. TWS 2025, 209, 112878. [Google Scholar] [CrossRef]



| Materials | Unidirectional CF-BMI Composite Laminate | Woven QF-BMI Composite Laminate | |
|---|---|---|---|
| Property | |||
| (MPa) | |||
| (MPa) | |||
| (MPa) | 11,000 | 9000 | |
| 0.15 | |||
| (MPa) | 6500 | ||
| (MPa) | |||
| (MPa) | 560 | ||
| (MPa) | |||
| (MPa) | 560 | ||
| (MPa) | |||
| Shear strength S (MPa) | 70 | ||
| (MPa) | 110,000 | ||
| (MPa) | 53 | ||
| (MPa) | 32 | ||
| (kJ/m2) | 0.51 | ||
| (kJ/m2) | 1.55 | ||
| Materials | Mechanical Parameters of Epoxy Adhesive Film J-116 | |
|---|---|---|
| Property | ||
| Young’s modulus E (MPa) | 2000 | |
| Poisson’s ratio v | 0.3 | |
| Yield stress σy (MPa) | 60 | |
| Fracture energy Gf (kJ/m2) | 0.5 | |
| Models | R2 | MAE | MBE | |
|---|---|---|---|---|
| Strength | ||||
| Shears strength | 0.99509 | 0.1611 | −0.048091 | |
| Tensile strength | 0.98788 | 1.826 | 0.011954 | |
| Sample Number | Parameter Value | Target Value | |||
|---|---|---|---|---|---|
| T (mm) | L (mm) | W (mm) | σS (MPa) | σΤ (MPa) | |
| 1 | 0.1 | 10 | 49.1 | 29.5 | 173.6 |
| 2 | 0.1 | 18.6 | 46.1 | 22.9 | 199.7 |
| 3 | 0.1 | 13.3 | 56 | 26.6 | 185.2 |
| 4 | 0.1 | 16.7 | 50.5 | 24.2 | 195.1 |
| 5 | 0.1 | 12.3 | 46.1 | 27.7 | 181.2 |
| 6 | 0.18 | 36.6 | 58.1 | 12.7 | 232.9 |
| … | … | … | … | … | … |
| 196 | 0.94 | 44.5 | 66 | 10.3 | 240.3 |
| 197 | 1.01 | 49.6 | 62 | 9.3 | 242.5 |
| 198 | 1.04 | 47.1 | 67.2 | 9.7 | 241.8 |
| 199 | 1.1 | 48.4 | 64.1 | 9.5 | 242.3 |
| 200 | 1.24 | 49.6 | 66 | 9.3 | 242.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zou, X.; Zhang, J.; Guo, R.; Xiang, H.; Zhan, L.; Wu, X. A Parametric Study of Epoxy-Bonded CF/QF-BMI Composite Joints Using a Method Combining RBF Neural Networks and NSGA-II Algorithm. Polymers 2025, 17, 1769. https://doi.org/10.3390/polym17131769
Yang X, Zou X, Zhang J, Guo R, Xiang H, Zhan L, Wu X. A Parametric Study of Epoxy-Bonded CF/QF-BMI Composite Joints Using a Method Combining RBF Neural Networks and NSGA-II Algorithm. Polymers. 2025; 17(13):1769. https://doi.org/10.3390/polym17131769
Chicago/Turabian StyleYang, Xiaobo, Xingyu Zou, Jingyu Zhang, Ruiqing Guo, He Xiang, Lihua Zhan, and Xintong Wu. 2025. "A Parametric Study of Epoxy-Bonded CF/QF-BMI Composite Joints Using a Method Combining RBF Neural Networks and NSGA-II Algorithm" Polymers 17, no. 13: 1769. https://doi.org/10.3390/polym17131769
APA StyleYang, X., Zou, X., Zhang, J., Guo, R., Xiang, H., Zhan, L., & Wu, X. (2025). A Parametric Study of Epoxy-Bonded CF/QF-BMI Composite Joints Using a Method Combining RBF Neural Networks and NSGA-II Algorithm. Polymers, 17(13), 1769. https://doi.org/10.3390/polym17131769







