Cure Kinetics-Driven Compression Molding of CFRP for Fast and Low-Cost Manufacturing
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. DSC Measurements
2.3. Rheological Measurements
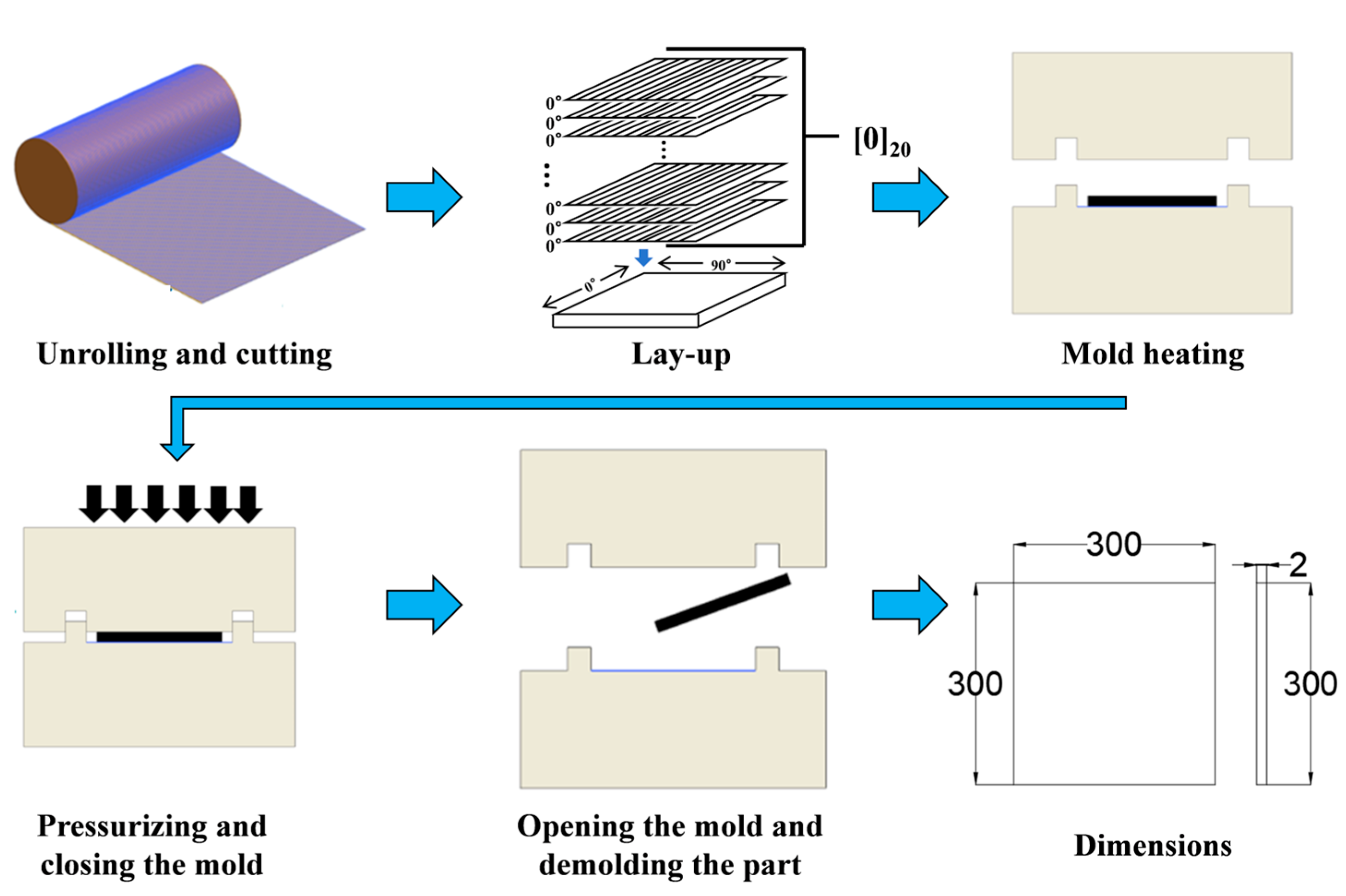
2.4. Compression Molding Process
2.5. Interlaminar Shear Strength Test
3. Results
3.1. Epoxy Curing Behavior Analysis
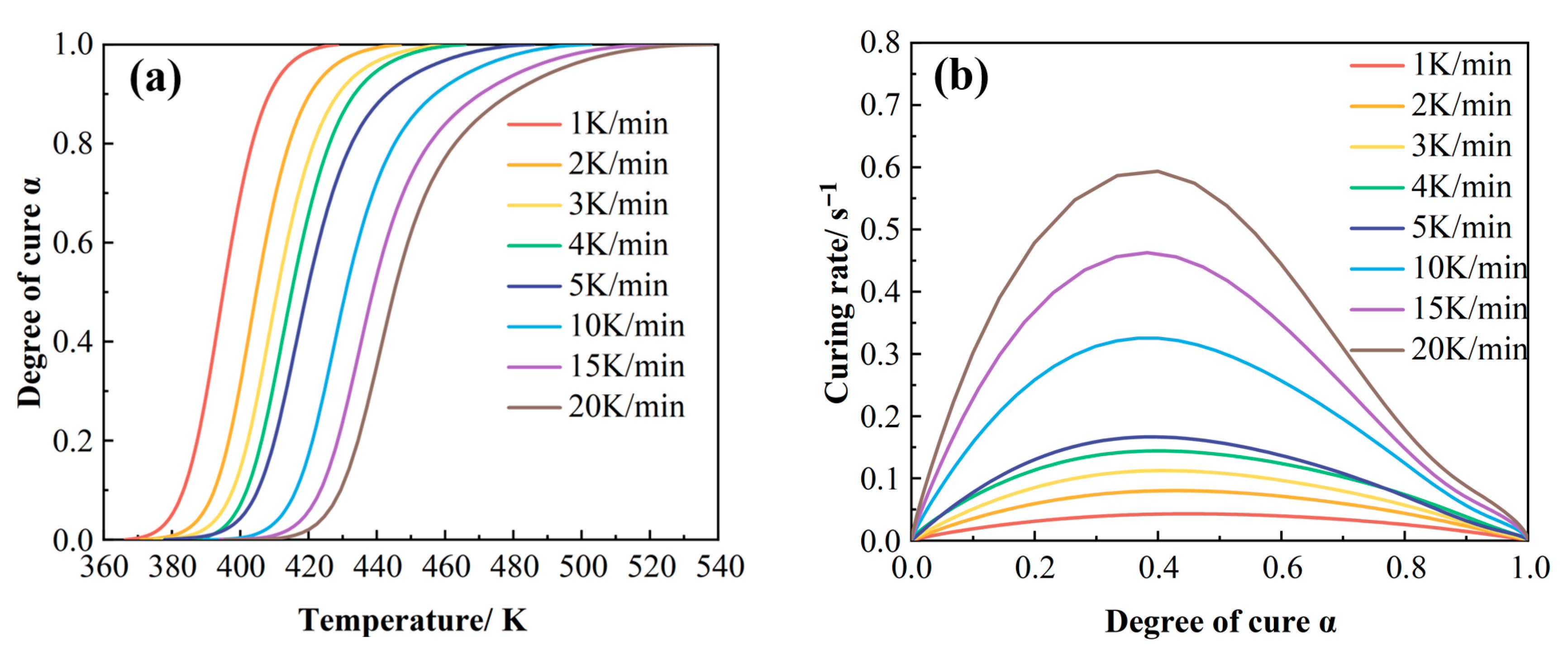
3.1.1. Dynamic Curing Kinetics Characterization and Modeling
3.1.2. Isothermal Curing Kinetics Considering the Heating Process
3.1.3. Dynamic Versus Isothermal Viscosity Test
3.2. Curing Cycle Optimization Analysis
3.2.1. Process Orthogonal Experiment Optimization
3.2.2. Weighted Scoring for Compression Molding Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFRP | Carbon fiber-reinforced polymer |
| MRCC | Manufacturer-recommended curing cycle |
| UV-FP | Ultraviolet-assisted frontal polymerization |
| DSC | Differential scanning calorimetry |
| FWO | Flynn–Wall–Ozawa |
| PSO | Particle swarm optimization |
| ILSS | Interlaminar shear strength |
| AHP | Analytic Hierarchy Process |
References
- Gutkin, R.; Green, C.J.; Vangrattanachai, S.; Pinho, S.T.; Robinson, P.; Curtis, P.T. On acoustic emission for failure investigation in CFRP: Pattern recognition and peak frequency analyses. Mech. Syst. Signal Process. 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Friedrich, K.; Almajid, A.A. Manufacturing Aspects of Advanced Polymer Composites for Automotive Applications. Appl. Compos. Mater. 2013, 20, 107–128. [Google Scholar] [CrossRef]
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber-reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019, 105, 2289–2308. [Google Scholar] [CrossRef]
- Al-Lami, A.; Hilmer, P.; Sinapius, M. Eco-efficiency assessment of manufacturing carbon fiber reinforced polymers (CFRP) in aerospace industry. Aerosp. Sci. Technol. 2018, 79, 669–678. [Google Scholar] [CrossRef]
- Ahmad, F.; Al Awadh, M.; Abas, M.; Noor, S.; Hameed, A. Optimization of Carbon Fiber Reinforced Plastic Curing Parameters for Aerospace Application. Appl. Sci. 2022, 12, 4307. [Google Scholar] [CrossRef]
- Gonzalez, J.A.; Farjas, J.; Blanco, N.; Costa, J.; Gascons, M.; Sanchez-Rodriguez, D. Towards time-reduced cure cycles of epoxy resins for mass production of composites maintaining the thermo-mechanical properties. J. Therm. Anal. Calorim. 2025, 150, 1205–1215. [Google Scholar] [CrossRef]
- Eom, S.Y.; Seo, S.B.; Lee, K.Y. Study on Cure Behavior of Low Temperature and Fast Cure Epoxy with Mercaptan Hardener. Polym.-Korea 2013, 37, 240–248. [Google Scholar] [CrossRef]
- Tarafdar, A.; Lin, W.; Naderi, A.; Wang, X.; Fu, K.; Hosein, I.D.; Wang, Y. UV-induced frontal polymerization for optimized in-situ curing of epoxy resin for excellent tensile and flexural properties. Compos. Commun. 2024, 46, 101832. [Google Scholar] [CrossRef]
- Tang, Y.; Fairclough, J.P.A. Electrical curing of carbon fibre composites with conductive epoxy resins. Compos. Part A Appl. Sci. Manuf. 2024, 185, 108296. [Google Scholar] [CrossRef]
- Xu, X.; Wang, X.; Cai, Q.; Wang, X.; Wei, R.; Du, S. Improvement of the Compressive Strength of Carbon Fiber/Epoxy Composites via Microwave Curing. J. Mater. Sci. Technol. 2016, 32, 226–232. [Google Scholar] [CrossRef]
- Muc, A.; Romanowicz, P.; Chwal, M. Description of the Resin Curing ProcessFormulation and Optimization. Polymers 2019, 11, 127. [Google Scholar] [CrossRef]
- de Calbiac, J.; Olivier, P.; Zbed, R.S.; Torres, M.; Broutelle, M.; Destarac, M.; Guerre, M. Assessing the Impact of the Off-Stoichiometric Epoxy/Amine Ratio on the Curing Kinetics and Properties of Space-Grade Disulfide-Based Vitrimer Resins. ACS Appl. Polym. Mater. 2025, 7, 5271–5279. [Google Scholar] [CrossRef]
- Farzanehfar, N.; Taheri, A.; Rafiemanzelat, F.; Jazani, O.M. Impact of multi-function SiO2-nanoscale ionic materials on the curing kinetics of epoxy resin: New approach to improve curing characteristics of thermoset polymers. Polym. Compos. 2025, 46, 7858–7881. [Google Scholar] [CrossRef]
- Yang, Y.; Lou, C.; Wang, H.; Yu, J. Synthesis and curing kinetics of O-aminoacetophenone-modified dicyandiamide curing agents for epoxy resin. Thermochim. ACTA 2025, 747, 179963. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhao, T.; Gong, Y.; Yu, Z. Synthesis, curing kinetics and properties of novel aromatic multifunctional epoxy resin. Eur. Polym. J. 2024, 219, 113375. [Google Scholar] [CrossRef]
- Jia, H.L.; Zhu, Y.D.; Yan, C.; Chen, M.D.; Chen, G.; Liu, D. Reliability evaluation of a new method developed for DSC curing kinetic model of epoxy resin. J. Appl. Polym. Sci. 2023, 140, e53986. [Google Scholar] [CrossRef]
- Yan, S.; Verestek, W.; Zeizinger, H.; Schmauder, S. Characterization of Cure Behavior in Epoxy Using Molecular Dynamics Simulation Compared with Dielectric Analysis and DSC. Polymers 2021, 13, 3085. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Qi, L.; He, W.; He, L. A novel approach on the study of cure kinetics for rheological isothermal and non-isothermal methods. Compos. Part B Eng. 2019, 162, 242–249. [Google Scholar] [CrossRef]
- GB/T 30969-2014; Test Method for Short-Beam Shear Strength of Polymer Matrix Composite Materials. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2014.
- Yang, X.; Zhan, L.; Jiang, C.; Zhao, X.; Guan, C.; Chang, T. Evaluating random vibration assisted vacuum processing of carbon/epoxy composites in terms of interlaminar shear strength and porosity. J. Compos. Mater. 2019, 53, 2367–2376. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Montoro, S.R.; Voorwald, H.J.C.; Cioffi, M.O.H. Porosity Characterization of Carbon Fiber/Epoxy Composite Using Hg Porosimetry and Other Techniques. Polym. Eng. Sci. 2020, 60, 841–849. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Ornaghi, H.L.; Voorwald, H.J.C.; Cioffi, M.O.H. Three-dimensional porosity characterization in carbon/glass fiber epoxy hybrid composites. Compos. Part A Appl. Sci. Manuf. 2019, 125, 105555. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Y.C.; Huang, P. Effect of cure cycle on curing process and hardness for epoxy resin. Express Polym. Lett. 2009, 3, 534–541. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, L.; Guo, X.; Cai, Z.; Huang, K. Study on curing kinetics of epoxy system and DFT simulation. J. Therm. Anal. Calorim. 2023, 148, 11069–11079. [Google Scholar] [CrossRef]
- Hardis, R.Z. Cure Kinetics Characterization and Monitoring of an Epoxy Resin for Thick Composite Structures. Master’s Thesis, Iowa State University, Ames, IA, USA, 2012. [Google Scholar]
- Liang, J.; Liu, L.; Qin, Z.; Zhao, X.; Li, Z.; Emmanuel, U.; Feng, J. Experimental Study of Curing Temperature Effect on Mechanical Performance of Carbon Fiber Composites with Application to Filament Winding Pressure Vessel Design. Polymers 2023, 15, 982. [Google Scholar] [CrossRef] [PubMed]
- Corcione, C.E.; Freuli, F.; Frigione, M. Cold-Curing Structural Epoxy Resins: Analysis of the Curing Reaction as a Function of Curing Time and Thickness. Materials 2014, 7, 6832–6842. [Google Scholar] [CrossRef]
- Puhurcuoglu, N.; Arman, Y. Parameter estimation of epoxy resin cure kinetics by dynamics DSC data. Polym. Adv. Technol. 2024, 35, e6498. [Google Scholar] [CrossRef]
- Tao, R.; Phansalkar, S.P.; Forster, A.M.; Han, B. Investigation of Cure Kinetics of Advanced Epoxy Molding Compound Using Dynamic Heating Scan: An Overlooked Second Reaction. In Proceedings of the 2023 IEEE 73rd Electronic Components and Technology Conference, ECTC, Orlando, FL, USA, 30 May–2 June 2023; pp. 1319–1326. [Google Scholar]
- Marotta, A.; Faggio, N.; Brondi, C. Curing Kinetics of Bioderived Furan-Based Epoxy Resins: Study on the Effect of the Epoxy Monomer/Hardener Ratio. Polymers 2022, 14, 5322. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, X.; Yu, X. Reaction mechanism, cure behavior and properties of a multifunctional epoxy resin, TGDDM, with latent curing agent dicyandiamide. RSC Adv. 2018, 8, 8248–8258. [Google Scholar] [CrossRef] [PubMed]
- Korotkov, R.; Shutov, V.; Orlov, A.; Bornosuz, N.; Kulemza, D.; Onuchin, D.; Shcherbina, A.; Gorbunova, I.; Sirotin, I. The Kinetic Study of the Influence of Common Modifiers on the Curing Process of Epoxy Vitrimers. Polymers 2024, 16, 392. [Google Scholar] [CrossRef]
- Anagwu, F.I.; Skordos, A.A. Cure kinetics, glass transition advancement and chemo-rheological modelling of an epoxy vitrimer based on disulphide metathesis. Polymer 2023, 288, 126427. [Google Scholar] [CrossRef]
- Bernath, A.; Kaerger, L.; Henning, F. Accurate Cure Modeling for Isothermal Processing of Fast Curing Epoxy Resins. Polymers 2016, 8, 390. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Fang, Y.; Zhou, A.; Jiang, P.; Shu, S.; Chen, L.; Wang, S.; Wei, L. Curing Kinetics and Mechanism Research of E44/T31 Insulation Paint. Mater. Sci.-Medzg. 2019, 25, 478–484. [Google Scholar] [CrossRef]
- Zheng, T.; Wang, X.; Lu, C.; Zhang, X.; Ji, Y.; Bai, C.; Chen, Y.; Qiao, Y. Studies on Curing Kinetics and Tensile Properties of Silica-Filled Phenolic Amine/Epoxy Resin Nanocomposite. Polymers 2019, 11, 680. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, H.; Chen, Y.; Kang, G.; Hua, L.; Feng, J. Study on Curing Kinetics and the Mechanism of Ultrasonic Curing of an Epoxy Adhesive. Polymers 2022, 14, 512. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, Y.; Meng, Q.; Zhang, L. Hyperspectral Image Classification based on Multiple Improved Particle Swarm Cooperative Optimization and SVM. In Proceedings of the 2012 21st International Conference on Pattern Recognition (ICPR 2012), Tsukuba, Japan, 11–15 November 2012; pp. 2274–2277. [Google Scholar]
- Politi, M.; Breuer, O.; Cohen, Y. Simulation and Experimental Validation of the Cure Process of an Epoxy-Based Encapsulant. Exp. Mech. 2023, 63, 1429–1444. [Google Scholar] [CrossRef]
- Wu, X.; Zhan, L.; Li, S.; Li, W. Study on the Cure Kinetics of Epoxy Resin Prepreg in Fiber Metal Laminates. In Proceedings of the 2016 International Conference on Biomaterials, Nanomaterials and Composite Materials (CBNCM 2016), Chengdu, China, 4–6 November 2016. [Google Scholar]
- Zhang, S.; Tang, H.; Tang, D.; Liu, T.; Liao, W. Effect of fabrication process on the microstructure and mechanical performance of carbon fiber reinforced PEEK composites via selective laser sintering. Compos. Sci. Technol. 2024, 246, 110396. [Google Scholar] [CrossRef]
- Davies, L.W.; Day, R.J.; Bond, D.; Nesbitt, A.; Ellis, J.; Gardon, E. Effect of cure cycle heat transfer rates on the physical and mechanical properties of an epoxy matrix composite. Compos. Sci. Technol. 2007, 67, 1892–1899. [Google Scholar] [CrossRef]
- Seretis, G.; Kouzilos, G.; Manolakos, D.; Provatidis, C. Multi-Objective Curing Cycle Optimization for Glass Fabric/Epoxy Composites Using Poisson Regression and Genetic Algorithm. Mater. Res. Ibero-Am. J. Mater. 2018, 21, e20170815. [Google Scholar] [CrossRef]
- Yang, X.; Zhan, L.; Jiang, C.; Zhao, X.; Guan, C. Effect of random vibration processing on void content in composite laminates. Polym. Compos. 2019, 40, 3122–3130. [Google Scholar] [CrossRef]
- Ashir, M.; Nocke, A.; Bulavinov, A.; Pinchuk, R.; Cherif, C. Influence of Defined Amount of Voids on the Mechanical Properties of Carbon Fiber-Reinforced Plastics. Polym. Compos. 2019, 40, E1049–E1056. [Google Scholar] [CrossRef]
- Shi, J.; Wang, W.; Liu, F.; Xun, G.; Yang, P. Effects of porosity on ultrasonic attenuation coefficient, shear properties and failure mechanisms of CF/EP laminates. Heliyon 2024, 10, e25288. [Google Scholar] [CrossRef] [PubMed]
- Oktora, D.; Ting, Y.-H.; Sukoyo. Multi-Objective Optimization of Injection Parameters and Energy Consumption Based on ANN-Differential Evolution. Appl. Sci. 2025, 15, 826. [Google Scholar] [CrossRef]
- Li, F.; Chu, M.; Tang, J.; Feng, C. Optimization of High Chromium Vanadium-Titanium Magnetite Electric Melting Process by Comprehensive Weighted Scoring Method. J. Northeast. Univ. Nat. Sci. 2016, 37, 1327–1331. [Google Scholar]
- Dhurkari, R.K. Improving the Prescriptive Power of Analytic Hierarchy Process. IEEE Trans. Eng. Manag. 2023, 71, 7456–7466. [Google Scholar] [CrossRef]
- Moragues, S.; Lenzano, M.G.; Lanfri, M.; Moreiras, S.; Lannutti, E.; Lenzano, L. Analytic hierarchy process applied to landslide susceptibility mapping of the North Branch of Argentino Lake, Argentina. Nat. Hazards 2021, 105, 915–941. [Google Scholar] [CrossRef]
- Li, Z.-R.; Jiang, M.-G.; Feng, X.-L.; Wang, S.-Y.; Zeng, Q.-T.; Chen, C.; Liu, W.-L.; Sun, W. Analysis of energy consumption characteristics and fracture characteristics of moraine grouting solidified body under uniaxial compression. Front. Earth Sci. 2023, 11, 1223785. [Google Scholar] [CrossRef]

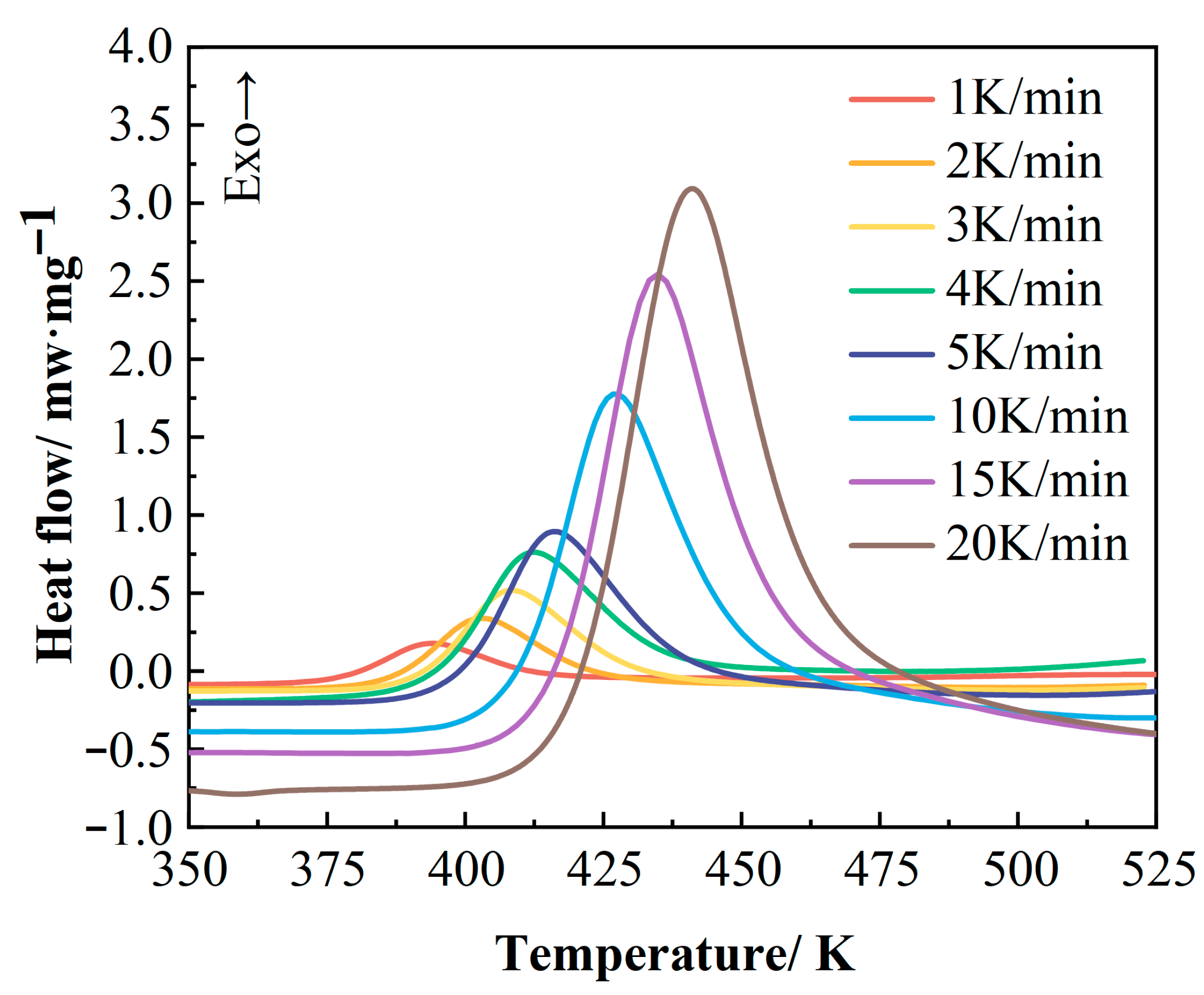
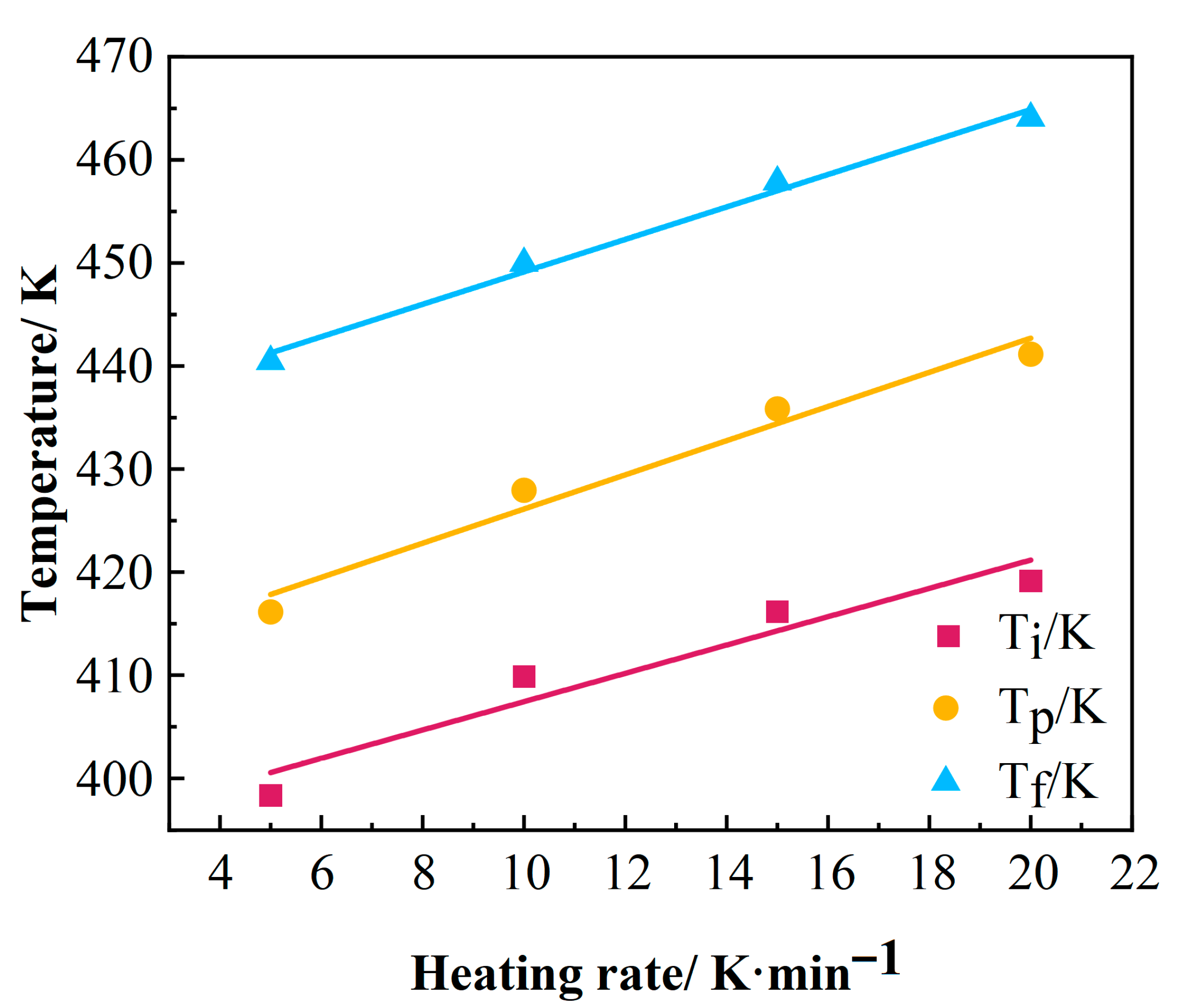
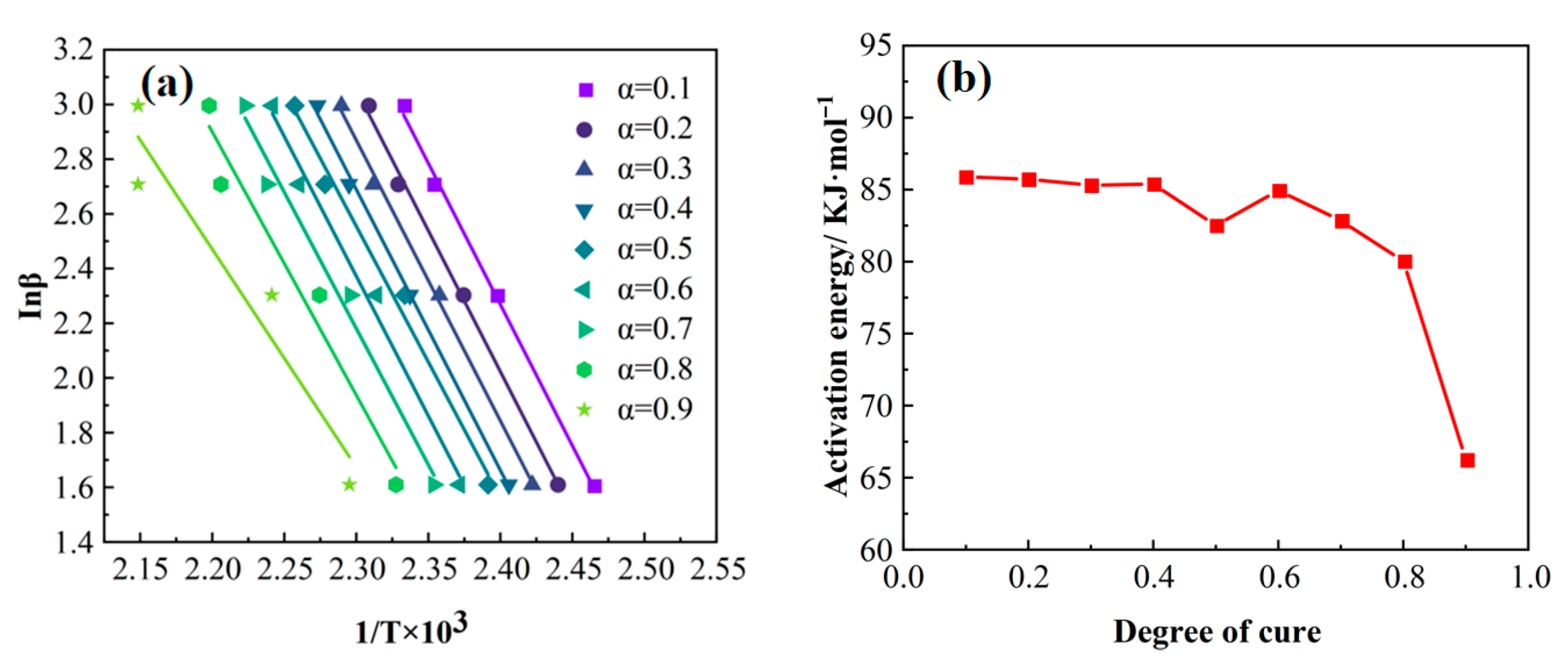
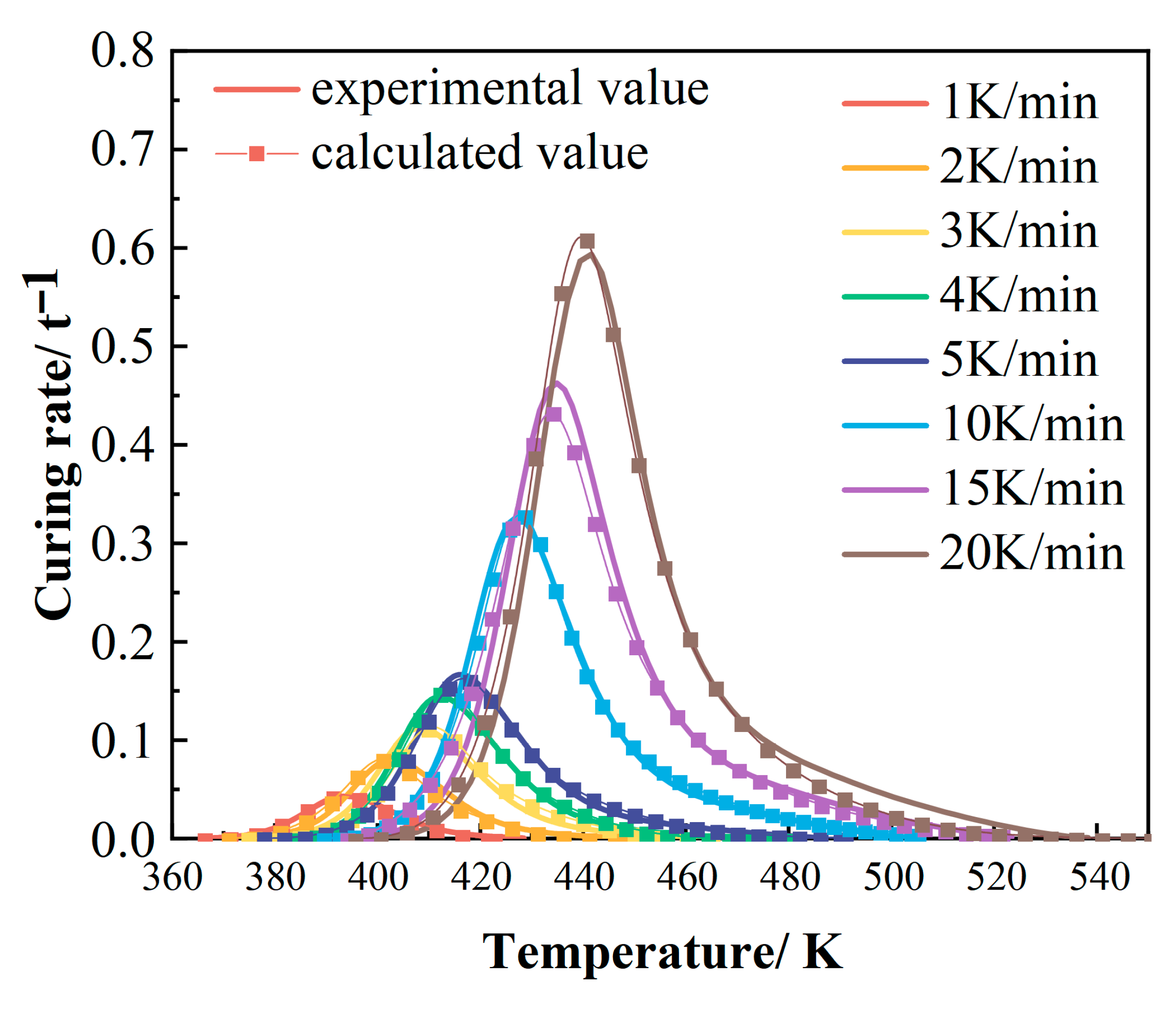
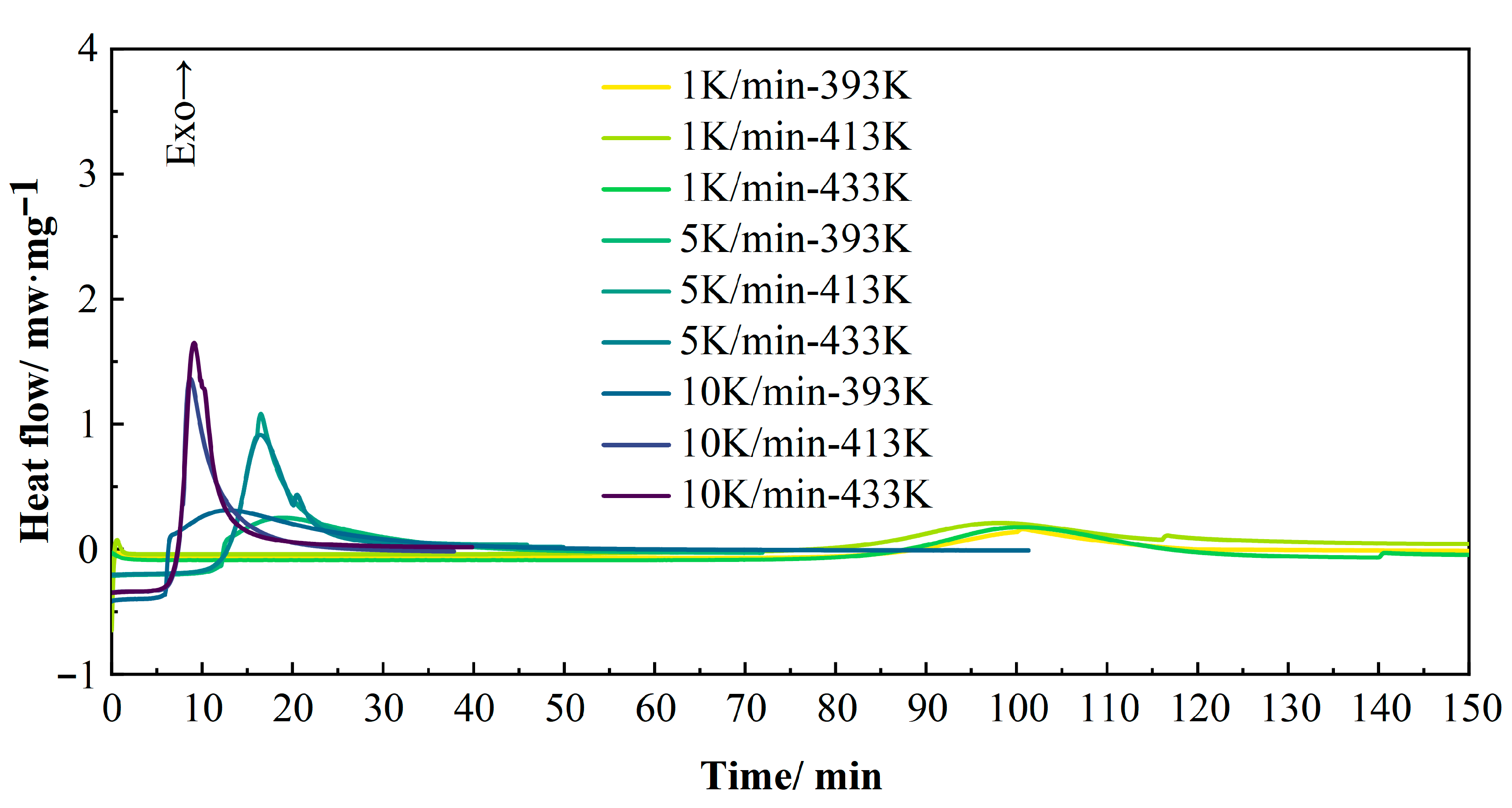

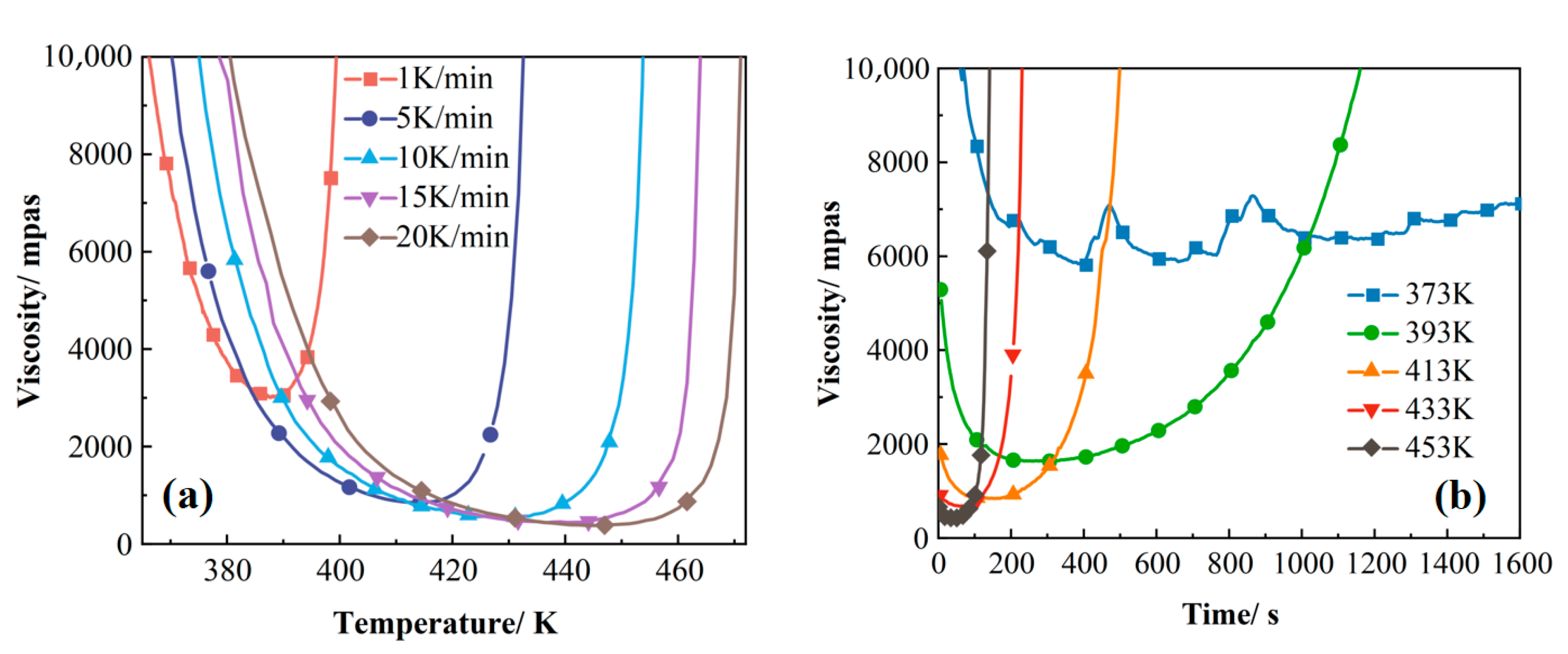


| Heating Rate (K/min) | Ti (K) | Tp (K) | Tf (K) | ∆HR (J/g) |
|---|---|---|---|---|
| 1 | 371.06 | 394.29 | 422.10 | 5.52 |
| 2 | 380.63 | 403.15 | 437.06 | 10.06 |
| 3 | 382.37 | 408.45 | 441.53 | 14.67 |
| 4 | 386.53 | 412.10 | 446.67 | 22.45 |
| 5 | 398.35 | 416.15 | 440.45 | 28.80 |
| 10 | 409.85 | 427.95 | 449.95 | 64.72 |
| 15 | 416.15 | 435.85 | 457.85 | 94.84 |
| 20 | 419.15 | 441.15 | 464.05 | 124.58 |
| A (min−1) | Energy (KJ/mol) | Order of Reaction |
|---|---|---|
| P1 = 18.25 | P5 = 62.67 | m = 0.546 |
| P2 = 3.29 | P6 = 9.58 | |
| P3 = −1.26 | P7 = 0.53 | n = 1.192 |
| P4 = −0.08 | P8 = 3.84 |
| Level | A Heating Rate (K/min) | B Temperature (K) | C Time (min) |
|---|---|---|---|
| 1 | 1 | 393 | 20 |
| 2 | 5 | 413 | 50 |
| 3 | 10 | 433 | 80 |
| Experiment | Heating Rate (K/min) | Temperature (K) | Holding Time (min) | Interlaminar Shear Strength (MPa) |
|---|---|---|---|---|
| 0-MRCC | 1 | 393 | 120 | 90.88 ± 2.11 |
| 1-A1B1C1 | 1 | 393 | 20 | 62.28 ± 4.15 |
| 2-A1B2C2 | 1 | 413 | 50 | 84.36 ± 2.90 |
| 3-A1B3C3 | 1 | 433 | 80 | 85.71 ± 2.68 |
| 4-A2B1C2 | 5 | 393 | 50 | 83.33 ± 2.95 |
| 5-A2B2C3 | 5 | 413 | 80 | 86.15 ± 3.05 |
| 6-A2B3C1 | 5 | 433 | 20 | 80.08 ± 2.54 |
| 7-A3B1C3 | 10 | 393 | 80 | 84.45 ± 2.64 |
| 8-A3B2C1 | 10 | 413 | 20 | 84.20 ± 2.38 |
| 9-A3B3C2 | 10 | 433 | 50 | 83.26 ± 2.31 |
| Factor | Heating Rate (K/min) | Temperature (K) | Time (min) |
|---|---|---|---|
| K1 | 232.35 | 230.06 | 226.56 |
| K2 | 249.56 | 254.71 | 250.95 |
| K3 | 251.91 | 249.05 | 256.31 |
| k1 | 77.45 | 76.69 | 75.52 |
| k2 | 83.19 | 84.90 | 83.65 |
| k3 | 83.97 | 83.02 | 85.44 |
| R | 6.52 | 8.22 | 9.92 |
| C > B > A | |||
| Experiment | Interlaminar Shear Strength (MPa) | Total Time (min) | Power Consumption (kWh) |
|---|---|---|---|
| MRCC | 90.88 ± 2.11 | 250 | 2.10 |
| 1-A1B1C1 | 62.28 ± 4.15 | 150 | 1.20 |
| 2-A1B2C2 | 84.36 ± 2.90 | 210 | 1.65 |
| 3-A1B3C3 | 85.71 ± 2.68 | 270 | 2.10 |
| 4-A2B1C2 | 83.33 ± 2.95 | 100 | 1.50 |
| 5-A2B2C3 | 86.15 ± 3.05 | 144 | 1.95 |
| 6-A2B3C1 | 80.08 ± 2.54 | 98 | 1.50 |
| 7-A3B1C3 | 84.45 ± 2.64 | 120 | 1.80 |
| 8-A3B2C1 | 84.20 ± 2.38 | 72 | 1.35 |
| 9-A3B3C2 | 83.26 ± 2.31 | 114 | 1.80 |
| C1 | C2 | C3 | |
|---|---|---|---|
| C1 | 1 | 3 | 5 |
| C2 | 1/3 | 1 | 2 |
| C3 | 1/5 | 1/2 | 1 |
| Experiment | Mechanical Property (Score) | Total Time (Score) | Energy Consumption (Score) | Synthesis Score | Ranking |
|---|---|---|---|---|---|
| MRCC | 1.00 | 0.10 | 0.00 | 0.66 | 7 |
| 1-A1B1C1 | 0.00 | 0.61 | 1.00 | 0.27 | 10 |
| 2-A1B2C2 | 0.77 | 0.30 | 0.50 | 0.62 | 8 |
| 3-A1B3C3 | 0.82 | 0.00 | 0.00 | 0.52 | 9 |
| 4-A2B1C2 | 0.74 | 0.86 | 0.67 | 0.76 | 2 |
| 5-A2B2C3 | 0.83 | 0.64 | 0.17 | 0.71 | 4 |
| 6-A2B3C1 | 0.62 | 0.87 | 0.67 | 0.69 | 6 |
| 7-A3B1C3 | 0.78 | 0.76 | 0.33 | 0.72 | 3 |
| 8-A3B2C1 | 0.77 | 1.00 | 0.83 | 0.83 | 1 |
| 9-A3B3C2 | 0.73 | 0.79 | 0.33 | 0.70 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Zhang, M.; Liu, Z.; Fu, X.; Liu, H.; Zhang, Y.; Yang, X. Cure Kinetics-Driven Compression Molding of CFRP for Fast and Low-Cost Manufacturing. Polymers 2025, 17, 2154. https://doi.org/10.3390/polym17152154
Wu X, Zhang M, Liu Z, Fu X, Liu H, Zhang Y, Yang X. Cure Kinetics-Driven Compression Molding of CFRP for Fast and Low-Cost Manufacturing. Polymers. 2025; 17(15):2154. https://doi.org/10.3390/polym17152154
Chicago/Turabian StyleWu, Xintong, Ming Zhang, Zhongling Liu, Xin Fu, Haonan Liu, Yuchen Zhang, and Xiaobo Yang. 2025. "Cure Kinetics-Driven Compression Molding of CFRP for Fast and Low-Cost Manufacturing" Polymers 17, no. 15: 2154. https://doi.org/10.3390/polym17152154
APA StyleWu, X., Zhang, M., Liu, Z., Fu, X., Liu, H., Zhang, Y., & Yang, X. (2025). Cure Kinetics-Driven Compression Molding of CFRP for Fast and Low-Cost Manufacturing. Polymers, 17(15), 2154. https://doi.org/10.3390/polym17152154





