Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes
Abstract
1. Introduction
2. Charge Regulation and Stretching of Weak Polyelectrolytes
2.1. Minimal Model of a Weak Flexible Polyelectrolyte
2.2. Constant Charge versus Constant-pH Simulations
2.3. Parameters Used in the Simulations
3. Effect of Charge Regulation in the Binding and Conformational Properties at Zero Force
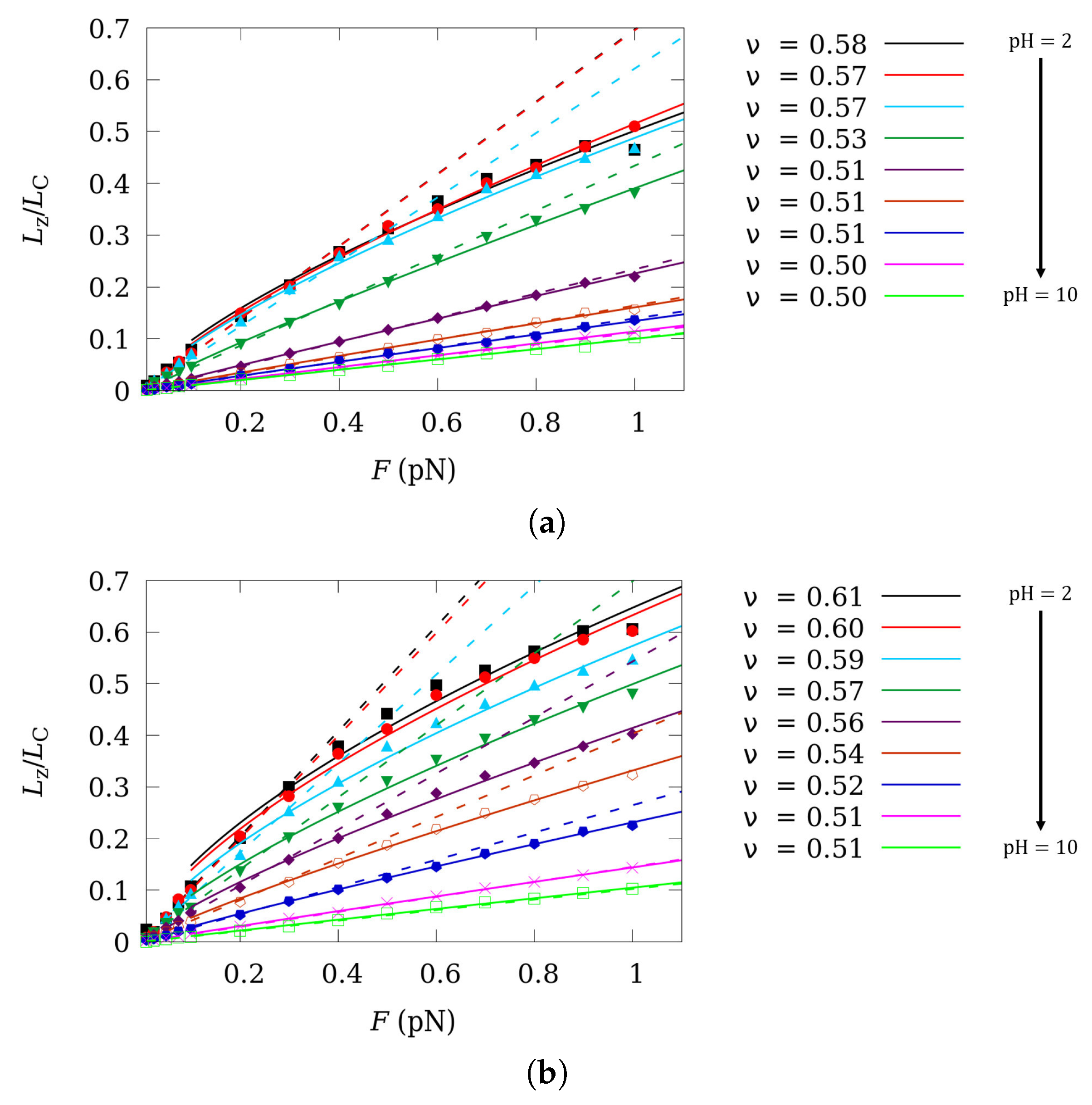
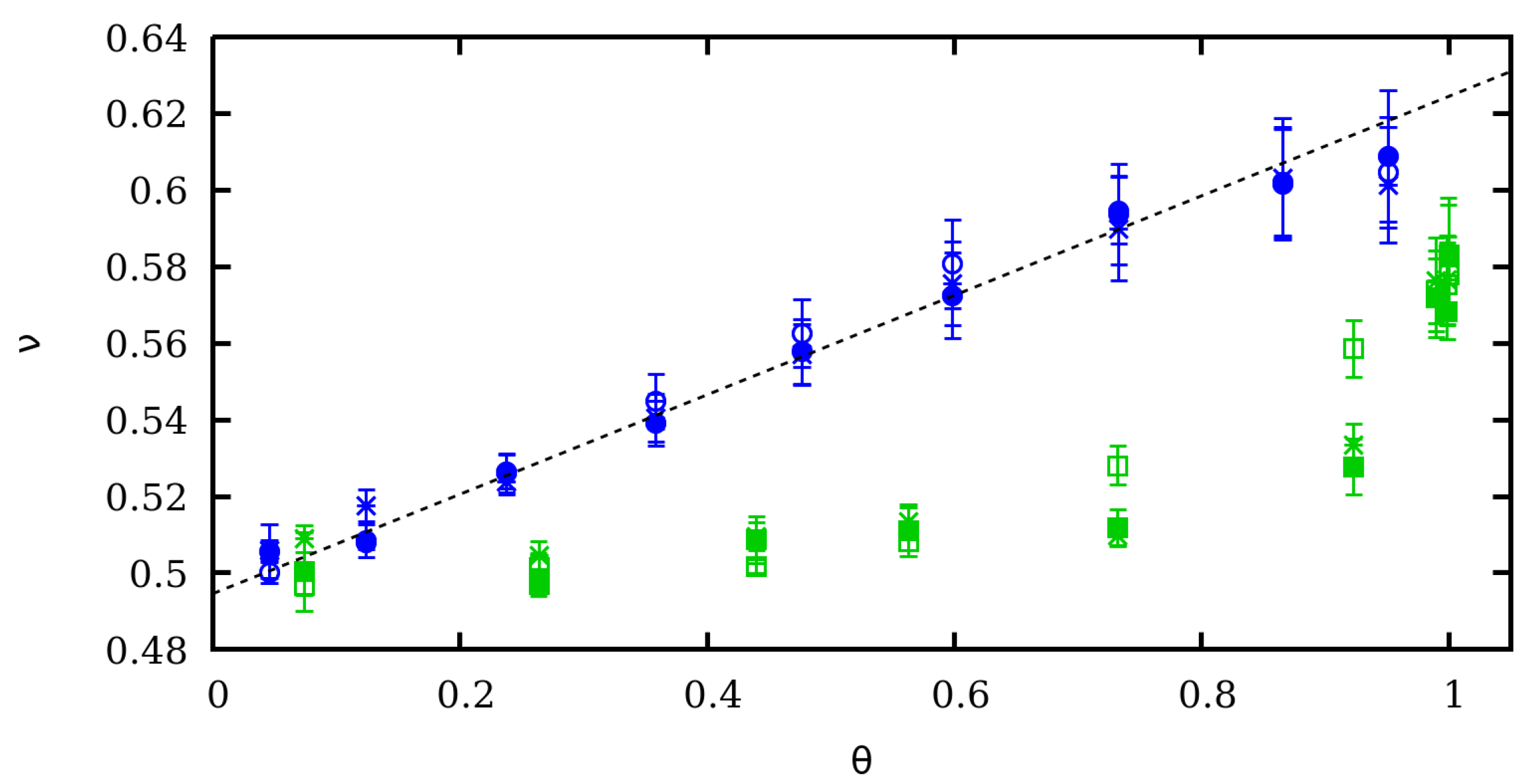
4. Scaling Properties of Mechanical Stretching in the Low Force Regime
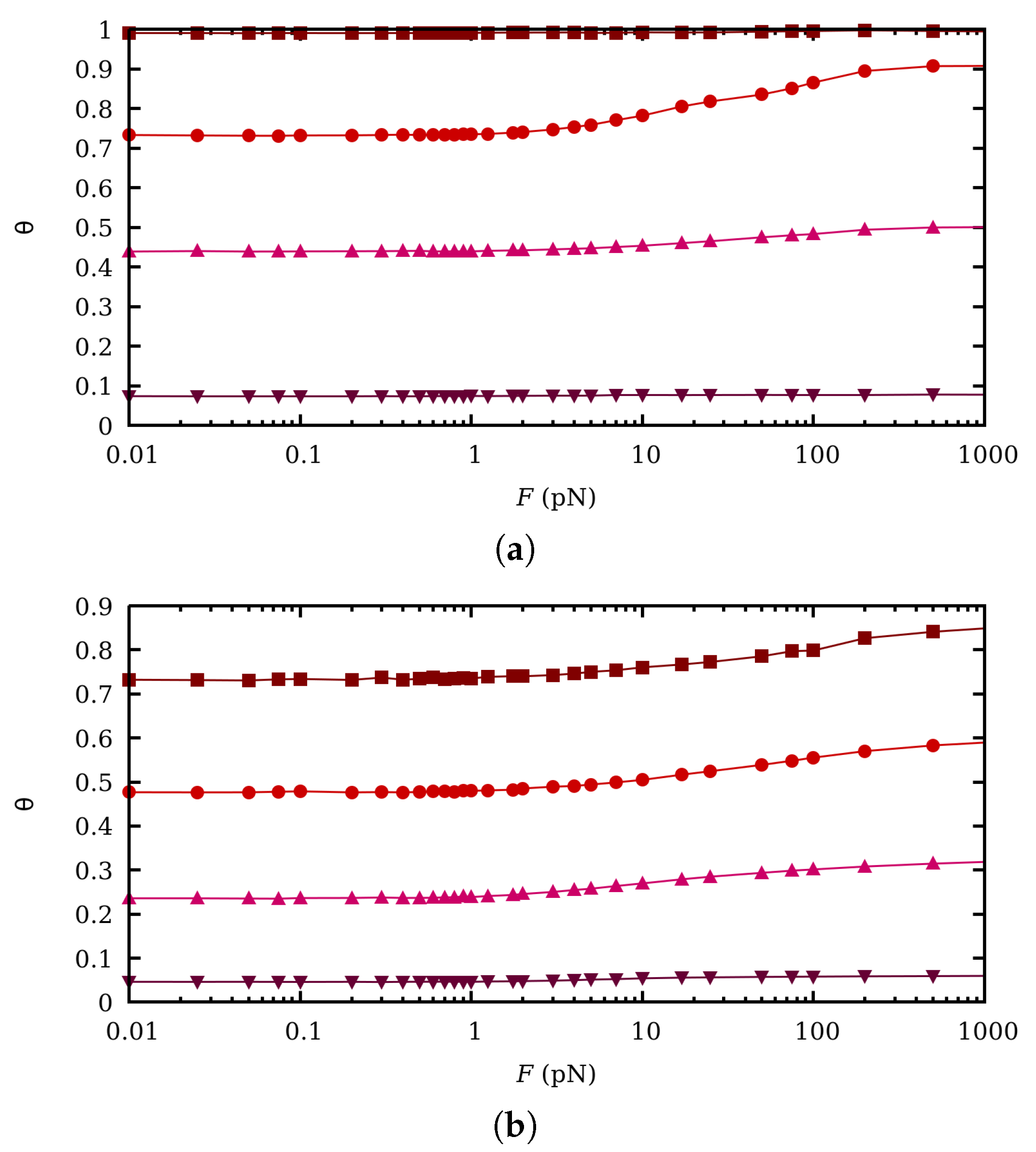
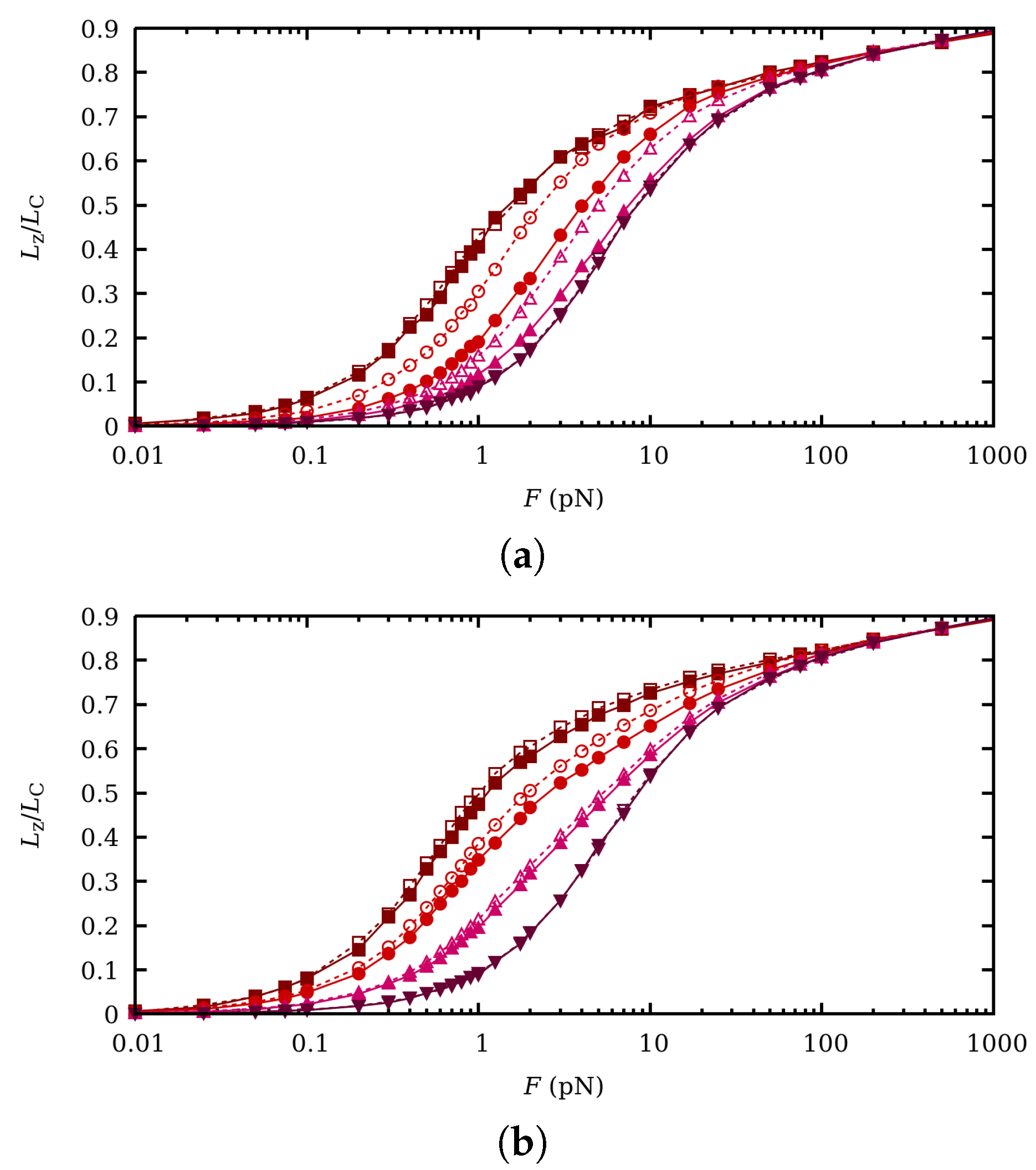
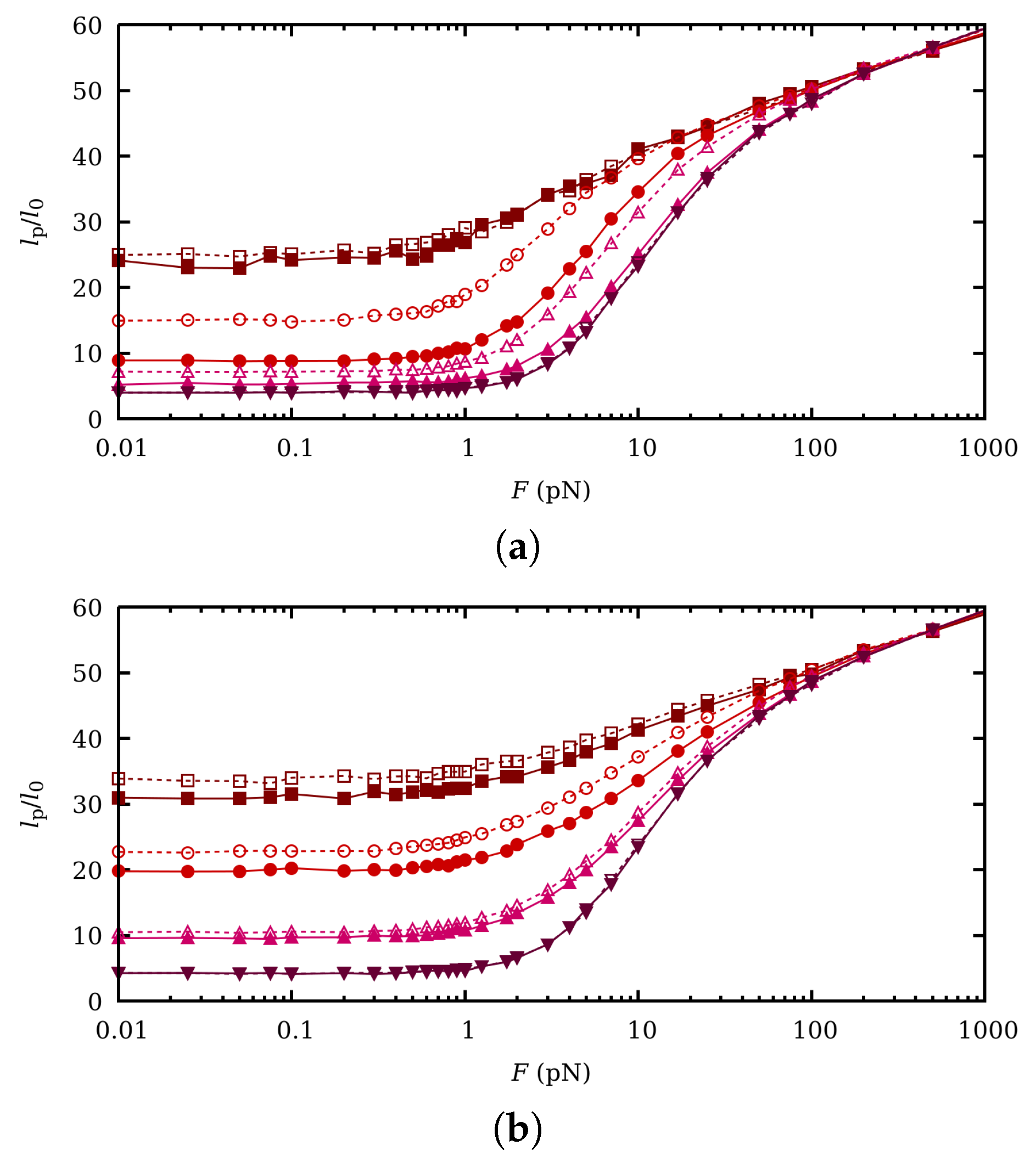
5. Influence of Charge Fluctuations in the Intermediate Force Regime
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ccMC | constant charge Monte Carlo |
| CF | Charge Fluctuation |
| CR | Charge Regulation |
| LPEI | Linear PolyEthylenImine |
| LR | Long Range |
| MC | Monte Carlo |
| RIS | Rotational Isomeric State |
| SB | Site Binding |
| SBRIS | Site Binding Rotational Isomeric State |
| SEV | Steric Excluded Volume |
| SGCMC | Semi-Grand Canonical Monte Carlo |
| SR | Short Range |
References
- Borkovec, M.; Jönsson, B.; Koper, G.J.M.J. Surface and Colloid Science; Matigeric, E., Ed.; Plenum Press: New York, NY, USA, 2001; Volume 10, Chapter 2; pp. 99–339. [Google Scholar]
- Lund, M.; Jo, B. Charge regulation in biomolecular solution. Q. Rev. Biophys. 2013, 46, 265–281. [Google Scholar] [CrossRef] [PubMed]
- Trefalt, G.; Behrens, S.H.; Borkovec, M. Charge Regulation in the Electrical Double Layer: Ion Adsorption and Surface Interactions. Langmuir 2016, 32, 380–400. [Google Scholar] [CrossRef] [PubMed]
- Hanakam, F.; Günther, G.; Lotz, S.; Alt, T.; Seelig, A. Binding of Hisactophilin I and II to Lipid Membranes Is Controlled by a pH-dependent myristoyl–histidine switch. Biochemistry 1996, 35, 11036–11044. [Google Scholar] [CrossRef] [PubMed]
- Narambuena, C.F.; Longo, G.S.; Szleifer, I. Lysozyme adsorption in pH-responsive hydrogel thin-films: The non-trivial role of acid-base equilibrium. Soft Matter 2015, 11, 6669–6679. [Google Scholar] [CrossRef]
- Lund, M.; Jönsson, B. On the Charge Regulation of Proteins. Biochemistry 2005, 44, 5722–5727. [Google Scholar] [CrossRef]
- Mason, A.C.; Jensen, J.H. Protein-protein binding is often associated with changes in protonation state. Proteins Struct. Funct. Bioinform. 2008, 71, 81–91. [Google Scholar] [CrossRef]
- Torres, P.; Bojanich, L.; Sanchez-Varretti, F.; Ramirez-Pastor, A.J.; Quiroga, E.; Boeris, V.; Narambuena, C.F. Protonation of β-lactoglobulin in the presence of strong polyelectrolyte chains: A study using Monte Carlo simulation. Colloids Surf. B Biointerfaces 2017, 160, 161–168. [Google Scholar] [CrossRef]
- Torres, P.B.; Quiroga, E.; Ramirez-Pastor, A.J.; Boeris, V.; Narambuena, C.F. Interaction between β-Lactoglobuline and Weak Polyelectrolyte Chains: A Study Using Monte Carlo Simulation. J. Phys. Chem. B 2019, 123, 8617–8627. [Google Scholar] [CrossRef]
- Carnal, F.; Clavier, A.; Stoll, S. Polypeptide-nanoparticle interactions and corona formation investigated by monte carlo simulations. Polymers 2016, 8, 203. [Google Scholar] [CrossRef]
- Hamacek, J.; Borkovec, M.; Piguet, C. Simple thermodynamics for unravelling sophisticated self-assembly processes. Dalton Trans. 2006, 1473–1490. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, T.; Wang, C.; Lin, Z.; Huang, G.; Sumer, B.D.; Gao, J. Molecular basis of cooperativity in pH-triggered supramolecular self-assembly. Nat. Commun. 2016, 7, 13214. [Google Scholar] [CrossRef] [PubMed]
- Cera, E.D. Stochastic linkage: Effect of random fluctuations on a twostate process Stochastic linkage: Effect of random fluctuations on a two-state process. J. Phys. Chem. 1991, 95, 5082–5086. [Google Scholar] [CrossRef]
- Svensson, B.; Jonsson, B.; Thulin, E. Binding of Calcium to Calmodulin and Its Tryptic Fragments: Theory and Experiment. Biochemistry 1993, 32, 2828–2834. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, B.; Anandakrishnan, R.; Ruscio, J.Z.; Onufriev, A.V. Statistics and physical origins of pK and ionization state changes upon protein-ligand binding. Biophys. J. 2010, 98, 872–880. [Google Scholar] [CrossRef] [PubMed]
- Hartig, S.M.; Greene, R.R.; Dikov, M.M.; Prokop, A.; Davidson, J.M. Multifunctional nanoparticulate polyelectrolyte complexes. Pharm. Res. 2007, 24, 2353–2369. [Google Scholar] [CrossRef] [PubMed]
- Whitten, S.T.; Garcia-Moreno, E.B.; Hilser, V.J. Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins. Proc. Natl. Acad. Sci. USA 2005, 102, 4282–4287. [Google Scholar] [CrossRef]
- Garcés, J.L.; Koper, G.J.M.; Borkovec, M. Ionization Equilibria and Conformational Transitions in Polyprotic Molecules and Polyelectrolytes. J. Phys. Chem. B 2006, 110, 10937–10950. [Google Scholar] [CrossRef]
- Garcés, J.L.; Madurga, S.; Borkovec, M. Coupling of conformational and ionization equilibria in linear poly (ethylenimine): A study based on the site binding/rotational isomeric state. Phys. Chem. Chem. Phys. 2014, 16, 4626–4638. [Google Scholar] [CrossRef]
- Garcés, J.L.; Madurga, S.; Rey-Castro, C.; Mas, F. Dealing with long-range interactions in the determination of polyelectrolyte ionization properties. Extension of the transfer matrix formalism to the full range of ionic strengths. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 275–284. [Google Scholar] [CrossRef]
- Blanco, P.M.; Madurga, S.; Mas, F.; Garcés, J.L. Coupling of charge regulation and conformational equilibria in linearweak polyelectrolytes: Treatment of long-range interactions via effective short-ranged and pH-dependent interaction parameters. Polymers 2018, 10, 811. [Google Scholar] [CrossRef]
- Giannotti, M.I.; Vancso, G.J. Interrogation of single synthetic polymer chains and polysaccharides by AFM-based force spectroscopy. ChemPhysChem 2007, 8, 2290–2307. [Google Scholar] [CrossRef] [PubMed]
- Rief, M.; Gautel, M.; Oesterhelt, F.; Fernandez, J.M.; Gaub, H.E. Immunoglobulin Domains by AFM Reversible Unfolding of Individual Titin Immunoglobulin Domains by AFM. Science 1997, 276, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Valiaev, A.; Lim, D.W.; Oas, T.G.; Chilkoti, A.; Zauscher, S. Force-Induced Prolyl Cis - Trans Isomerization in Elastin-like Polypeptides. J. Am. Chem. Soc. 2007, 129, 6491–6497. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, K.; Wang, Z.; Zhang, X. Host-enhanced π-π Interaction for water-soluble supramolecular polymerization. Chem. Eur. J. 2011, 17, 9930–9935. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Kouznetsova, T.B.; Niu, Z.; Ong, M.T.; Klukovich, H.M.; Rheingold, A.L.; Martinez, T.J.; Craig, S.L. Inducing and quantifying forbidden reactivity with single-molecule polymer mechanochemistry. Nat. Chem. 2015, 7, 323–327. [Google Scholar] [CrossRef] [PubMed]
- Radiom, M.; Kong, P.; Maroni, P.; Schäfer, M.; Kilbinger, A.F.M.; Borkovec, M. Mechanically induced cis-to-trans isomerization of carbon-carbon double bonds using atomic force microscopy. Phys. Chem. Chem. Phys. 2016, 18, 31202–31210. [Google Scholar] [CrossRef]
- Jacobson, D.R.; Mcintosh, D.B.; Stevens, M.J.; Rubinstein, M.; Saleh, O.A. Single-stranded nucleic acid elasticity arises from internal electrostatic tension. Proc. Natl. Acad. Sci. USA 2017, 114, 5095–5100. [Google Scholar] [CrossRef]
- Radiom, M.; Borkovec, M. Influence of ligand-receptor interactions on force-extension behavior within the freely jointed chain model. Phys. Rev. E 2017, 96, 062501. [Google Scholar] [CrossRef]
- Stevens, M.J.; Saleh, O.A. Simulations of Stretching a Strong, Flexible Polyelectrolyte. Macromolecules 2012, 45, 5757–5765. [Google Scholar] [CrossRef]
- Jacobson, D.R.; Mcintosh, D.B.; Saleh, O.A. The Snakelike Chain Character of Unstructured RNA. Biophys. J. 2013, 105, 2569–2576. [Google Scholar] [CrossRef]
- Stevens, M.J.; Berezneya, J.P.; Saleh, O.A. The Effect of Chain Stiffness and Salt on the Elastic Response of a Polyelectrolyte. J. Chem. Phys. 2018, 149, 163328. [Google Scholar] [CrossRef] [PubMed]
- Saleh, O.A.; McIntosh, D.B.; Pincus, P.; Ribeck, N. Nonlinear low-force elasticity of single-stranded DNA molecules. Phys. Rev. Lett. 2009, 102, 068301. [Google Scholar] [CrossRef] [PubMed]
- Mcintosh, D.B.; Saleh, O.A. Salt Species-Dependent Electrostatic Effects on ssDNA Elasticity. Macromolecules 2011, 44, 2328–2333. [Google Scholar] [CrossRef]
- Stevens, M.J.; Saleh, O.A. Simulations of Stretching a Strong, Flexible Polyelectrolyte: Using Long Chains To Access the Pincus Scaling Regime. Macromolecules 2013, 46, 6369–6373. [Google Scholar] [CrossRef]
- Blanco, P.M.; Madurga, S.; Mas, F.; Garcés, J.L. Effect of Charge Regulation and Conformational Equilibria in the Stretching Properties of Weak Polyelectrolytes. Macromolecules 2019, 52, 8017–8031. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Shumaker, J.B. Forces between Protein Molecules in Solution Arising from Fluctuations in Proton Charge and Configuration. Proc. Natl. Acad. Sci. USA 1952, 38, 863–871. [Google Scholar] [CrossRef]
- Odijk, T. Polyelectrolytes Near the Rod Limit. J. Polym. Sci. Polym. Phys. Ed. 1977, 15, 477–483. [Google Scholar] [CrossRef]
- Barrat, J.L.; Joanny, J.F. Persistence Length of Polyelectrolyte Chains. Europhys. Lett. 1993, 24, 333–338. [Google Scholar] [CrossRef]
- Ullner, M.; Jonsson, B. Monte Carlo study of titrating polyelectrolytes in the presence of salt. Macromolecules 1996, 29, 6645–6655. [Google Scholar] [CrossRef]
- Ullner, M. Comments on the Scaling Behavior of Flexible Polyelectrolytes within the Debye-Hückel Approximation. J. Phys. Chem. B 2003, 107, 8097–8110. [Google Scholar] [CrossRef]
- Ulrich, S.; Seijo, M.; Stoll, S. A Monte Carlo study of weak polyampholytes: Stiffness and primary structure influences on titration curves and chain conformations. J. Phys. Chem. B 2007, 111, 8459–8467. [Google Scholar] [CrossRef] [PubMed]
- Uyaver, S.; Seidel, C. First-order conformational transition of annealed polyelectrolytes in a poor solvent. Europhys. Lett. 2003, 64, 536–542. [Google Scholar] [CrossRef]
- Flory, P. Statistical Mechanics of Chain Molecules; John Wiley: New York, NY, USA, 1967. [Google Scholar]
- Sliozberg, Y.R.; Kröger, M.; Chantawansri, T.L. Fast equilibration protocol for million atom systems of highly entangled linear polyethylene chains Fast equilibration protocol for million atom systems of highly entangled linear polyethylene chains. J. Chem. Phys. 2016, 144, 154901. [Google Scholar] [CrossRef] [PubMed]
- Burak, Y.; Netz, R.R. Charge Regulation of Interacting Weak Polyelectrolytes. J. Phys. Chem. B 2004, 108, 4840–4849. [Google Scholar] [CrossRef]
- Livadaru, L.; Netz, R.R.; Kreuzer, H.J. Stretching response of discrete semiflexible polymers. Macromolecules 2003, 36, 3732–3744. [Google Scholar] [CrossRef]
- Saleh, O.A. Perspective: Single polymer mechanics across the force regimes. J. Phys. Chem. 2015, 142, 194902. [Google Scholar] [CrossRef] [PubMed]
- Pincus, P. Excluded Volume Effects and Stretched Polymer Chains. Macromolecules 1976, 9, 386–388. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, P.M.; Madurga, S.; Narambuena, C.F.; Mas, F.; Garcés, J.L. Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes. Polymers 2019, 11, 1962. https://doi.org/10.3390/polym11121962
Blanco PM, Madurga S, Narambuena CF, Mas F, Garcés JL. Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes. Polymers. 2019; 11(12):1962. https://doi.org/10.3390/polym11121962
Chicago/Turabian StyleBlanco, Pablo M., Sergio Madurga, Claudio F. Narambuena, Francesc Mas, and Josep L. Garcés. 2019. "Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes" Polymers 11, no. 12: 1962. https://doi.org/10.3390/polym11121962
APA StyleBlanco, P. M., Madurga, S., Narambuena, C. F., Mas, F., & Garcés, J. L. (2019). Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes. Polymers, 11(12), 1962. https://doi.org/10.3390/polym11121962