A Multi-Parameter Perturbation Solution and Experimental Verification for Bending Problem of Piezoelectric Cantilever Beams
Abstract
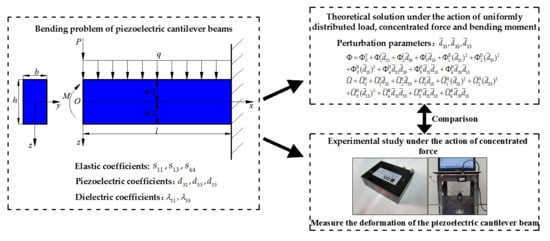
:1. Introduction
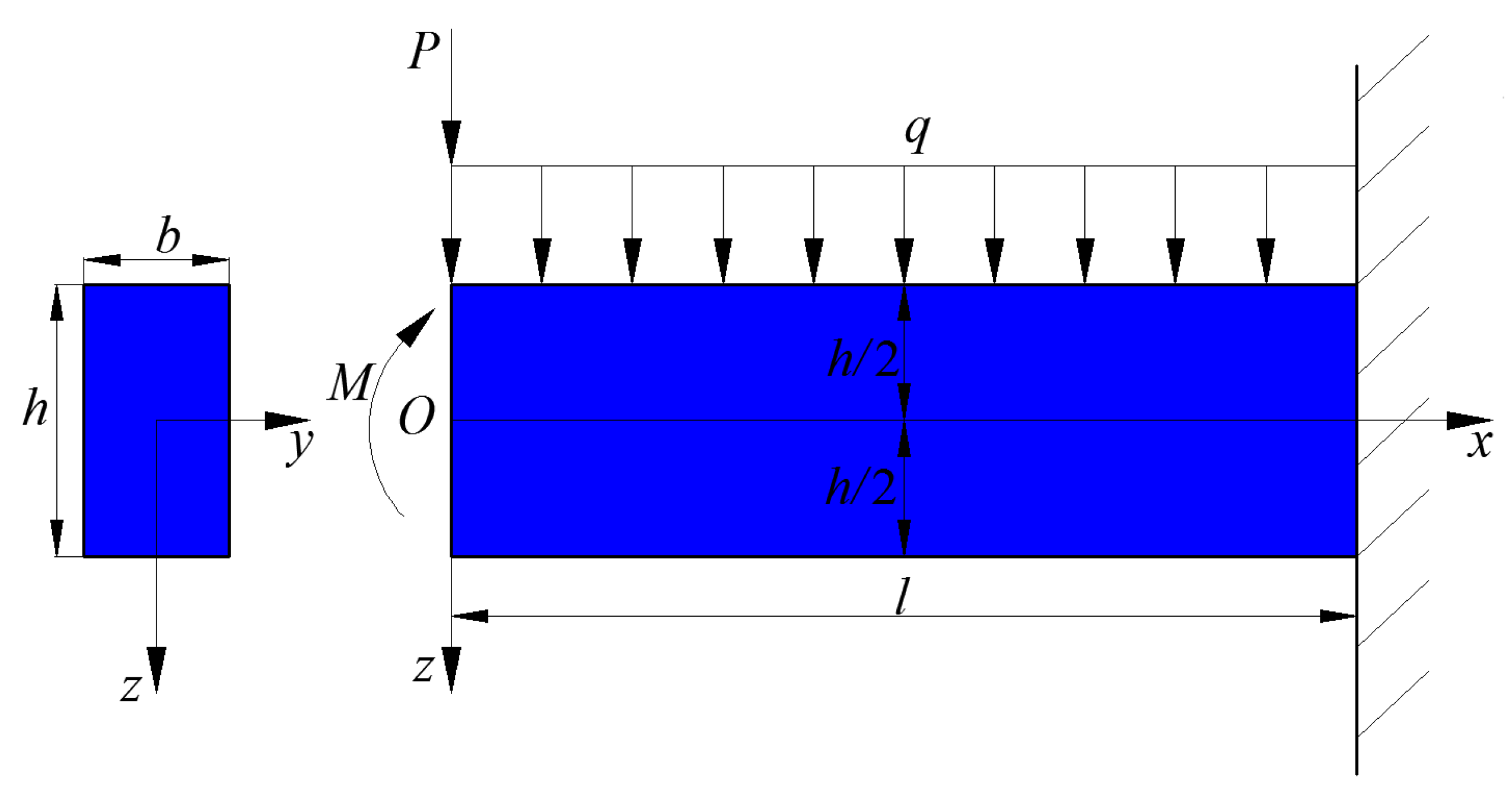
2. Mechanical Model and Basic Equations
3. Multi-parameter Perturbation Solution
4. Comparison of the Solution Presented Here and the Existing Solution
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Jiang, Y.G.; Gong, L.L.; Hu, X.H.; Zhao, Y.; Chen, H.W.; Feng, L.; Zhang, D.Y. Aligned P(VDF-TrFE) nanofibers for enhanced piezoelectric directional strain sensors. Polymers 2018, 10, 364. [Google Scholar] [CrossRef]
- Elnabawy, E.; Hassanain, A.; Shehata, N.; Popelka, A.; Nair, R.; Yousef, S.; Kandas, I. Piezoelastic PVDF/TPU nanofibrous composite membrane: Fabrication and characterization. Polymers 2019, 11, 1634. [Google Scholar] [CrossRef]
- Oh, W.J.; Lim, H.S.; Won, J.S.; Lee, S.G. Preparation of PVDF/PAR composites with piezoelectric properties by post-treatment. Polymers 2018, 10, 1333. [Google Scholar] [CrossRef]
- Kim, M.; Wu, Y.S.; Kan, E.C.; Fan, J. Breathable and flexible piezoelectric ZnO@PVDF fibrous nanogenerator for wearable applications. Polymers 2018, 10, 745. [Google Scholar] [CrossRef]
- Moghadam, A.; Kouzani, A.; Zamani, R.; Magniez, K.; Kaynak, A. Nonlinear large deformation dynamic analysis of electroactive polymer actuators. Smart Struct. Syst. 2015, 15, 1601–1623. [Google Scholar] [CrossRef]
- Nasri-Nasrabadi, B.; Kaynak, A.; Komeily-Nia, Z.; Li, J.; Zolfagharian, A.; Adams, S.; Kouzani, A. An electroactive polymer composite with reinforced bending strength, based on tubular micro carbonized-cellulose. Chem. Eng. J. 2018, 334, 1775–1780. [Google Scholar] [CrossRef]
- Gibeau, B.; Koch, C.R.; Ghaemi, S. Active control of vortex shedding from a blunt trailing edge using oscillating piezoelectric flaps. Phys. Rev. Fluids 2019, 4, 1–26. [Google Scholar] [CrossRef]
- Moretti, M.; Silva, E.C.N.; Reddy, J.N. Topology optimization of flex tensional piezoelectric actuators with active control law. Smart Mater. Struct. 2019, 28, 1–16. [Google Scholar] [CrossRef]
- Ji, H.L.; Qiu, J.H.; Wu, Y.P.; Zhang, C. Semi-active vibration control based on synchronously switched piezoelectric actuators. Int. J. Appl. Electrom. 2019, 59, 299–307. [Google Scholar] [CrossRef]
- Wang, Z.K.; Chen, G.C. A general solution and the application of space axisymmetric problem in piezoelectric material. Appl. Math. Mech. 1994, 15, 587–598. [Google Scholar]
- Lin, Q.R.; Liu, Z.X.; Jin, Z.L. A close form solution to simply supported piezoelectric beams under uniform exterior pressure. Appl. Math. Mech. 2000, 21, 617–624. [Google Scholar]
- Mei, F.L.; Zeng, D.S. State equation method of mechanical-electric coupling for a piezoelectric beam. J. Shandong Univ. Sci. Technol. 2002, 21, 9–12. [Google Scholar]
- Zhu, C.Z. Analytic solution to piezoelectric cantilever beam with concentrated force at free end. J. Nanjing Inst. Technol. 2001, 1, 12–15. [Google Scholar]
- Ding, H.J.; Jiang, A.M. Polynomial solutions to piezoelectric beams(Ι)-several exact solutions. Appl. Math. Mech. 2005, 26, 1009–1015. [Google Scholar]
- Ding, H.J.; Jiang, A.M. Polynomial solutions to piezoelectric beams(ΙΙ)-Analytical solutions to typical problems. Appl. Math. Mech. 2005, 26, 1016–1021. [Google Scholar]
- Ding, H.J.; Wang, G.Q.; Chen, W.Q. Green’s functions for a two-phase infinite piezoelectric plane. Proc. R. Soc. 1997, 453, 2241–2257. [Google Scholar] [CrossRef]
- Yang, D.Q.; Liu, Z.X. Analytical solution for bending of a piezoelectric cantilever beam under an end load. Chin. Q. Mech. 2003, 24, 327–333. [Google Scholar]
- Pang, X.M.; Qiu, J.H.; Zhu, K.J.; Du, J.Z. (K, Na)NbO3-based lead-free piezoelectric ceramics manufactured by two-step sintering. Ceram. Int. 2012, 38, 2521–2527. [Google Scholar] [CrossRef]
- Zhu, Q.; Yue, J.Z.; Liu, W.Q.; Wang, X.D.; Chen, J.; Hu, G.D. Active vibration control for piezoelectricity cantilever beam: an adaptive feed forward control method. Smart Mater. Struct. 2017, 26, 047003. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, G.; Xiang, M.J.; Sun, H.X.; Wang, X.Y.; Xie, X.Z. Vibration control for the nonlinear resonant response of a piezoelectric elastic beam via time-delayed feedback. Smart Mater. Struct. 2019, 28, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yang, D.Q. Analytical solution of the bending problem of piezoelectricity cantilever beam under uniformly distributed loading. Acta Mech. Solida Sin. 2002, 23, 366–372. [Google Scholar]
- Huang, B.B.; Shi, Z.F. Several analytical solutions for a functionally gradient piezoelectric cantilever. Acta Mater. Compos. Sin. 2002, 19, 106–113. [Google Scholar]
- Zhang, L.N.; Shi, Z.F. Analytical solution of simply-supported gradient piezoelectric beam. J. North. Jiaotong Univ. 2002, 26, 71–76. [Google Scholar]
- Wang, Q.; Quek, S.T.; Sun, C.T.; Liu, X. Analysis of piezoelectric coupled circular plate. Smart Mater. Struct. 2001, 10, 229–239. [Google Scholar] [CrossRef]
- Lian, Y.S.; He, X.T.; Shi, S.J.; Li, X.; Yang, Z.X.; Sun, J.Y. A multi-parameter perturbation solution for functionally graded piezoelectric cantilever beams under combined loads. Materials 2018, 11, 1222. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.L.; Li, Q.Z. The FPPM solutions for the problems of large deflection of axisymmetric circular plate. J. Chongqing Jianzhu Univ. 2003, 25, 32–36. [Google Scholar]
- Lian, Y.S.; He, X.T.; Liu, G.H.; Sun, J.Y.; Zheng, Z.L. Application of perturbation idea to well-known Hencky problem: A perturbation solution without small-rotation-angle assumption. Mech. Res. Commun. 2017, 83, 32–46. [Google Scholar] [CrossRef]
- Nowinski, J.L.; Ismail, I.A. Application of a multi-parameter perturbation method to elastostatics. J Theor. App. Mech. 1965, 2, 35–45. [Google Scholar]
- Chien, W.Z. Second order approximation solution of nonlinear large deflection problem of Yongjiang Railway Bridge in Ningbo. Appl. Math. Mech. 2002, 23, 493–506. [Google Scholar]
- He, X.T.; Chen, S.L. Biparametric perturbation solutions of the large deflection problem of cantilever beams. Appl. Math. Mech. 2006, 27, 404–410. [Google Scholar] [CrossRef]
- He, X.T.; Cao, L.; Li, Z.Y.; Hu, X.J.; Sun, J.Y. Nonlinear large deflection problems of beams with gradient: A biparametric perturbation method. App. Math. Comput. 2013, 219, 7493–7513. [Google Scholar] [CrossRef]
- He, X.T.; Cao, L.; Sun, J.Y.; Zheng, Z.L. Application of a biparametric perturbation method to large-deflection circular plate problems with a bimodular effect under combined loads. J. Math. Anal. Appl. 2014, 420, 48–65. [Google Scholar] [CrossRef]
- Ruan, X.P.; Danforth, S.C.; Safari, A.; Chou, T.W. Saint-Venant end effects in piezoceramic materials. Int. J. Solids Struct. 2000, 37, 2625–2637. [Google Scholar] [CrossRef]
- He, X.T.; Yang, Z.X.; Jing, H.X.; Sun, J.Y. One-dimensional theoretical solution and two-dimensional numerical simulation for functionally-graded piezoelectric cantilever beams with different properties in tension and compression. Polymers 2019, 11, 1–24. [Google Scholar]


| Elastic Constant (10−12 m2·N−1) | Piezoelectric Constant (10−12 C·N−1) | Dielectric Constant (10−8 F·m−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 16.4 | −5.74 | −7.22 | 18.8 | 47.5 | −172 | 374 | 584 | 1.505 | 1.531 |
| Loads(N) | The Deformation of the Cantilever End | ||
|---|---|---|---|
| Experimental Data (mm) | Theoretical Results (mm) | Relative Errors (%) | |
| 0.49 | 0.4069 | 0.3545 | 12.87 |
| 0.98 | 0.7527 | 0.7089 | 5.82 |
| 1.96 | 1.6072 | 1.4178 | 11.79 |
| Loads(N) | The Deformation of the Cantilever End | ||
|---|---|---|---|
| Piezoelectric Cantilever Beam (mm) | Cantilever Beam without Piezoelectric Properties (mm) | Difference (mm) | |
| 0.49 | 0.4069 | 0.5351 | 0.1282 |
| 0.98 | 0.7527 | 0.8463 | 0.0936 |
| 1.96 | 1.6072 | 1.9796 | 0.3724 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.-X.; He, X.-T.; Jing, H.-X.; Sun, J.-Y. A Multi-Parameter Perturbation Solution and Experimental Verification for Bending Problem of Piezoelectric Cantilever Beams. Polymers 2019, 11, 1934. https://doi.org/10.3390/polym11121934
Yang Z-X, He X-T, Jing H-X, Sun J-Y. A Multi-Parameter Perturbation Solution and Experimental Verification for Bending Problem of Piezoelectric Cantilever Beams. Polymers. 2019; 11(12):1934. https://doi.org/10.3390/polym11121934
Chicago/Turabian StyleYang, Zhi-Xin, Xiao-Ting He, Hong-Xia Jing, and Jun-Yi Sun. 2019. "A Multi-Parameter Perturbation Solution and Experimental Verification for Bending Problem of Piezoelectric Cantilever Beams" Polymers 11, no. 12: 1934. https://doi.org/10.3390/polym11121934
APA StyleYang, Z.-X., He, X.-T., Jing, H.-X., & Sun, J.-Y. (2019). A Multi-Parameter Perturbation Solution and Experimental Verification for Bending Problem of Piezoelectric Cantilever Beams. Polymers, 11(12), 1934. https://doi.org/10.3390/polym11121934