Critical Evaluation of Organic Thin-Film Transistor Models
Abstract
:1. Introduction
2. Materials and Methods
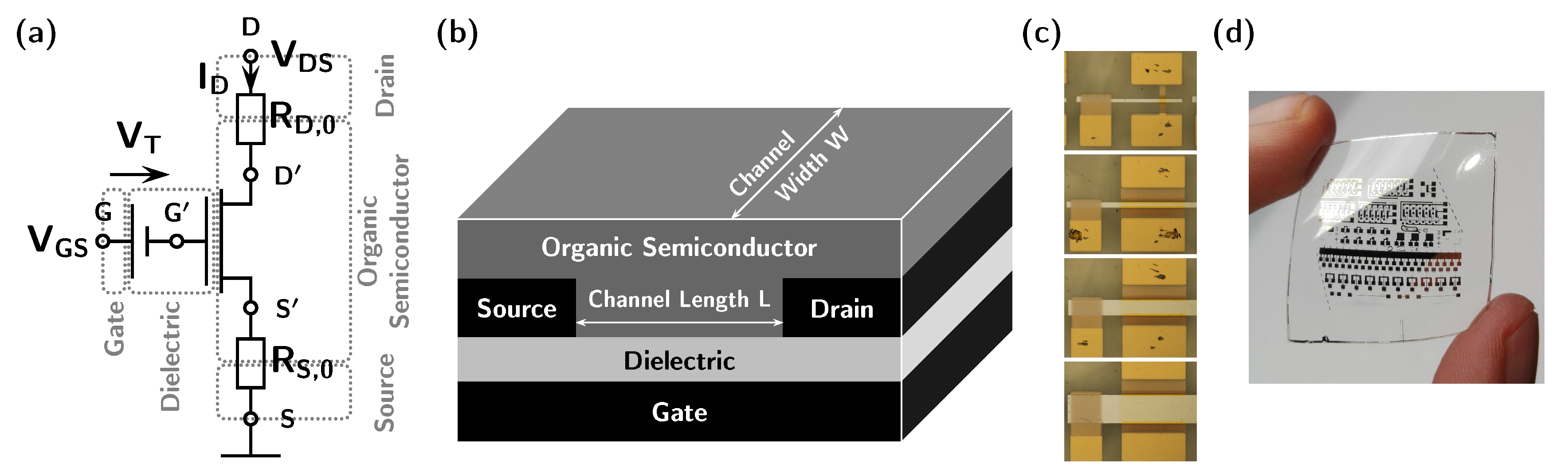
2.1. Equivalent Circuit Model
2.2. Fitting Procedure
2.3. Device Fabrication
3. Results
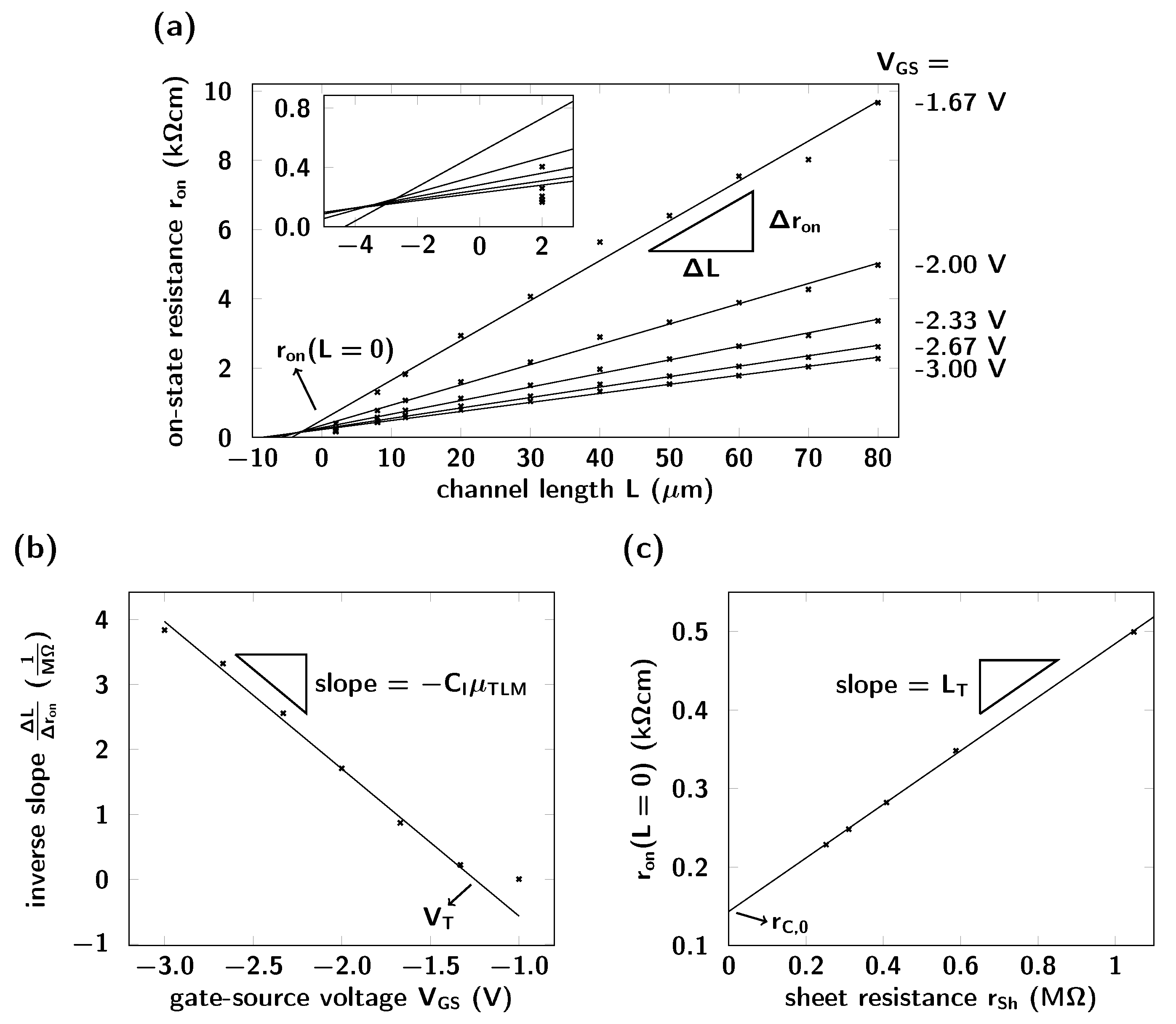
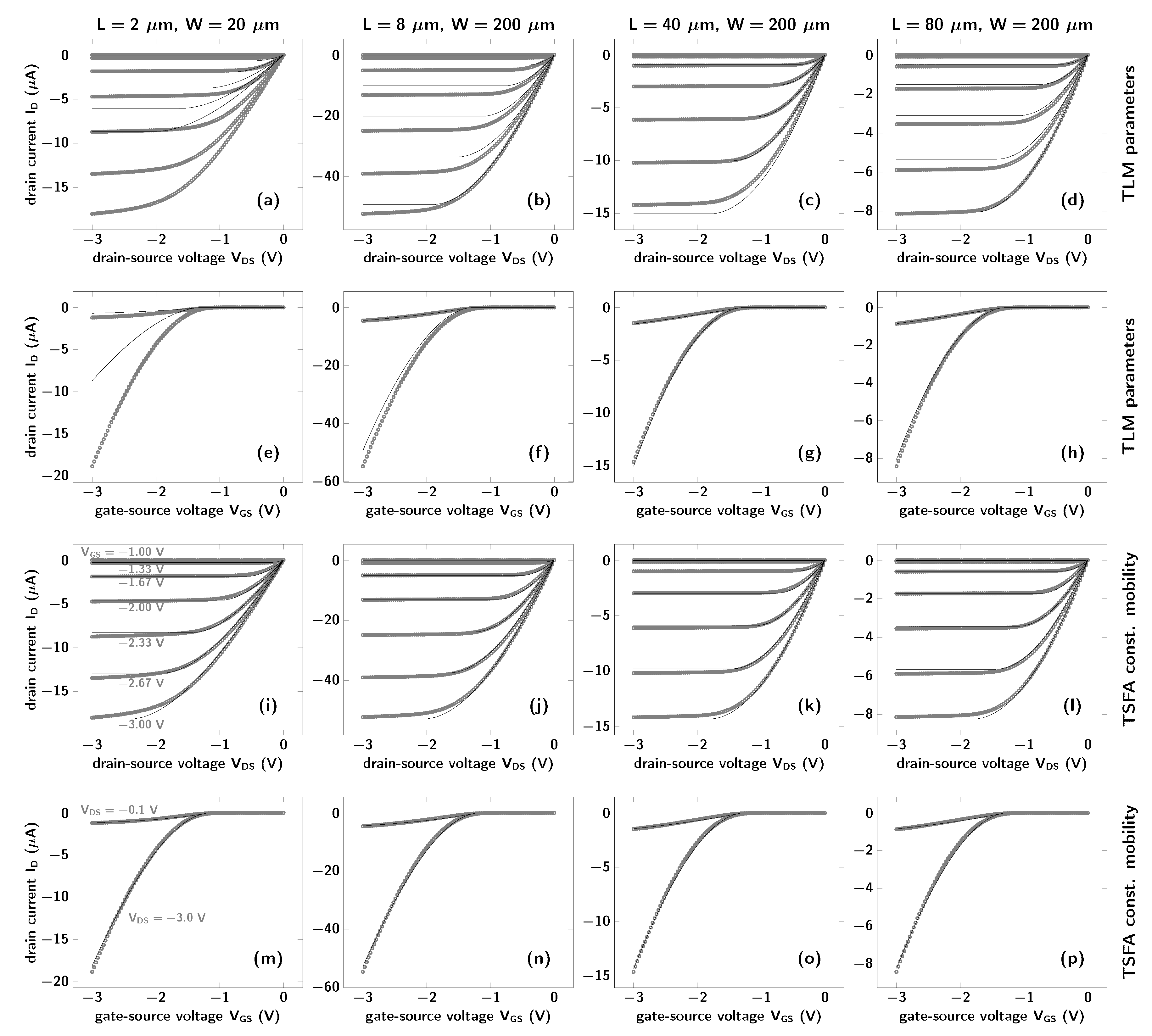
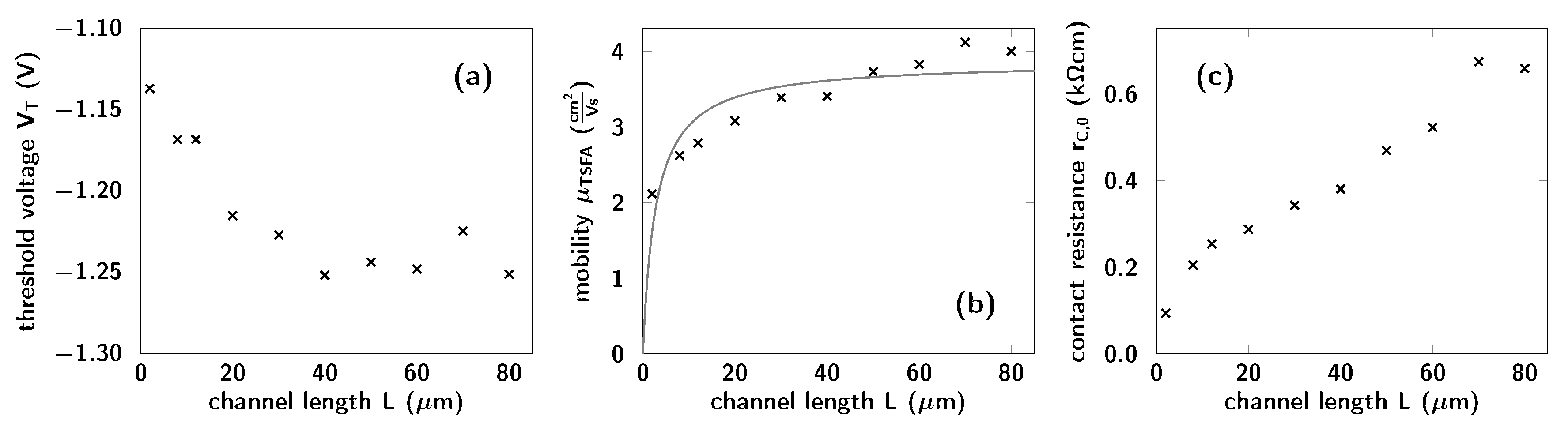
3.1. Conventional Transmission Line Method
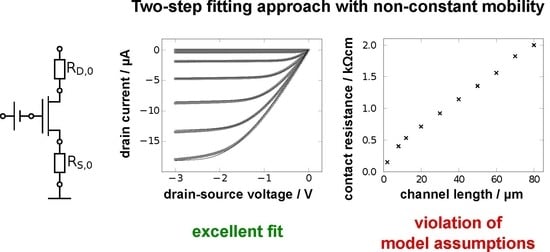
- The measured output characteristics (gray symbols in Figure 3a–d) must be linear for very small drain-source voltages ( V), and the slope of the curves must decrease monotonically as the absolute value of the drain-source voltage increases. An S-shape of the output curves in this regime is an indicator of a non-Ohmic contact resistance.
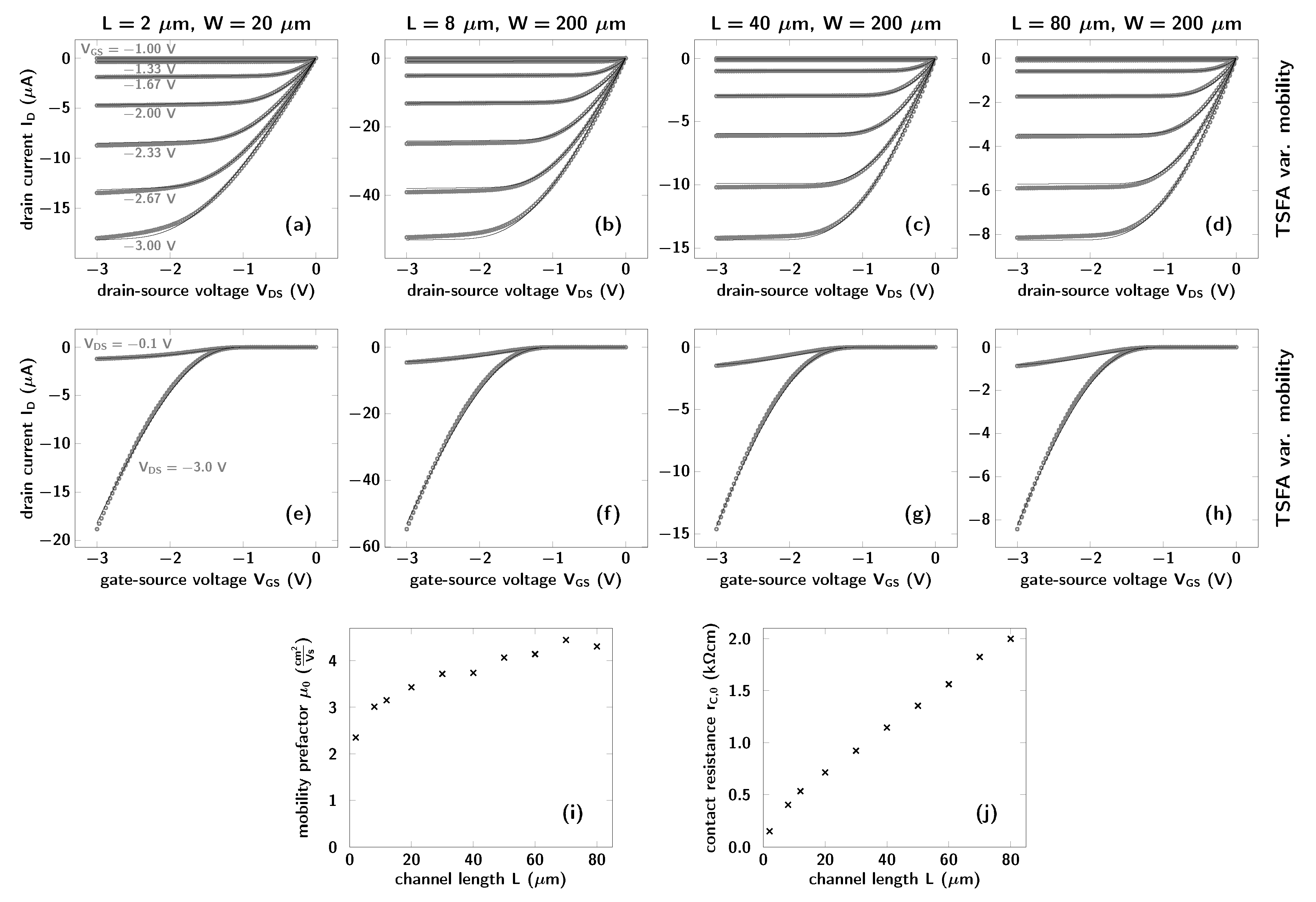
3.2. TSFA with Constant-Mobility Model
3.3. TSFA with Field- and Charge-Carrier-Density-Dependent Mobility
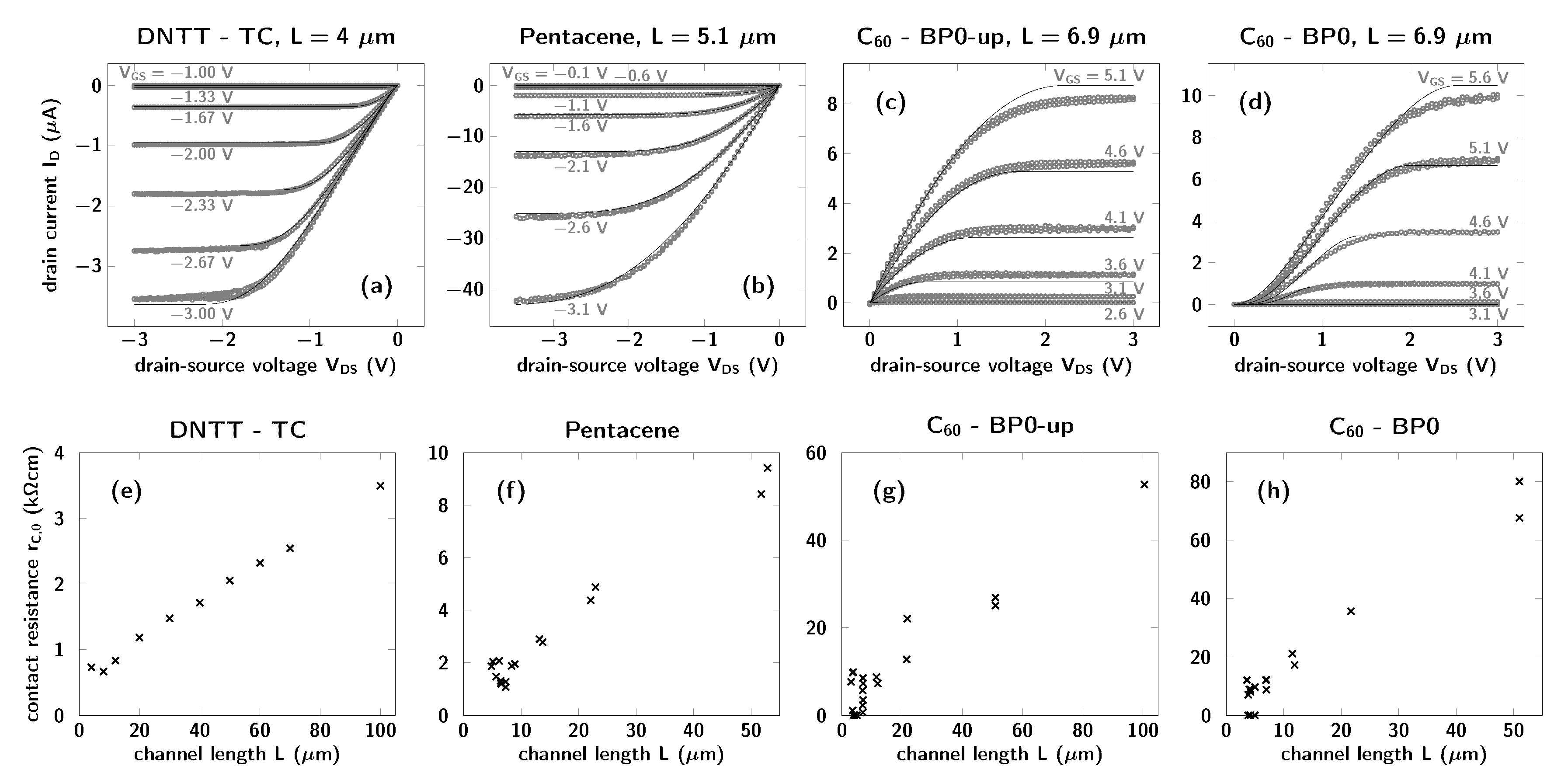
3.4. Testing Other Organic-TFT Technologies
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Guo, X.; Xu, Y.; Ogier, S.; Ng, T.N.; Caironi, M.; Perinot, A.; Li, L.; Zhao, J.; Tang, W.; Sporea, R.A.; et al. Current Status and Opportunities of Organic Thin-Film Transistor Technologies. IEEE Trans. Electron Devices 2017, 64, 1906–1921. [Google Scholar] [CrossRef]
- Paterson, A.F.; Singh, S.; Fallon, K.J.; Hodsden, T.; Han, Y.; Schroeder, B.C.; Bronstein, H.; Heeney, M.; McCulloch, I.; Anthopoulos, T.D. Recent Progress in High-Mobility Organic Transistors: A Reality Check. Adv. Mater. 2018, 30, 1801079. [Google Scholar] [CrossRef] [PubMed]
- Yamamura, A.; Watanabe, S.; Uno, M.; Mitani, M.; Mitsui, C.; Tsurumi, J.; Isahaya, N.; Kanaoka, Y.; Okamoto, T.; Takeya, J. Wafer-scale, layer-controlled organic single crystals for high-speed circuit operation. Sci. Adv. 2018, 4, eaao5758. [Google Scholar] [CrossRef] [PubMed]
- Ogier, S.D.; Matsui, H.; Feng, L.; Simms, M.; Mashayekhi, M.; Carrabina, J.; Terés, L.; Tokito, S. Uniform, high performance, solution processed organic thin-film transistors integrated in 1 MHz frequency ring oscillators. Org. Electron. 2018, 54, 40–47. [Google Scholar] [CrossRef]
- Pasveer, W.F.; Cottaar, J.; Tanase, C.; Coehoorn, R.; Bobbert, P.A.; Blom, P.W.M.; de Leeuw, D.M.; Michels, M.A.J. Unified Description of Charge-Carrier Mobilities in Disordered Semiconducting Polymers. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ou-Yang, W.; Weis, M. Electric-field enhanced thermionic emission model for carrier injection mechanism of organic field-effect transistors: Understanding of contact resistance. J. Phys. D Appl. Phys. 2017, 50, 035101. [Google Scholar] [CrossRef]
- Locci, S.; Morana, M.; Orgiu, E.; Bonfiglio, A.; Lugli, P. Modeling of Short-Channel Effects in Organic Thin-Film Transistors. IEEE Trans. Electron Devices 2008, 55, 2561–2567. [Google Scholar] [CrossRef]
- Marinov, O.; Deen, M.J.; Zschieschang, U.; Klauk, H. Organic Thin-Film Transistors: Part I—Compact DC Modeling. IEEE Trans. Electron Devices 2009, 56, 2952–2961. [Google Scholar] [CrossRef]
- Di Pietro, R.; Venkateshvaran, D.; Klug, A.; List-Kratochvil, E.J.W.; Facchetti, A.; Sirringhaus, H.; Neher, D. Simultaneous extraction of charge density dependent mobility and variable contact resistance from thin film transistors. Appl. Phys. Lett. 2014, 104, 193501. [Google Scholar] [CrossRef]
- Natali, D.; Caironi, M. Charge injection in solution-processed organic field-effect transistors: Physics, models and characterization methods. Adv. Mater. 2012, 24, 1357–1387. [Google Scholar] [CrossRef]
- Wang, S.D.; Yan, Y.; Tsukagoshi, K. Transition-Voltage Method for Estimating Contact Resistance in Organic Thin-Film Transistors. IEEE Electron Device Lett. 2010, 31, 509–511. [Google Scholar] [CrossRef]
- Takagaki, S.; Yamada, H.; Noda, K. Extraction of contact resistance and channel parameters from the electrical characteristics of a single bottom-gate/top-contact organic transistor. Jpn. J. Appl. Phys. 2016, 55, 03DC07. [Google Scholar] [CrossRef]
- Torricelli, F.; Ghittorelli, M.; Colalongo, L.; Kovacs-Vajna, Z.M. Single-transistor method for the extraction of the contact and channel resistances in organic field-effect transistors. Appl. Phys. Lett. 2014, 104, 093303. [Google Scholar] [CrossRef]
- Kanicki, J.; Libsch, F.R.; Griffith, J.; Polastre, R. Performance of thin hydrogenated amorphous silicon thin-film transistors. J. Appl. Phys. 1991, 69, 2339–2345. [Google Scholar] [CrossRef]
- Luan, S.; Neudeck, G.W. An experimental study of the source/drain parasitic resistance effects in amorphous silicon thin film transistors. J. Appl. Phys. 1992, 72, 766–772. [Google Scholar] [CrossRef]
- Natali, D.; Fumagalli, L.; Sampietro, M. Modeling of organic thin film transistors: Effect of contact resistances. J. Appl. Phys. 2007, 101, 014501. [Google Scholar] [CrossRef]
- Deen, M.J.; Marinov, O.; Zschieschang, U.; Klauk, H. Organic Thin-Film Transistors: Part II—Parameter Extraction. IEEE Trans. Electron Devices 2009, 56, 2962–2968. [Google Scholar] [CrossRef]
- Fischer, A.; Zündorf, H.; Kaschura, F.; Widmer, J.; Leo, K.; Kraft, U.; Klauk, H. Nonlinear Contact Effects in Staggered Thin-Film Transistors. Phys. Rev. Appl. 2017, 8, 054012. [Google Scholar] [CrossRef]
- Mayer, J.; Khairy, K.; Howard, J. Drawing an elephant with four complex parameters. Am. J. Phys. 2010, 78, 648–649. [Google Scholar] [CrossRef]
- Gundlach, D.J.; Royer, J.E.; Park, S.K.; Subramanian, S.; Jurchescu, O.D.; Hamadani, B.H.; Moad, A.J.; Kline, R.J.; Teague, L.C.; Kirillov, O.; et al. Contact-induced crystallinity for high-performance soluble acene-based transistors and circuits. Nat. Mater. 2008, 7, 216–221. [Google Scholar] [CrossRef]
- Kraft, U.; Takimiya, K.; Kang, M.J.; Rödel, R.; Letzkus, F.; Burghartz, J.N.; Weber, E.; Klauk, H. Detailed analysis and contact properties of low-voltage organic thin-film transistors based on dinaphtho[2,3- b:2’,3’f]thieno[3,2-b]thiophene (DNTT) and its didecyl and diphenyl derivatives. Org. Electron. 2016, 35, 33–40. [Google Scholar] [CrossRef]
- Petritz, A.; Krammer, M.; Sauter, E.; Gärtner, M.; Nascimbeni, G.; Schrode, B.; Fian, A.; Gold, H.; Cojocaru, A.; Karner-Petritz, E.; et al. Embedded Dipole Self-Assembled Monolayers for Contact Resistance Tuning in p-Type and n-Type Organic Thin Film Transistors and Flexible Electronic Circuits. Adv. Funct. Mater. 2018, 28, 1804462. [Google Scholar] [CrossRef]
- Shockley, W. A Unipolar “Field-Effect” Transistor. Proc. IRE 1952, 40, 1365–1376. [Google Scholar] [CrossRef]
- Vissenberg, M.C.J.M.; Matters, M. Theory of the field-effect mobility in amorphous organic transistors. Phys. Rev. B 1998, 57, 12964–12967. [Google Scholar] [CrossRef]
- Horowitz, G.; Hajlaoui, M.E.; Hajlaoui, R. Temperature and gate voltage dependence of hole mobility in polycrystalline oligothiophene thin film transistors. J. Appl. Phys. 2000, 87, 4456–4463. [Google Scholar] [CrossRef]
- Hall, R.B. The Poole-Frenkel effect. Thin Solid Films 1971, 8, 263–271. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hong, J.P.; Park, A.Y.; Lee, S.; Kang, J.; Shin, N.; Yoon, D.Y. Tuning of Ag work functions by self-assembled monolayers of aromatic thiols for an efficient hole injection for solution processed triisopropylsilylethynyl pentacene organic thin film transistors. Appl. Phys. Lett. 2008, 92, 143311. [Google Scholar] [CrossRef]
- Borchert, J.W.; Peng, B.; Letzkus, F.; Burghartz, J.N.; Chan, P.K.L.; Zojer, K.; Ludwigs, S.; Klauk, H. Small contact resistance and high-frequency operation of flexible, low-voltage, inverted coplanar organic transistors. Nat. Commun. 2019, submitted. [Google Scholar]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; OCLC: 488586029; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Rödel, R.; Letzkus, F.; Zaki, T.; Burghartz, J.N.; Kraft, U.; Zschieschang, U.; Kern, K.; Klauk, H. Contact properties of high-mobility, air-stable, low-voltage organic n-channel thin-film transistors based on a naphthalene tetracarboxylic diimide. Appl. Phys. Lett. 2013, 102, 233303. [Google Scholar] [CrossRef]
- Bittle, E.G.; Basham, J.I.; Jackson, T.N.; Jurchescu, O.D.; Gundlach, D.J. Mobility overestimation due to gated contacts in organic field-effect transistors. Nat. Commun. 2016, 7, 10908. [Google Scholar] [CrossRef] [PubMed]
- Uemura, T.; Rolin, C.; Ke, T.H.; Fesenko, P.; Genoe, J.; Heremans, P.; Takeya, J. On the Extraction of Charge Carrier Mobility in High-Mobility Organic Transistors. Adv. Mater. 2016, 28, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Fishchuk, I.I.; Arkhipov, V.I.; Kadashchuk, A.; Heremans, P.; Bässler, H. Analytic model of hopping mobility at large charge carrier concentrations in disordered organic semiconductors: Polarons versus bare charge carriers. Phys. Rev. B 2007, 76, 045210. [Google Scholar] [CrossRef]
| Name/Reference | Architecture | Semiconductor | Contact | (nm) | L (m) | W (m) |
|---|---|---|---|---|---|---|
| DNTT-BC [29] | BGBC | DNTT | Au/PFBT | 5.3 | 2–80 | 20–200 |
| DNTT-TC [21] | BGTC | DNTT | Au | 5.3 | 4–100 | 20–200 |
| Pentacene [22] | BGBC | Pentacene | Au/BP0-down | 18 | 4.85–52.90 | 1000 |
| C-BP0-up [22] | BGBC | C | Au/BP0-up | 18 | 3.0–100.5 | 1000 |
| C-BP0 [22] | BGBC | C | Au/BP0 | 18 | 3.6–51.0 | 1000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krammer, M.; Borchert, J.W.; Petritz, A.; Karner-Petritz, E.; Schider, G.; Stadlober, B.; Klauk, H.; Zojer, K. Critical Evaluation of Organic Thin-Film Transistor Models. Crystals 2019, 9, 85. https://doi.org/10.3390/cryst9020085
Krammer M, Borchert JW, Petritz A, Karner-Petritz E, Schider G, Stadlober B, Klauk H, Zojer K. Critical Evaluation of Organic Thin-Film Transistor Models. Crystals. 2019; 9(2):85. https://doi.org/10.3390/cryst9020085
Chicago/Turabian StyleKrammer, Markus, James W. Borchert, Andreas Petritz, Esther Karner-Petritz, Gerburg Schider, Barbara Stadlober, Hagen Klauk, and Karin Zojer. 2019. "Critical Evaluation of Organic Thin-Film Transistor Models" Crystals 9, no. 2: 85. https://doi.org/10.3390/cryst9020085
APA StyleKrammer, M., Borchert, J. W., Petritz, A., Karner-Petritz, E., Schider, G., Stadlober, B., Klauk, H., & Zojer, K. (2019). Critical Evaluation of Organic Thin-Film Transistor Models. Crystals, 9(2), 85. https://doi.org/10.3390/cryst9020085