Monolayer TiNI with Anisotropic Optical and Mechanical Properties
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
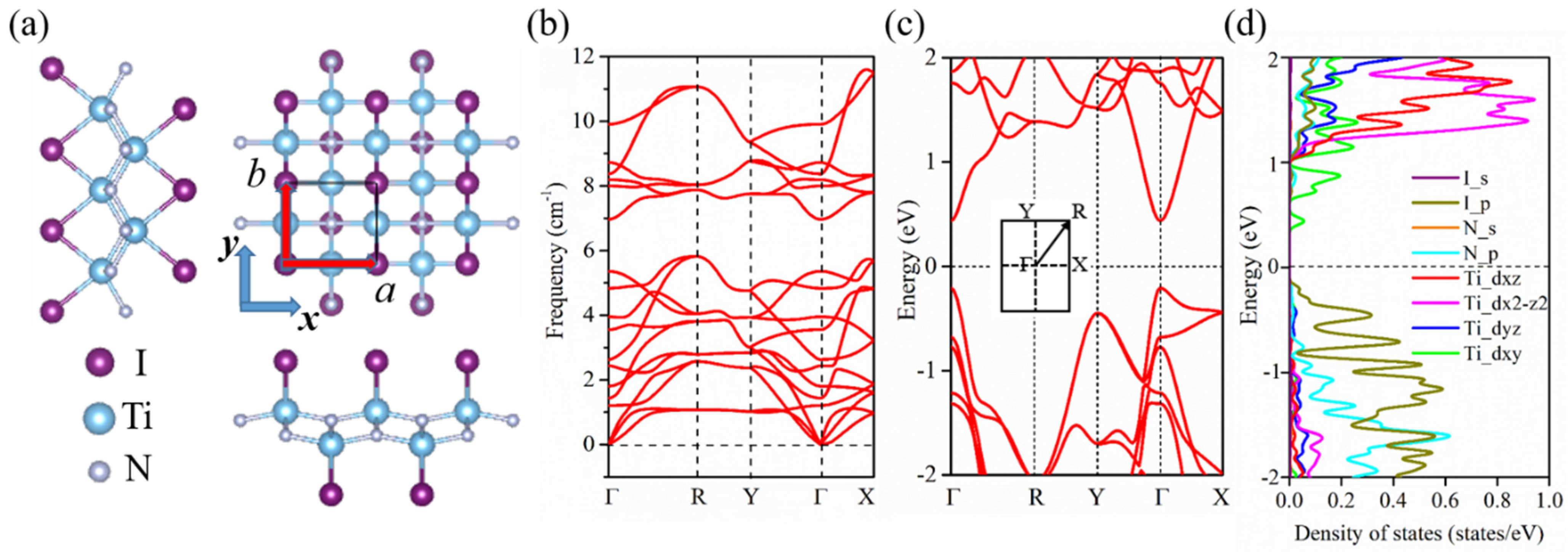
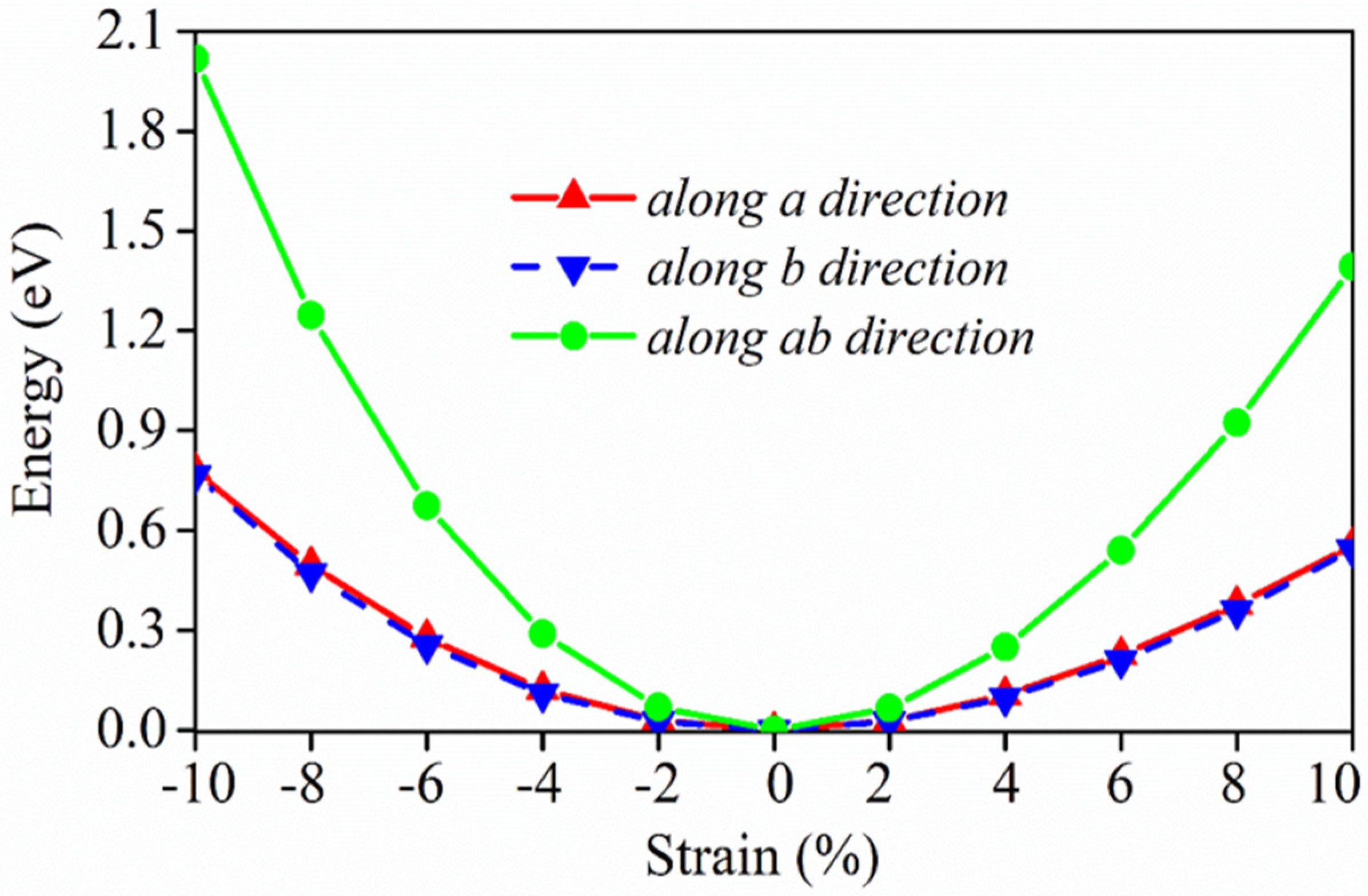
3.1. Energy Band and Structural Stability
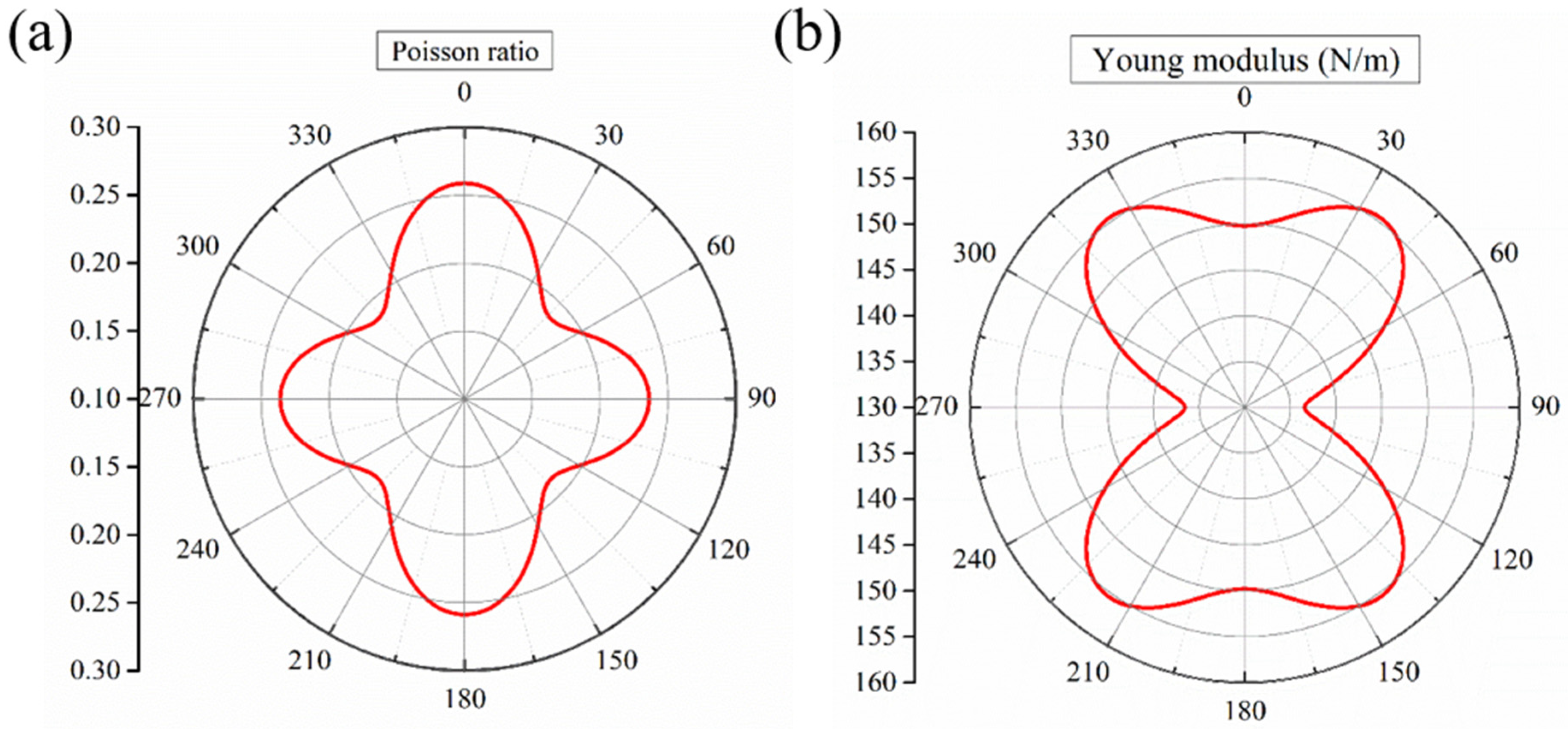
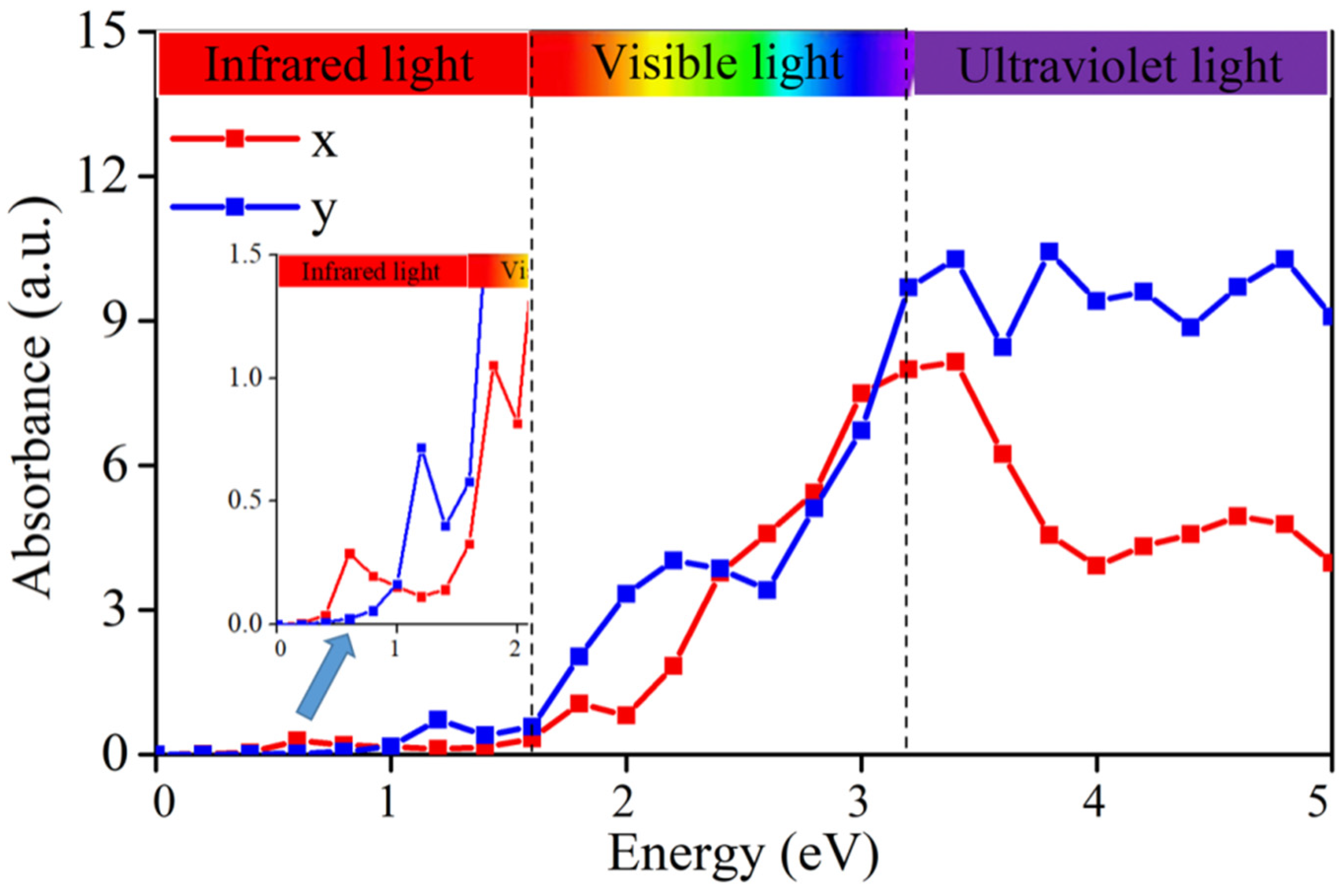
3.2. Mechanical and Optical Properties
3.3. Electronic Transport Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhao, X.; Wu, D.; Jing, Y.; Zhou, Z. High and anisotropic carrier mobility in experimentally possible Ti2CO2 (MXene) monolayers and nanoribbons. Nanoscale 2015, 7, 16020–16025. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Hao, Z.; Yu, S.; Huang, C.; Pan, Y.; Zhao, X. A wearable and deformable graphene-based affinity nanosensor for monitoring of cytokines in biofluids. Nanomaterials 2020, 10, 1503. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, Z.; Yu, S.; De Moraes, C.G.; Suh, L.H.; Zhao, X.; Lin, Q. An ultraflexible and stretchable aptameric graphene nanosensor for biomarker detection and monitoring. Adv. Funct. Mater. 2019, 29, 1905202. [Google Scholar] [CrossRef]
- Dhanabalan, S.C.; Ponraj, J.S.; Zhang, H.; Bao, Q. Present perspectives of broadband photodetectors based on nanobelts, nanoribbons, nanosheets and the emerging 2D materials. Nanoscale 2016, 8, 6410–6434. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, W.; Ma, Y.; Ji, J.; Cai, B.; Yang, S.A.; Zhu, Z.; Chen, Z.; Zeng, H. Antimonene oxides: Emerging tunable direct bandgap semiconductor and novel topological insulator. Nano Lett. 2017, 17, 3434–3440. [Google Scholar] [CrossRef]
- Zhang, C.-G.; Ji, W.-X.; Li, P.; Zhang, C.-W.; Wang, P.-J. Tuning the Electronic and Optical Properties of Two-dimensional AgBiP2Se6 and AgInP2Se6 Janus Monolayers. Chem. Phys. Lett. 2021, 780, 138933. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, W.; Li, S.; Li, P.; Zhang, C.; Wang, P.-J. 2D ternary nitrides XNY (X = Ti, Zr, Hf; YF, Cl, Br) with applications as photoelectric and photocatalytic materials featuring mechanical and optical anisotropy: A DFT study. J. Solid State Chem. 2021, 303, 122517. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, Z.; Wang, X.; Huang, C.; Lin, Q.; Zhao, X.; Pan, Y. A Flexible and regenerative aptameric graphene–Nafion biosensor for cytokine storm biomarker monitoring in undiluted biofluids toward wearable applications. Adv. Funct. Mater. 2021, 31, 2005958. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, Z.; Yang, C.; Wang, H.; Huang, C.; Zhao, X.; Pan, Y. Ultra-sensitive and rapid screening of acute myocardial infarction using 3D-affinity graphene biosensor. Cell Rep. Phys. Sci. 2022, 3, 100855. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, Y.; Ge, Y.; Zhang, S.; Zeng, H.; Zhang, H. 2D V-V binary materials: Status and challenges. Adv. Mater. 2019, 31, 1902352. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.; Guo, S.; Zhou, W.; Zhang, S. Uncovering the anisotropic electronic structure of 2D group VA-VA monolayers for quantum transport. IEEE Electron Device Lett. 2020, 42, 66–69. [Google Scholar] [CrossRef]
- Quio, J.; Kong, X.; Hu, Z.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 7, 4475. [Google Scholar] [CrossRef] [PubMed]
- Quhe, R.; Li, Q.; Zhang, Q.; Wang, Y.; Zhang, H.; Li, J.; Zhang, X.; Chen, D.; Liu, K.; Ye, Y. Simulations of quantum transport in sub-5-nm monolayer phosphorene transistors. Phys. Rev. Appl. 2018, 10, 024022. [Google Scholar] [CrossRef]
- Huang, S.; Tatsumi, Y.; Ling, X.; Guo, H.; Wang, Z.; Watson, G.; Puretzky, A.A.; Geohegan, D.B.; Kong, J.; Li, J. In-plane optical anisotropy of layered gallium telluride. ACS Nano 2016, 10, 8964–8972. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Leng, J.; Zhang, G. The grain boundary effect on mechanical and electronic transport properties of a striped borophene. Phys. Chem. Chem. Phys. 2020, 22, 21844–21850. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Kutana, A.; Zou, X.; Yakobson, B.I. Electro-mechanical anisotropy of phosphorene. Nanoscale 2015, 7, 9746–9751. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, L.; Huang, L.; Li, L.; Meng, L.; Gao, M.; Huan, Q.; Lin, X.; Wang, Y.; Du, S. Construction of 2D atomic crystals on transition metal surfaces: Graphene, silicene, and hafnene. Small 2014, 10, 2215–2225. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef]
- Liao, L.; Lin, Y.-C.; Bao, M.; Cheng, R.; Bai, J.; Liu, Y.; Qu, Y.; Wang, K.L.; Huang, Y.; Duan, X. High-speed graphene transistors with a self-aligned nanowire gate. Nature 2010, 467, 305–308. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Xia, X.; Shi, F.; Zhan, J.; Tu, J.; Fan, H.J. Transition metal carbides and nitrides in energy storage and conversion. Adv. Sci. 2016, 3, 1500286. [Google Scholar] [CrossRef] [PubMed]
- Ham, D.J.; Lee, J.S. Transition metal carbides and nitrides as electrode materials for low temperature fuel cells. Energies 2009, 2, 873–899. [Google Scholar] [CrossRef]
- Cao, B.; Veith, G.M.; Neuefeind, J.C.; Adzic, R.R.; Khalifah, P.G. Mixed close-packed cobalt molybdenum nitrides as non-noble metal electrocatalysts for the hydrogen evolution reaction. J. Am. Chem. Soc. 2013, 135, 19186–19192. [Google Scholar] [CrossRef]
- Yang, S.; Li, W.; Ye, C.; Wang, G.; Tian, H.; Zhu, C.; He, P.; Ding, G.; Xie, X.; Liu, Y. C3N-A 2D crystalline, hole-free, tunable-narrow-bandgap semiconductor with ferromagnetic properties. Adv. Mater. 2017, 29, 1605625. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B. Ultra high stiffness and thermal conductivity of graphene like C3N. Carbon 2017, 118, 25–34. [Google Scholar] [CrossRef]
- Makaremi, M.; Mortazavi, B.; Singh, C.V. Adsorption of metallic, metalloidic, and nonmetallic adatoms on two-dimensional C3N. J. Phys. Chem. C 2017, 121, 18575–18583. [Google Scholar] [CrossRef]
- Makaremi, M.; Grixti, S.; Butler, K.T.; Ozin, G.A.; Singh, C.V. Band engineering of carbon nitride monolayers by N-type, P-type, and isoelectronic doping for photocatalytic applications. ACS Appl. Mater. Interfaces 2018, 10, 11143–11151. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, S.; Ren, J.; Jia, Y.A.; Chen, C.; Komarneni, S.; Yang, D.; Yao, X. Electronic structure tuning in Ni3FeN/r-GO aerogel toward bifunctional electrocatalyst for overall water splitting. ACS Nano 2018, 12, 245–253. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, H.; Chen, J.; Xiong, T.; Balogun, M.-S.J.T.; Tong, Y. Efficient hydrogen evolution activity and overall water splitting of metallic Co4N nanowires through tunable d-orbitals with ultrafast incorporation of FeOOH. ACS Appl. Mater. Interfaces 2019, 11, 5152–5158. [Google Scholar] [CrossRef]
- Yan, H.; Xie, Y.; Wu, A.; Cai, Z.; Wang, L.; Tian, C.; Zhang, X.; Fu, H. Anion-modulated HER and OER activities of 3D Ni–V-based interstitial compound heterojunctions for high-efficiency and stable overall water splitting. Adv. Mater. 2019, 31, 1901174. [Google Scholar] [CrossRef] [PubMed]
- Guan, J.; Li, C.; Zhao, J.; Yang, Y.; Zhou, W.; Wang, Y.; Li, G.-R. FeOOH-enhanced bifunctionality in Ni3N nanotube arrays for water splitting. Appl. Catal. B Environ. 2020, 269, 118600. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Parlinski, K.; Li, Z.; Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Ozaki, T.; Nishio, K.; Kino, H. Efficient implementation of the nonequilibrium Green function method for electronic transport calculations. Phys. Rev. B 2010, 81, 035116. [Google Scholar] [CrossRef]
- Ozaki, T. Continued fraction representation of the Fermi-Dirac function for large-scale electronic structure calculations. Phys. Rev. B 2007, 75, 035123. [Google Scholar] [CrossRef] [Green Version]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Schurz, C.M.; Shlyk, L.; Schleid, T.; Niewa, R. Superconducting nitride halidesMNX(M=Ti, Zr, Hf;X=Cl, Br, I). Kristallogr. Z. 2011, 226, 395–416. [Google Scholar] [CrossRef]
- Juzatr, R.; Friedrichsen, H. Die Kristallstruktur von β-ZrNCl and β-ZrNBr. Z. Anorg. Allg. Chem. 1964, 332, 173–178. [Google Scholar] [CrossRef]
- Hu, Y.; Li, S.-S.; Ji, W.-X.; Zhang, C.-W.; Ding, M.; Wang, P.-J.; Yan, S.-S. Glide Mirror Plane Protected Nodal-Loop in an Anisotropic Half-Metallic MnNF Monolayer. J. Phys. Chem. Lett. 2019, 11, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-J.; Jeng, H.-T. High applicability of two-dimensional phosphorous in Kagome lattice predicted from first-principles calculations. Sci. Rep. 2016, 6, 23151. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Z.; Du, A.; Zhao, M. Band inversion and topological aspects in a TiNI monolayer. Phys. Chem. Chem. Phys. 2016, 18, 22154–22159. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon Press: Oxford, UK, 1954. [Google Scholar]
- Wang, J.; Yip, S.; Phillpot, S.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182. [Google Scholar] [CrossRef]
- Zhuo, Z.; Wu, X.; Yang, J. Two-dimensional phosphorus porous polymorphs with tunable band gaps. J. Am. Chem. Soc. 2016, 138, 7091–7098. [Google Scholar] [CrossRef]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Elastic properties of hydrogenated graphene. Phys. Rev. B 2010, 82, 235414. [Google Scholar] [CrossRef]
- Tauc, J. Optical properties and electronic structure of amorphous Ge and Si. Mater. Res. Bull. 1968, 3, 37–46. [Google Scholar] [CrossRef]
- Kaasbjerg, K.; Thygesen, K.S.; Jacobsen, K.W. Phonon-limited mobility in n-type single-layer MoS2 from first principles. Phys. Rev. B 2012, 85, 115317. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, C.; Ji, W.; Li, P.; Wang, P.; Li, S.; Yan, S. Silicon-based chalcogenide: Unexpected quantum spin Hall insulator with sizable band gap. Appl. Phys. Lett. 2016, 109, 182109. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, W.; Zhang, C.; Li, P.; Li, F.; Wang, P.; Li, S.; Yan, S. Large-gap quantum spin Hall state in functionalized dumbbell stanene. Appl. Phys. Lett. 2016, 108, 073104. [Google Scholar] [CrossRef]
- Li, P.; Wu, W.; Xu, Y.; Liu, J.; Wu, S.; Ye, Y.; Liang, C.; Zeng, X.C. Two-Dimensional IV–V Monolayers with Highly Anisotropic Carrier Mobility and Electric Transport Properties. J. Phys. Chem. Lett. 2021, 12, 1058–1065. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-J.; Li, M.; Zhang, C.-G.; Shi, K.-Y.; Wang, P.-J. Monolayer TiNI with Anisotropic Optical and Mechanical Properties. Crystals 2022, 12, 1202. https://doi.org/10.3390/cryst12091202
Li S-J, Li M, Zhang C-G, Shi K-Y, Wang P-J. Monolayer TiNI with Anisotropic Optical and Mechanical Properties. Crystals. 2022; 12(9):1202. https://doi.org/10.3390/cryst12091202
Chicago/Turabian StyleLi, Shu-Juan, Min Li, Cheng-Gong Zhang, Kun-Yue Shi, and Pei-Ji Wang. 2022. "Monolayer TiNI with Anisotropic Optical and Mechanical Properties" Crystals 12, no. 9: 1202. https://doi.org/10.3390/cryst12091202
APA StyleLi, S.-J., Li, M., Zhang, C.-G., Shi, K.-Y., & Wang, P.-J. (2022). Monolayer TiNI with Anisotropic Optical and Mechanical Properties. Crystals, 12(9), 1202. https://doi.org/10.3390/cryst12091202




