Some Issues on Crystal Plasticity Models Formulation: Motion Decomposition and Constitutive Law Variants

Abstract

In this paper, kinematic relations and constitutive laws in crystal plasticity are analyzed in the context of geometric nonlinearity description and fulfillment of thermodynamic requirements in the case of elastic deformation. We consider the most popular relations: in finite form, written in terms of the unloaded configuration, and in rate form, written in terms of the current configuration. The presence of a corotational derivative in the relations formulated in terms of the current configuration testifies to the fact that the model is based on the decomposition of motion into the deformation motion and the rigid motion of a moving coordinate system, and precisely the stress rate with respect to this coordinate system is associated with the strain rate. We also examine the relations of the mesolevel model with an explicit separation of a moving coordinate system and the elastic distortion of crystallites relative to it in the deformation gradient. These relations are compared with the above formulations, which makes it possible to determine how close they are. The results of the performed analytical calculations show the equivalence or similarity (in the sense of the response determined under the same influences) of the formulation and are supported by the results of numerical calculation. It is shown that the formulation based on the decomposition of motion with an explicit separation of the moving coordinate system motion provides a theoretical framework for the transition to a similar formulation in rate form written in terms of the current configuration. The formulation of this kind is preferable for the numerical solution of boundary value problems (in a case when the current configuration and, consequently, contact boundaries, are not known a priori) used to model the technological treatment processes.

1. Introduction

In recent decades, extensive research efforts have been made to develop a multilevel approach to constructing constitutive models for metals and alloys via the introduction of internal variables [1,2,3,4]. The crystal plasticity models obtained within the framework of this approach provide an opportunity to explicitly describe changes in the structure of the material (its anisotropic physical and mechanical macro-properties) and deformation mechanisms [5,6,7,8,9]. This validates the application of these models for studying and improvement of materials processing technologies, as well as for solving the problems associated with the development of new functional materials.

Crystal plasticity models can be divided into three classes. In statistical models aimed at describing the behavior of representative macrovolumes, consideration is given to a sample of uniformly deformed grains (reviews of the models of this class are provided in [10,11,12]. The application of modified statistical models makes it possible to take into account the interaction of neighboring grains, e.g., during the explicit description of the motion of dislocations across the boundary [13]. Self-consistent models are used to investigate the behavior of uniformly deformed grains in a matrix representing the effective characteristics of polycrystals. These models provide the fulfillment of equilibrium conditions; the effective characteristics are determined using statistical averaging methods. Reviews of the self-consistent models are given in [7,10,14]. Direct models based on the finite element method are recognized to be the most effective models for analyzing the non-uniform stress-strain state of grains (reviews of these models can be found in [7,8,9,15,16].

The crystal plasticity models mentioned above differ in the way of aggregation (combining the elements of a lower scale level into one element of a higher scale level), but all these models are based on the mesolevel relations used to describe crystallites, which led to the name “crystal plasticity”.

In the last decade, numerous attempts have been made to develop crystal plasticity models based on generalized, mainly gradient, continua [17,18,19,20]. However, most authors assumed that the material under study is a simple (first-order) material [21]. In this case, the basic structure of the mesolevel constitutive model aimed at taking into account intragranular dislocation slip and lattice rotation is composed of the following equations: constitutive law for the relationship between stresses and elastic component of deformation, kinematic relations (including equations for determining the lattice spin), relation for the determination of the inelastic component of deformation and equations for the description of hardening.

The description of hardening (usually through the evolutionary relations for the introduced internal variables “critical shear stresses”) is the important element of the model; there are many works devoted to the development of crystal plasticity in this direction (we mention here only some of the well-known works [22,23,24]). To date, other ratios of the basic structure of the model can be considered as the typical ratios, and therefore they are often dropped from the consideration in papers. However, researchers use several different types of basic formulations that differ in kinematic and constitutive relations. In our opinion, it is important to undertake a thorough analysis of these relations, which will enable their comparison in the context of geometric nonlinearity description and fulfillment of thermodynamic requirements. This is especially important given the fact that an intensively developing direction in crystal plasticity is related to the application of constitutive models for describing other, side by side with intragranular dislocation sliding, significant mechanisms and processes, such as twinning [8,25,26,27], phase transitions [8,28,29], grain boundary sliding [13,30,31,32], recrystallization [33,34,35]. In order to create advanced models, it is necessary to make a reasonable choice of a platform (the basic structure of the model).

In Section 2, popular formulations of mesolevel models are presented and analyzed. In the finite form, the models are formulated in the unloaded configuration, and in the rate form, in the actual configuration. The incorporation of a corotational derivative into the models formulated in the actual configuration means that the motion is decomposed into a rigid motion of the moving coordinate system and a deformation motion of the medium relative to it; the stress rate relative to the moving coordinate system is associated with the rate of this deformation. Section 3 considers the structure of kinematic and constitutive relations in the case when the component responsible for the rigid rotation of a moving coordinate system, relative to which the elastic distortions of the lattice are determined, is explicitly separated in the deformation gradient. An analytical comparison of different formulations and the results of numerical calculations are given in Section 4.

2. Some Well-Known Variants of Base Mesolevel Relations

In a number of works, linear constitutive relations with isotropic elastic law are used to describe small deformations [36]. However, since crystal plasticity models are usually focused on describing the behavior of materials at large displacement gradients, including changes in anisotropic properties at the macrolevel (texture formation), such approximation is rarely used. In addition, the application of anisotropic elastic law causes significant errors in the calculation of residual stress [37].

Let us consider the well-known variants of geometrically nonlinear anisotropic relations of the basic structure of crystal plasticity models, including the description of intragranular dislocation slip and crystallite lattice rotation. Single and double contractions are denoted by “·” and “:”, respectively, and the outer tensor product is denoted by “$\otimes$”.

2.1. Relations in Terms of the Unloaded Configuration (U-Model)

In many studies, the classical decomposition of the Kröner–Lee deformation gradient $\mathit{f}$ is explicitly utilized [38,39,40]:

$$\mathit{f}={\mathit{f}}^e\cdot {\mathit{f}}^p,$$

(1)

where ${\mathit{f}}^e,{\mathit{f}}^p$ denote the elastic and plastic components of the deformation gradient.

The crystal lattice rotation is associated with the orthogonal vector ${\mathit{r}}^e$ from the polar decomposition ${\mathit{f}}^e={\mathit{r}}^e\cdot {\mathit{u}}^e={\mathit{v}}^e\cdot {\mathit{r}}^e$, so the lattice spin is described by the relation:

$$\overline{\mathit{\omega }}={\dot{\mathit{r}}}^e\cdot {\mathit{r}}^e{}^T,$$

(2)

where the dot indicates the time derivative.

Constitutive relations are formulated in the “classical” unloaded configuration found from the actual configuration by applying an affine transformation with ${\left({\mathit{f}}^e\right)}^{-1}$:

$$\mathit{k}={\mathit{\pi }}_0:{\mathit{c}}^e,$$

(3)

where $\mathit{k}=J{({\mathit{f}}^e)}^{-1}\cdot \mathit{\sigma }\cdot {({\mathit{f}}^e)}^{-T}$ is the second Piola–Kirchhoff tensor defined in the unloaded configuration ($\mathit{\sigma }$ is the Cauchy stress tensor, $J=\det {\mathit{f}}^e$), ${\mathit{c}}^e=1/2\left({\left({\mathit{f}}^e\right)}^T\cdot {\mathit{f}}^e-\mathit{I}\right)$ is the elastic Green-Lagrange strain defined in the unloaded configuration, ${\mathit{\pi }}_0={\pi }^{ijmn}{\mathit{k}}_{0i}\otimes {\mathit{k}}_{0j}\otimes {\mathit{k}}_{0m}\otimes {\mathit{k}}_{0n}$ is the elastic tensor, in which ${\mathit{k}}_{0i}$ denotes the crystallographic basis in the reference configuration.

The plastic component of the deformation gradient ${\mathit{f}}^p$ is obtained from the relation:

$${\dot{\mathit{f}}}^p\cdot {({\mathit{f}}^p)}^{-1}={\displaystyle \sum _{k=1}^K{\dot{\gamma }}^{(k)}{\stackrel{o}{\mathit{b}}}^{(k)}\otimes {\stackrel{o}{\mathit{n}}}^{(k)}},$$

(4)

where ${\stackrel{o}{\mathit{b}}}^{(k)},{\stackrel{o}{\mathit{n}}}^{(k)}$ are the unit vectors of the slip direction and the normal to the slip plane in the reference configuration, and K is the number of the slip systems in a crystallite. Here, positive and negative dislocations (doubling of slip systems) are considered separately, which makes the specification of hardening laws more variable, and therefore we make use of this technique in our study.

In most models, the shear rates ${\dot{\gamma }}^{(k)}$ on the slip systems are determined by viscoplastic relations [41,42,43]:

$${\dot{\gamma }}^{(k)}={\dot{\gamma }}_0{\left(\frac{{\tau }^{(k)}}{{\tau }_c^{(k)}}\right)}^{m}H({\tau }^{(k)}-{\tau }_c^{(k)}),$$

(5)

where ${\tau }^{(k)}$, ${\tau }_c^{(k)}$ are the resolved and critical shear stresses on the k-th slip system, ${\dot{\gamma }}_0$ is the shear rate in the slip system in the case when the tangential stress approaches the critical shear stress, and m is the strain rate sensitivity exponent of the material, and H(·) is the Heaviside function. There are some papers, the authors of which propose different ways to determine the resolved shear stress; this issue deserves a separate discussion because it lies, strictly speaking, beyond the scope of this paper. For definiteness, we suppose that ${\tau }^{(k)}=\mathit{k}:{\mathit{n}}^{(k)}\otimes {\mathit{b}}^{(k)}$, where $\mathit{k}$ is the weighted Kirchhoff stress tensor ($\mathit{k}=J\mathit{\sigma }$), ${\mathit{b}}^{(k)},{\mathit{n}}^{(k)}$ are the unit vectors of the slip direction and the normal to the slip plane in the actual configuration.

In many works, Relation (5) are often supplemented with a term $\exp \left(-\frac{U}{\kappa \theta }\right)$, where $\kappa$ is the Boltzman constant, and $U$ is the model parameter (activation energy). This allows one to consider the dislocation motion as a function of temperature. There is also an approach that involves determination of the temperature-dependent parameters ${\dot{\gamma }}_0$, m [44] or formulations of corresponding relations for the critical stresses ${\tau }_c^{(k)}$ [24]. In any case, the initial critical stress values ${\tau }_c^{(k)}(0)$ should appear to be temperature-dependent.

Based on the literature review, we can conclude that the strain rate dependence of stresses in crystal plasticity can be taken into account in different ways. In most of the works ${\dot{\gamma }}_0=const$, and therefore the strain rate sensitivity is defined by the parameter m. The value of ${\dot{\gamma }}_0$ should match the strain rate in order to avoid the sawtooth stress-strain response (curve) of the material during the numerical implementation of the model. It should also be noted that in the general case, there is an interaction between the parameters ${\dot{\gamma }}_0$ and m. At high m, the elastoviscoplastic model is almost similar to the elastoplastic model. Relation (5) provides a point in the stress space in a small neighborhood of the yield surface defined by Schmid’s criterion: when the point is trying to move at great distance away from the neighborhood, significant relaxation of stresses is realized, and the point gets back to it. One can also use the relation ${\dot{\gamma }}_0=\eta d_u,d_u=\sqrt{\frac{2}{3}{\mathit{d}}^{\prime }:{\mathit{d}}^{\prime }}$ is the strain rate intensity, ${\mathit{d}}^{\prime }$ is the deviator of the stretching tensor $\mathit{d}$, $\eta$ is the model parameter (usually $\eta =1$) [24,45]. For the active slip systems, the shear stresses tend towards critical stresses [45]. In the framework of this approach, the effect of the strain rate on the material response is embedded into the evolutionary relations for critical stresses ${\tau }_c^{(k)}$.

The aim of this study is to analyze the kinematic relations and constitutive laws. To this end, we use, for definiteness, Relation (5) with constant ${\dot{\gamma }}_0$ in all cases under study and describe a hardening behavior according to a simple and well-known law [46,47,48] as:

$$\begin{array}{l}{\dot{\tau }}_c^{(k)}={\displaystyle \sum _{l=1}^K{h}^{(kl)}{\dot{\gamma }}^{(l)}},\\ h^{(kl)}=\left[q_{lat}+(1-q_{lat}){\delta }^{(kl)}\right]h^{(l)},h^{(l)}=h_0{\left|1-{\tau }_c^{\left(l\right)}/{\tau }_{sat}\right|}^a,\end{array}$$

(6)

where the latent hardening parameter $q_{lat}$ takes the values 1 and 1.4 for coplanar and noncoplanar slip systems (with numbers $k$ and $l$), respectively, and ${\delta }^{(kl)}$ is the Kronecker delta.

Thus, for definiteness, all the base models considered in our study involve Relations (5) and (6) so that the inelastic strain rate can be determined.

We will call the model, which uses the kinematic relations and constitutive laws (1)–(4), the “U-model” (the unloading configuration type of the model). The given base structure of the relations is employed in numerous works, for instance, in [8,47,48,49,50,51,52,53]. In [54], this model is termed the Kalidindi–Bronkhorst–Anand formulation [55].

2.2. Relations in Terms of the Actual Configuration with a Taylor Spin (T-Model)

The models are often formulated using the Jaumann type rate of the Cauchy stress. The law of elasticity is written in this case as [56,57]:

$${\mathit{\sigma }}^J=\dot{\mathit{\sigma }}-{\overline{\mathit{\omega }}}_T\cdot \mathit{\sigma }+\mathit{\sigma }\cdot {\overline{\mathit{\omega }}}_T=\mathit{\pi }:(\mathit{d}-{\mathit{d}}^p),$$

(7)

where $\mathit{\pi }$ is the elastic tensor in the actual configuration (defined for the current crystallographic orientation), $\mathit{d}$ is the stretching tensor (presented on the basis of the additive decomposition $\mathit{d}={\mathit{d}}^p+{\mathit{d}}^e$), the plastic part of which is determined as:

$${\mathit{d}}^p={\displaystyle \sum _{k=1}^K\frac{1}{2}{\dot{\gamma }}^{(k)}\left({\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)}+{\mathit{n}}^{(k)}\otimes {\mathit{b}}^{(k)}\right)}.$$

(8)

The spin ${\overline{\mathit{\omega }}}_T$ is calculated in the framework of the Taylor’s rotation model [58]:

$${\overline{\mathit{\omega }}}_T=\frac{1}{2}(\mathit{l}-{\mathit{l}}^T)+{\displaystyle \sum _{\kappa =1}^K\frac{1}{2}{\dot{\gamma }}^{(k)}({\mathit{n}}^{(k)}\otimes {\mathit{b}}^{(k)}-{\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)})},$$

(9)

where $\mathit{l}$ is the velocity gradient.

Some recent studies (e.g., [59,60]) have used the law of elasticity written as:

$${\mathit{\sigma }}^J=\dot{\mathit{\sigma }}-{\overline{\mathit{\omega }}}_T\cdot \mathit{\sigma }+\mathit{\sigma }\cdot {\overline{\mathit{\omega }}}_T=\mathit{\pi }:(\dot{\mathit{\epsilon }}-{\dot{\mathit{\epsilon }}}^p)-\mathit{\sigma }tr(\dot{\mathit{\epsilon }})$$

(10)

Apparently, these studies suggest that any strain rate can be defined as $\dot{\mathit{\epsilon }}$, yet $\dot{\mathit{\epsilon }}=\mathit{d}$ remains the most common option. The ${\dot{\mathit{\epsilon }}}^p$ is determined by making use of (8).

It is easy to see that, for $\dot{\mathit{\epsilon }}=\mathit{d}$, Relation (10) can be written in the form:

$${\mathit{k}}^J=\dot{\mathit{k}}-{\overline{\mathit{\omega }}}_T\cdot \mathit{k}+\mathit{k}\cdot {\overline{\mathit{\omega }}}_T=\tilde{\mathit{\pi }}:(\mathit{d}-{\mathit{d}}^p),$$

(11)

where $\overline{\mathit{\pi }}$ is the elastic tensor for establishing the relation between the stress rate and elastic strain rate shown above, $\tilde{\mathit{\pi }}=J\mathit{\pi }$.

Relation (11) and equivalent Relation (10) are supposed to be used instead of (7) since the internal energy density (per unit mass) is defined as:

$$u={\displaystyle \underset{0}{\overset{\tau }{\int }}\left(\frac{1}{\hat{\rho }}\mathit{\sigma }:\mathit{d}\right)dt}=\frac{1}{\stackrel{\circ }{\rho }}{\displaystyle \underset{0}{\overset{\tau }{\int }}\left(J\mathit{\sigma }:\mathit{d}\right)dt}=\frac{1}{\stackrel{\circ }{\rho }}{\displaystyle \underset{0}{\overset{\tau }{\int }}\left(\mathit{\kappa }:\mathit{d}\right)dt},$$

(12)

According to (12), at small deformations (at ${\overline{\mathit{\omega }}}_T=\mathbf{0}$ and for in case of change in volume) when (11) is fulfilled, there will be no energy dissipation during the purely elastic deformation, which does not provide (7). A detailed analysis of the fulfillment of the thermodynamic constraints is given in Section 2.3. Note that, due to the smallness of volume changes in metals and alloys, (11) and (7) give similar results.

The model that involves the kinematic relations and constitutive laws (8), (9), and (11) will be further called the “T-model” (Taylor spin model). The relations of such conceptual structure have been used in many papers, in particular, in [59,60,61]. Some variants of self-consistent models [7] are based on the mesolevel equations of the same structure but with correction of spin (9) via subtraction of the antisymmetric part of the Eshelby tensor for considered grain.

2.3. Analysis of the Formulations with an Emphasis on Describing Geometric Nonlinearity and Fulfillment of Thermodynamic Constraints

In many works cited above, it was shown that, due to the structure of the model relations, the dissipation of energy under inelastic deformation is positive within the framework of both U- and T-models.

The U-model elastic law (3) involves the energetic conjugate stress-strain measures, and this guarantees the absence of energy dissipation during purely elastic deformation. Besides, the finite form of the relations ensures that, after the purely elastic deformation of the material (being in the unloaded configuration) along any closed deformation trajectories, the stresses will be zero. Thus, the conservation conditions for purely elastic deformation [62] are fulfilled within the framework of the U-model.

At the same time, the U-model implies the necessity to perform numerical integration of (4) so that ${\mathit{f}}^p$ can be determined. This can violate the condition of isohoricity of plastic deformation and require corrective techniques. Therefore, ref. [54] proposes an alternative formulation for crystal plasticity that is based on the Kröner–Lee decomposition (also) and logarithmic strain measure, whose rate was decomposed additionally by using elastic corrector rates (defined on the basis of the plastic flow characteristics—shear rates on the slip systems). A major advantage is the lack of a necessity to calculate the exponent when determining ${\mathit{f}}^p$ at the end of each step. Meanwhile, we need to point out here that the interpretation of the physical meaning of the elastic law when considering it as a relation between the introduced complex measures of the stress-strain state (not only in the context of thermodynamics) is rather complicated. In addition, the fulfillment of the additivity condition for the components of the strain rate measure is guaranteed only if one slip system is active; in the general case, this condition is fulfilled approximately [54].

On the other hand, for the study of technological processes of thermomechanical processing, it is more convenient to formulate the boundary value problem in terms of the actual configuration in the rate form. This enables one to use numerical methods: a step-by-step solution with a redefinition of the configuration of the computational domain (including the contacting surfaces) can be realized. Another significant advantage of this formulation is an additive decomposition of the rate of inelastic deformation into contributions from various mechanisms. So, advanced crystal plasticity models taking into account grain boundary sliding were constructed on the basis of this structure [13,30,31,32]. The T-model, referring to this type of formulation, uses a transparent measure of the strain rate—stretching tensor $\mathit{d}$.

It should be noted that the use of the corotational derivative in Relation (11) suggests that the linear (verified) constitutive relation is assumed to be valid for the observer related to a moving coordinate system rotating with the Taylor spin [63]. This suggests that the motion is decomposed into the rigid motion of the moving coordinate system and the deformation motion with respect to it [64]. Note that, to be fully consistent with the issue, we should write the measure of the rate of elastic deformation on the right-hand side of (11) as $(\mathit{l}-{\mathit{l}}^p-{\overline{\mathit{\omega }}}_T)$, ${\mathit{l}}^p={\displaystyle \sum _{k=1}^K{\dot{\gamma }}^{(k)}{\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)}}$ [65]. However, due to the tensor symmetry, the results will be similar to those obtained when using $(\mathit{d}-{\mathit{d}}^p)$. In some studies, the authors explicitly say that they use linear constitutive relations written in the local coordinate systems of crystallites [66,67].

It is evident that, for the relations in terms of the actual configuration in the rate form, the key question is how to determine the spin of the moving coordinate system.

The determination of a hypoelastic law of the form (11), for which the above-mentioned conservation conditions are fulfilled under purely elastic deformation, is a well-known problem in the mechanics of solids [62]. The popular Zaremba–Jaumann [68,69] and Green–Naghdi [70] corotational derivatives do not guarantee the fulfillment of the conservation conditions. Therefore, a logarithmic corotational derivative without this drawback was developed [62,71,72]. However, in [63,73], one can find examples that illustrate the difficulties which can be encountered in modeling the multistage deformation processes (including unloading): if the purely elastic cyclic loading is realized upon completion of elastoplastic deformation and unloading, then the stress hysteresis will be observed. In [73,74], the logarithmic spin, called the kinetic logarithmic spin (k-logspin), was improved. The modernized spin makes it possible to meet the conservation conditions in the simulation of multi-stage deformation processes, including unloading, but the consideration is limited to anisotropic material. Thus, the problem of formulating a hypoelastic constitutive relation of the Form (11) for an anisotropic material that ensures the fulfillment of the conservative conditions has not yet been completely solved. Obviously, this is also the case for the crystal plasticity T-model.

So, both the U-model and the T-model have “a certain extent roughness” formulations, which still arouses the interest of researchers in finding a more elegant solution, with the leveling of these “roughness” formulations (see, e.g., [54]).

Note that, when formulating the T-model, the moving coordinate system (MCS) must be related to the crystallographic coordinate system since the components of the elastic tensor are assumed to be constant in the MCS. In other words, the MCS must be associated with the symmetry elements of the crystal.

According to the Taylor constrained rotation model, the displacement gradient at the mesoscale (grain level) is represented in the form [58]:

$$\mathit{l}={\overline{\mathit{\omega }}}_T+{\displaystyle \sum _{\kappa =1}^K{\dot{\gamma }}^{(k)}{\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)}},$$

(13)

whence, by taking the antisymmetric part, we obtain the relation for the lattice spin (9).

Traditionally, the Taylor model is used for rigid-plastic models (this follows from the symmetrized Relation (13)—all deformation is associated with the shears on the slip systems). The closeness of the spin (9) to the “material rotation” spin (2) was demonstrated [9,75]. In both cases, one cannot speak of a direct relation between the MCS and the symmetry elements of the lattice. We also note that during deformation, the crystallographic coordinate system (CSC) can be distorted, while the MCS remains rigid, and therefore, strictly speaking, their identification is an approximation of the mathematical model.

In [63,65,76], an approach to the formulation of geometrically nonlinear relations is proposed. The approach is based on a modified multiplicative decomposition of the deformation gradient with an explicit selection of rigid rotation of the MCS, which is associated with the symmetry elements of crystallites. In the next section, the equations of the corresponding mesoscale formulations are given in a brief form (in the finite form in the lattice unloaded configuration and in the rate form in the current configuration). In Section 4, these ratios are compared with the U-model and T-model and are utilized to compare these formulations to each other.

3. Modification of Mesolevel Relations with an Explicit Separation of the Rigid Moving Coordinate System with Respect to Which Elastic Distortion Is Defined

3.1. Relations in Terms of Lattice Unloaded Configuration (LU-Model)

In [63,76], it was proposed to modify the decomposition of motion at a mesolevel, i.e., to realize a multiplicative representation of the deformation gradient $\mathit{f}$ with an explicit separation of the rigid moving coordinate system (MCS) Op¹p²p³:

$$\mathit{f}={\mathit{f}}^e\cdot {\mathit{f}}^p={\overline{\mathit{f}}}^e\cdot \mathit{r}\cdot {\mathit{f}}^p.$$

(14)

Here, $\mathit{r}={\widehat{\mathit{k}}}_i\otimes \left({\widehat{\mathit{k}}}^i{|}_{t=0}\right)\equiv {\widehat{\mathit{k}}}_i\otimes {\mathit{k}}_{}^i$ is the proper orthogonal tensor which converts the reference basis MCS) ${\mathit{k}}_i^{}$ into the current basis ${\widehat{\mathit{k}}}_i$; in other words, $\mathit{r}$ is the tensor of rotation of the MCS from reference to actual configuration; ${\mathit{f}}^p$ is the component of the deformation gradient that transforms the initial configuration into the plastically deformed configuration, ${\overline{\mathit{f}}}^e$ is the component of the deformation gradient component that transforms the plastically deformed configuration into the actual configuration (this tensor also characterizes crystalline lattice distortion), and ${\overline{\mathit{f}}}^e$, ${\mathit{f}}^p$ are, in the general case, the non-symmetric second rank tensors.

The motion of the MCS is a rigid motion, and the motion relative to the MCS is a deformation motion: geometrically generalized nonlinear constitutive relations are formulated by an observer related to the MCS [65]. Relation (14) is a modification of the classical Kröner–Lee decomposition (1) via the explicit separation of the quasi-rigid motion $\mathit{r}$. Note that, in the general case, the tensor does not coincide with the orthogonal tensor ${\mathit{r}}^e$ in the polar expansion ${\mathit{f}}^e={\mathit{r}}^e\cdot {\mathit{u}}^e={\mathit{v}}^e\cdot {\mathit{r}}^e$ in the case when the spin of the corresponding MCS is defined (2).

For analytical calculations, we also introduce the crystallographic coordinate system (CCS) Oy¹y²y³ with basis q_i. Without loss of generality, we assume that, in the reference configuration, the CCS basis ${\mathit{q}}_i(0)$ is an orthonormal basis that coincides with ${\mathit{k}}_i$. Note that the lengths of the CCS basis vectors and the angles between them vary during deformation.

The constitutive laws are formulated in the context of the observer related to the MCS. This MCS is assumed to be linked to the symmetry axes of the material. Probably, the idea of the necessity of determining corotational derivatives with reference to the symmetric elements of the material (directors) was initially put forward by J. Mandel [77], yet, unfortunately, his study contains no specific relations for describing a crystallite lattice spin.

Based on the introduced multiplicative decomposition (14) and assuming that the elastic properties of the crystallite in MCS are constant, the constitutive elastoviscoplastic relation was formulated in terms of the unloaded configuration (unloading is carried out with ${({\overline{\mathit{f}}}^e)}^{-1}$, and the MCS remains fixed) [63,76]:

$$\overline{\mathit{k}}=\overline{\mathit{\pi }}:{\overline{\mathit{c}}}^e,$$

(15)

which includes the second Piola–Kirchhoff tensor $\overline{\mathit{k}}$, defined in the unloaded configuration, $\overline{\mathit{k}}={\overline{k}}^{ij}{\widehat{\mathit{k}}}_i\otimes {\widehat{\mathit{k}}}_j=J{({\overline{\mathit{f}}}^e)}^{-1}\cdot \mathit{\sigma }\cdot {({\overline{\mathit{f}}}^e)}^{-T}$ and the four-rank elastic tensor $\overline{\mathit{\pi }}={\overline{\pi }}^{ijmn}{\widehat{\mathit{k}}}_i\otimes {\widehat{\mathit{k}}}_j\otimes {\widehat{\mathit{k}}}_m\otimes {\widehat{\mathit{k}}}_n$, ${\overline{\mathit{c}}}^e$ is the elastic constituent of the right Cauchy–Green deformation tensor ${\overline{\mathit{c}}}^e={\overline{c}}^{ij}{\widehat{\mathit{k}}}_i\otimes {\widehat{\mathit{k}}}_j=1/2({({\overline{\mathit{f}}}^e)}^T\cdot {\overline{\mathit{f}}}^e-\mathit{I})$, and $\mathit{I}$ is the unit tensor. The accepted definition of the elastic tensor (its components are constant in the MCS) conforms to the principle of independence of constitutive relations from reference choice [21].

The plastic component of the deformation gradient ${\mathit{f}}^p$ is determined using the viscoplastic or elastoplastic relations applied to describe the intragranular dislocation slip. In the model, as in other compared models, we use Relations (4)–(6).

An important component of the constitutive model is the kinetic relation for the motion of the MCS. As noted above, it seems reasonable to relate the mesoscale MCSs and the symmetry elements of the crystal lattice [65,76,77]. Plastic deformations occur due to the movement of dislocations and they do not cause symmetry distortion, and therefore $\mathit{r}$ can be completely determined by the tensor ${\mathit{f}}^e$.

The elastic gradient ${\mathit{f}}^e={\overline{\mathit{f}}}^e\cdot \mathit{r}$ contains both the quasi-rigid motion (rotation) of the MCS and the distortion of the lattice relative to it. Generally speaking, there are different variants of this relation. In order to overcome this challenge, it is necessary to accept a hypothesis for the definition of $\mathit{r}$. We consider here one of the options. Let a relation between CCS and MCS be as follows: (1) the axes Oy¹ and Op¹ coincide at every instant of deformation (the vector ${\widehat{\mathit{k}}}_1$ is directed along the vector q₁); (2) the vector ${\widehat{\mathit{k}}}_2$ is located in the plane Oy¹y² at each instant of deformation. In [65], the following relation for the MCS spin is presented:

$$\begin{array}{ll}{\overline{\mathit{\omega }}}_1=\dot{\mathit{r}}\cdot {\mathit{r}}^T={\dot{\widehat{\mathit{k}}}}_i\otimes {\widehat{\mathit{k}}}_i=& -\left({\widehat{\mathit{k}}}_2\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_1\right){\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_2+\left({\widehat{\mathit{k}}}_2\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_1\right){\widehat{\mathit{k}}}_2\otimes {\widehat{\mathit{k}}}_1-\\ & -\left({\widehat{\mathit{k}}}_3\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_1\right){\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_3+\left({\widehat{\mathit{k}}}_3\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_1\right){\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_1-\\ & -\left({\widehat{\mathit{k}}}_3\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_2\right){\widehat{\mathit{k}}}_2\otimes {\widehat{\mathit{k}}}_3+\left({\widehat{\mathit{k}}}_3\cdot {\mathit{l}}^e\cdot {\widehat{\mathit{k}}}_2\right){\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_2.\end{array}$$

(16)

where ${\mathit{l}}^e={\dot{\mathit{f}}}^e\cdot {\mathit{f}}^e{}^{-1}$ is the elastic component of the velocity gradient. In [78], the authors described the way to define $\mathit{r}$ in finite form taking into account the above relation between the CCS and the MCS and showed the compliance of the obtained result with that obtained by integrating (16).

Expression (16) can take a more compact form [79]:

$${\overline{\mathit{\omega }}}_1=\mathit{I}\times ({\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_2\otimes {\widehat{\mathit{k}}}_3-{\widehat{\mathit{k}}}_2\otimes {\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_3+{\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_2):{\mathit{l}}^e$$

(17)

where «$\times$» denotes the vector product.

A model that involves kinematic Relations (4), (14), and (17) and constitutive law (15) is termed here the “LU1-model” (lattice unloading configuration type of model with spin 1).

Besides, the MCS can be related to other symmetry elements of the crystal lattice. As an alternative, we consider the case when the axes Oy³ and Op³ coincide at each instant of time (the vector ${\widehat{\mathit{k}}}_3$ is directed along the vector q₃), the vector k₁ is positioned at each instant of deformation in the plane Oy¹y³. Under these conditions, the spin can be calculated:

$${\overline{\mathit{\omega }}}_2=\mathit{I}\times (-{\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_2+{\widehat{\mathit{k}}}_2\otimes {\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_1+{\widehat{\mathit{k}}}_3\otimes {\widehat{\mathit{k}}}_1\otimes {\widehat{\mathit{k}}}_2):{\mathit{l}}^e.$$

(18)

We call the modified version of the LU-model with spin (18) the “LU2-model”.

Consider the issue regarding the difference between LU1-model and LU2-model.

We assume that, at equal kinematic effects $\mathit{f}$, the current positions of the MCS related to the symmetry axes of the lattice in different ways can be described by different tensors $\mathit{r}$ and $\mathit{r}*$ (due to the smallness of elastic distortions, these tensors are similar). So, the deformation gradient can be written as $\mathit{f}={\overline{\mathit{f}}}^e\cdot \mathit{r}\cdot {\mathit{f}}^p={\overline{\mathit{f}}}^e*\cdot \mathit{r}*\cdot {\mathit{f}}^p*$.

Based on the constitutive Relation (15), in the case when the orientation of the MCS is defined via the application of the tensor $\mathit{r}$, the Cauchy stress are established as:

$$\mathit{\sigma }=1/J{\overline{\mathit{f}}}^e\cdot \left(\overline{\mathit{\pi }}:1/2\left({\overline{\mathit{f}}}^e{}^T\cdot {\overline{\mathit{f}}}^e-\mathit{I}\right)\right)\cdot {\overline{\mathit{f}}}^{eT},$$

(19)

where $\overline{\mathit{\pi }}={\overline{\pi }}^{ijmn}{\widehat{\mathit{k}}}_i{\widehat{\mathit{k}}}_j{\widehat{\mathit{k}}}_m{\widehat{\mathit{k}}}_n={\overline{\pi }}^{ijmn}(\mathit{r}\cdot {\mathit{k}}_i\left)\right(\mathit{r}\cdot {\mathit{k}}_j\left)\right(\mathit{r}\cdot {\mathit{k}}_m\left)\right(\mathit{r}\cdot {\mathit{k}}_n)$. Relation (19) is easy to rearrange [80] into the form:

$$\mathit{\sigma }=1/J{\mathit{f}}^e\cdot \left({\overline{\pi }}^{ijmn}{\mathit{k}}_i\otimes {\mathit{k}}_j\otimes {\mathit{k}}_m\otimes {\mathit{k}}_n:1/2\left({\mathit{f}}^e{}^T\cdot {\mathit{f}}^e-\mathit{I}\right)\right)\cdot {\mathit{f}}^e{}^T$$

(20)

Analogously, when the position of the MCS position is defined via the application of the tensor $\mathit{r}*$, the Cauchy stress can be obtained from the relation:

$$\mathit{\sigma }*=1/J*{\mathit{f}}^e*\cdot \left({\overline{\pi }}^{ijmn}{\mathit{k}}_i\otimes {\mathit{k}}_j\otimes {\mathit{k}}_m\otimes {\mathit{k}}_n:1/2\left({\mathit{f}}^e{}^T*\cdot {\mathit{f}}^e*-I\right)\right)\cdot {\mathit{f}}^e{}^T*$$

(21)

Comparative analysis of (20) and (21) shows that the difference in the definitions of stresses obtained using the LU1- and LU2-models can be attributed to the fact that ${\mathit{f}}^e$ and ${\mathit{f}}^e*$ are determined in different ways in case of inelastic deformation. As noted above, the definition for shear stress can be expressed as ${\tau }^{(k)}=\mathit{k}:{\mathit{n}}^{(k)}\otimes {\mathit{b}}^{(k)}$. The unit vectors of the slip direction and the normal to the plane are found in terms of the actual configuration as ${\mathit{b}}^{(k)}={\mathit{f}}^e\cdot {\stackrel{o}{\mathit{b}}}^{(k)}/\Vert {\mathit{f}}^e\cdot {\stackrel{o}{\mathit{b}}}^{(k)}\Vert ,{\mathit{n}}^{(k)}={\mathit{f}}^e{}^{-T}\cdot {\stackrel{o}{\mathit{n}}}^{(k)}/\Vert {\mathit{f}}^e\cdot {\stackrel{o}{\mathit{n}}}^{(k)}\Vert$. It is evident that, at the elastic deformation stage and in a transition to plasticity (as ${\mathit{f}}^e={\mathit{f}}^e*$), the crystallographic characteristics will be the same, and therefore the reasons for the differences between ${\mathit{f}}^e$ and ${\mathit{f}}^e*$ that may occur are absent.

Thus, the mesostresses obtained within the framework of both LU1- and LU2-models are equal. The final orientations of the lattices determined using the models are different, though due to the smallness of elastic distortions, they differ only slightly [80]. Since the LU1-and LU2-models give almost the same definitions of stresses, we will call them an “LU-model” (if the case in point concerns the definition of stresses).

It is easy to show that the constitutive relation of the LU-model is independent of the imposed rigid motion [21]. Actually, let’s consider deformation gradient $\tilde{\mathit{f}}={\mathit{O}}^T\cdot \mathit{f}$, where $\mathit{O}=\mathit{O}(t)$($\mathit{O}(0)=\mathit{I}$) is the orthogonal tensor describing the rigid rotation added to the initial motion. For pure elastic deformation, we get ${\tilde{\mathit{f}}}^e={\mathit{O}}^T\cdot {\mathit{f}}^e$, and the analysis of (20) yields $\mathit{\sigma }({\tilde{\mathit{f}}}^e)={\mathit{O}}^T\cdot \mathit{\sigma }({\mathit{f}}^e)\cdot \mathit{O}$. In view of $\tilde{\mathit{\sigma }}={\mathit{O}}^T\cdot \mathit{\sigma }\cdot \mathit{O}$, we have $\tilde{\mathit{\sigma }}=\mathit{\sigma }({\tilde{\mathit{f}}}^e)$. Thus, measures of the stress-strain state with an imposed rigid movement are related by exactly the same function. It means that the principle of independence of the constitutive relation from the imposed rigid motion is fulfilled. Hence, it follows that at the onset of the plastic flow ${\tilde{\mathit{f}}}^p={\mathit{f}}^p$ is correct, and, as a result, the principle of independence of the constitutive law from the imposed rigid motion (i.e., $\tilde{\mathit{\sigma }}=\mathit{\sigma }({\tilde{\mathit{f}}}^e)$ will also be fulfilled in the case of inelastic deformation as well.

By virtue of the fact that the used stress and strain measures are energy conjugate, the requirement for the absence of stress hysteresis and energy dissipation in the arbitrary closed cycles of elastic deformations is fulfilled automatically in the LU-model [63], as in the U-model.

In the general case, other physically justified rotation models (in particular, those capable of taking into account the interaction of defects in neighboring crystallites [81] or the contribution of grain boundary sliding [13]) can be incorporated into the proposed approach to determine the MCS spin.

3.2. Rate Form Relations in Terms of the Actual Configuration (LR-Model)

From the formulation of the LU-model with the constitutive law in finite Form (15) through the corotational differentiation [64,76], we can pass to the rate analogue for the observer in the MCS:

$${\overline{\mathit{k}}}^{CR}=\overline{\mathit{\pi }}:{\overline{\mathit{c}}}^e{}^{CR},$$

(22)

where ${\overline{\mathit{k}}}^{CR}=\dot{\overline{\mathit{k}}}-{\overline{\mathit{\omega }}}_1\cdot \overline{\mathit{k}}+\overline{\mathit{k}}\cdot {\overline{\mathit{\omega }}}_1$, ${\overline{\mathit{c}}}^e{}^{CR}={\dot{\overline{\mathit{c}}}}^e-{\overline{\mathit{\omega }}}_1\cdot {\overline{\mathit{c}}}^e+{\overline{\mathit{c}}}^e\cdot {\overline{\mathit{\omega }}}_1$ (for implementation of this transition, we use the property of constancy of $\overline{\mathit{\pi }}$ for the observer in the MCS).

It was shown in [63,82] that, at ${\overline{\mathit{f}}}^e\approx \mathit{I}$ which is characteristic of metals, the following formulation in the rate form can be derived in terms of the current configuration.

Since, at ${\overline{\mathit{f}}}^e\approx \mathit{I}$, the unloaded and actual lattice configurations are close, the following estimate is valid for the velocity gradient:

$$\mathit{l}\approx {\dot{\overline{\mathit{f}}}}^e\cdot {\overline{\mathit{f}}}^e{}^{-1}+{\overline{\mathit{\omega }}}_1+\mathit{r}\cdot {\dot{\mathit{f}}}^p\cdot {\mathit{f}}^p{}^{-1}\cdot {\mathit{r}}^T={\overline{\mathit{\omega }}}_1+{\dot{\overline{\mathit{f}}}}^e\cdot {\overline{\mathit{f}}}^e{}^{-1}+{\displaystyle \sum _{k=1}^K{\dot{\gamma }}^{(k)}{\overline{\mathit{b}}}^{(k)}\otimes {\overline{\mathit{n}}}^{(k)}},$$

(23)

where ${\overline{\mathit{b}}}^{(k)},{\overline{\mathit{n}}}^{(k)}$ are the vectors of the slip direction and the normal to the slip plane in the unloaded lattice configuration, i.e., they are in the actual position of the MCS. If the unloaded and actual lattice configurations are in close proximity, then we can assume ${\overline{\mathit{b}}}^{(k)}={\mathit{b}}^{(k)},{\overline{\mathit{n}}}^{(k)}={\mathit{n}}^{(k)}$ for the latter relation and use ${\displaystyle \sum _{k=1}^K{\dot{\gamma }}^{(k)}{\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)}}$ as an approximation for the inelastic strain rate.

According to (23), the clear motion decomposition is established in the rate form: the velocity gradient $\mathit{l}$ is represented as a set of the MCS spin and the rate of elastic distortions and inelastic deformations determined by the observer related to this MCS.

Taking into account the described approximations, the constitutive law (22) is close to

$${\mathit{k}}^{cr}=\overline{\mathit{\pi }}:\left({\dot{\overline{\mathit{f}}}}^e\cdot {\overline{\mathit{f}}}^e{}^{-1}\right)=\overline{\mathit{\pi }}:\left(\mathit{l}-{\overline{\mathit{\omega }}}_1-{\displaystyle \sum _{k=1}^K{\dot{\gamma }}^{(k)}{\mathit{b}}^{(k)}\otimes {\mathit{n}}^{(k)}}\right)$$

(24)

where $\mathit{k}$ is the weighted Kirchhoff stress tensor, and ${\mathit{k}}^{cr}=\dot{\mathit{k}}+\mathit{k}\cdot {\overline{\mathit{\omega }}}_1-{\overline{\mathit{\omega }}}_1\cdot \mathit{k}$ is its corotational derivative. Let us call the model involving the kinematic Relations (8), (17), and (23) and a constitutive law (24) the “LR1-model” (lattice rate type of model with spin 1). We also consider an analogous LR2-model in which Relation (18) is used for the spin. It was shown in [80] that the Cauchy stress determined using the formulation of this kind depends only slightly on the way they are related to specific material symmetry elements.

From the above discussion, we can draw a conclusion that the formulations of the U- and LU-models can provide the fulfillment of the conservative conditions for elastic deformation. On the other hand, for the study of technological processes of thermomechanical treatment with an a priori unknown configuration of the computational domain (including contact with the tool), the formulations in terms of the actual configuration in the rate form offer the most promise. Another advantage of such formulations is the possibility of an additive decomposition of the inelastic deformation rate into the contributions of different deformation mechanisms. This explains why the T-model is also popular.

The formulation based on the decomposition of motion with an explicit separation of the motion of the moving coordinate system (LU-model) makes possible a theoretically substantiated transition to a similar formulation in the rate form in terms of the actual configuration (LR-model). As will be illustrated below, this helps to easily show that all the models considered here give a similar response under equal influences.

4. Results and Discussion

In this section, the issue regarding a comparison of the formulations for crystal plasticity models described above is considered.

4.1. Analytical Comparison

Based on the Equation of motion (14), constitutive law (3) for the U-model can be written as:

$$J{\mathit{r}}^T\cdot {({\overline{\mathit{f}}}^e)}^{-1}\cdot \mathit{\sigma }\cdot {({\overline{\mathit{f}}}^e)}^{-T}\cdot \mathit{r}={\overline{\pi }}^{ijmn}{\mathit{k}}_i\otimes {\mathit{k}}_j\otimes {\mathit{k}}_m\otimes {\mathit{k}}_n:1/2({\mathit{r}}^T\cdot {({\overline{\mathit{f}}}^e)}^T\cdot {\overline{\mathit{f}}}^e\cdot \mathit{r}-\mathit{I}),$$

(25)

where ${\mathit{k}}_i$ is the reference basis of the MCS related to the lattice symmetry.

The rearranged form of Relation (25) is:

$$J{({\overline{\mathit{f}}}^e)}^{-1}\cdot \mathit{\sigma }\cdot {({\overline{\mathit{f}}}^e)}^{-T}={\overline{\pi }}^{ijmn}(\mathit{r}\cdot {\mathit{k}}_i)\otimes (\mathit{r}\cdot {\mathit{k}}_j)\otimes (\mathit{r}\cdot {\mathit{k}}_m)\otimes (\mathit{r}\cdot {\mathit{k}}_n):1/2({({\overline{\mathit{f}}}^e)}^T\cdot {\overline{\mathit{f}}}^e-\mathit{I}).$$

(26)

Relation (26) can be represented as:

$$J{({\overline{\mathit{f}}}^e)}^{-1}\cdot \mathit{\sigma }\cdot {({\overline{\mathit{f}}}^e)}^{-T}={\overline{\pi }}^{ijmn}{\widehat{\mathit{k}}}_i\otimes {\widehat{\mathit{k}}}_j\otimes {\widehat{\mathit{k}}}_m\otimes {\widehat{\mathit{k}}}_n:1/2({({\overline{\mathit{f}}}^e)}^T\cdot {\overline{\mathit{f}}}^e-\mathit{I}).$$

(27)

Relation (27) corresponds to the constitutive law of the LU-model (15). Thus, the stresses in the U- and LU-models are equally determined. As shown in Section 3.1, the determined stresses are independent of the portion of the MCS motion in the deformation gradient. When we use models of this kind, it is important to keep in mind this distinction and verify separately texture description.

If, by analogy with the transition from the LU-model to the rate LR-model described in Section 3.2, we take for the U-model an MCS that moves with spin (2), then we get the rate formulation of the LR-model type, but with a corotational derivative of the Green–Naghdi type (the GN-model used, for instance, in [75,83,84]). In line with this assumption, the proposed model will give stresses close to those determined in the U-model.

In [75], the following relation between spins (2) and (9) is given:

$${\overline{\mathit{\omega }}}_{{\mathit{r}}^e}={\overline{\mathit{\omega }}}_T-(\mathit{B}:\mathit{\sigma })\cdot {\mathit{d}}^p+{\mathit{d}}^p\cdot (\mathit{B}:\mathit{\sigma }),$$

(28)

where $\mathit{B}$ is the four rank elastic compliance tensor, ${\mathit{d}}^p$ is defined using Formula (8). According to (28), by virtue of the smallness of elastic deformations $(\mathit{B}:\mathit{\sigma })$, the use of spin Relations (2) and (9) in the mesolevel model will cause slightly different stresses to occur (in other words, the proximity of the T-model and the GN-model is their characteristic feature).

Hence, we can suggest that at small elastic distortions, all the models examined should give a close response (stresses).

Table 1. Comparison of determination of stresses within the framework of different models (notation used here: «=»—precise coincidence of stresse obtained in the indicated models, «≈»—stresses are close; by “described” is meant the description of the essence of calculations with references to publications).

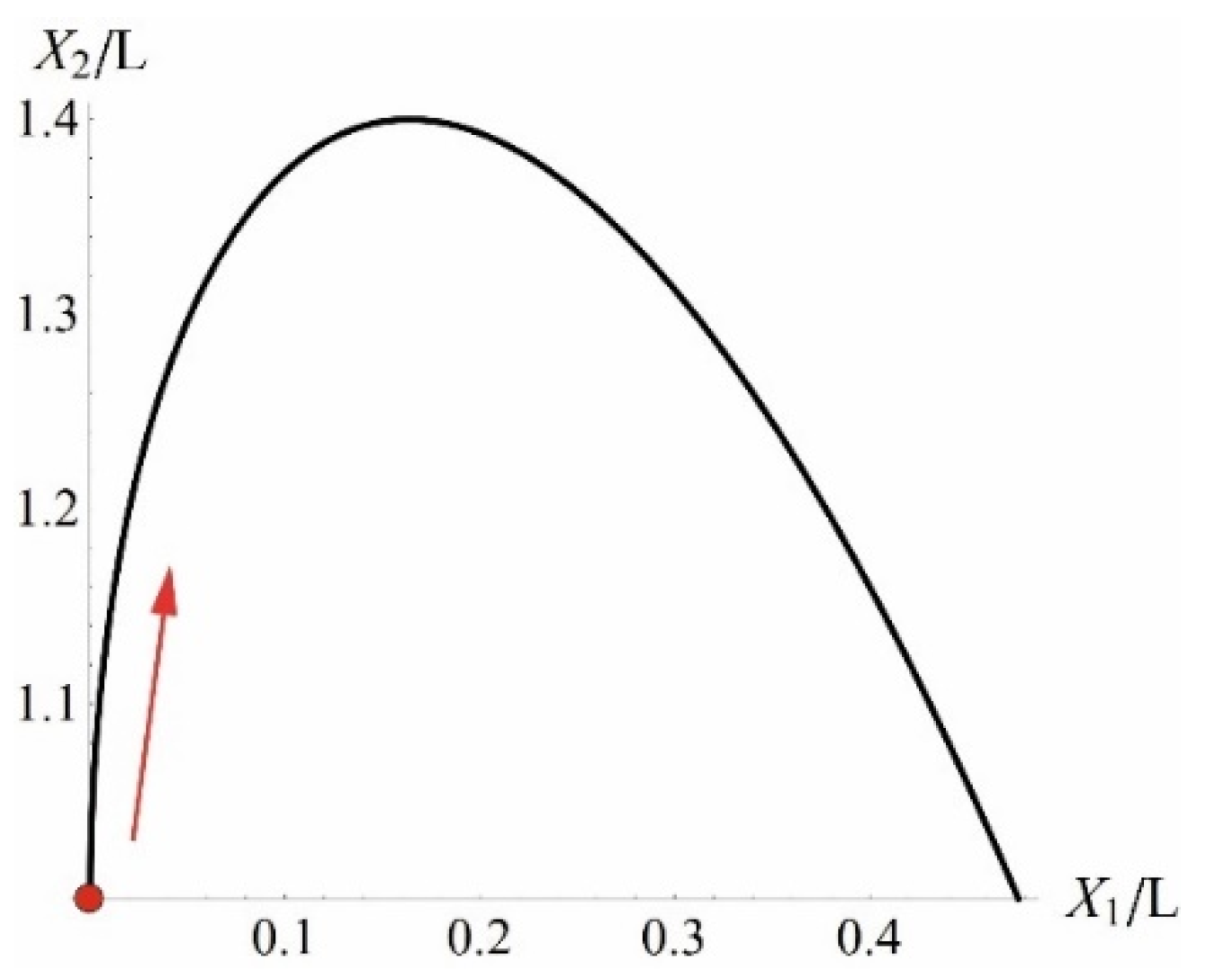
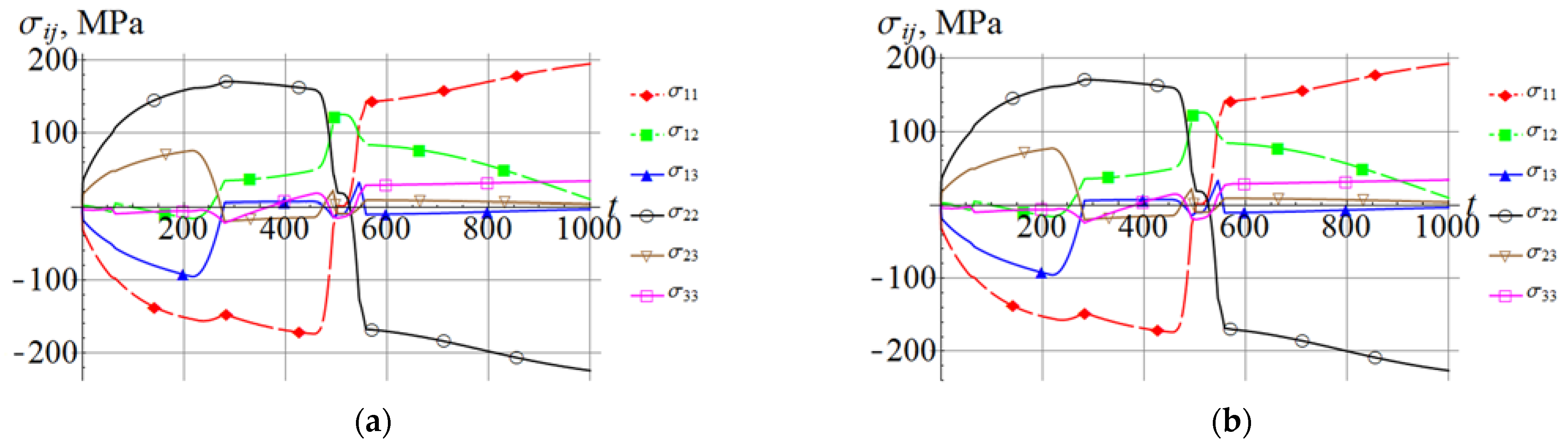
	U	T	LU	LR1	LR2	GN
U		≈ (described in Section 4.1, follows from U ≈ GN ≈ T)	= (shown in Section 4.1)	≈ (shown in Section 4.1, described in Section 3.2, follows from U = LU ≈ LR1)	≈ (shown in Section 4.1, described in Section 3.2, follows from U = LU ≈ LR2)	≈ (described in Section 4.1, S by analogy with LU ≈ LR1)
T			≈ (described in Section 4.1, follows from LU = U ≈ GN ≈ T)	≈ (described in Section 4.1, follows from LR1 ≈ LU = U ≈ ≈ GN ≈ T)	≈ (described in Section 4.1, follows from LR2 ≈ LU = U ≈ ≈ GN ≈ T)	≈ described in Section 4.1)
LU				≈ (described in Section 3.2)	≈ (described in Section 3.2)	≈ (described in Section 4.1, follows from LU = U ≈ GN)
LR1					≈ (described in Section 3.2)	≈ (described in Section 4.1, follows from LR1 ≈ LU = = U ≈ GN)
LR2						≈ (described in Section 4.1, follows from LR2 ≈ LU = = U ≈ GN)

presents information obtained when performing the analytical comparison of determination of stresses within the framework of different models.

In order to confirm the analytical results summarized in Table 1, we performed numerical calculations.

4.2. Illustrative Numerical Examples

We now turn to the consideration of the results obtained via the analysis of the application of kinematic relations and constitutive laws in the statistical constitutive model for simulating some kinematic loads imposed on the fcc polycrystal.

The representative volume included a sample of 343 crystallites, the initial orientations of which were distributed randomly according to a uniform law. The nominal properties of the polycrystal corresponded to those of copper. The mesolevel elastic property tensor contained the following independent components (constant for the observer in a rigid moving coordinate system linked with the lattice): ${\pi }_{1111}=168.4$ GPa, ${\pi }_{1122}=121.4$ GPa, ${\pi }_{1212}=75.4$ GPa [85]; the viscoplastic relations included ${\dot{\gamma }}_0=0.001$ s^–1, $1/m=0.012$; the hardening law parameters were $h_0=180$ MPa, $a=2.25$, ${\tau }_{sat}=148$ MPa, and the initial values of critical stresses for all slip systems were ${\tau }_c^{(k)}(0)={\tau }_{c0}^{}=16$ MPa ($k=1,\dots ,K$) [46,47]. Due to the significant nonlinearity of the systems of equations for all considered models, in particular, because of the presence of the Heaviside function in the viscoplastic law (5), which led to the necessity of discretization with a small time step to trace the activity of slip systems in crystallites, these equations were integrated using an explicit Euler method (in the calculations, the time step was 0.002 s). The results obtained with the aid of the LR1 model correspond satisfactorily to the experimental data for uniaxial compression and shear; the comparison of the results is given in [63].

We consider the affine deformations of the sample (corresponding to the representative volume of a polycrystal) subjected to uniformly distributed kinematic loads. Due to the uniform deformation, the radius vector of the material point at an arbitrary instant of time t is determined according to $\mathit{r}(t)=\mathit{f}(t)\cdot q^i{\mathit{p}}_i$, where $\mathit{f}(t)$ is the deformation gradient, $q^i$ stands for the Lagrangian coordinates of the considered point, and ${\mathit{p}}_i$ is the basis of the fixed laboratory coordinate system. The motion is determined by the deformation gradient (the choice of motion can be arbitrary):

$$\begin{array}{ll}\mathit{f}(t)=& \frac{1}{1+4h\sin (\omega t)}{\mathit{p}}_1{\mathit{p}}_1+(1+4h\sin (\omega t)){\mathit{p}}_2{\mathit{p}}_2+{\mathit{p}}_3{\mathit{p}}_3+\\ & +3h(1-cos(0.7\omega t)){\mathit{p}}_1{\mathit{p}}_2,\end{array}$$

(29)

where ω = 0.001π, $h=0.1$ is the constant parameter (deformation is considered within the time interval $t=[0,T],T=1000 \mathrm{s}$). For illustration, the trajectory of the point with Lagrangian coordinates (0, L, 0) m is given in Figure 1.

Figure 2 presents the time dependence of the Cauchy stress tensor components at a macrolevel (in the laboratory coordinate system) for the LU-model (Figure 2a, precise coincidence with the results of the U-model) and for LR1-model (Figure 2b).

We note the proximity of the results obtained (the curves plotted for the varying macrostress components are visually almost indistinguishable for all models examined in this study). For numerical assessment of the deviation in the results, we take the U-model as a base model and introduce the norm for comparing the results obtained using other models:

$${\Delta }_G={\Vert {\mathsf{\Sigma }}_{t\in [0,T]}{}^{(U)}-{\mathsf{\Sigma }}_{t\in [0,T]}{}^{(G)}\Vert }_{C_{L^2}^n},$$

(30)

where ${\mathsf{\Sigma }}_{t\in [0,T]}{}^{(U)}$ is the history of changes in stresses at $t=[0,1000 \mathrm{s}]$, obtained via the use of the U-model, ${\mathsf{\Sigma }}_{t\in [0,T]}{}^{(G)}$ is the history of changes in stresses at $t=[0,1000 \mathrm{s}]$ in case of the G-model (one of the models from Table 1). The norm is given based on the Riemann integral ${\Vert {\mathit{Y}}_{t\in \left[0,T\right]}\Vert }_{C_{L^2}^n}={\left(\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\mathit{Y}(t):{\mathit{Y}}^T(t)dt}\right)}^{1/2}$ in the space $C_{L^2}^n$ continuous at $t\in \left[0,T\right]$ on the vector-function dimension $n$; in the calculations $n=9$ (the number of the macrostress tensor component $\mathsf{\Sigma }$ that is equal to averaged mesostresses in crystallites).

Table 2. Deviation of the history of changes in macrostresses obtained via the use of the U-model from the history of changes in macrostresses determined in the framework of other models.

Model	U	T	LU	LR1	LR2	GN
$\mathrm{Norm}{\Delta }_G$, MPa	0	2.94	0	2.935	2.752	2.954
$\frac{{\Delta }_G}{{\Vert {\mathsf{\Sigma }}_{t\in [0,T]}{}^{(U)}\Vert }_{C_{L^2}^n}}$	0	0.013834	0	0.013813	0.012948	0.013903

(Zero deviations from Table 1 suggest that they do not exceed the order of the computer error when working with real numbers.).

summarizes the results for deviations in the macrostresses obtained by the U-model from those determined by other models.

Taking into account that the norms are integral over a sufficiently long period of time (T = 1000 s), the results summarized in Table 2 demonstrate the proximity of stresses obtained via the use of different formulations of mesolevel models, supporting thus the efficacy of theoretical statements given above (Table 1). Similar textures are obtained, which is indirectly confirmed by the proximity of macrostresses for the considered complex loading path. In [80], the issue of comparing the results of using some different spins (for other complex loading paths) was considered with an explicit analysis of the simulated lattice rotations.

Figure 3 shows the time dependence of the mesolevel stress components for a single crystallite (chosen arbitrarily). The initial orientations of the crystallographic and moving coordinate systems coincide and can be determined through the sequential rotation of the crystallographic system initially coincident with the coordinate system for the fcc-crystal around the Ox¹ axis with an angle ${\varphi }_1=4.078$, around the Ox² axis with an angle ${\varphi }_2=0.0739$, around the Ox³ axis with an angle ${\varphi }_3=2.149$ for the U-model (Figure 3a) and the LR1-model (Figure 3b).

Analysis of the results shown in Figure 3 demonstrates that the mesostresses for the crystallite under study, which were obtained within the framework of the models mentioned above, are similar.

Table 3. Deviation of the history of changes in mesostresses obtained via the use of the U-model for crystallite No1 from the history of changes in macrostresses determined within in the framework of other models.

Model	U	T	LU	LR1	LR2	GN
$\mathrm{Norm}{\delta }_G$, MPa	0	2.854	0	2.775	3.859	2.964
$\frac{{\delta }_G}{{\Vert {\mathit{\sigma }}_{t\in [0,T]}{}^{(U)}\Vert }_{C_{L^2}^n}}$	0	0.01145	0	0.011132	0.015481	0.011891

(Zero deviations from Table 1 suggest that they do not exceed the order of the computer error when working with real numbers.).

gives the norms for deviations in the mesostresses ${\delta }_G={\Vert {\sigma }_{t\in [0,T]}{}^{(U)}-{\sigma }_{t\in [0,T]}{}^{(G)}\Vert }_{C_{L^2}^n}$ for the considered models, which are similar to those for deviations in macrostresses (30).

The results shown in Figure 3 and in Table 3 indicate the proximity of mesostresses. This is typical for the overwhelming number of crystallites (i.e., for almost all random orientations). In special cases, deviations of the mesostress components (difference modulus) may, at a certain instant of time, exceed 50 MPa. This can be attributed to some specific features in the motion of a representative point in the stress space near the yield surface [86] in transitions between the neighborhoods of the vertices. After transitions, in a great number of crystallites, the stresses become similar (there is a separate publication devoted to the study of these special cases). Due to the small fraction of such crystallites (37 crystallites out of 343) and averaging, the macroscale stresses obtained on the basis of the statistical constitutive model data using mesolevel models differ insignificantly (Table 2).

The differences in stresses obtained at the macrolevel are significantly lower than the experimental data scatter for samples from one production batch. Indeed, for each material, there is no complete identity of samples even from the same batch due to the presence of many random factors during manufacturing, which leads to differences in the microstructure (distributions of crystallite orientations, dislocation densities, etc.) and, as a consequence, to different experimental dependences of stresses on deformations. For example, such scatters for copper alloy samples are given in [87,88].

It should be noted here that the U-model and LU-model offer the most promise for modeling purely elastic behavior (e.g., elastic cyclic loading during exploitation) since the constitutive law is presented in the finite form, and there is no stress hysteresis in closed elastic cycles. Moreover, due to the use of energetically conjugate stress and strain measures, no energy is dissipated during the elastic deformation.

On the other hand, crystal plasticity models are primarily used to describe large inelastic deformations and material structure evolution. In this regard, formulations in terms of the actual configuration hold more promise because the physical meaning of the stress tensor is clearer in this case, and, consequently, the simulation of hardening using evolutionary equations is facilitated. These arguments lend additional support to using this formulation in case of the boundary value problem and in some advanced constitutive models at different deformation mechanisms. The theoretical predictions and the results of the numerical experiments indicate that the response produced by these models is similar to that obtained using the U-model. So, it turns out that the formulation in rate form would be most suitable for constructing advanced constitutive models (e.g., with complex hardening laws). The point is that the hypotheses adopted for constructing the evolutionary equations of the model via the use of the internal variables determined in the unloaded configuration can give more significant errors than the small deviations from the strict fulfillment of conservative conditions for the formulations written in terms of the actual configuration.

Geometrically nonlinear crystal plasticity models are applied to anisotropic crystallites, and therefore the decomposition of motion, used in rate formulations in terms of the current configuration, must be constructed by taking into account the symmetry of the material. In other words, the moving coordinate system determining the rigid motion in motion decomposition must be associated with the elements of material symmetry so that its symmetry properties can be taken into account correctly. Above, some options for constructing constitutive models with the introduction of such moving coordinate systems have been considered.

5. Conclusions

We have analyzed the most popular relations of crystal plasticity models in the context of geometric nonlinearity description and fulfillment of thermodynamic constraints in case of elastic deformation. These models are focused on the description of significant inelastic deformations and material structure evolution caused by these deformations. That is why the formulations in the rate form written in terms of the current configuration seem preferable to constructing advanced constitutive models able to take into account different deformation mechanisms and their complex interactions. The main advantages of these formulations over the formulation in the finite form are as follows:

• clear physical meaning of the stress tensor, which simplifies simulations with evolutionary hardening equations;
• use of the clear measure of the strain rate (the stretching tensor) and the possibility of an additive decomposition of the strain rate into contributions from various mechanisms;
• ease of their use in the rate formulation of the boundary value problem under varying, a priori unknown, contact boundary conditions.

The use of a corotational derivative in such a formulation means that the model is based on the decomposition of motion into the deformation motion and the rigid motion of a moving coordinate system, the rate of stress change relative to which is associated with the strain rate.

We have obtained the relations of the mesolevel model with an explicit separation of the motion of the moving coordinate system and elastic distortion of crystallites with respect to this system in the deformation gradient. The MCS is related to the elements of the material symmetry of the anisotropic crystallite. The proposed formalism with an explicit consideration of the MCS allows us to reasonably pass from the formulation in terms of the unloaded lattice configuration in the finite form (where the thermodynamic constraints for purely elastic deformation are strictly fulfilled) to the close formulation in rate form written in terms of the current configuration.

We have compared these relations with a popular crystal plasticity formulation, which makes it possible to establish their proximity to one another. The results of the performed analytical calculations show the equivalence or similarity (in the sense of the response determined under the same loads) of the formulations under consideration. These conclusions were supported by the results of the numerical calculations. It should be noted that the proposed approach aimed to determine the spin of the MCS also could include other physically justified rotation models, e.g., those taking into account the interaction of defects of neighboring crystallites or the contribution from the mechanism of grain boundary sliding. Such models cannot be introduced into other known approaches to constructing constitutive relations via the use of kinematic variables without explicit consideration of the material symmetric properties.