New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach
Abstract
1. Introduction
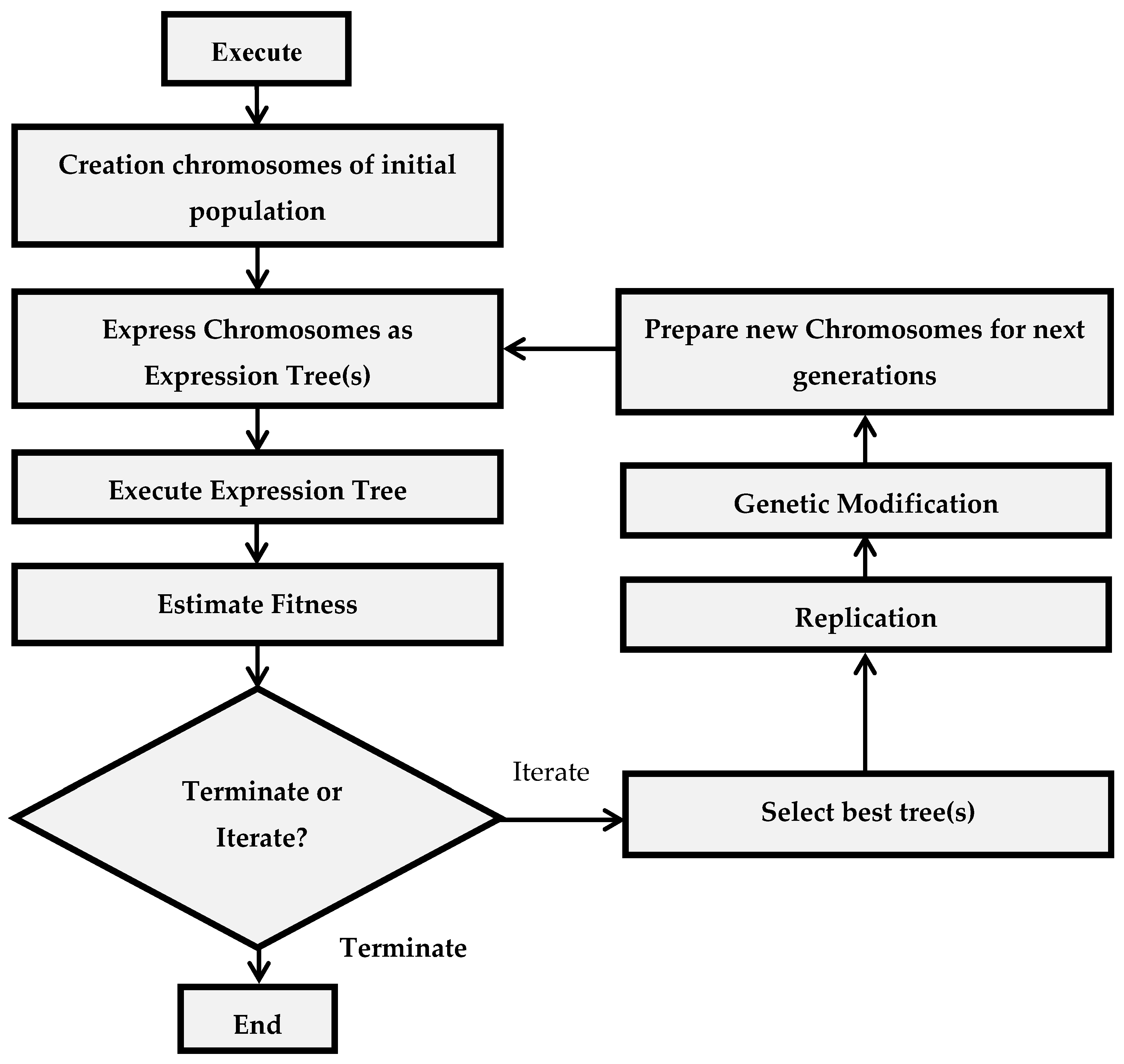
2. Comparison of Genetic Programming vs. Genetic Engineering Programming
3. Experimental Database
4. Development of Model
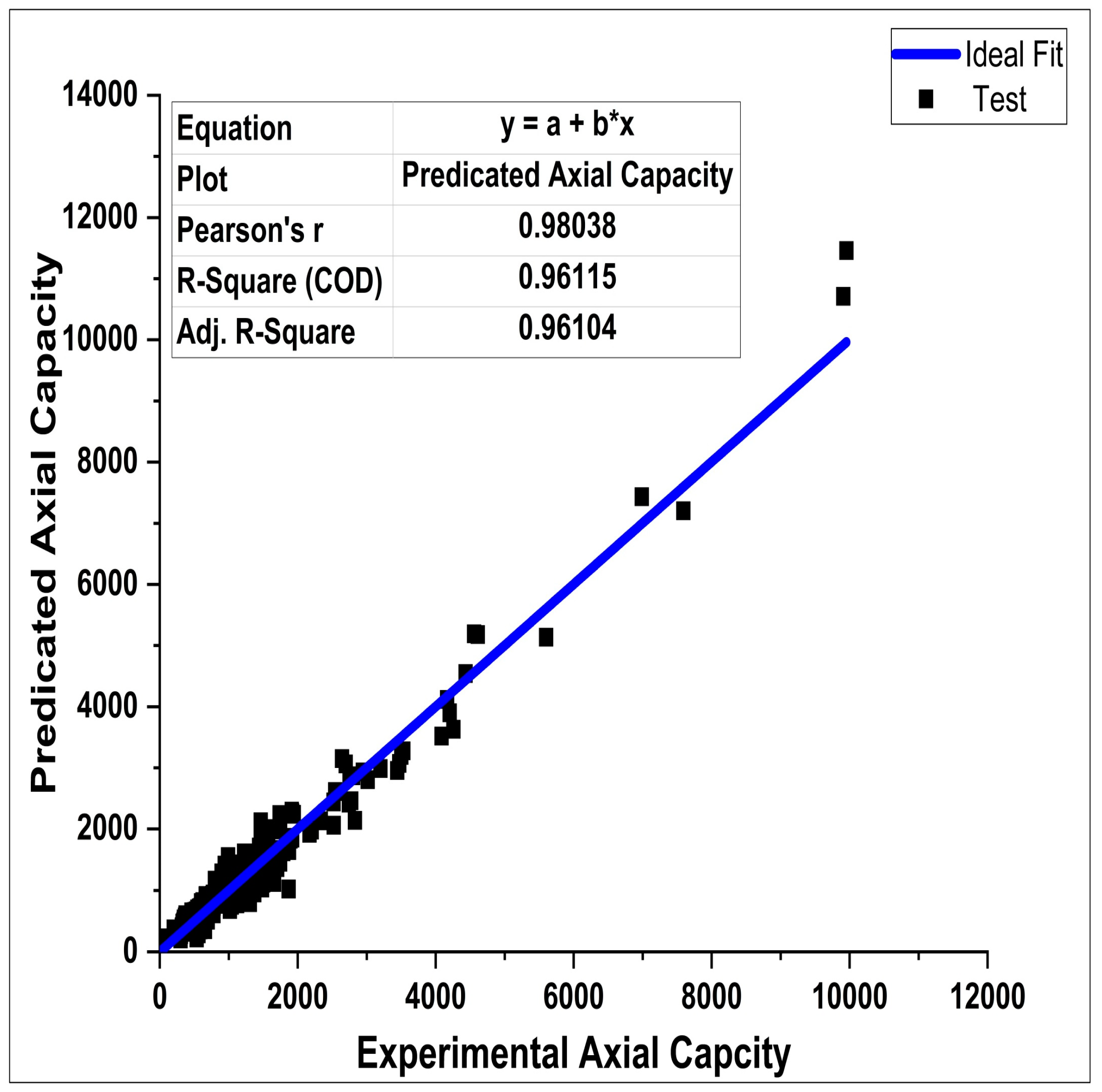
5. Results and Discussion
Model Performance, Validity and Comparative Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Concrete-filled steel tube |
| Artificial neutron network |
| Genetic programming |
| Genetic engineering programming |
| Expression trees |
| Mean absolute error |
| Root mean square error |
| Ultimate axial moment capacity |
| Nominal axial moment capacity |
| Euler’s bucking load |
| Nominal axial compressive strength exclusive of length effects |
| Steel section areas |
| Concrete area |
| Total composite cross-section area |
| Diameter of concrete core |
| Concrete elastic modulus |
| Steel elastic modulus |
| Concrete compressive strength |
| Steel section minimum yield strength |
| Concrete section moment of inertia |
| Steel section moment of inertia |
| Length effectiveness factor |
| Length of laterally braced member |
| Composite section effective stiffness |
| Elastic bucking load |
| Concrete contribution factor |
| 28-day characteristic strength of concrete cube |
| Triaxially contained concrete improved characteristic strength |
| Steel-tube nominal yield strength |
| Concrete characteristic strength |
| Reduced nominal yield strength of the steel casing |
| Effective length |
| Actual length |
| Concrete confinement coefficient |
| Steel tube confinement coefficient |
| = Relative slenderness |
| Effective flexural stiffness |
| Correction factor |
| Confinement factor |
| Confinement factor |
| Section modulus of composite cross section |
| Flexural strength index |
| = Objective function |
Appendix A
| S. No | Diameter | Thickness | Yield Strength | Compressive Strength | Length | Length/Diameter | Axial Capacity |
|---|---|---|---|---|---|---|---|
| 1 | 120.9 | 3.73 | 312 | 30.22 | 2311 | 19.11 | 725 |
| 2 | 166 | 5 | 288.1 | 63.70 | 1040 | 6.27 | 1862 |
| 3 | 88.9 | 5.842 | 406 | 50.50 | 1117.6 | 12.57 | 715.56 |
| 4 | 114.3 | 3.1 | 348 | 62.78 | 670 | 5.86 | 898 |
| 5 | 95 | 3.68 | 392 | 31.44 | 860 | 9.05 | 686 |
| 6 | 166 | 5 | 288.1 | 36.55 | 1040 | 6.27 | 1495 |
| 7 | 168.2 | 4.52 | 302 | 52.80 | 813 | 4.83 | 2113 |
| 8 | 114.3 | 3.1 | 348 | 62.78 | 670 | 5.86 | 904 |
| 9 | 219 | 7 | 273 | 46.50 | 1200 | 5.48 | 3200 |
| 10 | 114 | 6.34 | 486 | 45.00 | 850 | 7.46 | 1608 |
| 11 | 100 | 2.5 | 433.2 | 54.78 | 600 | 6.00 | 750 |
| 12 | 108 | 4 | 338.88 | 35.71 | 5400 | 50.00 | 210.7 |
| 13 | 219 | 7 | 273 | 46.50 | 1420 | 6.48 | 3070 |
| 14 | 215.9 | 4.08 | 292 | 28.67 | 2220 | 10.28 | 1650 |
| 15 | 152.4 | 1.55 | 294 | 43.25 | 914 | 6.00 | 721.5 |
| 16 | 114 | 6 | 486 | 45.00 | 850 | 7.46 | 1334 |
| 17 | 114.3 | 3.1 | 340 | 73.10 | 3370 | 29.48 | 379 |
| 18 | 95 | 3.66 | 338 | 30.00 | 2032 | 21.39 | 463 |
| 19 | 216 | 4.04 | 293 | 36.89 | 2220 | 10.28 | 2289 |
| 20 | 114.3 | 3.19 | 414 | 35.44 | 838 | 7.33 | 734 |
| 21 | 95 | 12.4 | 277 | 26.22 | 1420 | 14.95 | 907 |
| 22 | 108 | 4 | 337.6 | 43.12 | 756 | 7.00 | 785 |
| 23 | 152.4 | 1.55 | 330 | 32.11 | 1499 | 9.84 | 734 |
| 24 | 166 | 5 | 288.1 | 65.17 | 1040 | 6.27 | 1852 |
| 25 | 166 | 5 | 289.1 | 34.68 | 2700 | 16.27 | 1117.2 |
| 26 | 110 | 1.9 | 350 | 14.44 | 2200 | 20.00 | 252 |
| 27 | 120.9 | 3.76 | 312 | 26.78 | 1049 | 8.68 | 721 |
| 28 | 216 | 4.11 | 291 | 36.89 | 2220 | 10.28 | 2239 |
| 29 | 108 | 4.5 | 348.1 | 46.87 | 4023 | 37.25 | 318 |
| 30 | 190.7 | 6 | 505 | 57.40 | 3450 | 18.09 | 2130 |
| 31 | 166 | 5 | 288.1 | 53.11 | 1040 | 6.27 | 1695 |
| 32 | 108 | 4 | 338.88 | 35.71 | 864 | 8.00 | 766.36 |
| 33 | 95 | 12.75 | 277 | 26.22 | 1420 | 14.95 | 938 |
| 34 | 114 | 5.94 | 486 | 45.00 | 1750 | 15.35 | 1138 |
| 35 | 216 | 4.11 | 304 | 29.11 | 2220 | 10.28 | 1834 |
| 36 | 152.4 | 3.17 | 415 | 26.56 | 2271 | 14.90 | 939 |
| 37 | 114 | 4.68 | 332 | 45.00 | 850 | 7.46 | 1049 |
| 38 | 108 | 4.5 | 259.7 | 25.48 | 1620 | 15.00 | 524 |
| 39 | 108 | 4 | 338.88 | 35.71 | 3240 | 30.00 | 478.24 |
| 40 | 110 | 1.9 | 350 | 14.44 | 2200 | 20.00 | 219 |
| 41 | 76.48 | 1.73 | 369 | 32.56 | 609.45 | 7.97 | 330.04 |
| 42 | 166 | 5 | 274.4 | 36.43 | 1100 | 6.63 | 1985 |
| 43 | 127.1 | 2.95 | 376 | 77.20 | 711 | 5.59 | 1305 |
| 44 | 114.3 | 3.1 | 348 | 62.67 | 1020 | 8.92 | 888 |
| 45 | 110 | 1.9 | 350 | 40.50 | 2200 | 20.00 | 437 |
| 46 | 355.6 | 11.18 | 361 | 47.00 | 1880 | 5.29 | 11,460 |
| 47 | 88.9 | 5.85 | 400 | 49.75 | 508 | 5.71 | 992 |
| 48 | 127.3 | 1.63 | 334 | 77.20 | 711 | 5.59 | 1285 |
| 49 | 210 | 3 | 233.2 | 33.52 | 1040 | 4.95 | 1705 |
| 50 | 114.3 | 3.1 | 340 | 64.56 | 3720 | 32.55 | 293 |
| 51 | 355.6 | 4.72 | 281 | 27.00 | 1880 | 5.29 | 3517 |
| 52 | 114 | 3.41 | 291 | 43.75 | 2750 | 24.12 | 569 |
| 53 | 95 | 3.66 | 332 | 31.44 | 860 | 9.05 | 656 |
| 54 | 95 | 12.7 | 277 | 26.22 | 860 | 9.05 | 1034 |
| 55 | 108 | 4.5 | 358 | 106.00 | 1188 | 11.00 | 1194 |
| 56 | 121 | 3.73 | 333 | 27.11 | 1050 | 8.68 | 746 |
| 57 | 219 | 7 | 273 | 46.50 | 990 | 4.52 | 3278 |
| 58 | 168.4 | 4.52 | 302 | 52.80 | 813 | 4.83 | 2233 |
| 59 | 160 | 2.5 | 433.2 | 39.40 | 960 | 6.00 | 1426 |
| 60 | 121 | 3.71 | 313 | 30.67 | 2310 | 19.09 | 695 |
| 61 | 88.9 | 5.842 | 406 | 50.50 | 1422.4 | 16.00 | 712 |
| 62 | 88.9 | 5.72 | 400 | 48.25 | 1422 | 16.00 | 712 |
| 63 | 165.2 | 4.1 | 353 | 49.88 | 3965 | 24.00 | 1019 |
| 64 | 168.1 | 4.52 | 298 | 52.30 | 813 | 4.84 | 2233 |
| 65 | 92 | 3 | 260.7 | 26.07 | 1380 | 15.00 | 409 |
| 66 | 114 | 5.94 | 486 | 31.11 | 1280 | 11.23 | 1285 |
| 67 | 114 | 6.11 | 486 | 40.00 | 2750 | 24.12 | 941 |
| 68 | 168.8 | 5 | 302.4 | 40.50 | 2135 | 12.65 | 1130 |
| 69 | 108 | 4.5 | 348.1 | 31.91 | 4158 | 38.50 | 342 |
| 70 | 82.55 | 1.397 | 482.3 | 47.29 | 1422.4 | 17.23 | 294.59 |
| 71 | 114 | 3.23 | 290 | 36.67 | 1751 | 15.36 | 706 |
| 72 | 121 | 5.41 | 348 | 27.11 | 1050 | 8.68 | 1018 |
| 73 | 165.2 | 4.17 | 358.7 | 49.82 | 1321.6 | 8.00 | 1445 |
| 74 | 95 | 3.86 | 332 | 31.44 | 1420 | 14.95 | 567 |
| 75 | 95 | 12.6 | 279 | 26.22 | 860 | 9.05 | 1018 |
| 76 | 166 | 5 | 289.1 | 34.68 | 2700 | 16.27 | 1271.06 |
| 77 | 114.3 | 3.1 | 348 | 65.56 | 1335 | 11.68 | 794 |
| 78 | 108 | 4.5 | 358 | 106.00 | 1620 | 15.00 | 1018 |
| 79 | 114.3 | 3.1 | 348 | 67.22 | 2040 | 17.85 | 688 |
| 80 | 250 | 7 | 243 | 55.58 | 1480 | 5.92 | 4116 |
| 81 | 76.5 | 1.74 | 364 | 49.88 | 610 | 7.97 | 423 |
| 82 | 95 | 3.91 | 392 | 31.44 | 1420 | 14.95 | 606 |
| 83 | 108 | 4.5 | 358 | 106.00 | 756 | 7.00 | 1286 |
| 84 | 165 | 4.7 | 355 | 33.40 | 2475 | 15.00 | 1058 |
| 85 | 114 | 1.72 | 266 | 43.75 | 2750 | 24.12 | 353 |
| 86 | 95 | 12.6 | 275 | 25.89 | 1981 | 20.85 | 903 |
| 87 | 200 | 3 | 303.5 | 55.80 | 2002 | 10.01 | 1882 |
| 88 | 169 | 7.5 | 360 | 80.80 | 1768 | 10.46 | 2870 |
| 89 | 152.4 | 3.17 | 415 | 26.56 | 2271 | 14.90 | 881 |
| 90 | 121 | 3.86 | 332 | 30.67 | 2310 | 19.09 | 755 |
| 91 | 165.2 | 4.17 | 358.7 | 49.82 | 1982.4 | 12.00 | 1305 |
| 92 | 95 | 12.5 | 279 | 26.22 | 1420 | 14.95 | 947 |
| 93 | 108 | 4.5 | 348.1 | 31.91 | 3510 | 32.50 | 400 |
| 94 | 88.9 | 5.82 | 400 | 48.75 | 1727 | 19.43 | 614 |
| 95 | 88.9 | 5.842 | 406 | 50.50 | 812.8 | 9.14 | 918.925 |
| 96 | 166 | 5 | 288.1 | 52.90 | 1040 | 6.27 | 1764 |
| 97 | 121 | 5.44 | 327 | 30.67 | 2310 | 19.09 | 865 |
| 98 | 169.3 | 2.62 | 338.1 | 41.38 | 1830 | 10.81 | 689 |
| 99 | 121.01 | 3.66 | 300 | 27.11 | 1050 | 8.68 | 695 |
| 100 | 108 | 4 | 338.88 | 35.71 | 2160 | 20.00 | 672.28 |
| 101 | 166 | 5 | 284.2 | 51.24 | 870 | 5.24 | 1862 |
| 102 | 108 | 5 | 379.8 | 40.91 | 548 | 5.07 | 1084 |
| 103 | 114 | 3.35 | 291 | 45.00 | 850 | 7.46 | 785 |
| 104 | 108 | 4 | 338.88 | 35.71 | 1620 | 15.00 | 646.8 |
| 105 | 76.5 | 1.73 | 364 | 32.11 | 610 | 7.97 | 330 |
| 106 | 355.6 | 7.98 | 361 | 29.78 | 2083 | 5.86 | 7433 |
| 107 | 114 | 1.79 | 266 | 45.00 | 850 | 7.46 | 515 |
| 108 | 267.4 | 7 | 461 | 57.40 | 4800 | 17.95 | 3900 |
| 109 | 95 | 12.6 | 294 | 26.22 | 1980 | 20.84 | 917 |
| 110 | 114.3 | 3.1 | 348 | 62.67 | 1020 | 8.92 | 849 |
| 111 | 108 | 4.5 | 358 | 106.00 | 1188 | 11.00 | 1232 |
| 112 | 76 | 2 | 275 | 50.60 | 1556 | 20.47 | 330 |
| 113 | 216 | 6.3 | 411 | 36.89 | 2220 | 10.28 | 2932 |
| 114 | 114 | 5.73 | 486 | 40.00 | 2750 | 24.12 | 824 |
| 115 | 110 | 1.9 | 350 | 33.40 | 2200 | 20.00 | 374 |
| 116 | 219 | 4 | 325 | 61.44 | 1000 | 4.57 | 1980 |
| 117 | 267.4 | 7 | 461 | 57.40 | 1600 | 5.98 | 5190 |
| 118 | 88.9 | 5.81 | 400 | 47.62 | 1118 | 12.58 | 716 |
| 119 | 121 | 3.76 | 313 | 30.67 | 1050 | 8.68 | 837 |
| 120 | 108 | 4 | 338.88 | 35.71 | 2160 | 20.00 | 676.2 |
| 121 | 127 | 2.413 | 336 | 32.56 | 914 | 7.20 | 658.3 |
| 122 | 120.83 | 4.09 | 451.3 | 36.18 | 1050.04 | 8.69 | 1091.91 |
| 123 | 200 | 3 | 303.5 | 55.80 | 2001 | 10.01 | 1806 |
| 124 | 108 | 4 | 338.88 | 35.71 | 1080 | 10.00 | 783.02 |
| 125 | 82.55 | 1.397 | 482.3 | 47.29 | 1727.2 | 20.92 | 224.725 |
| 126 | 121.01 | 3.71 | 300 | 27.11 | 2310 | 19.09 | 641 |
| 127 | 140 | 2.5 | 433.2 | 47.43 | 840 | 6.00 | 1124 |
| 128 | 152.4 | 1.57 | 330 | 26.67 | 1499 | 9.84 | 681 |
| 129 | 120.65 | 4.09 | 451.3 | 41.72 | 1050.04 | 8.70 | 1155.7 |
| 130 | 215.9 | 6.02 | 350 | 36.44 | 2220 | 10.28 | 2869 |
| 131 | 121 | 5.49 | 348 | 27.11 | 2310 | 19.09 | 816 |
| 132 | 200 | 2 | 237.2 | 30.28 | 980 | 4.90 | 1411 |
| 133 | 82.55 | 1.397 | 482.3 | 47.29 | 812.8 | 9.85 | 400.5 |
| 134 | 108 | 4 | 338.88 | 35.71 | 2700 | 25.00 | 648.76 |
| 135 | 114.3 | 3.1 | 340 | 67.22 | 2700 | 23.62 | 516 |
| 136 | 108 | 4.5 | 348.1 | 31.91 | 3510 | 32.50 | 390 |
| 137 | 110 | 1.9 | 350 | 40.50 | 2200 | 20.00 | 368 |
| 138 | 114.3 | 3.19 | 414 | 35.44 | 838 | 7.33 | 756 |
| 139 | 114.3 | 3.1 | 340 | 67.22 | 2700 | 23.62 | 536 |
| 140 | 95 | 12.7 | 277 | 26.22 | 860 | 9.05 | 1008 |
| 141 | 108 | 4.5 | 348.1 | 46.87 | 3510 | 32.50 | 440 |
| 142 | 165 | 4.7 | 355 | 14.44 | 2477 | 15.01 | 800 |
| 143 | 140 | 5 | 378.3 | 37.53 | 840 | 6.00 | 1379 |
| 144 | 108 | 4.5 | 259.7 | 25.48 | 1994 | 18.46 | 495 |
| 145 | 152.4 | 1.55 | 330 | 32.11 | 1499 | 9.84 | 725 |
| 146 | 110 | 1.9 | 350 | 33.40 | 2200 | 20.00 | 368 |
| 147 | 219 | 4 | 325 | 56.60 | 1000 | 4.57 | 1931 |
| 148 | 114 | 4.44 | 332 | 45.00 | 850 | 7.46 | 902 |
| 149 | 108 | 4.5 | 348.1 | 46.87 | 4158 | 38.50 | 298 |
| 150 | 108 | 4 | 347.7 | 40.47 | 1620 | 15.00 | 672 |
| 151 | 152.7 | 3.15 | 421 | 26.89 | 1676.4 | 10.98 | 880.11 |
| 152 | 108 | 4 | 338.88 | 35.71 | 4320 | 40.00 | 294 |
| 153 | 108 | 4 | 338.88 | 35.71 | 1620 | 15.00 | 707.56 |
| 154 | 108 | 4.2 | 259.7 | 25.87 | 648 | 6.00 | 722 |
| 155 | 92 | 3 | 260.7 | 26.07 | 920 | 10.00 | 431 |
| 156 | 108 | 4 | 338.88 | 35.71 | 864 | 8.00 | 869.26 |
| 157 | 219 | 7 | 273 | 46.50 | 990 | 4.52 | 3278 |
| 158 | 108 | 4.5 | 344 | 40.91 | 548 | 5.07 | 917 |
| 159 | 107 | 4 | 379.8 | 38.32 | 542 | 5.07 | 889 |
| 160 | 108 | 4.5 | 259.7 | 25.48 | 648 | 6.00 | 665 |
| 161 | 219 | 7 | 273 | 46.50 | 990 | 4.52 | 3278 |
| 162 | 190.7 | 6 | 505 | 65.44 | 2300 | 12.06 | 2610 |
| 163 | 114 | 3.31 | 291 | 30.00 | 2320 | 20.35 | 535 |
| 164 | 95 | 12.6 | 275 | 25.89 | 861 | 9.06 | 1019 |
| 165 | 114.3 | 3.1 | 348 | 62.67 | 1020 | 8.92 | 845 |
| 166 | 140 | 5 | 378.3 | 42.63 | 840 | 6.00 | 1501 |
| 167 | 88.9 | 5.842 | 406 | 50.50 | 508 | 5.71 | 890 |
| 168 | 95 | 3.51 | 340 | 31.44 | 1980 | 20.84 | 488 |
| 169 | 108 | 4 | 338.88 | 35.71 | 4320 | 40.00 | 345.94 |
| 170 | 127.3 | 1.63 | 376 | 77.20 | 711 | 5.59 | 1285 |
| 171 | 95 | 3.76 | 332 | 31.44 | 1980 | 20.84 | 536 |
| 172 | 165 | 4.7 | 355 | 40.50 | 2476 | 15.01 | 1037 |
| 173 | 166 | 5 | 287.14 | 34.68 | 3700 | 22.29 | 958.44 |
| 174 | 127 | 2.413 | 336 | 27.11 | 914 | 7.20 | 627.2 |
| 175 | 114.3 | 3.1 | 340 | 73.10 | 3370 | 29.48 | 362 |
| 176 | 165 | 4.7 | 355 | 33.40 | 2475 | 15.00 | 1037 |
| 177 | 95 | 3.66 | 350 | 31.11 | 1981 | 20.85 | 529 |
| 178 | 114 | 1.73 | 266 | 40.00 | 1751 | 15.36 | 461 |
| 179 | 219 | 7 | 273 | 46.50 | 1640 | 7.49 | 2956 |
| 180 | 95 | 3.4 | 343 | 30.44 | 1980 | 20.84 | 473 |
| 181 | 210 | 2.5 | 237.2 | 32.93 | 1670 | 7.95 | 1323 |
| 182 | 95 | 3.78 | 392 | 31.44 | 1980 | 20.84 | 567 |
| 183 | 114 | 5.99 | 486 | 45.00 | 1750 | 15.35 | 1177 |
| 184 | 114 | 3.28 | 291 | 43.75 | 2750 | 24.12 | 667 |
| 185 | 108 | 4 | 338.88 | 35.71 | 5400 | 50.00 | 225.4 |
| 186 | 114.3 | 3.1 | 340 | 64.56 | 3720 | 32.55 | 305 |
| 187 | 108 | 4.5 | 259.7 | 25.48 | 1296 | 12.00 | 563 |
| 188 | 165 | 4.3 | 317.7 | 52.30 | 3640 | 22.06 | 987 |
| 189 | 114 | 3.29 | 291 | 30.00 | 2250 | 19.74 | 652 |
| 190 | 166 | 5 | 288.1 | 33.12 | 1040 | 6.27 | 1372 |
| 191 | 114.3 | 3.1 | 348 | 67.22 | 2040 | 17.85 | 617 |
| 192 | 168.3 | 4.47 | 302 | 29.33 | 813 | 4.83 | 1744 |
| 193 | 108 | 4 | 327.1 | 41.55 | 1188 | 11.00 | 686 |
| 194 | 140 | 5 | 378.3 | 51.25 | 840 | 6.00 | 1539 |
| 195 | 101.73 | 3.1 | 604.67 | 37.93 | 1524 | 14.98 | 800.1 |
| 196 | 152.4 | 1.55 | 294 | 43.25 | 914 | 6.00 | 733 |
| 197 | 219 | 7 | 273 | 46.50 | 1640 | 7.49 | 2956 |
| 198 | 168.8 | 2.64 | 200.2 | 42.13 | 1830 | 10.84 | 916 |
| 199 | 108 | 4 | 338.88 | 35.71 | 648 | 6.00 | 828.1 |
| 200 | 165.2 | 4.1 | 353 | 49.88 | 1322 | 8.00 | 1412 |
| 201 | 120.9 | 5.54 | 343 | 30.22 | 2311 | 19.11 | 867 |
| 202 | 114 | 6.14 | 486 | 34.44 | 2250 | 19.74 | 1000 |
| 203 | 166 | 5 | 313.6 | 51.24 | 1700 | 10.24 | 1460.2 |
| 204 | 219 | 7 | 273 | 46.50 | 1640 | 7.49 | 2956 |
| 205 | 76.5 | 1.73 | 364 | 31.11 | 1524 | 19.92 | 245 |
| 206 | 82.55 | 1.397 | 482.3 | 47.29 | 1117.6 | 13.54 | 356 |
| 207 | 95 | 12.8 | 283 | 26.22 | 1980 | 20.84 | 886 |
| 208 | 190.7 | 6 | 505 | 65.44 | 1150 | 6.03 | 3064 |
| 209 | 95 | 3.4 | 340 | 31.44 | 860 | 9.05 | 656 |
| 210 | 114 | 5.64 | 486 | 34.44 | 2250 | 19.74 | 902 |
| 211 | 240 | 10 | 269 | 58.80 | 1440 | 6.00 | 5135 |
| 212 | 152 | 1.65 | 270 | 83.00 | 900 | 5.92 | 1458 |
| 213 | 140 | 3 | 426.3 | 40.38 | 840 | 6.00 | 1208 |
| 214 | 216 | 6.05 | 395 | 29.11 | 2220 | 10.28 | 2462 |
| 215 | 108 | 4.5 | 348.1 | 46.87 | 4023 | 37.25 | 320 |
| 216 | 95 | 3.58 | 340 | 31.44 | 1420 | 14.95 | 576 |
| 217 | 169.3 | 2.62 | 338.1 | 45.13 | 1830 | 10.81 | 756 |
| 218 | 95 | 12.65 | 275 | 25.89 | 1420 | 14.95 | 930 |
| 219 | 114 | 6.21 | 486 | 40.00 | 2750 | 24.12 | 941 |
| 220 | 108 | 4.5 | 259.7 | 25.48 | 972 | 9.00 | 666 |
| 221 | 121 | 5.56 | 327 | 30.67 | 1050 | 8.68 | 1079 |
| 222 | 168.1 | 4.52 | 298 | 52.30 | 813 | 4.84 | 2113 |
| 223 | 216 | 4.06 | 289 | 29.11 | 2220 | 10.28 | 1023 |
| 224 | 114.3 | 3.1 | 340 | 73.10 | 3370 | 29.48 | 401 |
| 225 | 165.2 | 4.1 | 353 | 49.88 | 2974 | 18.00 | 1147 |
| 226 | 140 | 5.3 | 378.3 | 60.56 | 840 | 6.00 | 1664 |
| 227 | 127 | 2.39 | 289 | 42.75 | 1499 | 11.80 | 623 |
References
- El-Heweity, M.M. On the performance of circular concrete-filled high strength steel columns under axial loading. Alex. Eng. J. 2012, 51, 109–119. [Google Scholar] [CrossRef]
- Elbakry, H.M.F. A numerical approach for evaluating the stiffness of steel tube–R.C. beam composite joint. Alex. Eng. J. 2014, 53, 583–589. [Google Scholar] [CrossRef][Green Version]
- Jayalekshmi, S.; Jegadesh, J.S.S.; Goel, A. Empirical approach for determining axial strength of circular concrete filled steel tubular columns. J. Inst. Eng. Ser. A 2018, 99, 257–268. [Google Scholar] [CrossRef]
- Ekmekyapar, T.; AL-Eliwi, B.J.M. Concrete filled double circular steel tube (CFDCST) stub columns. Eng. Struct. 2017, 135, 68–80. [Google Scholar] [CrossRef]
- Chen, D.; Montano, V.; Huo, L.; Fan, S.; Song, G. Detection of subsurface voids in concrete-filled steel tubular (CFST) structure using percussion approach. Constr. Build. Mater. 2020, 262, 119761. [Google Scholar] [CrossRef]
- Chen, D.; Montano, V.; Huo, L.; Song, G. Depth detection of subsurface voids in concrete-filled steel tubular (CFST) structure using percussion and decision tree. Meas. J. Int. Meas. Confed. 2020, 163, 107869. [Google Scholar] [CrossRef]
- Rong, B.; Liu, S.; Li, Z.; Liu, R. Experimental and numerical studies of failure modes and load-carrying capacity of through-diaphragm connections. Trans. Tianjin Univ. 2018, 24, 387–400. [Google Scholar] [CrossRef]
- Alatshan, F.; Osman, S.A.; Mashiri, F.; Hamid, R. Explicit simulation of circular CFST stub columns with external steel confinement under axial compression. Materials 2019, 13, 23. [Google Scholar] [CrossRef]
- Akbar, A.; Farooq, F.; Shafique, M.; Aslam, F.; Alyousef, R.; Alabduljabbar, H. Sugarcane bagasse ash-based engineered geopolymer mortar incorporating propylene fibers. J. Build. Eng. 2020, 33, 101492. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Zhang, M.; Shen, Y.; Si, W. Prediction of ultimate axial capacity of square concrete-filled steel tubular short columns using a hybrid intelligent algorithm. Appl. Sci. 2019, 9, 2802. [Google Scholar] [CrossRef]
- Zhang, T.; Lyu, X.; Yu, Y. Prediction and analysis of the residual capacity of concrete-filled steel tube stub columns under axial compression subjected to combined freeze–thaw cycles and acid rain corrosion. Materials 2019, 12, 3070. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, T.-T.; Le, L.M.; Tran, V.Q.; Le, V.M.; Vu, H.-L.T.; Nguyen, Q.H.; Pham, B.T. Development of hybrid machine learning models for predicting the critical buckling load of I-shaped cellular beams. Appl. Sci. 2019, 9, 5458. [Google Scholar] [CrossRef]
- Chen, J.B.; Chan, T.M.; Castro, J.M. Parametric study on the flexural behaviour of circular rubberized concrete-filled steel tubes. In Tubular Structures XVI, Proceedings of the 16th International Symposium on Tubular Structures, ISTS 2017, Melbourne, Australia, 4–6 December 2017; CRC Press/Balkema: Leiden, The Netherlands, 2018; pp. 51–59. [Google Scholar]
- Farooq, F.; Akbar, A.; Khushnood, R.A.; Muhammad, W.L.B.; Rehman, S.K.U.; Javed, M.F. Experimental Investigation of Hybrid Carbon Nanotubes and Graphite Nanoplatelets on Rheology, Shrinkage, Mechanical, and Microstructure of SCCM. Materials 2020, 13, 230. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.S.; Liu, Y.; Zhuo, B.T.; Guo, Z.X.; Shahrooz, B.M. Axial compressive behavior of square CFST columns through direct measurement of load components. J. Struct. Eng. 2018. [Google Scholar] [CrossRef]
- Li, G.; Chen, B.; Yang, Z.; Feng, Y. Experimental and numerical behaviour of eccentrically loaded high strength concrete filled high strength square steel tube stub columns. Thin-Walled Struct. 2018, 127, 483–499. [Google Scholar] [CrossRef]
- Mendoza, R.; Yamamoto, Y.; Nakamura, H.; Miura, T. Numerical simulation of compressive failure behaviors of concrete-filled steel tube using coupled discrete model and shell finite element. In High Tech Concrete: Where Technology and Engineering Meet; Springer International Publishing: Berlin, Germany, 2018; pp. 1353–1361. [Google Scholar]
- Lai, Z.; Varma, A.H. Effective stress-strain relationships for analysis of noncompact and slender filled composite (CFT) members. Eng. Struct. 2016, 124, 457–472. [Google Scholar] [CrossRef]
- Chen, C.C.; Ko, J.W.; Huang, G.L.; Chang, Y.M. Local buckling and concrete confinement of concrete-filled box columns under axial load. J. Constr. Steel Res. 2012, 78, 8–21. [Google Scholar] [CrossRef]
- Mendoza, R.; Yamamoto, Y.; Nakamura, H.; Miura, T. Numerical evaluation of localization and softening behavior of concrete confined by steel tubes. Struct. Concr. 2018, 19, 1956–1970. [Google Scholar] [CrossRef]
- Jumaa, G.B.; Yousif, A.R. Predicting shear capacity of frp-reinforced concrete beams without stirrups by artificial neural networks, gene expression programming, and regression analysis. Adv. Civ. Eng. 2018. [Google Scholar] [CrossRef]
- Javed, M.F.; Amin, M.N.; Shah, M.I.; Khan, K.; Iftikhar, B.; Farooq, F.; Aslam, F.; Alyousef, R.; Alabduljabbar, H. Applications of Gene Expression Programming and Regression Techniques for Estimating Compressive Strength of Bagasse Ash based Concrete. Crystals 2020, 10, 737. [Google Scholar] [CrossRef]
- Javed, M.F.; Sulong, N.H.R.; Memon, S.A.; Rehman, S.K.U.; Khan, N.B. FE modelling of the flexural behaviour of square and rectangular steel tubes filled with normal and high strength concrete. Thin-Walled Struct. 2017, 119, 470–481. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A Newadaptive Algorithm for Solving Problems. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Ferreira%2C+C.%2C+Gene+Expression+Programming%3A+A+New+Adaptive+Algorithm+for+Solving+Problems.+Complex+Systems%2C+2001.+13%282%29%3A+p.+87-129.&btnG= (accessed on 17 December 2019).
- Sun, Y.; Li, G.; Zhang, J.; Qian, D.; Binh, G.E.; Pham, A. Prediction of the strength of rubberized concrete by an evolved random forest model. Adv. Civ. Eng. 2019. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20 August 1995; pp. 1137–1145. [Google Scholar]
- Le, L.M.; Ly, H.-B.; Pham, B.T.; Le, V.M.; Pham, T.A.; Nguyen, D.-H.; Tran, X.-T.; Le, T.-T. Hybrid artificial intelligence approaches for predicting buckling damage of steel columns under axial compression. Materials 2019, 12, 1670. [Google Scholar] [CrossRef]
- Sarir, P.; Chen, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Developing GEP tree-based, neuro-swarm, and whale optimization models for evaluation of bearing capacity of concrete-filled steel tube columns. Eng. Comput. 2019, 1, 3. [Google Scholar] [CrossRef]
- Elfahham, Y. Estimation and prediction of construction cost index using neural networks, time series, and regression. Alex. Eng. J. 2019, 58, 499–506. [Google Scholar] [CrossRef]
- Diab, A.M.; Elyamany, H.E.; Abd Elmoaty, A.E.M.; Shalan, A.H. Prediction of concrete compressive strength due to long term sulfate attack using neural network. Alex. Eng. J. 2014, 53, 627–642. [Google Scholar] [CrossRef]
- Mohamed, Y.S.; Shehata, H.M.; Abdellatif, M.; Awad, T.H. Steel crack depth estimation based on 2D images using artificial neural networks. Alex. Eng. J. 2019, 58, 1167–1174. [Google Scholar] [CrossRef]
- Mai, S.H.; Seghier, M.E.; Nguyen, P.L.; Jafari-Asl, J.; Thai, D.K. A hybrid model for predicting the axial compression capacity of square concrete-filled steel tubular columns. Eng. Comput. 2020, 1, 3. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Ren, R.; Wu, Z.; Ozbakkaloglu, T. Performance evaluation of recycled aggregate concrete-filled steel tubes under different loading conditions: Database analysis and modelling. J. Build. Eng. 2020, 30, 101308. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, W.; Ruan, X.; Tang, X. Experimental study on axial compression behavior and bearing capacity analysis of high titanium slag CFST columns. Appl. Sci. 2019, 9, 2021. [Google Scholar] [CrossRef]
- Dao, D.; Trinh, S.; Ly, H.-B.; Pham, B. Prediction of compressive strength of geopolymer concrete using entirely steel slag aggregates: Novel hybrid artificial intelligence approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
- Van Dao, D.; Ly, H.-B.; Vu, H.-L.T.; Le, T.-T.; Pham, B.T. Investigation and optimization of the C-ANN structure in predicting the compressive strength of foamed concrete. Materials 2020, 13, 1072. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.Q.; Ly, H.B.; Tran, V.Q.; Nguyen, T.A.; Le, T.T.; Pham, B.T. Optimization of artificial intelligence system by evolutionary algorithm for prediction of axial capacity of rectangular concrete filled steel tubes under compression. Materials 2020, 13, 1205. [Google Scholar] [CrossRef]
- Ly, H.-B.; Pham, B.T.; Le, L.M.; Le, T.-T.; Le, V.M.; Asteris, P.G. Estimation of axial load-carrying capacity of concrete-filled steel tubes using surrogate models. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.-B.; Tran, V.Q.; Nguyen, T.-A.; Phan, V.-H.; Le, T.-T.; Pham, B.T. A novel hybrid model based on a feedforward neural network and one step secant algorithm for prediction of load-bearing capacity of rectangular concrete-filled steel tube columns. Molecules 2020, 25, 3486. [Google Scholar] [CrossRef]
- Luat, N.V.; Shin, J.; Lee, K. Hybrid BART-based models optimized by nature-inspired metaheuristics to predict ultimate axial capacity of CCFST columns. Eng. Comput. 2020, 1, 3. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Nilsen, V.; Pham, L.T.; Hibbard, M.; Klager, A.; Cramer, S.M.; Morgan, D. Prediction of concrete coefficient of thermal expansion and other properties using machine learning. Constr. Build. Mater. 2019, 220, 587–595. [Google Scholar] [CrossRef]
- Fawagreh, K.; Medhat Gaber, M.; Elyan, E.; Gaber, M.M. Random forests: From early developments to recent advancements. Syst. Sci. Control Eng. Open Access J. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Ipek, S.; Güneyisi, E.M. Ultimate axial strength of concrete-filled double skin steel tubular column sections. Adv. Civ. Eng. 2019. [Google Scholar] [CrossRef]
- Güneyisi, E.M.; Gültekin, A.; Mermerdaş, K. Ultimate capacity prediction of axially loaded CFST short columns. Int. J. Steel Struct. 2016, 16, 99–114. [Google Scholar] [CrossRef]
- Yang, C.; Gao, P.; Wu, X.; Chen, Y.F.; Li, Q.; Li, Z. Practical formula for predicting axial strength of circular-CFST columns considering size effect. J. Constr. Steel Res. 2020, 168, 105979. [Google Scholar] [CrossRef]
- Avci-Karatas, C. Prediction of ultimate load capacity of concrete-filled steel tube columns using multivariate adaptive regression splines (MARS). Steel Compos. Struct. 2019, 33, 583–594. [Google Scholar]
- Wang, X.Y. Optimal design of the cement, fly ash, and slag mixture in ternary blended concrete based on gene expression programming and the genetic algorithm. Materials 2019, 12, 2448. [Google Scholar] [CrossRef]
- Alkroosh, I.S.; Sarker, P.K. Prediction of the compressive strength of fly ash geopolymer concrete using gene expression programming. Comput. Concr. 2019, 24, 295–302. [Google Scholar]
- Iqbal, M.F.; Liu, Q.-F.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Bolandi, H.; Banzhaf, W.; Lajnef, N.; Barri, K.; Alavi, A.H. An intelligent model for the prediction of bond strength of FRP bars in concrete: A soft computing approach. Technologies 2019, 7, 42. [Google Scholar] [CrossRef]
- Nour, A.I.; Güneyisi, E.M. Prediction model on compressive strength of recycled aggregate concrete filled steel tube columns. Compos. Part B Eng. 2019, 173, 106938. [Google Scholar] [CrossRef]
- Leon, L.P.; Gay, D. Gene expression programming for evaluation of aggregate angularity effects on permanent deformation of asphalt mixtures. Constr. Build. Mater. 2019, 211, 470–478. [Google Scholar] [CrossRef]
- Gunal, M.; Guven, A.; Asce, M. A genetic programming approach for prediction of local scour downstream hydraulic structures genetic programming approach for prediction of local scour downstream of hydraulic structures. Artic. J. Irrig. Drain. Eng. 2008. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming Mathematical Modeling by an Artificial Intelligence; Springer: Berlin, Germany, 2006; ISBN 3-540-32796-7. [Google Scholar]
- Ferreira, C. Gene expression programming in problem solving. In Soft Computing and Industry; Springer: London, UK, 2002; pp. 635–653. [Google Scholar]
- Tenpe, A.R.; Patel, A. Utilization of support vector models and gene expression programming for soil strength modeling. Arab. J. Sci. Eng. 2020, 45, 4301–4319. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Shahmansouri, A.A.; Fakoor, M. Post-fire compressive strength of recycled PET aggregate concrete reinforced with steel fibers: Optimization and prediction via RSM and GEP. Constr. Build. Mater. 2020, 252, 119057. [Google Scholar] [CrossRef]
- Momeni, M.; Hadianfard, M.A.; Bedon, C.; Baghlani, A. Damage evaluation of H-section steel columns under impulsive blast loads via gene expression programming. Eng. Struct. 2020, 219, 110909. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H. A robust data mining approach for formulation of geotechnical engineering systems. Eng. Comput. Int. J. Comput.-Aided Eng. 2011, 28, 242–274. [Google Scholar]
- Gandomi, A.H.; Babanajad, S.K.; Alavi, A.H.; Farnam, Y. Novel approach to strength modeling of concrete under triaxial compression. J. Mater. Civ. Eng. 2012. [Google Scholar] [CrossRef]
- Muduli, P.K.; Das, S.K.; Bhattacharya, S. CPT-based probabilistic evaluation of seismic soil liquefaction potential using multi-gene genetic programming. Georisk 2014, 8, 14–28. [Google Scholar] [CrossRef]
- Das, S.K. Artificial neural networks in geotechnical engineering: Modeling and application issues. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: Amsterdam, The Netherlands, 2013; pp. 231–270. ISBN 9780123982964. [Google Scholar]
- Fulcher, J. Computational intelligence: An introduction. Stud. Comput. Intell. 2008, 115, 3–78. [Google Scholar]
- Alabduljabbar, H.; Haido, J.H.; Alyousef, R.; Yousif, S.T.; McConnell, J.; Wakil, K.; Jermsittiparsert, K. Prediction of the flexural behavior of corroded concrete beams using combined method. Structures 2020, 25, 1000–1008. [Google Scholar] [CrossRef]
- Dunlop, P.; Smith, S. Estimating key characteristics of the concrete delivery and placement process using linear regression analysis. Civ. Eng. Environ. Syst. 2003, 20, 273–290. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Ferreira, C. Function finding and the creation of numerical constants in gene expression programming. In Advances in Soft Computing; Springer: London, UK, 2003; pp. 257–265. [Google Scholar]
- Babanajad, S.K.; Gandomi, A.H.; Alavi, A.H. New prediction models for concrete ultimate strength under true-triaxial stress states: An evolutionary approach. Adv. Eng. Softw. 2017, 110, 55–68. [Google Scholar] [CrossRef]
- Soleimani, S.; Rajaei, S.; Jiao, P.; Sabz, A.; Soheilinia, S. New prediction models for unconfined compressive strength of geopolymer stabilized soil using multi-gen genetic programming. Meas. J. Int. Meas. Confed. 2018, 113, 99–107. [Google Scholar] [CrossRef]
- Kupper, L.L. Probability, statistics, and decision for civil engineers. Technometrics 1971, 13, 211. [Google Scholar] [CrossRef]
- Frank, I.; Todeschini, R. The data analysis handbook. Data Handl. Sci. Technol. 1994, 14, 1–352. [Google Scholar]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Mirzahosseini, M.R.; Nejad, F.M. Nonlinear genetic-based models for prediction of flow number of asphalt mixtures. J. Mater. Civ. Eng. 2011, 23, 248–263. [Google Scholar] [CrossRef]
- Roy, P.P.; Roy, K. On some aspects of variable selection for partial least squares regression models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Lu, Z.; Zhao, Y. Suggested empirical models for the axial capacity of circular CFT stub columns. J. Constr. Steel Res. 2010. [Google Scholar] [CrossRef]
- Goode, C.; Narayanan, R. Design of concrete filled steel tubes to EC4. In Proceedings of the ASCCS Seminar on Concrete Filled Steel Tubes—A Comparison of International Codes and Practice, Innsbruck, Austria, 18 September 1997; pp. 1–25. [Google Scholar]
- Giakoumelis, G.; Lam, D. Axial capacity of circular concrete-filled tube columns. J. Constr. Steel Res. 2004, 60, 1049–1068. [Google Scholar] [CrossRef]
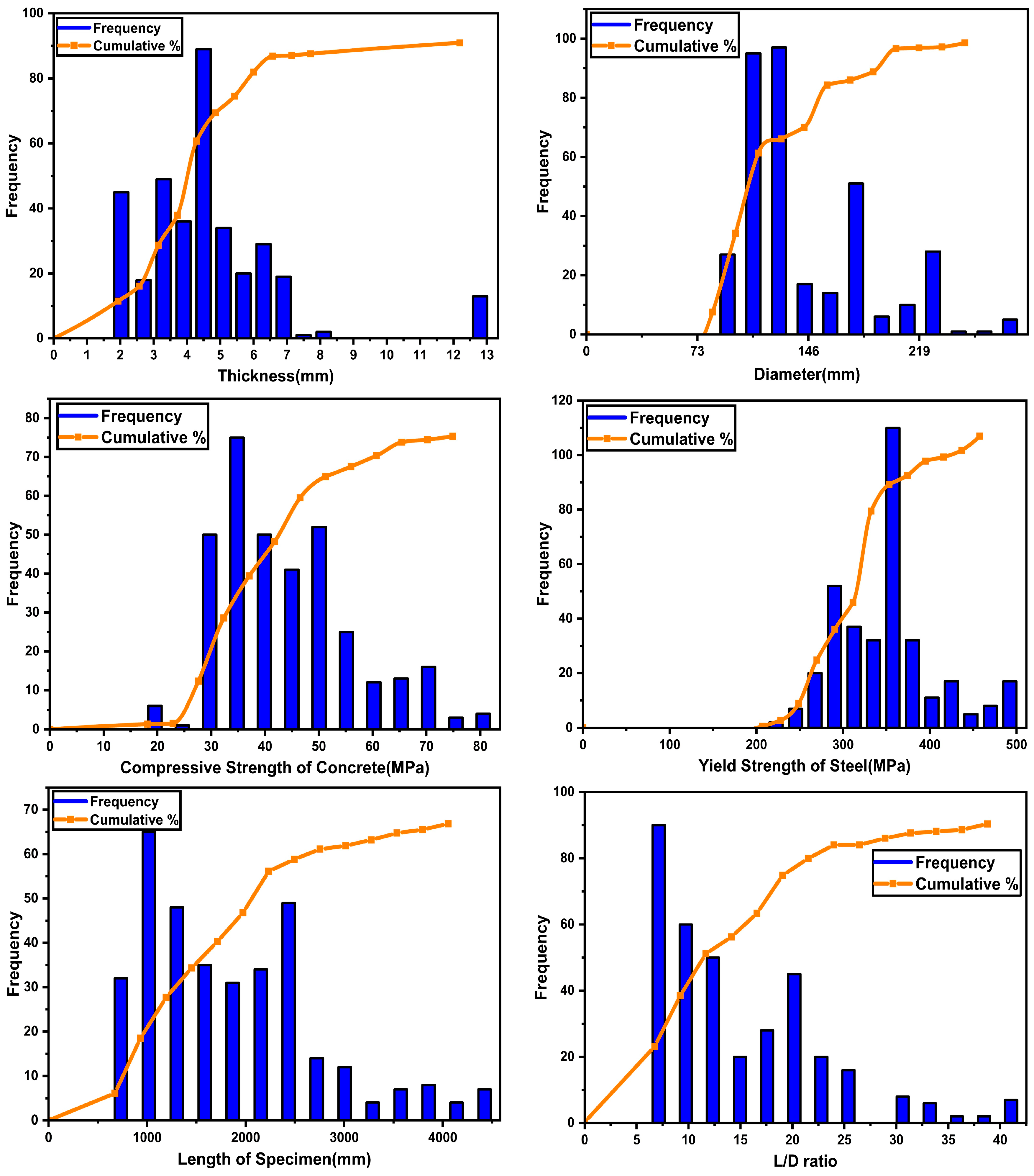

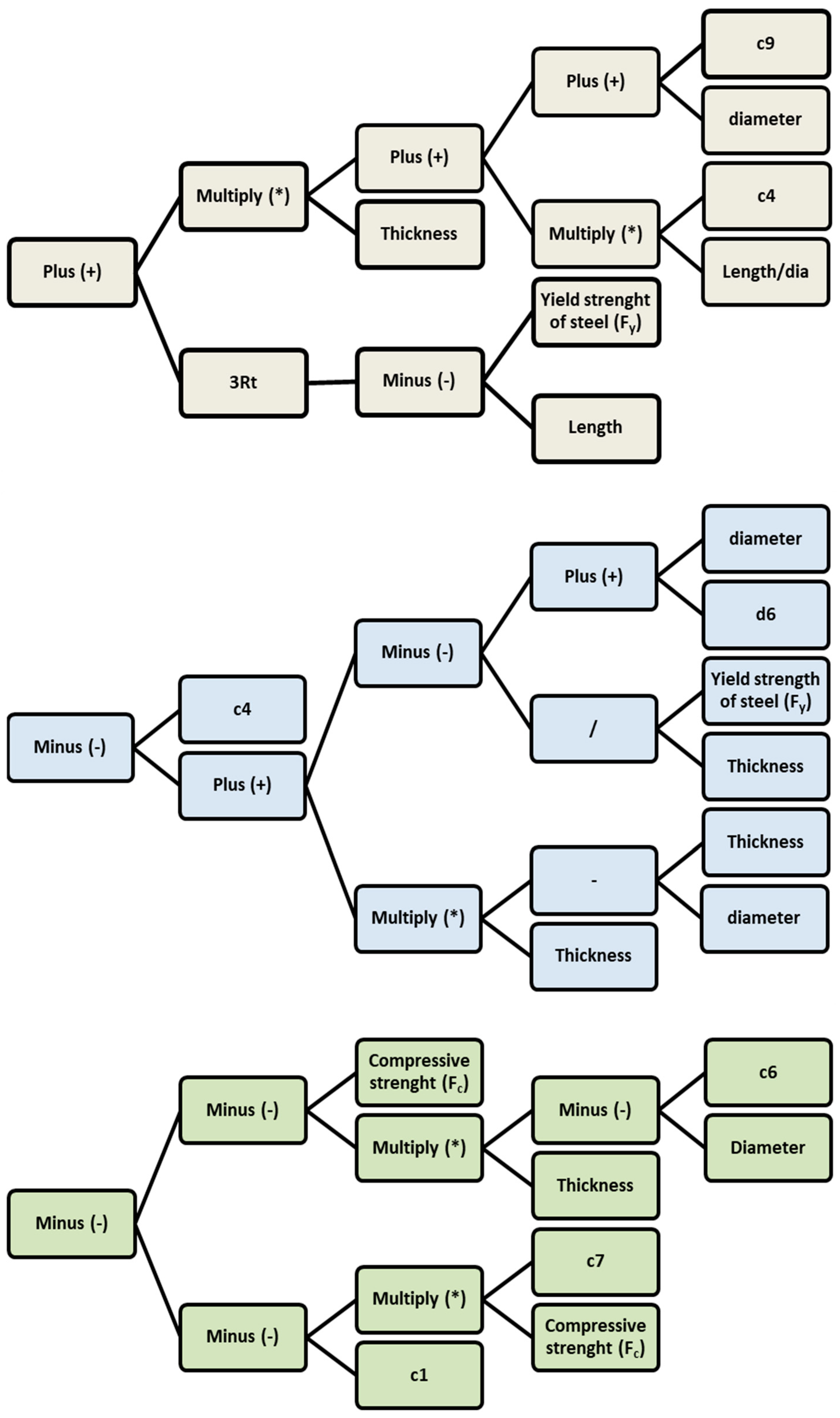
| Parameters | Diameter | Thickness | Yield Stress | Compressive Strength | Length | Length/Diameter | Test |
|---|---|---|---|---|---|---|---|
| Training set data | |||||||
| Mean | 137.9 | 4.6 | 344.9 | 43.9 | 36.4 | 1651.8 | 13.0 |
| Standard error | 4.8 | 0.2 | 5.4 | 1.5 | 1.4 | 81.1 | 0.7 |
| Median | 114.3 | 4.1 | 338.9 | 40.5 | 33.4 | 1420.0 | 10.3 |
| Mode | 108.0 | 5.0 | 348.0 | 35.7 | 29.0 | 1040.0 | 20.0 |
| Standard deviation | 54.4 | 2.5 | 61.2 | 17.3 | 15.9 | 917.2 | 7.9 |
| Sample variance | 2956.3 | 6.2 | 3744.4 | 298.6 | 254.3 | 841,300.1 | 62.6 |
| Kurtosis | 4.6 | 3.8 | 0.2 | 3.4 | 4.3 | 2.6 | 3.9 |
| Skewness | 1.9 | 1.8 | 0.8 | 1.6 | 1.8 | 1.5 | 1.7 |
| Range | 279.6 | 11.4 | 271.8 | 91.6 | 86.0 | 4892.0 | 45.5 |
| Minimum | 76.0 | 1.4 | 233.2 | 14.4 | 10.0 | 508.0 | 4.5 |
| Maximum | 355.6 | 12.8 | 505.0 | 106.0 | 96.0 | 5400.0 | 50.0 |
| Sum | 17,646.2 | 592.2 | 44,143.2 | 5615.7 | 4656.1 | 211,432.9 | 1663.8 |
| Count | 128.0 | 128.0 | 128.0 | 128.0 | 128.0 | 128.0 | 128.0 |
| Testing set data | |||||||
| Mean | 127.8 | 4.3 | 340.4 | 39.6 | 32.5 | 1806.0 | 15.0 |
| Standard error | 5.2 | 0.3 | 7.8 | 1.9 | 1.7 | 152.4 | 1.4 |
| Median | 114.0 | 4.0 | 340.0 | 35.7 | 29.0 | 1648.2 | 11.5 |
| Mode | 108.0 | 4.0 | 338.9 | 35.7 | 29.0 | 2700.0 | 6.0 |
| Standard deviation | 37.0 | 2.2 | 55.0 | 13.5 | 12.1 | 1077.3 | 9.9 |
| Sample variance | 1367.0 | 4.7 | 3021.6 | 182.2 | 147.1 | 1,160,607.4 | 97.2 |
| Kurtosis | 1.0 | 7.7 | 1.3 | 1.0 | 1.2 | −0.2 | 0.4 |
| Skewness | 1.4 | 2.3 | 0.7 | 1.1 | 1.2 | 0.8 | 1.1 |
| Range | 136.5 | 11.3 | 267.8 | 62.8 | 57.2 | 3812.0 | 35.5 |
| Minimum | 82.6 | 1.4 | 237.2 | 14.4 | 10.0 | 508.0 | 4.5 |
| Maximum | 219.0 | 12.7 | 505.0 | 77.2 | 67.2 | 4320.0 | 40.0 |
| Sum | 6388.6 | 214.0 | 17,017.5 | 1982.3 | 1626.9 | 90,302.2 | 751.0 |
| Count | 50.0 | 50.0 | 50.0 | 50.0 | 50.0 | 50.0 | 50.0 |
| Validation set data | |||||||
| Mean | 137.3 | 4.5 | 347.2 | 42.2 | 34.8 | 1755.6 | 13.8 |
| Standard error | 5.7 | 0.3 | 10.2 | 1.7 | 1.5 | 127.2 | 1.2 |
| Median | 114.3 | 4.1 | 338.9 | 40.2 | 33.0 | 1572.0 | 10.9 |
| Mode | 108.0 | 4.0 | 486.0 | 35.7 | 29.0 | 1640.0 | 6.0 |
| Standard deviation | 43.9 | 2.3 | 79.1 | 13.3 | 11.9 | 985.3 | 9.0 |
| Sample variance | 1927.1 | 5.1 | 6256.5 | 175.8 | 141.8 | 970,885.0 | 81.2 |
| Kurtosis | 0.4 | 4.5 | 1.0 | 0.5 | 0.9 | 2.3 | 3.8 |
| Skewness | 1.1 | 1.8 | 1.0 | 1.0 | 1.1 | 1.4 | 1.7 |
| Range | 190.9 | 11.4 | 404.5 | 57.5 | 52.8 | 4892.0 | 45.2 |
| Minimum | 76.5 | 1.4 | 200.2 | 25.5 | 20.2 | 508.0 | 4.8 |
| Maximum | 267.4 | 12.8 | 604.7 | 83.0 | 73.0 | 5400.0 | 50.0 |
| Sum | 8236.8 | 271.1 | 20,831.6 | 2534.8 | 2089.2 | 105,337.0 | 830.1 |
| Count | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Variable | Diameter | Thickness | Steel Yield Strength | Compressive Strength | Length | Length/Diameter |
|---|---|---|---|---|---|---|
| Diameter | 1 | 0.367 | −0.197 | 0.123 | 0.246 | −0.293 |
| Thickness | 0.367 | 1 | 0.031 | −0.041 | 0.091 | −0.102 |
| Steel yield strength | −0.197 | 0.031 | 1 | 0.088 | −0.028 | 0.075 |
| Compressive strength | 0.123 | −0.041 | 0.088 | 1 | −0.016 | −0.102 |
| Length | 0.246 | 0.091 | −0.028 | −0.016 | 1 | 0.813 |
| Length/diameter | −0.293 | −0.102 | 0.075 | −0.102 | 0.813 | 1 |
| Parameter | Settings | |
|---|---|---|
| General | ||
| Chromosomes | 30 | |
| Genes | 3 | |
| Head size | 8 | |
| Gene size | 26 | |
| Linking function | Addition | |
| Function set | +, −, ×, ÷, √,3√ | |
| Genetic operators | ||
| Mutation rate | 0.0138 | |
| Inversion rate | 0.00546 | |
| IS Transposition rate | 0.00546 | |
| RIS transposition rate | 0.00546 | |
| One-point recombination rate | 0.00277 | |
| Two-point recombination rate | 0.00277 | |
| Gene recombination rate | 0.00755 | |
| Gene transposition rate | 0.00277 | |
| Numerical constants | ||
| Constants per gene | 10 | |
| Data type | Floating Point | |
| Lower bound | −10 | |
| Upper bound | 10 | |
| Model | Experimental Axial Capacity vs. Predicted Axial Capacity | ||
|---|---|---|---|
| R2 | MAE | RMSE | |
| Learning | 0.97 | 134.8 | 210.3 |
| Validation | 0.98 | 153.9 | 226.1 |
| Testing | 0.99 | 124.3 | 173.7 |
| Equation No: | Code Specification | Ultimate Axial Moment Capacity (NU) | Limitations |
|---|---|---|---|
| 1 | AS5100.6 (2004) | ||
| 2 | AISC (2005) | ||
| 3 | BS5400 | ||
| 4 | DBJ (1999) | ||
| 5 | AIJ (2001) | ||
| 6 | EC4 (2004) |
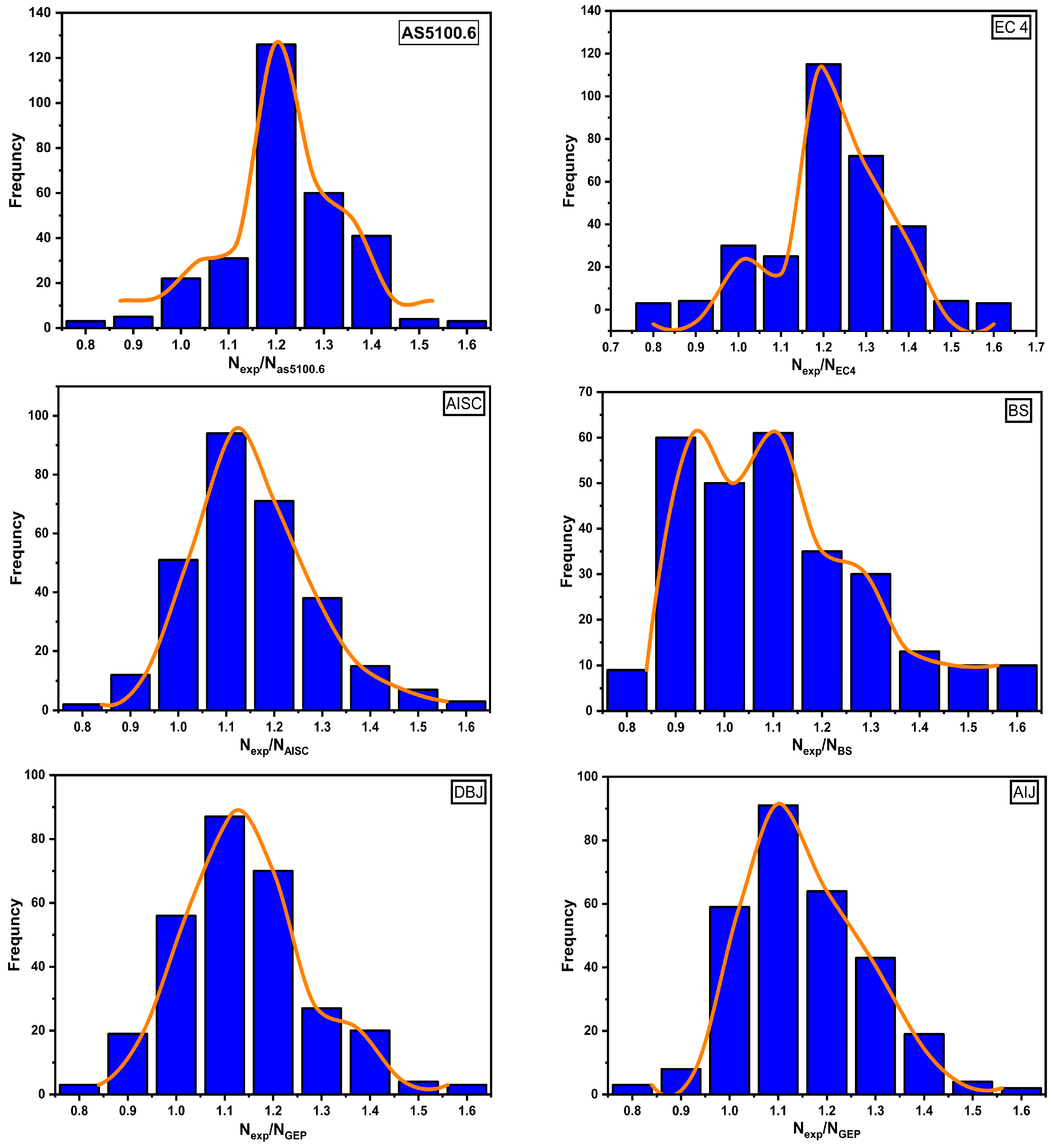
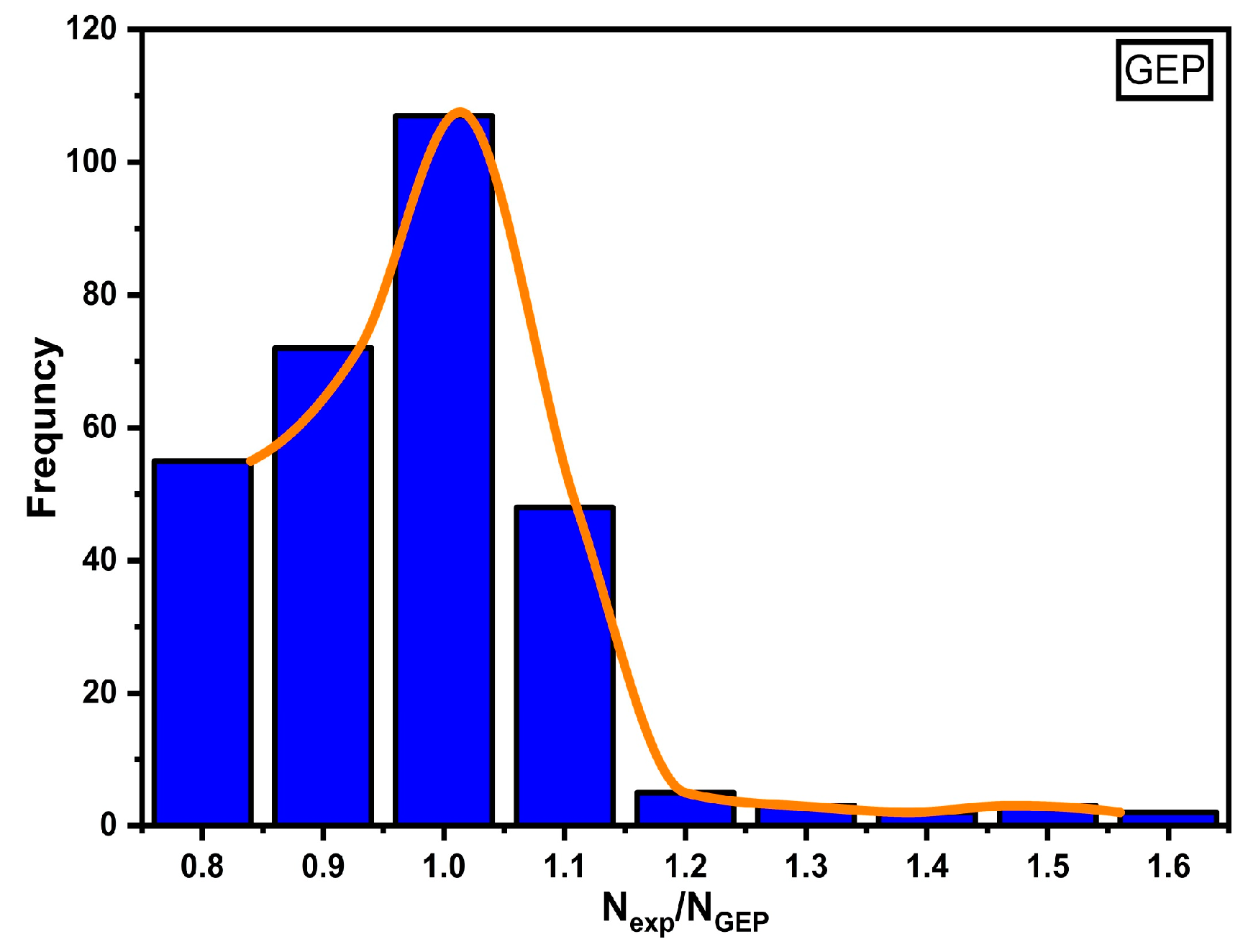
| Statistical Parameters | GEP | AS5100.6 | EC4 | AISC | BS | DBJ | AIJ |
|---|---|---|---|---|---|---|---|
| Rsq | 0.98 | 0.98 | 0.98 | 0.97 | 0.96 | 0.97 | 0.97 |
| MAE | 138.7 | 249.4 | 220.6 | 333.5 | 205.0 | 228.0 | 194.4 |
| RMSE | 258.0 | 484.7 | 452.9 | 701.4 | 352.9 | 512.0 | 408.4 |
| 0.1 | 0.2 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 | |
| Average | 1.2 | 1.1 | 1.2 | 1.0 | 1.0 | 0.9 | 1.2 |
| Maximum | 1.2 | 1.6 | 1.7 | 2.0 | 1.7 | 1.5 | 1.2 |
| Minimum | 0.7 | 0.7 | 0.8 | 0.6 | 0.5 | 0.6 | 0.8 |
| SD | 0.1 | 0.1 | 0.1 | 0.1 | 0.3 | 0.2 | 0.1 |
| COV | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 |
| Sr. No | Formula | Condition | GEP |
|---|---|---|---|
| 1 | Equation (5) | R > 0.8 | 0.973 |
| 2 | 0.85 < K < 1.15 | 0.983 | |
| 3 | 0.85 < K′ < 1.15 | 1.003 | |
| 4 | Rm > 0.5 | 0.838 | |
| is squared correlation coefficient between predicted and experimental values | 0.999 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U. New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals 2020, 10, 741. https://doi.org/10.3390/cryst10090741
Javed MF, Farooq F, Memon SA, Akbar A, Khan MA, Aslam F, Alyousef R, Alabduljabbar H, Rehman SKU. New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals. 2020; 10(9):741. https://doi.org/10.3390/cryst10090741
Chicago/Turabian StyleJaved, Muhammad Faisal, Furqan Farooq, Shazim Ali Memon, Arslan Akbar, Mohsin Ali Khan, Fahid Aslam, Rayed Alyousef, Hisham Alabduljabbar, and Sardar Kashif Ur Rehman. 2020. "New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach" Crystals 10, no. 9: 741. https://doi.org/10.3390/cryst10090741
APA StyleJaved, M. F., Farooq, F., Memon, S. A., Akbar, A., Khan, M. A., Aslam, F., Alyousef, R., Alabduljabbar, H., & Rehman, S. K. U. (2020). New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals, 10(9), 741. https://doi.org/10.3390/cryst10090741












