One-Dimensional Alternating Extended Hubbard Model at Quarter-Filling and Its Applications to Structural Instabilities of Organic Conductors
Abstract
:1. Introduction
2. Alternating Extended Hubbard Model
The Model and Its Continuum Limit
3. Renormalization Group Results
3.1. Formulation and Coupling Constants
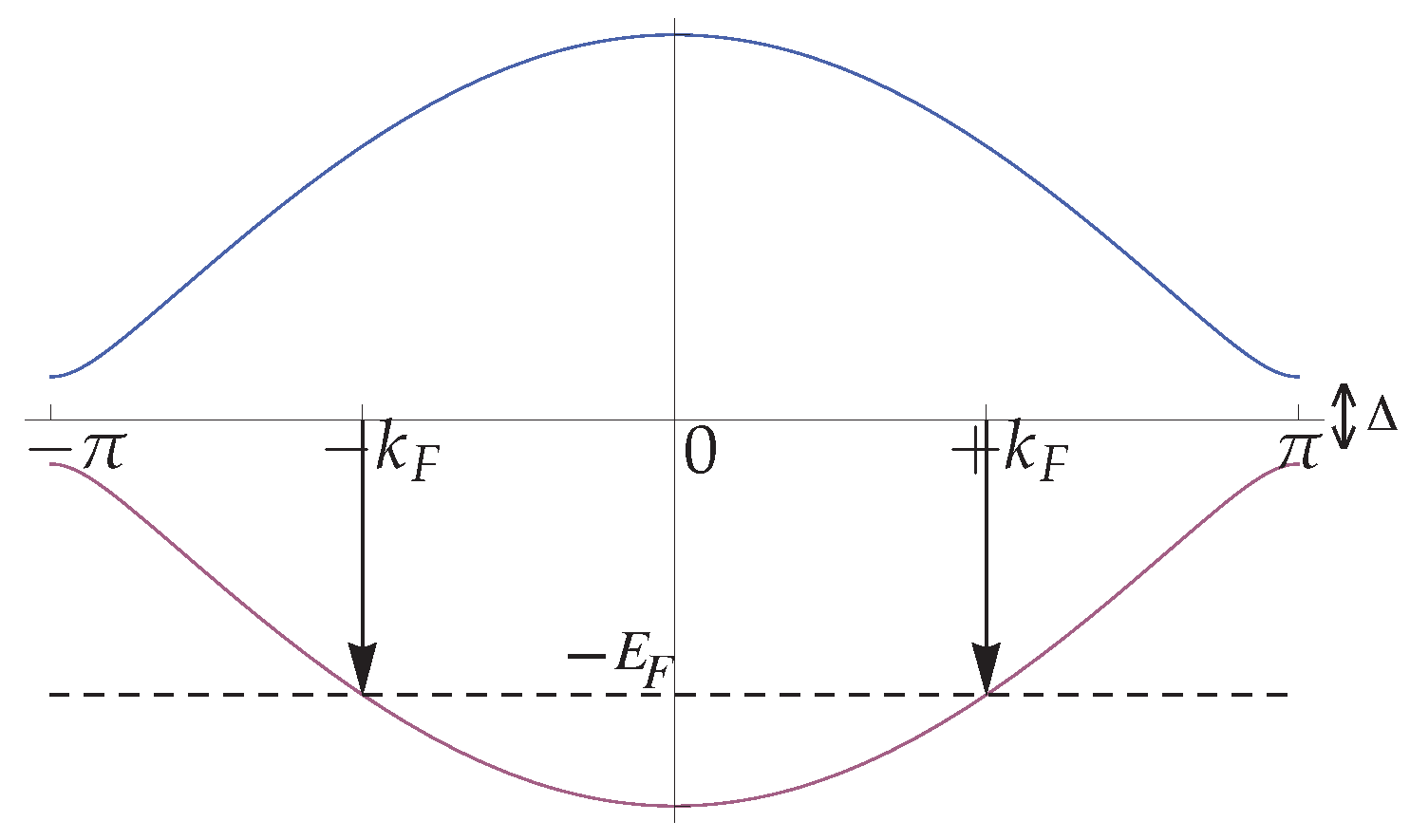
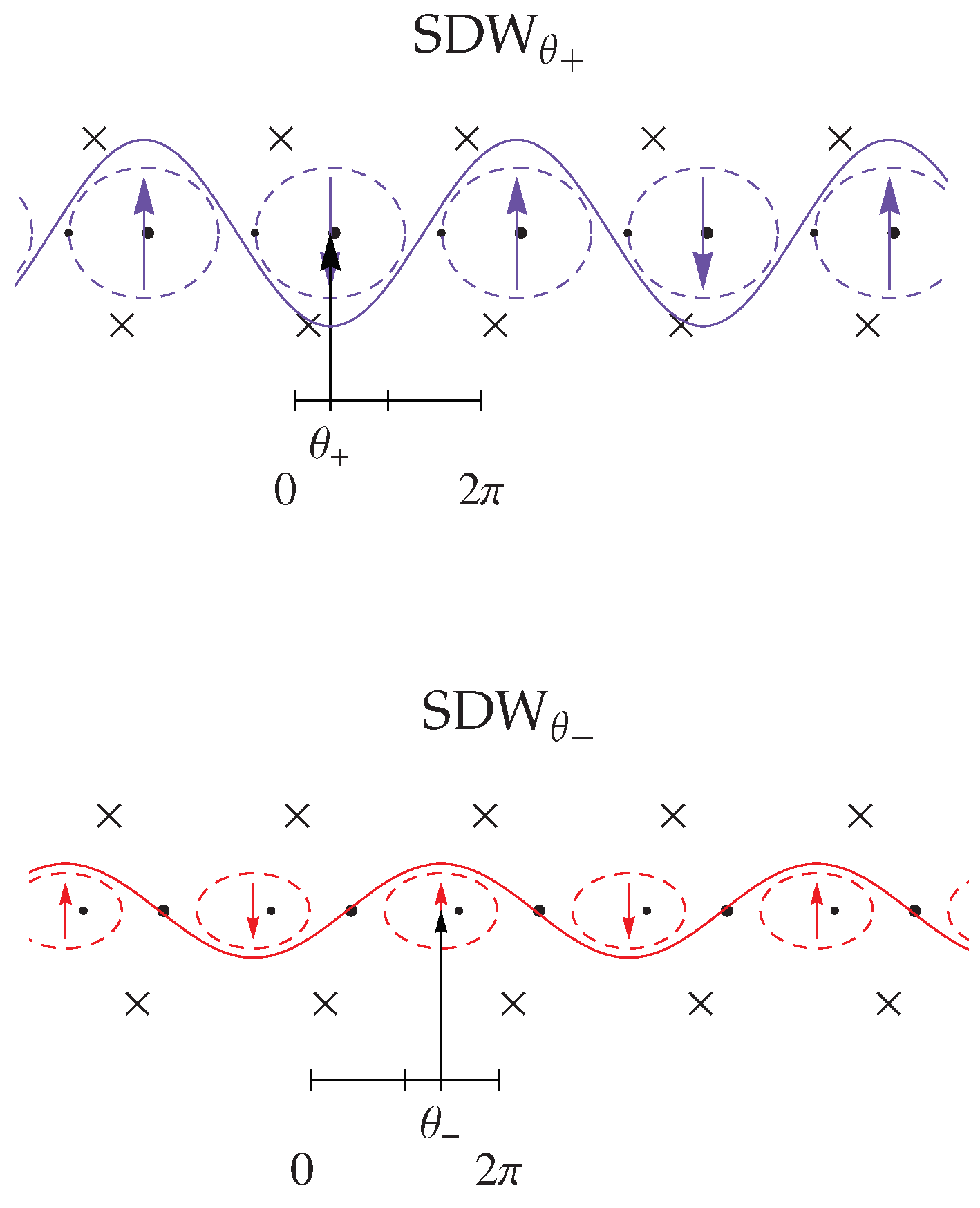
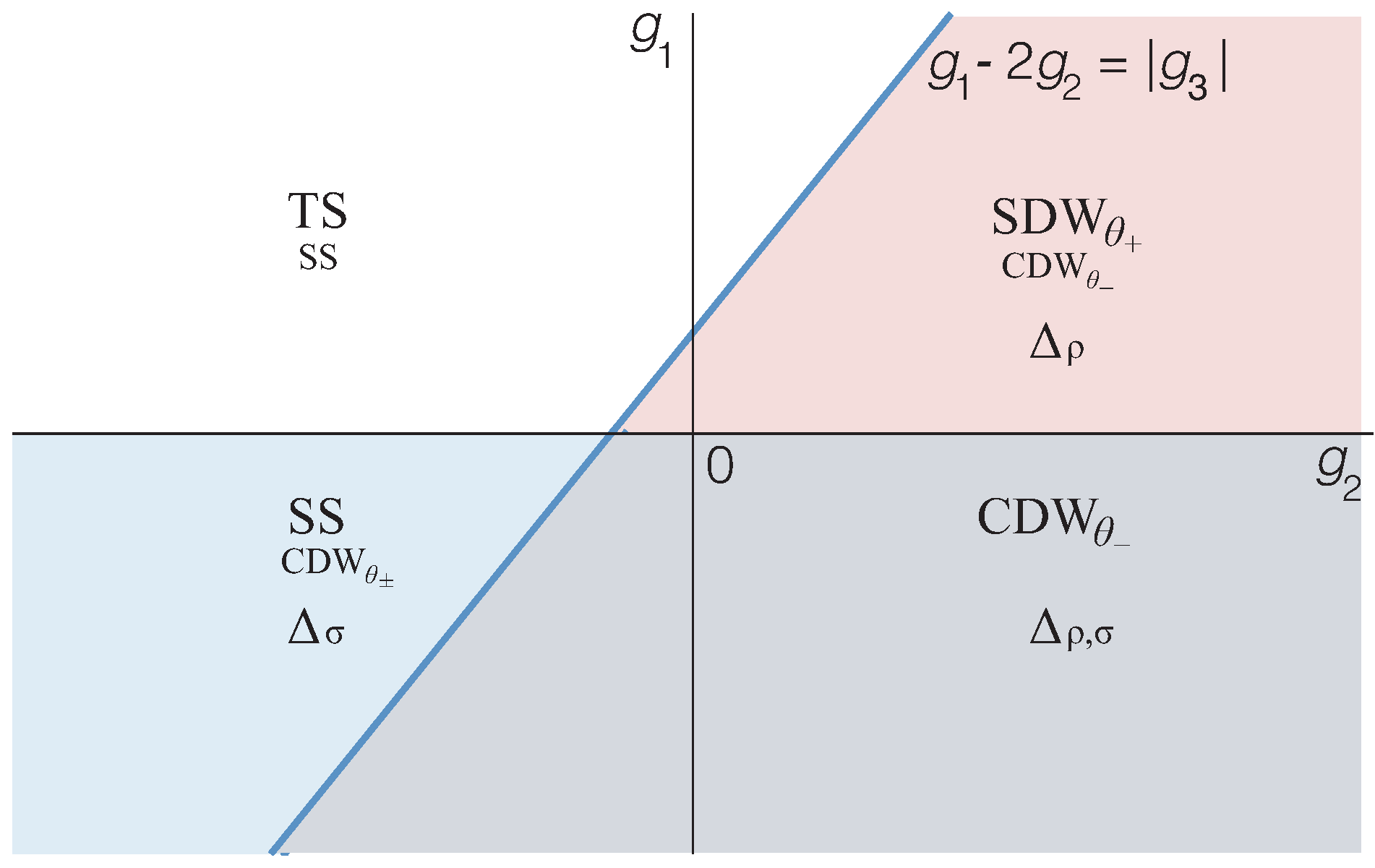
3.2. Response Functions and Phase Diagram
4. Applications
4.1. Anion Ordering in [(TMTSF)TMTTF]ReO
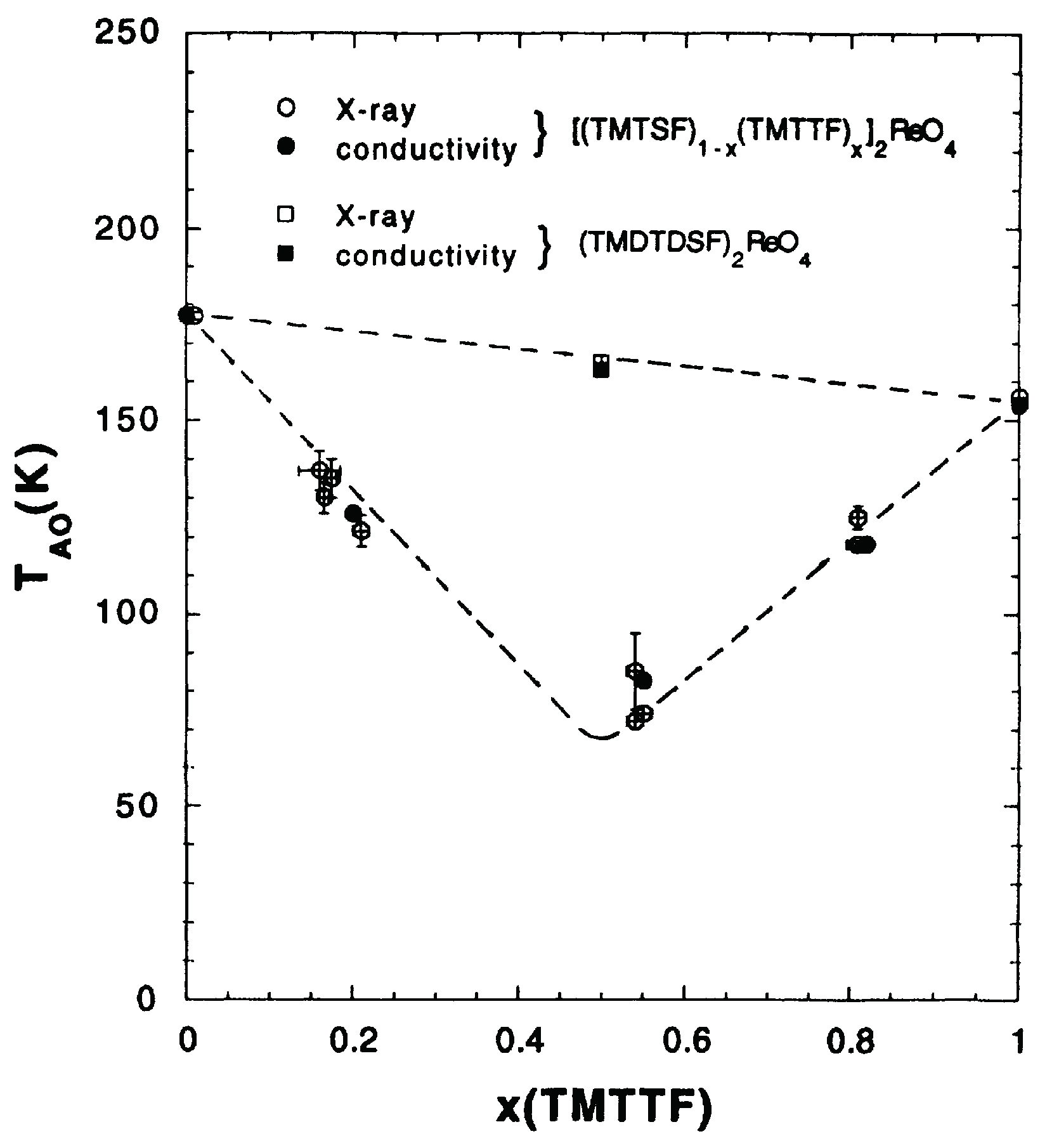
4.1.1. Experimental Features
4.1.2. Electron–Anion Interaction
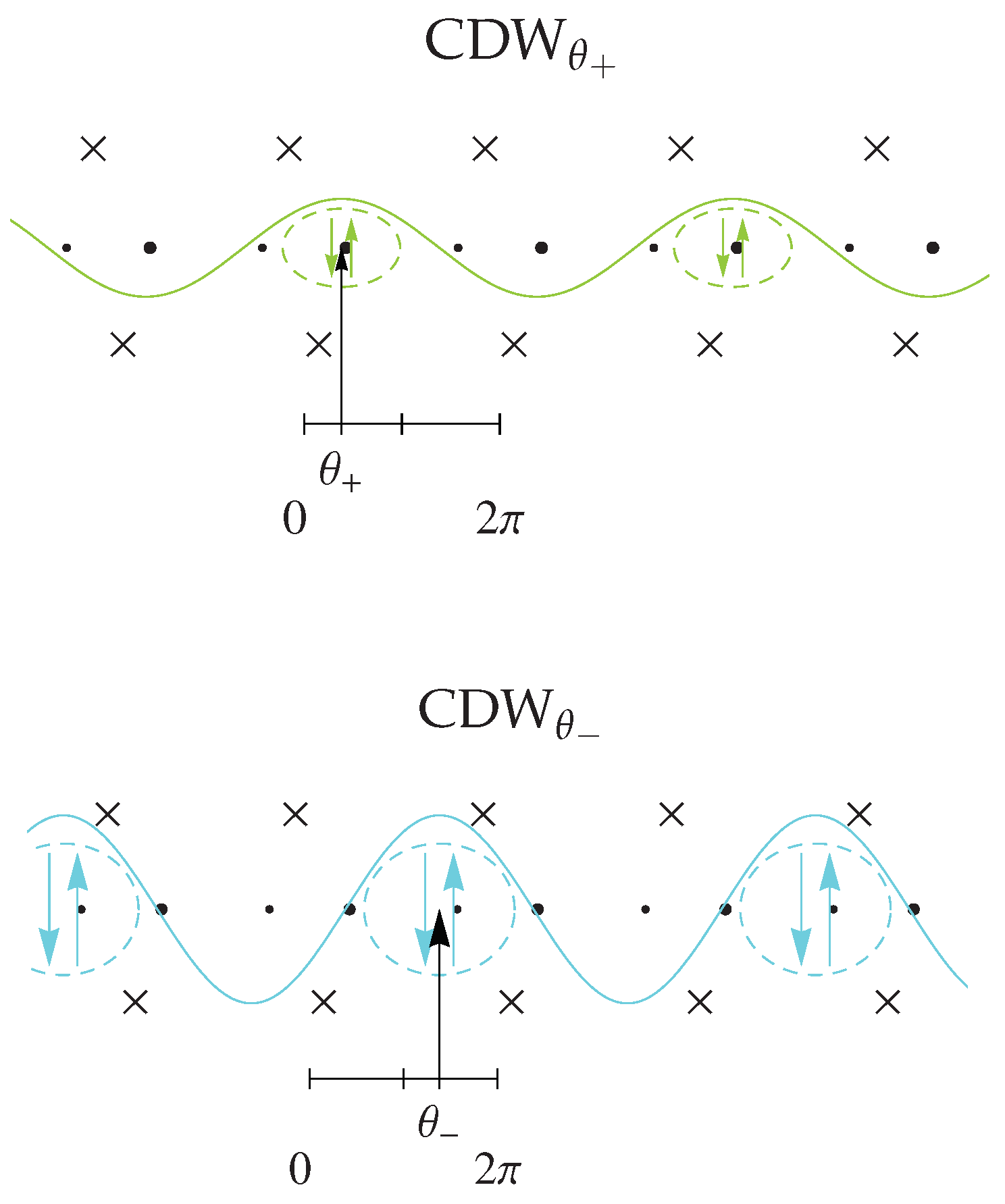
4.1.3. Anion Ordering
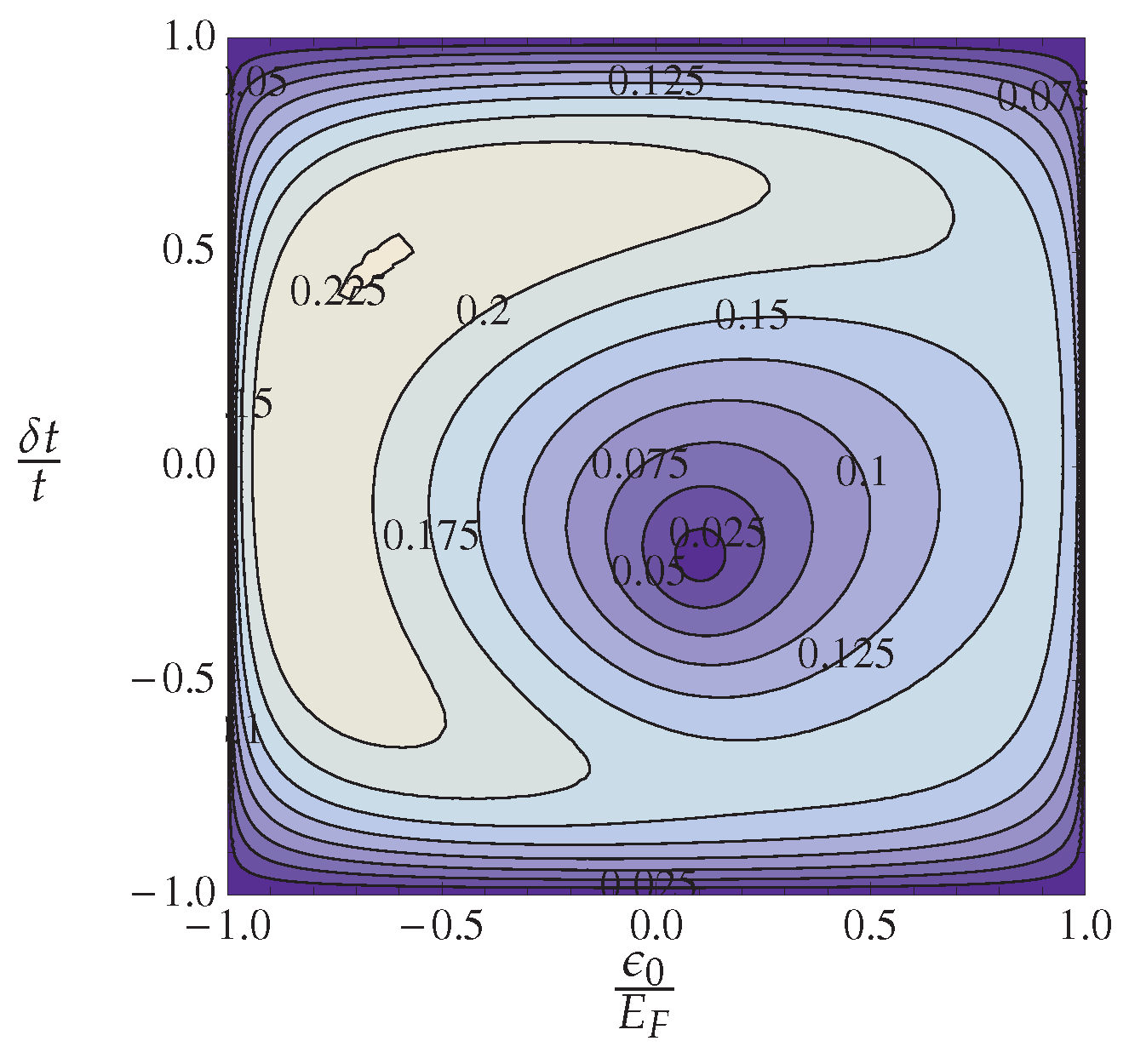
4.1.4. Theory and Experiment
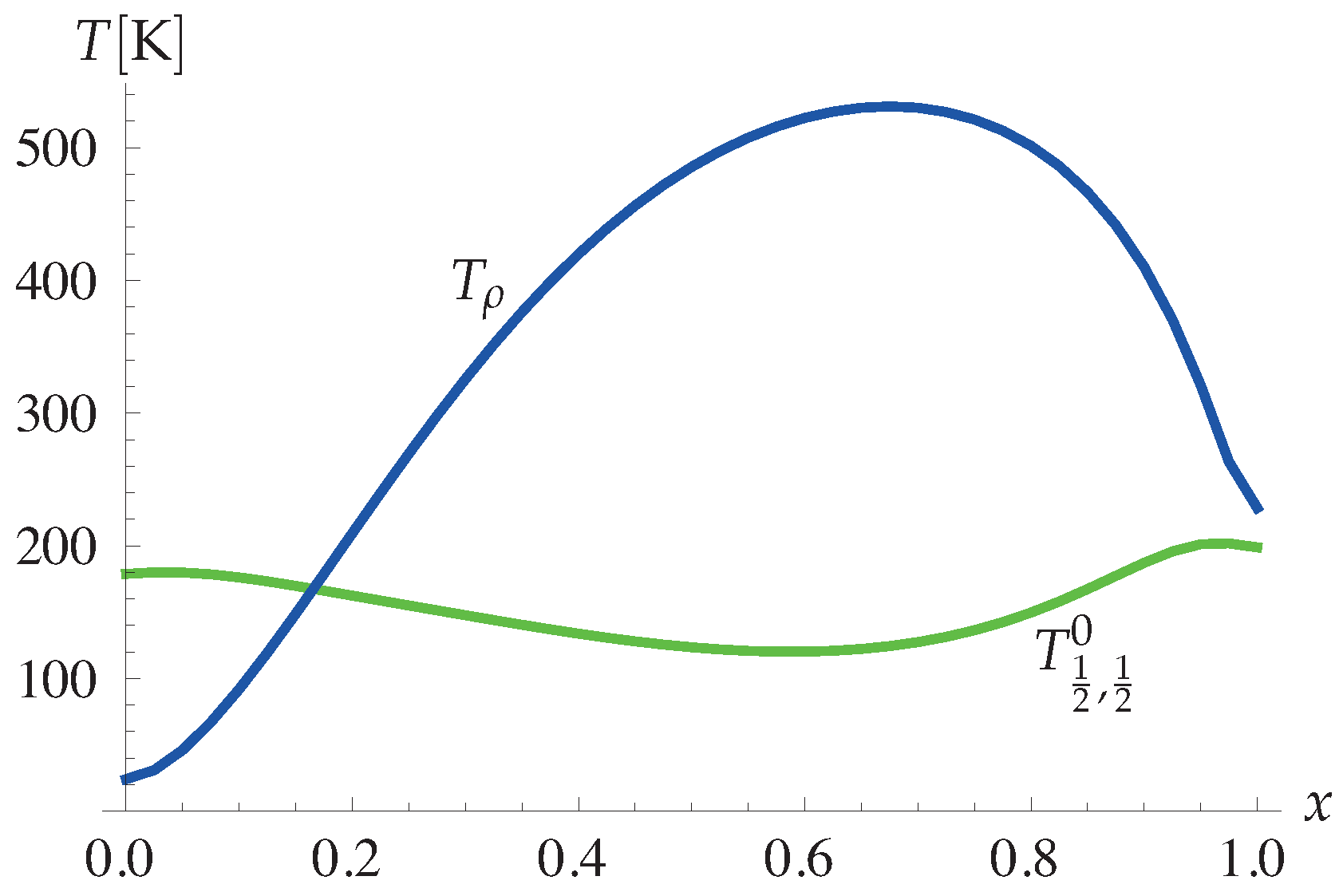
4.2. Interplay between the Spin-Peierls and Charge Ordered States
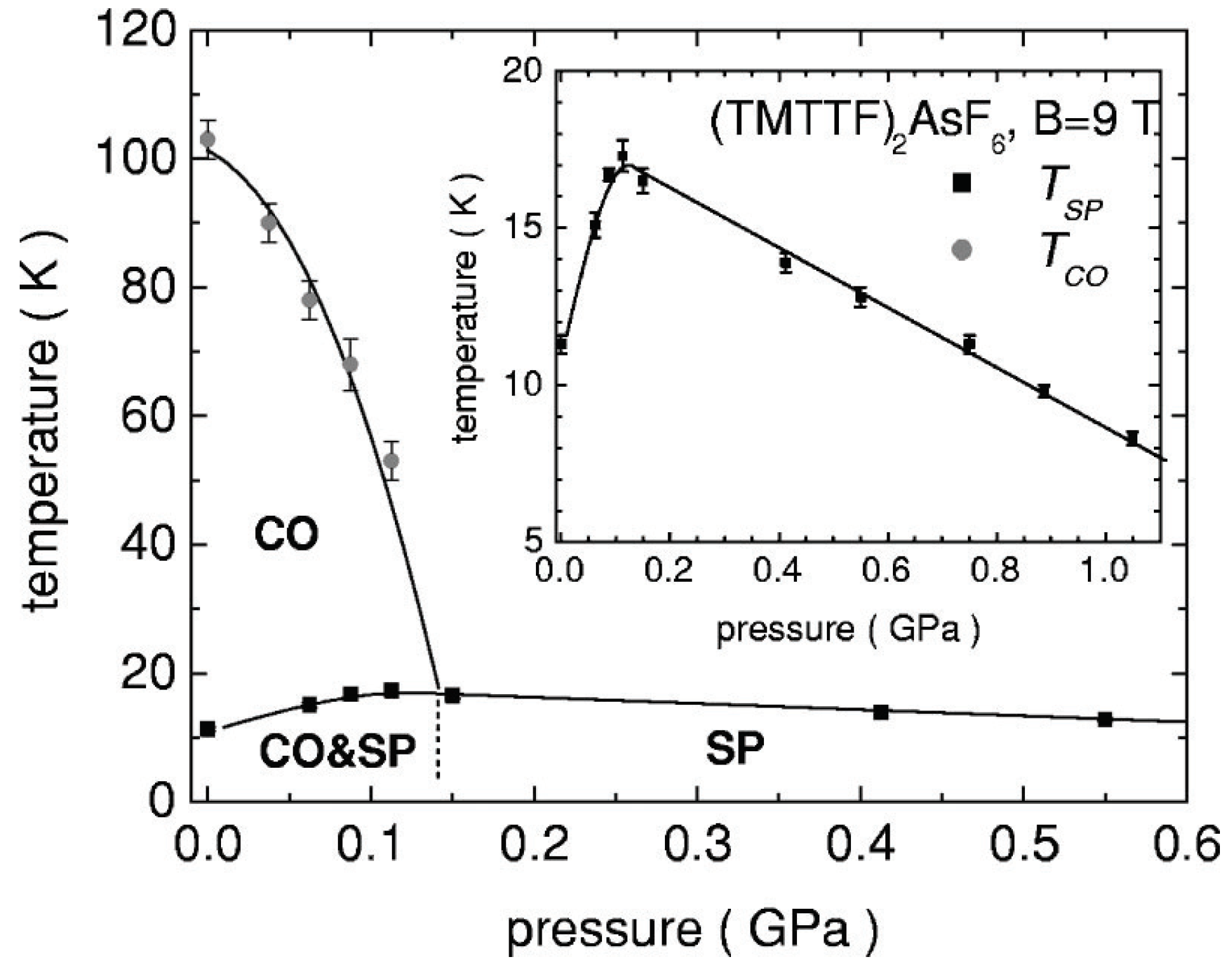
4.2.1. Experiments
4.2.2. Electron–Lattice Coupling
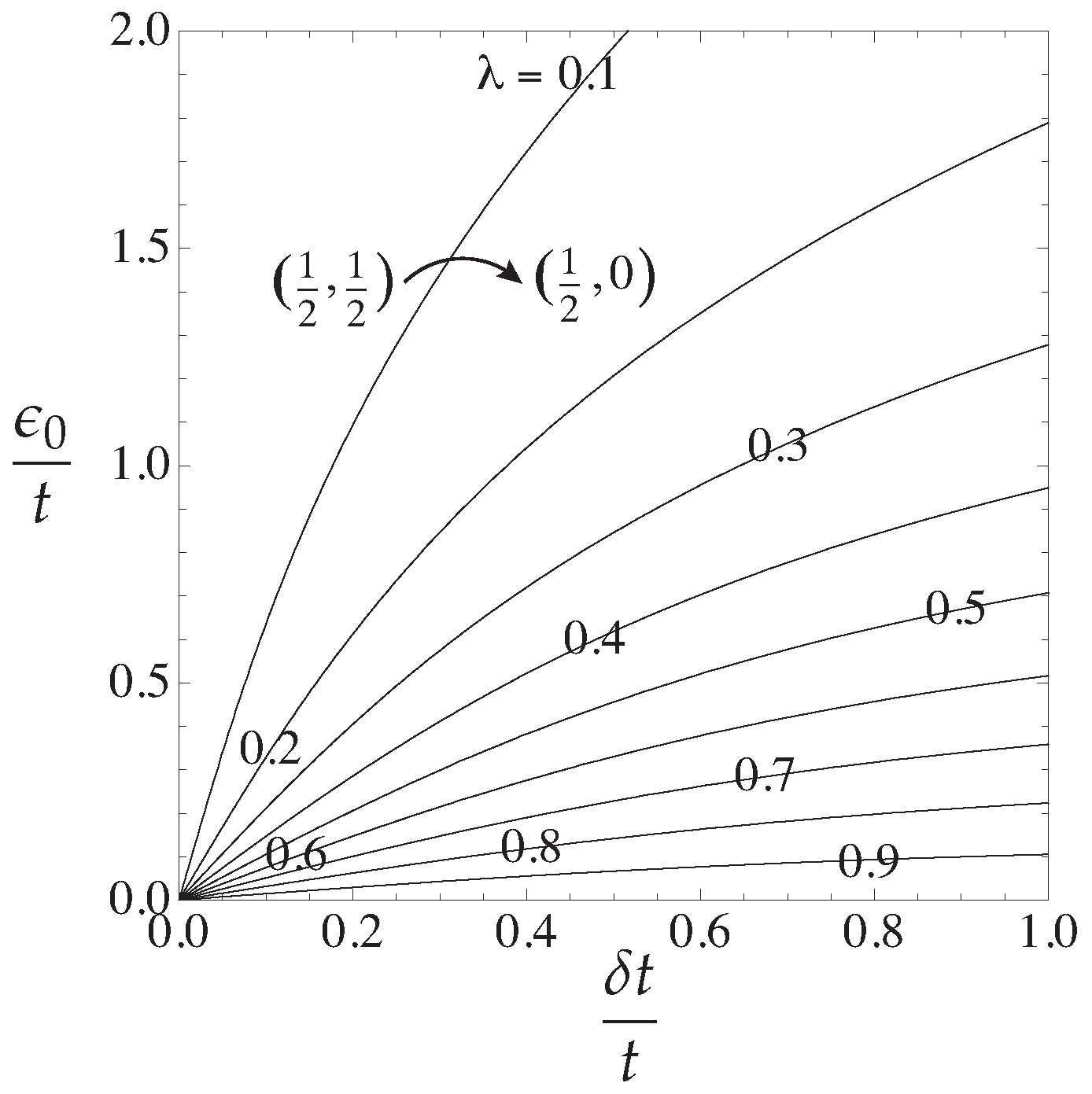
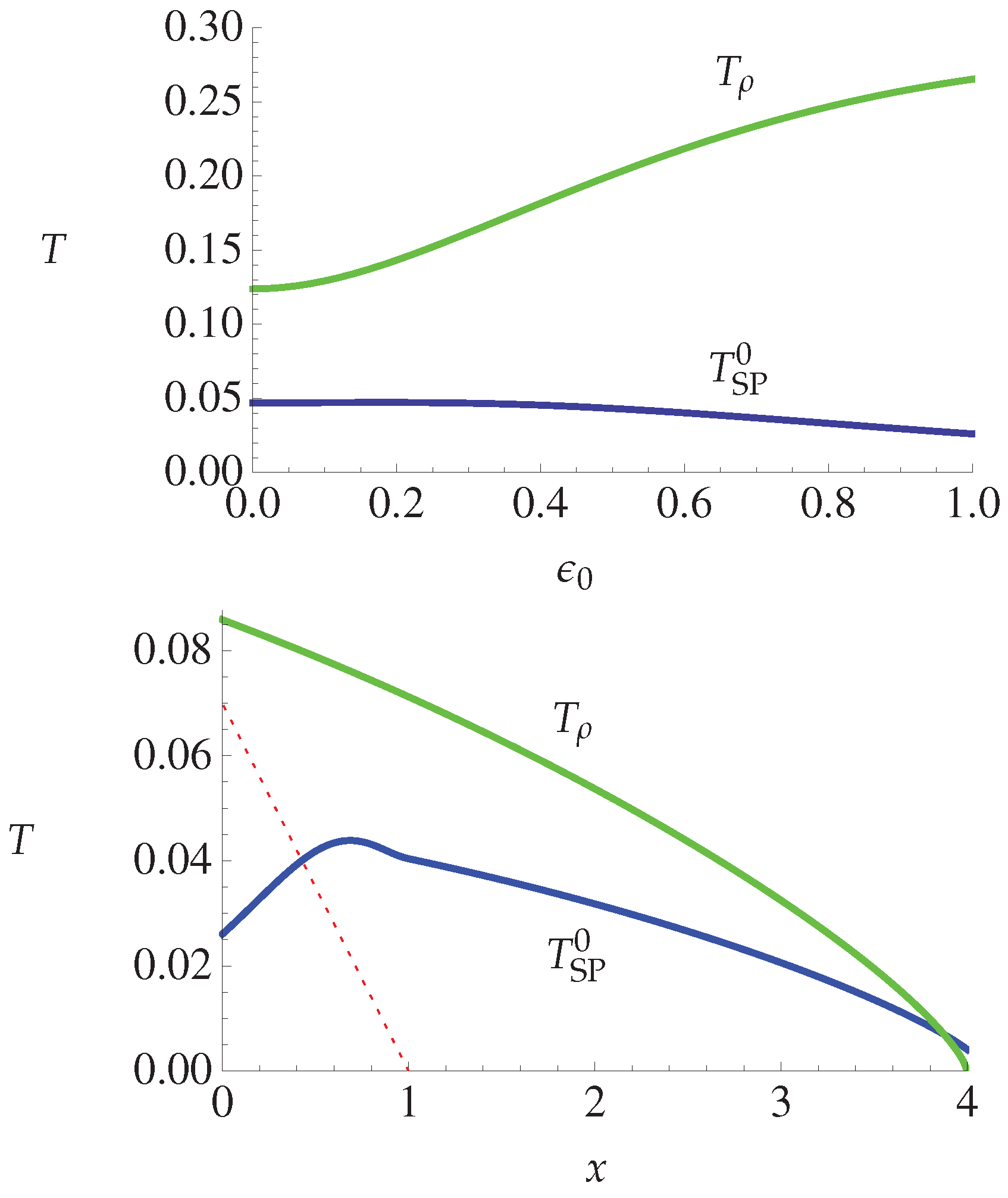
4.2.3. Spin-Peierls Instability
4.2.4. Theory and Experiment
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jérome, D.; Schulz, H.J. Organic conductors and superconductors. Adv. Phys. 1982, 31, 299. [Google Scholar] [CrossRef]
- Ishiguro, T.; Yamaji, K. Organic Superconductors; Springer-Verlag Series in Solid-State Science; Springer: Berlin/Heidelberg, Germeny, 1990; Volume 88. [Google Scholar]
- Bourbonnais, C.; Jérome, D. The normal phase of quasi-one-dimensional organic superconductors. In Advances in Synthetic Metals, Twenty Years of Progress in Science and Technology; Bernier, P., Lefrant, S., Bidan, G., Eds.; Elsevier: New York, NY, USA, 1999; pp. 206–261. [Google Scholar]
- Bourbonnais, C.; Jérome, D. Interacting electrons In quasi-one-Dimensional organic superconductors. In The Physics of Organic Superconductors and Conductors; Springer Series in Materials Science; Lebed, A., Ed.; Springer: Heidelberg, Germany, 2008; Volume 110, p. 357. [Google Scholar]
- Brown, S.E.; Chaikin, P.M.; Naughton, M.J. La tour des sels de Bechgaard. In The Physics of Organic Superconductors and Conductors; Springer Series in Materials Science; Lebed, A., Ed.; Springer: Heidelberg, Germany, 2008; Volume 110, p. 49. [Google Scholar]
- Seo, H.; Hotta, C.; Fukuyama, H. Towards systematic understanding of diversity of electronic properties in low-dimensional molecular solids. Chem. Rev. 2004, 104, 5005. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.E. The Bechgaard salts and relatives. Physica C 2015, 514, 279. [Google Scholar] [CrossRef]
- Dressel, M. Ordering phenomena in quasi-one-dimensional organic conductors. Naturwissenschaften 2007, 94, 527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dressel, M.; Dumm, M.; Knoblauch, T.; Masino, M. Comprehensive optical investigations of charge order in organic chain compounds (TMTTF)2X. Crystals 2012, 2, 528–578. [Google Scholar] [CrossRef] [Green Version]
- Pouget, J.P. Interplay between electronic and structural degrees of freedom in quarter-filled low dimensional organic compounds. Physica B 2015, 460, 45. [Google Scholar] [CrossRef]
- Pouget, J.P.; Alemany, P.; Canadell, E. Donor-anion interactions in quarter-filled low-dimensional organic conductors. Mater. Horizons 2018, 5, 590. [Google Scholar] [CrossRef] [Green Version]
- Rosslhuber, R.; Rose, E.; Ivek, T.; Pustogow, A.; Breier, T.; Geiger, M.; Schrem, K.; Untereiner, G.; Dressel, M. Structural and electronic properties of (TMTTF)2X salts with tetrahedral anions. Crystals 2018, 8, 121. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Mazumdar, S. From charge- and spin-ordering to superconductivity in the organic charge-transfer solids. Phys. Rep. 2019, 788, 1. [Google Scholar] [CrossRef] [Green Version]
- Barisic, S.; Brazovskii, S. Recent Developments in Condensed Matter Physics; Devreese, J.T., Ed.; Plenum: New York, NY, USA, 1981; Volume 1, p. 327. [Google Scholar]
- Emery, V.J.; Bruinsma, R.; Barisic, S. Electron-electron umklapp scattering in organic superconductors. Phys. Rev. Lett. 1982, 48, 1039. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Larkin, A.I. Possible states of quasi-unidimensional systems. Sov. Phys. JETP 1972, 34, 422. [Google Scholar]
- Solyom, J. The Fermi gas model of one-dimensional conductors. Adv. Phys. 1979, 28, 201. [Google Scholar] [CrossRef] [Green Version]
- Emery, V.J. Highly Conducting One-Dimensional Solids; Devreese, J.T., Evrard, R.E., van Doren, V.E., Eds.; Plenum: New York, NY, USA, 1979; p. 247. [Google Scholar]
- Brazovskii, S.; Yakovenko, Y. On the theory of organic superconducting materials. Sov. Phys. JETP 1985, 62, 1340. [Google Scholar]
- Caron, L.G.; Bourbonnais, C. Importance of one-dimensional correlations in the phase diagram of the (TMTTF)2-(TMTSF)2X salts. Phys. B + C 1986, 143, 453. [Google Scholar] [CrossRef]
- Bourbonnais, C.; Caron, L.G. New mechanisms of phase transition in quasi-one dimensional conductors. Europhys. Lett. 1988, 5, 209. [Google Scholar] [CrossRef]
- Moret, R.; Pouget, J.P.; Comès, R.; Bechgaard, K. X-ray scattering evidence for anion ordering in the low-temperature phase of Di(Tetramethyltetraselanafulvalenium) Perrhenate. Phys. Rev. Lett. 1982, 49, 1008–1012. [Google Scholar] [CrossRef]
- Moret, R.; Pouget, J.P.; Comes, R.; Bechgaard, K. Structural phase transitions in (TMTSF)2X and (TMTTF)2X: A survey with some new results. J. Phys. Colloq. 1983, 44, C3-957. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Petit, S.; Andre, G.; Moradpour, A.; Pouget, J.P. Neutron scattering evidence for a lattice displacement at the charge ordering transition of (TMTTF)2PF6. Physica B 2010, 405, S95. [Google Scholar] [CrossRef]
- Riera, J.; Poilblanc, D. Influence of anion potential on the charge ordering in the charge-transfer salts. Phys. Rev. B 2001, 63, R241102. [Google Scholar] [CrossRef] [Green Version]
- Ilakovac, V.; Ravy, S.; Pouget, J.P.; Lenoir, C.; Boubekur, K.; Batail, P.; Babic, S.D.; Biskup, N.; Korin-Hamzic, B.; Tomic, S.; et al. Enhanced charge localization in the organic alloys [(TMTSF)1-xTMTTFx]2ReO4. Phys. Rev. B 1994, 50, 7136. [Google Scholar] [CrossRef] [PubMed]
- Penc, K.; Mila, F. Charge gap in the one-dimensional Hubbard model at quarter-filling. Phys. Rev. B 1994, 50, 11429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsuchiizu, M.; Yoshioka, H.; Suzumura, Y. Theoretical study of the charge gap of organic conductors Bechgaard salts. J. Phys. Soc. Jpn. 1999, 68, 1809. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.; Brazovskii, S. Ferroelectric Mott-Hubbard phase of organic (TMTTF)2X conductors. Phys. Rev. Lett. 2001, 86, 4080. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coulon, C.; Parkin, S.S.P.; Laversanne, R. Structureless transition and strong localization effects in bis-tetramethyltetrathiafulvalenium salts [(TMTTF)2X]. Phys. Rev. B 1985, 31, 3583. [Google Scholar] [CrossRef] [PubMed]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge Ordering in the TMTTF Family of Molecular Conductors. Phys. Rev. Lett. 2000, 85, 1698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nad, F.; Monceau, P.; Carcel, C.; Fabre, J.M. Charge ordering phase transition in the quasi-one-dimensional conductor (TMTTF)2AsF6. J. Phys. Condens. Matter 2000, 12, L435. [Google Scholar] [CrossRef]
- Seo, H.; Fukuyama, H. Antiferromagnetic phases of one-dimensional quarter-felled organic conductors. J. Phys. Soc. Jpn. 1997, 66, 1249. [Google Scholar] [CrossRef] [Green Version]
- Mazumdar, S.; Clay, R.T.; Campbell, D.K. Bond-order and charge-density waves in the isotropic interacting two-dimensional quarter-filled band and the insulating state proximate to organic superconductivity. Phys. Rev. B 2000, 62, 13400. [Google Scholar] [CrossRef] [Green Version]
- Riera, J.; Poilblanc, D. Coexistence of charge-density waves, bond-order waves, and spin-density waves in quasi-one-dimensional charge-transfer salts. Phys. Rev. B 2000, 62, R16243. [Google Scholar] [CrossRef] [Green Version]
- Giamarchi, T. Mott transition in one dimension. Physica 1997, B230-232, 975. [Google Scholar] [CrossRef] [Green Version]
- Pouget, J.; Moret, R.; Comes, R.; Bechgaard, K.; Fabre, J.M.; Giral, L. X-ray diffuse scattering of some (TMTSF)2X and (TMTTF)2X salts. Mol. Cryst. Liq. Cryst. 1982, 79, 129. [Google Scholar] [CrossRef]
- Creuzet, F.; Bourbonnais, C.; Caron, L.G.; Jérome, D.; Bechgaard, K. A 13C NMR study of the interplay between the spin-Peierls and antiferromagnetic ground states in (TMTTF)2PF6 under pressure. Synth. Met. 1987, 19, 289. [Google Scholar] [CrossRef]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103(R). [Google Scholar] [CrossRef] [Green Version]
- Sugiura, M.; Suzumura, Y. Competition of dimerization and charge ordering in the pin-Peierls state of organic conductors. J. Phys. Soc. Jpn. 2003, 72, 1458. [Google Scholar] [CrossRef] [Green Version]
- Kuwabara, M.; Seo, H.; Ogata, M. Coexistence of charge order and spin-Peierls lattice distortion in one-dimensional organic conductors. J. Phys. Soc. Jpn. 2003, 72, 225. [Google Scholar] [CrossRef]
- Tsuchiizu, M.; Yoshioka, H.; Suzumura, Y. Crossover from quarter-filling to half-filling in a one-dimensional electron system with a dimerized and quarter-filled band. J. Phys. Soc. Jpn. 2001, 70, 1460. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Mazumdar, S.; Campbell, D.K. Pattern of charge ordering in quasi-one-dimensional organic charge-transfer solids. Phys. Rev. B 2003, 67, 115121. [Google Scholar] [CrossRef] [Green Version]
- Castet, F.; Fritsch, A.; Ducasse, L. Determination of coulombic interaction parameters of the extended Hubbard model in the organic conductors. J. Phys. I (France) 1996, 6, 583. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Gorkov, L.P.; Dzyaloshinskii, I. Possibility of superconductivity type phenomena in a one-dimensional system. Sov. Phys. JETP 1966, 23, 489. [Google Scholar]
- Bourbonnais, C.; Caron, L.G. Renormalization group approach to quasi-one-dimensional conductors. Int. J. Mod. Phys. B 1991, 05, 1033. [Google Scholar] [CrossRef]
- Kimura, M. Possible phases and some properties of the one metal with the half-filled band. Prog. Theor. Phys. 1975, 63, 955. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, C.S.; Pedersen, H.J.; Mortensen, K.; Rindorf, G.; Thorup, N.; Torrance, J.B.; Bechgaard, K. An unusual metal-insulator transition: bis(tetramethyltetraselenafulvalenium)-perrhenate (TMTSF)2ReO4. J. Phys. C Solid State Phys. 1982, 15, 2651. [Google Scholar] [CrossRef]
- Pustogow, A.; Petersein, T.; Kolatschek, S.; Engel, L.; Dressel, M. Electronic correlations versus lattice interactions: Interplay of charge and anion orders in (TMTTF)2X. Phys. Rev. B 2016, 94, 195125. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Senhaji, A.; Pouget, J.P.; Johanssen, I.; Bechgaard, K. Structural investigation of the (TMDTDSF)2X series of organic conductors. Synth. Met. 1991, 42, 1711. [Google Scholar] [CrossRef]
- Auban, P.; Jérome, D.; Johannsen, I.; Bechgaard, K. Physical properties of the new organic conductor series di(tetramethyl-dithiadiselenafulvalene) X; X = BF4, ClO4, ReO4, PF6, AsF6, SbF6. Synth. Met. 1991, 41, 2285. [Google Scholar] [CrossRef]
- Gotschy, B.; Auban-Senzier, P.; Farrall, A.; Bourbonnais, C.; Jerome, D.; Canadell, E.; Henriques, R.T.; Johanssen, I.; Bechgaard, K. One-dimensional physics in organic conductors (TMDTDSF)2X, X = PF6, ReO4:77Se-NMR experiments. J. Phys. I (France) 1992, 2, 677. [Google Scholar] [CrossRef]
- Grant, P.M. Electronic structure of the 2:1 charge transfer salts of tmtcf. J. Phys. Colloq. 1983, 44, C3 847. [Google Scholar] [CrossRef]
- Jacko, A.C.; Feldner, H.; Rose, E.; Lissner, F.; Dressel, M.; Valenti, R.; Jeschke, H.O. Electronic properties of Fabre charge-transfer salts under various temperature and pressure conditions. Phys. Rev. B 2013, 87, 155139. [Google Scholar] [CrossRef] [Green Version]
- Sato, N.; Saito, G.; Inokuchi, H. Ionization potentials and polarization energies of tetraselenafulvalene (TSF) derivatives determined from ultraviolet photoelectron spectroscopy. Chem. Phys. 1983, 76, 79. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Mayerle, J.J.; Engler, E.M. Anion ordering in (TMTTF)2ReO4. J. Phys. (Paris) Coll. 1983, 44, C3-1105. [Google Scholar]
- Coulon, C.; Delhaes, P.; Flandrois, S.; Lagnier, R.; Bonjour, E.; Fabre, J. A new survey of the physical properties of the (TMTTF)2X series. Role of the counterion ordering. J. Phys. (Paris) 1982, 43, 1059. [Google Scholar] [CrossRef]
- Laversanne, R.; Coulon, C.; Gallois, B.; Pouget, J.P.; Moret, R. Structural and electrical properties of (TMTTF)2MF6 salts (M = P, As, Sb). Role of the anions. J. Phys. (Paris) Lett. 1984, 45, L393. [Google Scholar] [CrossRef] [Green Version]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in polyaecetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Barišić, S.; Labbé, J.; Friedel, J. Tight-binding and transition-metal superconductivity. Phys. Rev. Lett. 1970, 25, 919. [Google Scholar] [CrossRef]
- Caron, L.G.; Bourbonnais, C.; Creuzet, F.; Jerome, D. Evolution of the spin-Peierls transition in the (TMTTF)2X salts (X = PF6, PF6 Br) under pressure. Synth. Met. 1987, 19, 69. [Google Scholar] [CrossRef]
- Bourbonnais, C.; Dumoulin, B. Theory of lattice and electronic fluctuations in weakly localized spin-Peierls systems. J. Phys. I (France) 1996, 6, 1727. [Google Scholar] [CrossRef] [Green Version]
- Scalapino, D.J.; Imry, Y.; Pincus, P. Generalized Ginzburg-Landau theory of pseudo-one dimensional systems. Phys. Rev. B 1975, 11, 2042. [Google Scholar] [CrossRef]
- Ducasse, L.; Abderrabba, A.; Hoarau, J.; Pesquer, M.; Gallois, B.; Gaultier, J. Temperature dependence of the transfer integrals in the (TMTSF)2X and (TMTTF)2X families. J. Phys. C 1986, 19, 3805. [Google Scholar] [CrossRef]
- Caron, L.G.; Creuzet, F.; Butaud, P.; Bourbonnais, C.; Jérome, D.; Bechgaard, K. Spin-Peierls and antiferromagnetic transition in (TMTTF)2PF6: EPR and NMR measurements and theory. Synth. Met. 1988, 27B, 123. [Google Scholar] [CrossRef]
- Chow, D.; Wzietek, P.; Foglatti, D.; Alavi, B.; Tantillo, D.J.; Merlic, C.A.; Brown, S.E. Singular behavior in the pressure-tuned competition between spin-Peierls and antiferromagnetic ground states of (TMTTF)2PF6. Phys. Rev. Lett. 1998, 81, 3984. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, F.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.A.; Brown, S.E. Electron-lattice coupling and broken symmetries of the molecular salt ?(TMTTF)2SbF6. Phys. Rev. B 2004, 70, R121101. [Google Scholar] [CrossRef] [Green Version]
- De Souza, M.; Squillante, L.; Sônego, C.; Menegasso, P.; Foury-Leylekian, P.; Pouget, J.P. Probing the ionic dielectric constant contribution in the ferroelectric phase of the Fabre salts. Phys. Rev. B 2018, 97, 045122. [Google Scholar] [CrossRef] [Green Version]
- De Souza, M.; Pouget, J.P. Charge-ordering transition in (TMTTF)2X explored via dilatometry. J. Phys. Condens. Matter 2013, 25, 343201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
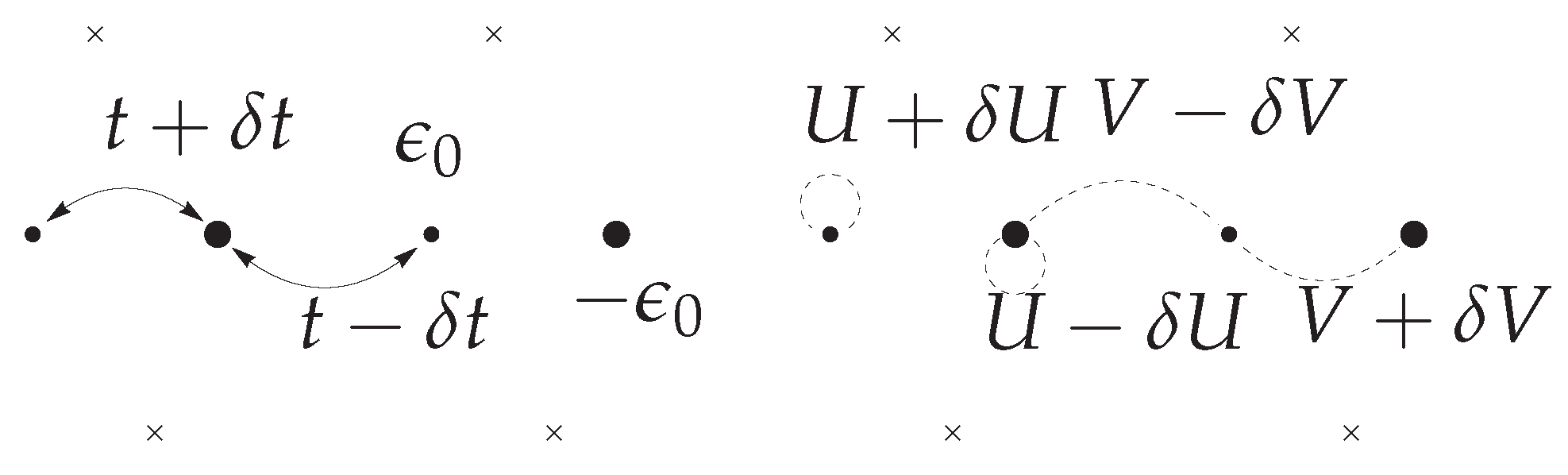

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ménard, M.; Bourbonnais, C. One-Dimensional Alternating Extended Hubbard Model at Quarter-Filling and Its Applications to Structural Instabilities of Organic Conductors. Crystals 2020, 10, 942. https://doi.org/10.3390/cryst10100942
Ménard M, Bourbonnais C. One-Dimensional Alternating Extended Hubbard Model at Quarter-Filling and Its Applications to Structural Instabilities of Organic Conductors. Crystals. 2020; 10(10):942. https://doi.org/10.3390/cryst10100942
Chicago/Turabian StyleMénard, M., and C. Bourbonnais. 2020. "One-Dimensional Alternating Extended Hubbard Model at Quarter-Filling and Its Applications to Structural Instabilities of Organic Conductors" Crystals 10, no. 10: 942. https://doi.org/10.3390/cryst10100942
APA StyleMénard, M., & Bourbonnais, C. (2020). One-Dimensional Alternating Extended Hubbard Model at Quarter-Filling and Its Applications to Structural Instabilities of Organic Conductors. Crystals, 10(10), 942. https://doi.org/10.3390/cryst10100942




