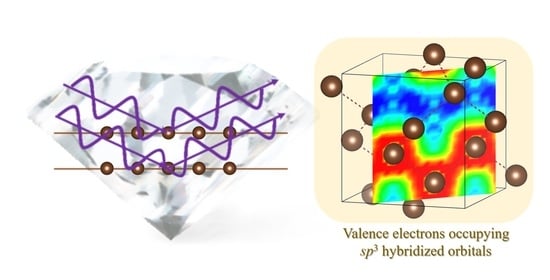
Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction
Abstract
1. Introduction
2. Methods
3. Results and Discussion
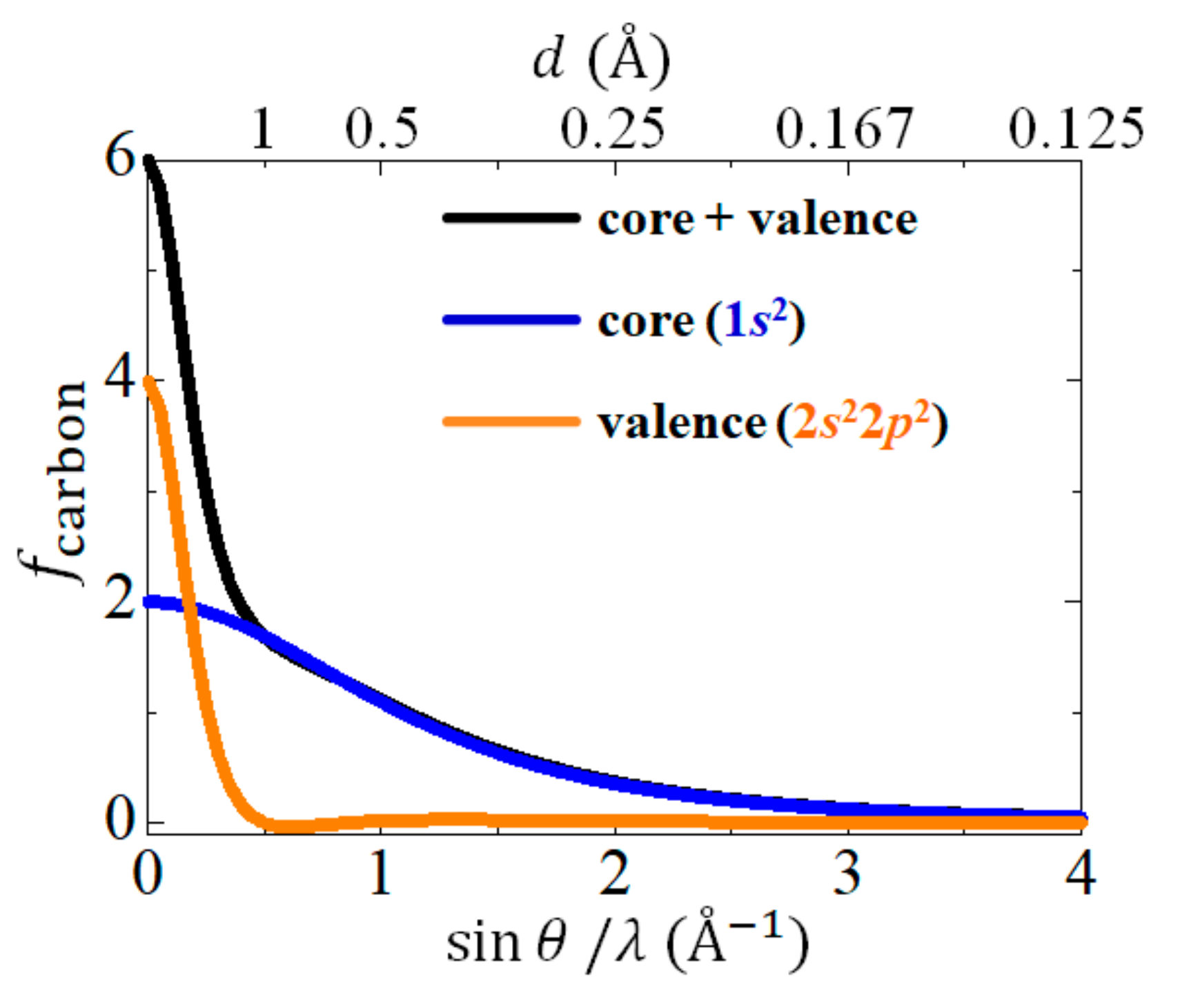
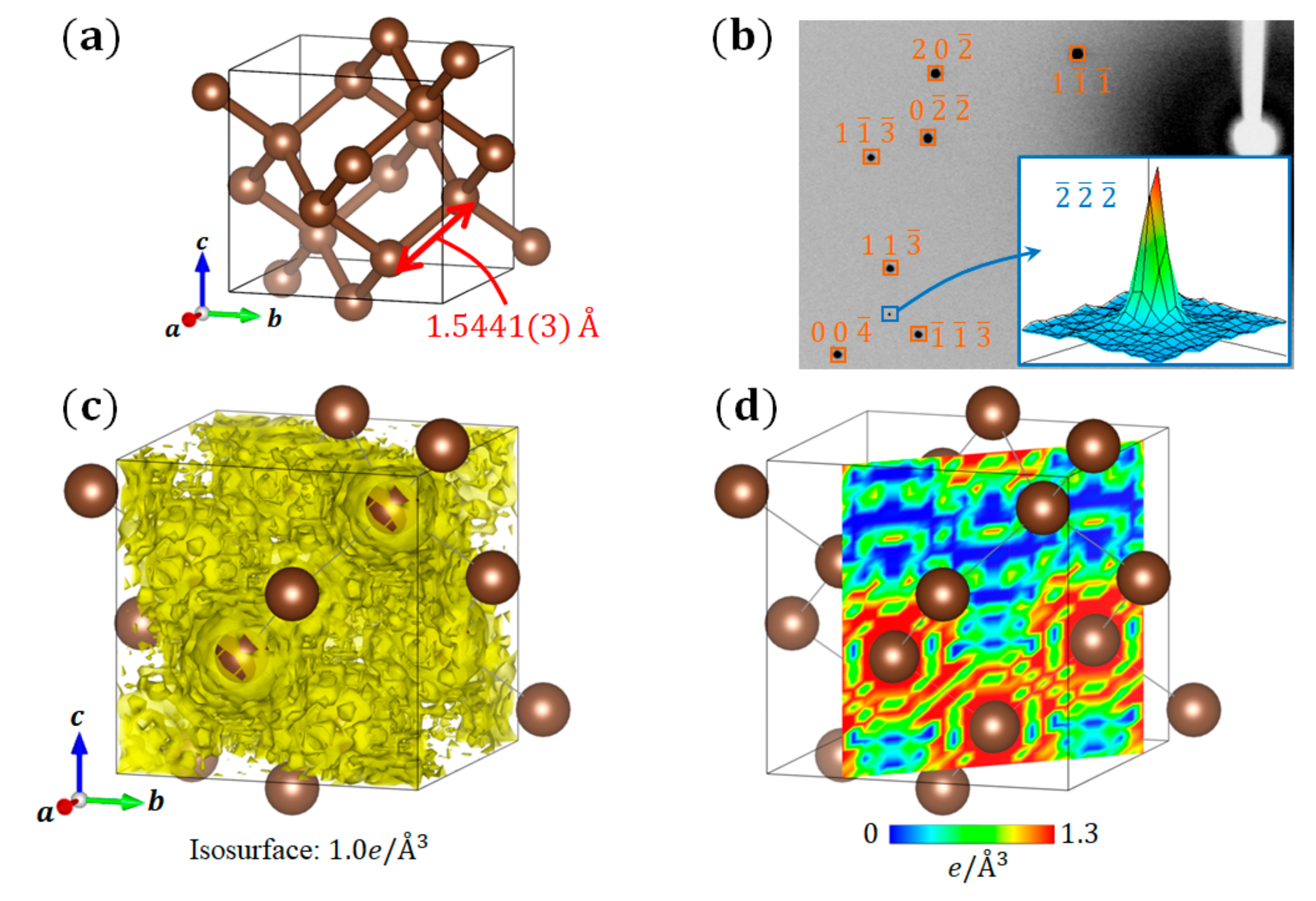
3.1. Diamond
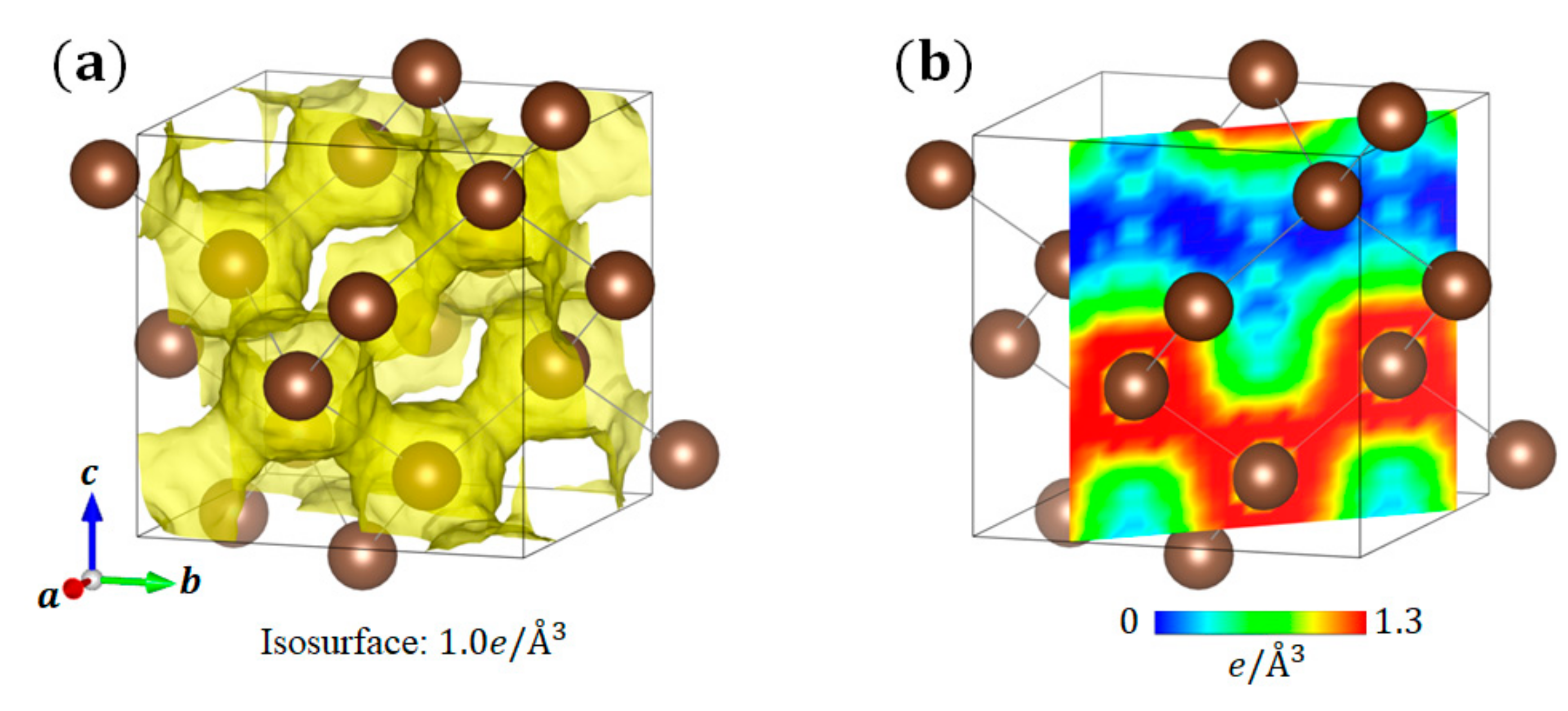
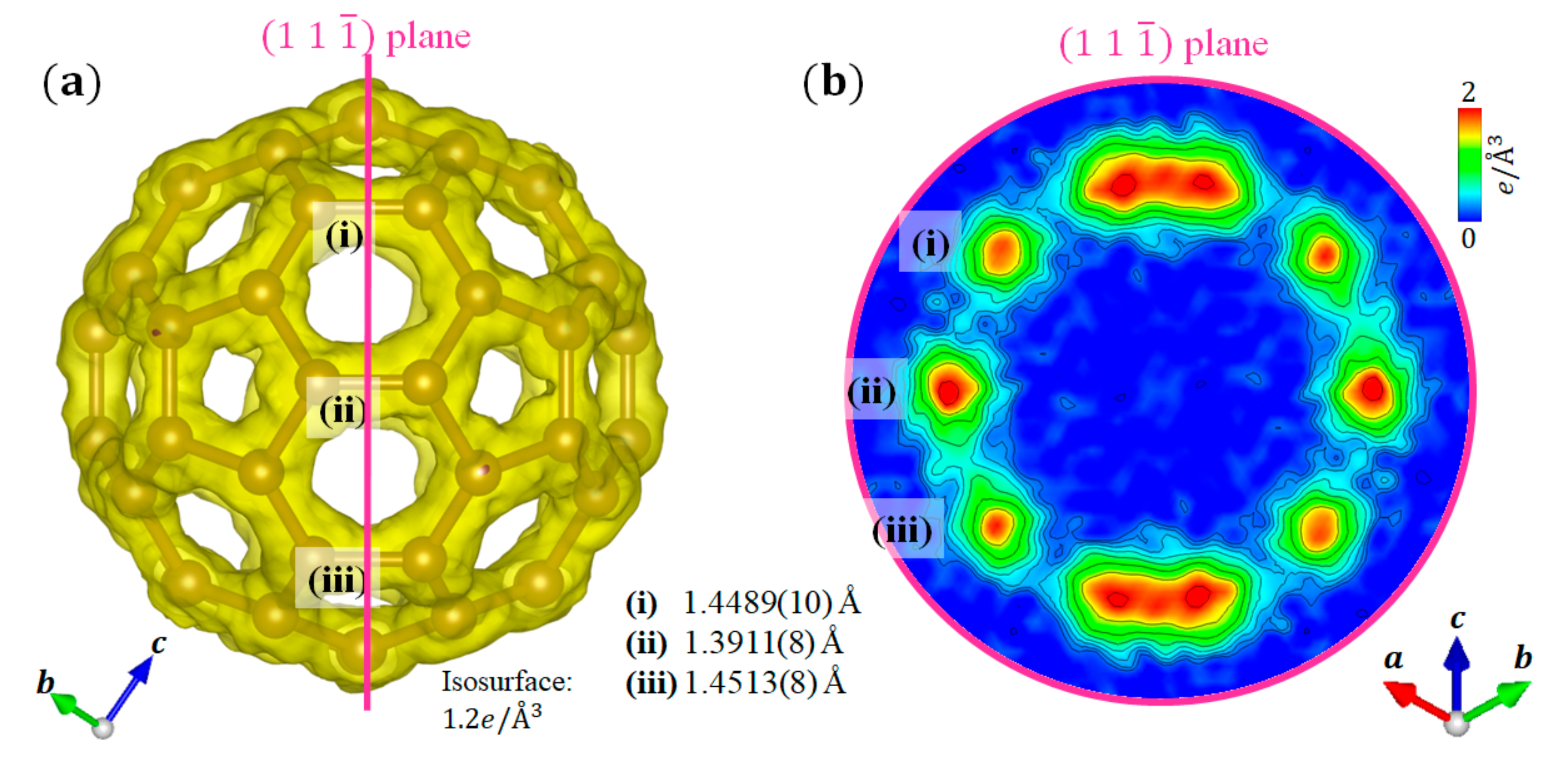
3.2. C60 Fullerene
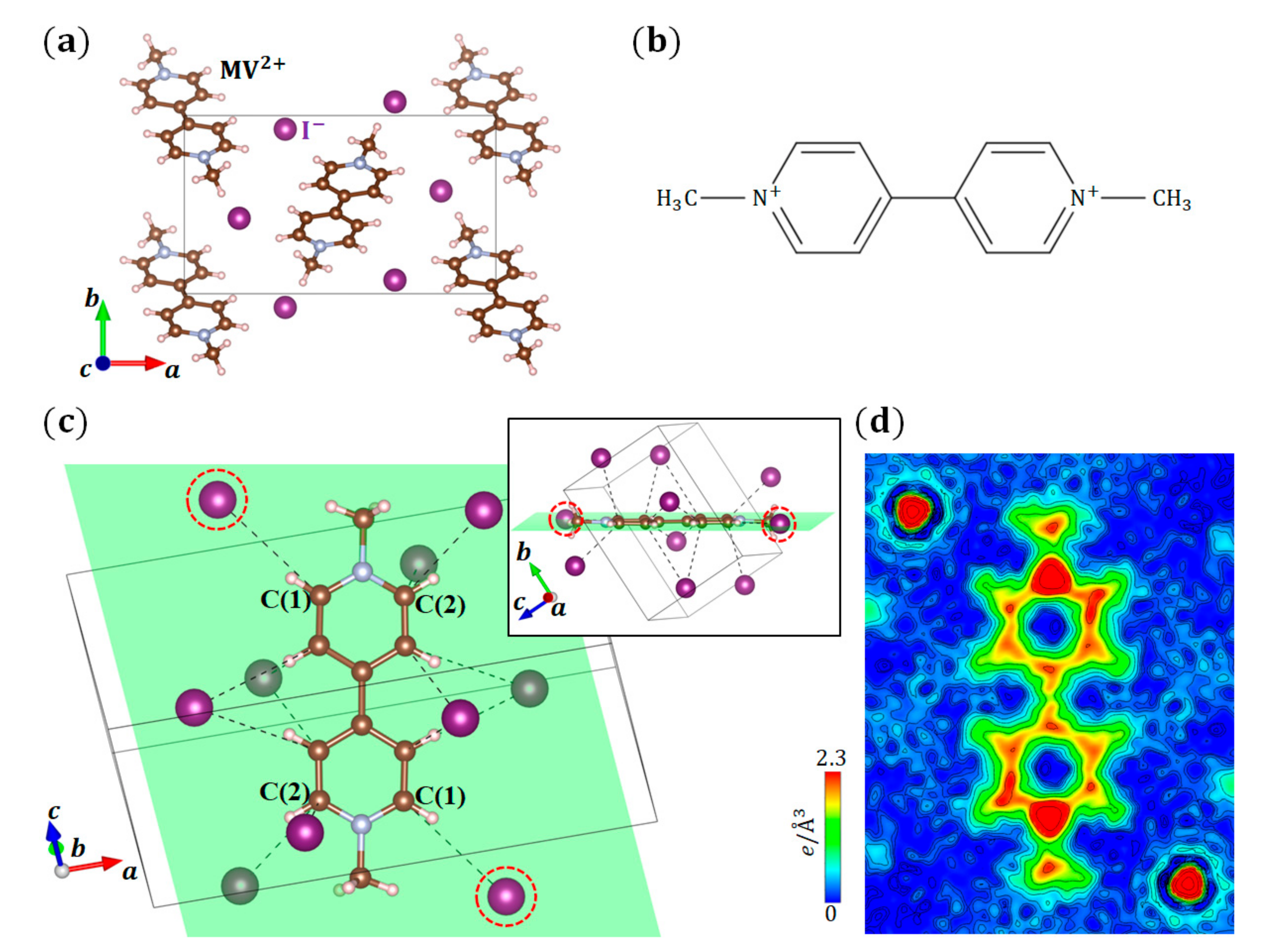
3.3. (MV)I2
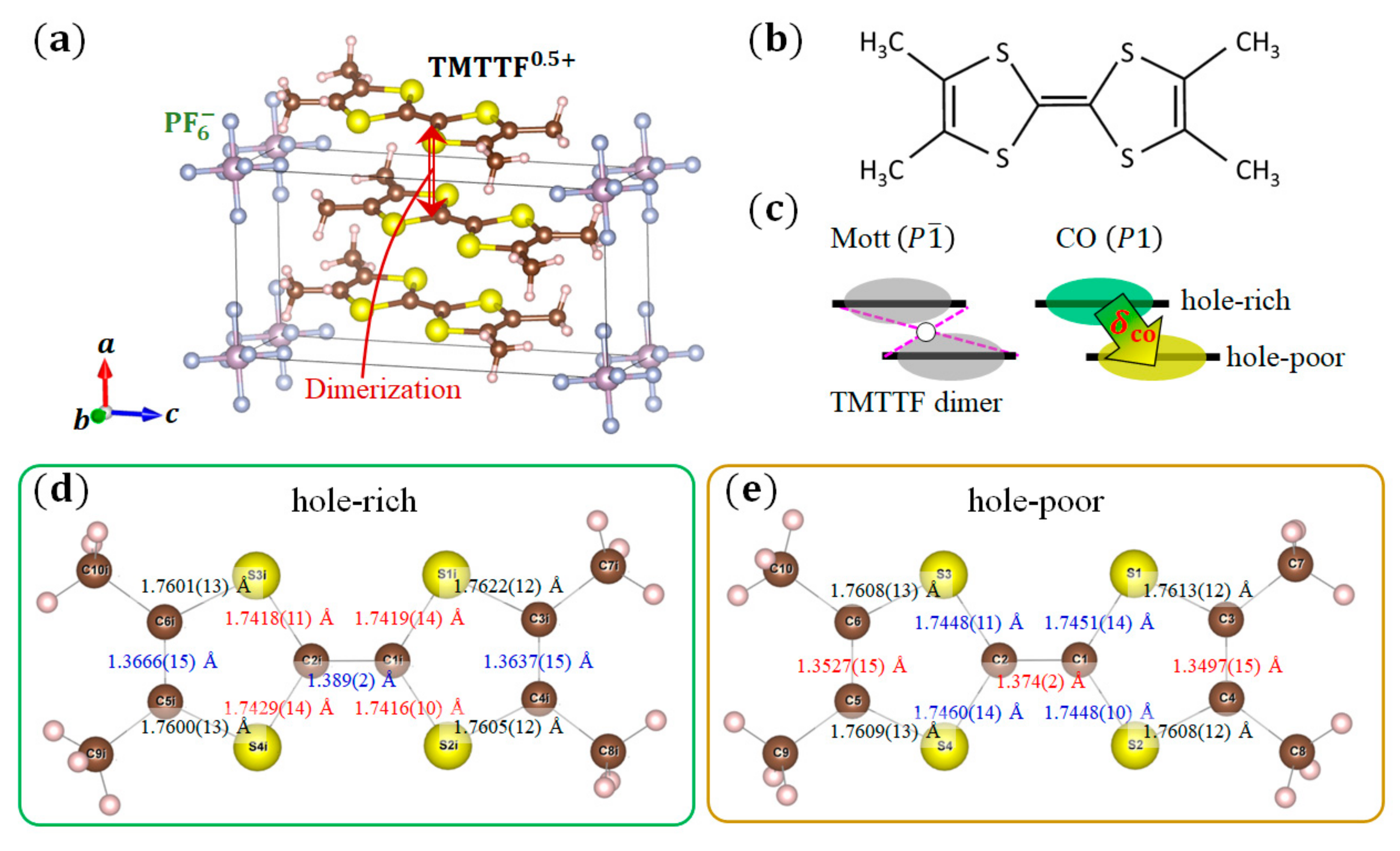
3.4. (TMTTF)2X
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| CCDC Deposit Number | 2036797 |
|---|---|
| Temperature (K) | 30 |
| Wavelength () | 0.35044 |
| Space group | |
| a () | 14.0279(6) |
| V () | 2760.4(2) |
| Z | 24 |
| F (000) | 1440 |
| (sinθ/λ)Max () | 1.11 |
| NTotal,obs | 65,092 |
| NUnique,obs | 4920 |
| Average redundancy | 11.4 |
| Completeness (%) | 100 |
| # of reflections () | 5424 |
| R () | 4.36 |
| wR () | 3.73 |
| GOF () | 1.21 |
References
- Albright, T.A.; Burdett, J.K.; Whangbo, M.H. Orbital Interactions in Chemistry; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Beveridge, D.L. Approximate Molecular Orbital Theory of Nuclear and Electron Magnetic Resonance Parameters. In Semiempirical Methods of Electronic Structure Calculation. Modern Theoretical Chemistry; Segal, G.A., Ed.; Springer: Boston, MA, USA, 1977; Volume 8, pp. 163–214. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Orbital Physics in Transition-Metal Oxides. Science 2000, 288, 462–468. [Google Scholar] [CrossRef] [PubMed]
- Itatani, J.; Levesque, J.; Zeidler, D.L.; Niikura, H.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Puschnig, P.; Berkebile, S.; Fleming, A.J.; Koller, G.; Emtsev, K.; Seyller, T.; Riley, J.D.; Ambrosch-Draxl, C.; Netzer, F.P.; Ramsey, M.G. Reconstruction of Molecular Orbital Densities from Photoemission Data. Science 2009, 326, 702–706. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y.; Akimitsu, J. Observation of Orbital Ordering in K2CuF4. J. Phys. Soc. Jpn. 1976, 40, 1333–1338. [Google Scholar] [CrossRef]
- Murakami, Y.; Hill, J.P.; Gibbs, D.; Blume, M.; Koyama, I.; Tanaka, M.; Kawata, H.; Arima, T.H.; Tokura, Y.; Hirota, K.; et al. Resonant X-ray Scattering from Orbital Ordering in LaMnO3. Phys. Rev. Lett. 1998, 81, 582–585. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. Sect. A Cryst. Phys. Diffraction Theor. Gen. Crystallogr. 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Kitou, S.; Fujii, T.; Kawamoto, T.; Katayama, N.; Maki, S.; Nishibori, E.; Sugimoto, K.; Takata, M.; Nakamura, T.; Sawa, H. Successive Dimensional Transition in (TMTTF)2PF6 Revealed by Synchrotron X-ray Diffraction. Phys. Rev. Lett. 2017, 119, 065701. [Google Scholar] [CrossRef] [PubMed]
- Kitou, S.; Manjo, T.; Katayama, N.; Shishidou, T.; Arima, T.H.; Taguchi, Y.; Tokura, Y.; Nakamura, T.; Yokoyama, T.; Sugimoto, K.; et al. Collapse of the simple localized 3d1 orbital picture in Mott insulator. Phys. Rev. Res. 2020, 2, 033503. [Google Scholar] [CrossRef]
- Sugimoto, K.; Ohsumi, H.; Aoyagi, S.; Nishibori, E.; Moriyoshi, C.; Kuroiwa, Y.; Sawa, H.; Takata, M. Extremely High Resolution Single Crystal Diffractometry for Orbital Resolution using High Energy Synchrotron Radiation at SPring-8. AIP Conf. Proc. 2010, 1234, 887. [Google Scholar] [CrossRef]
- Blessing, R.H. Data Reduction and Error Analysis for Accurate Signal Crystal Diffraction Intensities. Crystallogr. Rev. 1987, 1, 3–58. [Google Scholar] [CrossRef]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Krist. Cryst. Mater. 2014, 229, 345. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Su, Z.; Coppens, P. Relativistic X-ray Elastic Scattering Factors for Neutral Atoms Z= 1–54 from Multiconfiguration Dirac–Fock Wavefunctions in the 0–12Å−1 sinθ/λ Range, and Six-Gaussian Analytical Expressions in the 0–6Å−1 Range. Acta Crystallogr. Sect. A Found. Crystallogr. 1997, 53, 749–762. [Google Scholar] [CrossRef]
- Pavone, P.; Karch, K.; Schütt, O.; Strauch, D.; Windl, W.; Giannozzi, P.; Baroni, S. Ab initiolattice dynamics of diamond. Phys. Rev. B 1993, 48, 3156–3163. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Krätschmer, W.; Lamb, L.D.; Fostiropoulos, K.; Huffman, D.R. Solid C60: A new form of carbon. Nature 1990, 347, 354–358. [Google Scholar] [CrossRef]
- David, W.I.F.; Ibberson, R.M.; Matthewman, J.C.; Prassides, K.; Dennis, T.J.S.; Hare, J.P.; Kroto, H.W.; Taylor, R.; Walton, D.R.M. Crystal structure and bonding of ordered C60. Nature 1991, 353, 147–149. [Google Scholar] [CrossRef]
- Fischer, J.E.; Heiney, P.A.; McGhie, A.R.; Romanow, W.J.; Denenstein, A.M.; McCauley, J.P.; Smith, A.B. Compressibility of Solid C60. Science 1991, 252, 1288–1290. [Google Scholar] [CrossRef] [PubMed]
- Heiney, P.A.; Fischer, J.E.; McGhie, A.R.; Romanow, W.J.; Denenstein, A.M.; McCauley, J.P., Jr.; Smith, A.B.; Cox, D.E. Orientational ordering transition in solid C60. Phys. Rev. Lett. 1991, 66, 2911–2914. [Google Scholar] [CrossRef]
- Liu, S.; Lu, Y.J.; Kappes, M.M.; Ibers, J.A. The Structure of the C60 Molecule: X-ray Crystal Structure Determination of a Twin at 110 K. Science 1991, 254, 408–410. [Google Scholar] [CrossRef]
- David, W.I.F.; Ibberson, R.M.; Dennis, T.J.S.; Hare, J.P.; Prassides, K. Structural Phase Transitions in the Fullerene C60. Europhysics Lett. 1992, 18, 219–225. [Google Scholar] [CrossRef]
- Bürgi, H.B.; Blanc, E.; Schwarzenbach, D.; Liu, S.; Lu, Y.J.; Kappes, M.M.; Ibers, J.A. The Structure of C60: Orientational Disorder in the Low-Temperature Modification of C60. Angew. Chem. Int. Ed. 1992, 31, 640–643. [Google Scholar] [CrossRef]
- Saito, S.; Oshiyama, A. Cohesive mechanism and energy bands of solid C60. Phys. Rev. Lett. 1991, 66, 2637–2640. [Google Scholar] [CrossRef] [PubMed]
- Russell, J.H.; Wallwork, S.C. The crystal structures of the dichloride and isomorphous dibromide and diiodide of the N,N’-dimethyl-4,4′-bipyridylium ion. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 1527–1533. [Google Scholar] [CrossRef]
- Galigné, J.L.; Liautard, B.; Peytavin, S.; Brun, G.; Fabre, J.M.; Torreilles, E.; Giral, L. Etude structurale du bromure de tétraméthyltétrathiafulvalène, (TMTTF)2Br. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1978, 34, 620–624. [Google Scholar] [CrossRef]
- Jérome, D.; Schulz, H.J. Organic conductors and superconductors. Adv. Phys. 1982, 31, 299–490. [Google Scholar] [CrossRef]
- Jérome, D. The Physics of Organic Superconductors. Science 1991, 252, 1509–1514. [Google Scholar] [CrossRef] [PubMed]
- Pouget, J.P.; Ravy, S. Structural Aspects of the Bechgaard Salts and Related Compounds. J. Phys. I 1996, 6, 1501–1525. [Google Scholar] [CrossRef]
- Dressel, M.; Dumm, M.; Knoblauch, T.; Masino, M. Comprehensive Optical Investigations of Charge Order in Organic Chain Compounds (TMTTF)2X. Crystals 2012, 2, 528–578. [Google Scholar] [CrossRef]
- Nad, F.; Monceau, P.; Carcel, C.; Fabre, J.M. Dielectric response of the charge-induced correlated state in the quasi-one-dimensional conductor (TMTTF)2PF6. Phys. Rev. B 2000, 62, 1753–1756. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.Y.; Brazovskii, S. Ferroelectric Mott-Hubbard Phase of Organic (TMTTF)2X Conductors. Phys. Rev. Lett. 2001, 86, 4080. [Google Scholar] [CrossRef] [PubMed]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge Ordering in the TMTTF Family of Molecular Conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef]
- Nakamura, M.; Furukawa, K.; Hara, T. Redistribution of Charge in the Proximity of the Spin-Peierls Transition: 13C NMR Investigation of (TMTTF)2PF6. J. Phys. Soc. Jpn. 2007, 76, 64715. [Google Scholar] [CrossRef]
- Nakamura, M. Possible Charge Ordering Patterns of the Paramagnetic Insulating States in (TMTTF)2X. J. Phys. Soc. Jpn. 2003, 72, 213–216. [Google Scholar] [CrossRef]
- Jacobsen, C.S.; Tanner, D.B.; Bechgaard, K. Optical and infrared properties of tetramethyltetraselenafulvalene [(TMTSF)2X] and tetramethyltetrathiafulvalene [(TMTTF)2X] compounds. Phys. Rev. B 1983, 28, 7019–7032. [Google Scholar] [CrossRef]
- Świetlik, R.; Barszcz, B.; Pustogow, A.; Dressel, M. Raman spectroscopy evidence of domain walls in the organic electronic ferroelectrics (TMTTF)2X (X=SbF6, AsF6, PF6). Phys. Rev. B 2017, 95, 085205. [Google Scholar] [CrossRef]
- Pouget, J.P.; Moret, R.; Comes, R.; Bechgaard, K.; Fabre, J.M.; Giral, L. X-ray Diffuse Scattering Study of Some (TMTSF)2X and (TMTTF)2X Salts. Mol. Cryst. Liq. Cryst. 1982, 79, 485–499. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Le Bolloc’h, D.; Hennion, B.; Ravy, S.; Moradpour, A.; Pouget, J.P. Neutron-scattering evidence for a spin-Peierls ground state in (TMTTF)2PF6. Phys. Rev. B 2004, 70, 180–405. [Google Scholar] [CrossRef]
- Coulon, C.; Parkin, S.S.P.; Laversanne, R. Structureless transition and strong localization effects in bis-tetramethyltetrathiafulvalenium salts [(TMTTF)2X]. Phys. Rev. B 1985, 31, 3583–3587. [Google Scholar] [CrossRef]
- De Souza, M.; Foury-Leylekian, P.; Moradpour, A.; Pouget, J.P.; Lang, M. Evidence for Lattice Effects at the Charge-Ordering Transition in (TMTTF)2X. Phys. Rev. Lett. 2008, 101, 216–403. [Google Scholar] [CrossRef]
- Foury-Leylekian, P.; Petit, S.; Andre, G.; Moradpour, A.; Pouget, J.P. Neutron scattering evidence for a lattice displacement at the charge ordering transition of (TMTTF)2PF6. Phys. B Condens. Matter 2010, 405B, S95–S97. [Google Scholar] [CrossRef]
- Umland, T.C.; Allie, S.; Kuhlmann, T.; Coppens, P. Relation between geometry and charge transfer in low-dimensional organic salts. J. Phys. Chem. 1988, 92, 6456–6460. [Google Scholar] [CrossRef]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The Intermolecular Interaction of Tetrathiafulvalene and Bis(ethylenedithio)tetrathiafulvalene in Organic Metals. Calculation of Orbital Overlaps and Models of Energy-band Structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar] [CrossRef]
- A Computer Program Package for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental and Theoretical Structure Factors. Available online: https://www.chem.gla.ac.uk/~louis/xd-home/ (accessed on 3 November 2020).
- Nad, F.; Monceau, P.; Carcel, C.; Fabre, J.M. Charge ordering phase transition in the quasi-one-dimensional conductor (TMTTF)2AsF6. J. Phys. Condens. Matter 2000, 12, L435–L440. [Google Scholar] [CrossRef]
- Zámborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103. [Google Scholar] [CrossRef]
- Fujiyama, S.; Nakamura, M. Redistribution of Electronic Charges in Spin-Peierls State in (TMTTF)2AsF6 Observed by 13C NMR. J. Phys. Soc. Jpn. 2006, 75, 14705. [Google Scholar] [CrossRef]
- Pouget, J.P. Structural Aspects of the Bechgaard and Fabre Salts: An Update. Crystals 2012, 2, 466–520. [Google Scholar] [CrossRef]
- Seo, H.; Fukuyama, H. Antiferromagnetic Phases of One-Dimensional Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 1997, 66, 1249–1252. [Google Scholar] [CrossRef]
- Mazumdar, S.; Clay, R.T.; Campbell, D.K. Bond-order and charge-density waves in the isotropic interacting two-dimensional quarter-filled band and the insulating state proximate to organic superconductivity. Phys. Rev. B 2000, 62, 13400–13425. [Google Scholar] [CrossRef]
- Shibata, Y.; Nishimoto, S.; Ohta, Y. Charge ordering in the one-dimensional extended Hubbard model: Implication to the TMTTF family of organic conductors. Phys. Rev. B 2001, 64, 235107. [Google Scholar] [CrossRef]
- The Cambridge Crystallographic Data Centre. Available online: https://www.ccdc.cam.ac.uk/structures/ (accessed on 3 November 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kitou, S.; Hosogi, Y.; Kitaura, R.; Naito, T.; Nakamura, T.; Sawa, H. Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction. Crystals 2020, 10, 998. https://doi.org/10.3390/cryst10110998
Kitou S, Hosogi Y, Kitaura R, Naito T, Nakamura T, Sawa H. Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction. Crystals. 2020; 10(11):998. https://doi.org/10.3390/cryst10110998
Chicago/Turabian StyleKitou, Shunsuke, Yuto Hosogi, Ryo Kitaura, Toshio Naito, Toshikazu Nakamura, and Hiroshi Sawa. 2020. "Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction" Crystals 10, no. 11: 998. https://doi.org/10.3390/cryst10110998
APA StyleKitou, S., Hosogi, Y., Kitaura, R., Naito, T., Nakamura, T., & Sawa, H. (2020). Direct Observation of Molecular Orbitals Using Synchrotron X-ray Diffraction. Crystals, 10(11), 998. https://doi.org/10.3390/cryst10110998