Dislocation Analysis in SiGe Heterostructures by Large-Angle Convergent Beam Electron Diffraction
Abstract
1. Introduction
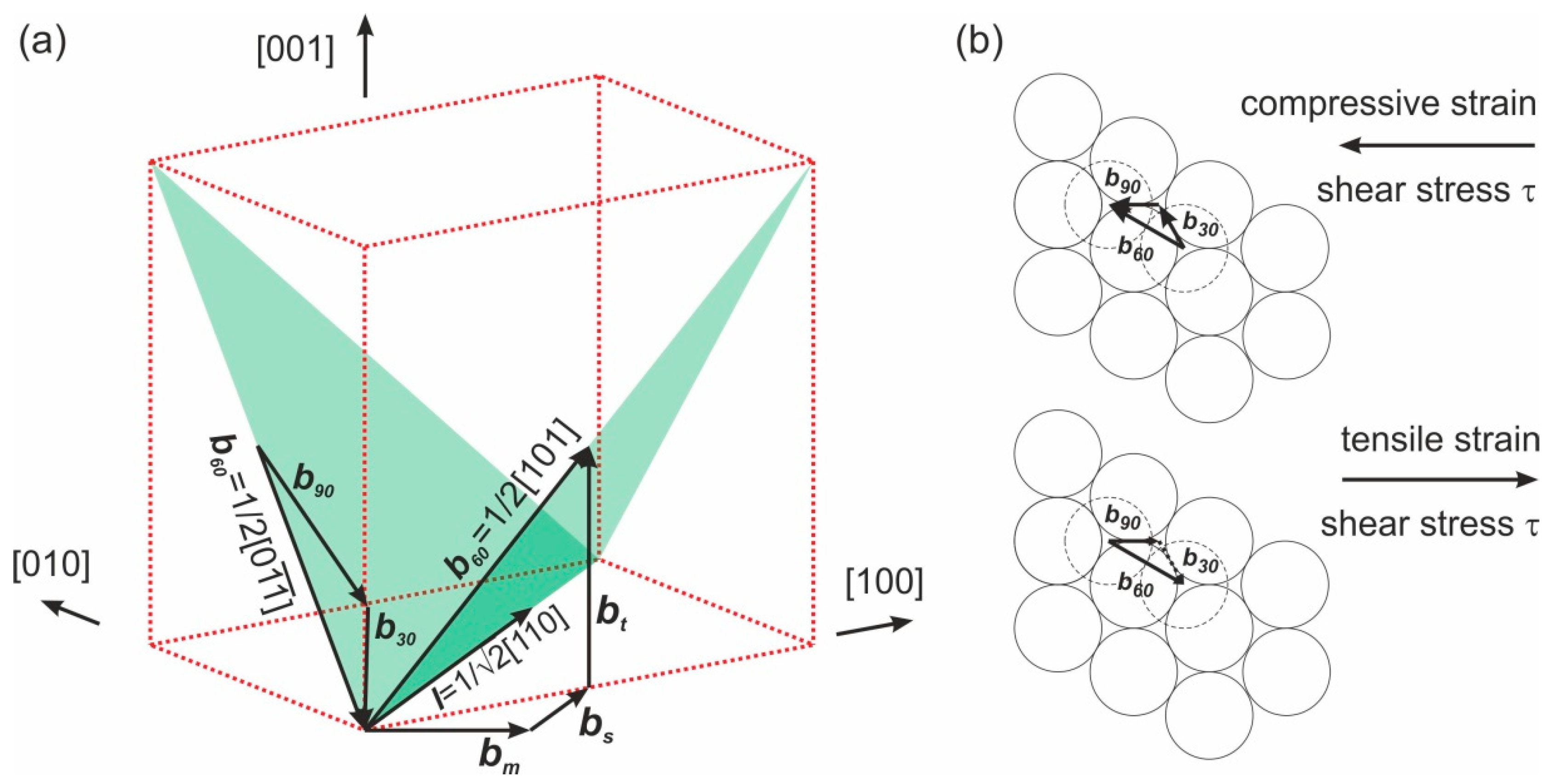
2. Dislocations in SiGe Heterostructures
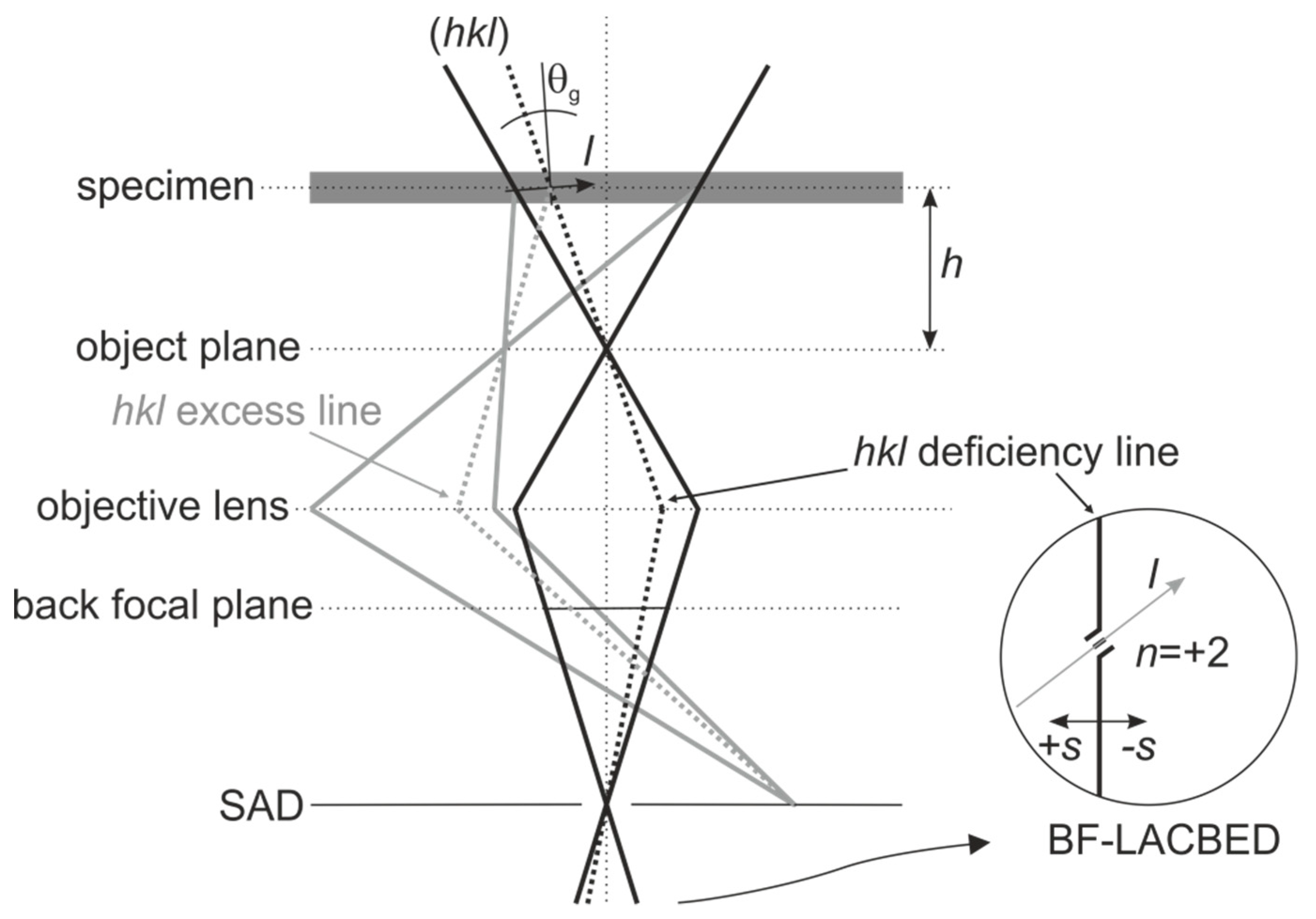
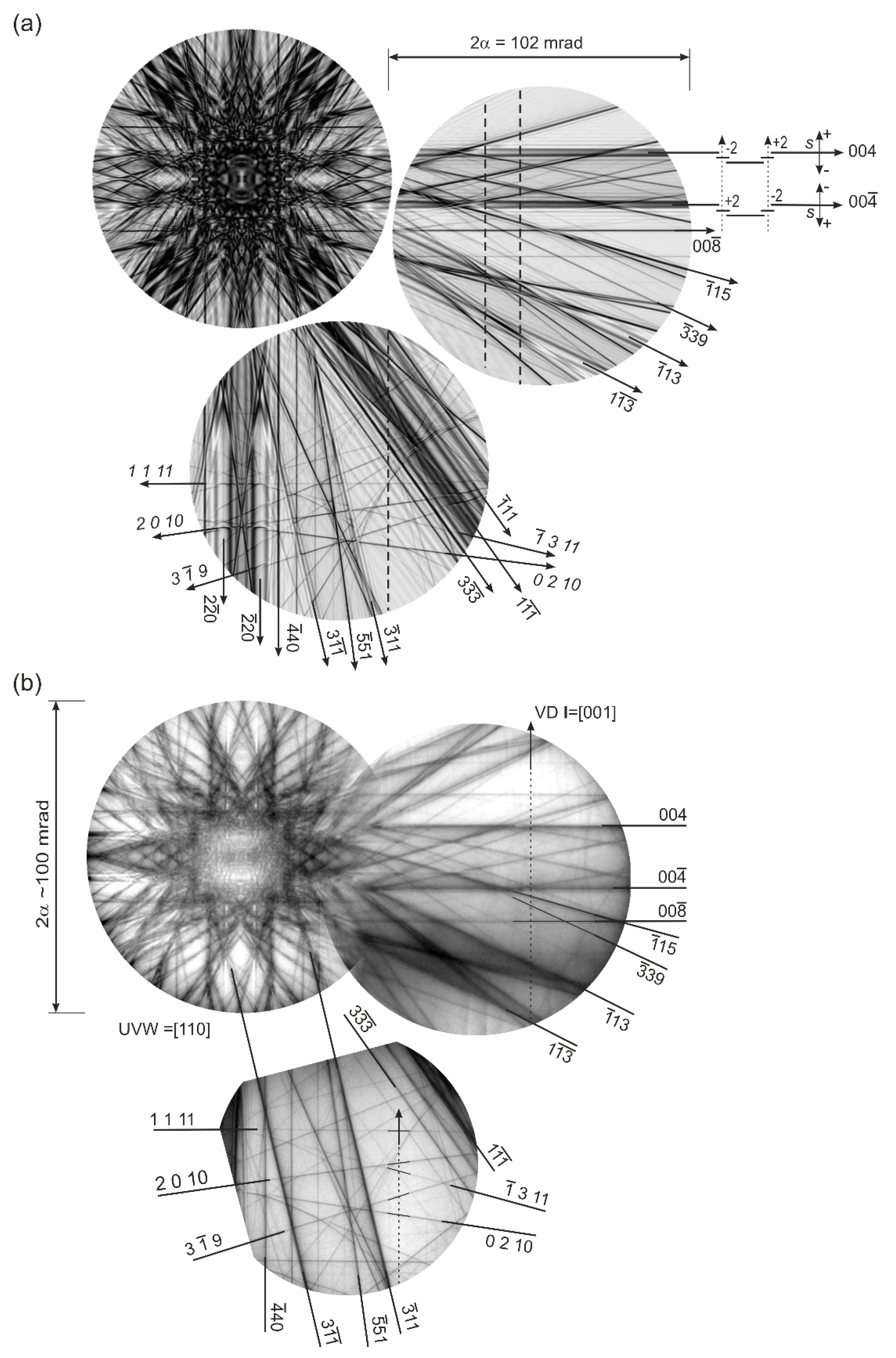
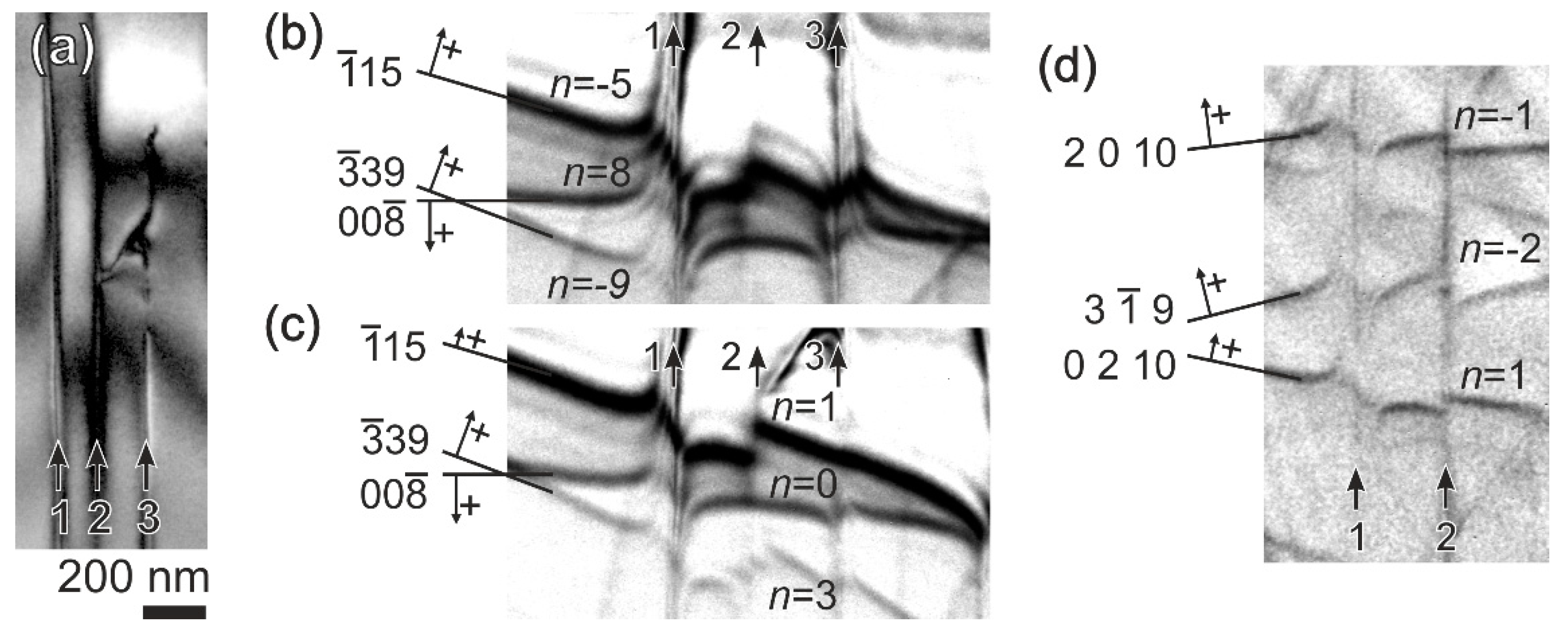
3. Large-Angle Convergent-Beam Electron Diffraction for Dislocation Analysis in SiGe
4. Conclusions and Perspectives
- (1)
- Method for non-expensive analytic standard TEMs.
- (2)
- Thicker specimens—advantages for specimen preparation.
- (3)
- Thicker specimens—less specimen artifacts.
- (4)
- Modern instruments can allow fast and automatic recording in scanning mode.
- (5)
- Software can allow automatic identification.
Funding
Acknowledgments
Conflicts of Interest
References
- Maszara, W.P.; Goetz, G.; Caviglia, A.; McKitterick, J.B. Bonding of silicon wafers for silicon-on-insulator. J. Appl. Phys. 1988, 64, 4943–4950. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Zhu, Z.H.; Crouse, D.; Lo, Y.H. Electrical properties of wafer-bonded GaAs/Si heterojunctions. Appl. Phys. Lett. 1998, 73, 2337–2339. [Google Scholar] [CrossRef]
- Liang, J.; Nishida, S.; Arai, M.; Shigekawa, N. Effects of thermal annealing process on the electrical properties of p+-Si/n-SiC heterojunctions. Appl. Phys. Lett. 2014, 104, 161604. [Google Scholar] [CrossRef]
- Rosenblad, C.; Deller, H.R.; Dommann, A.; Meyer, T.; Schroeter, P.; von Känel, H. Silicon epitaxy by low-energy plasma enhanced chemical vapor deposition. J. Vac. Sci. Technol. A Vac. Surf. Film 1998, 16, 2785–2790. [Google Scholar] [CrossRef]
- Kazior, T.E. Beyond Cmos: Heterogeneous integration of III-V devices, RF MEMS and other dissimilar materials/devices with Si CMOS to create intelligent microsystems. Philos. Trans. R. Soc. A 2014, 372, 20130105. [Google Scholar] [CrossRef]
- Kimoto, T.; Nishino, H.; Yoo, W.S.; Matsunami, H. Growth mechanism of 6H-SiC in step-controlled epitaxy. J. Appl. Phys. 1993, 73, 726–732. [Google Scholar] [CrossRef]
- Ieong, M.; Doris, B.; Kedzierski, J.; Rim, K.; Yang, M. Silicon device scaling to the sub-10-nm regime. Science 2004, 306, 2057–2060. [Google Scholar] [CrossRef]
- Wang, G.L.; Moeen, M.; Abedin, A.; Kolahdouz, M.; Luo, J.; Qin, C.L.; Zhu, H.L.; Yan, J.; Yin, H.Z.; Li, J.F.; et al. Optimization of SiGe selective epitaxy for source/drain engineering in 22 nm node complementary metal-oxide semiconductor (CMOS). J. Appl. Phys. 2013, 114, 123511. [Google Scholar] [CrossRef]
- Wirths, S.; Geiger, R.; von den Driesch, N.; Mussler, G.; Stoica, T.; Mantl, S.; Ikonic, Z.; Luysberg, M.; Chiussi, S.; Hartmann, J.M.; et al. Lasing in direct-bandgap GeSn alloy grown on Si. Nat. Photonics 2015, 9, 88–92. [Google Scholar] [CrossRef]
- Groiss, H.; Glaser, M.; Schatzl, M.; Brehm, M.; Gerthsen, D.; Roth, D.; Bauer, P.; Schäffler, F. Free-running Sn precipitates: An efficient phase separation mechanism for metastable Ge1−xSnx epilayers. Sci. Rep. 2017, 7, 16144. [Google Scholar] [CrossRef]
- Michel, J.; Liu, J.; Kimerling, L.C. High-performance Ge-on-Si photodetectors. Nat. Photonics 2010, 4, 527–534. [Google Scholar] [CrossRef]
- Camacho-Aguilera, R.E.; Cai, Y.; Patel, N.; Bessette, J.T.; Romagnoli, M.; Kimerling, L.C.; Michel, J. An electrically pumped germanium laser. Opt. Express 2012, 20, 11316. [Google Scholar] [CrossRef] [PubMed]
- Schatzl, M.; Hackl, F.; Glaser, M.; Rauter, P.; Brehm, M.; Spindlberger, L.; Simbula, A.; Galli, M.; Fromherz, T.; Schäffler, F. Enhanced Telecom Emission from Single Group-IV Quantum Dots by Precise CMOS-Compatible Positioning in Photonic Crystal Cavities. ACS Photonics 2017, 4, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Grydlik, M.; Brehm, M.; Hackl, F.; Groiss, H.; Fromherz, T.; Schäffler, F.; Bauer, G. Inverted Ge islands in {111} faceted Si pits—A novel approach towards SiGe islands with higher aspect ratio. New J. Phys. 2010, 12, 063002. [Google Scholar] [CrossRef]
- Zhang, J.J.; Montalenti, F.; Rastelli, A.; Hrauda, N.; Scopece, D.; Groiss, H.; Stangl, J.; Pezzoli, F.; Schäffler, F.; Schmidt, O.G.; et al. Collective shape oscillations of sige islands on pit-patterned Si(001) substrates: A coherent-growth strategy enabled by self-regulated intermixing. Phys. Rev. Lett. 2010, 105, 166102. [Google Scholar] [CrossRef]
- Thewalt, M.L.W.; Harrison, D.A.; Reinhart, C.F.; Wolk, J.A.; Lafontaine, H. Type II band alignment in Si1−xGex/Si(001) quantum wells: The ubiquitous type I luminescence results from band bending. Phys. Rev. Lett. 1997, 79, 269–272. [Google Scholar] [CrossRef]
- Grydlik, M.; Hackl, F.; Groiss, H.; Glaser, M.; Halilovic, A.; Fromherz, T.; Jantsch, W.; Schäffler, F.; Brehm, M. Lasing from glassy Ge quantum dots in crystalline Si. ACS Photonics 2016, 3, 298–303. [Google Scholar] [CrossRef]
- Groiss, H.; Spindlberger, L.; Oberhumer, P.; Schäffler, F.; Fromherz, T.; Grydlik, M.; Brehm, M. Photoluminescence enhancement through vertical stacking of defect-engineered Ge on Si quantum dots. Semicond. Sci. Technol. 2017, 32, 02LT01. [Google Scholar] [CrossRef]
- Schmidt, O.G.; Eberl, K. Self-assembled Ge/Si dots for faster field-effect transistors. IEEE Trans. Electron Devices 2001, 48, 1175–1179. [Google Scholar] [CrossRef]
- Thompson, S.E.; Armstrong, M.; Auth, C.; Cea, S.; Chau, R.; Glass, G.; Hoffman, T.; Klaus, J.; Ma, Z.; Mcintyre, B.; et al. A logic nanotechnology featuring strained-silicon. IEEE Electron Device Lett. 2004, 25, 191–193. [Google Scholar] [CrossRef]
- Jovanovic, V.; Biasotto, C.; Nanver, L.K.; Moers, J.; Grutzmacher, D.; Gerharz, J.; Mussler, G.; Van Der Cingel, J.; Zhang, J.J.; Bauer, G.; et al. N-channel MOSFETs fabricated on SiGe dots for strain-enhanced mobility. IEEE Electron Device Lett. 2010, 31, 1083–1085. [Google Scholar] [CrossRef]
- Pernot, G.; Stoffel, M.; Savic, I.; Pezzoli, F.; Chen, P.; Savelli, G.; Jacquot, A.; Schumann, J.; Denker, U.; Mönch, I.; et al. Precise control of thermal conductivity at the nanoscale through individual phonon-scattering barriers. Nat. Mater. 2010, 9, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.T.; Wang, S.Y.; Lee, S.W. Designer Ge/Si composite quantum dots with enhanced thermoelectric properties. Nanoscale 2014, 6, 3593–3598. [Google Scholar] [CrossRef] [PubMed]
- Thumfart, L.; Carrete, J.; Vermeersch, B.; Ye, N.; Truglas, T.; Feser, J.; Groiss, H.; Mingo, N.; Rastelli, A. Thermal transport through Ge-rich Ge/Si superlattices grown on Ge(0 0 1). J. Phys. D Appl. Phys. 2018, 51, 014001. [Google Scholar] [CrossRef]
- Hӱtch, M.J.; Putaux, J.L.; Thibault, J. Stress and strain around grain-boundary dislocations measured by high-resolution electron microscopy. Philos. Mag. 2006, 86, 4641–4656. [Google Scholar] [CrossRef]
- Bolkhovityanov, Y.B.; Deryabin, A.S.; Gutakovskii, A.K.; Sokolov, L.V. Mechanism of induced nucleation of misfit dislocations in the Ge-on-Si(001) system and its role in the formation of the core structure of edge misfit dislocations. Acta Mater. 2013, 61, 617–621. [Google Scholar] [CrossRef]
- Bolkhovityanov, Y.B.; Gutakovskii, A.K.; Deryabin, A.S.; Sokolov, L.V. Specific features of plastic relaxation of a metastable GexSi1−x layer buried between a silicon substrate and a relaxed germanium layer. Phys. Solid State 2014, 56, 247–253. [Google Scholar] [CrossRef]
- Bolkhovityanov, Y.B.; Gutakovskii, A.K.; Deryabin, A.S.; Sokolov, L.V. Experimental observation of motion of edge dislocations in Ge/GexSi1−x/Si(001) (x = 0.2–0.6) heterostructures. J. Exp. Theor. Phys. 2016, 123, 832–837. [Google Scholar] [CrossRef]
- Bolkhovityanov, Y.B.; Deryabin, A.S.; Gutakovskii, A.K.; Sokolov, L.V. Unzipping and movement of Lomer-type edge dislocations in Ge/GeSi/Si(001) heterostructures. J. Cryst. Growth 2018, 483, 265–268. [Google Scholar] [CrossRef]
- Dou, W.; Benamara, M.; Mosleh, A.; Margetis, J.; Grant, P.; Zhou, Y.; Al-Kabi, S.; Du, W.; Tolle, J.; Li, B.; et al. Investigation of GeSn Strain Relaxation and Spontaneous Composition Gradient for Low-Defect and High-Sn Alloy Growth. Sci. Rep. 2018, 8, 5640. [Google Scholar] [CrossRef]
- Arroyo Rojas Dasilva, Y.; Rossell, M.D.; Keller, D.; Gröning, P.; Isa, F.; Kreiliger, T.; Von Känel, H.; Isella, G.; Erni, R. Analysis of edge threading dislocations b = 1/2 <110> in three dimensional Ge crystals grown on (001)-Si substrates. Appl. Phys. Lett. 2015, 107, 093501. [Google Scholar] [CrossRef]
- Arroyo Rojas Dasilva, Y.; Rossell, M.D.; Isa, F.; Erni, R.; Isella, G.; von Känel, H.; Gröning, P. Strain relaxation in epitaxial Ge crystals grown on patterned Si(001) substrates. Scr. Mater. 2017, 127, 169–172. [Google Scholar] [CrossRef]
- Arroyo Rojas Dasilva, Y.; Isa, F.; Isella, G.; Erni, R.; von Känel, H.; Gröning, P.; Rossell, M.D. Effect of thermal annealing on the interface quality of Ge/Si heterostructures. Scr. Mater. 2019, 170, 52–56. [Google Scholar] [CrossRef]
- Tanaka, M.; Tsuda, K. Convergent-beam electron diffraction. Microscopy 2011, 60, 245–267. [Google Scholar] [CrossRef]
- Stranski, I.N.; Krastanow, L. Berichtigung zur Arbeit—“Zur Theorie der orientierten Ausscheidung von Ionenkristallen aufeinander”. Mon. Chem. 1939, 72, 76. [Google Scholar] [CrossRef]
- Brehm, M.; Groiss, H.; Bauer, G.; Gerthsen, D.; Clarke, R.; Paltiel, Y.; Yacoby, Y. Atomic structure and composition distribution in wetting layers and islands of germanium grown on silicon (001) substrates. Nanotechnology 2015, 26, 485702. [Google Scholar] [CrossRef][Green Version]
- Rosenauer, A.; Remmele, T.; Gerthsen, D.; Tillmann, K.; Förster, A. Atomic scale strain measurements by the digital analysis of transmission electron microscopic lattice images. Optik 1997, 105, 99–107. [Google Scholar]
- Hӱtch, M.J.; Snoeck, E.; Kilaas, R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy 1998, 74, 131–146. [Google Scholar] [CrossRef]
- Marée, P.M.J.; Barbour, J.C.; Van Der Veen, J.F.; Kavanagh, K.L.; Bulle-Lieuwma, C.W.T.; Viegers, M.P.A. Generation of misfit dislocations in semiconductors. J. Appl. Phys. 1987, 62, 4413–4420. [Google Scholar] [CrossRef]
- Wegscheider, W.; Eberl, K.; Abstreiter, G.; Cerva, H.; Oppolzer, H. Novel relaxation process in strained Si/Ge superlattices grown on Ge (001). Appl. Phys. Lett. 1990, 57, 1496–1498. [Google Scholar] [CrossRef]
- Kvam, E.P.; Hull, R. Surface orientation and stacking fault generation in strained epitaxial growth. J. Appl. Phys. 1993, 73, 7407–7411. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Y.W.; Fox, B.; Lu, C. Molecular dynamics study of dislocation formation in a [001] face-centered-cubic epitaxial island under tensile stress. Appl. Phys. Lett. 2004, 84, 714–716. [Google Scholar] [CrossRef]
- Bedell, S.W.; Reznicek, A.; Yang, B.; Hovel, H.J.; Ott, J.A.; Fogel, K.; Domenicucci, A.G.; Sadana, D.K. Development of stacking faults in strained silicon layers. In Proceedings of the IEEE International SOI Conference, Honolulu, HI, USA, 3–6 October 2005; pp. 144–145. [Google Scholar]
- Hartmann, J.M.; Abbadie, A.; Rouchon, D.; Barnes, J.P.; Mermoux, M.; Billon, T. Structural properties of tensile-strained Si layers grown on Si1−xGex virtual substrates (x = 0.2, 0.3, 0.4 and 0.5). Thin Solid Films 2008, 516, 4238–4246. [Google Scholar] [CrossRef]
- Pachinger, D.; Groiss, H.; Teuchtmann, M.; Hesser, G.; Schäffler, F. Surfactant-mediated Si quantum dot formation on Ge(001). Appl. Phys. Lett. 2011, 98, 223104. [Google Scholar] [CrossRef]
- Pachinger, D.; Groiss, H.; Lichtenberger, H.; Stangl, J.; Hesser, G.; Schäffler, F. Stranski-Krastanow growth of tensile strained Si islands on Ge (001). Appl. Phys. Lett. 2007, 91, 233106. [Google Scholar] [CrossRef]
- Lee, M.L.; Antoniadis, D.A.; Fitzgerald, E.A. Challenges in epitaxial growth of SiGe buffers on Si (111), (110), and (112). Thin Solid Films 2006, 508, 136–139. [Google Scholar] [CrossRef]
- Norris, D.J.; Myronov, M.; Leadley, D.R.; Walther, T. Comparison of cross-sectional transmission electron microscope studies of thin germanium epilayers grown on differently oriented silicon wafers. J. Microsc. 2017, 268, 288–297. [Google Scholar] [CrossRef]
- Hrauda, N.; Zhang, J.J.; Groiss, H.; Gerharz, J.C.; Etzelstorfer, T.; Stangl, J.; Holý, V.; Deiter, C.; Seeck, O.H.; Bauer, G. Closely spaced SiGe barns as stressor structures for strain-enhancement in silicon. Appl. Phys. Lett. 2013, 102, 032109. [Google Scholar] [CrossRef]
- Hrauda, N.; Zhang, J.J.; Groiss, H.; Etzelstorfer, T.; Holý, V.; Bauer, G.; Deiter, C.; Seeck, O.H.; Stangl, J. Strain relief and shape oscillations in site-controlled coherent SiGe islands. Nanotechnology 2013, 24, 335707. [Google Scholar] [CrossRef]
- Gatti, R.; Boioli, F.; Grydlik, M.; Brehm, M.; Groiss, H.; Glaser, M.; Montalenti, F.; Fromherz, T.; Schäffler, F.; Miglio, L. Dislocation engineering in SiGe heteroepitaxial films on patterned Si (001) substrates. Appl. Phys. Lett. 2011, 98, 121908. [Google Scholar] [CrossRef]
- Grydlik, M.; Boioli, F.; Groiss, H.; Gatti, R.; Brehm, M.; Montalenti, F.; Devincre, B.; Schäffler, F.; Miglio, L. Misfit dislocation gettering by substrate pit-patterning in SiGe films on Si(001). Appl. Phys. Lett. 2012, 101, 013119. [Google Scholar] [CrossRef]
- Bollani, M.; Chrastina, D.; Ruggeri, R.; Nicotra, G.; Gagliano, L.; Bonera, E.; Mondiali, V.; Marzegalli, A.; Montalenti, F.; Spinella, C.; et al. Anisotropic extended misfit dislocations in overcritical SiGe films by local substrate patterning. Nanotechnology 2016, 27, 425301. [Google Scholar] [CrossRef] [PubMed]
- Montalenti, F.; Rovaris, F.; Bergamaschini, R.; Miglio, L.; Salvalaglio, M.; Isella, G.; Isa, F.; von Känel, H. Dislocation-free SiGe/Si heterostructures. Crystals 2018, 8, 257. [Google Scholar] [CrossRef]
- Groiss, H.; Glaser, M.; Marzegalli, A.; Isa, F.; Isella, G.; Miglio, L.; Schäffler, F. Burgers Vector Analysis of Vertical Dislocations in Ge Crystals by Large-Angle Convergent Beam Electron Diffraction. Microsc. Microanal. 2015, 21, 637–645. [Google Scholar] [CrossRef] [PubMed]
- Marzegalli, A.; Isa, F.; Groiss, H.; Müller, E.; Falub, C.V.; Taboada, A.G.; Niedermann, P.; Isella, G.; Schäffler, F.; Montalenti, F.; et al. Unexpected dominance of vertical dislocations in high-misfit Ge/Si(001) films and their elimination by deep substrate patterning. Adv. Mater. 2013, 25, 4408–4412. [Google Scholar] [CrossRef]
- Williams, D.W.; Carter, C.B. Transmission Electron Microscopy, 2nd ed.; Springer Science+Business Media: New York, NY, USA, 2009; pp. 441–461. [Google Scholar]
- Ishida, Y.; Ishida, H.; Kohra, K.; Ichinose, H.; Ichinose, H. Determination of the Burgers vector of a dislocation by weak-beam imaging in a HVEM. Philos. Mag. A 1980, 42, 453–462. [Google Scholar] [CrossRef]
- Spiecker, E. Novel TEM methods for large-area analysis of misfit dislocation networks in semiconductor heterostructures. Philos. Mag. 2006, 86, 4941–4963. [Google Scholar] [CrossRef]
- Stenkamp, D.; Jäger, W. Dislocations and their dissociation in SixGe1−x alloys. Philos. Mag. A 1992, 65, 1369–1382. [Google Scholar] [CrossRef]
- Bonnet, R.; Loubradou, M.; Youssef, S.; Rouvière, J.L.; Fournel, F. Alternate dissociation of the screw dislocations in a (001) buried small-angle twist boundary in silicon. Philos. Mag. 2009, 89, 413–434. [Google Scholar] [CrossRef]
- Vijayalakshmi, M.; Saroja, S.; Mythili, R. Convergent beam electron diffraction—A novel technique for materials characterisation at sub-microscopic levels. Sadhana 2003, 28, 763–782. [Google Scholar] [CrossRef]
- Tsuda, K.; Tanaka, M. Refinement of crystal structural parameters using two-dimensional energy-filtered CBED patterns. Acta Cryst. 1999, 55, 939–954. [Google Scholar] [CrossRef] [PubMed]
- Ogata, Y.; Tsuda, K.; Tanaka, M. Determination of the electrostatic potential and electron density of silicon using convergent-beam electron diffraction. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Saito, R.; Ueno, K.; Harada, Y. Large-Angle Convergent-Beam Electron Diffraction. J. Electron Microsc. 1980, 29, 408–412. [Google Scholar]
- Tanaka, M.; Terauchi, M.; Kaneyama, T. Convergent-Beam Electron Diffraction II; JEOL Ltd.: Akishima, Tokyo, Japan, 1988. [Google Scholar]
- Morniroli, J.P. CBED and LACBED characterization of crystal defects. J. Microsc. 2006, 223, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.F.; Cherns, D.; Steeds, J.W. Effects of elastic relaxation on large-angle convergent-beam electron diffraction from cross-sectional specimens of GexSi1−x/Si strained-layer superlattices. Philos. Mag. A 1994, 70, 1091–1105. [Google Scholar] [CrossRef]
- Cherns, D.; Touaitia, R.; Preston, A.R.; Rossouw, C.J.; Houghton, D.C. Convergent beam electron diffraction studies of strain in Si/SiGe superlattices. Philos. Mag. A 1991, 64, 597–612. [Google Scholar] [CrossRef]
- Rossouw, C.J.; Spellward, P.; Perovic, D.D.; Cherns, D. Dynamical zone-axis electron diffraction contrast of boron-doped Si multilayers. Philos. Mag. A 1994, 69, 255–265. [Google Scholar] [CrossRef]
- Cherns, D.; Hovsepian, A.; Jäger, W. Profiling Ge islands in Si by large angle convergent beam electron diffraction. J. Electron Microsc. 1998, 47, 211–215. [Google Scholar] [CrossRef]
- Kürnsteiner, P.; Commenda, C.; Arenholz, E.; Samek, L.; Stifter, D.; Groiss, H. Investigation of nanoscale twinning in an advanced high manganese twinning-induced plasticity steel. Materialia 2018, 1, 70–77. [Google Scholar] [CrossRef]
- Carpenter, R.W.; Spence, J.C.H. Three-dimensional strain-field information in convergent-beam electron diffraction patterns. Acta Crystallogr. A 1982, 38, 55–61. [Google Scholar] [CrossRef]
- Cherns, D.; Preston, A.R. Convergent beam diffraction studies of crystal effects. In Proceedings of the 11th International Congress on Electron Microscopy, Kyoto, Japan, 31 August–7 September 1986; Imura, T., Marusa, S., Suzuki, T., Eds.; The Japanese Society of Electron Microscopy: Tokyo, Japan, 1986; Volume 1, p. 721. [Google Scholar]
- Cherns, D.; Preston, A.R. Convergent beam diffraction studies of interfaces, defects, and multilayers. J. Electron Microsc. Tech. 1989, 13, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.T.; Preston, A.R.; Steeds, J.W. Dislocation contrast in large angle convergent-beam electron diffraction patterns. Philos. Mag. A 1992, 65, 863–888. [Google Scholar] [CrossRef]
- Cherns, D.; Morniroli, J.P. Analysis of partial and stair-rod dislocations by large angle convergent beam electron diffraction. Ultramicroscopy 1994, 53, 167–180. [Google Scholar] [CrossRef]
- Morniroli, J.P.; Marceau, R.K.W.; Ringer, S.P.; Boulanger, L. LACBED characterization of dislocation loops. Philos. Mag. 2006, 86, 4883–4900. [Google Scholar] [CrossRef]
- Wang, R. Defocus convergent beam electron diffraction determination of Burgers vectors of dislocations in quasicrystals. Micron 2000, 31, 475–486. [Google Scholar] [CrossRef]
- Morniroli, J.P.; Marceau, R.K.W.; Ringer, S.P. New developments in the characterization of dislocation loops from LACBED patterns. J. Microsc. 2006, 223, 246–248. [Google Scholar] [CrossRef]
- Jäger, C.; Spiecker, E.; Morniroli, J.P.; Jäger, W. Analysis of dislocation loops by means of large-angle convergent beam electron diffraction. J. Phys. Condens. Matter 2002, 14, 12777–12782. [Google Scholar] [CrossRef]
- Morniroli, J.P.; Cherns, D. Analysis of grain boundary dislocations by large angle convergent beam electron diffraction. Ultramicroscopy 1996, 62, 53–63. [Google Scholar] [CrossRef]
- Rousseau, K.; Eymery, J.; Fournel, F.; Morniroli, J.P.; Rouviere, J.L. (001) Silicon surfacial grain boundaries obtained by direct wafer bonding process: Accurate control of the structure before bonding. Philos. Mag. 2005, 85, 2415–2448. [Google Scholar] [CrossRef]
- Texier, M.; Regula, G.; Lancin, M.; Pichaud, B. LACBED study of extended defects in 4H-SiC. Philos. Mag. Lett. 2006, 86, 529–537. [Google Scholar] [CrossRef]
- Onda, S.; Watanabe, H.; Kito, Y.; Kondo, H.; Uehigashi, H.; Hosokawa, N.; Hisada, Y.; Shiraishi, K.; Saka, H. Transmission electron microscope study of a threading dislocation with and its effect on leakage in a 4H-SiC MOSFET. Philos. Mag. Lett. 2013, 93, 439–447. [Google Scholar] [CrossRef]
- Onda, S.; Watanabe, H.; Okamoto, T.I.; Kondo, H.; Uehigashi, H.; Saka, H. Threading dislocation with b=c+2a in 4H-SiC as determined by LACBED. Philos. Mag. Lett. 2015, 95, 489–495. [Google Scholar] [CrossRef]
- Hadorn, J.P.; Tanuma, R.; Kamata, I.; Tsuchida, H. Direct evaluation of threading dislocations in 4H-SiC through large-angle convergent beam electron diffraction. Philos. Mag. 2019. [Google Scholar] [CrossRef]
- Spiecker, E.; Jäger, W. Burgers vector analysis of large area misfit dislocation arrays from bend contour contrast in transmission electron microscope images. J. Phys. Condens. Matter 2002, 14, 12767–12776. [Google Scholar] [CrossRef]
- Spiecker, E.; Schöne, J.; Rajagopalan, S.; Jäger, W. Novel TEM method for large-area analysis of misfit dislocation networks in semiconductor heterostructures. In Microscopy of Semiconducting Materials; Springer: Berlin/Heidelberg, Germany, 2006; Volume 86, pp. 117–130. [Google Scholar]



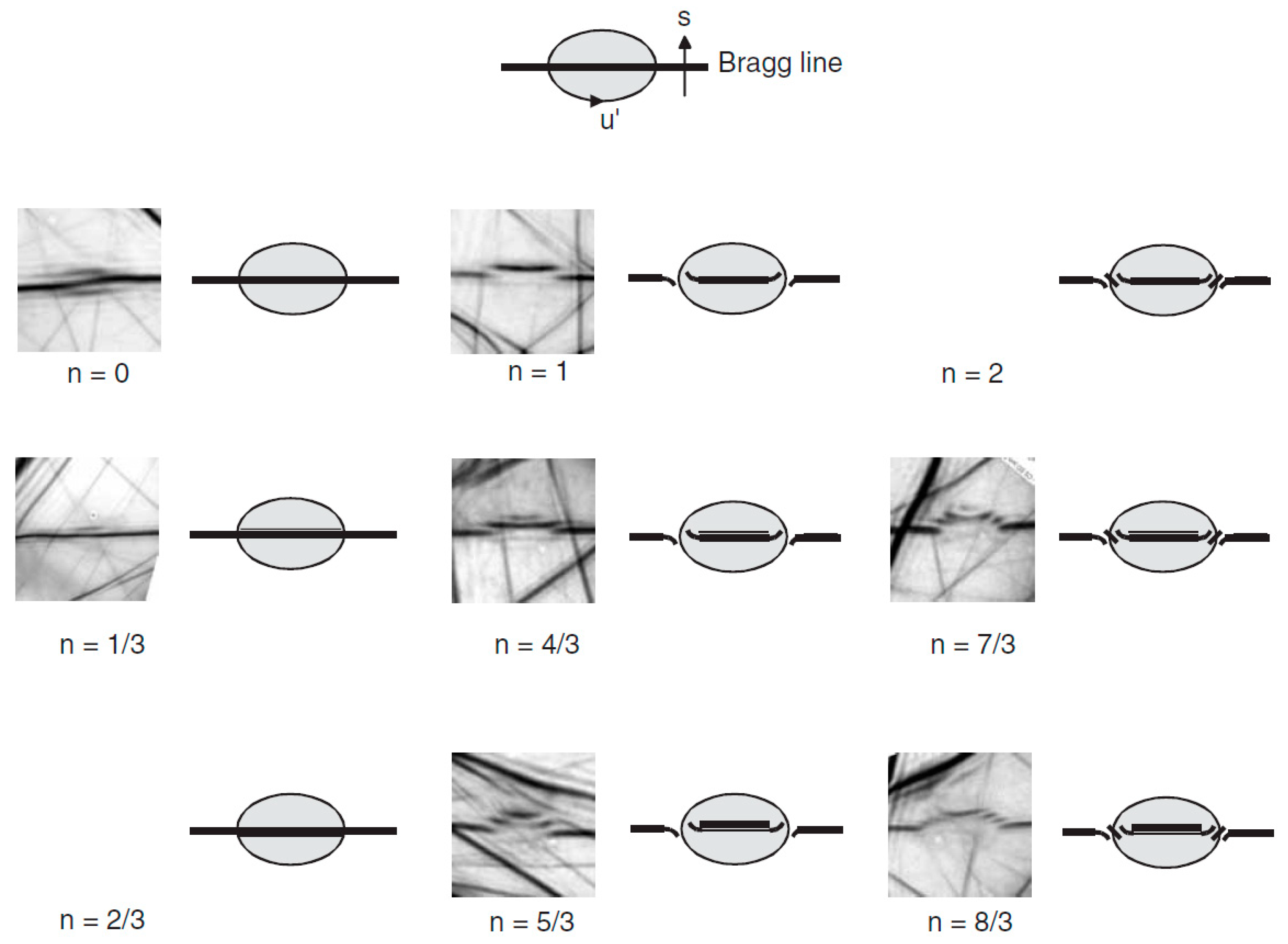
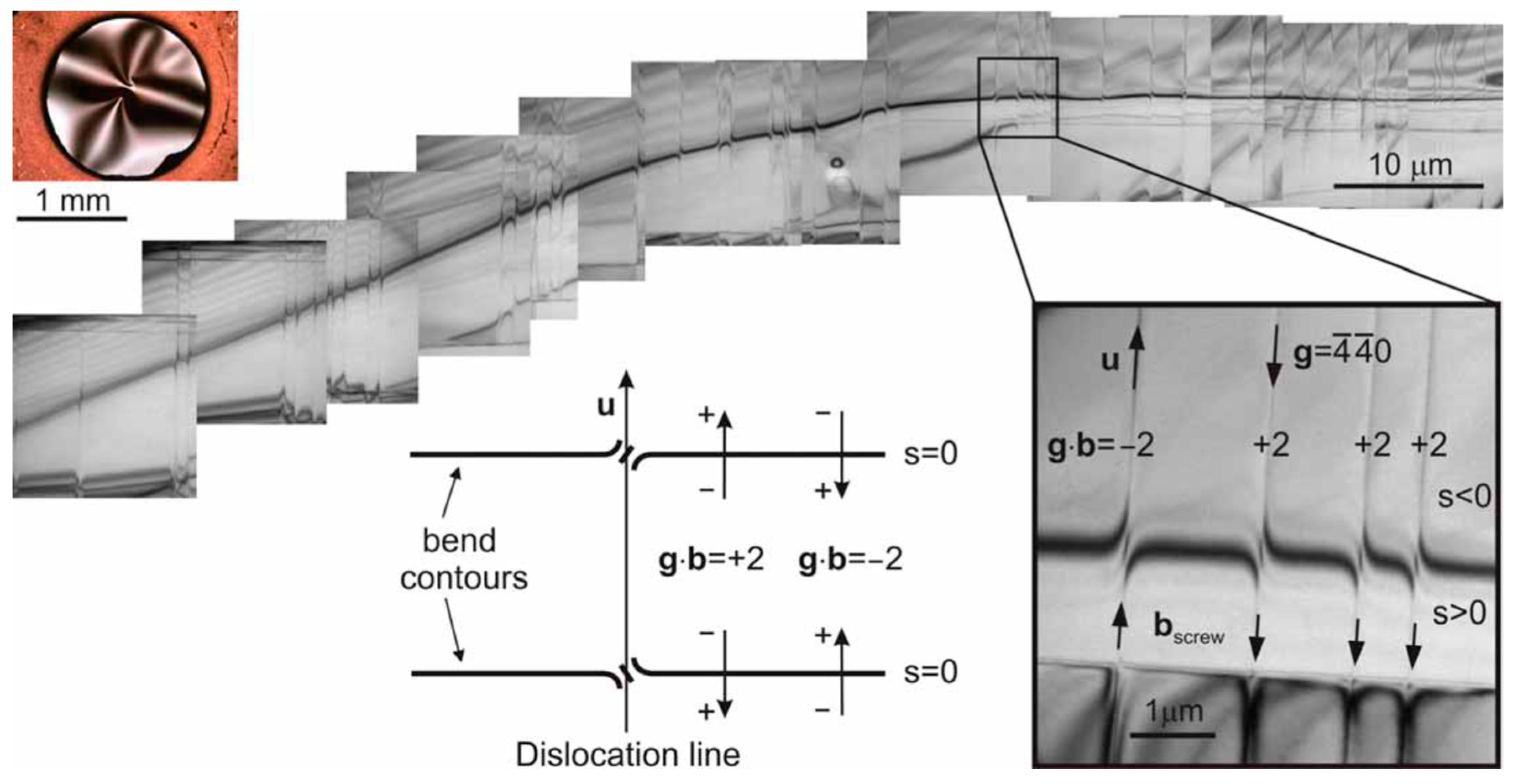
| DP[ 1 1 0 ] | ZOLZ hkl-lines | SOLZ hkl-lines / | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| g→ | 004 | 1 1 1 1 | 2 0 10/0 2 10 | / | / | 0 2 10/2 0 10 | |||||
| b↓ | |||||||||||
| 1/2[ 1 1 0 ] | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1/2[ 1 0 ] | 2 | 1 | 0 | 0 | 1 | 3 | 0 | −1/1 | 2/−2 | −2/2 | 1/−1 |
| 1/2[ 1 0 1 ] | −1 | 0 | 2 | −4 | 2 | 3 | 6 | 6/5 | 5/7 | 6/4 | 5/6 |
| 1/2[ 0 1 ] | 1 | 1 | 2 | −4 | 3 | 6 | 5 | 4/5 | 6/4 | 3/5 | 5/4 |
| 1/2[ 0 1 1 ] | 1 | 1 | 2 | −4 | 3 | 6 | 6 | 5/6 | 7/5 | 4/6 | 6/5 |
| 1/2[ 0 1 ] | −1 | 0 | 2 | −4 | 2 | 3 | 5 | 5/4 | 4/6 | 5/3 | 4/5 |
| [ 1 0 0 ] | −2 | −1 | 0 | 0 | −1 | −3 | 1 | 2/0 | −1/3 | 3/−1 | 0/2 |
| [ 0 1 0 ] | 2 | 1 | 0 | 0 | 1 | 3 | 1 | 0/2 | 3/−1 | −1/3 | 2/0 |
| [ 0 0 1 ] | 0 | 1 | 4 | −8 | 5 | 9 | 11 | 10 | 11 | 9 | 10 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groiss, H. Dislocation Analysis in SiGe Heterostructures by Large-Angle Convergent Beam Electron Diffraction. Crystals 2020, 10, 5. https://doi.org/10.3390/cryst10010005
Groiss H. Dislocation Analysis in SiGe Heterostructures by Large-Angle Convergent Beam Electron Diffraction. Crystals. 2020; 10(1):5. https://doi.org/10.3390/cryst10010005
Chicago/Turabian StyleGroiss, Heiko. 2020. "Dislocation Analysis in SiGe Heterostructures by Large-Angle Convergent Beam Electron Diffraction" Crystals 10, no. 1: 5. https://doi.org/10.3390/cryst10010005
APA StyleGroiss, H. (2020). Dislocation Analysis in SiGe Heterostructures by Large-Angle Convergent Beam Electron Diffraction. Crystals, 10(1), 5. https://doi.org/10.3390/cryst10010005





