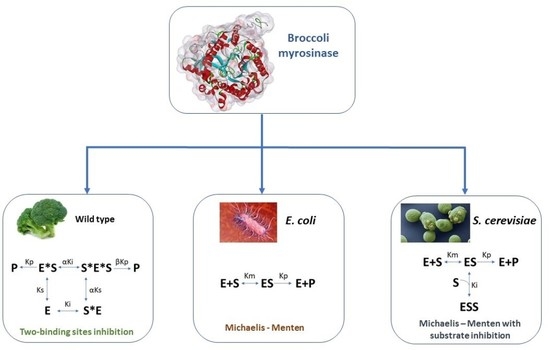
Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH
Abstract
:1. Introduction
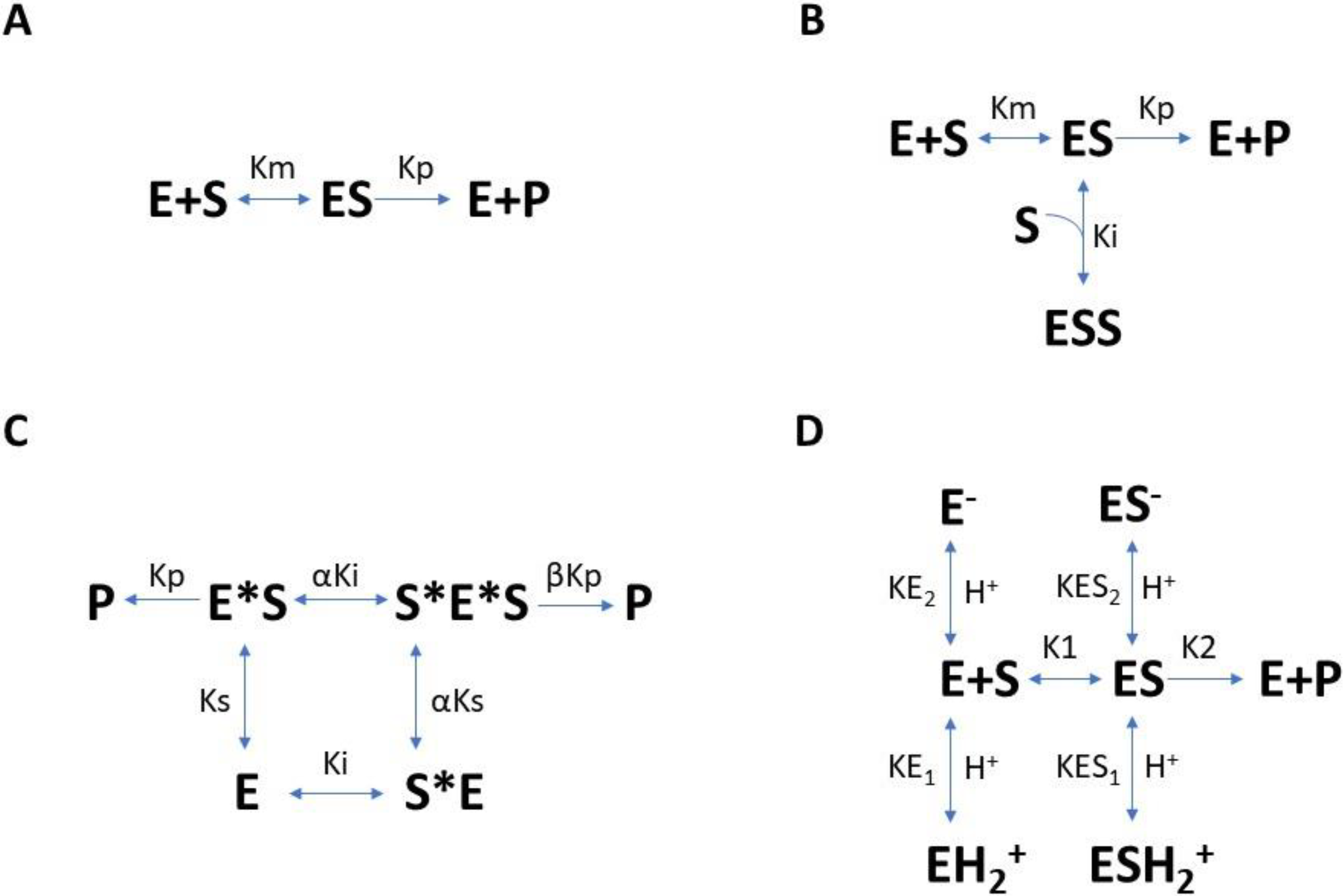
2. Enzyme Kinetics Models
2.1. Substrate-Dependent Models
2.2. Temperature-Dependent Models
2.3. pH-Dependent Models
3. Results and Discussion
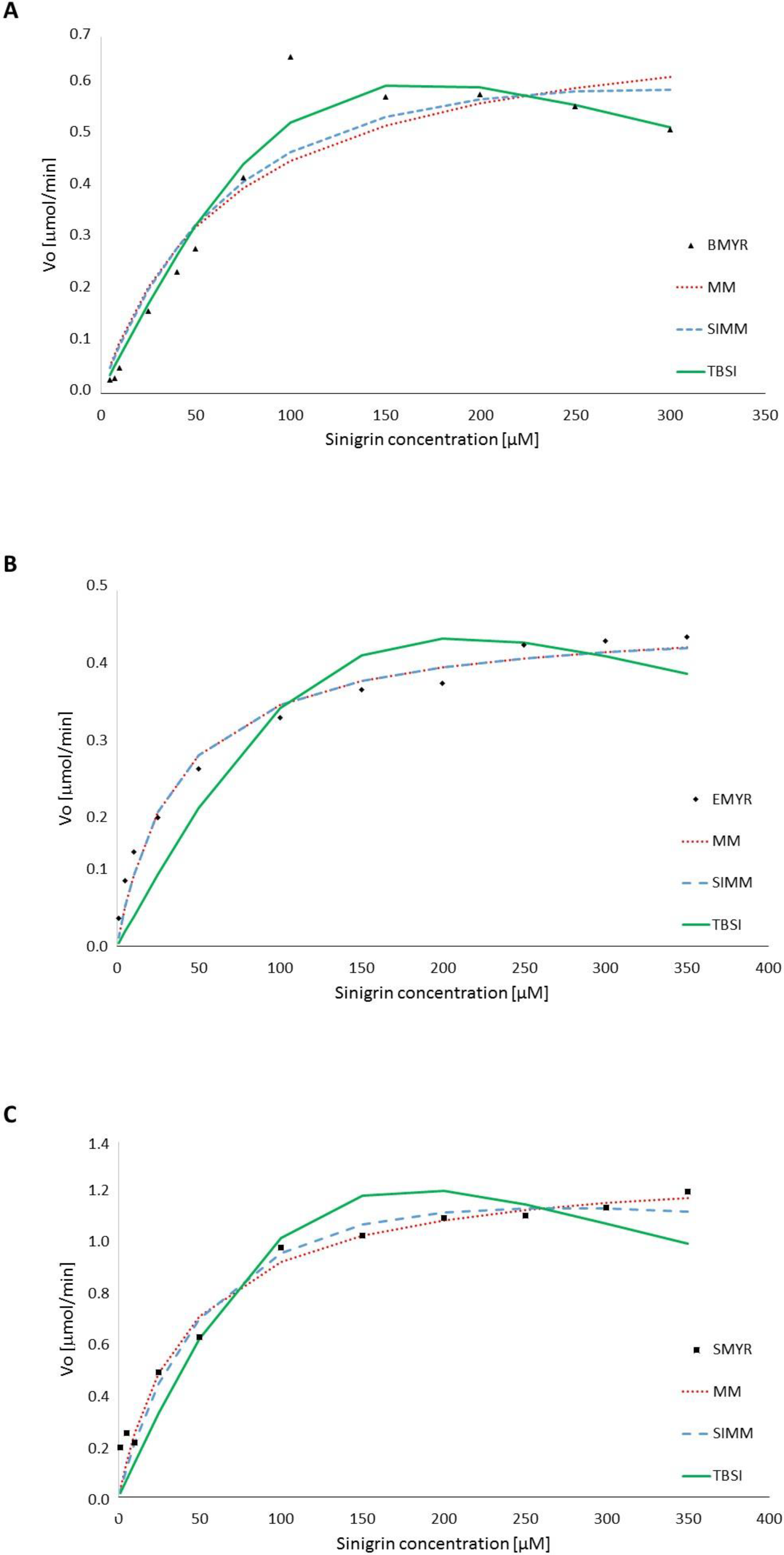
3.1. Enzyme Kinetics in Terms of Substrate Concentration
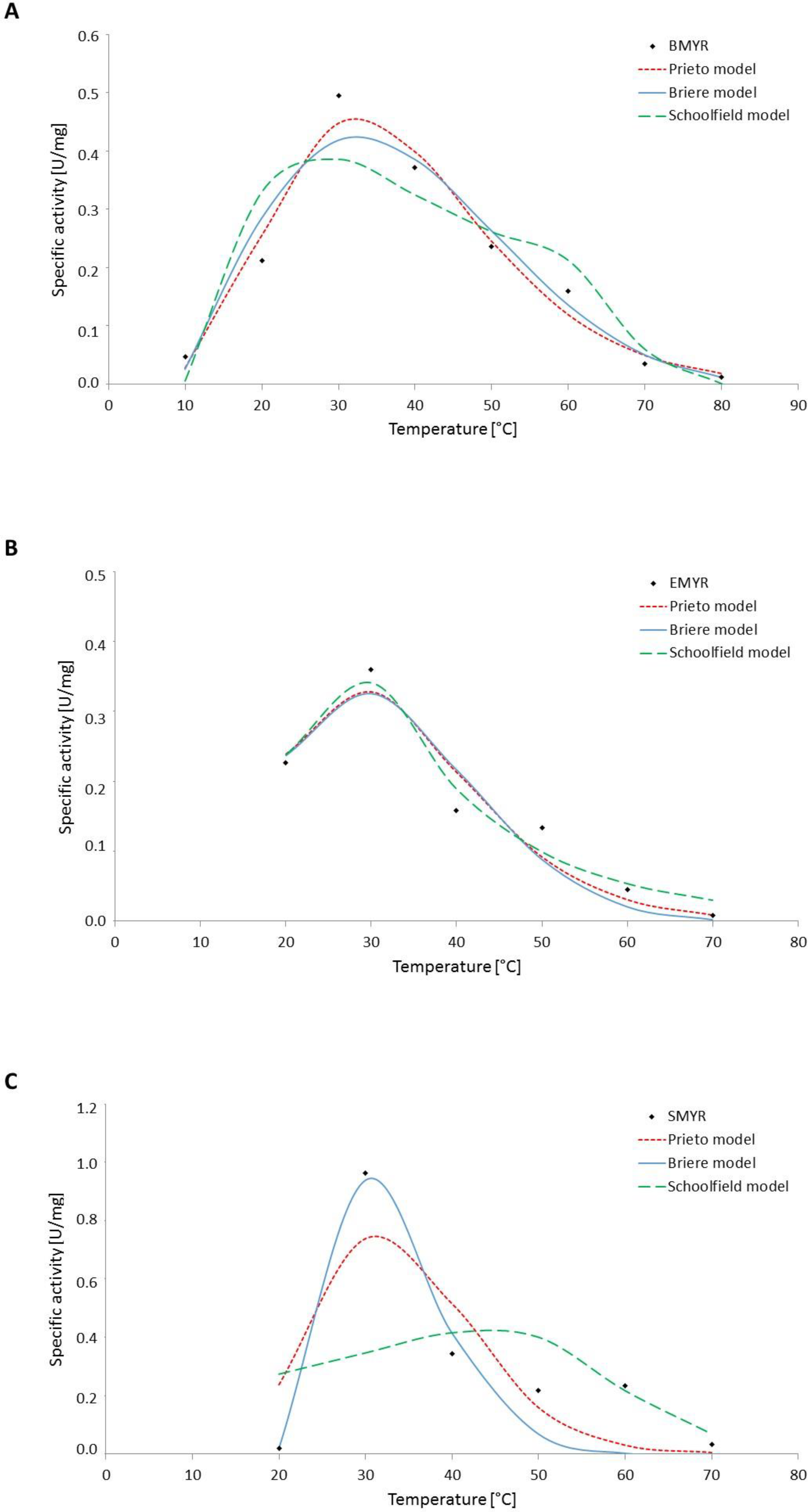
3.2. Effect of Temperature on Myrosinase Kinetics
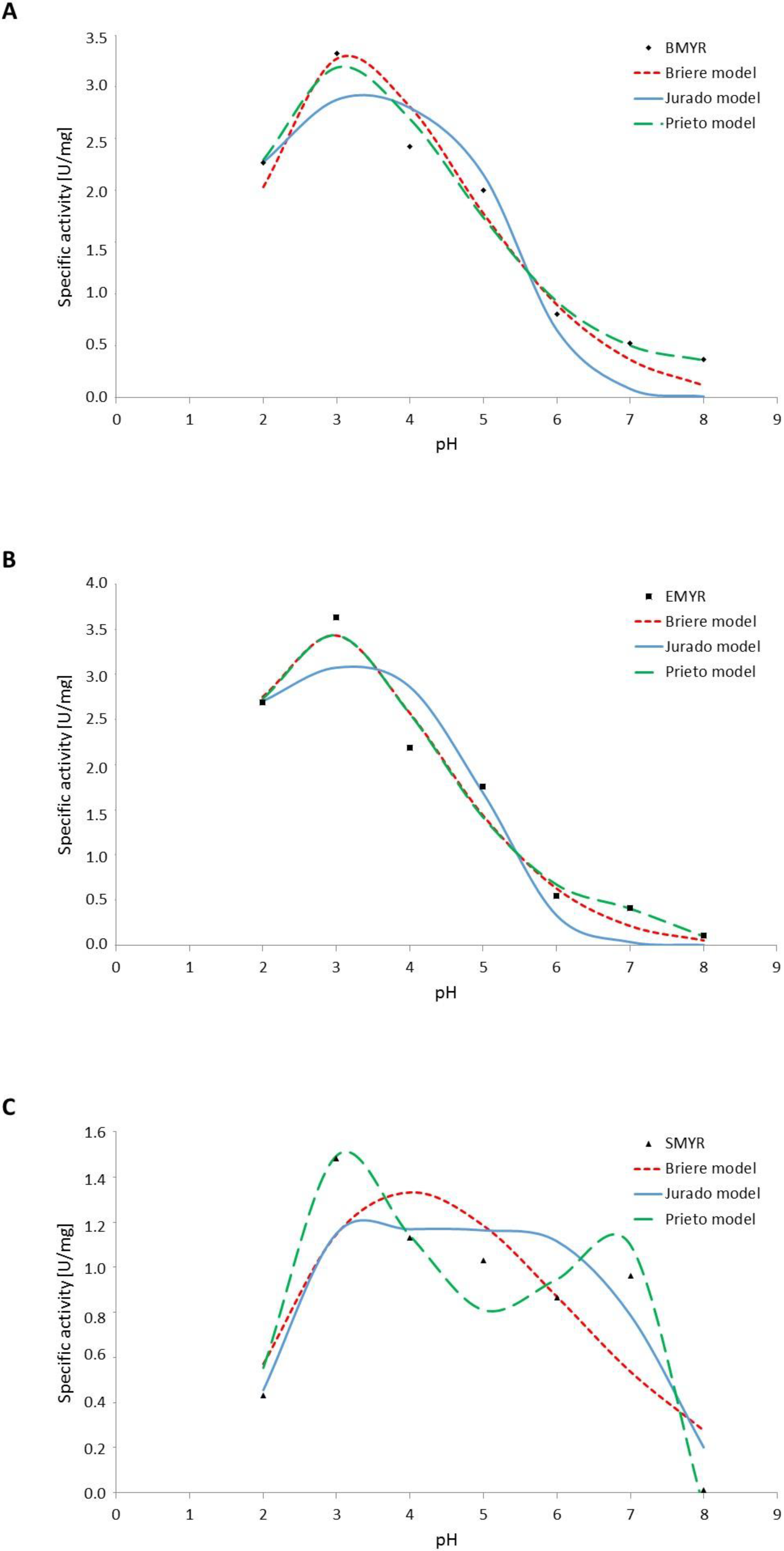
3.3. Effect of pH on Myrosinases Kinetics
4. Material and Methods
4.1. Myrosinase Production and Isolation
4.2. Myrosinase Kinetics
4.3. Modeling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Backenköhler, A.; Eisenschmidt, D.; Schneegans, N.; Strieker, M.; Brandt, W.; Wittstock, U. Iron is a centrally bound cofactor of specifier proteins involved in glucosinolate breakdown. PLoS ONE 2018, 13, e0205755. [Google Scholar] [CrossRef]
- Mahn, A.; Castillo, A. Potential of Sulforaphane as a Natural Immune System Enhancer: A Review. Molecules 2021, 26, 752. [Google Scholar] [CrossRef]
- Hossain, S.; Liu, Z.; Wood, R.J. Histone deacetylase activity and vitamin D-dependent gene expressions in relation to sulforaphane in human breast cancer cells. J. Food Biochem. 2019, 00, e13114. [Google Scholar] [CrossRef]
- Georgikou, C.; Yin, L.; Gladkich, J.; Xiao, X.; Sticht, C.; De la Torre, C.; Gretz, N.; Gross, W.; Schäfer, M.; Karakhanova, S.; et al. Inhibition of miR30a-3p by sulforaphane enhances gap junction intercellular communication in pancreatic cancer. Cancer Lett. 2020, 469, 238–245. [Google Scholar] [CrossRef]
- Rosenbergová, Z.; Kántorová, K.; Šimkovic, M.; Breier, A.; Rebros, M. Optimisation of Recombinant Myrosinase Production in Pichia pastoris. Int. J. Mol. Sci. 2021, 22, 3677. [Google Scholar] [CrossRef]
- Santín-Márquez, R.; Alarcón-Aguilar, A.; López-Diazguerrero, N.E.; Chondrogianni, N.; Königsberg, M. Sulforaphane-role in aging and neurodegeneration. GeroScience 2019, 41, 655–670. [Google Scholar] [CrossRef]
- Zeren, S.; Bayhan, Z.; Kocak, F.E.; Kocak, C.; Akcılar, R.; Bayat, Z.; Simsek, H.; Duzgun, S.A. Gastroprotective effects of sulforaphane and thymoquinone against acetylsalicylic acideinduced gastric ulcer in rats. J. Surg. Res. 2016, 203, 348e359. [Google Scholar] [CrossRef]
- Pereyra, K.V.; Andrade, D.C.; Toledo, C.; Schwarz, K.; Uribe-Ojeda, A.; Ríos-Gallardo, A.P.; Mahn, A.; Del Rio, R. Dietary supplementation of a sulforaphane-enriched broccoli extract protects the heart from acute cardiac stress. J. Funct. Foods 2020, 75, 104267. [Google Scholar] [CrossRef]
- Sakorn, P.; Rakariyatham, N.; Niamsup, H.; Nongkunsarn, P. Rapid detection of myrosinase-producing fungi: A plate method based on opaque barium sulphate formation. World J. Microbiol. Biotechnol. 2002, 18, 73–74. [Google Scholar] [CrossRef]
- Francis, F.; Lognay, G.; Wathelet, J.P.; Haubruge, E. Characterisation of aphid myrosinase and degradation studies of glucosinolates. Arch. Insect Biochem. Physiol. 2002, 50, 173–182. [Google Scholar] [CrossRef]
- Hanschen, F.S.; Klopsch, R.; Olivero, T.; Schreiner, M.; Vverkerk, R.; Dekker, M. Optimizing isothiocyanate formation during enzymatic glucosinolate breakdown by adjusting pH value, temperature and dilution in Brassica vegetables and Arabidopsis thaliana. Sci. Rep. 2017, 7, 40807. [Google Scholar] [CrossRef] [PubMed]
- Bhat, R.; Vyas, D. Myrosinase: Insights on structural, catalytic, regulatory, and environmental interactions. Crit. Rev. Biotechnol. 2019, 39, 508–523. [Google Scholar] [CrossRef] [PubMed]
- Mahn, A.; Angulo, A.; Cabañas, F. Purification and Characterization of Broccoli (Brassica oleracea var. italica) Myrosinase (β-Thioglucosidase Glucohydrolase). J. Agric. Food Chem. 2014, 62, 11666–11671. [Google Scholar] [CrossRef] [PubMed]
- Bellostas, N.; Petersen, I.L.; Sorensen, J.C.; Sorensen, H. A fast and gentle method for the isolation of myrosinase complexes from Brassicaceous seeds. J. Biochem. Biophys. Met. 2008, 70, 918–925. [Google Scholar] [CrossRef]
- Šamec, D.; Redovnikovic, I.R.; Salopek-Sondi, B. Comparative analysis of phytochemicals and activity of endogenous enzymes associated with their stability, bioavailability and food quality in five Brassicaceae sprouts. Food Chem. 2018, 269, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Halkier, B.A. Functional Expression and Characterization of the Myrosinase MYR1 from Brassica napus in Saccharomyces cerevisiae. Protein Expr. Purif. 1999, 17, 414–420. [Google Scholar] [CrossRef]
- Härtel, F.V.; Brandt, A. Characterization of a Brassica napus Myrosinase Expressed and Secreted by Pichia pastoris. Protein Expr. Purif. 2002, 24, 221–226. [Google Scholar] [CrossRef]
- Husebye, H.; Arzt, S.; Burmeister, W.P.; Hartel, F.W.; Brandt, A.; Rossiter, J.T.; Bones, A. Crystal structure at 1.1 A resolution of an insect myrosinase from Brevicoryne brassicae shows its close relationship to b-glucosidases. Insect Biochem. Mol. Biol. 2005, 35, 1311–1320. [Google Scholar] [CrossRef]
- Burmeister, W.P.; Cottaz, S.; Driguez, H.; Iori, R.; Palmieri, S.; Henrissat, B. The crystal structures of Sinapis alba myrosinase and a covalent glycosyl–enzyme intermediate provide insights into the substrate recognition and active-site machinery of an S-glycosidase. Structure 1997, 5, 663–676. [Google Scholar] [CrossRef] [Green Version]
- Román, J.; Castillo, A.; Cottet, L.; Mahn, A. Kinetic and structural study of broccoli myrosinase and its interaction with different glucosinolates. Food Chem. 2018, 254, 87–94. [Google Scholar] [CrossRef]
- Román, J.; Castillo, A.; Cottet, L.; Mahn, A. Molecular modeling of broccoli myrosinase and its interaction with different ligands. Chem. Eng. Trans. 2018, 64, 373–378. [Google Scholar]
- Curiqueo, C.; Mahn, A.; Castillo, A. Broccoli myrosinase expression in Escherichia coli and Saccharomyces cerevisiae. Biomolecules 2022, 12, 233. [Google Scholar] [CrossRef]
- Bernardi, R.; Finiguerra, M.G.; Rossi, A.A.; Palmieri, S. Isolation and Biochemical Characterization of a Basic Myrosinase from Ripe Crambe abyssinica Seeds, Highly Specific for epi-Progoitrin. J. Agric. Food Chem. 2003, 51, 2737–2744. [Google Scholar] [CrossRef] [PubMed]
- Vastenhout, K.J.; Tornberg, R.H.; Johnson, A.L.; Amolins, M.W.; Mays, J.R. HPLC-Based Method to Evaluate Kinetics of Glucosinolate Hydrolysis by Sinapis alba Myrosinase. Anal. Biochem. 2014, 465, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Pardini, A.; Tamasi, G.; De Rocco, F.; Bonechi, C.; Consumi, M.; Leone, G.; Magnani, A.; Rossi, C. Kinetics of glucosinolate hydrolysis by myrosinase in Brassicaceae tissues: A high-performance liquid chromatography approach. Food Chem. 2021, 355, 129634. [Google Scholar] [CrossRef]
- Korzekwa, K.R.; Krishnamachary, N.; Shou, M.; Ogai, A.; Parise, R.A.; Rettie, A.E.; Gonzalez, F.J.; Tracy, T.S. Evaluation of atypical cytochrome P450 kinetics with two-substrate models: Evidence that multiple substrates can simultaneously bind to cytochrome P450 active sites. Biochemistry 1998, 37, 4137–4147. [Google Scholar] [CrossRef]
- Wu, B. Substrate inhibition kinetics in drug metabolism reactions. Drug Metab. Rev. 2011, 43, 440–456. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Lu, P.; Tang, C.; Mei, Q.; Sandig, G.; Rodrigues, A.D.; Rushmore, T.H.; Shou, M. Substrate Inhibition Kinetics for Cytochrome P450-Catalyzed Reactions. Drug Metab. Dispos. 2001, 29, 368. [Google Scholar]
- Kambiré, M.S.; Gnanwa, J.M.; Boa, D.; Kouadio, E.J.P.; Kouamé, L.P. Modeling of enzymatic activity of free β-glucosidase from palm weevil, Rhynchophorus palmarum Linn. (Coleoptera: Curculionidae) larvae: Effects of pH and temperature. Biophys. Chem. 2021, 276, 106611. [Google Scholar] [CrossRef]
- Al-Turki, A.I.; Dock, W.A. Myrosinase Activity in Soil. Soil Sci. Soc. Am. J. 2003, 67, 139–145. [Google Scholar] [CrossRef]
- Prieto, M.A.; Vázquez, J.A.; Murado, M.A. Comparison of several mathematical models for describing the joint effect of temperature and ph on glucanex activity. Biotechnol. Prog. 2011, 28, 372–381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briere, J.-F.; Pracros, P.; Le Roux, A.-Y.; Pierre, J.-S. A Novel Rate Model of Temperature-Dependent Development for Arthropods. Environ. Entomol. 1999, 28, 22–29. [Google Scholar] [CrossRef]
- Sharpe, P.J.H.; Schoolfield, R.M.; Butler, G.D. Distribution Model of Heliothis Zea (Lepidoptera: Noctuidae) Development Times. Can. Entomol. 1981, 113, 845–856. [Google Scholar] [CrossRef]
- Schoolfield, R.M.; Sharpe, P.J.H.; Magnuson, C.E. Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J. Theor. Biol. 1981, 88, 719–731. [Google Scholar] [CrossRef]
- Jurado, E.; Camacho, F.; Luzón, G.; Vicaria, J.M. Kinetic models of activity for β-galactosidases: Influence of pH, ionic concentration and temperature. Enzyme Microb. Technol. 2004, 34, 33–40. [Google Scholar] [CrossRef]
- Mitra, N.; Sinha, S.; Ramya, T.N.C.; Surolia, A. N-linked oligosaccharides as outfitters for glycoprotein folding, form and function. Trends Biochem. Sci. 2006, 31, 156–163. [Google Scholar] [CrossRef]
- Lee, H.S.; Qi, Y.; Im, W. Effects of N-glycosylation on protein conformation and dynamics: Protein Data Bank analysis and molecular dynamics simulation study. Sci. Rep. 2015, 5, 8926. [Google Scholar] [CrossRef]
- Ning, H.; Zhang, J.-M.; Li, D.-Q.; Wang, M.; Sun, X.-P.; Zhu, Y.J.; Meijer, J.; Wang, Q.-H. Characterization of a Novel β-thioglucosidase CpTGG1 in Carica papaya and its Substrate-dependent and Ascorbic Acid-independent O-β-glucosidase Activity. J. Integr. Plant Biol. 2010, 52, 879–890. [Google Scholar] [CrossRef]
- Wang, M.; Li, D.; Sun, X.; Zhu, Y.J.; Nong, H.; Zhang, J. Characterization of a root-specific β-thioglucoside glucohydrolase gene in Carica papaya and its recombinant protein expressed in Pichia pastoris. Plant Sci. 2009, 177, 716–723. [Google Scholar] [CrossRef]
- Andersson, D.; Chakrabarty, R.; Bejai, S.; Zhang, J.; Rask, L.; Meijer, J. Myrosinases from root and leaves of Arabidopsis thaliana have different catalytic properties. Phytochemistry 2009, 70, 1345–1354. [Google Scholar] [CrossRef]
- Li, X.; Kushad, M.M. Purification and characterization of myrosinase from horseradish (Armoracia rusticana) roots. Plant Physiol. Biochem. 2005, 43, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Ghawi, S.K.; Methven, L.; Rastall, R.A.; Niranjan, K. Thermal and high hydrostatic pressure inactivation of myrosinase from green cabbage: A kinetic study. Food Chem. 2012, 131, 1240–1247. [Google Scholar] [CrossRef]
- Mahn, A.; Quintero, J.; Castillo, N.; Comett, R. Effect of Ultrasound-Assisted Blanching on Myrosinase Activity and Sulforaphane Content in Broccoli Florets. Catalysts 2020, 10, 616. [Google Scholar] [CrossRef]
- Van Eylen, D.; Oey, I.; Hendrickx, M.; Van Loey, A. Behavior of mustard seed (Sinapis alba L.) myrosinase during temperature/pressure treatments: A case study on enzyme activity and stability. Eur. Food Res. Technol. 2008, 226, 545–553. [Google Scholar] [CrossRef]
- Pace, C.N.; Grimsley, G.R.; Scholtz, J.M. Protein Ionizable Groups: pK Values and Their Contribution to Protein Stability and Solubility. J. Biol. Chem. 2009, 284, 13285–13289. [Google Scholar] [CrossRef] [Green Version]
- Kohen, A.; Jonsson, T.; Klinman, J.P. Effects of Protein Glycosylation on Catalysis: Changes in Hydrogen Tunneling and Enthalpy of Activation in the Glucose Oxidase Reaction. Biochemistry 1997, 36, 2603–2611. [Google Scholar] [CrossRef]
| Model | Source | Kinetic Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Vmax (µmol/min) | Km (µM) | Ks (µM) | Ki (M) | β | α | R2 (%) | RMSE | ||
| MM (Equation (1)) | BMYR | 0.76 | 0.07 | - | - | - | - | 94.7 | 0.08 |
| EMYR | 0.42 | 0.04 | - | - | - | - | 99.1 | 0.02 | |
| SMYR | 1.33 | 0.04 | - | - | - | - | 98.9 | 0.07 | |
| SIMM (Equation (2)) | BMYR | 0.96 | 0.09 | - | 1.01 | - | - | 96.0 | 0.07 |
| EMYR | 0.42 | 0.04 | - | 160.00 | - | - | 99.1 | 0.02 | |
| SMYR | 1.75 | 0.07 | - | 1.01 | - | - | 99.0 | 0.08 | |
| TBSI (Equation (3)) | BMYR | 143.02 | - | 19.88 | 88.58 | 0.10 | 50.93 | 98.4 | 0.05 |
| EMYR | 124.46 | - | 33.68 | 62.00 | 0.10 | 93.43 | 97.2 | 0.05 | |
| SMYR | 65.184 | - | 4.83 | 87.48 | 0.11 | 14.13 | 97.6 | 0.14 | |
| Gene | Source | Expression System | Km (mM) | Vmax (μmol/min) | Reference |
|---|---|---|---|---|---|
| CpTGG1 | Carica papaya | P. pastoris | 2.83 | 59.9 | [38] |
| CpTGG2 | Carica papaya | P. pastoris | 2.24 | 24.3 | [39] |
| TGG4 | Arabidopsis thaliana | P. pastoris | 0.25 | 12.2 | [40] |
| TGG5 | Arabidopsis thaliana | P. pastoris | 0.55 | 48.1 | [40] |
| TGG1 | Arabidopsis thaliana | P. pastoris | 0.05 | 2.30 | [40] |
| Myr1 | Brassica napus | P. pastoris | 1.00 | 15.0 | [17] |
| Myr | Armoracia rusticana | - | 0.13 | 0.62 | [41] |
| Myr | Brassica oleracea | - | 0.07 | 0.76 | [20] |
| Myr | Brassica oleracea | E. coli | 0.04 | 0.42 | [22] |
| Myr | Brassica oleracea | S. cerevisiae | 0.04 | 1.33 | [22] |
| Model | Source | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Prieto (Equation (5)) | n | a | b | R2 (%) | RMSE | ||||
| BMYR | 5.76 | 2.83 × 10−7 | 0.17 | 98.6 | 0.03 | ||||
| EMYR | 6.35 | 1.19 × 10−7 | 0.22 | 96.3 | 0.04 | ||||
| SMYR | 12.72 | 2.05 × 10−8 | 0.40 | 84.8 | 0.16 | ||||
| Briere (Equation (6)) | α | m | Tmin (°C) | Tmax (°C) | |||||
| BMYR | 8.0 × 10−6 | 0.18 | 8 | 104 | 97.1 | 0.04 | |||
| EMYR | 2.0 × 10−6 | 0.16 | 12 | 87 | 95.8 | 0.09 | |||
| SMYR | 1.4 × 10−1 | 0.14 | 19 | 73 | 95.8 | 0.06 | |||
| Schoolfield (Equation (7)) | ∆H_H (KJ/mol) | ∆H_L (KJ/mol) | ∆H_A (KJ/mol) | n25 (d−1) | T1/2_L (°C) | T1/2_H (°C) | |||
| BMYR | 93.46 | 182.34 | 19.29 | 0.26 | 19.45 | 67.48 | 99.0 | 0.06 | |
| EMYR | 127.85 | 62.80 | 14.67 | 0.26 | 17.50 | 35.57 | 94.0 | 0.09 | |
| SMYR | 251.21 | 523.35 | 41.87 | 0.82 | 22.00 | 37.00 | 92.2 | 0.14 | |
| Enzyme | Ea (kJ/mol) Activation (10–30 °C) | Vmax (30 °C) (µmol/min) | R2 (%) | Ea (kJ/mol) Inactivation (30–70 °C) | V (60 °C) (µmol/min) | V (70 °C) (µmol/min) | R2 (%) |
|---|---|---|---|---|---|---|---|
| EMYR | −34.1 | 0.44 | 86.6 | 76.1 | 0.04 ± 0.00 | 0.01 ± 0.00 | 89.3 |
| BMYR | −83.5 | 0.65 | 97.0 | 52.8 | 0.18 ± 0.01 | 0.07 ± 0.01 | 92.6 |
| SMYR | −288.1 | 1.20 | 88.9 | 72.2 | 0.16 ± 0.03 | 0.04 ± 0.02 | 98.4 |
| Model | Source | Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| Briere (Equation (8)) | α (×106) | m | pH_min | pH_max | R2 | RMSE | ||
| BMYR | 9.56 × 10−6 | 1.0 · 10−1 | 1 | 15 | 98.3 | 0.24 | ||
| EMYR | 4.84 × 10−5 | 1.0 · 10−1 | 1 | 14 | 98.5 | 0.24 | ||
| SMYR | 1.3 × 10−1 | 1.7 · 10−1 | 1 | 14 | 82.5 | 0.27 | ||
| Jurado (Equation (12)) | Vmax (U/mg) | pkES1 | pkES2 | |||||
| BMYR | 2.90 | 3.4 | 5.5 | 97.2 | 0.34 | |||
| EMYR | 3.10 | 3.1 | 5.1 | 96.0 | 0.40 | |||
| SMYR | 1.17 | 4.2 | 7.3 | 90.8 | 0.21 | |||
| Prieto (Equation (9)) | b0 | b2 | b22 | b33 | b44 | |||
| BMYR | −9.13 | 10.65 | −3.13 | 0.36 | −0.01 | 98.8 | 0.17 | |
| EMYR | −11.59 | 14.12 | −4.51 | 0.57 | −0.03 | 98.5 | 0.23 | |
| SMYR | −14.98 | 15.64 | −5.27 | 0.74 | −0.04 | 96.8 | 0.13 | |
| Specific Activity at 30° (U/mg) | ||
|---|---|---|
| pH 7.0 | pH 3.0 | |
| BMYR | 0.50 | 3.30 |
| EMYR | 0.38 | 3.60 |
| SMYR | 1.00 | 1.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez, A.; Castillo, A.; Mahn, A. Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH. Catalysts 2022, 12, 683. https://doi.org/10.3390/catal12070683
Jiménez A, Castillo A, Mahn A. Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH. Catalysts. 2022; 12(7):683. https://doi.org/10.3390/catal12070683
Chicago/Turabian StyleJiménez, Adielis, Antonio Castillo, and Andrea Mahn. 2022. "Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH" Catalysts 12, no. 7: 683. https://doi.org/10.3390/catal12070683
APA StyleJiménez, A., Castillo, A., & Mahn, A. (2022). Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH. Catalysts, 12(7), 683. https://doi.org/10.3390/catal12070683